Archivo de la etiqueta: trigonometria

Geometría Moderna I: Trigonometría

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada presentaremos las razones trigonométricas respecto de un ángulo agudo en un triángulo rectángulo, estas pueden ser vistas como funciones si consideramos el ángulo como una variable, veremos como extender estas funciones a ángulos de cualquier magnitud y algunas identidades trigonométricas.

Razones trigonométricas

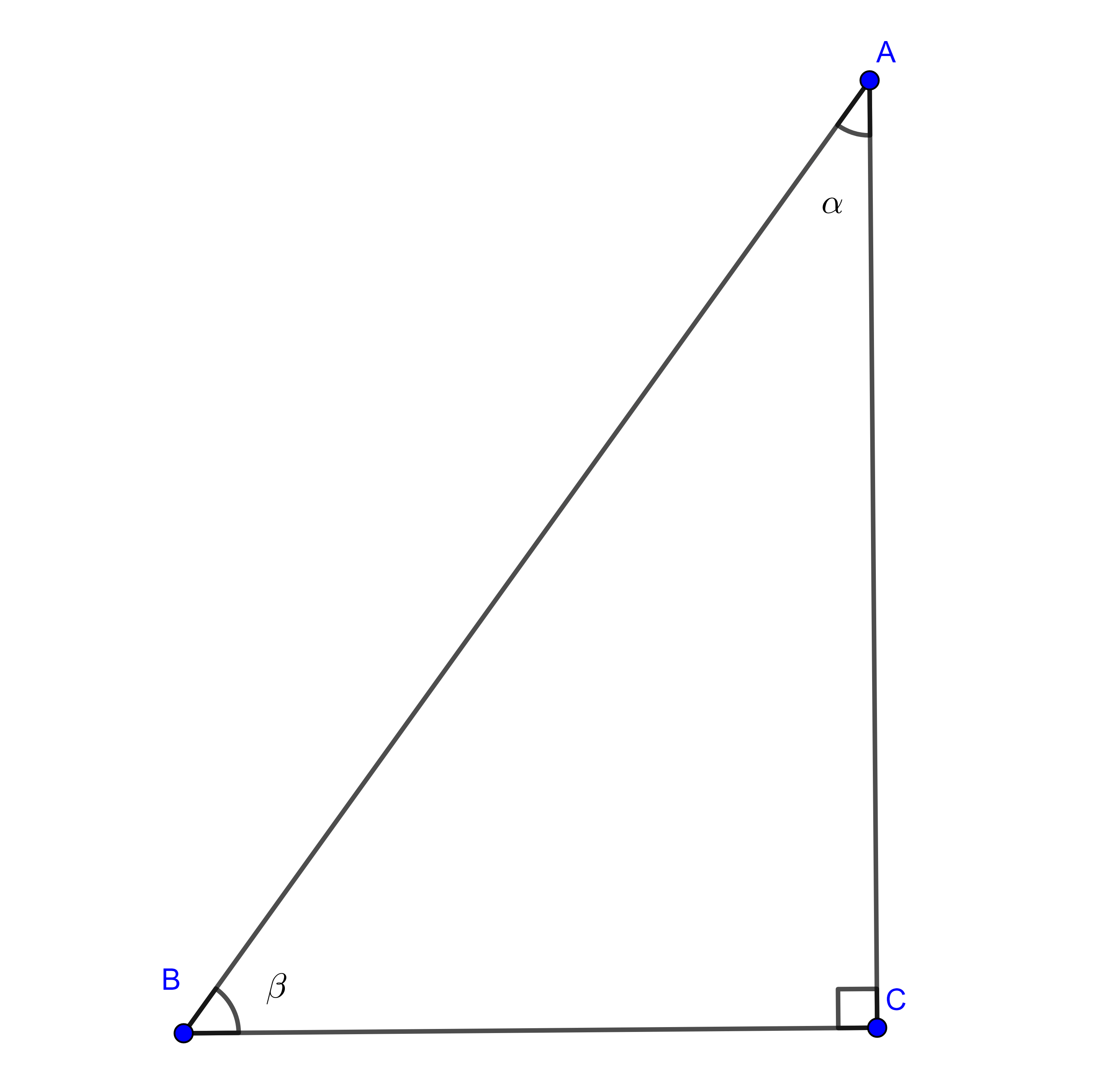
Definiciones. Consideremos un triángulo rectángulo $\triangle ABC$ donde $AB$ es la hipotenusa y sea $\alpha =  \angle BAC$, decimos que $BC$ es el cateto opuesto a $\alpha$ y $AC$ es el cateto adyacente a $\alpha$.

Definimos las razones trigonométricas respecto del ángulo $\alpha$ como sigue:

El seno del ángulo $\alpha$ como $\dfrac{c.opuesto}{hipotenusa}$ y lo denotamos como $\sin \alpha = \dfrac{BC}{AB}$.
El coseno del ángulo $\alpha$ como $\dfrac{c.adyacente}{hipotenusa}$ y lo denotamos como $\cos \alpha = \dfrac{AC}{AB}$.
La tangente del ángulo $\alpha$ como $\dfrac{c.opuesto}{c.adyacente}$ y lo denotamos como $\tan \alpha = \dfrac{BC}{AC}$.
La cosecante del ángulo $\alpha$ como como $\dfrac{hipotenusa}{c.opuesto}$ y lo denotamos como $\csc \alpha = \dfrac{AB}{BC}$.
La secante del ángulo $\alpha$ como $\dfrac{hipotenusa}{c.adyacente}$  y lo denotamos como $\sec \alpha = \dfrac{AB}{AC}$.
La cotangente del ángulo $\alpha$ como $\dfrac{c.adyacente}{c.opuesto}$ y lo denotamos como $\cot \alpha = \dfrac{AC}{BC}$.

Figura 1

Si consideramos el ángulo complementario a $\alpha$, $\beta = \angle CBA$, entonces de las definiciones se siguen las siguientes relaciones:

$\sin \alpha = \cos \beta$, $\cos \alpha = \sin \beta$, $\tan \alpha = \dfrac{\sin \alpha}{\cos \alpha}$, $\tan \alpha \tan \beta = 1$.

$\csc \alpha = \sec \beta$, $\sec \alpha = \csc \beta$, $\cot \alpha = \dfrac{\cos \alpha}{\sin \alpha}$, $\cot \alpha \cot \beta = 1$.

Círculo trigonométrico

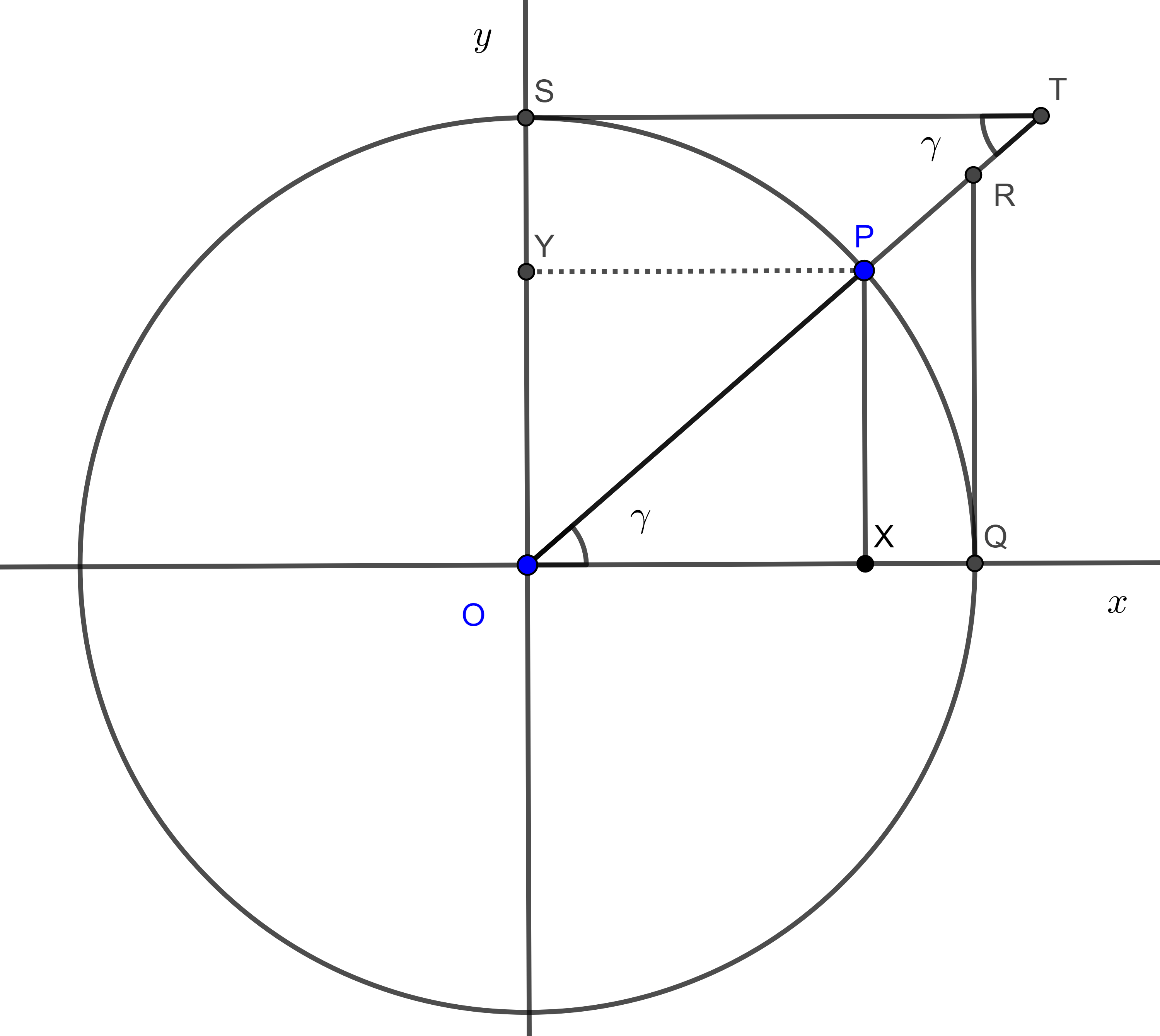
Consideremos $(O, 1)$ un círculo con centro en $O$ de radio $1$, por $O$ trazamos dos rectas perpendiculares $x$ e $y$, tomamos un punto $P \in (O, 1)$ en el cuadrante formado por el rayo derecho $Ox$ y el rayo superior $Oy$ y trazamos las proyecciones $X$, $Y$ de $O$ a las rectas $x$, $y$ respectivamente.

El triángulo $\triangle OPX$ es rectángulo y su hipotenusa $OP = 1$, si consideramos el ángulo $\angle XOP = \gamma$ entonces
$\sin \gamma = PX$ y
$\cos \gamma = OX$.

Figura 2

Tracemos la tangente a $(O, 1)$ por $Q$, la intersección entre $x$ y $(O, 1)$, tomemos $R$ como la intersección entre la tangente y $OP$ entonces $RQ \parallel PX$ y los triángulos $\triangle OPX$ y $\triangle ORQ$ son semejantes por lo tanto
$\tan \gamma = \dfrac{PX}{OX} = \dfrac{RQ}{OQ} = RQ$ y
$\sec \gamma = \dfrac{OP}{OX} = \dfrac{OR}{OQ} = OR$.

Ahora trazamos la tangente a $(O, 1)$ por $S$, la intersección de $y$ con $(O, 1)$, tomamos $T$ como la intersección de la tangente con $OP$ entonces $ST \parallel x$, por lo tanto $\gamma = \angle STO$ y así $\triangle OPX$ y $\triangle TOS$ son semejantes, por lo tanto,
$\csc \gamma = \dfrac{OP}{PX} = \dfrac{OT}{OS} = OT$ y 
$\cot \alpha = \dfrac{OX}{PX} = \dfrac{ST}{OS} = ST$.

Con esta construcción podemos extender las definiciones de función trigonométrica para ángulos agudos a ángulos de cualquier magnitud trasladando el punto $P$ alrededor de la circunferencia $(O, 1)$ y tomando las proyecciones de $P$, $X$ e $Y$ a las rectas $x$ e $y$ respectivamente que tomaremos como positivas si se encuentran en los rayos derecho y superior o negativas si se encuentran en los rayos izquierdos e inferior de las rectas $x$, $y$ respectivamente.

De esta manera todas las razones trigonométricas quedan determinadas por el valor de $\sin \gamma = PX$ y $\cos \gamma = OX$.

Teorema 1, identidad pitagórica. Sea $0 \leq \gamma < 2\pi$ entonces, $\sin^2 \gamma + \cos^2 \gamma = 1$.

Demostración. Aplicamos el teorema de Pitágoras al triángulo rectángulo $\triangle OPX$, (figura 2).

$1 = PX^2 + OX^2 = \sin^2 \gamma + \cos^2 \gamma$.

$\blacksquare$

Ley extendida de senos

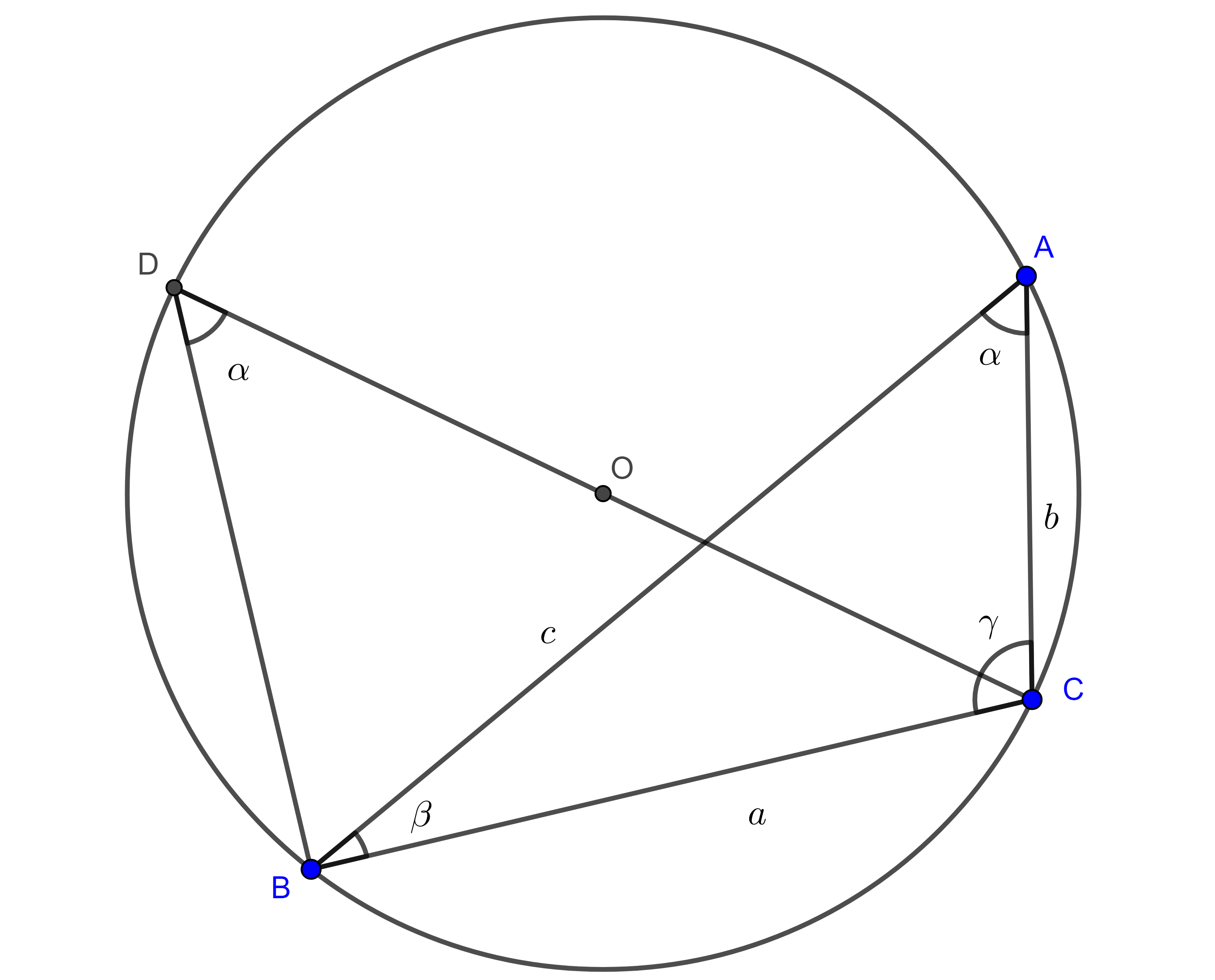
Teorema 2, ley extendida de los senos. Sean $\triangle ABC$ y $(O, R)$ su circuncírculo, etiquetemos $\angle BAC = \alpha$, $\angle CBA = \beta$, $\angle ACB = \gamma$ y $a = BC$, $b = AC$, $c = AB$ las longitudes de sus lados, entonces
$\dfrac{\sin \alpha}{a} = \dfrac{\sin \beta}{b} = \dfrac{\sin \gamma}{c} = \dfrac{1}{2R}$.

Demostración. Tracemos $D$ el punto diametralmente opuesto a $C$, entonces $\angle BDC = \alpha$, pues subtienden el mismo arco.

$\angle CBD$ es un ángulo recto, pues $CD$ es diámetro, por lo tanto $\sin \alpha = \sin \angle BDC = \dfrac{a}{CD}$.

Por lo tanto, $\dfrac{\sin \alpha}{a} = \dfrac{1}{2R}$.

Figura 3

De manera análoga podemos ver que
$\sin \beta = \dfrac{b}{2R}$ y
$\sin \gamma = \dfrac{c}{2R}$.

Por lo tanto, $\dfrac{\sin \alpha}{a} = \dfrac{\sin \beta}{b} = \dfrac{\sin \gamma}{c} = \dfrac{1}{2R}$.

$\blacksquare$

Corolario. El seno de un ángulo inscrito en una circunferencia de diámetro $1$ es igual a la cuerda que abarca dicho ángulo.

Demostración. Se sigue de sustituir $2R = 1$ en el teorema anterior.

$\blacksquare$

Ley de cosenos

Teorema 3, ley de cosenos. Sean $\triangle ABC$, $\angle BAC = \alpha$, $\angle CBA = \beta$, $\angle ACB = \gamma$ y $a = BC$, $b = AC$, $c = AB$ las longitudes de sus lados, entonces se da la siguiente igualdad:
$c^2 = a^2 + b^2 – 2ab \cos \gamma$.

Demostración. Trazamos $D$ el pie de la perpendicular a $BC$ desde $A$ y aplicamos el teorema de Pitágoras a $\triangle ABD$ y $\triangle ADC,$ de donde obtenemos

$\begin{equation} c^2 = AD^2 + (a – DC)^2 = AD^2 + a^2 – 2a(DC) + DC^2, \end{equation}$
$b^2 = AD^2 + DC^2$
$\Leftrightarrow$ $\begin{equation} AD^2 = b^2 – DC^2. \end{equation}$

Figura 4

Sustituimos $(2)$ en $(1)$ y obtenemos $c^2 = b^2 + a^2 – 2a(DC)$.

Por otro lado $\cos \gamma = \dfrac{DC}{b}$ $\Leftrightarrow$ $b \cos \gamma = DC$.

Así que $c^2 = a^2 + b^2 – 2ab \cos \gamma$.

De manera similar se puede ver que
$a^2 = b^2 + c^2 – 2bc \cos \alpha$ y
$b^2 = a^2 + c^2 – 2ac \cos \beta$.

$\blacksquare$

El seno de la suma

Teorema 4, el seno de la suma de dos ángulos. Sean $\alpha$ y $\beta$ ángulos agudos entonces $\sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$.

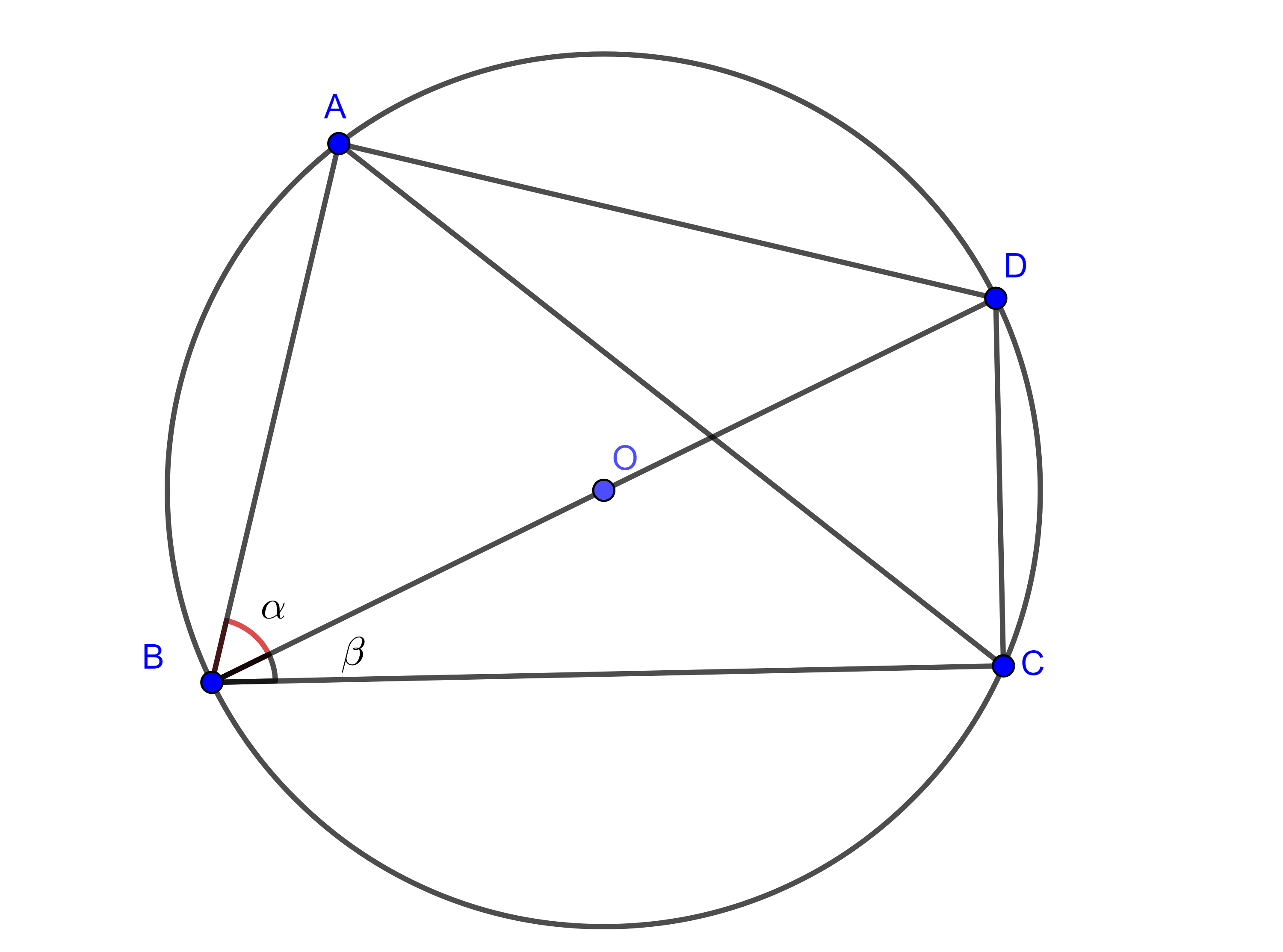
Demostración. Sea $\square ABCD$ cíclico tal que $BD = 1$ es diámetro del circuncírculo, $\angle DBA = \alpha$ y $\angle CBD =\beta$.

Figura 5

Como consecuencia del corolario tenemos que $AC = \sin (\alpha + \beta)$, ademas $\triangle BAD$ y $\triangle DCB$ son triángulos rectángulos pues $DB$ es diámetro.

Se sigue que
$AB = \cos \alpha$,
$CD = \sin \beta$,
$AD = \sin \alpha$ y
$BC = \cos \beta$.

El teorema de Ptolomeo nos dice que
$\begin{equation} AC \times BD = AB \times CD + BC \times AD. \end{equation}$

Por lo tanto, $\sin (\alpha + \beta) = \cos \alpha \sin \beta +\sin \alpha \cos \beta$.

$\blacksquare$

El coseno de la suma

Teorema 5, el coseno de la suma de dos ángulos. Sean $\alpha \ne 0$ y $\beta$ ángulos agudos tales que $\alpha + \beta < \dfrac{\pi}{2}$ entonces $\cos (\alpha + \beta) = \cos \alpha \cos \beta – \sin \alpha \sin \beta$.

Demostración. Sea $\square ABCD$ cíclico tal que $BC = 1$ es diámetro del circuncírculo, $\angle CBD = \alpha$ y $\angle DBA = \beta$.

Figura 6

Como $\triangle BAC$ y $\triangle BDC$ son triángulos rectángulos y $BC = 1$ tenemos que
$AC = \sin (\alpha + \beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha$ (teorema 4),
$BD = \cos \alpha$,
$AB = \cos (\alpha + \beta)$,
$CD = \sin \alpha$,
$AD = \sin \angle DCA = \sin \beta$ (corolario).

Por el teorema de Ptolomeo $(3)$, aplicado a $\square ABCD$ obtenemos:
$\cos (\alpha + \beta) \sin \alpha + \sin \beta$
$= (\sin \alpha \cos \beta + \sin \beta \cos \alpha) \cos \alpha$
$= \sin \alpha \cos \beta \cos \alpha + \sin \beta \cos^2 \alpha$
$ = \sin \alpha \cos \beta \cos \alpha + (\sin \beta)(1 – \sin^2 \alpha)$ (teorema 1)
$= \sin \alpha \cos \beta \cos \alpha – \sin \beta \sin^2 \alpha + \sin \beta$.

$\Leftrightarrow$$\cos (\alpha + \beta) \sin \alpha = \sin \alpha \cos \beta \cos \alpha – \sin \beta \sin^2 \alpha$.

Por lo tanto, $\cos (\alpha + \beta) = \cos \beta \cos \alpha -\sin \beta \sin \alpha$.

$\blacksquare$

Seno y coseno del ángulo medio

Teorema 6, el seno y el coseno del ángulo medio. Sea $\alpha \ne 0$ un ángulo agudo entonces
$\sin \dfrac{\alpha}{2} = \sqrt{\dfrac{1 – \cos \alpha}{2}}$ y $\cos \dfrac{\alpha}{2} = \sqrt{\dfrac{1 + \cos \alpha}{2}}$.

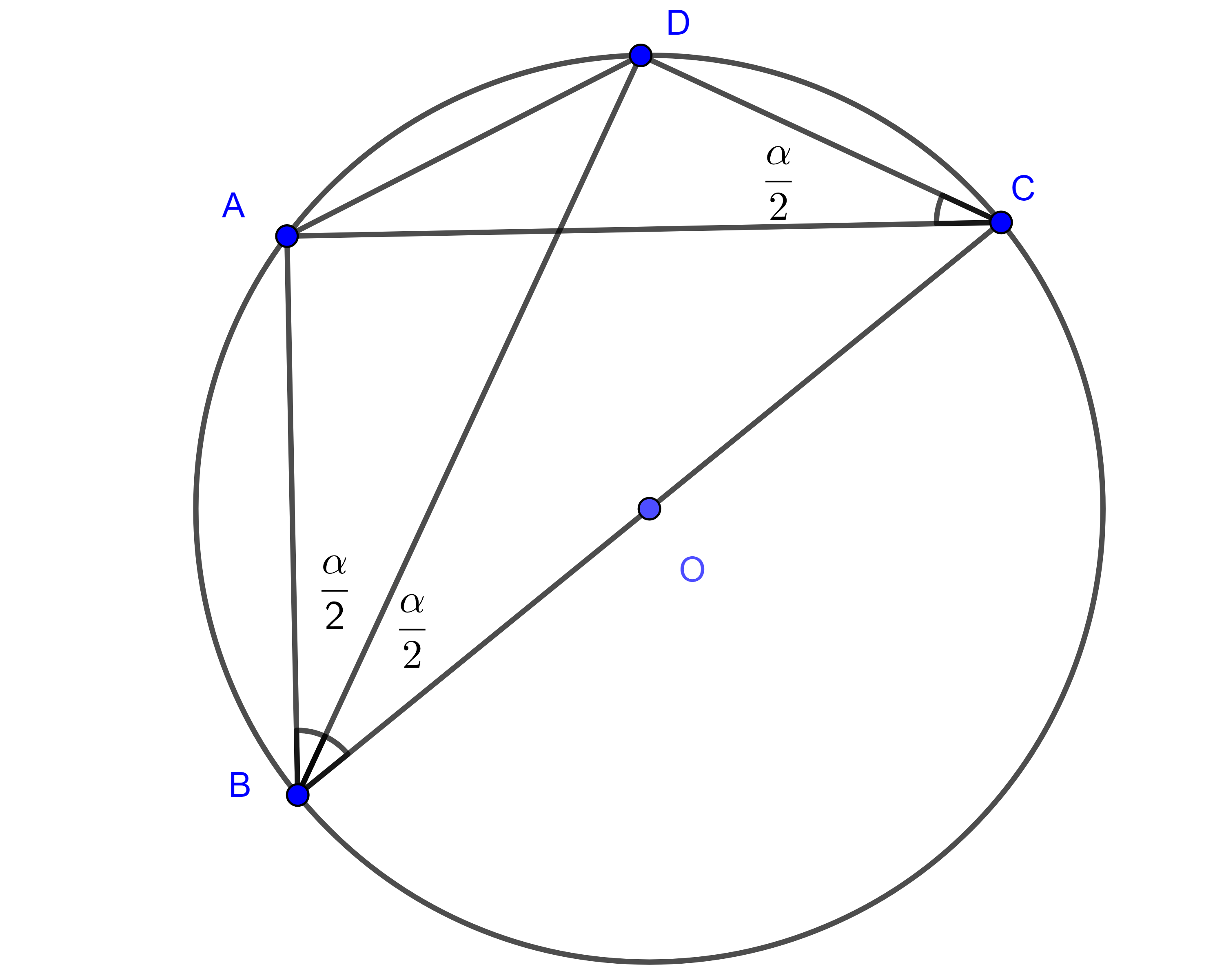
Demostración. Sea $\square ABCD$ cíclico tal que $BC = 1$ es diámetro y $\angle CBD = \angle DBA = \dfrac{\alpha}{2}$.

Figura 7

Ya que $\triangle BAC$ y $\triangle BDC$ son triángulos rectángulos podemos ver que
$AC = \sin \alpha$,
$BD = \cos \dfrac{\alpha}{2}$,
$AB = \cos \alpha$,
$CD = \sin \dfrac{\alpha}{2}$,
$AD = \sin \angle DCA = \sin \dfrac{\alpha}{2}$ (corolario).

Aplicando Ptolomeo $(3)$ y el teorema 4 obtenemos:
$\cos \alpha \sin \dfrac{\alpha}{2} + \sin \dfrac{\alpha}{2} = \sin \alpha \cos \dfrac{\alpha}{2} $
$= \sin (\dfrac{\alpha}{2} +\dfrac{\alpha}{2}) \cos \dfrac{\alpha}{2} = 2 \sin \dfrac{\alpha}{2} \cos^2 \dfrac{\alpha}{2}$.

Por lo tanto, $2 \sin \dfrac{\alpha}{2} \cos^2 \dfrac{\alpha}{2} = \sin \dfrac{\alpha}{2} (\cos \alpha + 1)$ $\Rightarrow$  
$\begin{equation} \cos^2 \dfrac{\alpha}{2} = \dfrac{\cos \alpha + 1}{2}. \end{equation}$

De donde se sigue que $\cos \dfrac{\alpha}{2} = \sqrt{\dfrac{\cos \alpha + 1}{2}}$.

Ahora sustituimos la identidad pitagórica en la ecuación $(4)$ y obtenemos:
$1 – \sin^2 \dfrac{\alpha}{2} = \dfrac{\cos \alpha + 1}{2}$
$\Leftrightarrow$
$\sin \dfrac{\alpha}{2} = \sqrt{\dfrac{1 – \cos \alpha}{2}}$.

$\blacksquare$

Más adelante…

En la siguiente entrada estudiaremos algunas propiedades relacionadas con el incírculo y los excÍrculos de un triángulo, así como también sobre sus centros y radios.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. $i)$ A partir de un triangulo equilátero deriva los valores de las seis razones trigonométricas para los ángulos $\dfrac{\pi}{3}$ y $\dfrac{\pi}{6}$,
    $ii)$ A partir de un triángulo rectángulo isósceles deduce los valores de las seis razones trigonométricas para el ángulo $\dfrac{\pi}{4}$.
  2. Recordemos que consideramos la magnitud de un ángulo central como positiva, si recorremos el arco de circunferencia que subtiende dicho ángulo en el sentido contrario al de las manecillas del reloj y negativa en caso contraio, muestra que para cualquier valor de $\alpha$ se cumple que:
    $i)$ $\sin (-\alpha) = -\sin \alpha$,
    $ii)$ $\cos (-\alpha) = \cos \alpha$,
    $iii)$ $\sin (\pi – \alpha) = \sin \alpha$,
    $iv)$ $\cos (\pi – \alpha) = -\cos \alpha$,
    $v)$ $\sec^2 \alpha = 1 + \tan^2 \alpha$.
  3. Sean $\alpha$ y $\beta$ ángulos agudos tales que $\alpha \geq \beta$, muestra geométricamente:
    $i)$ el seno de la diferencia de dos ángulos, $\sin (\alpha – \beta) = \sin \alpha \cos \beta – \sin \beta \cos \alpha$,
    $ii)$ el coseno de la diferencia de dos ángulos, $\cos (\alpha – \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$.
  4.  Sean $\alpha$ y $\beta$ ángulos agudos prueba que:
    $i)$ $\sin \alpha \cos \beta = \dfrac{\sin (\alpha + \beta) + \sin (\alpha – \beta)}{2}$,
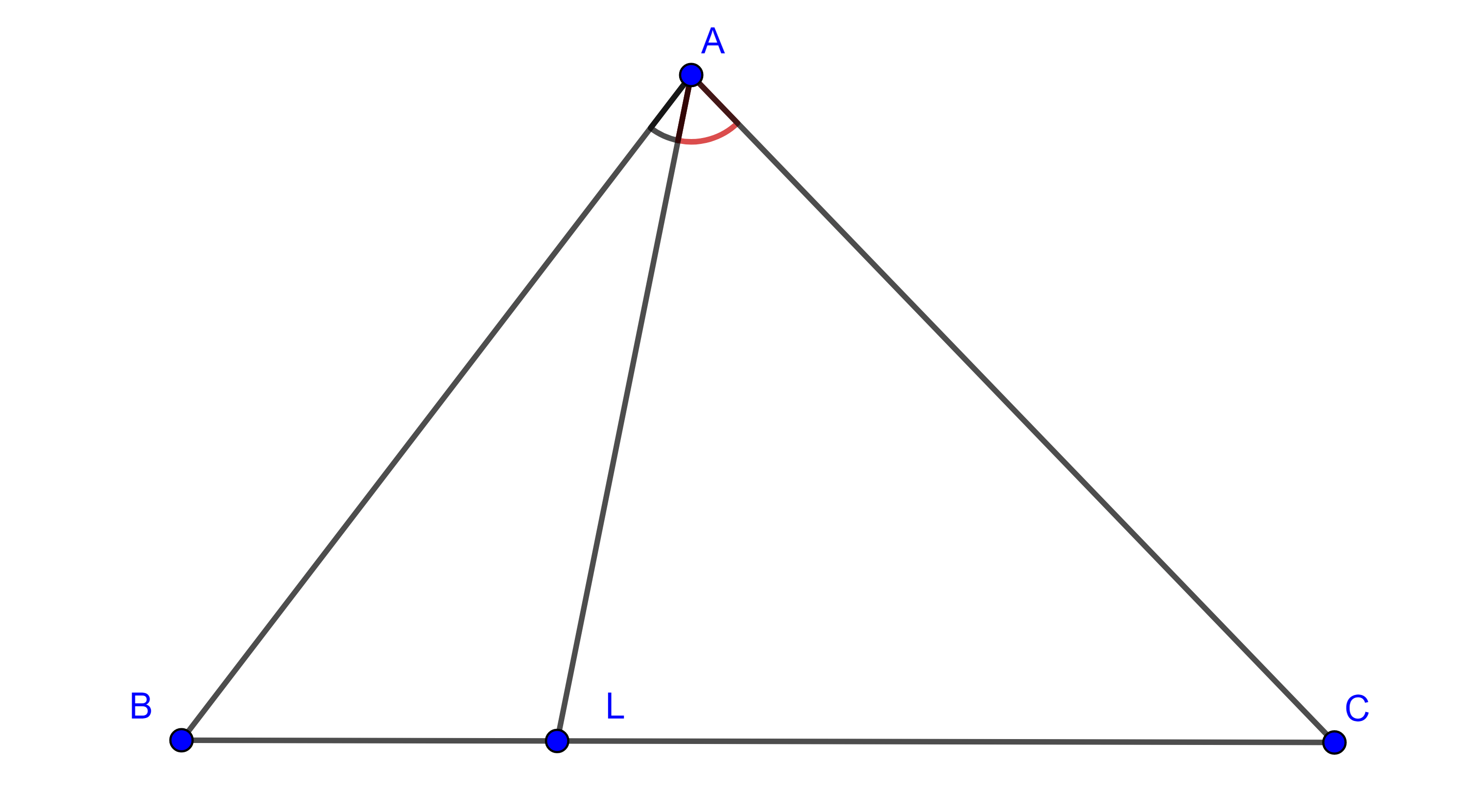
    $ii)$ $\cos \alpha \sin \beta = \dfrac{\sin (\alpha + \beta) – \sin (\alpha – \beta)}{2}$.
  5. Sea $\triangle ABC$, por $A$ traza cualquier recta que corte a $BC$ en $L$, muestra que $\dfrac{BL}{LC} = \dfrac{AB \sin \angle BAL}{AC \sin \angle LAC}$.
Figura 8
  1. Demuestra que si $\dfrac{\sin \alpha}{\sin \beta} = \dfrac{\sin \delta}{\sin \gamma}$ y $\alpha + \beta = \delta + \gamma < \pi$ entonces $\alpha = \delta$ y $\beta = \gamma$.
  2. Sea $\triangle ABC$ con $a = BC$, $b = AC$, $c = AB$, $\alpha = \angle BAC$, $\beta = \angle CBA$, $\gamma = \angle ACB$, demuestra las siguientes formulas para calcular el área de $\triangle ABC$:
    $i)$ $(\triangle ABC) = \dfrac{ac \sin \beta}{2} = \dfrac{ab \sin \gamma}{2} = \dfrac{bc \sin \alpha}{2}$,
    $ii)$ $(\triangle ABC) = \dfrac{a^2 \sin \beta \sin \gamma}{2 \sin (\beta + \gamma)} = \dfrac{b^2 \sin \alpha \sin \gamma}{2 \sin (\alpha + \gamma)} = \dfrac{c^2 \sin \alpha \sin \beta}{2 \sin (\alpha + \beta)}$.

Entradas relacionadas

Fuentes

  • Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 69-78.
  • Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 55-62.
  • Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 89-95.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Problemas de exponencial, logaritmo y trigonometría en los complejos

Por Claudia Silva

Deja un comentario

Introducción

En entradas anteriores, vimos la construcción de los números complejos, sus operaciones y varias de sus características algebraicas. Conociendo ya las funciones exponencial y logaritmo, así como las funciones trigonométricas seno y coseno, vamos a iniciar con un breve análisis geométrico de la función exponencial. Posteriormente pasaremos a hacer unos ejercicios simples de operar dichas funciones en números complejos concretos.

Geometría de la exponencial compleja

Para empezar, estudiamos qué le hace la función exponencial al plano complejo de manera geométrica. Para hacer esto, tomamos varias rectas en el plano complejo para entender en qué se transforman tras aplicarles la función exponencial.

A grandes rasgos, cuando tomamos una recta vertical, la imagen de esta le da la vuelta al origen repetidamente. Cuando tomamos una recta horizontal, su imagen es un rayo que emana del origen (sin tocarlo).

En este video se explican estas ideas de manera visual.

Calcular una exponencial compleja

Lo siguiente que haremos es resolver un ejercicio de calcular la exponencial de un número complejo. Recuerda que, por definición, se tiene que $$e^{x+iy}=e^x\text{cis}(y).$$

Ejercicio. Expresa $e^{4+\frac{\pi}{6}i}$ en la forma $x+iy$.

Problema de logaritmo complejo

Recuerda que el logaritmo complejo funciona como inverso de la función exponencial. Para que esto sea cierto, tenemos que restringir la exponencial a una franja del plano complejo.

Por definición, tenemos que $$L(z)=\ln \norm{z} + \text{arg}(z)i.$$ Para que la definición funcione bien, es necesario que tomemos el argumento en el intervalo $(-\pi,\pi]$.

Resolveremos el siguiente ejercicio.

Ejercicio. Calcula $L\left(\frac{1}{2}+\frac{\sqrt{3}}{2} i\right)$.

Problema de trigonometría compleja

Por último, haremos un ejercicio de calcular una función trigonométrica compleja. Sólo necesitaremos la definición de la función coseno, pero por conveniencia, a continuación recordamos tanto la definición de seno, como la de coseno.

\begin{align*}
\cos(z)=\frac{e^{zi}+e^{-zi}}{2},
\sin(z)=\frac{e^{zi}-e^{-zi}}{2}.
\end{align*}

Con esto en mente, resolveremos el siguiente ejercicio.

Ejercicio. Calcula $\cos\left(\frac{\pi}{2}+\frac{\pi}{2} i\right)$.

Más tarde les subo fotos por si alguien tiene dificultades para ver los videos.

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Exponencial, logaritmo y trigonometría en los complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Gracias a las entradas anteriores ya hemos desarrollado un buen manejo de los números complejos. Sabemos cómo se construyen y cómo hacer operaciones básicas, incluyendo obtener conjugados, la forma polar, sacar normas y elevar a potencias. También hemos aprendido a resolver varias ecuaciones en los complejos: cuadráticas, sistemas lineales y raíces $n$-ésimas. Todo esto forma parte de los fundamentos algebraicos de $\mathbb{C}$. Ahora hablaremos un poco de la exponencial, el logaritmo y trigonometría en los complejos.

Aunque mencionaremos un poco de las motivaciones detrás de las definiciones, no profundizaremos tanto como con otros temas. Varias de las razones para elegir las siguientes definiciones tienen que ver con temas de ecuaciones diferenciales y de análisis complejo, que no se estudian sino hasta semestres posteriores.

Función exponencial compleja

Recordemos que, para un real $y$, definimos $\text{cis}(y)=\cos y + i \sin y$. La función $\text{cis}$ y la exponenciación en los reales nos ayudarán a definir la exponencial compleja.

Definición. Definimos la función $\exp:\mathbb{C}\to \mathbb{C}$ como $$\exp(x+yi)=e^x\text{cis}(y).$$

Ejemplo 1. Se tiene que $$\exp\left(1+\frac{\pi}{2} i\right) = e^1 \text{cis}\left(\frac{\pi}{2}\right) = ei.$$

$\triangle$

Ejemplo 2. Se tiene que $$\exp(\pi i) = e^0\text{cis}(\pi) = (1)(-1)=-1.$$ Como veremos más abajo, esto lo podemos reescribir como la famosa identidad de Euler $$e^{\pi i}+1=0.$$

$\triangle$

Ejemplo 3. Se tiene que $$\exp(2+3i)=e^2\text{cis}(3).$$ Como $\cos(3)$ y $\sin(3)$ no tienen ningún valor especial, esta es la forma final de la expresión.

$\triangle$

Propiedades de la función exponencial compleja

Una buena razón para definir la exponencial así es que si $y=0$, entonces la definición coincide con la definición en los reales: $$\exp(x)=e^x\text{cis}(0)=e^x.$$ Si $x=0$, tenemos que $\exp(iy)=\text{cis}(y)$, de modo que si $w$ tiene norma $r$ y argumento $\theta$, podemos reescribir su forma polar como $$w=r\exp(\theta i),$$ y una forma alternativa de escribir el teorema de De Moivre es $$w^n=r^n\exp(n\theta i).$$

Otra buena razón para definir la exponencial compleja como lo hicimos es que se sigue satisfaciendo que las sumas en la exponencial se abren en productos.

Proposición. Para $w$ y $z$ complejos se tiene que $$E(w+z)=E(w)E(z).$$

Demostración. Escribamos $w=a+bi$ y $z=c+di$ con $a,b,c$ y $d$ reales. Tenemos que
\begin{align*}
\exp(w+z)&=\exp((a+c)+(b+d)i)\\
&=e^{a+c}\text{cis}(b+d).
\end{align*}

Por propiedades de la exponencial en $\mathbb{R}$ tenemos que $e^{a+c}=e^ae^c$. Además, por cómo funciona la multiplicación compleja en términos polares, tenemos que $\text{cis}(b+d)=\text{cis}(b)\text{cis}(d)$. Usando estas observaciones podemos continuar con la cadena de igualdades,

\begin{align*}
&=e^ae^c\text{cis}(b)\text{cis}(d)\\
&=(e^a\text{cis}(b)) (e^c\text{cis}(d))\\
&=\exp(a+bi)\exp(c+di)\\
&=\exp(w)\exp(z).
\end{align*}

$\square$

Como $\exp$ extiende a la exponencial real y se vale abrir las sumas de exponentes en productos, puede ser tentador usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$. Hay que tener cuidado con esta interpretación, pues hasta ahora no hemos dicho qué quiere decir «elevar a una potencia». Cuando lo hagamos, veremos que usar la notación $e^{x+yi}$ sí tiene sentido, pero por el momento hay que apegarnos a la definición.

Hay otras buenas razones para definir la exponencial compleja como lo hicimos. Una muy importante es que es la solución a una ecuación diferencial muy natural. Más adelante, en tu formación matemática, verás esto.

Función logaritmo complejo

Con el logaritmo natural $\ln$ en $\mathbb{R}$ y la multifunción argumento podemos extender el logaritmo a $\mathbb{C}$.

Definición. Definimos la función $L:\mathbb{C}\setminus \{0\} \to \mathbb{C}$ como $$L(z)=\ln \Vert z \Vert + \arg(z) i.$$

Hay que ser un poco más precisos, pues $\arg(z)$ es una multifunción y toma varios valores. Cuando estamos trabajando con logaritmo, lo más conveniente por razones de simetría es que tomemos el argumento en el intervalo $(-\pi,\pi]$. En cursos posteriores hablarás de «otras» funciones logaritmo, y de por qué ésta es usualmente una buena elección.

Ejemplo. Los logaritmos de $i$ y de $-1$ son, respectivamente,
\begin{align*}
L(i)&=\ln \Vert i \Vert + \arg(i) i = \ln(1) + \frac{\pi}{2} i =\frac{\pi}{2} i\\
L(-1)&=\ln \Vert -1 \Vert + \arg(-1) i = \ln(1)+\pi i = \pi i.
\end{align*}

$\triangle$

Propiedades del logaritmo complejo

La función $\exp$ restringida a los números con parte imaginaria en $(-\pi,\pi]$ es invertible y su inversa es $L$. Esto justifica en parte la definición de logaritmo. Demostrar esto es sencillo y queda como tarea moral.

La función $L$ restringida a los reales positivos coincide con la función logaritmo natural, pues para $z=x+0i=x$, con $x>0$ se tiene que $\arg(x)=0$ y entonces $$L(z)=L(x)=\Vert x\Vert+\arg(x)i=x.$$

Como en el caso real, la función logaritmo abre productos en sumas, pero con un detalle que hay que cuidar.

Proposición. Para $w$ y $z$ complejos no $0$, se tiene que $L(wz)$ y $L(w)+L(z)$ difieren en un múltiplo entero de $2\pi i$.

Con la función logaritmo podemos definir potencias de números complejos.

Definición. Para $w,z$ en $\mathbb{C}$ con $w\neq 0$, definimos $$w^z=\exp(zL(w)).$$

Ejemplo. En particular, podemos tomar $w=e$, de donde \begin{align*}e^z&=\exp(zL(e))\\&=\exp(z\ln(e))\\&=\exp(z),\end{align*} de donde ahora sí podemos justificar usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$.

$\square$

Esta definición de exponenciación en $\mathbb{C}$ es buena, en parte, porque se puede probar que se satisfacen las leyes de los exponentes.

Proposición. Para $w, z_1, z_2$ en $\mathbb{C}$, con $w\neq 0$, se cumple que $$z^{w_1+w_2}=z^{w_1}z^{w_2}$$ y que $$(z^{w_1})^{w_2}=z^{w_1w_2}.$$

La demostración es sencilla y se deja como tarea moral.

Funciones trigonométricas complejas

Finalmente, definiremos las funciones trigonométricas en $\mathbb{C}$. Para ello, nos basaremos en la función exponencial que ya definimos.

Definición. Para $z$ cualquier complejo, definimos $$\cos(z)=\frac{e^{iz}+e^{-iz}}{2}$$ y $$\sin(z)=\frac{e^{iz}-e^{-iz}}{2}.$$

Una de las razones por las cuales esta definición es buena es que extiende a las funciones trigonométricas reales. En efecto, si $z=x+0i=x$ es real, entonces $\cos(z)$ es \begin{align*}
\frac{e^{iz}+e^{-iz}}{2}&=\frac{\text{cis}(x)+\text{cis}(-x)}{2}\\
&=\frac{2\cos(x)}{2}\\
&=\cos(x),
\end{align*} y de manera similar para $\sin(z)$.

Las funciones trigonométricas en $\mathbb{C}$ siguen cumpliendo varias propiedades que cumplían en $\mathbb{R}$.

Proposición. Para $w$ y $z$ complejos, se tiene que
\begin{align*}
\cos(w+z)=\cos(w)\cos(z)-\sin(w)\sin(z)\\
\sin(w+z)=\sin(w)\cos(z)+\sin(z)\cos(w).
\end{align*}

Demostración. Procedemos por definición. Tenemos que
\begin{align*}
4&\cos(w)\cos(z)\\
&=(e^{iw}+e^{-iw})(e^{iz}+e^{-iz})\\
&=(e^{i(w+z)}+e^{i(w-z)}+e^{i(z-w)}+e^{i(-z-w)})
\end{align*}

y que
\begin{align*}
4&\sin(w)\sin(z)\\
&=(e^{iw}-e^{-iw})(e^{iz}-e^{-iz})\\
&=(e^{i(w+z)}-e^{i(w-z)}-e^{i(z-w)}+e^{i(-z-w)}),
\end{align*}

de modo que
\begin{align*}
4(\cos(w)&\cos(z)-\sin(w)\sin(z))\\
&=2(e^{i(w+z)}+e^{-i(w+z)})\\
&=4\cos(w+z).
\end{align*}

Dividiendo entre $4$ ambos lados de la igualdad, obtenemos la primer identidad. La segunda se demuestra de manera análoga, y queda como tarea moral.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Determina los valores de $\exp(3+\frac{3\pi}{4}i)$ y de $L(-i)$.
  2. Muestra que para $z$ con parte imaginaria en $(-\pi,\pi]$ se tiene que $L(\exp(z))=z$.
  3. Determina el valor de $(1+i)^{1+i}$.
  4. Muestra las leyes de los exponentes para la exponenciación en $\mathbb{C}$.
  5. Determina el valor de $\sin(i)$ y de $\cos(1+i)$.
  6. Muestra la identidad de seno de la suma de ángulos en $\mathbb{C}$.
  7. Investiga qué otras propiedades de las funciones trigonométricas reales se extienden al caso complejo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Multiplicación en forma polar y fórmula de De Moivre

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En la entrada anterior hablamos de las coordenadas rectangulares y polares de un número complejo. También, definimos la forma polar de un número complejo. En esta entrada hablaremos de cómo con la forma polar, de los elementos de $\mathbb{C}$, podemos entender fácilmente su multiplicación. Además, usaremos esto para demostrar la fórmula de De Moivre, que nos dice cómo encontrar las potencias de un complejo.

Como pequeño recordatorio, la forma polar del complejo $z=x+iy$ es $z=r(\cos \theta + i \sin \theta)$, en donde $r$ es la norma de $z$ y $\theta$ es el ángulo que hace con el eje real positivo, pensándolo como el punto $(x,y)$. Esto queda resumido por la siguiente figura:

Complejo en forma rectangular y polar
Complejo en forma rectangular y polar

Forma polar, multiplicación y recordatorio trigonométrico

Para ver cómo la forma polar de los complejos nos ayuda a entender la multiplicación en $\mathbb{C}$, necesitamos recordar las siguientes fórmulas trigonométricas
\begin{align*}
\sin (\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha\\
\cos(\alpha+\beta) = \cos \alpha \cos \beta – \sin \beta \sin \alpha.
\end{align*}

Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r (\cos\alpha+ i \sin \alpha)\\
z&=s(\cos \beta + i \sin \beta)
\end{align*}

y los multiplicamos con la definición, su producto tendría parte real $$rs(\cos\alpha\cos \beta – \sin \alpha\sin \beta) = rs\cos (\alpha+\beta)$$ y parte imaginaria $$rs(\sin \alpha \cos \beta+ \sin\beta\cos\alpha)=rs\sin (\alpha+\beta).$$

Además, como la norma es multiplicativa, tenemos que la norma de $wz$ es $rs$. Con esto mostramos que la forma polar de $wz$ es exactamente $$wz=(rs)(\cos(\alpha+\beta)+i\sin(\alpha+\beta)).$$ Esto queda resumido en el siguiente resultado

Proposición. Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r \text{cis}(\alpha)\\
z&=s\text{cis}(\beta),
\end{align*} entonces la forma polar del producto es $$wz=rs\text{cis}(\alpha+\beta).$$

Otra forma de decirlo es que «al multiplicar complejos, multiplicamos normas y sumamos argumentos». Podemos también ver el resultado de forma geométrica mediante la siguiente figura, en donde marcamos con rojo y azul los factores, y con negro al producto.

Interpretación geométrica de la multiplicación en los complejos
Interpretación geométrica de la multiplicación en los complejos

Ejemplo. Vamos a encontrar la forma rectangular del producto de los complejos
\begin{align*}w& =7 \text{cis}\left( \frac{2\pi}{5} \right)\quad\text{y}\\ z&=2\text{cis}\left(\frac{3\pi}{5}\right).\end{align*}

Por la proposición anterior, el producto es exactamente el complejo
\begin{align*}
14 \text{cis}\left(\frac{2+3}{5}\pi \right)=14 \text{cis} (\pi).
\end{align*}

Esta es la forma polar del producto. Por un problema anterior, sabemos que $\text{cis}(\pi)=-1$, de modo que la forma rectangular del producto es $-14$.

Si tenemos un complejo no nulo en forma polar, podemos entender fácilmente su inverso multiplicativo. Esto está dado por la siguiente proposición, cuya demostración es sencilla y se deja como tarea moral.

Proposición. Sea $w\neq 0$ un complejo con forma polar $w=r\text{cis}(\theta)$. Su inverso multiplicativo es el complejo $r^{-1}\text{cis}(-\theta)$.

Ejemplo. Determinemos el inverso multiplicativo del complejo $$w=\sqrt{3}\text{cis}\left(\frac{3\pi}{7}\right).$$ Para ello, basta usar la proposición anterior, de donde $$w^{-1}=\frac{1}{\sqrt{3}} \text{cis}\left(-\frac{3\pi}{7}\right)=\frac{\sqrt{3}}{3}\text{cis}\frac{11\pi}{7}.$$

$\triangle$

Fórmula de De Moivre

La proposición para multiplicación de complejos se vuelve todavía más útil si la usamos iteradamente para hacer potencias de complejos.

Teorema (fórmula de De Moivre). Si $z$ es un complejo de norma $r$ y argumento $\theta$ y $n$ es un entero positivo, entonces $z^n$ es el complejo de norma $r^n$ y argumento $n\theta$. En otras palabras, si $z=r(\cos \theta + i \sin \theta)=r\text{cis}(\theta)$, entonces $$z^n=r^n (\cos (n\theta)+i\sin (n\theta))= r^n \text{cis} (n\theta).$$

Demostración. Procedemos por inducción sobre $n$. El caso $n=1$ es inmediato. Supongamos que el resultado es cierto para $n$, es decir, que $$z^n=r^n \text{cis} (n\theta).$$

Por hipótesis inductiva, tenemos entonces que la norma de $z^n$ es $r^n$, de modo que $z^{n+1}=z^n z$ tiene norma $r^nr=r^{n+1}$.

También por hipótesis inductiva, $z^n$ tiene argumento $n\theta$. Por cómo funciona la multiplicación compleja, el argumento de $z^{n+1}=z^n z$ es la suma de los argumentos de $z^n$ y $z$, es decir, $n\theta + \theta = (n+1)\theta$. Esto muestra que $$z^{n+1}=r^{n+1}\text{cis}((n+1)\theta),$$ y con esto acabamos el paso inductivo.

$\square$

Ejemplos de aplicación de fórmula de De Moivre

Ejemplo. Veremos quién es la décima potencia del complejo $$z=\sqrt{3}\text{cis} \left(\frac{4\pi}{5}\right).$$ Como este número ya está escrito en forma polar, podemos aplicarle directamente la fórmula de De Moivre:
\begin{align*}
z^{10}&=3^{10/2} \text{cis}\left(\frac{40\pi}{5}\right)\\
&=3^5 \text{cis} (8\pi)\\
&=3^5\\
&=243.
\end{align*}

$\triangle$

El ejemplo anterior nos dice que $z^{10}=243$. En otras palabras, $z$ es una raíz $10$-ésima de $243$. Pero existen otras raíces $10$-ésimas de 243, por ejemplo, tiene dos raíces reales $\sqrt[10]{243}$ y $-\sqrt[10]{243}$. ¿Cuántas raíces tiene entonces en total? ¿Quiénes son? Esto lo veremos en la siguiente entrada.

Veamos otro ejemplo en el que se aplica la fórmula de De Moivre.

Problema. Evalúa la expresión $(1+i)^{30}$, expresando el resultado final en forma rectangular.

Solución. Comenzamos expresando a $(1+i)$ en forma polar. Para ello, notamos que $\Vert 1+i \Vert = \sqrt{2}$, y que $1+i$ hace un ángulo de $\frac{\pi}{4}$ con el eje real positivo. Por el teorema de De Moivre, tenemos que

\begin{align*}
z^{30}&=\sqrt{2}^{30}\text{cis}\left(\frac{30\pi}{4}\right)\\
&=2^{15}\text{cis}\left(\frac{6\pi}{4} \right) \\
&=2^{15}\text{cis}\left(\frac{3\pi}{2} \right) \\
&=2^{15}(-i)\\
&=-2^{15}i.
\end{align*}

En la segunda igualdad usamos que $\frac{30\pi}{4}$ y $\frac{6\pi}{4}$ difieren en un múltiplo entero de $2\pi$. En la cuarta usamos la forma polar de $-i$.

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que para un complejo $z\neq 0$ escrito en forma polar $z=r\text{cis}(\theta)$, su inverso multiplicativo tiene forma polar $r^{-1}\text{cis} (-\theta)$.
  2. Evalúa la multiplicación $wz$, donde $w=2\text{cis}\left(\frac{5\pi}{7}\right)$ y $z=-5\text{cis}\left(\frac{7\pi}{5}\right)$. Expresa la respuesta forma polar.
  3. Haz la multiplicación $wz$, donde $w=3\text{cis}\left(\frac{\pi}{2}\right)$ y $z=4\text{cis}\left(\frac{\pi}{3}\right)$. Expresa la respuesta en forma rectangular.
  4. Sea $z=7\text{cis}\left(\frac{5\pi}{7}\right)$. Expresa $z^3$ en forma polar.
  5. Sea $z=\sqrt[3]{5} \text{cis}\left(\frac{\pi}{3}\right)$. Expresa $z^9$ en forma rectangular.
  6. Toma el complejo $z=-2+2i$. Evalúa la expresión $$1+z+\ldots+z^{29}.$$ Sugerencia: Usa primero la fórmula de suma de términos de una sucesión geométrica, y después la fórmula de De Moivre.

Puedes practicar más estos temas viendo los videos y haciendo los ejercicios de la página de Khan Academy, de su sección de números complejos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: El teorema fundamental del cálculo

Por Fabian Ferrari

Deja un comentario

Introducción

Ya platicamos de continuidad, diferenciabilidad e integrales, así como de otros temas de cálculo. En esta sección reuniremos varias de estas ideas a través de uno de los resultados más importantes: el teorema fundamental del cálculo. Este teorema nos exhibe la relación que hay entre la derivada y la integral, distinguiéndolas como procedimientos inversos el uno del otro.

El teorema nos dice que si tenemos una función $F(x)$ derivable sobre un intervalo $[a, b]$, entonces

\begin{equation*}
\int_{a}^{b} \! F^\prime(t) \, dt = F(b)-F(a).
\end{equation*}

Ahora bien, si nuestra función $F(t)$ es derivable en $[0,x]$, tenemos que

\begin{equation*}
\int_{0}^{x} \! F^\prime(t) \, dt = F(x)-F(0),
\end{equation*}

a lo que le sigue que

\begin{equation*}
F(x)=\int_{0}^{x} \! F^\prime(t) \, dt + F(0).
\end{equation*}

Esto nos recuerda a la constante de integración

\begin{equation*}
F(x)=\int_{0}^{x} \! F^\prime(t) \, dt + C.
\end{equation*}

Es decir, tenemos que $C=F(0)$.

Aquí en el blog, en la entrada «Teoremas fundamentales de los cuadraditos» damos la intuición acerca de este teorema, comenzando con el caso discreto. Puedes leerlo antes de continuar.

Usar el teorema fundamental del cálculo para obtener una identidad trigonométrica

Veamos un ejemplo. Tenemos que la derivada de la función $F(t)=\sin^2 t$ es $F^\prime (t)=2\cos t\sin t$. Por el teorema fundamental del cálculo, la integral de $F'(t)$ en el intervalo $[0,x]$ está dada por

\begin{equation*}
\int_{0}^{x}\! 2 \sin t \cos t \, dt=\sin^2x,
\end{equation*}

en donde usamos que $F(0)=\sin^2(0)=0$.

Por otro lado, resolviendo la integral utilizando el cambio de variable $u=\cos t$, tenemos que $$\int_{0}^{x}\! 2 \sin t \cos t \, dt= \left. -\cos^2t \right |_0^x= -\cos^2x+1.
$$

Igualando ambos valores de la integral, tenemos que $\sin^2x=-\cos^2 x+1$. De aquí obtenemos la identidad trigonométrica pitagórica $\sin^2 x+\cos^2x=1$ para toda $x$.

Veamos ahora un problema en el que, mediante el problema fundamental del cálculo,

Problema. Aplicando el teorema fundamental del calculo halla $$\int_{a}^{b}\! \sec x\, dx.$$

Sugerencia pre-solución. Formula un problema equivalente multiplicando y dividiendo la expresión por $\sec x + \tan x$. Intenta identificar la expresión resultante como la derivada de otra función.

Solución. Para resolver este problema tenemos que hallar una función $F(x)$ de tal forma que $F^\prime (x)= \sec x$.

Para ello, tenemos que notar que

\begin{align*}
\sec x &=\sec x \left(\frac{ \sec x + \tan x}{\sec x+ \tan x}\right)\\ &=\frac{\sec^2x+\sec x \tan x}{\sec x+\tan x}.
\end{align*}

Y entonces la derivada de $\ln (\sec x + \tan x)$ es igual a

\begin{align*}
\left(\frac{1}{\sec x + \tan x}\right)&(\sec^2x+\sec x \tan x)\\
&=\frac{\sec^2x+\sec x \tan x}{\sec x+\tan x}\\&=\sec x.
\end{align*}

Proponemos a la función

\begin{equation*}
F(x)=\ln (\sec x + \tan x)
\end{equation*}

dado que

\begin{equation*}
F^\prime (x)=\sec x.
\end{equation*}

Ahora, aplicando el teorema fundamental del cálculo tenemos que

\begin{align*}
\int_{a}^{b}\! \sec x\, dx&=F(b)-F(a)\\&=\ln (\sec b + \tan b)-\ln (\sec a + \tan a)
\end{align*}

$\square$

Segundo teorema fundamental del cálculo

Veamos una implicación del teorema fundamental del cálculo, que también se le conoce como el «segundo teorema fundamental del cálculo».

Para una función $f: [a,b] \to \mathbb{R}$ continua en el intervalo $[a,b]$ se tiene que:

\begin{equation*}
\frac{d}{dx}\left(\int_{a}^{x}\! f(t)\, dt\right)=f(x)
\end{equation*}

Problema. Determina $$\frac{d}{dx}\left(\int_{3x-1}^{0} \! \frac{1}{t+4}\, dt\right).$$

Sugerencia pre-solución. Usa el segundo teorema fundamental del cálculo y la regla de la cadena.

Solución. Como $$\int_{3x-1}^{0} \! \frac{1}{t+4}\, dt=-\int_{0}^{3x-1} \! \frac{1}{t+4}\, dt,$$ tenemos entonces que

$$\frac{d}{dx}\left(\int_{3x-1}^0 \frac{1}{t+4} \, dt\right)= – \frac{d}{dx}\left(\int_{0}^{3x-1} \frac{1}{t+4} \, dt\right).$$

Por otro lado, consideremos las funciones

\begin{align*}
f(x)&=\int_{0}^{x} \! \frac{1}{t+4}\, dt \quad \text{y}\\
g(x)&=3x-1.
\end{align*}

Aplicando el teorema fundamental del cálculo y derivando tenemos que

\begin{align*}
f^\prime (x)&=\frac{1}{x+4} \quad \text{y}\\
g^\prime (x)&=3.
\end{align*}

Notemos que

\begin{align*}
(f \circ g)(x)&=f( g(x) )\\&=f(3x-1)\\&=\int_{0}^{3x-1}\! \frac{1}{t+4}\, dt.
\end{align*}

Así, aplicando la regla de la cadena, tenemos que

\begin{align*}
-\frac{d}{dx}\left(\int_{0}^{3x-1} \! \frac{1}{t+4}\, dt\right)&=-\frac{d}{dx}(f(g(x))\\&=-f^\prime (g(x)) g^\prime(x)\\
&=-\frac{1}{(3x-1)+4}\cdot 3\\
&=-\frac{1}{x+1}.
\end{align*}

$\square$

Veamos un último problema en el que se usa la segunda forma del teorema fundamental del cálculo.

Problema: Supongamos que $f$ es una función continua para toda $x$, la cual satisface la ecuación

\begin{equation}
\int_{0}^{x} \! f(t)\, dt= \int_{x}^{1} \! t^2f(t) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C,
\end{equation}

donde $C$ es una constante. Encuentra la forma explícita de la función $f(x)$ y determina el valor de la constante $C$.

Sugerencia pre-solución.

Solución. De la ecuación, tenemos lo siguiente

\begin{equation*}
\frac{d}{dx}\left(\int_{0}^{x} \! f(t)\, dt\right)= \frac{d}{dx}\left(\int_{x}^{1} \! t^2f(t) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C \right)
\end{equation*}

Como $f$ es continua para toda $x$, por el teorema fundamental del cálculo en su segunda forma tenemos que

\begin{equation*}
\frac{d}{dx} \left( \int_{0}^{x} \! f(t)\, dt \right)= f(x)
\end{equation*}

y

\begin{align*}
\frac{d}{dx} \left( \int_{x}^{1} \! t^2f(t)\, dt \right)&= – \frac{d}{dx} \left( \int_{1}^{x} \! t^2f(t)\, dt \right)\\&= -x^2f(x).
\end{align*}

Entonces, derivando ambos lados de la expresión original nos resulta la ecuación

\begin{equation*}
f(x)=-x^2f(x)+2x^{15}+2x^{17},
\end{equation*}

de la cual se obtiene

\begin{align*}
f(x) (x^2+1)&=2x^{15}+2x^{17}\\
&=2x^{15}(x^2+1)
\end{align*}

Así, tenemos que

\begin{equation*}
f(x)=2x^{15}.
\end{equation*}

Sustituyendo $f(t)=2t^{15}$ en la ecuación (1), tenemos que

\begin{equation*}
\int_{0}^{x} \! 2t^{15}\, dt= \int_{x}^{1} \! t^2(2t^{15}) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C
\end{equation*}

Así,

\begin{align*}
\int_{0}^{x} \! 2t^{15}\, dt&= \int_{x}^{1} \! t^2(2t^{15}) \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\int_{0}^{x} \! 2t^{15}\, dt &= -\int_{1}^{x} \! 2t^{17} \, dt +\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\left. \frac{2t^{16}}{16} \right|_{0}^{x} &= – \left. \left(\frac{2t^{18}}{18} \right) \right|_{1}^{x}+\frac{x^{16}}{8}+\frac{x^{18}}{9}+C\\
\frac{x^{16}}{8} &= – \left( \frac{x^{18}}{9}-\frac{1}{9}\right)+\frac{x^{16}}{8}+\frac{x^{18}}{19}+C\\
\end{align*}

Con ello, tenemos que

\begin{equation*}
C+\frac{1}{9}=0.
\end{equation*}

Por lo tanto la función que satisface la ecuación es $f(x)=2x^{15}$ y el valor de la constante es $C= – \frac{1}{9}$.

$\square$

Más problemas

Hay más ejemplos de problemas relacionados con la aplicación del teorema fundamental del cálculo en la Sección 6.9 del libro Problem Solving through Problems de Loren Larson.