Introducción
En geometría euclidiana existen los Teoremas de Miquel, dados por el matemático Auguste Miquel, los cuales son relacionados con circunferencias concurrentes.
Teoremas de Miquel
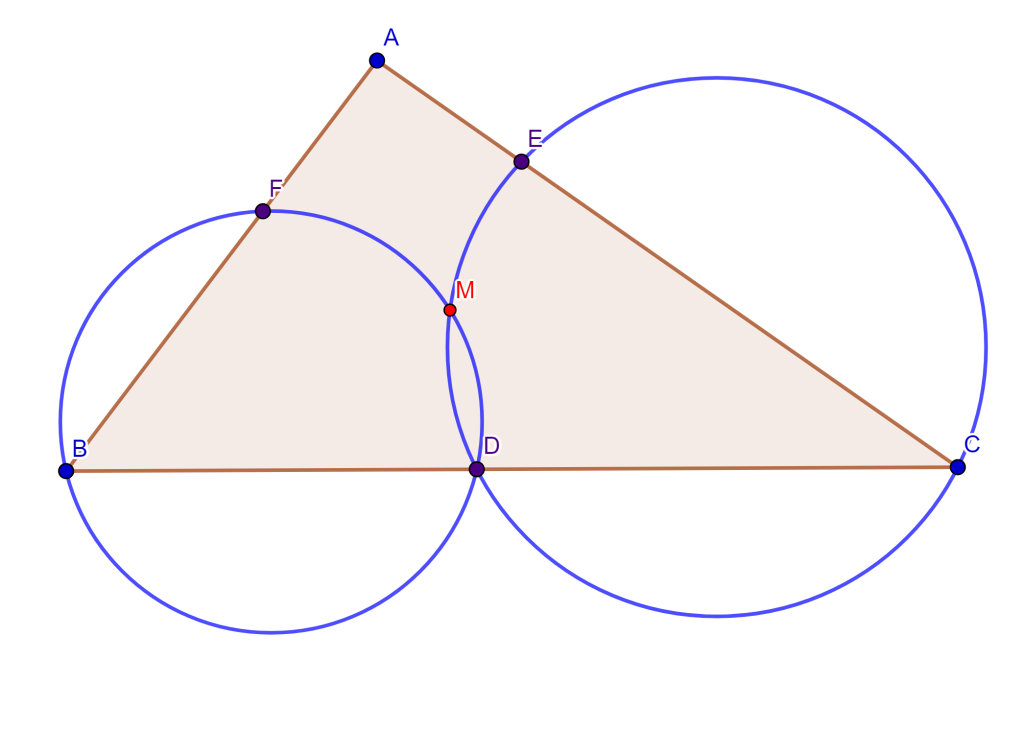
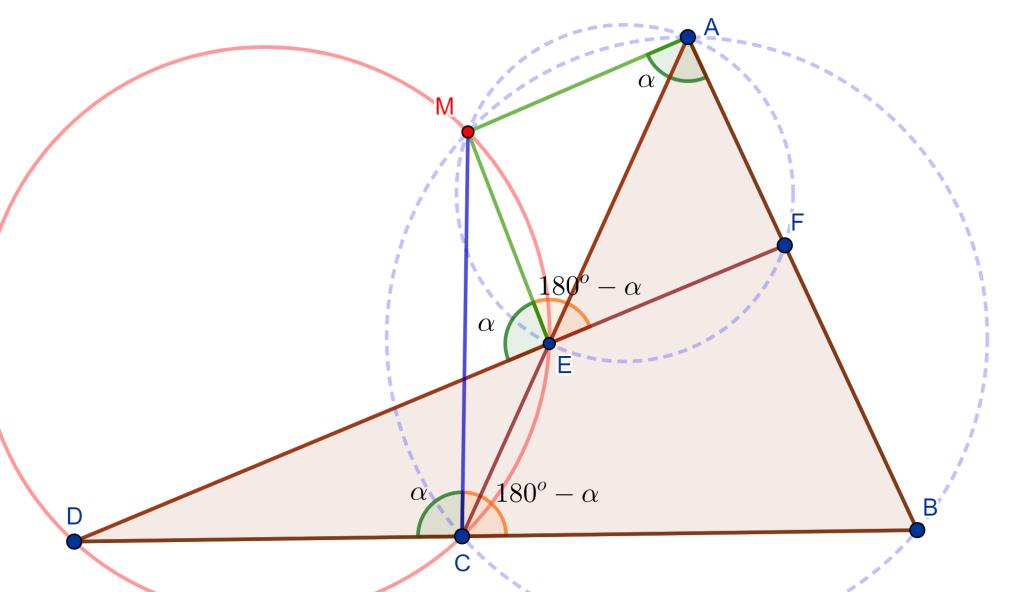
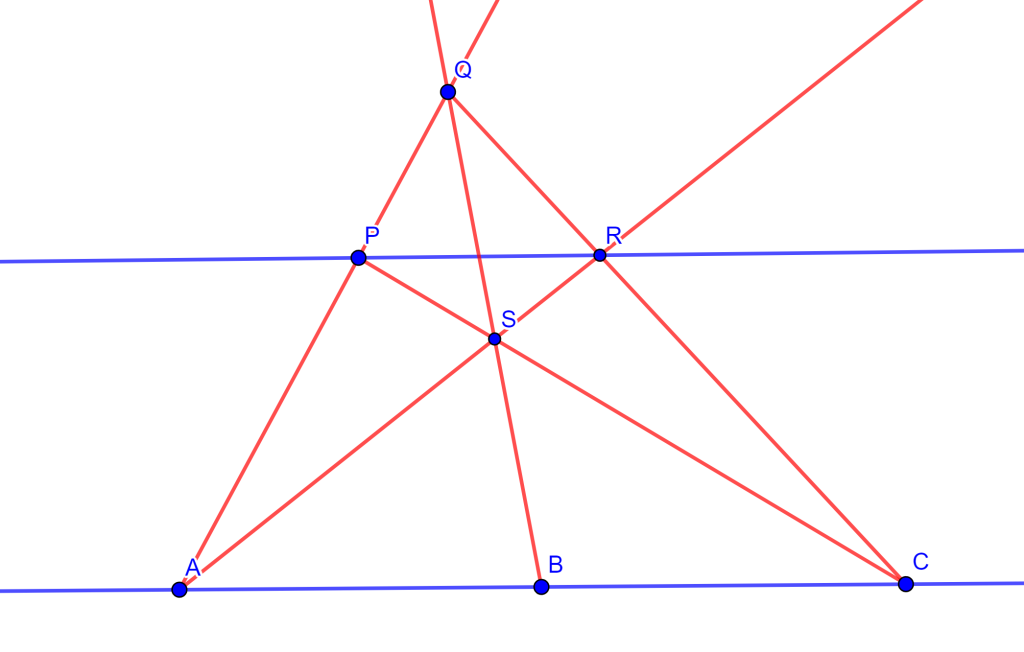
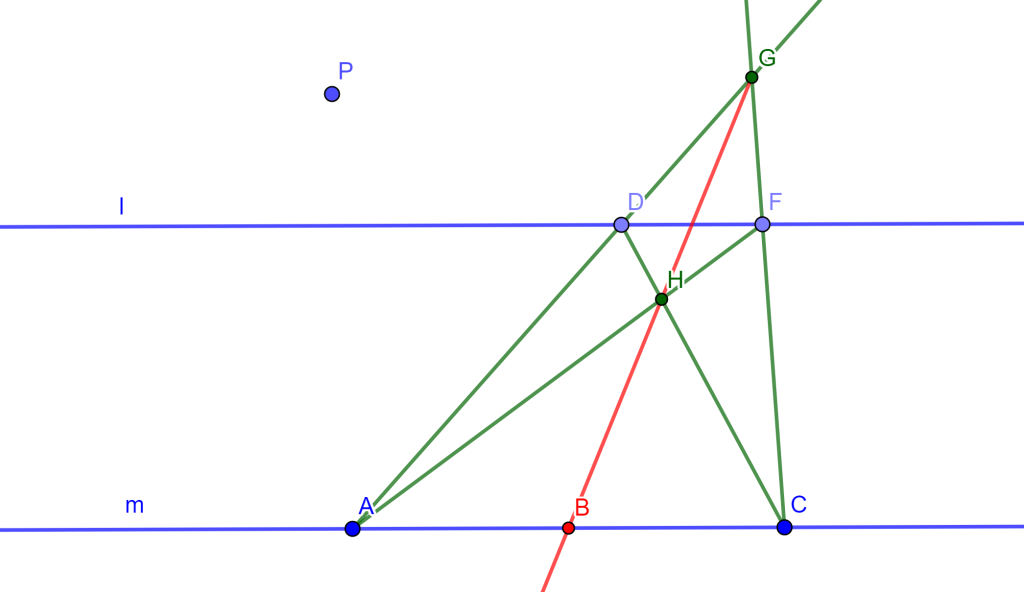
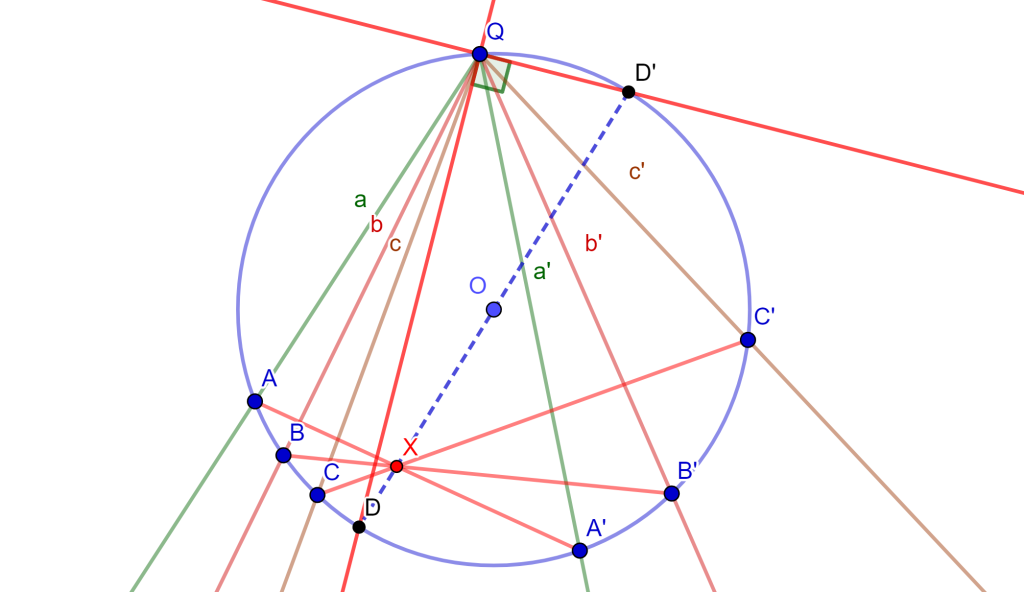
Teorema de Miquel: Dado el triángulo $\triangle ABC$ y $DEF$ tres puntos cualesquiera en los lados $BC$, $CA$ y $AB$ respectivamente, entonces los circuncirculos de $AEF$, $BFD$ y $CDE$ se intersecan en un punto en común, este es el punto de Miquel.
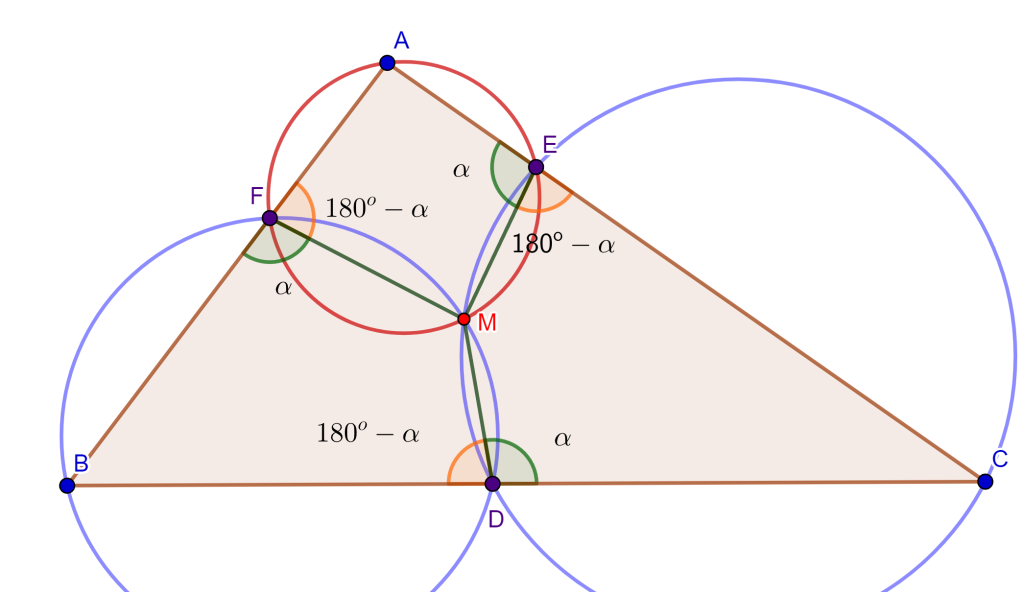
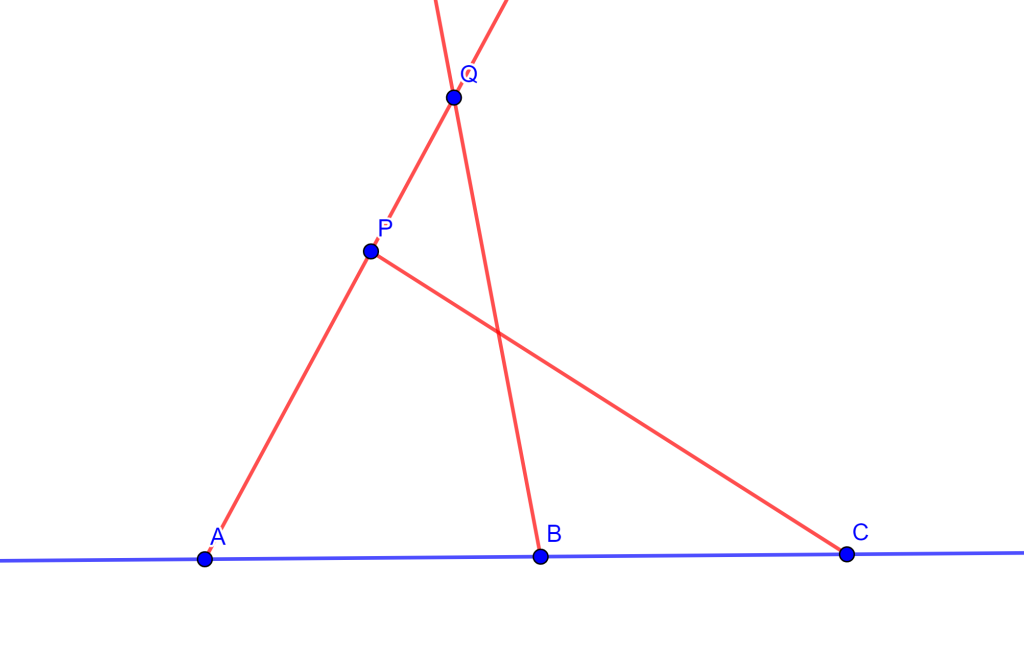
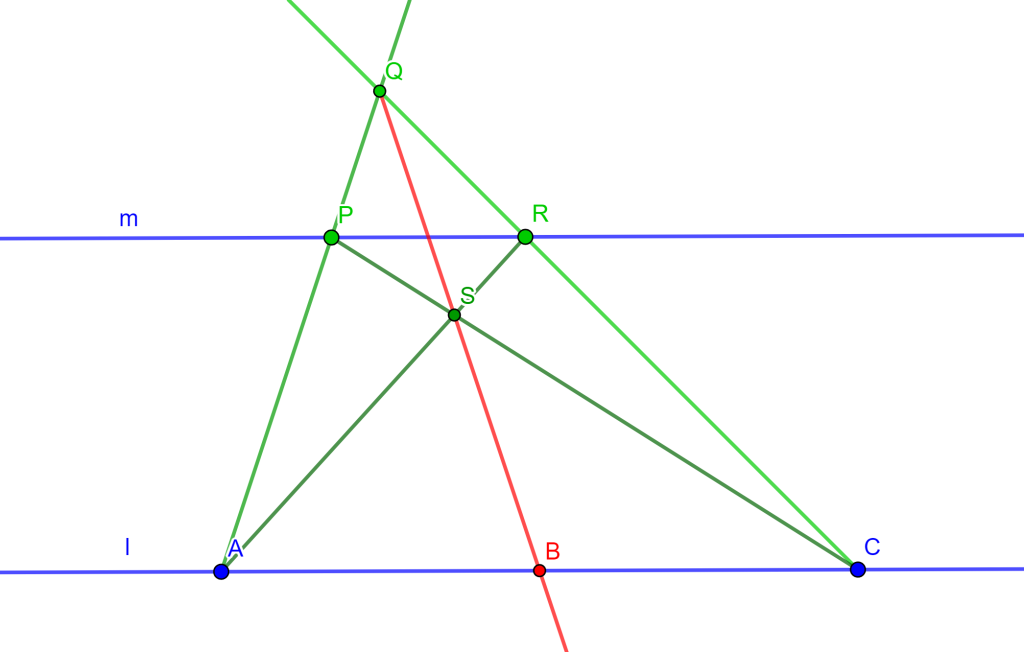
Demostración Sea el triángulo $\triangle ABC$ y sean los tres puntos $DEF$ en los lados de $BC$, $CA$ y $AB$ respectivamente, entonces los circuncirculos $CDE$ y $BFD$ se intersecan en un punto $M$. Solo falta demostrar que el cuadrilátero $AFOE$ es cíclico, ya que probaría que la circunferencia $AFE$ pasa por el punto $M$.
Tracemos $FM$, $ME$ y $MD$, de esta forma se tienen los tres cuadriláteros $FMDB$, $MECD$ y $FAEM$. Tenemos el ángulo $\angle AEM = \alpha $ donde el ángulo $\angle CEM = 180^o – \alpha$, como el cuadrilátero $MECD$ es cíclico entonces el ángulo $\angle MDC = \alpha $, por lo cual el ángulo $\angle MDB = 180 ^o – \alpha$.
Ahora, como el ángulo $\angle MDB = 180^o – \alpha$ y el cuadrilátero $FMDB$ es cíclico, entonces el ángulo $\angle BFM = \alpha$, por lo cual el ángulo $\angle MFA = 180 ^o – \alpha$.
Si observamos el cuadrilátero $FAEM$ sus dos ángulos opuestos $\angle MFA$ y $\angle AEM$ suman $180^o$, por lo cual el cuadrilátero $FAEM$ es cíclico. Por lo tanto, el circuncirculo de $FAE$ pasa por el punto $M$ y los tres circuncirculos se intersecan en el punto $M$ ($M$ es el punto de Miquel).
$\square$
El punto $M$ es el punto de Miquel con respecto al triángulo $\triangle ABC$
El triángulo $DEF$ cuando $D$, $E$ y $F$ no son colineales, es llamado un triángulo de Miquel $M$.
Los tres circuncirculos de $AEF$, $BFD$ y $CDE$ son llamadas las circunferencias de Miquel de los puntos $D$, $E$ y $F$.
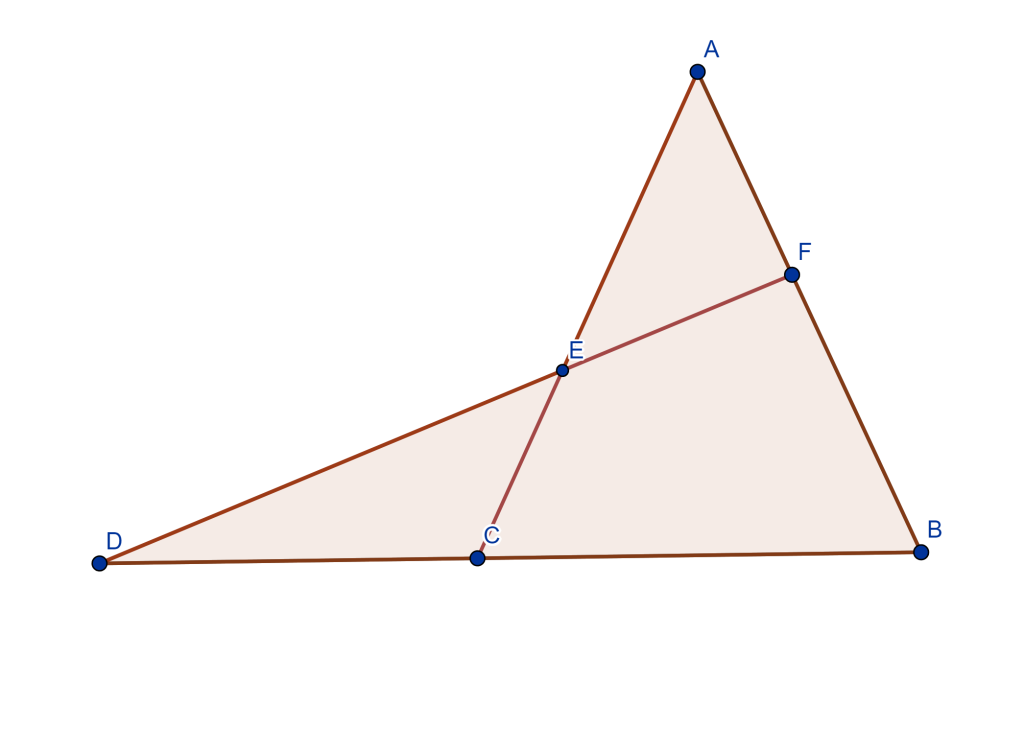
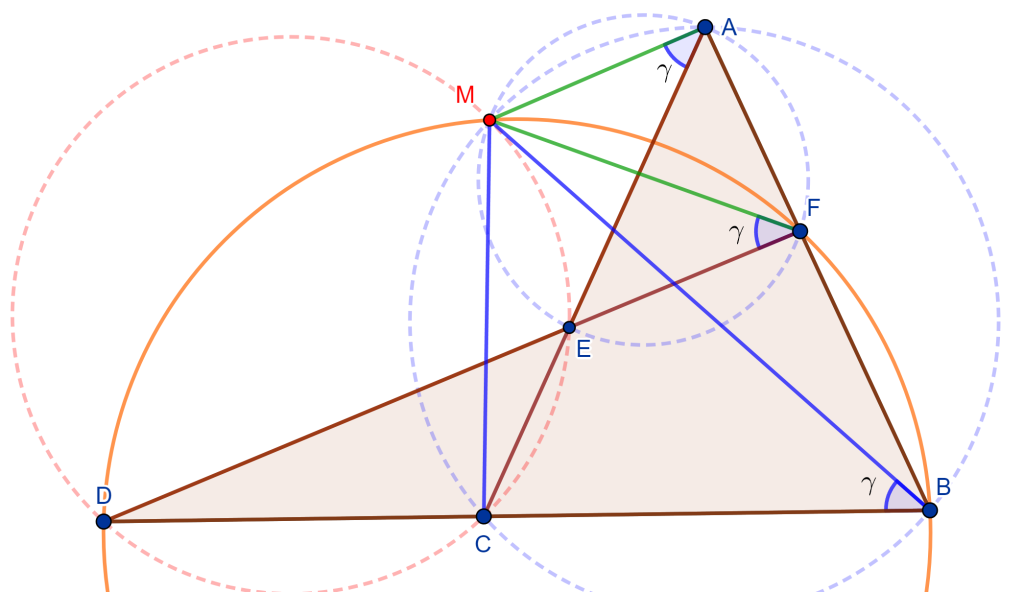
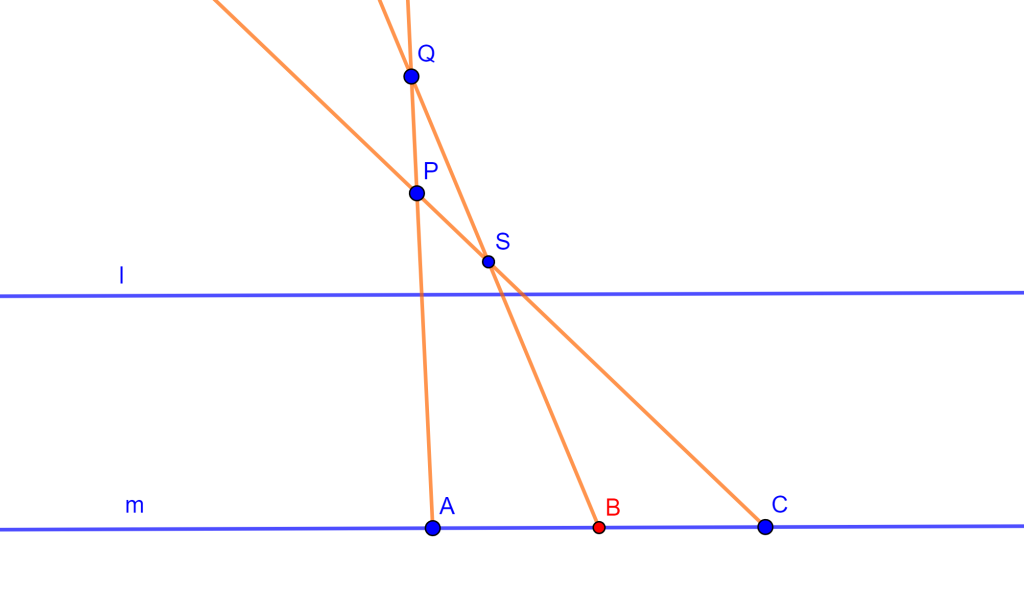
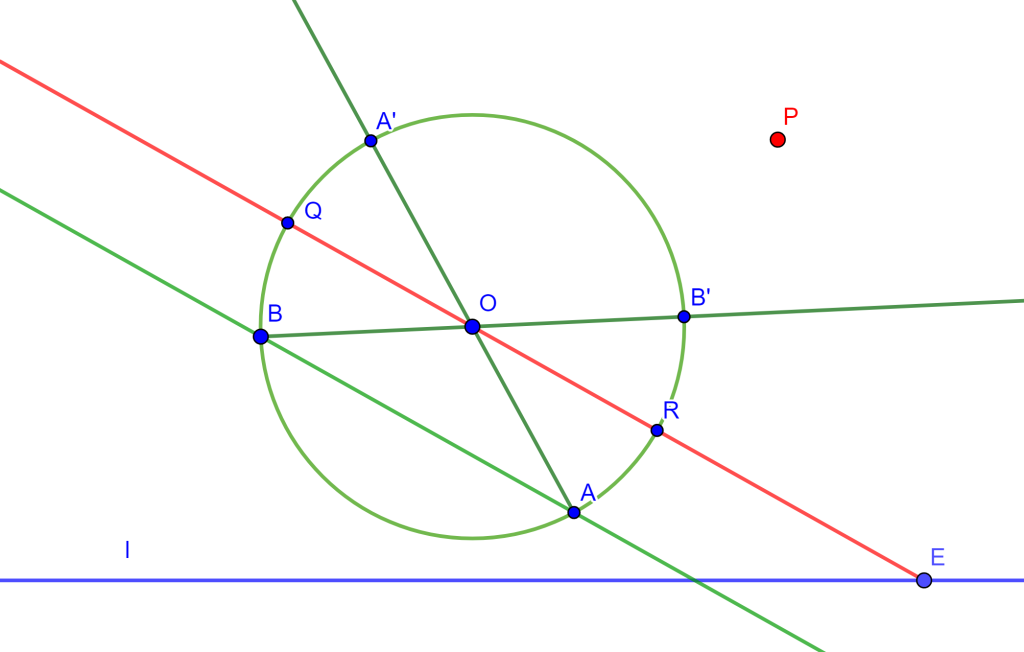
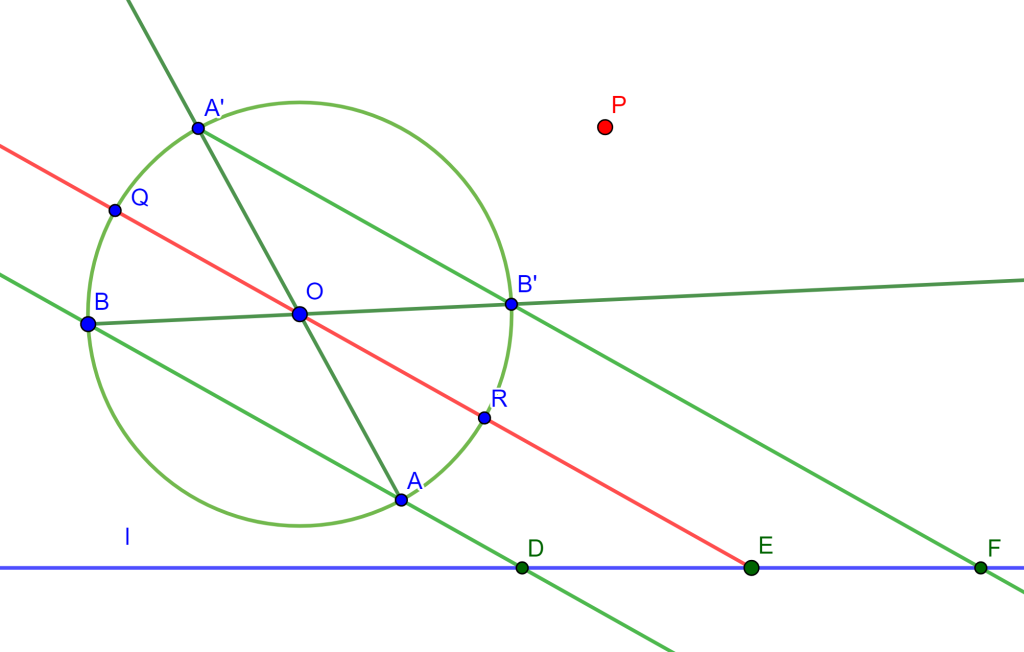
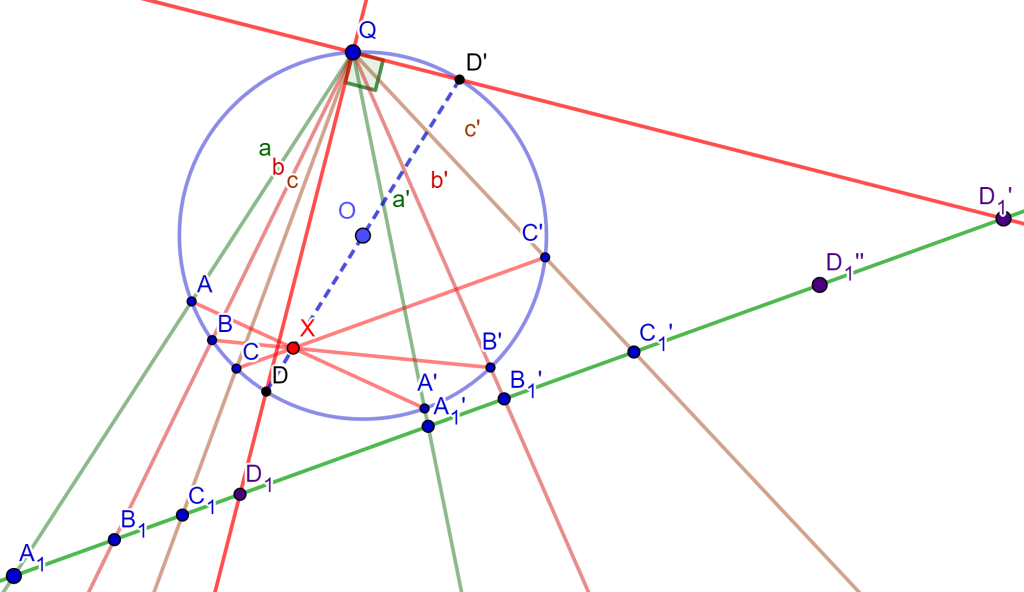
Teorema (Cuadrilátero Completo): Sea $ABCDEF$ un cuadrilátero completo, entonces las circunferencias circunscritas de los cuatro triángulos $EAD$, $EBC$, $FAB$ y $FDC$ tienen un punto en común, $M$ llamado punto de Miquel.
Demostración
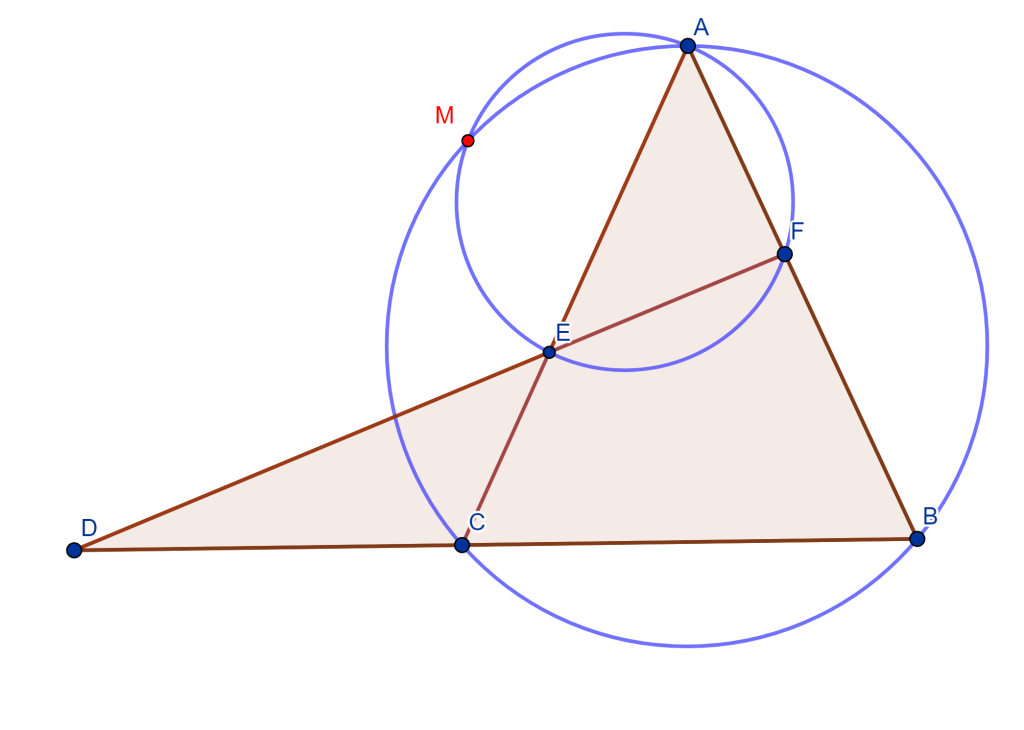
De los triángulos $AEF$ y $ACB$ trazamos sus circunferencias circunscritas que se cortan en un punto $M$.
Mostremos que el cuadrilátero $MECD$ es cíclico, ya que mostraría que su circunferencia circunscrita pasa por $M$.
Observemos el ángulo $\angle DCM = \alpha$ y $\angle MCB = 180 ^o – \alpha$, ahora tenemos el cuadrilátero cíclico $MCBA$ entonces el ángulo $\angle MAB = \alpha$, el cuadrilátero cíclico $MAFE$ tiene el ángulo $\angle MAF = \alpha$ entonces $\angle MEF = 180 ^o – \alpha$.
Como $\angle MEF = 180^o – \alpha$ entonces $\angle MED = \alpha$, ahora veamos el cuadrilátero $MECD$ tiene los ángulos $\angle MED = \alpha $ y $\angle DCM = \alpha$, lo que nos lleva a que el cuadrilátero $MECD$ es cíclico y su circunferencia circunscrita pasa por $M$.
Falta por demostrar que el cuadrilátero $MDBF$ es cíclico.
Sea el ángulo $\angle MFE = \gamma$, el cuadrilátero $MAFE$ es cíclico, entonces tiene un ángulo $\angle MAE = \gamma = \angle MFE$. Observemos ahora el cuadrilátero $MCBA$ cíclico, con su ángulo $\angle MAC = \gamma$ y como es cíclico entonces el ángulo $\angle MBC = \gamma$.
Notemos que el cuadrilátero $MDBF$ tiene los ángulos $\angle MFD = \gamma$ y $\angle MBD = \gamma$, por lo cual el cuadrilátero $MDBF$ es cíclico, entonces su circunferencia circunscrita pasa por $M$.
Por lo tanto, las circunferencias circunscritas de los cuatro triángulos $EAD$, $EBC$, $FAB$ y $FDC$ tienen un punto en común $M$ llamado punto de Miquel $M$.
$\square$
Círculo de Miquel
Respecto a las cuatro circunferencias del cuadrilátero completo con centros $O_1, O_2, O_3 $ y $O_4$ y el punto de Miquel $M$ son conciclicos. Por lo cual la circunferencia que contiene a estos cinco puntos se llama Círculo de Miquel.
Teoremas de la línea de Simson del punto de Miquel
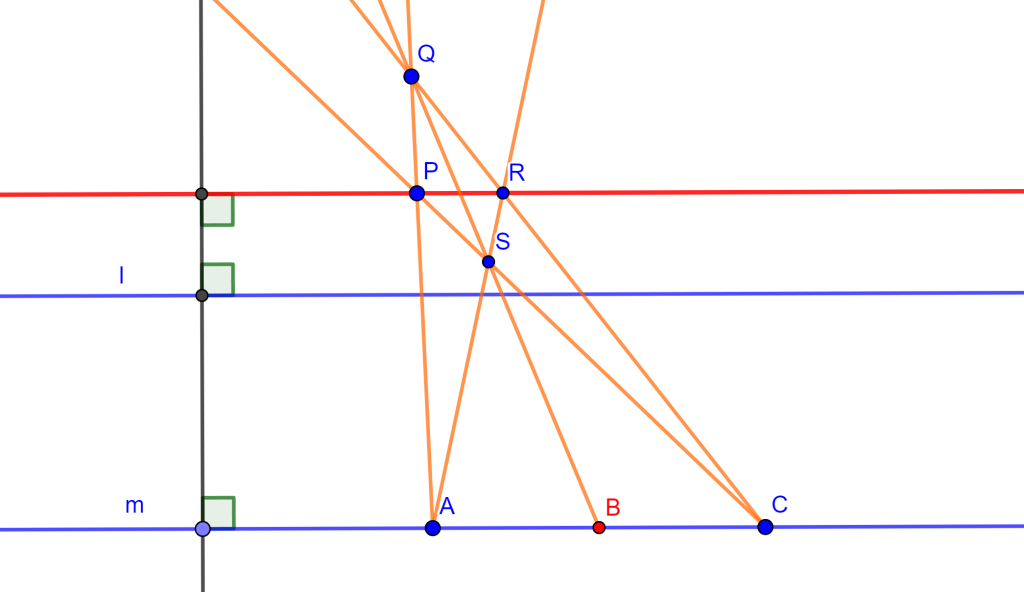
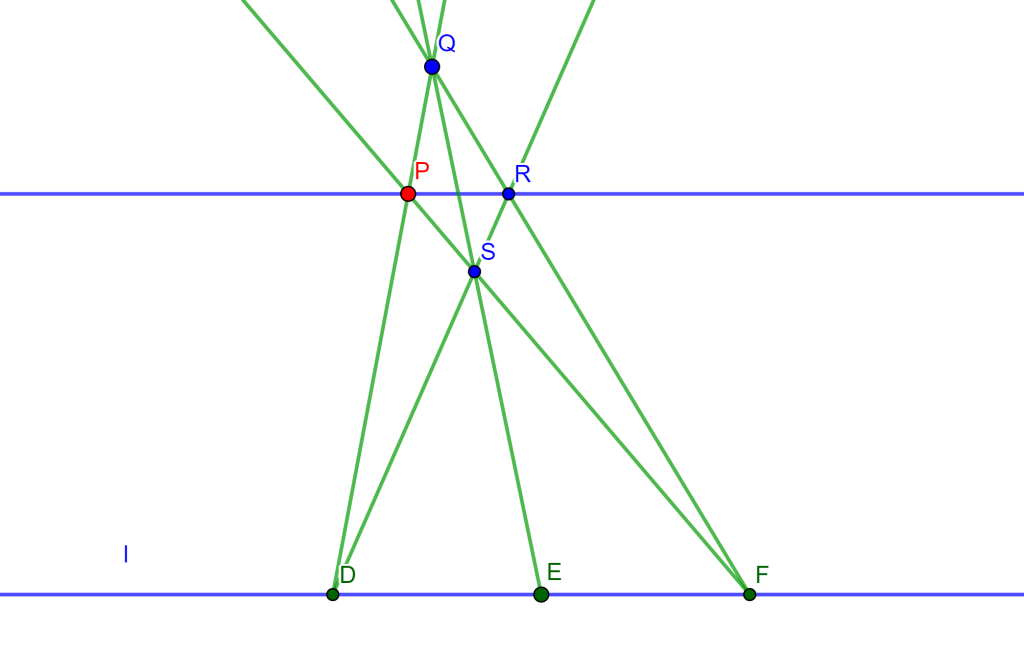
Teorema 1 (Línea de Simson) Sea una circunferencia circunscrita de un triángulo con un punto cualquiera de esta circunferencia, bajamos perpendiculares a los tres lados, entonces los pies de estas perpendiculares están en una línea recta (Línea de Simson).
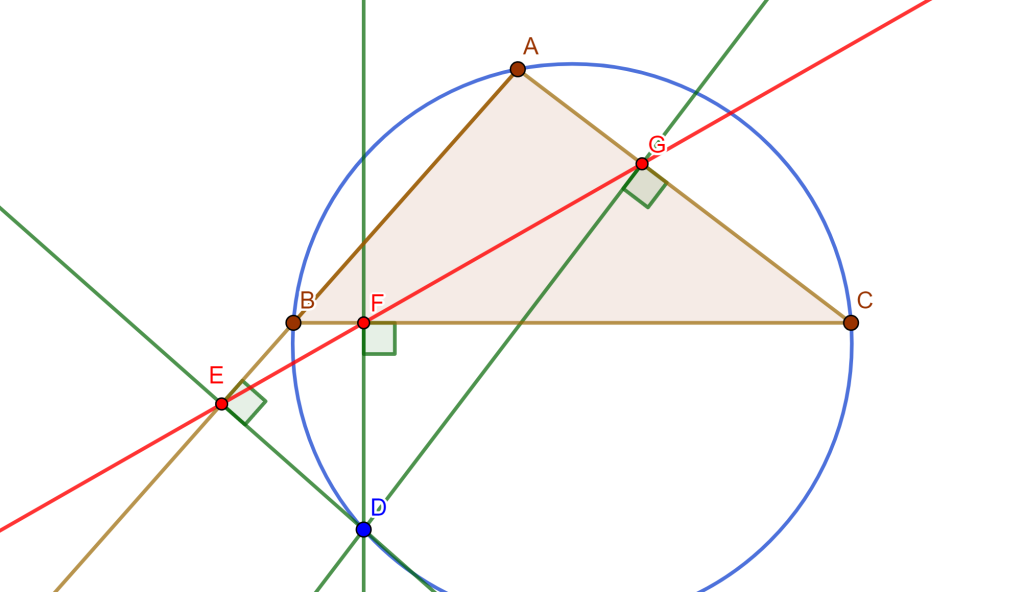
Teorema 2 (Línea de Simson) Los pies de las perpendiculares de $M$ de los cuatro lados del cuadrilátero completo son colineales.
Teoremas del pentágono y los seis círculos de Miquel
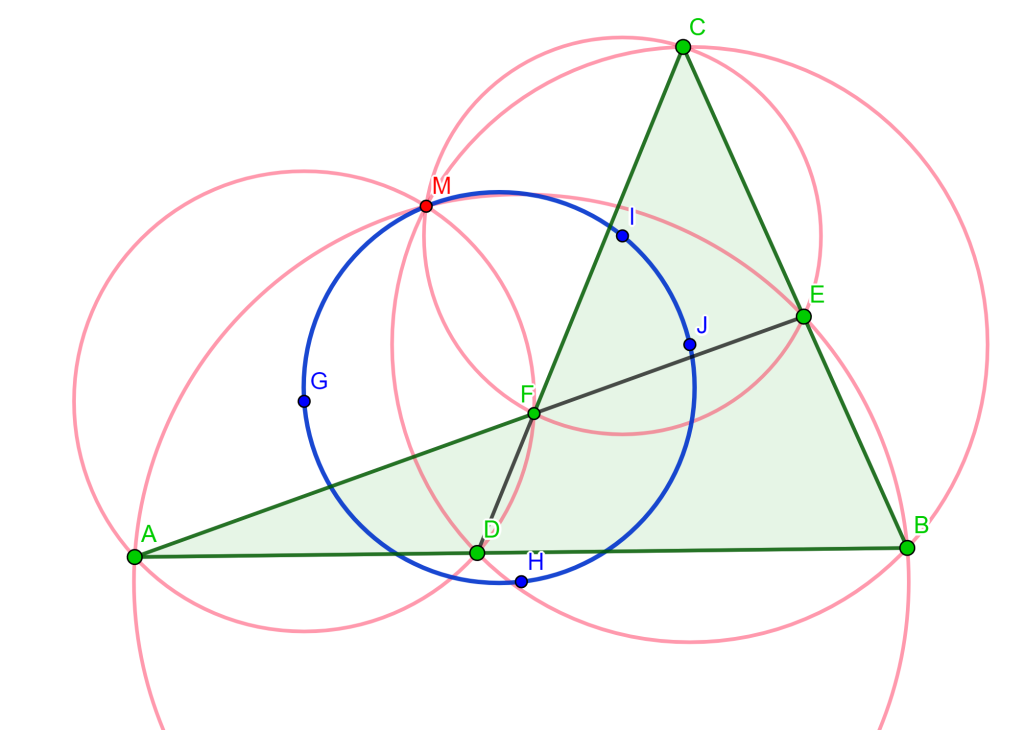
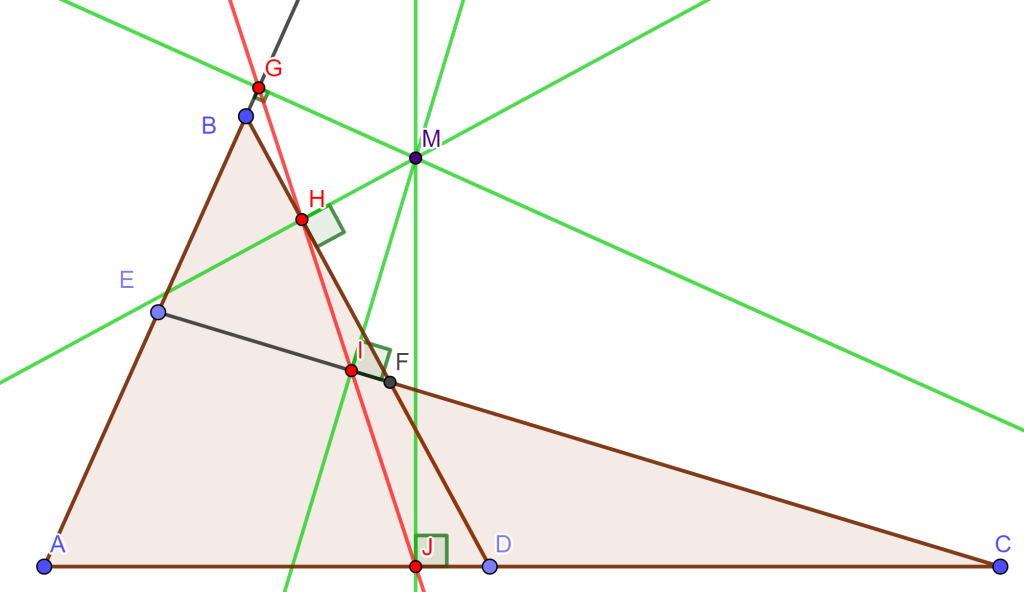
Teorema del Pentágono Sea $ABCDE$ un pentágono cualquiera, prolongando todos los lados, estos se intersecan en los puntos $F$, $G$, $H$, $I$ y $J$, entonces los puntos de intersección de las cinco circunferencias circunscritas $ABF$, $BCG$, $CDH$, $DEI$ y $EAJ$ son conciclicos.
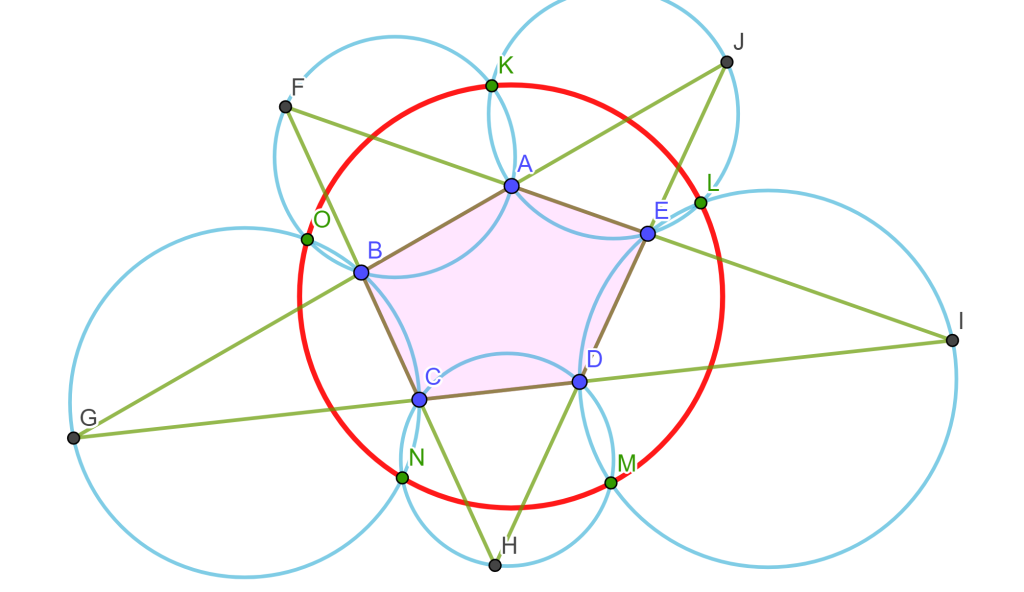
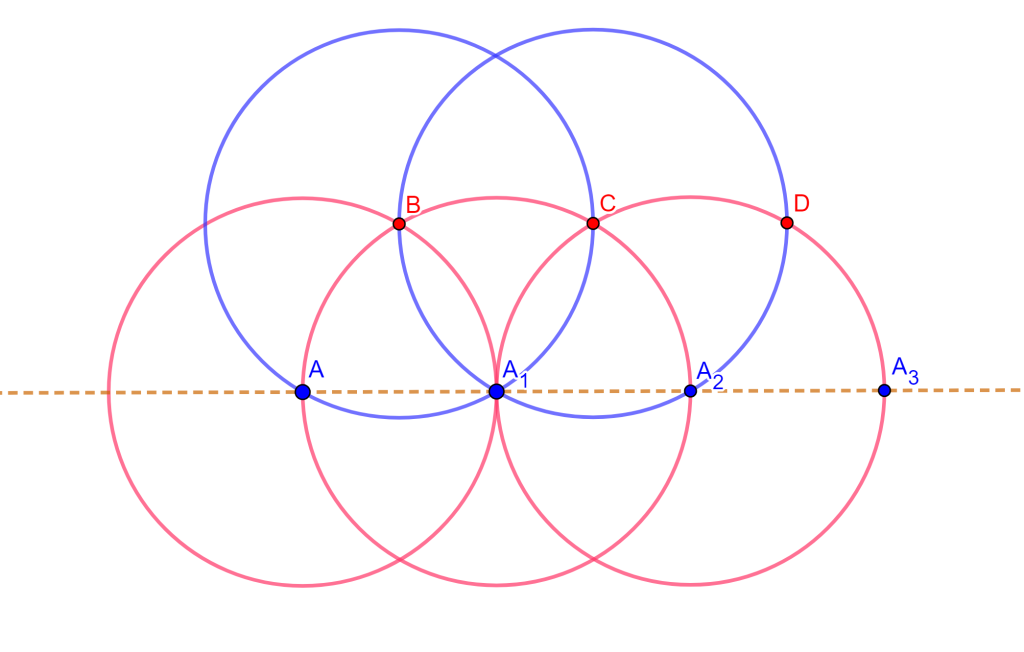
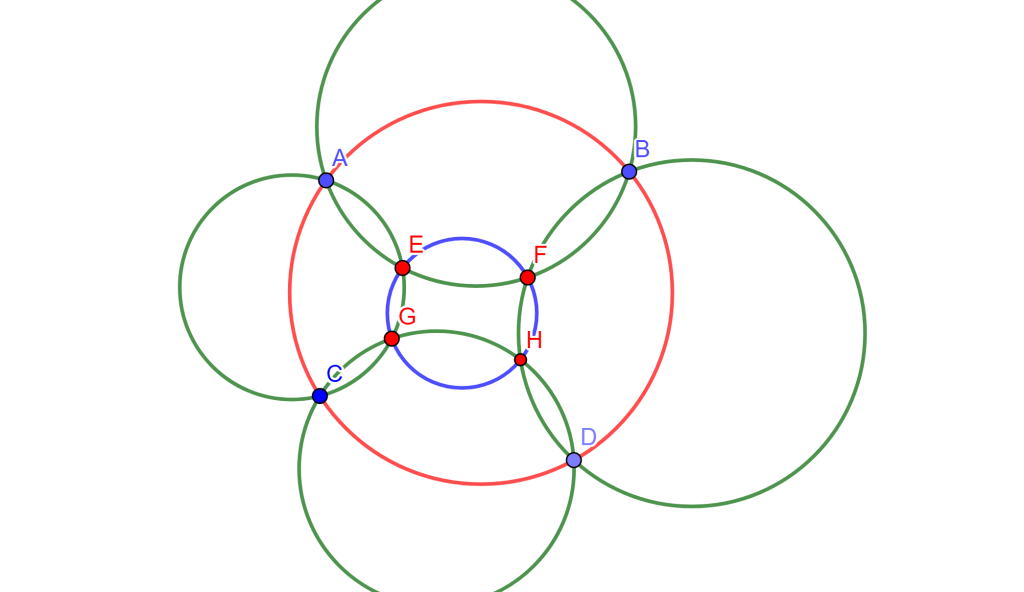
Teorema de los seis círculos Sean los puntos $A$, $B$, $C$ y $D$ de una circunferencia y las circunferencias que pasan por los pares de puntos adyacentes, las intersecciones de estas circunferencias en $E$, $F$, $G$ y $H$ se encuentran en una sexta circunferencia en común.
Más adelante…
Al igual que los Teoremas de Miquel, se abordarán ahora los Teoremas de Carnot.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Teorema de Stewart
- Siguiente entrada del curso: Teorema de Carnot