Archivo de la etiqueta: algebra

2.2. NÚCLEO, NULIDAD, IMAGEN Y RANGO: definiciones, ejemplos y propiedades

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

INTRODUCCIÓN

Analizaremos 4 nuevos conceptos. Dos de ellos son conjuntos y los otros dos son dimensiones de esos conjuntos.

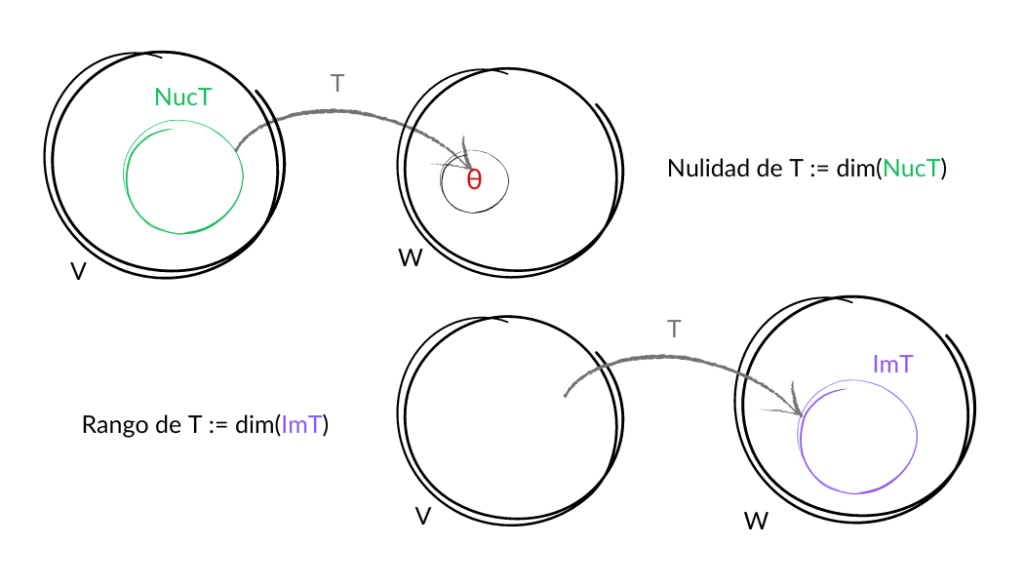
Representación gráfica del núcleo y la imagen de una transformación $T$.

Al ir avanzando en el análisis del concepto de núcleo, podrás ver que una de las aplicaciones inmediatas es pensar al núcleo como el conjunto formado por las soluciones de un sistema de ecuaciones lineales homogéneo asociado a la matriz que representa la transformación lineal. Pero todo con calma…

NÚCLEO E IMAGEN DE UNA TRANSFORMACIÓN LINEAL

Definición: Sean $V$ y $W$ $K$ – espacios vectoriales y $T\in\mathcal{L}(V,W)$.
El núcleo de $T$ es $Núc(T)=\{v\in V|T(v)=\theta_W\}$.
La imagen de $T$ es $Im(T)=\{T(v)|v\in V\}$.

Nota: El núcleo de una transformación $T$, también suele llamarse kernel y se denota como $ker(T)$.

  • Sean $K$ un campo y $T:K^\infty\longrightarrow K^\infty$ lineal donde $\forall (x_1,x_2,x_3,…)\in K^\infty (T(x_1,x_2,x_3,…)=(x_2,x_3,x_4,…))$.
    $Núc(T)=\{(x_1,0_K,0_K,…)\in K^\infty | x_1\in K\}$ ; $Im(T)=K^\infty$

Justificación. Para el núcleo de $T$: $T(x_1,x_2,x_3,…)=(0_K,0_K,0_K,…)$ syss $(x_2,x_3,x_4,…)=(0_K,0_K,0_K,…)$ syss $x_i=0_K$ para toda $i\in\{2,3,4,…\}$
Para la imagen de $T$: Sea $(y_1,y_2,y_3,…)\in K^\infty$. $T(0_K,y_1,y_2,…)=(y_1,y_2,y_3,…)$

  • Sea $T:\mathbb{R}^2\longrightarrow\mathbb{R}^2$ donde $\forall (x,y)\in\mathbb{R}^2(T(x,y)=(x,0))$
    $Núc(T)=\{(0,y)\in\mathbb{R}^2|y\in\mathbb{R}\}$ ; $Im(T)=\{(x,0)\mathbb{R}^2|x\in\mathbb{R}\}$

Justificación. Para el núcleo de $T$: $T(x,y)=(0,0)$ syss $(x,0)=(0,0)$ syss $x=0$
Para la imagen de $T$: Sea $(a,0)\in \{ (x,0)\in\mathbb{R}^2|x\in\mathbb{R}^2\}$. $T(a,0)=(a,0)$.

  • Sean $K$ campo, $A\in\mathcal{M}_{m\times n}(K)$ y $T:K^n\longrightarrow K^m$ donde $\forall X\in K^n(T(X)=AX)$
    $Núc(T)$ es el conjunto de las soluciones del sistema homogéneo con matriz de coeficientes $A$ ; $Im(T)$ es el espacio generado por las columnas de $A$

Justificación. Para el núcleo de $T$: $T(X)=\theta_{m\times 1}$ syss $AX=\theta_{m\times 1}$ syss $X$ es solución del sistema homogéneo con matriz de coeficientes $A$
Para la imagen de $T$: $Im(T)=\{AX:X\in K^n\}$$=\left\{ \begin{equation*} \begin{pmatrix} a_{11} & … & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & … & a_{mn} \end{pmatrix} \begin{pmatrix} x_1\\ \vdots \\ x_n & \vdots & a_{mn} \end{pmatrix} \end{equation*} : x_1,x_2,…,x_n\in K \right\}$$=\left\{ \begin{equation*} \begin{pmatrix} a_{11}x_1 + … + a_{1n}x_n \\ … \\ a_{m1}x_1 + … + a_{mn}x_n \end{pmatrix} \end{equation*} : x_1,x_2,…,x_n\in K \right\}$$=\left\{ \begin{equation*} x_1\begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix} + … + x_n\begin{pmatrix} a_{1n}\\ \vdots \\ a_{mn} \end{pmatrix} \end{equation*} : x_1,x_2,…,x_n\in K \right\}$$=\langle\begin{equation*} \begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix},…,\begin{pmatrix} a_{11}\\ \vdots \\ a_{m1} \end{pmatrix} \end{equation*} \rangle$

Proposición: Sean $V,W$ $K$ – espacios vectoriales, $T\in\mathcal{L}(V,W)$. Se cumple que:

a) $Núc(T)\leqslant V$
b) $Im(T)\leqslant W$

Demostración: Para cada inciso es necesario demostrar dos propiedades:

a) P.D. $\theta_V\in Núc(T)$ y $\forall\lambda\in K$ $\forall u,v\in Núc(T) (\lambda u + v\in Núc(T))$

Por la Obs. tenemos que $T(\theta_V)=\theta_W$, por lo tanto, $\theta_V\in Núc(T)$

Sean $\lambda\in K$ y $u,v\in Núc(T)$.
Entonces $T(u)=\theta_W=T(v)$
Además, $T(\lambda u+v)=\lambda T(u)+T(v)$ por ser $T$ lineal.
Así, $T(\lambda u+v)=\lambda\theta_W +\theta_W=\theta_W$.
De donde $\lambda u + v\in Núc(T)$

b) P.D. $\theta_W\in Im(T)$ y $\forall\lambda\in K$ $\forall u,v\in Im(T) (\lambda u + v\in Im(T))$

Por la Obs. tenemos que $\theta_V\in V$ cumple que $T(\theta_V)=\theta_W$, por lo tanto, $\theta_W\in Im(T)$.

Sean $\lambda\in K$ y $w,z\in Im(T)$.
Entonces $\exists x,y\in Núc(T) (T(x)=w\wedge T(y)=z)$
Además, $T(\lambda u+v)=\lambda T(u)+T(v)$ por ser $T$ lineal.
Así, $T(\lambda u+v)=\lambda\theta_W +\theta_W=\theta_W$.
De donde $\lambda u + v\in Núc(T)$

NULIDAD Y RANGO DE UNA TRANSFORMACIÓN LINEAL

Definición: Sea $T$ una transformación lineal con $Núc (T)$ de dimensión finita. Decimos que la dimensión de $Núc(T)$ es la nulidad de $T$.

Definición: Sea $T$ una transformación lineal con $Im (T)$ de dimensión finita. Decimos que la dimensión de $Im(T)$ es el rango de $T$.

Ejemplo

  • Sea $K=\mathbb{R}$ y sean $V=\mathcal{P}_3$ y $W=\mathcal{P}_2$ $K$ – espacios vectoriales.
    Sea $T:V\longrightarrow W$ donde $\forall p(x)\in T(p(x))=p'(x)$
    La nulidad de $T$ es $1$ y su rango es $3$

Justificación. Los polinomios con derivada cero son únicamente las constantes. Así, $Núc(T)=\{a|a\in\mathbb{R}\}$ que tiene dimensión $1$.

Todo polinomio de grado $2$ se puede obtener derivando un polinomio de grado $3$. Basta con integrar el polinomio de grado $2$ para encontrar la estructura de los polinomios de grado $3$ que cumplen lo deseado. De modo que $W\subseteq Im(T)$ y como $Im(T)\subseteq W$ por definición, entonces $Im(T)=W$ que tiene dimensión $3$

Por lo tanto, el núcleo y la imagen son de dimensión finita y la nulidad de $T$ es $1$ y su rango es $3$

Tarea Moral

  1. Sean $V$ y $W$ esp. vect. y sea $T:V\longrightarrow W$ lineal. Sea $\{ y_1, y_2, …, y_k\}$ un subconjunto l.i. de $Im(T)$.
    Si $S=\{ x_1,x_2,…,x_k \}$ se selecciona de tal forma que $\forall i\in \{ 1,2,…,k\}(T(x_i)=y_i)$, demostrar que $S$ es l.i.
  2. Para la transformación lineal $T:\mathbb{R}^3\longrightarrow \mathbb{R}^2$ con $T(a_1,a_2,a_3)=(a_1 + 2a_2, 2a_3 – a_1)$ encuentra bases para $Nuc(T)$ e $Im(T)$.
  3. Sea $P: \mathcal{M}_{m\times m}(F) \longrightarrow \mathcal{M}_{m\times m}(F)$ definida por $\forall A\in \mathcal{M}_{m\times m}(F) \left( P(A)_{i,j}=\frac{A_{i,j} + A_{i,j}^{t}}{2} \right)$.

Más adelante…

En la siguiente entrada veremos el vínculo que existe entre la dimensión del núcleo, de la imagen y del espacio vectorial (dominio) de una transformación lineal. Esta relación numérica nos permite calcular cualquiera de estas dimensiones si tenemos conocimiento de las otras dos.

Entradas relacionadas

Álgebra Lineal II: Unicidad de la forma canónica de Jordan

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En la entrada anterior enunciamos el teorema de la forma canónica de Jordan y demostramos la existencia de dicha forma bajo ciertas hipótesis. Como corolario, quedó pensar cuál es la versión para matrices. En esta entrada enunciamos la versión para matrices (totalmente equivalente a la de transformaciones lineales) y nos enfocamos en mostrar la unicidad de la forma canónica de Jordan.

Unicidad de la forma canónica de Jordan

El siguiente teorema es totalmente análogo al enunciado en la entrada anterior. Recuerda que $\leq$ es un orden total fijo de $F$ (en $\mathbb{R}$, es el orden usual).

Teorema. Sea $A$ una matriz $M_n(F)$ cuyo polinomio característico $\chi_A(X)$ se divide en $F$. Entonces, existen únicos valores $\lambda_1\leq \ldots \leq \lambda_n$ en $F$ y únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} para los cuales $A$ es similar a la siguiente matriz de bloques de Jordan:

$$\begin{pmatrix} J_{\lambda_1,k_1} & 0 & \cdots & 0 \\ 0 & J_{\lambda_2,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{\lambda_d,k_d}\end{pmatrix}.$$

Usaremos esta versión para demostrar la unicidad, lo cual también implicará la unicidad para la versión de transformaciones lineales.

Mediante la demostración de existencia de la entrada anterior, llegamos a que si el polinomio característico de $A$ es

$$\chi_A(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r},$$

entonces $A$ es similar a una matriz conformada por matrices de bloques de Jordan $J_1,J_2,\ldots,J_r$, en donde cada $J_i$ es de tamaño $m_i$ y de bloques de Jordan de eigenvalor $\lambda_i$.

Si $A$ fuera similar a otra matriz $K$ de bloques de Jordan, podríamos agrupar por eigenvalores de los bloques $\kappa_1< \ldots < \kappa_s$ en matrices de bloques de Jordan tamaños $o_1,\ldots,o_s$, digamos $K_1,\ldots,K_s$. El polinomio característico de $K$ sería entonces

$$\chi_{K}(X)=(X-\kappa_1)^{o_1}(X-\kappa_2)^{o_2}\cdots(X-\kappa_s)^{o_s}.$$

Pero $K$ es similar a $A$, y entonces deben tener el mismo polinomio característico, así que conciden en raíces y multiplicidad. Esto demuestra que $r=s$ y como los $\lambda_i$ y los $\kappa_i$ están ordenados, también demuestra las igualdades $\lambda_i=\kappa_i$ y $m_i=o_i$ para todo $i\in\{1,\ldots,r\}.$

Sólo nos queda argumentar la igualdad entre cada $J_i$ y $K_i$ para $i\in\{1,\ldots,r\}$. Pero ambas una forma canónica de Jordan para la transformación nilpotente que se obtiene de restringir $T_{A-\lambda_i I}$ a $\ker(T_{A-\lambda_i I}^{m_i})$. Por la unicidad que demostramos para la forma canónica de Jordan para transformaciones nilpotentes, concluimos que $J_i=K_i$. Esto termina la demostración de la unicidad de la forma canónica de Jordan.

$\square$

Una receta para encontrar la forma canónica de Jordan

Ya con el teorema demostrado, ¿cómo juntamos todas las ideas para encontrar la forma canónica de Jordan de una matriz $A$ en $M_n(F)$ cuyo polinomio característico se divida en $F$? Podemos proceder como sigue.

  1. Encontramos el polinomio característico $\chi_A(X)$ y su factorización, digamos $$\chi_A(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r}.$$
  2. Nos enfocamos en encontrar las matrices de bloque de Jordan $J_i$ para cada eigenvalor $\lambda_i$. Sabemos que la matriz $J_i$ será de tamaño $m_i$.
  3. Para saber exactamente cuál matriz de bloques de Jordan es $J_i$, pensaremos en que tiene $b_1,b_2,\ldots,b_{m_i}$ bloques de Jordan de eigenvalor $\lambda_i$ de tamaños $1,2, \ldots,m_i$. Consideramos la matriz $A_i=A-\lambda_i I$. Los $b_1,\ldots,b_{m_i}$ son la solución al siguiente sistema de ecuaciones en las variables $x_1,\ldots,x_{m_i}$.
    \begin{align*}
    m_i&= 1\cdot x_1 + 2\cdot x_2 + 3 \cdot x_3 + \ldots + m_i \cdot x_{m_i}\\
    m_i-n+\text{rango}(A_i-\lambda_i I)&=0\cdot x_1 + 1\cdot x_2 + 2 \cdot x_3 + \ldots + (m_i-1) \cdot x_{m_i}\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^2)&= 0 \cdot x_1 + 0 \cdot x_2 + 1 \cdot x_3 + \ldots + (m_i-2)\cdot x_{m_i}\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^3)&= 0 \cdot x_1 + 0 \cdot x_2 + 0 \cdot x_3 + \ldots + (m_i-3)\cdot x_{m_i}\\
    &\vdots\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^{m_i-1})&= 0\cdot x_1 + 0 \cdot x_2 + 0 \cdot x_3 + \ldots + 1 \cdot x_{m_i}.
    \end{align*}
  4. Juntamos todos los $J_i$ en una misma matriz y los ordenamos apropiadamente.

El paso número $3$ está motivado por lo que sabemos de las matrices nilpotentes, y es bueno que pienses por qué se estudia específicamente ese sistema de ecuaciones para cada eigenvalor $\lambda_i$ y multiplicidad $m_i$.

Ejemplo de obtener la forma canónica de Jordan

Veamos un ejemplo del procedimiento descrito en la sección anterior.

Ejemplo. Encontraremos la forma canónica de Jordan de la siguiente matriz: $$A=\begin{pmatrix}-226 & -10 & -246 & 39 & 246\\234 & 23 & 236 & -46 & -236\\-198 & -20 & -192 & 41 & 195\\-93 & 10 & -122 & 10 & 122\\-385 & -30 & -393 & 74 & 396\end{pmatrix}.$$

Con herramientas computacionales, podemos darnos cuenta de que el polinomio característico de esta matriz es $$\chi_A(X)=X^{5} – 11 X^{4} + 46 X^{3} – 90 X^{2} + 81 X- 27.$$

Este polinomio se puede factorizar como $$(X-1)^2(X-3)^3.$$ Así, la submatriz de bloques de Jordan $J_1$ de eigenvalor $1$ tendrá tamaño $2$ y la $J_3$ de eigenvalor $3$ tendrá tamaño $3$. Pero, ¿de qué tamaño son cada uno de los bloques de Jordan en cada una de estas matrices?

Para respondernos esto para $J_1$, notamos que sus bloques son de tamaño $1$ y $2$ solamente. Si hay $b_1$ bloques de tamaño $1$ y $b_2$ bloques de tamaño $2$, por la teoría desarrollada arriba tendremos:

\begin{align*}
b_1+2b_2&=2\\
b_2&=2-5+\text{rango}(A-I)=2-5+4=1.
\end{align*}

El rango de $A-I$ lo obtuvimos computacionalmente, pero recuerda que también puede ser obtenido con reducción gaussiana. Resolviendo el sistema, $b_2=1$ y entonces $b_1=0$. Concluimos que en $J_1$ hay un bloque de Jordan de tamaño $2$.

Para $J_3$, reciclemos las variables $b_i$ (para no introducir nuevas). Los bloques pueden ser de tamaño $1,2,3$. Supongamos que de estos tamaños respectivamente hay $b_1,b_2,b_3$ bloques. Los $b_i$ cumplen:

\begin{align*}
b_1+2b_2+3b_3&=3\\
b_2+2b_3&=3-5+\text{rango}(A-3I)=3-5+3=1\\
b_3&=3-5+\text{rango}((A-3I)^2)=3-5+2=0.
\end{align*}

Así, $b_3=0$, y en consecuencia $b_2=1$ y entonces $b_1=1$. Concluimos que $J_3$ tiene un bloque de tamaño $1$ y uno de tamaño $3$. Por lo tanto, la forma canónica de Jordan de $A$ es:

$$\begin{pmatrix} J_1 & 0 \\ 0 & J_3 \end{pmatrix} = \begin{pmatrix} J_{1,2} & 0 & 0 \\ 0 & J_{3,1} & 0 \\ 0 & 0 & J_{3,2} \end{pmatrix} = \begin{pmatrix}1 & 1 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0\\0 & 0 & 3 & 0 & 0\\0 & 0 & 0 & 3 & 1\\0 & 0 & 0 & 0 & 3\end{pmatrix}$$

$\triangle$

Otro problema sobre forma canónica de Jordan

La receta anterior funciona en general y da la forma canónica de Jordan. Esto es algo que probablemente en la práctica en aplicaciones no tendrás que hacer manualmente nunca, pues hay herramientas computacionales que te pueden ayudar. Sin embargo, es importante entender con profundidad el teorema y la receta de manera teórica, pues hay problemas conceptuales en los que no podrás usar herramientas computacionales. A continuación veremos un ejemplo.

Problema. Sea $A$ una matriz en $M_6(\mathbb{R})$ con polinomio característico $$\chi_A(X)=X^6-2X^4+X^2.$$

  • ¿Cuántas posibilidades hay para la forma canónica de Jordan de $A$?
  • Demuestra que si el rango de $A$ es $5$, entonces $A$ no es diagonalizable.

Solución. Podemos factorizar el polinomio característico de $A$ como sigue:

$$\chi_A(X)=X^2(X+1)^2(X-1)^2.$$

Así, la forma canónica de Jordan está conformada por una matriz de bloques de Jordan $J_0$ de eigenvalor $0$ y tamaño $2$; una $J_1$ de eigenvalor $1$ y tamaño $2$; y una $J_{-1}$ de eigenvalor $-1$ y tamaño $2$.

Cada $J_i$ tiene dos chances: o es un bloque de Jordan de tamaño $2$, o son dos bloques de Jordan de tamaño $1$. Así, en total tenemos $2\cdot 2 \cdot 2=8$ posibilidades.

Si $A$ es de rango $5$, entonces tendríamos en las cuentas de cantidad de bloques $b_1$ y $b_2$ para eigenvalor $0$ que

\begin{align*}
b_1+2b_2&=2\\
b_2&=2-6+\text{rango}(A)=2-6+5=1,
\end{align*}

de donde en $J_0$ tendría $1$ bloque de tamaño $2$ y ninguno de tamaño $1$. Si $A$ fuera diagonalizable, su diagonalización sería una forma canónica de Jordan donde para eigenvalor $0$ se tendrían $2$ bloques de tamaño $1$ y ninguno de tamaño $2$. Así, $A$ tendría dos formas canónicas de Jordan distintas, lo cual es imposible.

$\square$

Más adelante…

Con esta entrada terminamos de demostrar el teorema de la forma canónica de Jordan, uno de los teoremas más bonitos de álgebra lineal. ¿Te das cuenta de todo lo que utilizamos en su demostración? Forma matricial de transformaciones lineales, el teorema de Cayley-Hamilton, polinomio característico, subespacios estables, teoría de dualidad, sistemas de ecuaciones lineales, resultados auxiliares de polinomios, etc. Es un resultado verdaderamente integrador.

En la siguiente entrada, la última del curso, hablaremos de algunas de las consecuencias del teorema de la forma canónica de Jordan. Discutiremos cómo lo podemos utilizar para clasificar a las matrices por similaridad. Veremos una aplicación con respecto a una matriz y su transpuesta. También, esbozaremos un poco de por qué en cierto sentido el resultado no sólo vale para las matrices cuyo polinomio se divide sobre el campo, sino que para cualquier matriz. Con ello terminaremos el curso.

Tarea moral

  1. Calcula la forma canónica de Jordan $J$ de la matriz $$A=\begin{pmatrix} 1 & 0 & -3 \\ 1 & -1 & -6 \\ -1 & 2 & 5 \end{pmatrix}.$$ Además de encontrar $J$, encuentra de manera explícita una matriz invertible $P$ tal que $A=P^{-1}JP$.
  2. Calcula la forma canónica de Jordan de la matriz $$\begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 2 \end{pmatrix}$$
  3. Explica y demuestra cómo obtener lo siguiente para una matriz de bloques de Jordan:
    • Su polinomio característico.
    • Su polinomio mínimo.
    • Su determinante.
    • Su traza.
    • Sus eigenespacios.
  4. Justifica con más detalle por qué la receta que se propone para calcular la forma canónica de Jordan en efecto funciona. Necesitarás varios de los argumentos que dimos en la entrada anterior.
  5. Demuestra que una matriz $A\in M_n(F)$ para la cual su polinomio característico se divide en $F$ es diagonalizable si y sólo si cada bloque de cada matriz de bloques de la forma canónica de Jordan tiene tamaño $1$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

1.3. ESPACIOS VECTORIALES: propiedades

Por Jennyfer Paulina Bennetts Castillo

Deja un comentario

Nota: Para simplificar notación (sobre todo en las demostraciones): $0_K$ será $0$; $\theta_V$ será $\theta$ y dependiendo de los elementos que se operen, serán las operaciones del campo o del espacio vectorial. Y en las justificaciones de pasos, tendremos que un número $m$ seguido $K$, hará referencia a la propiedad $m$ de la definición de campo y análogamente si el número $m$ es seguido por $V$ será la propiedad $m$ de la definición de espacio vectorial.

Recordemos que, por ahora, dado $u$ en un espacio vectorial, tenemos que $\tilde u$ denota a su inverso aditivo.

Proposición (1): Sean $K$ un campo y $V$ un $K$ – espacio vectorial.
1. $0_K \cdot_V u = \theta_V$ $\forall u \in V$
2. $\lambda \cdot_V \theta_V = \theta_V$ $\forall \lambda\in K$

Demostración: Sean $u \in V$, $\lambda\in K$.

1. Tenemos por distributividad en $V$ que $(0+0)u=0u+0u$.
Y además, por ser $0$ el neutro de $K$ y $\theta$ el neutro de $V$, $(0+0)u=0u=\theta+0u$.
Así, $0u+0u=\theta+0u$.
De donde, $\widetilde{0u}+(0u+0u)=(\theta+0u)+\widetilde{0u}$

$\begin{align*}
\Rightarrow &(\widetilde{0u}+0u)+0u=\theta+(0u+\widetilde{0u})\tag{asociat. $+_V$}\\
\Rightarrow &\theta+0u=\theta+\theta\tag{inv. ad. $V$}\\
\Rightarrow &0u=\theta\tag{neu. ad. $V$}\\
\end{align*}$

2. Tenemos por distributividad en $V$ que $\lambda(\theta+\theta)= \lambda\theta+\lambda\theta$.
Y además, por ser $\theta$ el neutro de $V$, $\lambda(\theta+\theta)=\lambda\theta$.
Así, $\lambda\theta+\lambda\theta=\lambda\theta$.
De donde, $\widetilde{\lambda\theta}+(\lambda\theta+\lambda\theta)=\lambda\theta\widetilde{\lambda\theta}$

$\begin{align*}
\Rightarrow &(\widetilde{\lambda\theta}+\lambda\theta)+\lambda\theta=\lambda\theta_V+\widetilde{\lambda\theta}\tag{asociat. $+_V$}\\
\Rightarrow &\theta+\lambda\theta=\theta\tag{inv. ad. $V$}\\
\Rightarrow &\lambda\theta=\theta\tag{neu. ad. $V$}\\
\end{align*}$

Proposición (2): Sean $K$ un campo y $V$ un $K$ – espacio vectorial.
Para todo $u \in V$, $(-1_K)\cdot_V u$ es el inverso aditivo de $u$.

Demostración: Sea $u\in V$.
Veamos que $u+(-1_K)u=\theta$

$\begin{align*}
u+(-1_K)u&=1_Ku+(-1_K)u\tag{propiedad 5. campo}\\
&=(1_K+(-1_K))u\tag{distrib. 7.1 $V$}\\
&=0u\tag{inv. ad. $K$}\\
&=\theta\tag{Prop. (1)}\\
\therefore u+(-1_K)u=\theta
\end{align*}$

Nota: Dada $u \in V$ denotaremos por $-u$ a su inverso aditivo.

Obs.* Existen resultados análogos para las dos proposiciones anteriores pero en el caso de los campos, y sus pruebas son también análogas.

Corolario: Sean $K$ un campo y $V$ un $K$ – espacio vectorial.
$(-\lambda)u=-(\lambda u)=\lambda(-u)$ $\forall \lambda \in K$ , $\forall u \in V$

Demostración: Sean $\lambda\in K, u\in V$.
Por un lado,
\begin{align*}
\lambda(-u)&=\lambda((-1_K)u)\tag{Prop. (2)}\\
&=(\lambda(-1_K))u\tag{propiedad 6. campo}\\
&=(-\lambda)u\tag{Obs.*}\\
\therefore\lambda(-u)=(-\lambda)u
\end{align*}
Por otro lado,
\begin{align*}
(-\lambda)u&=((-1_K)\lambda)u\tag{Obs.*}\\
&=(-1_K)(\lambda u)\tag{propiedad 6. campo}\\
&=-(\lambda u)\tag{Prop. (2)}\\
\therefore (-\lambda)u=-(\lambda u)
\end{align*}

Proposición (3): Sea $K$ un campo y $V$ un $K$ – espacio vectorial.
Si $\lambda\cdot_V u = \theta_V$, entonces se cumple al menos uno de los siguientes casos:
1. $\lambda = 0_K$
2. $u = \theta_V$

Demostración: Sup. que $\lambda u=\theta$.
Tenemos dos posibilidades:
i) $\lambda=0$
ii) $\lambda\not=0$

Si se cumple i), entonces ya tenemos el caso 1.

Sup. que se cumple ii). Veamos que $u=\theta$.
Como nuestra hipótesis es que $\lambda\not=0$ y $\lambda\in K$, con $K$ un campo, entonces $\exists(\lambda^{-1})\in K$ inverso multiplicativo de $\lambda$. Así,

$\begin{align*}
\lambda u=\theta\Rightarrow &(\lambda^{-1})(\lambda u)=(\lambda^{-1})\theta\\
\Rightarrow &((\lambda^{-1})\lambda)u=(\lambda^{-1})\theta\tag{propiedad 6. esp. vect.}\\
\Rightarrow &((\lambda^{-1})\lambda)u=\theta\tag{Prop. (1)}\\
\Rightarrow &1_Ku=\theta\tag{inv. mult. $K$}\\
\Rightarrow &u=\theta\tag{propiedad 5. campo}\\
\end{align*}$

Nota: En adelante, $K$ denotará un campo.

TAREA MORAL

Sea $K$ un campo. Sea $V$ un $K$ – espacio vectorial. Demuestra que para cualesquiera $u,v,w \in V$ se cumplen las siguientes propiedades de cancelación:

  1. Si $u+v=w+v$, entonces $u=w$.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Primero sup. que $u+v=w+v$ y justifiquemos por qué tiene que suceder que $u=w$.
    • Podemos sumar a la derecha de cada lado de la igualdad el inverso de $v$.
    • Una vez hecho eso, utiliza la asociatividad de la suma en $V$, luego la definición del inverso de $v$ y por último la definición del neutro aditivo en $V$.
  1. Si $v+u=v+w$, entonces $u=w$.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Primero sup. que $u+v=w+v$ y justifiquemos por qué tiene que suceder que $u=w$.
    • Piensa en qué propiedad de la $+$ en $V$ te permite tener una ecuación de la forma que se presenta en el $1$. Una vez teniendo esa forma, por lo que ya probaste, obtienes lo que se necesitaba.
      • Observa que haciendo un proceso totalmente análogo a este inciso, se obtiene que también se cumple la cancelación si es de la forma $u+v=v+w$, o bien, de la forma $v+u=w+v$.

MÁS ADELANTE…

Ahora vamos a usar el concepto de espacio vectorial para obtener otro concepto: subespacio.

Entradas relacionadas

1.2. ESPACIOS VECTORIALES: definición y ejemplos

Por Jennyfer Paulina Bennetts Castillo

2 respuestas

INTRODUCCIÓN

A partir del interés de establecer métodos para resolver ecuaciones de tercer grado por medio de radicales, los matemáticos se encuentran con las raíces negativas e imaginarias. El concepto de número imaginario logra superponerse al paradigma y encuentra su lugar a través de su representación geométrica.

El físico William Rowan Hamilton se interesó por establecer propiedades de las operaciones entre números complejos y sostuvo que el álgebra tenía una relación muy estrecha con la física. Motivado con esta idea, establece conjuntos de números dotados de una estructura algebraica con una representación espacial muy útil para los trabajos en física. Sus propiedades resultan similares a las que actualmente se tienen para el producto escalar y vectorial.

Los cuaterniones de Hamilton son números de la forma: $P=a+bi+cj+dk$.
Donde $a,b,c,d\in\mathbb{R}$ y $k=ij=-ji$ es una unidad imaginaria.

En el álgebra lineal el concepto de «vector» adquiere su significado más general.

ESPACIO VECTORIAL

Definición: Sean $V$ un conjunto y sea $K$ un campo (con las operaciones $+_K$ y $\cdot_K$). Sean $+_V: V \times V \longrightarrow V$ y $\cdot_V: K \times V \longrightarrow V$ operaciones. Decimos que $V,+_V,\cdot_V$ es un espacio vectorial sobre el campo $K$, o bien un $K$ – espacio vectorial (y a los elementos de $K$ les llamamos vectores), si $+_V$ y $\cdot_V$ cumplen lo siguiente:

  1. $+_V$ es asociativa
    $\forall u,v,w \in V:$
    $(\,u+_V(v+_V w)=(u+_V v)+_V w\,)$
  2. $+_V$ es conmutativa
    $\forall u,v \in V:$
    $(\,u+_V v=v+_V u\,)$
  3. Existe neutro aditivo
    $\exists \theta_V \in V:$
    $\forall u \in V (\,\theta_V +_V u = u +_V \theta_V = u\,)$
  4. Todo elemento $u \in V$ tiene inverso aditivo
    $\forall u \in V:$
    $\exists \tilde {u} \in V (\,u+_V \tilde {u} = \tilde {u} +_V u = \theta_V\,)$
  1. $\forall u \in V:$
    $1_K \cdot_V u = u$
  2. $\forall \lambda,\mu \in K \forall u \in V:$
    $\lambda\cdot_K(\mu\cdot_K u)=(\lambda\cdot_K\mu)\cdot_V u$
  3. $\cdot_V$ es distributiva
    7.1 $\forall \lambda,\mu \in K \forall u \in V:$
    $(\lambda+_K\mu)\cdot_V u = (\lambda\cdot_V u)+(\mu\cdot_V u)$
    7.2 $\forall \lambda \in K \forall u,v \in K:$
    $\lambda\cdot_V(u+v)=\lambda\cdot_V u+\lambda\cdot_V v$

Nota: Es común encontrar la expresión «$V$ es un $K$ – espacio vectorial con las operaciones $+, \cdot$» en lugar de «$V,+,\cdot$ es un $K$ – espacio vectorial», al igual que «$V$ es un $K$ – espacio vectorial» sin la referencia a las operaciones cuando se trata de las usuales (se suponen por obviedad).

Nota: Para evitar confusiones, en caso de ser necesario, denotaremos por $u+_V v$ a la suma de los vectores $u$ y $v$, y por $\lambda\cdot_V v$ al producto del escalar $\lambda$ por el vector $v$, pero una vez que nos habituemos a ellas las denotaremos simplemente por $u+v$ y $\lambda v$.

Ejemplos:

  • $\mathbb{R}^n$ es un $\mathbb{R}$ – espacio vectorial con la suma y el producto por escalar usuales.
  • $<(1,1,1)> = \{\lambda(1,1,1):\lambda \in \mathbb{R} \}$ es un $\mathbb{R}^n$ – espacio vectorial.
  • Sea $K$ campo. $\mathcal{M}_{m\times n}(K)$ (las matrices con $m$ renglones y $n$ columnas, con entradas en $K$) es un $K$ – espacio vectorial con las operaciones usuales de suma y producto por escalar.
  • Sea $K$ campo. $K[x]$ (los polinomios en $x$ con coeficientes en $K$) es un $K$ – espacio vectorial con la suma y el producto por escalar usuales.
  • Sea $K$ campo. $K^{n} = \{(x_{1}, x_{2},…,x_{n}) : x_{1},x_{2},…,x_{n} \in K \}$ es un $K$ – espacio vectorial con la suma entrada a entrada y el producto definido como sigue:
    Sean $(x_{1},x_{2},…,x_{n}) \in K^{n}$, $\lambda \in K$. $\lambda \cdot (x_{1},x_{2},…,x_{n})=(\lambda x_{1}, \lambda x_{2},…,\lambda x_{n})$
  • Sea $K$ campo. $K^{\infty} = \{(x_{1}, x_{2},…) : x_{1},x_{2},… \in K \}$ es un $K$ – espacio vectorial con la suma entrada a entrada y el producto definido como sigue:
    Sean $(x_{1},x_{2},…) \in K^{n}$, $\lambda \in K$. $\lambda \cdot (x_{1},x_{2},…)=(\lambda x_{1}, \lambda x_{2},…)$

EJEMPLO FUNCIONES

Sea $K$ campo. $V=\{f|f:K \longrightarrow K\}$ es un $K$ – espacio vectorial con las operaciones $+_V$ y $\cdot_V$ definidas como sigue:

Sean $f,g \in V$, $\lambda \in K$.
$f +_V g : K \longrightarrow K$
$(f +_V g )(x) = f(x) +_K g(x)$ para todo $x\in K$ donde $+_K$ es la suma en $K$.

Sean $f \in V$, $\lambda \in K$.
$\lambda \cdot_V f : K \longrightarrow K$
$(\lambda \cdot_V f )(x) =\lambda \cdot_K f(x)$ para todo $x\in K$
donde $\cdot_K$ es el producto en $K$.

DEMOSTRACIÓN

Vamos a ver que las operaciones $+_V$, $\cdot_V$ cumplen las ocho condiciones suficientes y necesarias (por definición) para que $V$ sea espacio vectorial:

Sean $f,g,h \in V$, $\lambda, \mu \in K$.
Sea $x \in K$ arbitrario.

  1. P.D. $+_V$ es asociativa
    $i. e.$ $(f +_V g) +_V h = f +_V (g +_V h)$

Obs. 1 Tenemos que $f +_V g, g +_V h \in V$. Así, $(f +_V g) +_V h, f +_V (g +_V h) \in V$. Así que sólo falta ver que $(f +_V g) +_V h$ y $f +_V (g +_V h)$ tienen la misma regla de correspondencia.

$\begin{align*}
((f +_V g) +_V h)(x) &= (f +_V g)(x) +_K h(x)\tag{def. $+_V$}\\
&= (f(x) +_K g(x)) +_K h(x)\tag{def. $+_V$}\\
&= f(x) +_K (g(x) +_K h(x))\tag{asociat. $+_K$}\\
&= f(x) +_K (g +_V h)(x)\tag{def. $+_V$}\\
&= (f +_V (g +_V h))(x)\tag{def. $+_V$}\\
\therefore (f +_V g) +_V h &= f +_V (g +_V h)
\end{align*}$

  1. P.D. $+_V$ es conmutativa
    $i.e.$ $f +_V g = g +_V f$

Obs. 2 Tenemos que $f +_V g, g +_V f \in V$. Así que sólo falta ver que $f +_V g$ y $g +_V f$ tienen la misma regla de correspondencia.

$\begin{align*}
(f +_V g)(x) &= f(x) +_K g(x)\tag{def. $+_V$}\\
&= g(x) +_K f(x)\tag{conmutat. $+_K$}\\
&= (g +_V f)(x)\tag{def. $+_V$}\\
\therefore f +_V g &= g +_V f
\end{align*}$

  1. P.D. Existe neutro aditivo
    $i.e.$ $\exists \theta_V \in V:$
    $\theta_V +_V f = f +_V \theta_V = f$

Proponemos:
$\theta_V : K \longrightarrow K$ con
$\theta_V(x) = 0_K$ para todo $x\in K$
donde $0_K$ es neutro aditivo de $K$.

Obs. 3 Por construcción $\theta_V \in V$. Así, $f +_V \theta_V, \theta_V +_V f \in V$. Además, por $2$, se cumple que $\forall f \in V (\theta_V +_V f = f +_V \theta_V)$. Entonces sólo falta ver que $f +_V \theta_V$ y $f$ tienen la misma regla de correspondencia.

$\begin{align*}
(f +_V \theta_V)(x) &= f(x) +_K \theta_V(x)\tag{def. $+_V$}\\
&= f(x) +_K 0_K\tag{def. $\theta_V$}\\
&= f(x)\tag{neutro ad.}\\
\therefore \theta_V +_V f = f +_V \theta_V
\end{align*}$

  1. P.D. Todo elemento $f \in V$ tiene inverso aditivo
    $i.e.$ $\exists \tilde{f} \in V:$
    $f+ \tilde{f} = \tilde{f} + f = \theta_V$

Proponemos:
$\tilde{f} : K \longrightarrow K$ con
$\tilde{f}(x)=(-f(x))$ para todo $x\in K$
donde $(-f(x))$ es el inverso aditivo de $f(x) \in K$.

Obs. 4 Por construcción $\tilde{f} \in V$. Así, $f +_V \tilde{f}, \tilde{f} +_V f \in V$. Además, por $2$, se cumple que $\forall f \in V (f +_V \tilde{f} = \tilde{f} +_V f \in V)$. Entonces sólo falta ver que $f +_V \tilde{f}$ y $\theta_V$ tienen la misma regla de correspondencia.

$\begin{align*}
(f +_V \tilde{f})(x) &= f(x) +_K \tilde{f}(x)\tag{def. $+_V$}\\
&= f(x) +_K (-f(x)) \tag{def. $\tilde{f}$}\\
&= 0_K\tag{inv. ad.}\\
&= \theta_V (x)\tag{def. $\theta_V$}\\
\therefore f +_V \tilde{f} = \tilde{f} +_V f = \theta_V
\end{align*}$

  1. P.D. $1_K \cdot_V f = f$

Sea $1_K$ el neutro multiplicativo en $K$.

Obs. 5 Por construcción $1_K \in K$. Así, $1_K \cdot_V f \in V$. Así que sólo falta ver que $1_K \cdot_V f$ y $f$ tienen la misma regla de correspondencia.

$\begin{align*}
(1_K \cdot_V f)(x) &= 1_K \cdot_K f(x)\tag{def. $\cdot_V$}\\
&= f(x)\tag{neut. mult.}\\
\therefore 1_V \cdot_V f = f
\end{align*}$

  1. P.D. $\lambda\cdot_V(\mu\cdot_V f)=(\lambda\cdot_K\mu)\cdot_V f$

Obs. 6 Por construcción $\mu\cdot_V f \in V$. Así, $\lambda\cdot_V(\mu\cdot_V f) \in V$. También tenemos que $\lambda\cdot_K\mu\in K,$ por lo cual $(\lambda\cdot_K\mu)\cdot_V f\in V$ Entonces sólo falta ver que $\lambda\cdot_V(\mu\cdot_V f)$ y $(\lambda\cdot_K\mu)\cdot_V f$ tienen la misma regla de correspondencia.

$\begin{align*}
(\lambda\cdot_V(\mu\cdot_V f))(x) &= \lambda \cdot_K (\mu\cdot_V f)(x)\tag{def. $\cdot_V$}\\
&= \lambda\cdot_K(\mu\cdot_K f(x))\tag{def. $\cdot_V$}\\
&= (\lambda\cdot_K\mu)\cdot_K f(x)\tag{asociat. $\cdot_K$}\\
&= ((\lambda\cdot_K\mu)\cdot_V f)(x)\tag{def. $\cdot_V$}\\
\therefore \lambda\cdot_V(\mu\cdot_V f)=(\lambda\cdot_K\mu)\cdot_V f
\end{align*}$

  1. P.D. Se cumple la distributividad (7.1)
    $i.e.$ $(\lambda +_K \mu)\cdot_V f=(\lambda\cdot_V f) +_V (\mu\cdot_V f)$

Obs. 7 Tenemos que $\lambda,\mu,\lambda +_K \mu \in K$. Así, $(\lambda +_K \mu)\cdot_V f, (\lambda\cdot_V f) +_V (\mu\cdot_V f) \in V$. Así que solo falta ver que $(\lambda +_K \mu)\cdot_V f$ y $(\lambda\cdot_V f) +_V (\mu\cdot_V f)$ tienen la misma regla de correspondencia.

$\begin{align*}
((\lambda +_K \mu)\cdot_V f)(x) &= (\lambda +_K \mu)\cdot_K f(x)\tag{def. $+_V$}\\
&= (\lambda\cdot_K f(x)) +_K (\mu\cdot_K f(x))\tag{distrib.}\\
&= ((\lambda\cdot_V f)(x)) +_K ((\mu\cdot_V f)(x))\tag{def. $\cdot_V$}\\
&= ((\lambda\cdot_V f) +_V (\mu\cdot_V f))(x))\tag{def. $\cdot_V$}\\
\therefore (\lambda +_K \mu)\cdot_V f=(\lambda\cdot_V f) +_V (\mu\cdot_V f)
\end{align*}$

  1. P.D. Se cumple la distributividad (7.2)
    $i.e.$ $\lambda \cdot_V (f +_V g)= (\lambda \cdot_V f) +_V(\lambda \cdot_V g)$

Obs. 8 Tenemos que $\lambda \cdot_V (f +_V g), \lambda \cdot_V f, \lambda \cdot_V g \in V$. Así, $(\lambda \cdot_V f) +_V(\lambda \cdot_V g) \in V$. Entonces sólo falta ver que $\lambda \cdot_V (f +_V g)$ y $(\lambda \cdot_V f) +_V(\lambda \cdot_V g)$ tienen la misma regla de correspondencia.

$\begin{align*}
(\lambda \cdot_V (f +_V g))(x) &= \lambda \cdot_K (f +_V g)(x)\tag{def. $\cdot_V$}\\
&= \lambda \cdot_K (f(x) +_K g(x))\tag{def. $+_V$}\\
&= (\lambda \cdot_K f(x)) +_K (\lambda \cdot_K g(x))\tag{distrib.}\\
&= ((\lambda \cdot_V f)(x)) +_K ((\lambda \cdot_V g)(x))\tag{def. $\cdot_V$}\\
&= ((\lambda \cdot_V f) +_V (\lambda \cdot_V g))(x)\tag{def. $+_V$}\\
\therefore \lambda \cdot_V (f +_V g)= (\lambda \cdot_V f) +_V(\lambda \cdot_V g)
\end{align*}$

Por lo tanto $V=\{f|f:K \longrightarrow K\}$ es un $K$ – espacio vectorial con las operaciones $+_V$ y $\cdot_V$ trabajadas.

TAREA MORAL

  1. Encuentra un $K$ campo dentro de los ejemplos de la entrada anterior con el cual $\mathcal{M}_{m\times n}(K)$ sea un $K$ – espacio vectorial con una cantidad finita de elementos. Si $K$ no es concreto, exhibe un caso particular de ese campo y una vez que lo hagas, muestra todos los elementos del espacio vectorial obtenido.
  1. Demuestra que el neutro aditivo de $V$, un $K$ – espacio vectorial, es único.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Sabemos por la definición de espacio vectorial, que existe $\theta_V$ neutro.
    • Primero sup. que existe ${\theta_V}’ \in V$ que también lo es. Con el objetivo de demostrar que $\theta_V = {\theta_V}’$.
    • Ahora justifica cada una de las siguientes igualdades:
      $\theta_V = \theta_V +_V {\theta_V}’ = {\theta_V}’$
  1. Demuestra que los inversos aditivos en $V$ son únicos.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Sea $u \in V$. Sabemos por la definición de campo, que existe $\tilde{u} \in V$ inverso aditivo de $u$.
    • Primero sup. que existe $\tilde{u}’ \in V$ que también lo es. Con el objetivo de demostrar que $\tilde{u} = \tilde{u}’$.
    • Ahora justifica cada una de las siguientes igualdades:
      $\tilde{u} = \tilde{u} +_V \theta_V = \tilde{u} + (u + \tilde{u}’) = (\tilde{u} + u) + \tilde{u}’$
    • Completa la demostración con las igualdades necesarias y justifícalas.

MÁS ADELANTE…

Ahora analizaremos algunas propiedades de los espacios vectoriales, una de ellas nos dice quién es el elemento neutro dado el espacio vectorial. Además de dos identidades del elemento neutro.

Entradas relacionadas

1.1. CAMPO Y SUBCAMPO: definiciones y ejemplos

Por Jennyfer Paulina Bennetts Castillo

2 respuestas

INTRODUCCIÓN

El ser humano ha hecho un fascinante trabajo construyendo modelos para facilitar la resolución de problemas concretos. Muchos de estos problemas tienen un carácter lineal, es decir, pueden plantearse mediante ecuaciones lineales con coeficientes en algún «conjunto especial» de números y con unas cuantas variables.

El Papiro Rhind considera ecuaciones de primer grado y es el documento matemático más antiguo hallado.

Así es, nos facilitamos la vida reduciendo casi todo a «talachita»: operaciones. Y como buena rama de las matemáticas, esto de «operar» vamos a abstraerlo. Ya no sólo se tratará de números, si no de conjuntos (de «lo que sea») y operaciones («las que sean») que cumplan ciertas condiciones.

CAMPO

Definición: Sea $K$ un conjunto con dos operaciones binarias $+: K \times K \longrightarrow K$ y $\cdot: K \times K \longrightarrow K$. Decimos que $K$ es un campo (y a sus elementos los llamamos escalares) si se cumplen las siguientes propiedades:

  • $+$ es asociativa
    $\forall \alpha ,\beta ,\gamma \in K:$
    $\alpha+(\beta+\gamma)=(\alpha+\beta)+\gamma$
  • $+$ es conmutativa
    $\forall \alpha,\beta \in K:$
    $\alpha+\beta=\beta+\alpha$
  • Existe un neutro aditivo
    $\exists 0_K \in K:$
    $\forall \alpha \in K (0_K + \alpha = \alpha + 0_K = \alpha)$
  • Todo elemento $\alpha \in K$ tiene un inverso aditivo
    $\forall \alpha \in K:$
    $\exists (-\alpha) \in K (\alpha+ (-\alpha) = (-\alpha)+\alpha = 0_K)$
  • $\cdot$ distribuye a $+$
    $\forall \alpha,\beta,\gamma \in K:$
    $\alpha\cdot(\beta + \gamma)=\alpha\cdot\beta + \alpha\cdot\gamma$
  • $\cdot$ es asociativa
    $\forall \alpha,\beta,\gamma \in K:$
    $\alpha\cdot(\beta\cdot\gamma)=(\alpha\cdot\beta)\cdot\gamma$
  • $\cdot$ es conmutativa
    $\forall \alpha,\beta \in K:$
    $\alpha\cdot\beta=\beta\cdot\alpha$
  • Existe un neutro multiplicativo
    $\exists 1_K \not= 0_K \in K:$
    $\forall \alpha \in K (1_K \cdot \alpha = \alpha \cdot 1_K = \alpha)$
  • Todo elemento $\alpha \not= 0_K \in K$ tiene un inverso multiplicativo
    $\forall \alpha \not= 0_K \in K:$
    $\exists \alpha^{-1} \in K (\alpha \cdot \alpha^{-1} = \alpha^{-1} \cdot \alpha = 1_K)$

Nota: En un campo vectorial: los neutros (aditivo y multiplicativo) y los inversos (aditivos y multiplicativos) son únicos. Por ello, desde la definición se han denotado de esa manera. Como parte de la tarea moral al final de esta entrada encontrarás ideas para realizar las demostraciones de estas unicidades.

Nota: Para simplificar notación, el producto $\alpha\cdot\beta$ se suele denotar como $\alpha\beta$.

Nota: Si es necesario aclarar que las operaciones con las que se está trabajando están definidas en el campo $K$, se suelen denotar como $+_K$ y $\cdot_K$.

Ejemplos:

  • $\mathbb{R} , \mathbb{Q} , \mathbb{C}$
    con la suma y producto usual respectivamente
  • $\{y+y\sqrt{2} : x,y \in \mathbb{Q}\}$
    con la suma y el producto usual
  • $\mathbb{Z}_p = \{\overline {0},\overline {1},…,\overline {p-1}\}$
    donde $p$ es primo y $\forall \overline {x}, \overline {y} \in \mathbb{Z}_p$ las operaciones son
    $\overline {x} + \overline {y} = \overline {x+y}$
    $\overline {x} \cdot \overline{y} = \overline {x \cdot y}$
    con $x+y$ la suma usual en $\mathbb{Z}$, $x \cdot y$ el producto usual en $\mathbb{Z}$

¿Cómo funciona $\mathbb{Z}_n$ con $n \in \mathbb{N}$?

$\mathbb{Z}_n$ con $n\in\mathbb{N}^+$ es el conjunto llamado enteros módulo $n$ cuyos $n$ elementos son de la forma $\overline {k}$ $= \{a \in \mathbb{Z} | a \equiv k (mód\, n) \} = \{a \in \mathbb{Z} | a – k = mn, m \in \mathbb{Z} \}$. Es decir, la clase de $k$, con $k \in \mathbb{Z}$ es el conjunto de los números enteros $a$ tales que $a-k$ es múltiplo de $n$.

Obs *. $\overline {k} = \overline {l}$ para toda $l \equiv k$ $(mód\, n)$ pues los elementos de $\overline {k}$ son aquellos congruentes entre sí, módulo $n$.

Ejemplo concreto: $\mathbb{Z}_3$

Tenemos que $\mathbb{Z}_3 = \{ \overline {0}, \overline {1}, \overline {2} \} = \{ \{…, -9, -6, -3, 0, 3, 6, 9, … \}, $$\{…, -8, -5, -2, 1, 4, 7, 10, …\}, $$\{…, -7, -4, -1, 2, 5, 8, 11, … \} \}$

Comprobemos que $\mathbb{Z}_3$ es un campo con las operaciones definidas anteriormente.

Tabla de Cayley de $\mathbb{Z}_3$:

$+$$\overline {0}$$\overline {1}$$\overline {2}$
$\overline {0}$$\overline {0+0} = \overline {0}$$\overline {0+1} = \overline {1}$$\overline {0+2} = \overline {2}$
$\overline {1}$$\overline {1+0} = \overline {1}$$\overline {1+1} = \overline {2}$ $\overline {1+2} = \overline {3} = \overline {0}$
$\overline {2}$$\overline {2+0} = \overline {2}$$\overline {2+1} = \overline {3} = \overline {0}$$\overline {2+2} = \overline {4} = \overline {1}$
$\cdot$$\overline {0}$$\overline {1}$$\overline {2}$
$\overline {0}$$\overline {0 \cdot 0} = \overline {0}$$\overline {0 \cdot 1} = \overline {0}$$\overline {0 \cdot 2} = \overline {0}$
$\overline {1}$$\overline {1 \cdot 0} = \overline {0}$$\overline {1 \cdot 1} = \overline {1}$ $\overline {1 \cdot 2} = \overline {2} = \overline {2}$
$\overline {2}$$\overline {2 \cdot 0} = \overline {0}$$\overline {2 \cdot 1} = \overline {2}$$\overline {2 \cdot 2} = \overline {4} = \overline {1}$

Así, es fácil ver que:

  • $+$ y $\cdot$ son asociativas y conmutativas.
  • El único neutro aditivo es $\overline {0}$.
  • El único neutro multiplicativo es $\overline {1}$.
  • Dado $\overline {k} \in \mathbb{Z}_3$ su único inverso aditivo es $\overline {-k}$.
  • Dado $\overline {k} \not= \overline {0} \in \mathbb{Z}_3$ su único inverso multiplicativo es $\overline {k}$

Existencia y exhibición de inversos multiplicativos en $\mathbb{Z}_p$

Ahora veamos un resultado que será muy útil para entender por qué $\mathbb{Z}_n$ con $n \in \mathbb{N}^+$ es un campo si y sólo si $n$ es un primo y para saber cómo obtener el inverso multiplicativo de un elemento dado.

Sea $K=\mathbb{Z}_n$.
Sea $\overline{k}\not= 0_K\in K$. Con el fin de simplificar la demostración, tomaremos $k\in\{0,1,…,n-1\}$ recordando que, de este modo, estamos considerando cualquier posible elemento de $\mathbb{Z}_n$.
$\overline{k}$ tiene inverso $\overline{j}\in K$ si y sólo si

$\begin{align*}
&\overline{k}\cdot\overline{j}=\overline{1}\\
\Leftrightarrow &\overline{k\cdot j}=\overline{1}\tag{def. $\cdot_K$}\\
\Leftrightarrow &k\cdot j\,\equiv 1 (mód\, n)\tag{Obs *}\\
\Leftrightarrow &k\cdot j \,-\, 1 = qn, q \in \mathbb{Z}\tag{def. $a \equiv b (mód\, n)$}\\
\Leftrightarrow &k \cdot j + (-q) \cdot n = 1, (-q) \in \mathbb{Z}\\
\Leftrightarrow &(k,n)\text{ divide a } 1\tag{Prop.del máximo común divisor}\\
\therefore (k,n) = 1
\end{align*}$

Para que $K = \mathbb{Z}_n$ sea un campo, necesitamos que cada $\overline {k} \not= 0_K \in K$ tenga inverso multiplicativo. Por lo tanto se debe cumplir que $(k,n) = 1$ para toda $k \in \{ 0, 1, …, n-1 \}$. Notamos que si $n$ no fuera primo, entonces $n = ab$ con $2 \le a,b \le n-1$. De modo que existe $a \in \{ 1, …, n-1 \}$ tal que $(a,n) = a \not= 1$ y entonces en este caso $K = \mathbb{Z}_n$ no es un campo. A la inversa, si $K = \mathbb{Z}_p$ con $p$ un primo, entonces para cada $a \in \{1, …, n-1 \}$ tenemos que $(a,p)=1$, y por lo anterior $\overline {a}$ tiene un inverso multiplicativo. Así, $K = \mathbb{Z}_p$ es un campo.

Además, dado $\overline {k} \not= \overline {0} \in \mathbb{Z}_p$ con $p$ primo, sabemos, por ser $\mathbb{Z}_p$ un campo, que existe su inverso multiplicativo $\overline {j} \in \mathbb{Z}_p$ y se cumple que $(k,n) = 1$. Para encontrar el inverso multiplicativo de $\overline {k}$ bastaría encontrar $l,m \in \mathbb{Z}$ tales que $k \cdot l + m \cdot n = 1$, para lo cual podemos usar el algorimo de Euclides, y así obtendremos que si tomamos $j=l$, entonces $\overline {j}$ es el elemento que queríamos.

SUBCAMPO

Definición: Sean $K$ un campo y $\tilde {K} \subseteq K$. Decimos que $\tilde {K}$ es un subcampo de $K$ si $\tilde {K}$ con las operaciones restringidas de $K$ es por sí mismo un campo.

Ejemplos:

  • $\mathbb{Q}$ es un subcampo de $\mathbb{R}$
  • $\mathbb{R}$ es un subcampo de $\mathbb{C}$

Propiedad

  • Si $K$ es un campo, entonces cualquiera de sus elementos $\alpha$ cumple que
    $\alpha \cdot 0_K = 0_K$.

Demostración: Sea $\alpha \in K$.
Sea $(-\alpha) \in K$ su inverso aditivo.
Como $0_K$ es el neutro aditivo, $0_K + 0_K = 0_K$.
De donde,

$\begin{align*}
&\alpha \cdot (0_K + 0_K) = \alpha \cdot 0_K\\
\Rightarrow &\alpha \cdot 0_K + \alpha \cdot 0_K = \alpha \cdot 0_K\tag{distrib.}\\
\Rightarrow &(\alpha \cdot 0_K + \alpha \cdot 0_K) + (-(\alpha \cdot 0_K)) = \alpha \cdot 0_K + (-(\alpha \cdot 0_K))\tag{inv. ad.}\\
\Rightarrow &\alpha \cdot 0_K + (\alpha \cdot 0_K +( -(\alpha \cdot 0_K))) = \alpha \cdot 0_K + (-(\alpha \cdot 0_K))\tag{asociat.}\\
\Rightarrow &\alpha \cdot 0_K + 0_K = 0_K\tag{inv. ad.}\\
\Rightarrow &\alpha \cdot 0_K = 0_K\tag{neutro ad.}\\
\end{align*}$

Nota: Es por esta afirmación que se definen los inversos multiplicativos para los elementos distintos de $0_K$.

Característica de un campo

Definición: Sea $K$ un campo. Se le llama característica de $K$, y se denota como $car(K)$ al menor número natural $n$ tal que $\underbrace{1_K + … + 1_K}_{n} = 0_K$ si acaso existe.
En caso contrario, decimos que $car(K)$ es cero.

Obs. La característica de un campo no puede ser 1 (es decir, si no es cero, entonces es mayor o igual a 2) pues por definición $1_K \not= 0_K$. Y más que eso, resulta que si no es cero, entonces es un número primo.

Ejemplos:

  • $car(\mathbb{Z}_p) = p$
    donde $p$ es primo.

Justificación:
Sea $K = \mathbb{Z}_p = \{\overline {0},\overline {1},…,\overline {p-1}\}$ con cada uno de esos elementos distintos entre sí.
De modo que $p$ es el mínimo natural tal que $\underbrace{1_K + … + 1_K}_{p} = \underbrace{\overline{1} + … + \overline{1}}_{p}$
$= \overline {\underbrace{1 + … + 1}_{p}} = \overline{p} = \overline{0}$

  • $car(\mathbb{Q}) = car(\mathbb{R}) = car(\mathbb{C}) = 0$

Justificación:
Sea $K\in \{\mathbb{Q}, \mathbb{R},\mathbb{C} \}$.
$\underbrace{1_K + … + 1_K}_{n} = n \cdot (1_K) = n \not= 0_K$ $\forall n \in \mathbb{N}, n \not=0$

Propiedades

  • Si $K$ es un campo tal que $car(K) = 0$, entonces $K$ no tiene cardinalidad finita.

Demostración: Como $car(K) = 0$, entonces $\underbrace{1_K + … + 1_K}_{n} \not= 0_K \in K$ para cualquier $n \in \mathbb{N}$.
Así, $\{ 1_K, 1_K + 1_K, …, \underbrace{1_K + … + 1_K}_{n}, … \} \subseteq K$ y no es difícil concluir que cada uno de los elementos de este subconjunto son distintos, de modo que tiene cardinalidad no finita.

  • Si $K$ es un campo tal que $car(K) = 2$, entonces $\alpha + \alpha = 0_K$ para cualquier $\alpha \in K$.

Demostración: Por ser $1_K \in K$ el neutro aditivo de $K$ y por las propiedades de campo obtenemos que
$\alpha + \alpha = 1_K \cdot (\alpha + \alpha) = 1_K \cdot \alpha + 1_K \cdot \alpha =$$\alpha \cdot 1_K + \alpha \cdot 1_K = \alpha \cdot (1_K + 1_K)$
Como $car(K) = 2$, entonces $1_K + 1_K = 0_K$, por lo cual $\alpha \cdot (1_K + 1_K) = \alpha \cdot 0_K = 0_K$

  • En general, si $K$ es un campo tal que $car(K) = n \not= 0_K$, entonces $\underbrace{\alpha +…+ \alpha}_{n} = 0_K$ para cualquier $\alpha \in K$.

Demostración: Por ser $1_K \in K$ el neutro aditivo de $K$ y por las propiedades de campo obtenemos que
$\underbrace{ \alpha + … + \alpha }_{n} = 1_K \cdot (\underbrace{ \alpha + … + \alpha }_{n}) =$$\underbrace{ 1_K \cdot \alpha +…+ 1_K \cdot \alpha}_{n}= \underbrace{ \alpha \cdot 1_K +…+ \alpha \cdot 1_K}_{n} =$$\alpha \cdot ( \underbrace{ 1_K +…+ 1_K}_{n})$.
Como $car(K) = n$, entonces $\underbrace{ 1_K +…+ 1_K}_{n} = 0_K$, por lo cual $\alpha \cdot ( \underbrace{ 1_K +…+ 1_K}_{n}) = \alpha \cdot 0_K = 0_K$

Tarea Moral

Sea $K$ un campo. Demuestra la unicidad de:

  1. El neutro aditivo en $K$.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Sabemos por la definición de campo, que existe $0_K$ neutro aditivo.
    • Primero sup. que existe ${0_K}’ \in K$ que también lo es. Con el objetivo de demostrar que $0_K = {0_K}’$.
    • Ahora justifica cada una de las siguientes igualdades:
      $0_K = 0_K + {0_K}’ = {0_K}’$
  1. Los inversos aditivos en $K$.
    Para lograrlo, se te sugiere realizar lo siguiente:
    • Sea $\alpha \in K$. Sabemos por la definición de campo, que existe $(-\alpha) \in K$ inverso aditivo de $\alpha$.
    • Primero sup. que existe $(-\alpha)’ \in K$ que también lo es. Con el objetivo de demostrar que $(-\alpha) = (-\alpha)’$.
    • Ahora justifica cada una de las siguientes igualdades:
      $(-\alpha) = (-\alpha) + 0_K = (-\alpha) + (\alpha + (-\alpha)’)$$= ((-\alpha) + (\alpha)) + (-\alpha)’$
    • Completa la demostración con las igualdades necesarias y justifícalas.
  1. El neutro multiplicativo en $K$.
    Para lograrlo, se te sugiere realizar igualdades análogas al neutro aditivo y justificar cada una.
  1. Los inversos multiplicativos en $K$.
    Para lograrlo, se te sugiere realizar igualdades análogas a los inversos aditivos y justificar cada una.

Más adelante…

Ahora el concepto de campo vamos a usarlo para obtener un nuevo concepto básico y central en este curso: espacio vectorial.

Entradas relacionadas