Introducción

Dados un ángulo y una circunferencia nos podemos preguntar si podemos calcular la magnitud del ángulo dado con algún ángulo que tenga como vértice el centro de la circunferencia dada. En esta entrada estudiaremos algunos resultados que nos permitirán establecer dicha relación.

Definición 1. Un ángulo central en una circunferencia es un ángulo formado por dos radios.

Denotamos a una circunferencia con centro en $O$ como $\mathrm{\Gamma }(O)$.

Ángulo inscrito

Definición 2. Decimos que un segmento es una cuerda de una circunferencia si sus extremos pertenecen a la circunferencia y el segmento no contiene al centro de la circunferencia, si contiene al centro entonces es un diámetro.

Un ángulo inscrito en una circunferencia es un ángulo formado por dos cuerdas o una cuerda y un diámetro que tienen un extremo en común sobre la circunferencia.

Teorema 1, de la medida del ángulo inscrito. Un ángulo inscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.

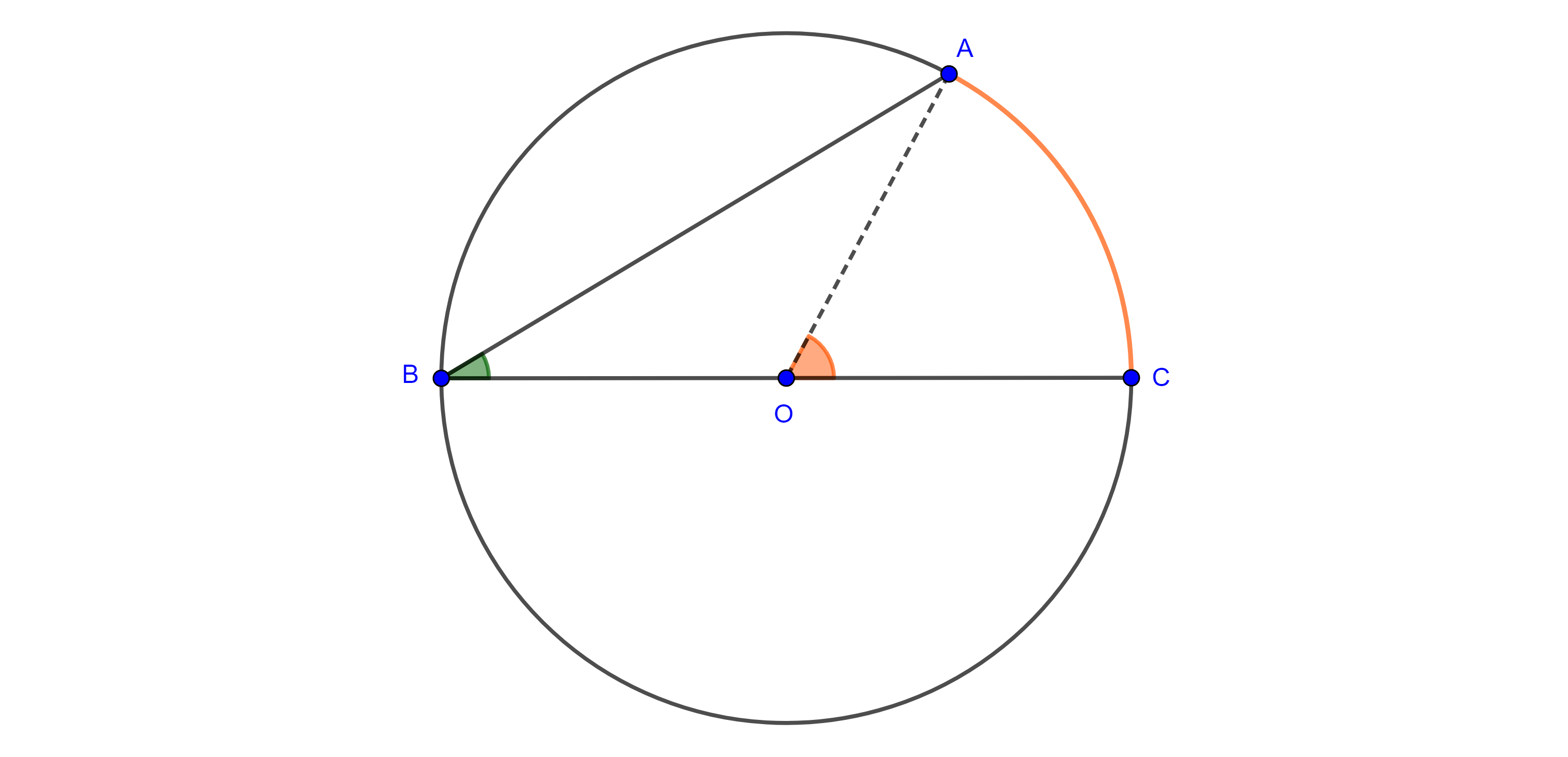
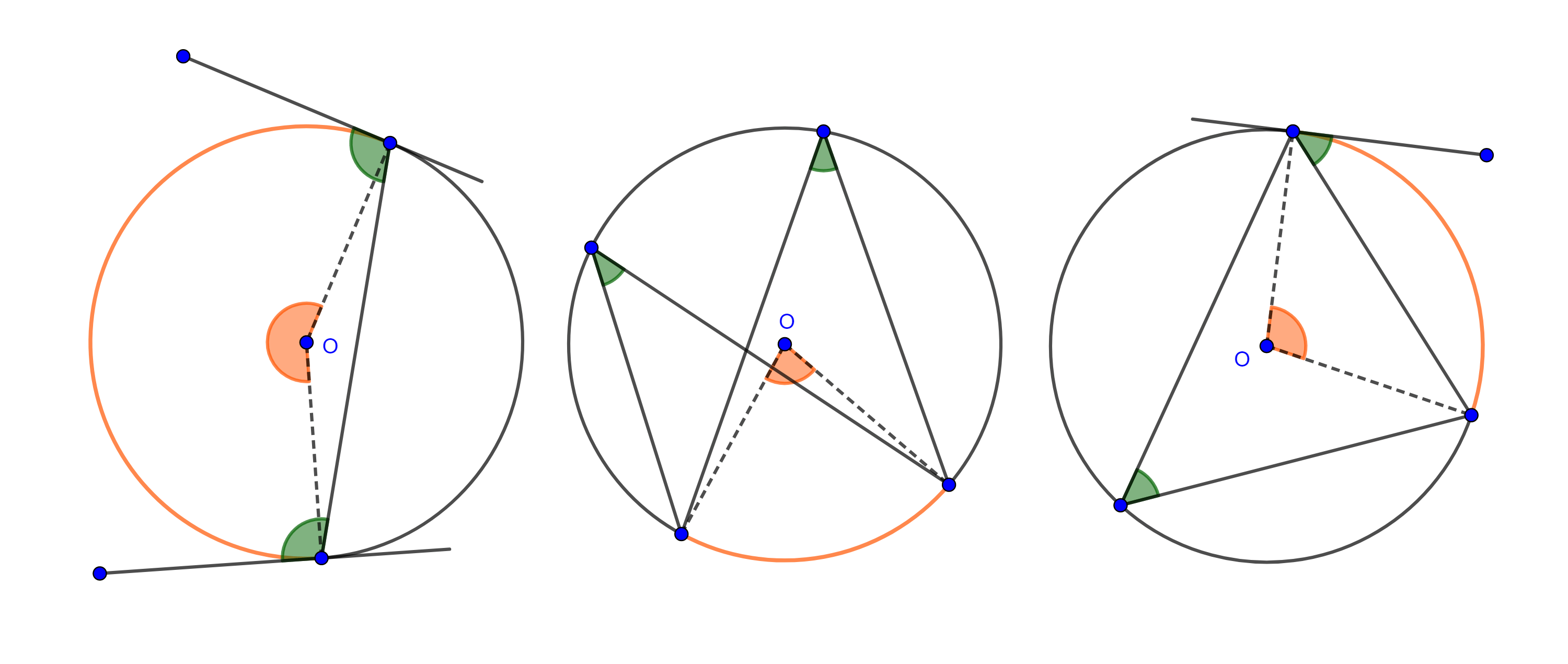
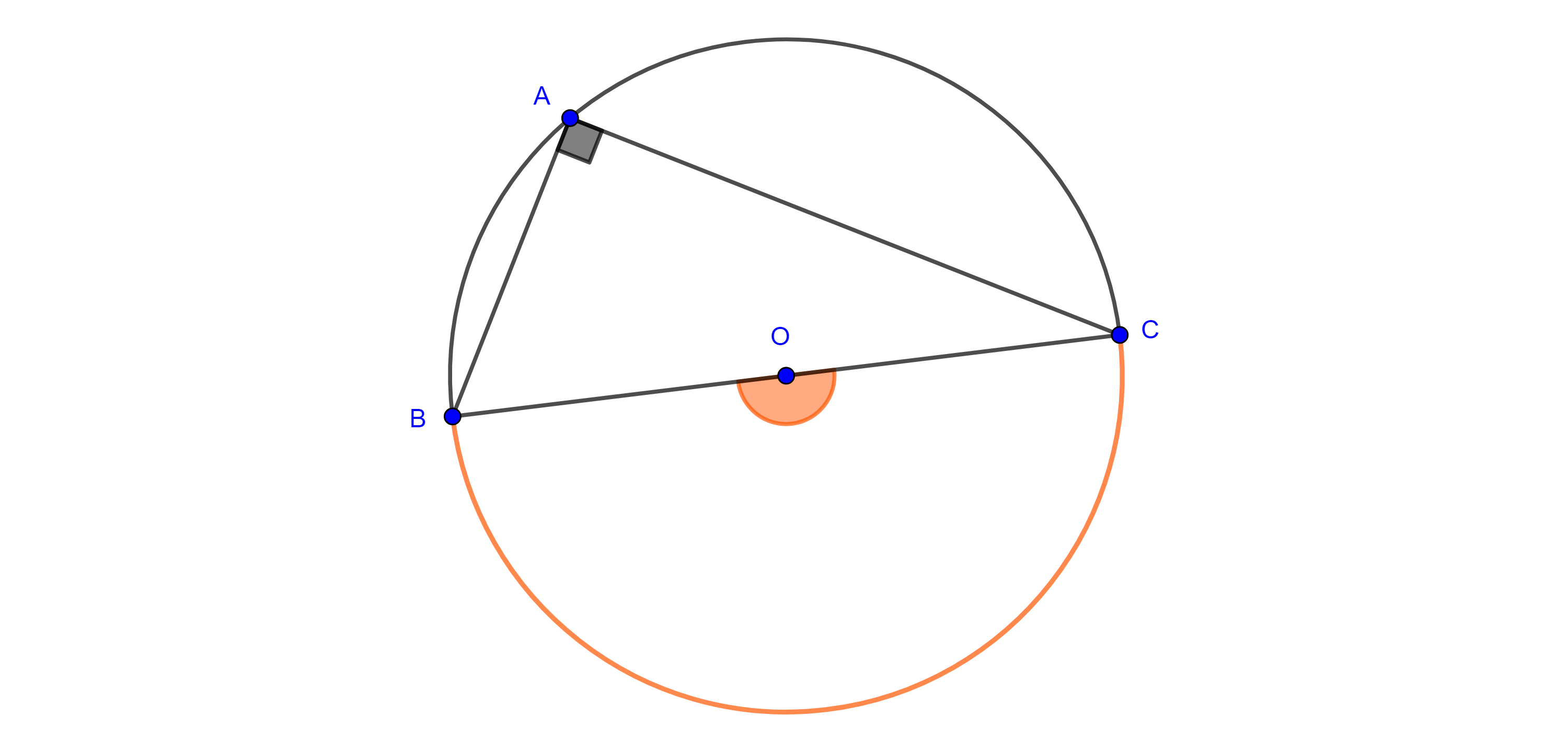
Demostración. Sea $\mathrm{\angle }CBA$ un ángulo inscrito en $\mathrm{\Gamma }(O)$.

Caso 1. $BC$ es diámetro, entonces $\mathrm{△}AOB$ es isósceles y por tanto $\mathrm{\angle }BAO=\mathrm{\angle }CBA$.

Como $\mathrm{\angle }COA$ es un ángulo exterior de $\mathrm{△}AOB$ entonces es igual a la suma de los ángulos interiores no adyacentes a él,
$\Rightarrow \mathrm{\angle }COA=\mathrm{\angle }CBA+\mathrm{\angle }BAO=2\mathrm{\angle }CBA$
$\Rightarrow \mathrm{\angle }CBA={\displaystyle \frac{\mathrm{\angle }COA}{2}}$.

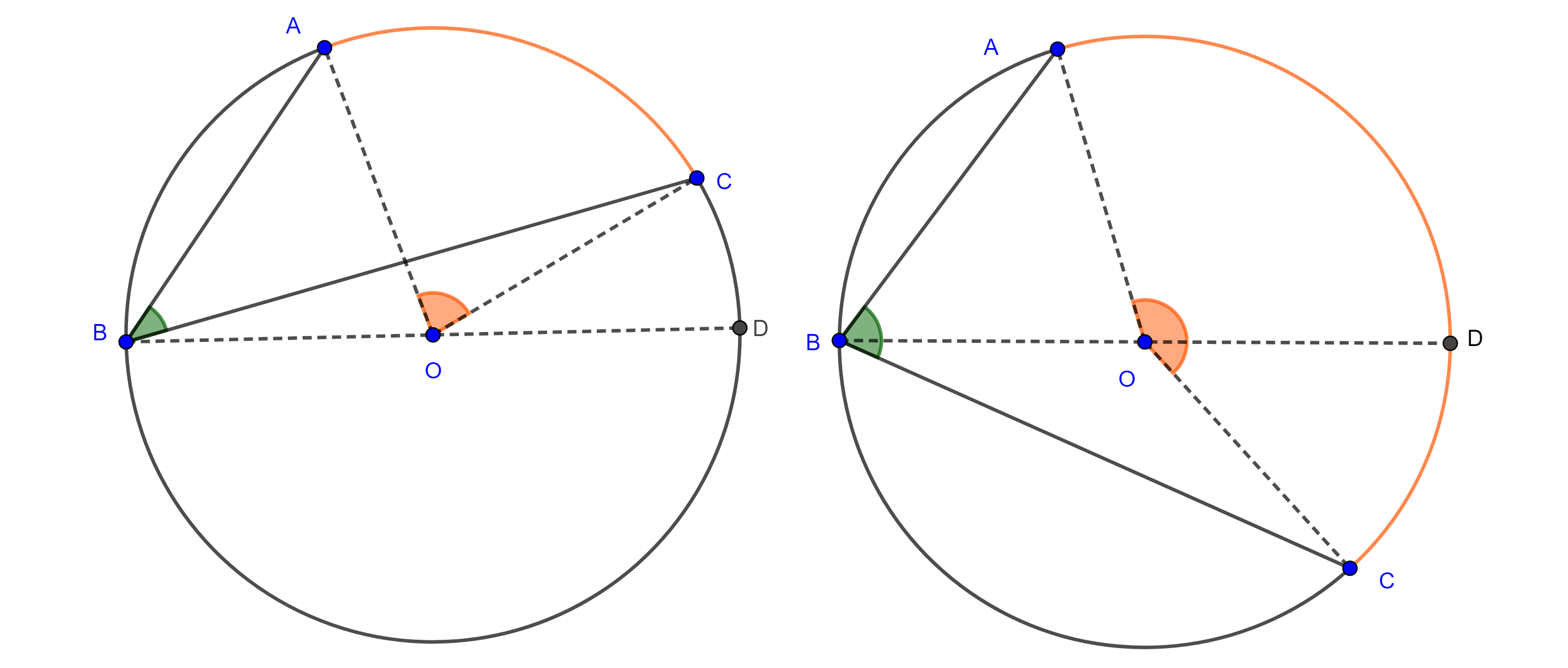
Caso 2. Ambos lados del ángulo son cuerdas, trazamos el diámetro $BO$ y consideramos $D=BO\cap \mathrm{\Gamma }(O)$.

Si $AB$ y $BC$ están en un mismo lado respecto de $BD$ (izquierda figura 2), entonces
$\mathrm{\angle }CBA=\mathrm{\angle }DBA–\mathrm{\angle }DBC$ y por el caso 1,
$\Rightarrow \mathrm{\angle }CBA={\displaystyle \frac{\mathrm{\angle }DOA}{2}}–{\displaystyle \frac{\mathrm{\angle }DOC}{2}}={\displaystyle \frac{\mathrm{\angle }COA}{2}}$.

Si $AB$ y $BC$ están en lados distintos respecto de $BD$ (derecha figura 2), entonces
$\mathrm{\angle }CBA=\mathrm{\angle }CBD+\mathrm{\angle }DBA$ y por el caso 1,
$\Rightarrow \mathrm{\angle }CBA={\displaystyle \frac{\mathrm{\angle }COD}{2}}+{\displaystyle \frac{\mathrm{\angle }DOA}{2}}={\displaystyle \frac{\mathrm{\angle }COA}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Ángulo semiinscrito

Definición 3. Decimos que una recta es tangente a una circunferencia en un punto si la recta es perpendicular al radio que pasa por el punto.  

Definición 4. Decimos que un ángulo es semiinscrito en una circunferencia, si el ángulo está formado por una recta tangente a la circunferencia y una cuerda que tiene como extremo el punto de tangencia.

Teorema 2, de la medida del ángulo semiinscrito. Un ángulo semiinscrito en una circunferencia es igual a la mitad del ángulo central que abarca el mismo arco de circunferencia.

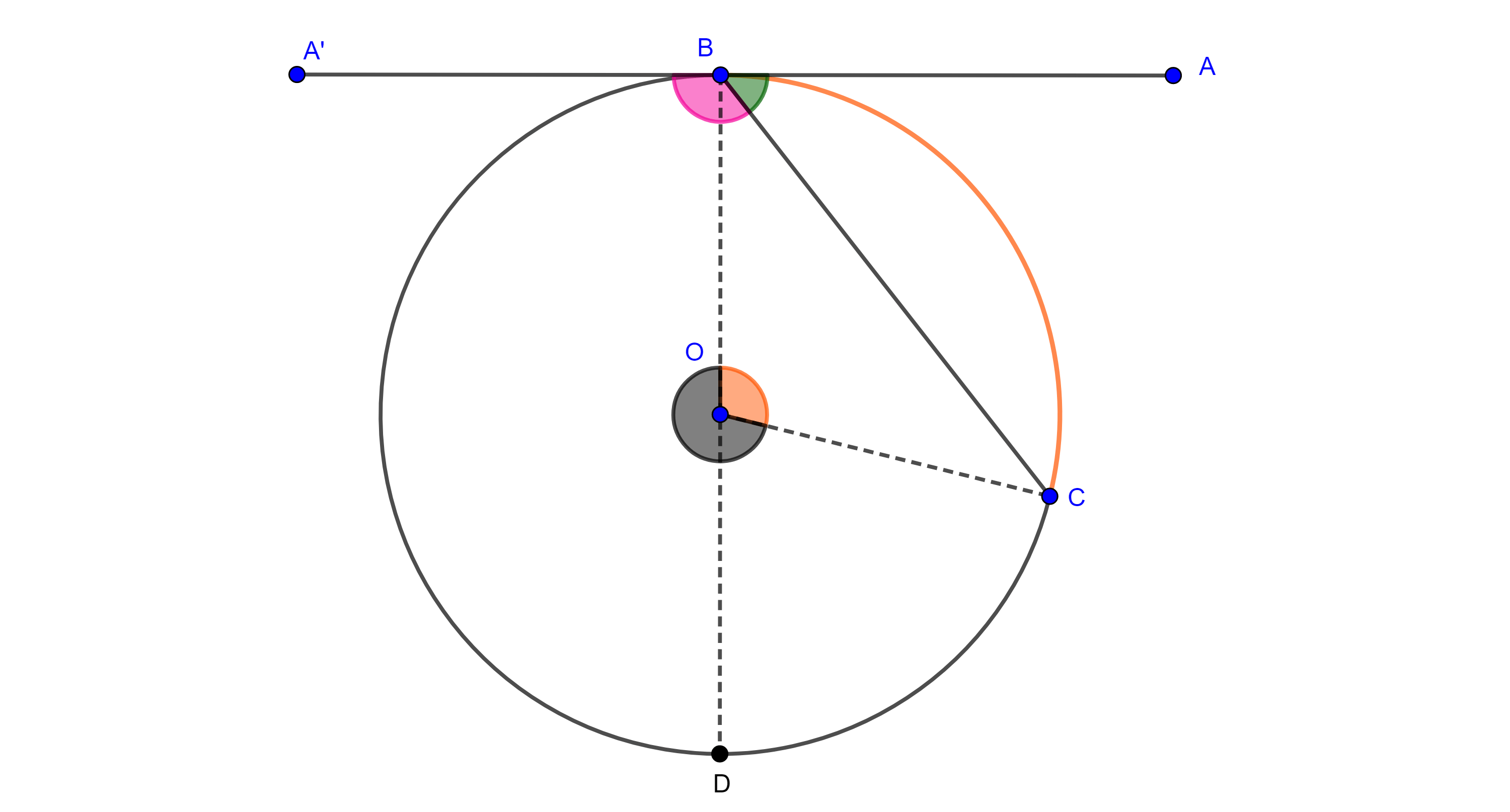
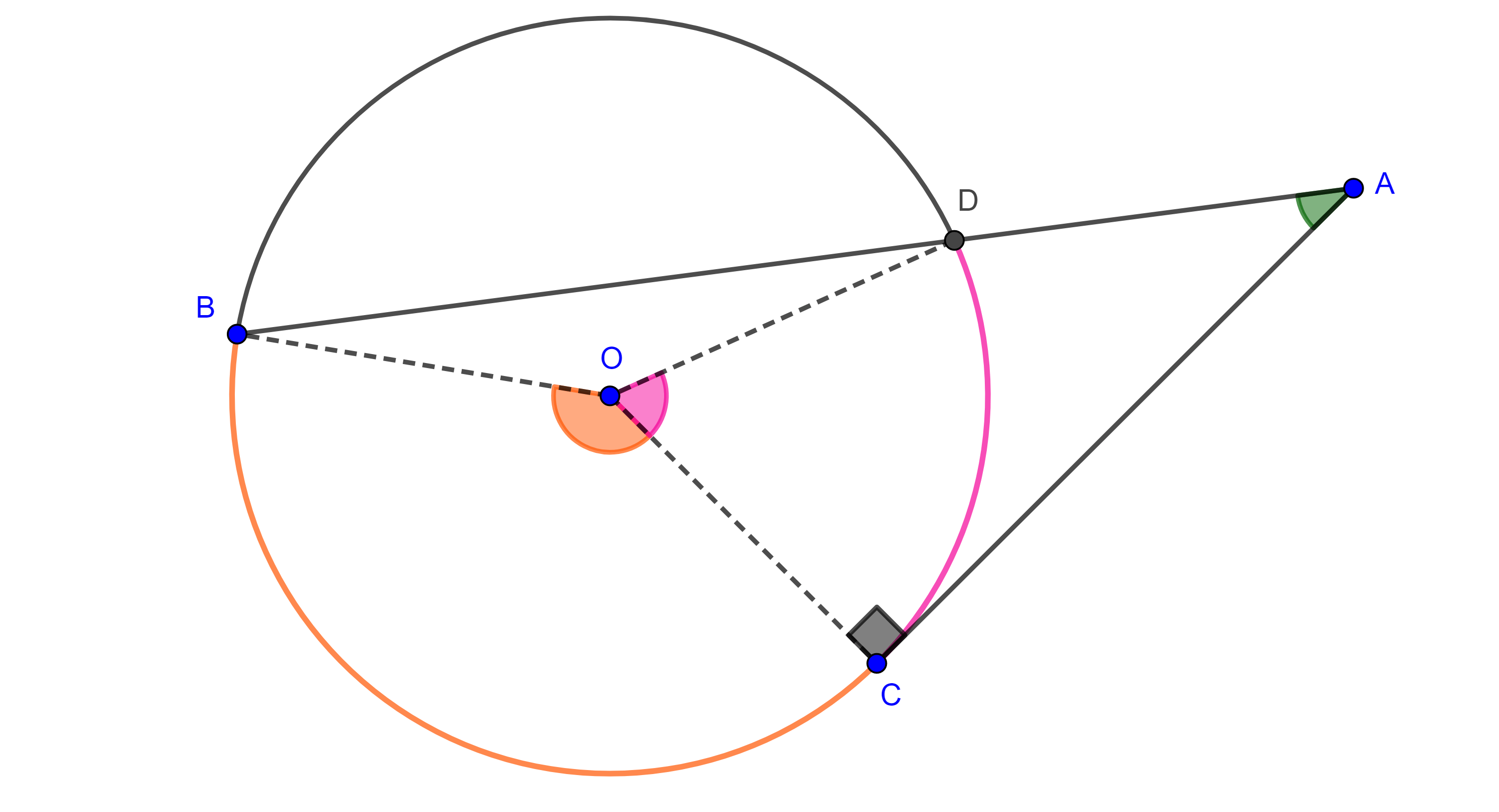
Demostración. Sea $\mathrm{\angle }CBA$ un ángulo inscrito en $\mathrm{\Gamma }(O)$, con $AB$ tangente a $\mathrm{\Gamma }(O)$ en $B$, consideremos $D=BO\cap \mathrm{\Gamma }(O)$.

$\mathrm{\angle }DBC$ es inscrito, por el teorema 1, $\mathrm{\angle }DBC={\displaystyle \frac{\mathrm{\angle }DOC}{2}}$
$\Rightarrow \mathrm{\angle }CBA=\mathrm{\angle }DBA–\mathrm{\angle }DBC={\displaystyle \frac{\pi }{2}}–{\displaystyle \frac{\mathrm{\angle }DOC}{2}}$
$={\displaystyle \frac{\mathrm{\angle }DOB}{2}}–{\displaystyle \frac{\mathrm{\angle }DOC}{2}}={\displaystyle \frac{\mathrm{\angle }COB}{2}}$.

Por otro lado, consideremos $A^{\prime }\in AB$ pero del lado opuesto a $A$ respecto de $B$, entonces,
$\mathrm{\angle }{A}^{\prime }BC=\mathrm{\angle }ABD+\mathrm{\angle }DBC={\displaystyle \frac{\pi }{2}}+{\displaystyle \frac{\mathrm{\angle }DOC}{2}}$
$={\displaystyle \frac{\mathrm{\angle }BOD}{2}}+{\displaystyle \frac{\mathrm{\angle }DOC}{2}}={\displaystyle \frac{\mathrm{\angle }BOC}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Ángulo interior

Definición 5. Si el vértice de un ángulo está en el interior de una circunferencia decimos que el ángulo es interior a la circunferencia.

Teorema 3, de la medida del ángulo interior. Un ángulo interior a una circunferencia es igual a la semisuma del ángulo central que abarca el mismo arco que el ángulo interior y del ángulo central que abarca el mismo arco que el opuesto por el vértice.

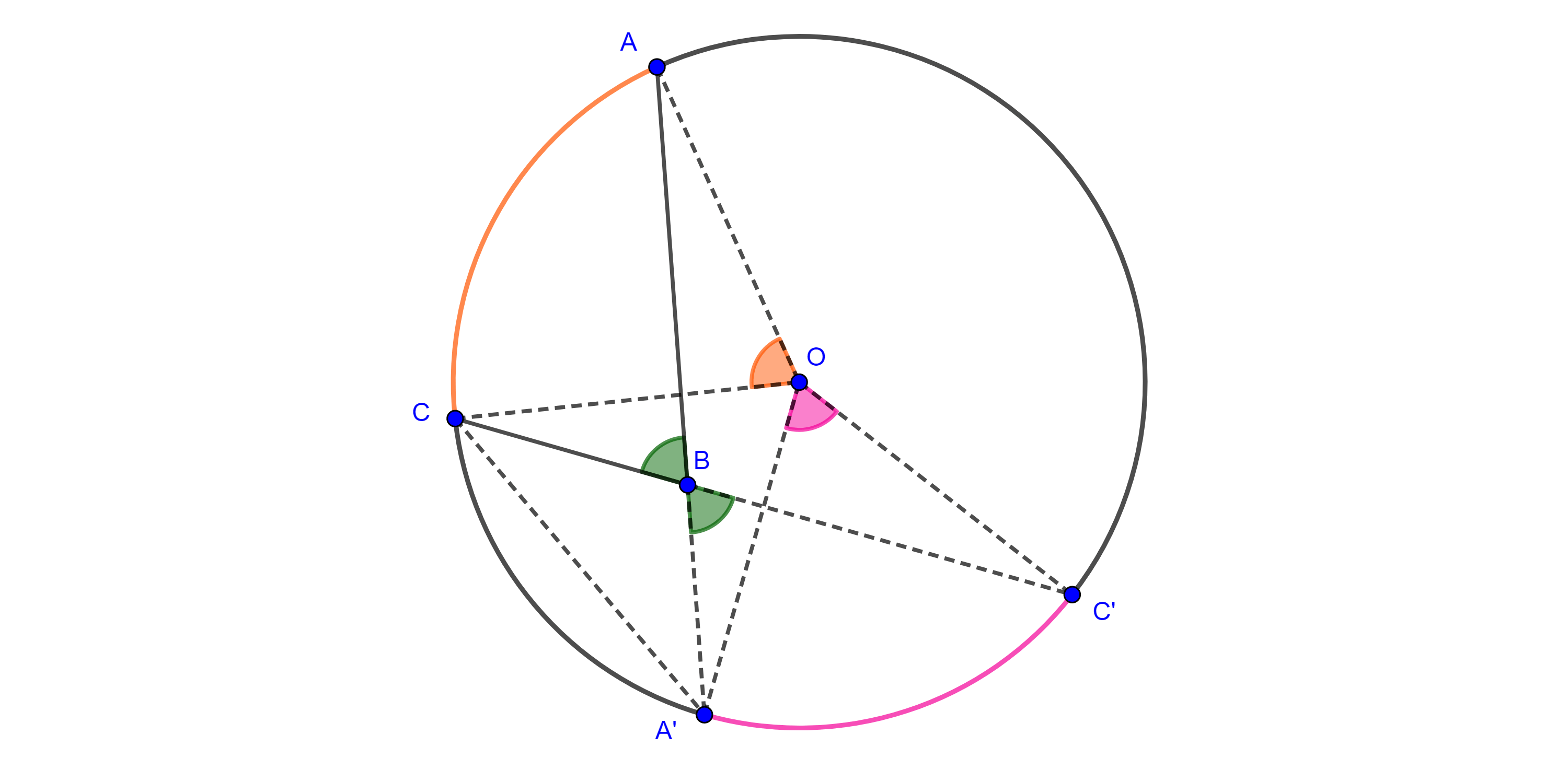
Demostración.  Sea $\mathrm{\angle }ABC$ un ángulo interior a $\mathrm{\Gamma }(O)$ con $A$, $C\in \mathrm{\Gamma }(O)$, consideremos $A^{\prime }=AB\cap \mathrm{\Gamma }(O)$ y $C^{\prime }=CB\cap \mathrm{\Gamma }(O)$.

Como $\mathrm{\angle }ABC$ es un ángulo exterior de $\mathrm{△}{A}^{\prime }BC$ es igual a la suma de los ángulos interiores no adyacentes a él, además $\mathrm{\angle }A{A}^{\prime }C$ y  $\mathrm{\angle }{A}^{\prime }C{C}^{\prime }$ son inscritos y por el teorema 1,
$\Rightarrow \mathrm{\angle }ABC=\mathrm{\angle }A{A}^{\prime }C+\mathrm{\angle }{A}^{\prime }C{C}^{\prime }={\displaystyle \frac{\mathrm{\angle }AOC+\mathrm{\angle }{A}^{\prime }O{C}^{\prime }}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Ángulo exterior (lados secantes)

Definición 6. Una recta secante a una circunferencia es una recta que la interseca en dos puntos distintos.

Definición 7. Decimos que un ángulo es exterior a una circunferencia si su vértice se encuentra fuera de la circunferencia y los lados que forman el ángulo son tangentes o secantes a la circunferencia.

Teorema 4, de la medida del ángulo exterior. Un ángulo exterior a una circunferencia es igual a la mitad de la diferencia de los ángulos centrales que abarcan arcos cuyos extremos son las intersecciones de cada lado del ángulo con la circunferencia.

Caso 1. Ambos lados del ángulo son secantes a la circunferencia.

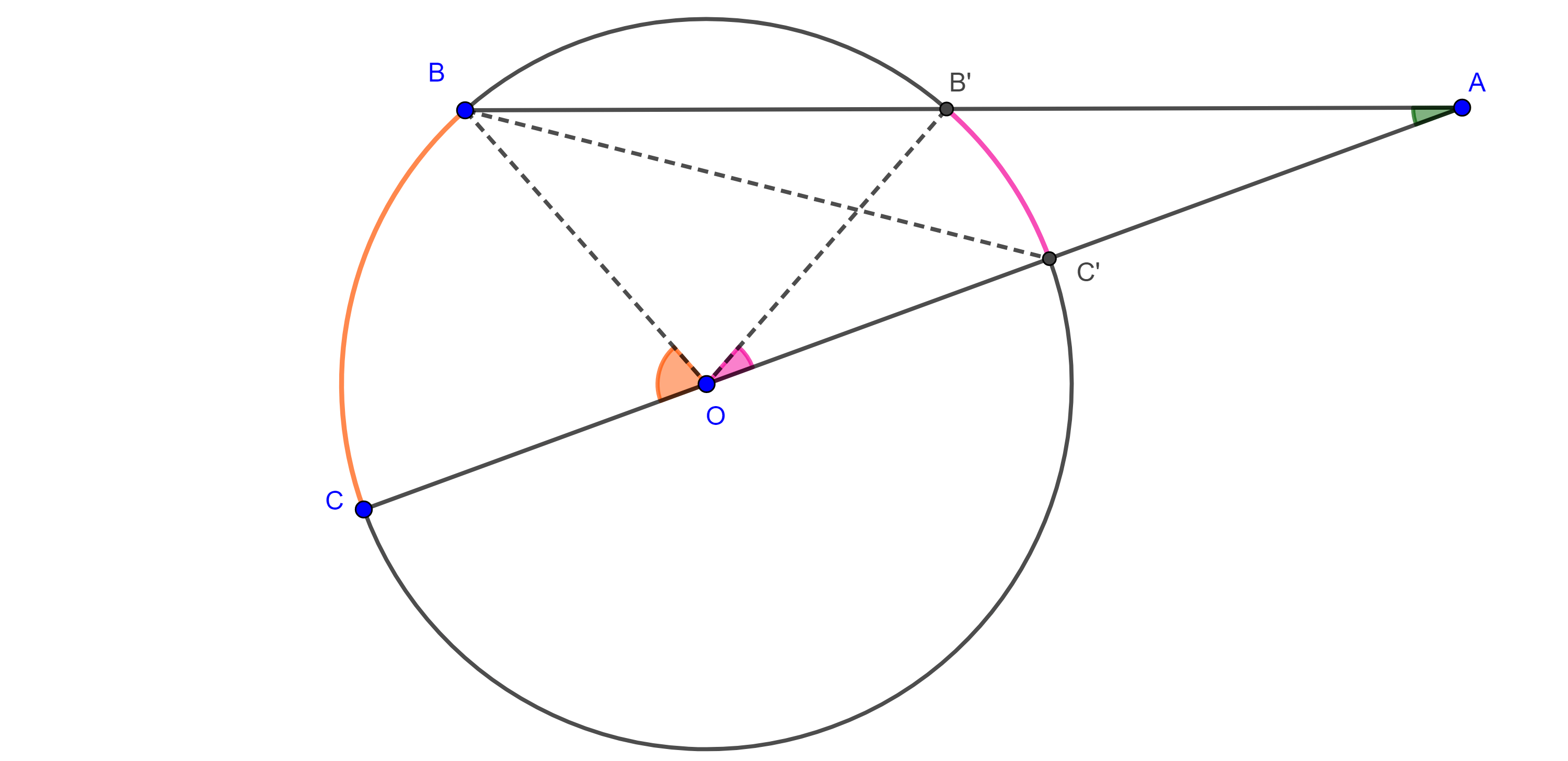
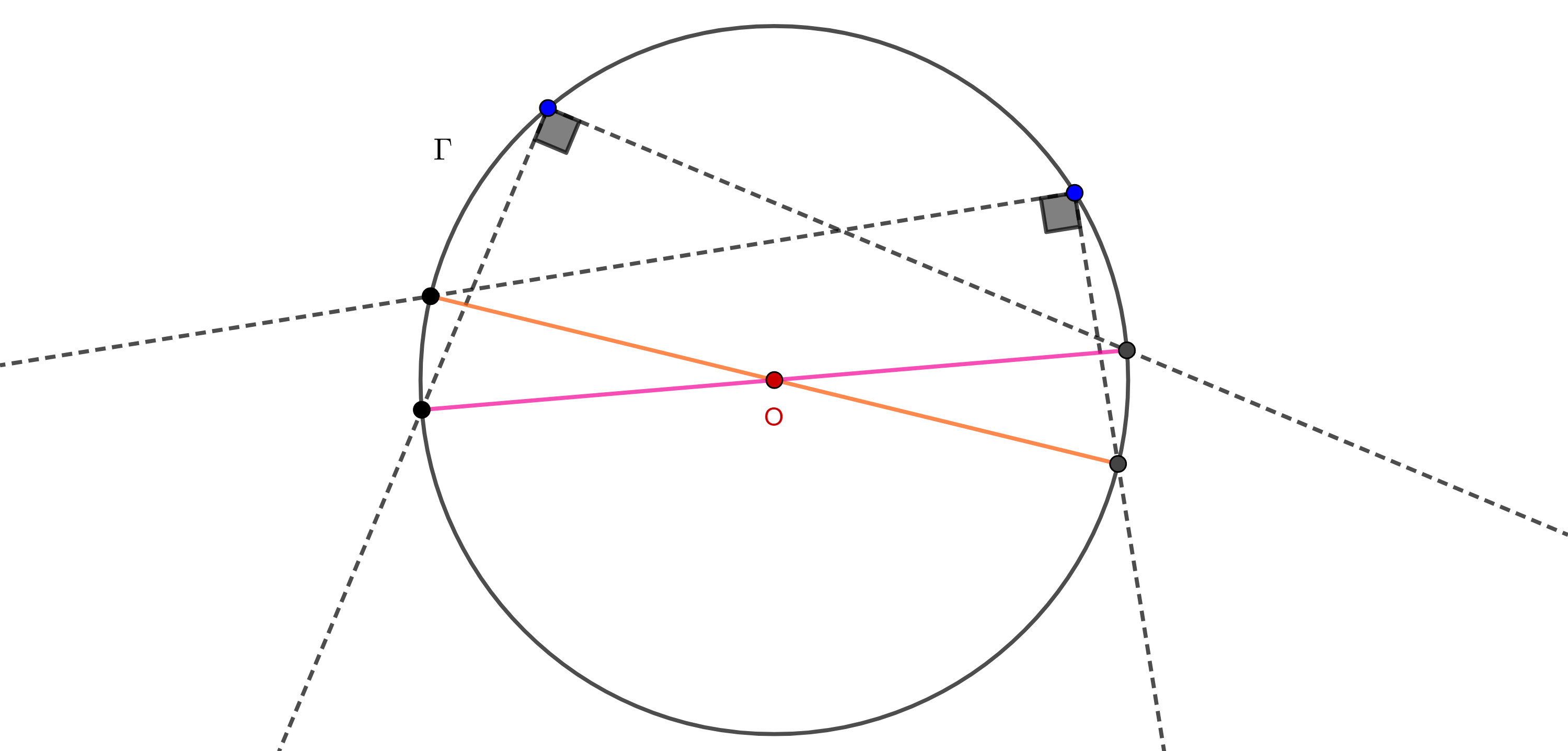
Demostración. Sea $\mathrm{\angle }BAC$ un ángulo exterior a $\mathrm{\Gamma }(O)$.

Supongamos que $B$, $C\in \mathrm{\Gamma }(O)$ y consideremos $B^{\prime }=AB\cap \mathrm{\Gamma }(O)$ y $C^{\prime }=AC\cap \mathrm{\Gamma }(O)$.

Veamos primero el caso particular en el que $C{C}^{\prime }$ es diámetro entonces $\mathrm{\angle }B{C}^{\prime }C$ es un ángulo exterior de $\mathrm{△}A{C}^{\prime }B$, por tanto,
$\mathrm{\angle }B{C}^{\prime }C=\mathrm{\angle }A+\mathrm{\angle }{C}^{\prime }B{B}^{\prime }$

Como $\mathrm{\angle }B{C}^{\prime }C$ y $\mathrm{\angle }{C}^{\prime }B{B}^{\prime }$ son ángulos inscritos, por el teorema 1,
$\Rightarrow \mathrm{\angle }A=\mathrm{\angle }B{C}^{\prime }C–\mathrm{\angle }{C}^{\prime }B{B}^{\prime }={\displaystyle \frac{\mathrm{\angle }BOC–\mathrm{\angle }{C}^{\prime }O{B}^{\prime }}{2}}$.

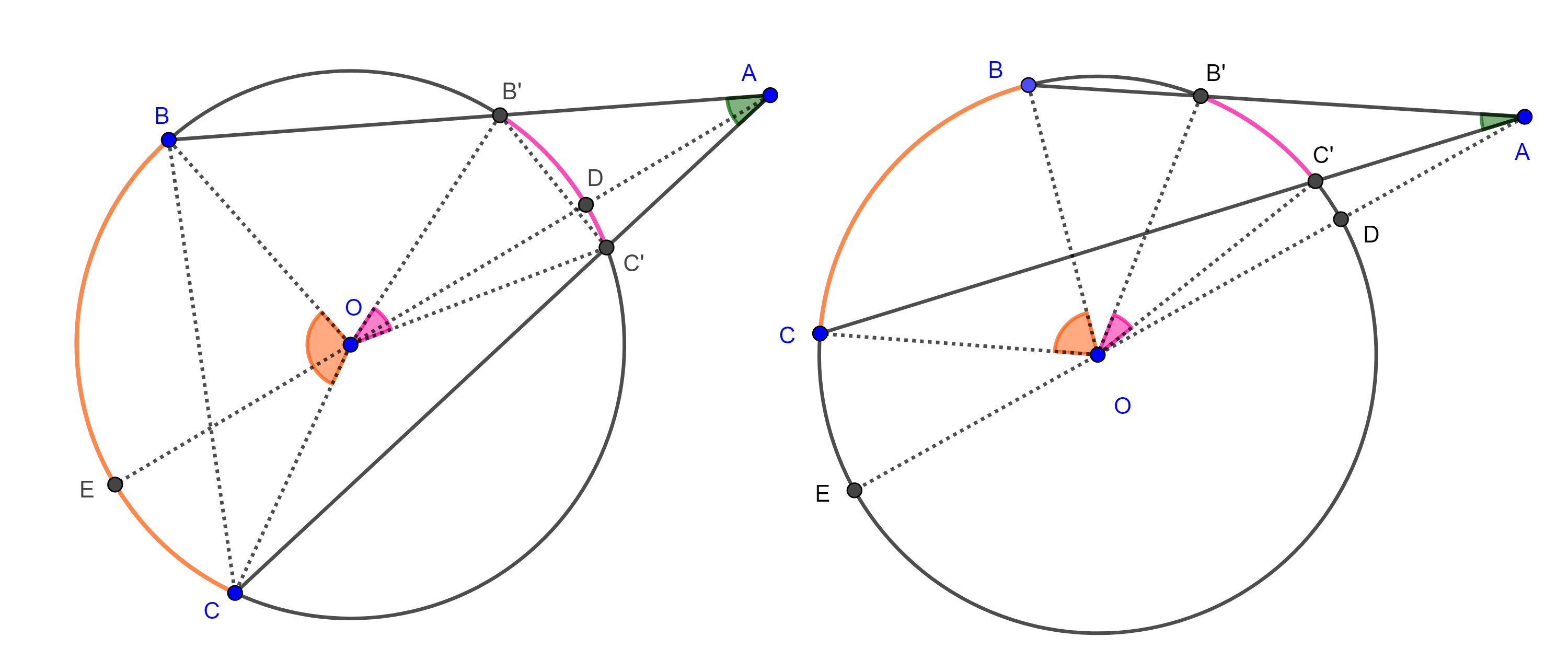
Para el caso general sean $D$ y $E$ las intersecciones de $AO$ con $\mathrm{\Gamma }(O)$.

Si $B$ y $C$ están en lados distintos respecto de $DE$ (izquierda figura 6), entonces
$\mathrm{\angle }A=\mathrm{\angle }BAE+\mathrm{\angle }EAC$, y por el caso particular,
$\Rightarrow \mathrm{\angle }BAE={\displaystyle \frac{\mathrm{\angle }BOE–\mathrm{\angle }DO{B}^{\prime }}{2}}$ y $\mathrm{\angle }EAC={\displaystyle \frac{\mathrm{\angle }EOC–\mathrm{\angle }{C}^{\prime }OD}{2}}$
$\Rightarrow \mathrm{\angle }A={\displaystyle \frac{\mathrm{\angle }BOE+\mathrm{\angle }EOC–(\mathrm{\angle }{C}^{\prime }OD+\mathrm{\angle }DO{B}^{\prime })}{2}}={\displaystyle \frac{\mathrm{\angle }BOC–\mathrm{\angle }{C}^{\prime }O{B}^{\prime }}{2}}$.

Si $B$ y $C$ están en el mismo lado respecto de $DE$ (derecha figura 6), entonces
$\mathrm{\angle }BAC=\mathrm{\angle }BAE–\mathrm{\angle }CAE$ y por el caso particular, 
$\mathrm{\angle }BAE={\displaystyle \frac{\mathrm{\angle }BOE–\mathrm{\angle }DO{B}^{\prime }}{2}}$ y $\mathrm{\angle }CAE={\displaystyle \frac{\mathrm{\angle }COE–\mathrm{\angle }DO{C}^{\prime }}{2}}$
$\Rightarrow \mathrm{\angle }A=\mathrm{\angle }BAC={\displaystyle \frac{(\mathrm{\angle }BOE–\mathrm{\angle }COE)–(\mathrm{\angle }DO{B}^{\prime }–\mathrm{\angle }DO{C}^{\prime })}{2}}={\displaystyle \frac{\mathrm{\angle }BOC–\mathrm{\angle }{C}^{\prime }O{B}^{\prime }}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Ángulo exterior (lados tangentes)

Caso 2. Ambos lados del ángulo son tangentes a la circunferencia.

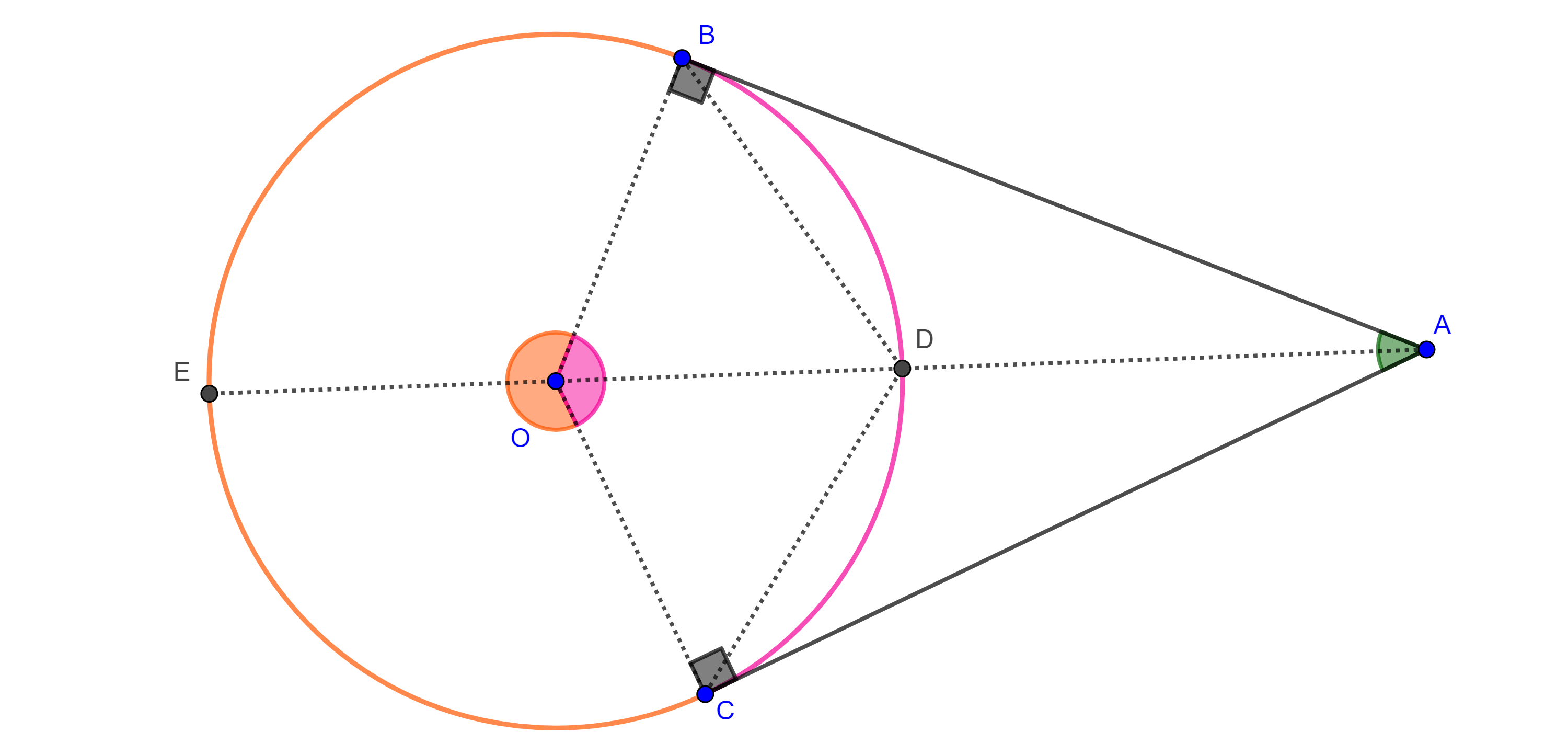
Demostración. Sea $\mathrm{\angle }BAC$ un ángulo exterior a $\mathrm{\Gamma }(O)$.

Supongamos que $B$, $C\in \mathrm{\Gamma }(O)$ y consideremos $D$ y $E$ las intersecciones de $AO$ con $\mathrm{\Gamma }(O)$.

Como $\mathrm{\angle }BDE$ y $\mathrm{\angle }EDC$ son ángulos exteriores de $\mathrm{△}ADB$ y $\mathrm{△}ADC$ respectivamente, entonces
$\mathrm{\angle }BDE=\mathrm{\angle }BAD+\mathrm{\angle }DBA$ y $\mathrm{\angle }EDC=\mathrm{\angle }DAC+\mathrm{\angle }ACD$
$\Rightarrow \mathrm{\angle }A=\mathrm{\angle }BAD+\mathrm{\angle }DAC=(\mathrm{\angle }BDE–\mathrm{\angle }DBA)+(\mathrm{\angle }EDC–\mathrm{\angle }ACD)$
$=(\mathrm{\angle }BDE+\mathrm{\angle }EDC)–(\mathrm{\angle }ACD+\mathrm{\angle }DBA)=\mathrm{\angle }BDC–(\mathrm{\angle }ACD+\mathrm{\angle }DBA)$

$\mathrm{\angle }ACD$ y $\mathrm{\angle }DBA$ son ángulos semiinscritos y $\mathrm{\angle }BDC$ es un ángulo inscrito, por los teoremas 1 y 2 tenemos
$\mathrm{\angle }ACD={\displaystyle \frac{\mathrm{\angle }COD}{2}}$, $\mathrm{\angle }DBA={\displaystyle \frac{\mathrm{\angle }DOB}{2}}$ y $\mathrm{\angle }BDC={\displaystyle \frac{\mathrm{\angle }BOC}{2}}$,  
$\Rightarrow \mathrm{\angle }A={\displaystyle \frac{\mathrm{\angle }BOC–(\mathrm{\angle }COD+\mathrm{\angle }DOB)}{2}}={\displaystyle \frac{\mathrm{\angle }BOC–\mathrm{\angle }COB}{2}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Caso 3. Un lado del ángulo es tangente a la circunferencia y el otro es secante.

La demostración de este caso queda como ejercicio.

Ejemplos

Proposición 1. Dos ángulos ya sean inscritos o semiinscritos que abarcan el mismo arco de circunferencia son iguales.

Demostración. Por los teoremas 1 y 2, un ángulo inscrito y un ángulo semiinscrito son iguales a la mitad del ángulo central que abarca el mismo arco, si dos ángulos abarcan el mismo arco entonces el ángulo central es el mismo para ambos y por transitividad son iguales.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Teorema 5, de Tales. Sean $A$, $B$ y $C$ puntos distintos en una circunferencia entonces $BC$ es diámetro si y solo si $A$ es un ángulo recto.

 Demostración. Sea $\mathrm{\Gamma }(O)$ la circunferencia a la que pertenecen $A$, $B$ y $C$, el resultado se sigue del hecho de que el ángulo central que abarca el mismo arco que $\mathrm{\angle }A$ es $\mathrm{\angle }BOC$ y aplicar el teorema del ángulo inscrito.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Problema. Dado un círculo $\mathrm{\Gamma }$ construir su centro.

Solución. Construimos dos ángulos rectos inscritos en la circunferencia, tomando dos puntos distintos como vértice.

Por el teorema de Tales, las intersecciones de los lados de cada ángulo formaran dos diámetros distintos de la circunferencia y su intersección será el centro de la circunferencia.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Proposición 2. Las rectas tangentes trazadas desde un punto exterior a una circunferencia son iguales.

Demostración. Sean $\mathrm{\Gamma }(O)$ y $A$ un punto exterior, por $A$ trazamos $AB$ y $AC$ tangentes a $\mathrm{\Gamma }(O)$ en $B$ y en $C$ respectivamente (figura 7).

Consideremos los radios $OB$ y $OC$ entonces $OB=OC$, y por definición de tangencia, $OB\perp AB$ y $OC\perp AC$.

Los triángulos rectángulos $\mathrm{△}AOB$ y $\mathrm{△}AOC$ tienen a $AO$ como lado en común, por criterio de congruencia hipotenusa-cateto $\mathrm{△}AOB\cong \mathrm{△}AOC$, por tanto, $AB=AC$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$ 

Más adelante…

Apoyándonos de los resultados vistos aquí, en la siguiente entrada daremos una caracterización de arco de circunferencia y veremos la circunferencia de Apolonio.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Sean $A$ y $C$ dos puntos fijos en una circunferencia, muestra que para cualesquiera dos puntos $B$ y $D$ en la misma circunferencia se tiene que $\mathrm{\angle }ABC=\mathrm{\angle }ADC$ o $\mathrm{\angle }ABC$ y $\mathrm{\angle }CDA$ son suplementarios.
2.  Prueba que una recta es tangente a una circunferencia si y solo si la recta y la circunferencia tienen un solo punto en común.
3. Demuestra el teorema 4 en el caso en el que el un lado del ángulo exterior es secante a la circunferencia y el otro es tangente, es decir, en la figura 11 muestra que
   $\mathrm{\angle }BAC={\displaystyle \frac{\mathrm{\angle }BOC–\mathrm{\angle }COD}{2}}$.

4. Dados una circunferencia y un punto fuera de ella, construye las rectas tangentes a la circunferencia dada trazadas desde el punto dado.
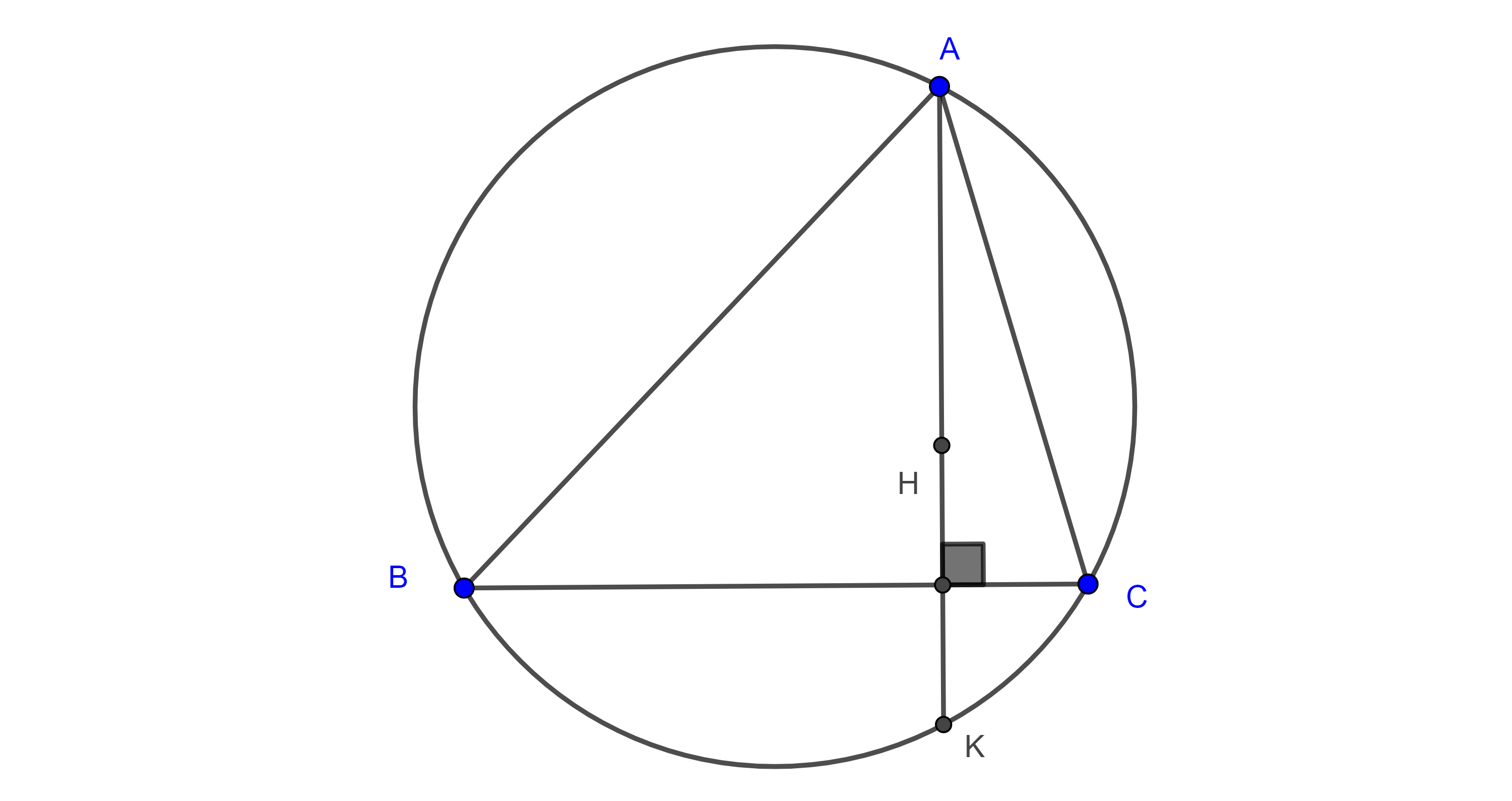
5. Sean $\mathrm{△}ABC$, $K$ la intersección de la altura trazada desde $A$ con el circuncírculo de $\mathrm{△}ABC$ y $H$ el ortocentro de $\mathrm{△}ABC$, muestra que $BC$ biseca a $HK$.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Puntos notables del triángulo.
• Siguiente entrada del curso: Circunferencia de Apolonio.
• Otros cursos.

Fuentes

• Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 133-140.
• Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 34-40.
• Wikipedia
• Geometría interactiva

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»