Introducción

El teorema de Ptolomeo nos da una caracterización del cuando un cuadrilátero convexo es cíclico en términos de los productos entre sus lados y sus diagonales. Necesitaremos antes una caracterización diferente de cuadrilátero cíclico.

Cuadriláteros cíclicos

Definición. Si los vértices de un polígono están en una misma circunferencia decimos que está inscrito en ella o que es cíclico.

Teorema 1. Un cuadrilátero convexo es cíclico si y solo si los ángulos opuestos son suplementarios.

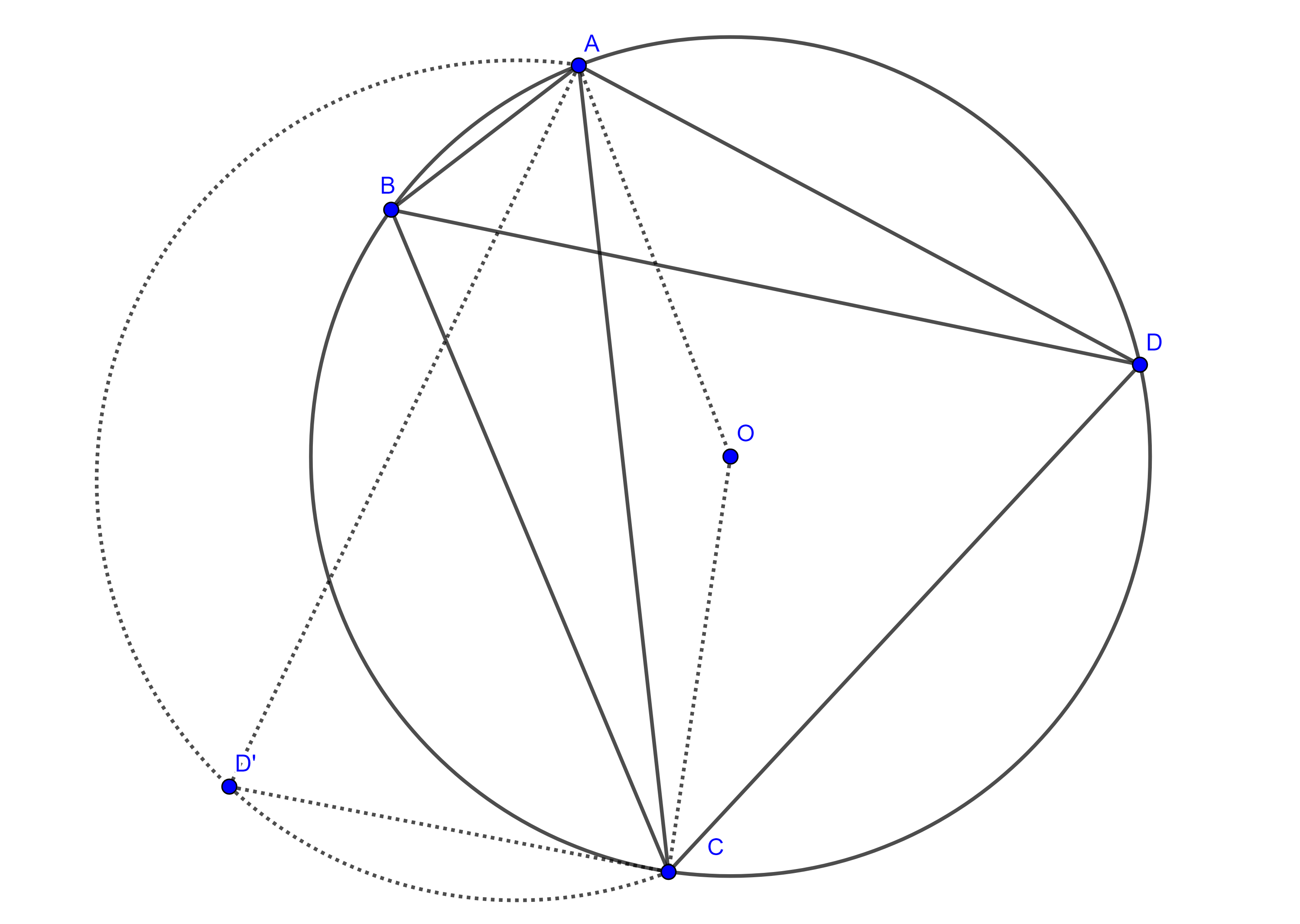
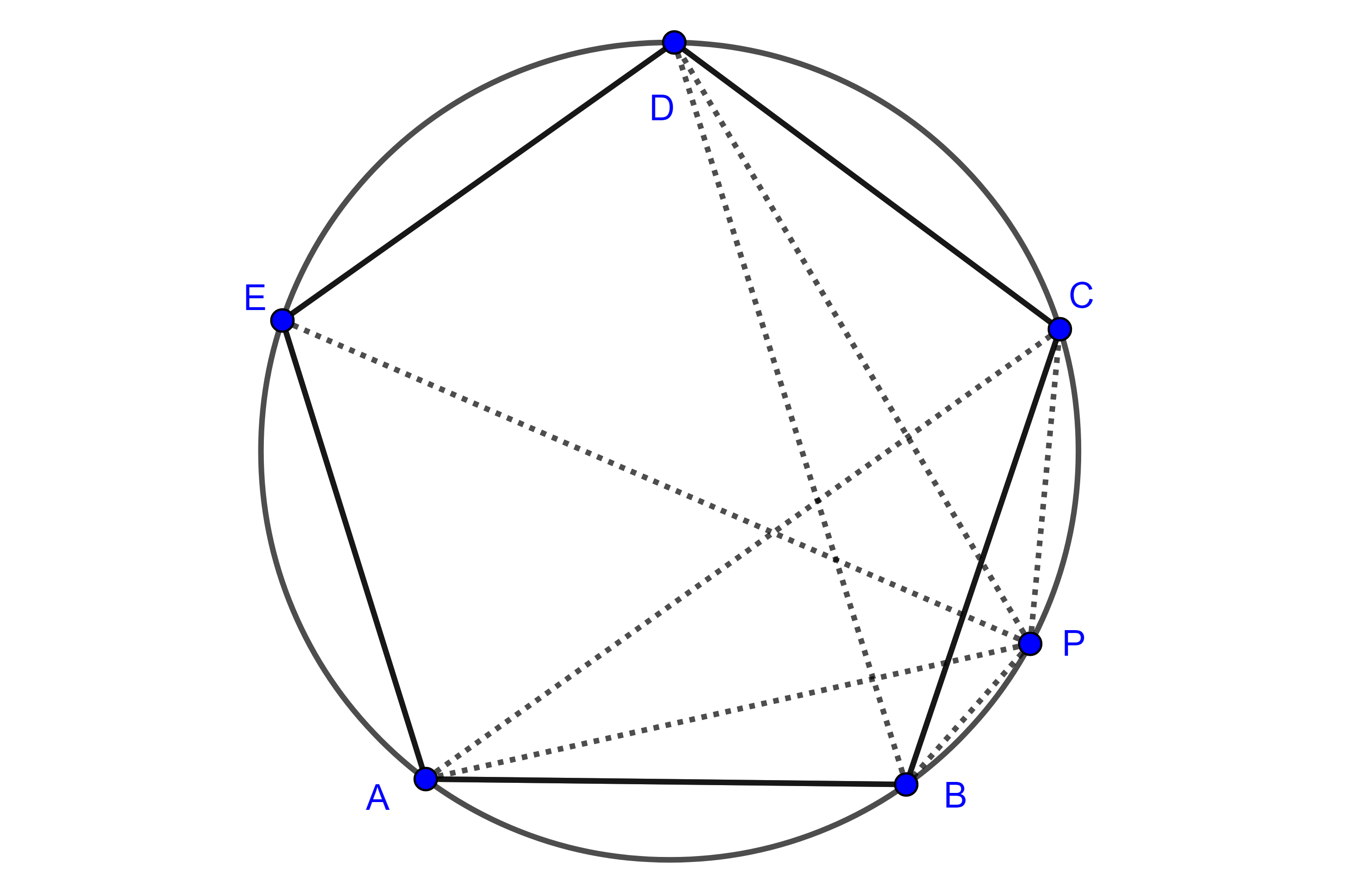
Demostración. Sea $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ un cuadrilátero cíclico inscrito en $(O,r)$, la circunferencia con centro en $O$.

Los ángulos opuestos $\mathrm{\angle }ADC$ y $\mathrm{\angle }CBA$ son subtendidos por los arcos $AC$ y $CA$ respectivamente y por el teorema de la medida del ángulo inscrito tenemos que
$\mathrm{\angle }ADC+\mathrm{\angle }CBA={\displaystyle \frac{\mathrm{\angle }AOC}{2}}+{\displaystyle \frac{\mathrm{\angle }COA}{2}}={\displaystyle \frac{2\pi }{2}}=\pi$.

De manera análoga se ve que $\mathrm{\angle }BAD$ y $\mathrm{\angle }DCB$ son suplementarios.

Por lo tanto, los ángulos opuestos de un cuadrilátero cíclico son suplementarios.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Ahora supongamos que los ángulos opuestos $\mathrm{\angle }ADC$ y $\mathrm{\angle }CBA$ de $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ son suplementarios.

Consideremos el circuncírculo de $\mathrm{△}ABC$, entonces todos los puntos en el arco $\stackrel{⌢}{CA}$ que no contiene a $B$ subtienden un ángulo $\mathrm{\angle }ADC$ suplementario a $\mathrm{\angle }CBA$, pero este lugar geométrico es único.

Por lo tanto $D\in \stackrel{⌢}{CA}$ y en consecuencia $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ es cíclico.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Teorema de Ptolomeo

Teorema 2, desigualdad de Ptolomeo. En todo cuadrilátero convexo la suma de los productos entre lados opuestos es mayor o igual al producto de las diagonales, y la igualdad se da si y solo si es el cuadrilátero es cíclico.

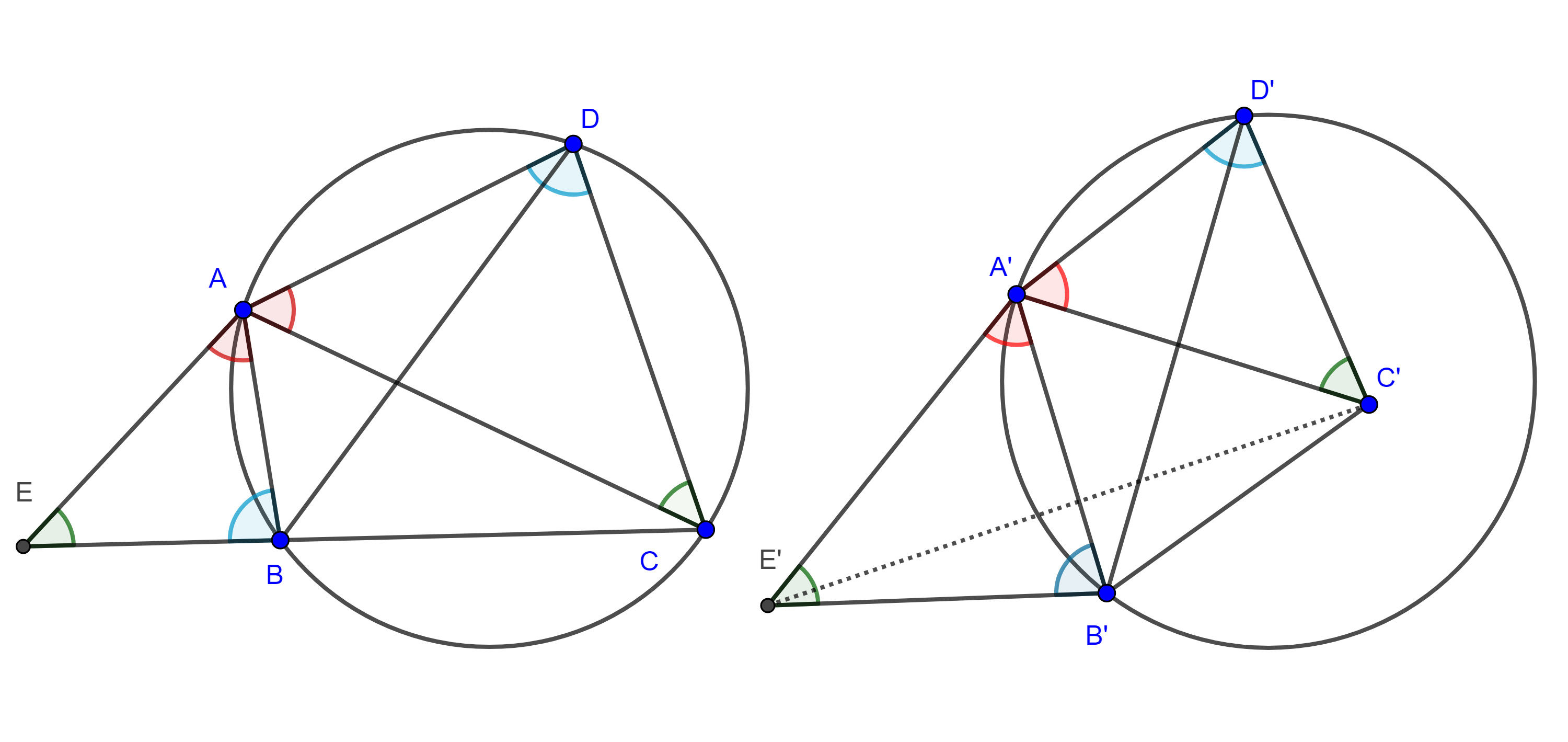
Demostración. Sea $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ un cuadrilátero convexo, construyamos sobre el segmento $AB$ (figura 2), un triángulo $\mathrm{△}ABE$ semejante a $\mathrm{△}ADC$ tal que $\mathrm{\angle }ABE=\mathrm{\angle }ADC$ y $\mathrm{\angle }BAE=\mathrm{\angle }CAD$ entonces

$\begin{array}{}\text{(1)}& {\displaystyle \frac{EA}{CA}}={\displaystyle \frac{BA}{DA}}\iff {\displaystyle \frac{EA}{BA}}={\displaystyle \frac{CA}{DA}}.\end{array}$

Dado que $\mathrm{\angle }CAE=\mathrm{\angle }BAD$ y por $(1)$, por criterio lado, ángulo, lado, los triángulos $\mathrm{△}EAC$ y $\mathrm{△}BAD$ son semejantes, entonces de la primera y segunda relaciones de semejanza tenemos que
${\displaystyle \frac{EB}{CD}}={\displaystyle \frac{AB}{AD}}$ y ${\displaystyle \frac{EC}{BD}}={\displaystyle \frac{AC}{AD}}$
$\iff$ $EB={\displaystyle \frac{AB\times CD}{AD}}$ y $EC={\displaystyle \frac{AC\times BD}{AD}}$.

Ahora notemos que tenemos dos casos:

Caso 1. (izquierda figura 2)
$B\in EC$ $\iff$ $\mathrm{\angle }CBA+\mathrm{\angle }ADC=\mathrm{\angle }CBA+\mathrm{\angle }ABE=\pi$ $\iff$ $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ es cíclico,
y en tal caso $EC=EB+BC$ $\iff$ ${\displaystyle \frac{AC\times BD}{AD}}={\displaystyle \frac{AB\times CD}{AD}}+BC$
$\iff$ $AC\times BD=AB\times CD+AD\times BC$.

Caso 2. (derecha figura 2)
$E$, $B$ y $C$ son tres puntos no colineales $\iff$ $\mathrm{\angle }CBA+\mathrm{\angle }ADC=\mathrm{\angle }CBA+\mathrm{\angle }ABE\ne \pi$ $\iff$ $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ no es cíclico, entonces aplicando la desigualdad del triángulo a $\mathrm{△}EBC$ tenemos que
$EC<EB+BC$ $\iff$ $AC\times BD<AB\times CD+AD\times BC$.

De lo anterior se sigue que $AB\times CD+AD\times BC\ge AC\times BD$, con la igualdad si y solo si $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ es cíclico.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Construcción del cuadrilátero cíclico

Problema 1. Construir un cuadrilátero convexo y cíclico dados sus cuatro lados $a$, $b$, $c$ y $d$.

Solución. Notemos primero que es necesario que la suma de cualesquiera tres de los lados dados sea mayor que el lado restante.

Si un lado es mayor que la suma de los otros tres no es posible construir ningún cuadrilátero y si es igual entonces solo es posible construir un cuadrilátero degenerado donde todos los vértices están alineados.

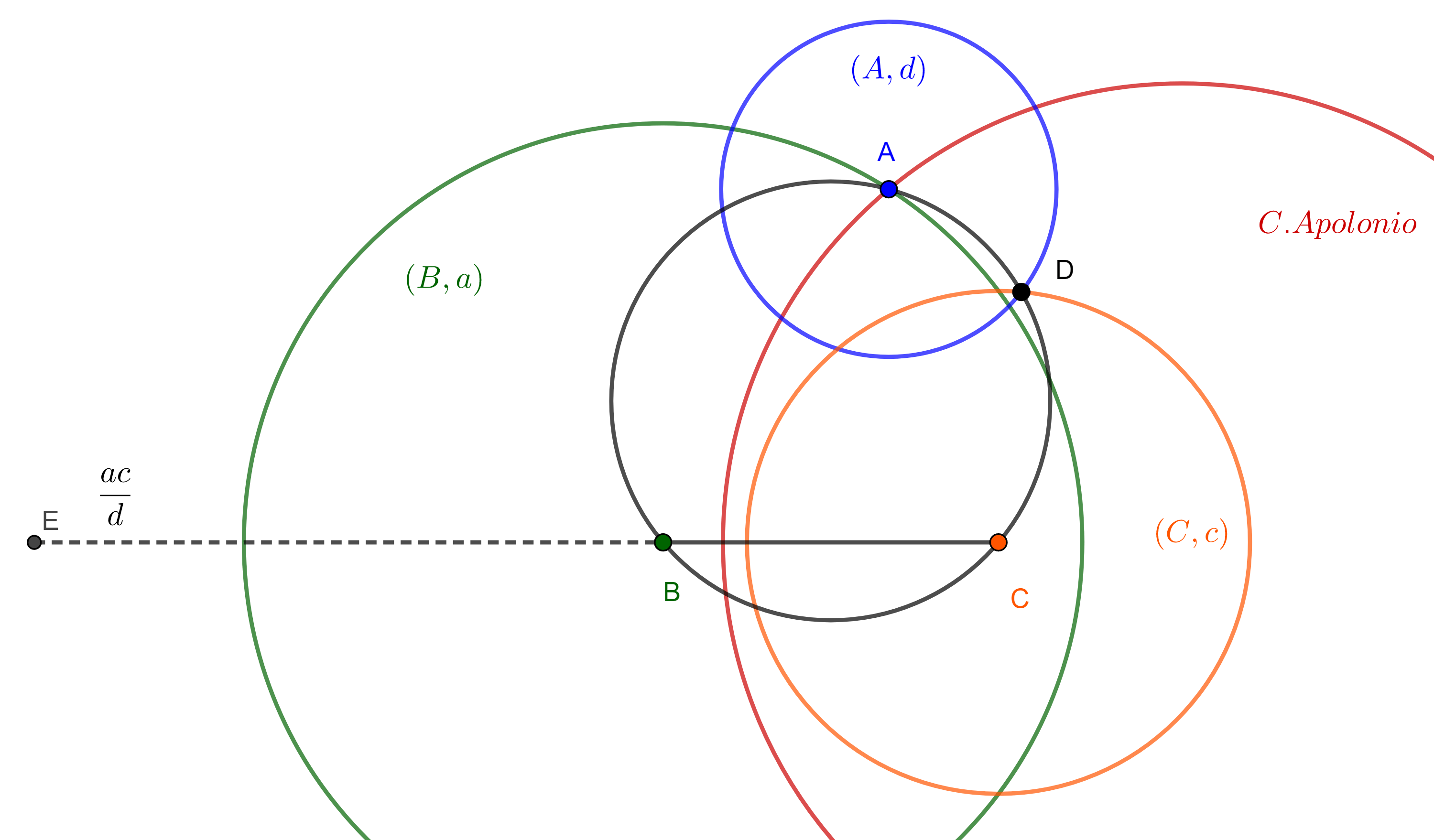
Supongamos que $AB=a$, $BC=b$, $CD=c$ y $DA=d$, la prueba del teorema de Ptolomeo nos sugiere una manera de resolver este problema.

Trazamos el segmento $BC$ y lo extendemos del lado de $B$ hasta un punto $E$ tal que $EB={\displaystyle \frac{ac}{d}}$, el cual es posible construir pues podemos construir el producto de dos magnitudes y el inverso de una magnitud dadas.

Aquí usaremos que $B\in EC$ $\iff$ $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ es cíclico y que los triángulos $\mathrm{△}ABE$ y $\mathrm{△}ADC$ son semejantes, como en la prueba anterior.

La razón de semejanza está dada por ${\displaystyle \frac{AE}{AC}}={\displaystyle \frac{BE}{CD}}={\displaystyle \frac{ac}{dc}}={\displaystyle \frac{a}{d}}$.

Esto último nos dice que la razón entre las distancias de $A$ a los puntos $E$ y $C$ es una razón fija por lo tanto $A$ esta en la circunferencia de Apolonio determinada por $E$, $C$ y la razón ${\displaystyle \frac{a}{d}}$.

Por otro lado, el vértice $A$ se encuentra en la circunferencia con centro en $B$ y radio $a$, por lo tanto, $A$ esta determinado por la intersección de $(B,a)$ y la circunferencia de Apolonio mencionada.

Ahora que conocemos la diagonal $AC$ podemos completar el triángulo $\mathrm{△}ACD$ trazando circunferencias $(A,d)$ y $(C,c)$, una de las intersecciones será el cuarto vértice del cuadrilátero buscado.

Por construcción $\mathrm{△}ABE$ y $\mathrm{△}ADC$ son semejantes por lo que $\mathrm{\angle }CBA$ y $\mathrm{\angle }ADC$ son suplementarios.

Por lo tanto $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ es cíclico.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Distancia de los vértices de un polígono cíclico a un punto del circuncírculo

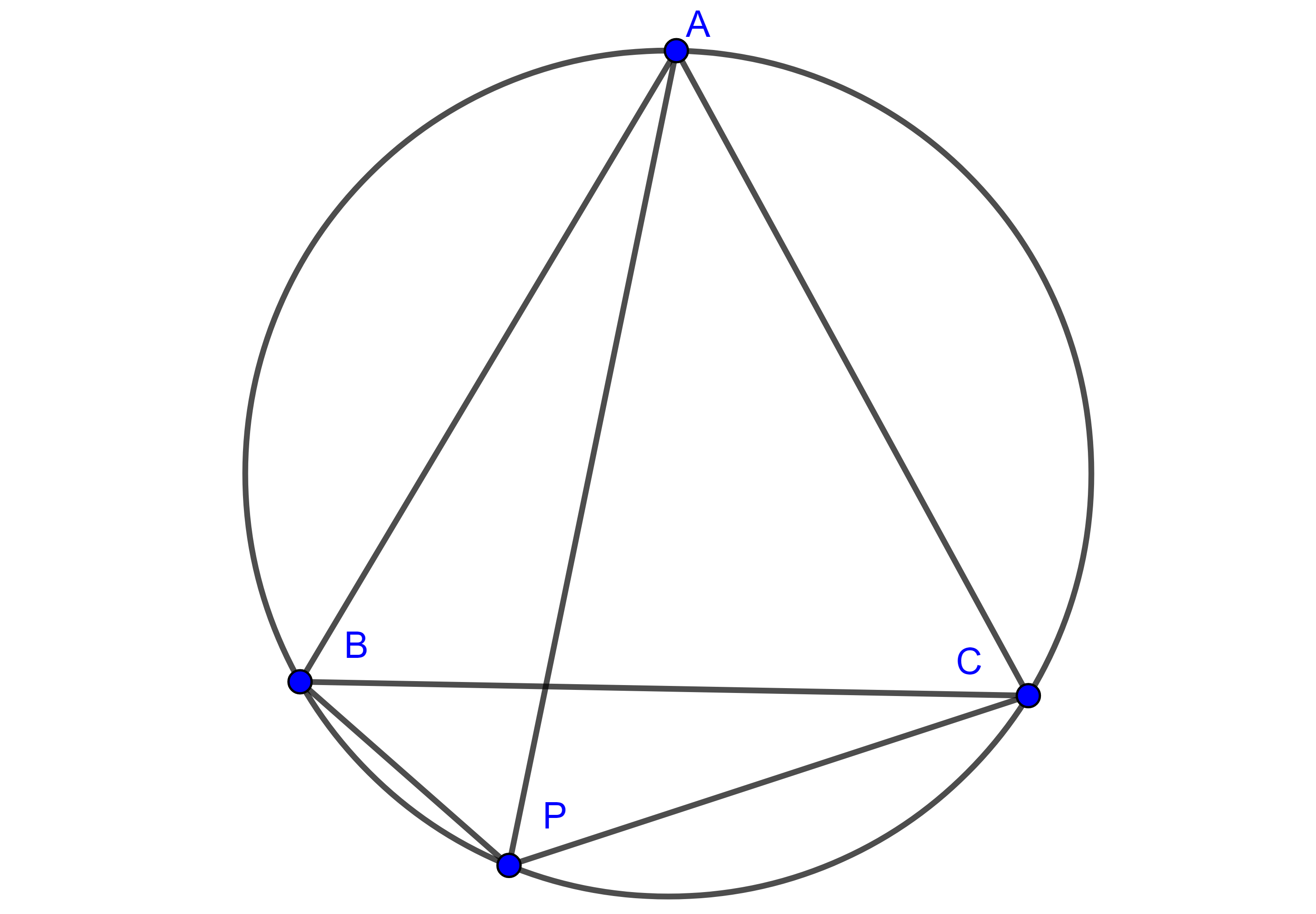
Problema 2. Sean $\mathrm{△}ABC$ isósceles con $AB=AC$ y $P$ un punto en el arco $\stackrel{⌢}{BC}$ del circuncírculo de $\mathrm{△}ABC$, muestra que ${\displaystyle \frac{PA}{PB+PC}}={\displaystyle \frac{AC}{BC}}$.

Solución. Aplicando el teorema de Ptolomeo a $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABPC$ tenemos que
$PA\times BC=AB\times PC+AC\times PB$
$=AC\times PC+AC\times PB=AC(PC+PB)$.

Por lo tanto, ${\displaystyle \frac{PA}{PB+PC}}={\displaystyle \frac{AC}{BC}}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Problema 3. Sean $ABCDE$ un pentágono regular inscrito en una circunferencia y $P$ un punto en el arco $\stackrel{⌢}{BC}$, muestra que $PA+PD=PB+PC+PE$.

Solución. Como el pentágono es regular, entonces sus diagonales tienen la misma longitud.

Aplicando el teorema de Ptolomeo a $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABPC$  y $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}BPCD$ obtenemos
$BC\times PA=AB\times PC+AC\times PB=BC\times PC+AC\times PB$
$BC\times PD=PB\times CD+PC\times BD=PB\times BC+PC\times AC$.

Sumando estas dos últimas igualdades tenemos
$\begin{array}{}\text{(2)}& BC(PA+PD)=BC(PB+PC)+AC(PB+PC).\end{array}$

Por otra parte dado que $\mathrm{△}BEC$ es isósceles podemos aplicar el resultado del problema anterior y obtenemos ${\displaystyle \frac{PE}{PB+PC}}={\displaystyle \frac{EC}{BC}}$

$\iff$ $\begin{array}{}\text{(3)}& {\displaystyle \frac{PE\times BC}{PB+PC}}=EC=AC.\end{array}$

Sustituyendo $(3)$ en $(2)$ resulta
$BC(PA+PD)=BC(PB+PC)+{\displaystyle \frac{PE\times BC}{PB+PC}}(PB+PC)$.

Por lo tanto, $PA+PD=PB+PC+PE$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Hexágono cíclico

Problema 4. Sea $ABCDEF$ un hexágono convexo inscrito en una circunferencia. Consideremos las diagonales que dividen al hexágono en dos cuadriláteros cíclicos, $AD=d$, $CF=e$ y $BE=f$ y los lados del hexágono que no comparten vértices con dichas diagonales $BC=a$, $EF=a^{\prime }$, $DE=b$, $AB=b^{\prime }$, $AF=c$, $CD=c^{\prime }$ respectivamente, entonces $def=a{a}^{\prime }d+b{b}^{\prime }e+c{c}^{\prime }f+abc+a^{\prime }{b}^{\prime }{c}^{\prime }$.

Demostración. Aplicando el teorema de Ptolomeo a $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ y $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}BCDE$ obtenemos
$ad+b^{\prime }{c}^{\prime }=AC\times BD$ y $ab+c^{\prime }f=BD\times CE$.

Multiplicamos por $a^{\prime }$ y $c$ respectivamente y después sumamos el resultado y obtenemos:
$a{a}^{\prime }d+a^{\prime }{b}^{\prime }{c}^{\prime }+abc+c{c}^{\prime }f$
$=a^{\prime }(AC\times BD)+c(BD\times CE)=BD(a^{\prime }AC+cCE)$.

Aplicando Ptolomeo a $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ACEF$ obtenemos $a^{\prime }AC+cCE=eAE$.

Por lo tanto $a{a}^{\prime }d+a^{\prime }{b}^{\prime }{c}^{\prime }+abc+c{c}^{\prime }f=BD(eAE)=e(BD\times AE)$.

Ahora consideramos $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABDE$ y por el teorema de Ptolomeo obtenemos
$BD\times AE=df-b{b}^{\prime }$.

En consecuencia tenemos $a{a}^{\prime }d+a^{\prime }{b}^{\prime }{c}^{\prime }+abc+c{c}^{\prime }f=e(df–b{b}^{\prime })$.

Por lo tanto, $def=a{a}^{\prime }d+b{b}^{\prime }e+c{c}^{\prime }f+abc+a^{\prime }{b}^{\prime }{c}^{\prime }$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Más adelante…

En la próxima entrada estudiaremos trigonometría y mostraremos algunas identidades trigonométricas aplicando el teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que un cuadrilátero convexo es cíclico si y solo si:
   $i)$ un ángulo interno formado con una diagonal y un lado es igual al ángulo interno formado con la otra diagonal y el lado opuesto,
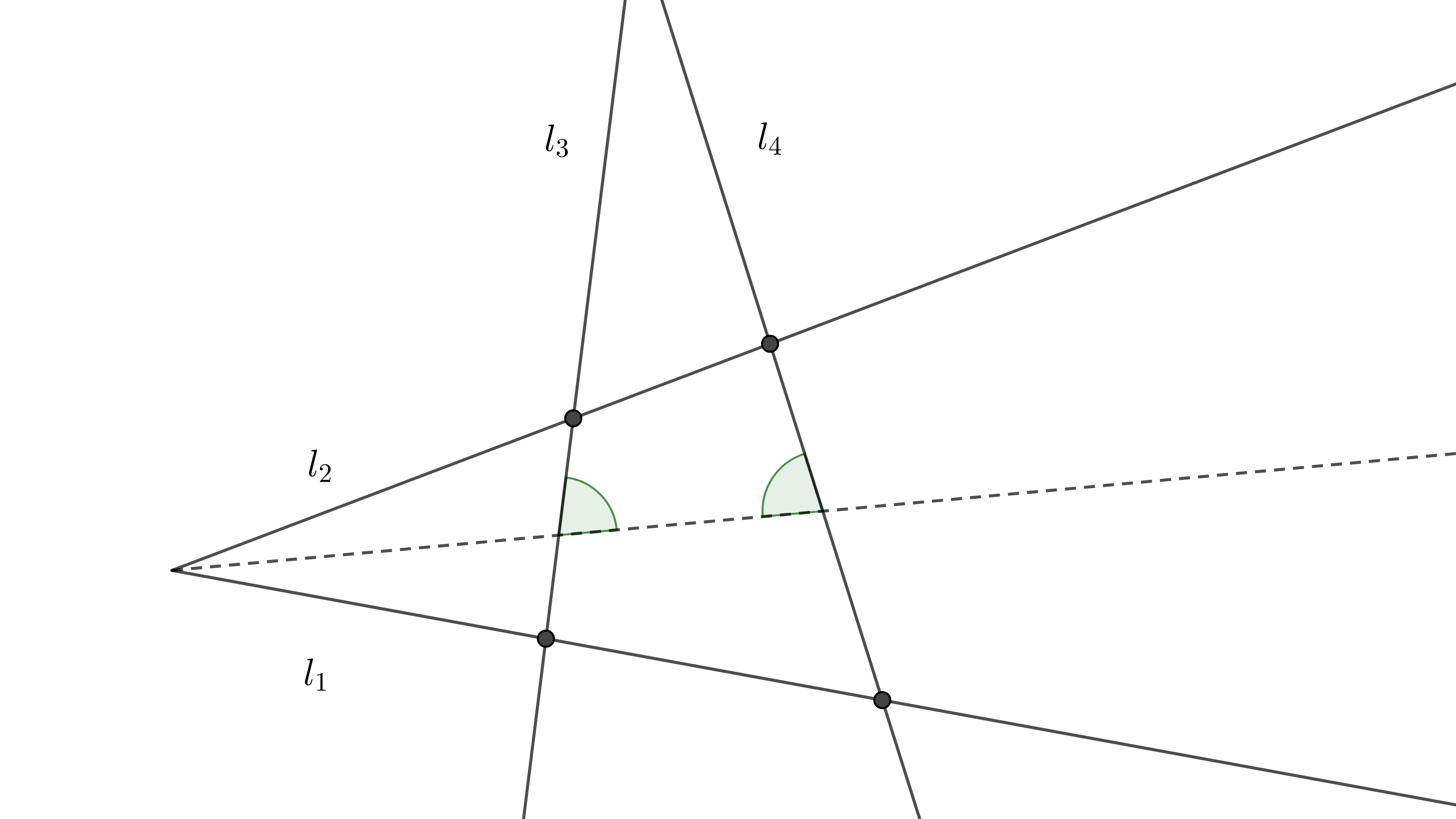
   $ii)$ las mediatrices de los lados del cuadrilátero son concurrentes.
2. Sean $l_1$, $l_2$ y $l_3$, $l_4$ dos pares de rectas tales que la bisectriz del primer par es transversal al segundo par y forma ángulos internos iguales entonces decimos que $l_3$ y $l_4$ son antiparalelas respecto a $l_1$ y $l_2$. Muestra que un cuadrilátero convexo es cíclico si y solo si un par de lados opuestos es antiparalelo respecto al otro par de lados opuestos.

3. Como podrás haber notado nuestra construcción del cuadrilátero cíclico no es única pues partimos de una suposición arbitraria, que $AB=a$, $BC=b$, $CD=c$ y $DA=d$ para $a$, $b$, $c$ y $d$ dados. Muestra que es posible construir tres cuadriláteros cíclicos diferentes con los mismos lados y que de estos se obtienen tres diagonales diferentes.
4. Expresa la razón de las diagonales de un cuadrilátero cíclico en términos de sus lados.
5. Considera $\mathrm{△}ABC$ equilátero y $P$ un punto en el arco $\stackrel{⌢}{BC}$ del circuncírculo de $\mathrm{△}ABC$, prueba que $PA=PB+PC$.
6. Sean $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$ un cuadrado y $P\in \stackrel{⌢}{BC}$ del circuncírculo de $\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}ABCD$, muestra que ${\displaystyle \frac{PA+PC}{PD+PB}}={\displaystyle \frac{PD}{PA}}$.
7. Si $ABCDEF$ es un hexágono regular y $P\in \stackrel{⌢}{BC}$ del circuncírculo de $ABCDEF$, muestra que $PE+PF=PA+PB+PC+PD$.
8. Sean $\mathrm{△}ABC$ equilátero, $P\in \stackrel{⌢}{BC}$ del circuncírculo de $\mathrm{△}ABC$ y $D$ la intersección de $BC$ con $AP$, demuestra que ${\displaystyle \frac{1}{PD}}={\displaystyle \frac{1}{PB}}+{\displaystyle \frac{1}{PC}}$.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Potencia de un punto.
• Siguiente entrada del curso: Trigonometría.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 127-131.
• Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 15-19, 31-34.
• Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 33-35.
• Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 62-66.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»