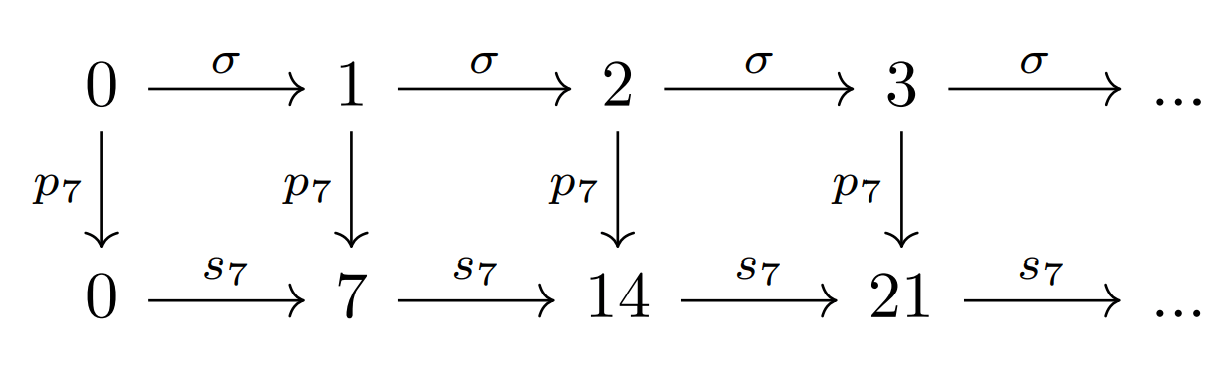Archivo de la etiqueta: multiplicación

Álgebra Superior I: Suma y producto de naturales y sus propiedades

Por Guillermo Oswaldo Cota Martínez

Introducción

La función suma

Usaremos el teorema de recursión que revisamos en la entrada pasada para definir la función suma entre números naturales.

Primero, recordemos qué nos menciona este teorema:

Teorema (Recursión Débil): Sea $X$ un conjunto y $x_{0} \in X$ . Supongamos que tenemos una función $f : X \to X$ . Entonces existe una única función $ϕ : N \to X$ tal que:

$ϕ (0) = x_{0}$
$ϕ (σ (n)) = f (ϕ (n)) .$

Ahora, definamos la función suma como sigue: La función sumar $n$ unidades a un número estará dada por $s_{n} : N \to N$ dada por:

$s_{n} (0) = n$
$s_{n} (σ (m)) = σ (s_{n} (m))$

Notación: Para cada par de números naturales $n, m$ , escribiremos $s_{n} (m) = n + m .$
Y por el teorema de recursión, esta es una función bien definida. Ahora veamos cuál es esta función. La primera condición nos dice que la función evaluada en el $0$ es $n$ . Ahora veamos cómo es que esta función se define para los siguientes números, nota que si aplicamos la segunda condición, obtenemos que $s_{n} (σ (0)) = σ (s_{n} (0)) .$ Recordando cómo definimos la función sucesora, sustituimos $σ (0)$ por $1$ para obtener que $s_{n} (1) = σ (s_{n} (0)) = σ (n) .$ De tal manera que $s_{n} (1) = n + 1 .$ De manera similar se puede comprobar que $s_{n} (2) = n + 2 .$ Y de manera recursiva, podemos demostrar que $\begin{aligned} s_{n} (3) & = n + 3 \\ s_{n} (4) & = n + 4 \\ s_{n} (5) & = n + 5 \\ ⋮ \\ s_{n} (m) & = n + m \\ ⋮ \end{aligned}$ Como podrás observar, la función $s_{n}$ corresponde a sumarle a un número $n$ unidades. Formalmente así es como se defina la suma entre dos números. Veamos a continuación algunas propiedades de la suma. Como dato adicional, nota que para todo número natural $n$ , $s_{n} (1) = σ (n)$ .

Propiedades de la suma

Proposición. La suma es asociativa, esto quiere decir, para $n, m, k \in N$ se cumple que: $s_{n} (s_{m} (k)) = s_{n + m} (k) .$
Demostración. Sean $n, m, k \in N$ . Lo que queremos demostrar es que $n + (m + k) = (n + m) + k .$ Para ello, nota que bastará probar que $s_{n} \circ s_{m} = s_{n + m}$ . Para ello notemos que

$s_{n} (s_{m} (0)) = s_{n} (m) = m + n$
$s_{n} (s_{m} (σ (k))) = s_{n} (σ (s_{m} (k))) = σ (s_{n} (s_{m} (k)))$

Por otro lado, por definición de la suma:

$s_{n + m} (0) = n + m$
$s_{n + m} (σ (k)) = σ (s_{n + m} (k))$

Esto quiere decir que tanto $s_{n} \circ s_{m}$ como $s_{n + m}$ cumplen las dos condiciones del teorema de recursión, y este nos asegura que $s_{n + m} = s_{n} \circ s_{m}$ pues el teorema asegura que la función que cumple dichas dos condiciones es única.

Proposición. La suma es conmutativa. Es decir, para $n, m, k \in N$ se cumple que: $s_{n} (m) = s_{m} (n) .$

Demostración. Sea $n \in N$ . Haremos la demostración por inducción sobre $m$ .
Base inductiva. Notemos que $s_{n} (0) = n$ . Por otro lado, se puede demostrar sin mucha dificultad que $s_{0} (n) = n$ (se deja como tarea moral la demostración de este enunciado). De esta manera $s_{n} (0) = s_{0} (m) .$

Hipótesis de inducción. Supongamos que $m \in N$ es tal que $s_{n} (m) = s_{m} (n) .$

Paso inductivo. Ahora demostraremos que $s_{n} (σ (m)) = s_{σ (m)} (n) .$ Para ello notemos que $s_{n} (σ (m)) = σ (s_{n} (m))$ Ahora, aplicando la hipótesis de inducción, tenemos que $σ (s_{n} (m)) = σ (s_{m} (n)) .$ Ahora, nota que $$ \begin{align*}
\sigma(s_m(n)) &= s_m(\sigma(n)) \

& = s_m(s_1(n))\

&= s_{m+1}(n) \

&= s_{\sigma(m)}(n)
\end{align*}$$

Estas últimas dos igualdades son válidas debido a la asociatividad de la suma. Es una vez concluido esto último que podemos seguir la cadena de igualdades. Esto resulta en que $s_{n} (σ (m)) = s_{σ (m)} (n) .$ Como se quería demostrar.

La multiplicación

Cuando apenas estamos aprendiendo a sumar, alguna vez nos encontramos con una abreviación de sumar los mismos términos. Por ejemplo, nos dicen que si tenemos tres grupos de perros, cada uno con cinco perros, entonces podríamos contar el número total de perros con la siguiente expresión:

$5 + 5 + 5$

$3$ grupos de perros con $5$ perros cada uno

Quizá no es tan tardado en escribir $5 + 5 + 5$ , y llegaríamos a la conclusión de que hay $15$ perros en total. Pero ahora ¿Qué pasaría si tenemos trescientos grupos de perros con cinco perros cada uno? Pues la notación se complica, pues para escribirlo, deberíamos anotar $5 + 5 \underset{296 veces}{\underset{⏟}{+ \dots +}} 5 + 5$ , es decir, sumar $5$ unas $300$ veces.

$300$ grupos de perros con $5$ perros cada uno

Es por esto que se llega a la noción de multiplicación, pues al considerar la primera suma, bien podemos escribir: $5 + 5 + 5 = 3 \times 5.$ Y la segunda suma: $5 + 5 \underset{296 veces}{\underset{⏟}{+ \dots +}} 5 + 5 = 300 \times 5 .$

Ahora, nota que la primera suma se puede expresar como $(5 + 5) + 5 = (2 \times 5) + 5$ De manera que sabemos que $3 \times 5 = (s (1) \times 5) + 5 .$

De igual forma $(s (298) \times 5) + 5 = 300 \times 5$ Eso generalizando a cualquier número $n \in N$ lo escribiríamos como $s (n) \times 5 = (n \times 5) + 5$ Y para cualquier número $m \in N$ : $s (n) \times m = (n \times m) + m$

Definición de la multiplicación

Sean $n, m \in N$ , la multiplicación entre números naturales la definiremos como la función $\times : N \to N$ tal que:

$\begin{aligned} 0 & \times n = 0 \\ s (n) & \times m = (n \times m) + m \end{aligned}$

Nota que esta es una definición recursiva, pues la definición de la multiplicación del sucesor de un elemento depende de la multiplicación del mismo elemento.

Usando el hecho de que sabemos que la multiplicación con el $0$ siempre es $0$ , podemos obtener una propiedad interesante al ver qué pasa cuando multiplicamos cualquier elemento con el $1$ , pues resultará que la multiplicación se comportará como la identidad cuando multiplicamos con el $1$ .

Proposición. Para cualquier número natural $m$ , $1 \times m = m$ .

Demostración. Notemos que por definición $0 \times m = 0$ , de manera que $1 \times m = s (0) \times m$ .

A su vez, podemos usar la otra propiedad de la multiplicación para sustituir el término $s (0)$ : $s (0) \times m = (0 \times m) + m = m$ Llegando así al resultado deseado.

Otra proposición interesante es que esta operación es conmutativa, y es algo que sabemos por sentido común, pues podríamos escribir que $3 \times 5 = 5 + 5 + 5 = 15 = 3 + 3 + 3 + 3 + 3 = 5 \times 3$ Nuestro sentido común nos lo dice, sin embargo para demostrar esto, deberemos usar inducción matemática.

Proposición. La multiplicación de números naturales es conmutativa.

Demostración. Para esto notemos que podemos definir la multiplicación de cada número natural $m$ en términos de el teorema débil de recursividad como:
${\begin{cases} f_{m} (0) & = 0 \\ f_{m} (n + 1) & = m \times n + m \end{cases}$
Ahora definamos la función $g_{m} (n) = n \times m$ y veamos que es la misma que $f$ .
Notemos que cualquier suma de $0$ consigo misma es $0$ , haciendo que $g_{m} (0) = 0$ esto se puede demostrar por inducción y resulta una tarea que puede poner en práctica tus habilidades para este tipo de demostraciones.

Notemos que adicionalmente:
$\begin{aligned} g_{m} (n + 1) & = (n + 1) \times m \\ = (n \times m) + m \\ = g_{m} (n) + m \end{aligned}$
Demostrando que $g_{m}$ también cumple la definición de $f_{m}$ . Como el teorema de recursión débil nos garantiza que $f_{m}$ es única, entonces $g_{m} = f_{m}$ , esto quiere decir que $m \times n = n \times m$ .

Como esto sucede para cualquier número natural $m$ , entonces es cierta la siguiente afirmación: « $\forall m, n \in N, m \times n = n \times m$ ».

Más adelante…

Ahora que hemos visto la suma y multiplicación de los números naturales, hablaremos un poco más de los conjuntos y su relación con los números naturales introduciendo «el tamaño de los conjuntos» o «cardinalidad».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que para todo número natural $n$ , $s_{n} (1) = σ (n)$ .
Demuestra que para todo número natural $n$ , $s_{0} (n) = n$ .
Demuestra que la multiplicación es asociativa.
Demuestra que $0 \times n = n \times 0$ .

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Principio de recursión en los números naturales
Siguiente entrada del curso: Cardinalidad de conjuntos finitos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior II: El producto en los enteros

Por Ana Ofelia Negrete Fernández

Deja un comentario

Introducción

En la entrada anterior hablamos de cómo se construye el conjunto $Z$ de los números enteros y cómo definir una operación de suma en él. Vimos que esta operación de suma tenía cuatro propiedades clave: asociatividad, conmutatividad, existencia de un neutro y de inversos. A partir de ello definimos también la operación de resta. En esta entrada continuaremos con la construcción de las operaciones en $Z$ . Ahora definiremos el producto de números enteros.

Intuición del producto de enteros y su definición formal

La definición de la suma de los enteros resultó ser muy sencilla. Si tenemos enteros $\overset{―}{(a, b)}$ y $\overset{―}{(c, d)}$ entonces para hacer la suma simplemente «sumamos entrada a entrada» para obtener $\overset{―}{(a + c, b + d)}$ . Uno podría pensar que para hacer el producto de enteros esto debe ser igual de fácil, definiendo al producto simplemente como $\overset{―}{(a c, b d)}$ . Sin embargo, esta definición no funciona, pues no tiene muchas de las propiedades valiosas que debería tener una operación de producto.

Antes de dar la definición, recordemos nuestra intuición de qué quería decir cada pareja $(a, b)$ . En la entrada anterior, a cada pareja la asociábamos con la ecuación $a = x + b$ . La relación de equivalencia que dimos consistía en asociar a las parejas cuyas ecuaciones daban la misma solución. De manera informal, podemos pensar entonces a la pareja $(a, b)$ como si fuera $a - b$ . Pero ojo: esto sólo es intuición, pues $a$ y $b$ son elementos de $N$ y ahí no hay operación de resta.

De cualquier forma, esta intuición es valiosa, pues nos sugiere cuál debería de ser la definición de producto. De manera intuitiva, queremos que suceda $(a - b) (c - d) = a c - a d - b c + b d = (a c + b d) - (a d + b c)$ , y aquí cada término entre paréntesis sí es un natural válido: $a c + b d$ y $a d + b c$ , así que el resultado correspondería a la pareja $(a c + b d, a d + b c)$ . Es muy interesante que esta intuición informal en verdad da una buena definición de producto.

Definición. El producto en $Z$ es la función $⋆ : Z \times Z \to Z$ tal que para enteros $\overset{―}{(a, b)}$ y $\overset{―}{(c, d)}$ , se tiene que $\overset{―}{(a, b)} ⋆ \overset{―}{(c, d)} = \overset{―}{(a c + b d), (a d + b c)} .$

Como en el caso de la suma, estamos usando un símbolo especial para el producto en $Z$ , de modo que podamos distinguirlo del producto en $N$ . Así como en el caso de la suma, sólo haremos la distinción explícita en este momento. Usualmente nos referiremos al producto de enteros $\overset{―}{(a, b)}$ y $\overset{―}{(c, d)}$ como $\overset{―}{(a, b)} \cdot \overset{―}{(c, d)}$ , o simplemente como $\overset{―}{(a, b)} \overset{―}{(c, d)}$ . Esto será claro por el contexto.

El producto en $Z$ está bien definido

Nuestra definición de producto en $Z$ es un poco extraña, así que debemos dedicar algo de trabajo a verificar que en realidad es el producto tal y como siempre lo habíamos conocido. La primer cosa que debemos hacer es ver que el producto en $Z$ está bien definido, es decir, que el resultado es el mismo independientemente de los representantes que se elijan para realizar la multiplicación.

Proposición. El producto en $Z$ está bien definido.

Demostración. Comencemos con parejas $(a, b) \sim (e, f)$ y $(c, d) \sim (g, h)$ . Como $(a, b) \sim (e, f)$ , entonces $a + f = b + e .$ También, $(c, d) \sim (g, h)$ , implica que $c + h = d + g .$

Usando la definición de producto de dos enteros, se tiene por un lado que
$\overset{―}{(a, b)} \overset{―}{(c, d)} = \overset{―}{(a c + b d, a d + b c)} .$

Por otro lado, tenemos

$\overset{―}{(e, f)} \overset{―}{(g, h)} = \overset{―}{(e g + f h, e h + f g)} .$

Así, debemos demostrar que $\overset{―}{(a c + b d, a d + b c)} = \overset{―}{(e g + f h, e h + f g)}$ . Poniendo en términos de la relación de equivalencia, se deberá cumplir que $(a c + b d) + (e h + f g) = (a d + b c) + (e g + f h) .$

Multiplicando las primeras igualdades que encontramos, tenemos lo siguiente:
$\begin{aligned} (a + f) (c + h) & = (b + e) (d + g) \\ a c + a h + f c + f h & = b d + b g + e d + e g . \end{aligned}$

Sumemos $b d + f h$ en ambos lados de la ecuación y usemos nuevamente las hipótesis para obtener las siguientes igualdades:

$\begin{aligned} (b d + f h) + a c + a h + f c + f h & = (b d + f h) + b d + b g + e d + e g \\ (a c + b d) + h (a + f) + f (c + h) & = b (d + g) + d (b + e) + (e g + f h) \\ (a c + b d) + h (b + e) + f (d + g) & = b (c + h) + d (a + f) + (e g + f h) \\ (a c + b d + e h + f g) + h b + d f & = (b c + a d + e g + f h) + h b + d f \\ a c + b d + e h + f g & = a d + b c + e g + f h . \end{aligned}$

Esto es justo lo que queríamos mostrar.

En la demostración anterior estamos usando las propiedades de las operaciones en $N$ ya prácticamente sin enunciarlas. A estas alturas ya podemos hacer eso, pues hemos trabajado bastante con ellas. Sin embargo, es importante que de vez en cuando te preguntes por qué se vale cada una de las igualdades.

Propiedades del producto en $Z$

Ya que hemos definido el producto en los enteros, es importante verificar que hay algunas propiedades que se cumplen. Esto nos permitirá más adelante trabajar sin problema con el producto de enteros, como se ha hecho desde la educación básica.

Proposición. Se satisfacen las siguientes propiedades para la operación de producto en $Z$ .

Asociatividad. Para enteros $\overset{―}{(a, b)}$ , $\overset{―}{(c, d)}$ y $\overset{―}{(e, f)}$ se satisface que $(\overset{―}{(a, b)} \overset{―}{(c, d)}) \overset{―}{(e, f)} = \overset{―}{(a, b)} (\overset{―}{(c, d)} \overset{―}{(e, f)}) .$
Conmutatividad. Para enteros $\overset{―}{(a, b)}$ y $\overset{―}{(c, d)}$ se satisface que $\overset{―}{(a, b)} \overset{―}{(c, d)} = \overset{―}{(c, d)} \overset{―}{(a, b)} .$
Neutro. Existe un elemento neutro, es decir, existe un entero $\overset{―}{(m, n)}$ tal que para cualquier entero $\overset{―}{(a, b)}$ se cumple que $\overset{―}{(a, b)} \overset{―}{(m, n)} = \overset{―}{(a, b)} .$
Los únicos elementos que tienen inverso multiplicativo son $\overset{―}{(1, 0)}$ y $\overset{―}{(0, 1)}$ .

Demostración. Las demostraciones de la asociatividad y la conmutatividad quedan como tarea moral. La sugerencia es desarrollar ambos lados de las igualdades usando la definición de producto, y luego utilizar propiedades del producto y la suma en $N$ .

El elemento que sirve como neutro para el producto es el $\overset{―}{(1, 0)}$ . En efecto, usando la definición tenemos que: $\overset{―}{(a, b)} \overset{―}{(1, 0)} = \overset{―}{(a \cdot 1 + b \cdot 0, a \cdot 0 + b \cdot 1)} = \overset{―}{(a, b)} .$

Es sencillo ver que los elementos indicados sí tienen inverso. El inverso de $\overset{―}{(1, 0)}$ es él mismo y el inverso de $\overset{―}{(0, 1)}$ también es él mismo. En efecto:

$\begin{aligned} \overset{―}{(1, 0)} \overset{―}{(1, 0)} & = \overset{―}{(1 \cdot 1 + 0 \cdot 0, 1 \cdot 0 + 0 \cdot 1)} = \overset{―}{(1, 0)} \\ \overset{―}{(0, 1)} \overset{―}{(0, 1)} & = \overset{―}{(0 \cdot 0 + 1 \cdot 1, 0 \cdot 1 + 1 \cdot 0)} = \overset{―}{(1, 0)} . \end{aligned}$

Para ver que estos son los únicos elementos que tienen inversos, supongamos que algún otro entero $\overset{―}{(a, b)}$ tiene inverso multiplicativo $\overset{―}{(c, d)}$ . Esto querría decir que $\overset{―}{(a c + b d, a d + b c)} = \overset{―}{(1, 0)}$ , que en términos de la relación de equivalencia se traduce a $a c + b d = a d + b c + 1.$

Si $a = b$ , la igualdad no se puede dar pues tendríamos $a c + a d = a d + a c + 1$ , que es imposible. Por tricotomía en $N$ , tenemos entonces que $a > b$ o $a < b$ . Resolveremos el caso $a > b$ y el caso $a < b$ quedará como tarea moral.

Si $a = b + 1$ , entonces la igualdad queda como $(b + 1) c + b d = (b + 1) d + b c + 1$ , que se simplifica a $c = d + 1$ . Esto nos da la solución $\overset{―}{(a, b)} = \overset{―}{(c, d)} = \overset{―}{(1, 0)}$ .

En otro caso, tenemos $a \geq b + 2$ y por lo tanto podemos escribir $a = b + 1 + k$ con $k \geq 1$ . La igualdad queda entonces como $(b + 1 + k) c + b d = (b + 1 + k) d + b c + 1.$ Desarrollando y simplificando tenemos que $c + k c = d + k d + 1.$ Si $d \geq c$ , el lado derecho claramente es más grande, así que no hay solución. De este modo, $d < c$ y por lo tanto podemos escribir $c = d + l$ con $l \geq 1$ . Usando esta igualdad en $c + k c = d + k d + 1$ , llegamos a la igualdad $d + l + k d + k l = d + k d + 1,$ que se simplifica a $l (k + 1) = 1.$ Pero como $k \geq 1$ , entonces $k + 1 \geq 2$ y como además $l \geq 1$ , tenemos $l (k + 1) \geq 2$ , así que en este caso no tenemos soluciones.

Las propiedades anteriores se pueden enunciar únicamente en términos de la operación de producto. Además de estas propiedades, hay otra que nos dice cómo el producto interactúa con la operación suma en $Z$ .

Proposición. Se cumple la ley distributiva para la suma y el producto, es decir, para enteros $\overset{―}{(a, b)}$ , $\overset{―}{(c, d)}$ y $\overset{―}{(e, f)}$ se cumple que $\overset{―}{(a, b)} (\overset{―}{(c, d)} + \overset{―}{(e, f)}) = \overset{―}{(a, b)} \overset{―}{(c, d)} + \overset{―}{(a, b)} \overset{―}{(e, f)} .$

Demostración. Realizando la operación correspondiente al lado izquierdo tenemos:

$\begin{aligned} \overset{―}{(a, b)} (\overset{―}{(c, d)} + \overset{―}{(e, f)}) & = \overset{―}{(a, b)} \overset{―}{(c + e, d + f)} \\ = \overset{―}{(a (c + e) + b (d + f), a (d + f) + b (c + e))} \\ = \overset{―}{(a c + a e + b d + b f, a d + a f + b c + b e)} . \end{aligned}$

Observa cómo aquí se está usando la propiedad distributiva, pero en $N$ .

Realizando la operación correspondiente al lado derecho tenemos:

$\begin{aligned} \overset{―}{(a, b)} \overset{―}{(c, d)} + \overset{―}{(a, b)} \overset{―}{(e, f)} & = \overset{―}{(a c + b d, a d + b c)} + \overset{―}{(a e + b f, a f + b e)} \\ = \overset{―}{(a c + b d + a e + b f, a d + b d + a f + b e)} . \end{aligned}$

Usando la conmutatividad de la suma en $N$ , obtenemos que esta expresión es igual a la del lado izquierdo, como queríamos.

Divisores de cero y cancelación

Hasta donde hemos platicado, los enteros tienen suma, resta y producto. Sin embargo, en los enteros todavía no tenemos una operación de división. Esto causa un par de dificultades. Una de estas es que cuando queremos resolver ecuaciones del estilo $a = b x$ con $a$ y $b$ enteros y $x$ un entero por determinar, no podemos simplemente «pasar la $b$ dividiendo» y obtener $x = a / b$ . Otra dificultad es que cuando tenemos una igualdad del estilo $a b = a c$ tampoco podemos simplemente «dividir entre $a$ ».

La primer dificultad la estudiaremos más a detalle cuando entremos a teoría de números qué es lo que sí se puede hacer en $Z$ . Para la segunda, resulta que de cualquier forma podemos concluir casi siempre que $b = c$ .

Antes de demostrar esto, veamos un resultado intermedio auxiliar. La siguiente proposición a veces se enuncia como que $Z$ no tiene divisores de cero, o bien como que si el producto de dos enteros es cero, entonces alguno de ellos debe de ser cero.

Proposición. Si $\overset{―}{(a, b)}$ , $\overset{―}{(c, d)}$ pertenecen a $Z$ y $\overset{―}{(a, b)} \overset{―}{(c, d)} = \overset{―}{(0, 0)}$ , entonces $\overset{―}{(a, b)} = \overset{―}{(0, 0)}$ o $\overset{―}{(c, d)} = \overset{―}{(0, 0)}$ .

Demostración. Para que el producto $\overset{―}{(a, b)} \overset{―}{(c, d)} = \overset{―}{(a c + b d, a d + b c)}$ sea igual al entero $\overset{―}{(0, 0)}$ , debe suceder que $a c + b d + 0 = a d + b c + 0,$ es decir, que $a c + b d = a d + b c$ . A partir de esto, debemos de demostrar que o bien $a = b$ , o bien que $c = d$ . Supongamos que $a \neq b$ (en otro caso, ya tenemos lo buscado). Por tricotomía, debe pasar $a > b$ ó $a < b$ .

Si $a > b$ , entonces existe un entero $k > 1$ tal que $a = b + k$ , de modo que tenemos las siguientes igualdades:

$\begin{aligned} a c + b d & = a d + b c \\ (b + k) c + b d & = (b + k) d + b c \\ b c + k c + b d & = b d + k d + b c \\ k c & = k d . \end{aligned}$

Como $k >= 1$ , podemos usar la cancelación del producto en $N$ para obtener $c = d$ , como queríamos. Falta el caso $a < b$ , pero es análogo al anterior. Los detalles quedan como tarea moral.

Ahora sí podemos demostrar que en $Z$ se vale cancelar factores distintos de cero.

Proposición. Sean $\overset{―}{(a, b)}$ , $\overset{―}{(c, d)}$ , $\overset{―}{(e, f)}$ elementos en $Z$ . Supongamos que $\overset{―}{(a, b)} \neq \overset{―}{(0, 0)}$ y que $\overset{―}{(a, b)} \overset{―}{(c, d)} = \overset{―}{(a, b)} \overset{―}{(e, f)} .$

Entonces $\overset{―}{(c, d)} = \overset{―}{(e, f)}$ .

Demostración. Tenemos las siguientes igualdades:

$\begin{aligned} \overset{―}{(a, b)} \overset{―}{(c, d)} & = \overset{―}{(a, b)} \overset{―}{(e, f)} \\ \overset{―}{(a, b)} \overset{―}{(c, d)} - \overset{―}{(a, b)} \overset{―}{(e, f)} & = 0 \\ \overset{―}{(a, b)} (\overset{―}{(c, d)} - \overset{―}{(e, f)}) & = 0. \end{aligned}$

Para pasar de la primera a la segunda, estamos restando de ambos lados, lo cual es válido en $Z$ . De la segunda igualdad a la tercera se está usando la ley distributiva para la resta (ver Tarea moral). A partir de aquí podemos usar la proposición anterior. Como $\overset{―}{(a, b)}$ no es cero, entonces $\overset{―}{(c, d)} - \overset{―}{(e, f)} = 0$ . De aquí se obtiene $\overset{―}{(c, d)} = \overset{―}{(e, f)}$ , que es lo que queríamos mostrar.

Más adelante…

Ya tenemos las operaciones para los números enteros. Aún nos falta introducir un concepto muy importante: el de orden. Esto lo haremos en la siguiente entrada. Además, veremos que la noción de orden en $Z$ es compatible con sus operaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Realiza por definición el producto de los enteros $\overset{―}{(8, 3)}$ y $\overset{―}{(3, 5)}$ . ¿Lo que obtienes tiene sentido con el hecho de que $5 \cdot (- 2) = - 10$ ?
Demuestra que el producto en $Z$ es asociativo y conmutativo.
Para terminar la demostración de que $Z$ no tiene divisores de cero, muestra que si se tienen naturales $a, b, c, d$ tales que $a c + b d = a d + b c$ y $a < b$ , entonces $c = d$ . Recuerda que debes trabajar todo en $N$ , en donde no se pueden restar elementos.
Termina la demostración de que en $Z$ los únicos elementos con inversos multiplicativos son $\overset{―}{(1, 0)}$ y $\overset{―}{(0, 1)}$ . Tendrás que llegar a que en el caso faltante la única solución es $\overset{―}{(a, b)} = \overset{―}{(c, d)} = \overset{―}{(0, 1)}$ .
Enuncia y demuestra una ley distributiva para la resta.
Si definiéramos al producto de dos enteros $\overset{―}{(a, b)}$ y $\overset{―}{(c, d)}$ como el entero $\overset{―}{(a c, b d)}$ , ¿cuáles de las propiedades que hemos discutido en esta entrada fallarían?

Entradas relacionadas

Ir a: Álgebra Superior II
Entrada anterior del curso: Construcción de los enteros y su suma
Siguiente entrada del curso: El orden en los enteros

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Compatibilidad del orden con las operaciones de los naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En las entradas anteriores, nos encargamos de definir con toda formalidad la estructura con la que hemos estado familiarizados desde hace mucho; sin embargo, en principio, la forma en que definimos el orden y las distintas operaciones, no parece ser que.

Para finalizar con el estudio de los números naturales, veremos las importantes relaciones que hay entre el orden que definimos para $N$ en la entrada anterior, y las operaciones que hemos trabajado a lo largo de este tema. Para esto, nuevamente ocuparemos el Principio de Inducción.

Una equivalencia del orden

Aunque como mencionamos en la introducción, la forma en que definimos el orden, no parece tener mucha relación con las operaciones definidas, usando la definición de la suma, podemos dar una definición equivalente del orden en $N$ , en el siguiente teorema, demostramos que en efecto, ambas caracterizaciones son equivalentes.

Teorema.Si $n, m$ son números naturales, se tiene que $n < m$ si y sólo si existe $k \in N ∖ {0}$ tal que n+k=m.

Demostración. Procedamos por inducción sobre $n$ .

Si $n = 0$ , si $0 < m$ , entonces $m \in N ∖ {0}$ y $n + m = 0 + m = m$ . Recíprocamente, si existe $k \in N ∖ {0}$ tal que $0 + k = m$ , tendremos que $k = m$ , por lo que $m \neq 0$ y por lo tanto $0 < m$ . Con esto probamos la base de inducción.

Supongamos que el resultado es válido para alguna $n$ y probemos que el resultado para $σ (n)$ es decir, que si $m \in N$ se tiene que $σ (n) < m \Leftrightarrow$ existe $k \in N ∖ {0}$ tal que $σ (n) + k = m$ .

Verifiquemos la ida de la demostración. Supongamos que $σ (n) < m$ , entonces $n < m$ , por lo que por la hipótesis de inducción concluimos que existe $k \neq 0$ tal que $n + k = m$ , como $k \neq 0$ , existe $k^{'}$ tal que $σ (k^{'}) = k$ , entonces tenemos que

$\begin{aligned} m & = n + k \\ = n + σ (k^{'}) \\ = σ (n) + k^{'} \end{aligned}$

Notemos además que $k^{'} \neq 0$ , ya que si $k^{'} = 0$ , entonces $m = σ (n)$ lo cual es un contradicción.

Para el regreso, supongamos que existe $k \neq 0$ tal que $σ (n) + k = m$ y demostremos que $σ (n) \in m$ . Como $σ (n) + k = m$ , concluimos que $n + σ (k) = m$ , por lo que $n < m$ y por lo visto en la entrada de La relación de orden en los naturales, tendremos que $σ (n) \leq m$ . Si $σ (n) = m$ , entonces cancelando, obtenemos que $k = 0$ , lo cual es absurdo, entonces solo queda que $σ (n) < m$ . Con esto concluimos la inducción y la prueba.

El orden y las operaciones

Con el anterior resultado, es más fácil ver las relaciones que tendrán el orden con las operaciones, por ejemplo, la siguiente.

Teorema. Si $n < m$ y $l \in N$ , entonces $n + l < m + l$ .

Demostración. Como $n < m$ , entonces existe $k \neq 0$ tal que $n + k = m$ , de donde $n + l + k = m + l$ , pero justo esa es la definición de que $n + l < m + l$ .

Corolario. Si $a < b$ y $c < d$ , entonces $a + c < b + d$ .

Demostración. Como $a < b$ , entonces $a + c < b + c$ , y como $c < d$ , tenemos que $b + c < b + d$ . Por la transitividad del orden, obtenemos el resultado.

Finalizamos la entrada, marcando la relación entre el orden y la multiplicación.

Teorema. Si $n < m$ y $l \in N ∖ {0}$ , entonces $n \cdot l < m \cdot l$

Demostración. Como $n < m$ entonces existe $k \neq 0$ tal que $n + k = m$ , por lo que $n l + l k = m l$ , sin embargo, como $l$ y $k$ son distintos de cero, entonces $l k$ también es distinto de cero, por lo que $n l < m l$ justo como debíamos probar.

Más adelante…

Con esta entrada, terminamos el estudio de los números naturales, por lo que en la siguiente entrada empezaremos con el estudio de los números enteros. Sin embargo, toda la teoría que hemos desarrollado hasta el momento será la base para poder dar una definición precisa de qué son los números enteros. También nos ayudará a definir sus operaciones, así que nos encontraremos con más oportunidades para practicar nociones de los números naturales.

Hay que hacer una especial mención a los principios de inducción y de buen orden, ya que jugarán un papel crucial a la hora de estudiar las propiedades de los enteros, que nos servirán para desarrollar lo que conocemos como teoría de números.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que si $a < b$ y $c < d$ , entonces $a c < b d$ , no es necesario suponer que los números son distintos de cero.
Si $n < m$ y $l \neq 0$ , entonces $n^{l} < m^{l}$ . Sugerencia, usa inducción sobre $l$ .
Si $n < m$ y $l \neq 0$ , entonces $l^{n} < l^{m}$ .
Si $n < m$ , entonces $n! < m!$ .
Demuestra que si $n, m \in N ∖ {0}$ , entonces $(1 + m)^{n} \geq 1 + n m$ .

Entradas relacionadas

Ir a Álgebra Superior II
Entrada anterior del curso: El principio del Buen Orden
Siguiente entrada del curso: Introducción a estructuras algebraicas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Definición del producto y sus propiedades básicas

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada anterior, nos dedicamos a buscar una definición apropiada para la suma de números naturales, y después nos dedicamos a probar las propiedades más elementales que esta operación satisface.

Ahora es el turno de la multiplicación o producto, que se definirá de forma similar a la suma, ya que ocuparemos el teorema de Recursión Débil, y para probar sus propiedades ocuparemos el principio de Inducción.

Te motivamos a releer la entrada anterior y pensar unos momentos en el ejercicio 5 de la entrada anterior.

Definición del producto

Así como con la suma, recurriremos a una definición recursiva, la cual existe en virtud del teorema de Recursión.

Definición. Sea $m \in N$ , defnimos la función $p_{m} : N ⟶ N$ , como la función que satisface las propiedades siguientes:

$p_{m} (0) = 0$ .
$p_{m} (σ (n)) = s_{m} ((p_{m} (n))$ .

Denotaremos a $p_{m} (n)$ como $m \cdot n$ , o simplemente como $m n$

Ejemplo. Para aclarar la definición anterior, consideremos $p_{7}$ y realicemos el diagrama conmutativo correspondiente a su definición recursiva.

Recordemos que las flechas indican a donde es mandado cada elemento bajo cada función, entonces las flechas verticales, justamente son las que nos indican los valores de $p_{7}$ en cada número natural, observemos que estos valores coinciden con la conocida tabla del $7$ .

$△$

Aprendiendo a multiplicar por uno

En este momento, demostraremos las propiedades más importantes del producto. Tenemos la fortuna de que contamos con una buena cantidad de propiedades de las funciones $s_{n}$ , las cuales ya podremos usar sin ningún problema, más aún, para simplificar la notación haremos uso de la notación $m + n$ , en vez de la notación $s_{m} (n)$ , cada vez que se pueda.

Siguiendo la idea anterior, mencionamos la siguiente identidad, que es solo una reformulación del punto (2) de la definición del producto, pero que nos servirá para esclarecer la mayor parte de las pruebas.

Observación. $a \cdot σ (n) = a + (a \cdot n)$ .

Para referir a esta observación en una demostración ocuparemos el símbolo $\overset{*}{=}$ .

Proposición. Para toda $n \in N$ , se tiene que $p_{1} (n) = n$ , es decir, $1 \cdot n = n$

Demostración. Como se esperaba, la prueba es por inducción sobre $n$ .

Base inductiva: Por la definición de $p_{1}$ , tenemos que $p_{1} (0) = 0$ .

Hipótesis de inducción: Supongamos que para algún $n$ , se tiene que $p_{1} (n) = n$

Paso inductivo: Debemos demostrar que $p_{1} (σ (n)) = σ (n)$ , esto se sigue por las siguientes igualdades

$\begin{aligned} p_{1} (σ (n)) & \overset{*}{=} 1 + (p_{1} (n)) \\ \overset{H.I.}{=} 1 + n = σ (n) . \end{aligned}$

Donde la última igualdad se da recordando que en la entrada anterior probamos que $s_{1} (n) = σ (n)$ .

Con esto hemos aprendido a multiplicar por $1$ .

Aprendiendo a multiplicar por cero

Proposición. Para toda $n \in N$ , se tiene que $p_{0} (n) = 0$ .

Demostración. Procedamos por inducción sobre $n$ , la base inductiva es directa de la definición, ya que $p_{0} (0) = 0$ .

Nuestra hipótesis de inducción consiste en suponer que para alguna $n$ se tiene que $p_{0} (n) = 0$ . Entonces queda demostrar que $p_{0} (σ (n)) = 0$ . Esto se sigue de las siguientes igualdades.

$\begin{aligned} p_{0} (σ (n)) & \overset{*}{=} 0 + p_{0} (n) \\ \overset{H.I.}{=} 0 + 0 = 0 \end{aligned}$

La propiedad distributiva izquierda

La siguiente propiedad es una de las más famosas, ya que nos permitirá relacionar la suma y el producto, además jugará un papel importante en la demostración de las siguientes propiedades.

Proposición (propiedad distributiva izquierda). Si $a, b, n$ son números naturales, entonces $p_{s_{a} (b)} (n) = s_{p_{a} (n)} (p_{b} (n))$ , u ocupando la notación familiar $(a + b) \cdot n = (a \cdot n) + (b \cdot n)$ .

Demostración. Procedamos por inducción, como podrás notar con todas estas demostraciones, la inducción será sobre la variable que aparezca más a la derecha de nuestras expresiones, es decir, la inducción será sobre $n$ .

Base inductiva: Por la definición del producto tenemos que, $(a + b) \cdot 0 = 0$ , y por las propiedades que demostramos para la suma, concluimos que $0 = 0 + 0$ , sin embargo; de nuevo por la definición del producto, $0 = (a \cdot n)$ y $0 = (b \cdot n)$ , uniendo todas estas igualdades concluimos que $(a + b) \cdot 0 = (a \cdot n) + (b \cdot n)$ , justo como queremos.

Hipótesis de inducción: Supongamos que para algún $n$ se tiene que $(a + b) \cdot n = (a \cdot n) + (b \cdot n)$ .

Paso inductivo: Debemos probar que $(a + b) \cdot σ (n) = (a \cdot σ (n)) + (b \cdot σ (n))$ . Por la observación que hicimos, tenemos

$\begin{aligned} (a + b) \cdot σ (n) & \overset{*}{=} (a + b) + ((a + b) \cdot n) \\ \overset{H.I.}{=} (a + b) + ((a \cdot n) + (b \cdot n)) \end{aligned}$

A partir de aquí, el resultado se seguirá usando la asociatividad y la conmutatividad de la suma, en la siguiente cadena de igualades detallamos la demostración paso a paso ¿Puedes identificar cómo ocupamos las propiedades de la suma?.

$\begin{aligned} (a + b) + ((a \cdot n) + (b \cdot n)) & = a + (b + ((a \cdot n) + (b \cdot n))) \\ = a + ((b + (a \cdot n)) + (b \cdot n)) \\ = a + (((a \cdot n) + b) + (b \cdot n)) \\ = a + ((a \cdot n) + (b + (b \cdot n))) \\ = (a + (a \cdot n)) + (b + (b \cdot n)) \\ \overset{*}{=} (a \cdot σ (n)) + (b \cdot σ (n)) \end{aligned}$

Aunque la prueba anterior fue un poco más confusa que las anteriores, las consecuencias que tendrá esta proposición serán sumamente importantes.

El producto es conmutativo

Como mencionamos, la asociatividad y la conmutatividad, serán una consecuencia de las propiedades distributivas, por el momento veamos que en efecto el producto conmuta.

Proposición (conmutatividad). Si $m, n \in N$ , entonces $m \cdot n = n \cdot m$ .

Demostración. Una vez más hagamos la prueba por inducción sobre $n$

Base inductiva: Por definición tenemos que $m \cdot 0 = 0$ , además $p_{0} (m) = 0$ por lo demostrado antes, es decir que $m \cdot 0 = 0 = 0 \cdot m$

Hipótesis de inducción: Supongamos que para alguna $n$ , se tiene que $m \cdot n = n \cdot m$ .

Paso inductivo: Debemos probar que $m \cdot σ (n) = σ (n) \cdot m$ . Esto se sigue ya que

$\begin{aligned} m \cdot σ (n) & \overset{*}{=} m + (m \cdot n) \\ \overset{H.I.}{=} m + (n \cdot m) \end{aligned}$

Pero ya demostramos que $m = 1 \cdot m$ , usando esto y la propiedad ditributiva, podemos concluir que

$\begin{aligned} m + (n \cdot m) & = (1 \cdot m) + (n \cdot m) \\ = (1 + n) \cdot m = σ (n) \cdot m \end{aligned}$

Con la conmutatividad, podemos probar de manera inmediata el siguiente resultado

Corolario (propiedad distributiva derecha). Si $a, b, n$ son números naturales, entonces $a \cdot (b + n) = (a \cdot b) + (a \cdot n)$ .

La prueba queda como un ejercicio moral, en parte porque su prueba no requiere Inducción. Con este resultado, podemos probar la propiedad asociativa del producto.

El producto es asociativo

Con la propiedad distributiva derecha , podemos dar la demostración de la propiedad asociativa del producto.

Proposición (asociatividad). Si $a, b, n$ son números naturales, se tiene que $a \cdot (b \cdot n) = (a \cdot b) \cdot n$ .

Demostración. De nuevo procedamos por inducción sobre $n$

Base inductiva: Notemos que por definición, para cualquier número natural $m$ se tiene que $0 = p_{m} (0) = m \cdot 0$ . Con esto en mente tenemos que, $(a \cdot b) \cdot (0) = 0 = a \cdot 0 = a \cdot (b \cdot 0)$ que es justo la base de inducción.

Hipótesis de Inducción: Supongamos que para alguna $n \in N$ , tenemos que $(a \cdot b) \cdot n = a \cdot (b \cdot n)$

Paso Inductivo: Demostremos que $(a \cdot b) \cdot σ (n) = a \cdot (b \cdot σ (n))$ . Como

$\begin{aligned} (a \cdot b) \cdot σ (n) & \overset{*}{=} (a \cdot b) + (a \cdot b) \cdot n \\ \overset{H.I.}{=} (a \cdot b) + a \cdot (b \cdot n) \\ = a \cdot (b + b \cdot n) \\ \overset{*}{=} a \cdot (b \cdot σ (n)) \end{aligned}$

la igualdad que no está justificada es la aplicación de la propiedad distributiva.

Ley de la cancelación

Para concluir con las propiedades del producto, enunciamos la propiedad de la cancelación del producto, recordemos que esta propiedad también es válida para la suma. Para hacer esta prueba necesitamos trabajar un poco.

Recordemos el ejercicio 2 de la Tarea moral de la entrada Principio de inducción y teoremas de recursión, el cual ya hemos ocupado anteriormente:

Si $n \neq 0$ , entonces existe $a \in N$ tal que $n = σ (a)$

De la misma forma, el ejercicio 1 de la Tarea moral de la entrada pasada dice que:

Si $a, b \in N$ son tales que $a + b = 0$ , entonces $a = b = 0$

Con estos resultados en mente probamos el siguiente lema.

Lema. Si $n \neq 0$ y $m \in N$ es tal que $m \cdot n = 0$ , entonces $m = 0$ .

Demostración. Como $n \neq 0$ , entonces existe $a \in N$ , tal que $n = σ (a)$ , entonces tenemos que

$\begin{aligned} 0 & = m \cdot n \\ = m \cdot σ (a) \\ \overset{*}{=} m + (m \cdot a) . \end{aligned}$

Entonces tenemos que $m \cdot a = 0$ y que $m = 0$ que es lo que debíamos probar.

Es común usar una equivalencia lógica del enunciado anterior, la cual dice:

Si $n, m \in N ∖ {0}$ , entonces $n \cdot m \in N ∖ {0}$

Proposición (ley de cancelación). Si $m, n$ son números naturales y $a \neq 0$ y cumplen que $a \cdot n = a \cdot m$ , entonces, $n = m$

Demostración. De nuevo, procedamos por inducción sobre $n$

Base inductiva: Supongamos que $n = 0$ y $a \neq 0$ , entonces $a \cdot m = a \cdot n = a \cdot 0 = 0,$ por el Lema tenemos que $m = 0 = n$ .

Hipótesis de inducción: Supongamos que para algún $n$ , tenemos que si $a \neq 0$ y $a \cdot n = a \cdot m$ , entonces $n = m$ .

Paso inductivo: Probemos para $σ (n)$ , sea $a \neq 0$ y supongamos que $a \cdot σ (n) = a \cdot m$ .

Como $σ (n) \neq 0$ , y por hipótesis, $a \neq 0$ , entonces por la equivalencia del lema, concluimos que $a \cdot σ (n) \neq 0$ , de donde $a \cdot m \neq 0$ , esto implica que $m \neq 0$ , por lo que existe $b$ tal que $m = σ (b)$ , entonces podemos escribir

$\begin{aligned} a + a \cdot n & \overset{*}{=} a \cdot σ (n) \\ = a \cdot m \\ = a \cdot σ (b) \\ \overset{*}{=} a + a \cdot b \end{aligned}$

Ocupando la ley de cancelación de la suma, tenemos que $a \cdot n = a \cdot b$ .

Pero por hipótesis de inducción debemos de tener que $n = b$ , esto quiere decir que $σ (n) = σ (b) = m$ , justo como debíamos probar.

Con esta prueba concluimos las propiedades más fundamentales del producto.

Resumen de las propiedades del producto

Para finalizar con la entrada, haremos un compendio de las propiedades que demostramos

Para todo $n$ natural, se tiene que $1 \cdot n = n = n \cdot 1$
Para todo $n$ natural, se tiene que $0 \cdot n = 0 = n \cdot 0$
Para $l, m, n$ naturales cualesquiera se tiene que $(l + m) \cdot n = (l \cdot n) + (m \cdot n)$
Para $m, n$ naturales se tiene que $m \cdot n = n \cdot m$
Para $l, m, n$ naturales cualesquiera se tiene que $l \cdot (m + n) = (l \cdot m) + (l \cdot n)$
Para $l, m, n$ naturales cualesquiera se tiene que $(l \cdot m) \cdot n = l \cdot (m \cdot n)$
Para $m, n$ naturales con $m \neq 0$ , si $m \cdot n = 0$ , entonces $n = 0$
Para $l, m, n$ naturales con $l \neq 0$ , si $l \cdot n = l \cdot m$ , entonces $n = m$

Más adelante…

Con las propiedades de la suma y del producto en nuestra bolsa de herramientas, tenemos ya una rica teoría que desarrollar; nos falta aún definir una relación muy familiar en el conjunto $N$ , el orden, al cual ya hemos apelado en la demostración del teorema de la Recursión Débil.

Por el momento estudiaremos con mayor detalle los conjuntos infinitos, donde veremos la importancia de los naturales dentro de esta clase de conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Prueba la Propiedad distributiva derecha.
Usando únicamente la ley de cancelación el producto, demuestra el Lema previo a la demostración de la ley de cancelación.
¿Qué pasa si en el enunciado de la ley de la cancelación, no asumimos que $a \neq 0$ ?
Demuestra usando el Lema previo a la demostración de la ley de cancelación que si $n, m \in N ∖ {0}$ , entonces $n \cdot m \in N ∖ {0}$ .
Da una definición recursiva de las funciones $η_{m} (n) = m^{n}$ y prueba las leyes de los exponentes.

Entradas relacionadas

Ir a: Álgebra Superior II
Entrada anterior del curso: Definición de la suma y sus propiedades básicas
Entrada siguiente del curso: Otras definiciones recursivas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Matrices de bloques

Por Julio Sampietro

2 respuestas

Introducción

En esta entrada definimos el concepto de submatriz y estudiamos las llamadas matrices de bloques que esencialmente son matrices grandes obtenidas por matrices más pequeñas (esto tendrá sentido después de algunos ejemplos). Las matrices de bloque aparecen frecuentemente en muchas áreas y permiten realizar cálculos que podrían ser bastante complicados de otra manera.

Dentro de este curso, nos encontraremos con las matrices de bloque cuando hablemos de solución de ecuaciones lineales y de encontrar inversas de matrices usando el método de reducción gaussiana.

Definición de matrices de bloques

Definición. Una submatriz de una matriz $A \in M_{m, n} (F)$ es una matriz que se obtiene al quitar filas y/o columnas de $A$ .

Notamos que $A$ es submatriz de si misma. Una matriz puede partirse en submatrices marcando líneas verticales u horizontales en la matriz. Llamamos a una matriz de este estilo una matriz de bloques y a las submatrices marcadas las llamamos bloques.

Unos ejemplos de matrices de bloques:

$\begin{array}{r} (\begin{array}{ccc} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 0 & 0 & 9 \end{array}), (\begin{array}{ccc} 1 & 0 & 1 \\ 2 & 5 & - 3 \end{array}), \\ (\begin{array}{cccc} 1 & 0 & 0 & 2 \\ 5 & 16 & 2 & 0 \\ 17 & 19 & - 5 & 3 \\ 117 & 0 & 0 & 11 \end{array}) . \end{array}$

Como mencionamos en la introducción, podemos ver a una matriz de bloques como una ‘matriz de matrices’: una matriz de bloques en $M_{m, n} (F)$ típica se ve como

$\begin{array}{r} (\begin{array}{c} A_{11} & A_{12} & \dots & A_{1 k} \\ A_{21} & A_{22} & \dots & A_{2 k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ A_{l 1} & A_{l 2} & \dots & A_{l k} \end{array}), \end{array}$

en donde cada submatriz $A_{i j}$ es una matriz de tamaño $m_{i} \times n_{j}$ para algunos enteros positivos $m_{1}, \dots, m_{l}$ y $n_{1}, \dots, n_{k}$ tales que $m_{1} + \dots + m_{l} = m$ y $n_{1} + \dots + n_{k} = n$ . La matriz tiene entonces $l$ filas de bloques y $k$ columnas de bloques.

Si $l = k$ , llamamos a los bloques $A_{11}, \dots, A_{k k}$ los bloques diagonales y decimos que $A$ es diagonal por bloques si todos los bloques aparte de los diagonales son la matriz cero del tamaño correspondiente. Es decir, una matriz diagonal por bloques es de la forma

$\begin{array}{r} A = (\begin{array}{c} A_{11} & 0 & \dots & 0 \\ 0 & A_{21} & \dots & 0 \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & A_{k k} . \end{array}) \end{array}$

Observa que sólo estamos pidiendo que $k = l$ , es decir, que haya la misma cantidad de filas de bloques y de columnas de bloques. Sin embargo, no es necesario que la matriz $A$ sea cuadrada para que sea diagonal por bloques.

Por más que la definición en abstracto pueda ocultar su sentido práctico, uno siempre reconoce una matriz diagonal por bloques cuando la ve.

Ejemplo. La matriz

$\begin{array}{r} (\begin{array}{c} 1 & - 1 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 15 & - 2 \end{array}) \end{array}$

es diagonal por bloques, y los resaltamos con las líneas de división

$\begin{array}{r} (\begin{array}{cccc} 1 & - 1 & 0 & 0 \\ 0 & 2 & 0 & 0 \\ 0 & 0 & 3 & 0 \\ 0 & 0 & 15 & - 2 \end{array}) . \end{array}$

La matriz
$\begin{array}{r} (\begin{array}{c} 2 & - 1 & 0 & 0 \\ 8 & 3 & 0 & 0 \\ 0 & 3 & 0 & 0 \\ 0 & 0 & 0 & - 2 \\ 0 & 0 & 1 & 0 \end{array}) \end{array}$

también es diagonal por bloques, aunque los bloques no necesariamente sean cuadrados. Resaltamos la lineas divisorias a continuación:

$\begin{array}{r} (\begin{array}{cccc} 2 & - 1 & 0 & 0 \\ 8 & 3 & 0 & 0 \\ 2 & 3 & 0 & 0 \\ 0 & 0 & 0 & - 2 \\ 0 & 0 & 1 & 0 \end{array}) . \end{array}$

Los bloques diagonales son $\begin{array}{r} (\begin{array}{c} 2 & - 1 \\ 8 & 3 \\ 2 & 3 \end{array}) \end{array}$ y $\begin{array}{r} (\begin{array}{c} 0 & - 2 \\ 1 & 0 \end{array}) . \end{array}$

$△$

Operaciones con matrices de bloques

Al ser ‘matrices de matrices’, las matrices de bloques se comportan adecuadamente con las operaciones de suma y producto de matrices que conocemos. Enunciamos esto con más detalle en la siguiente proposición que no demostraremos. Las demostraciones son directas pero tediosas.

Proposición.

Si
$\begin{array}{r} A = (\begin{array}{c} A_{11} & A_{12} & \dots & A_{1 k} \\ A_{21} & A_{22} & \dots & A_{2 k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ A_{l 1} & A_{l 2} & \dots & A_{l k} \end{array}) \end{array}$ y $\begin{array}{r} B = (\begin{array}{c} B_{11} & B_{12} & \dots & B_{1 k} \\ B_{21} & B_{22} & \dots & B_{2 k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ B_{l 1} & B_{l 2} & \dots & B_{l k} \end{array}) \end{array}$
son matrices de bloques con $A_{i j}$ y $B_{i j}$ del mismo tamaño para cada $i, j$ (es decir, la partición es igual) entonces
$\begin{array}{r} A + B = (\begin{array}{c} A_{11} + B_{11} & A_{12} + B_{12} & \dots & A_{1 k} + B_{1 k} \\ A_{21} + B_{21} & A_{22} + B_{22} & \dots & A_{2 k} + B_{2 k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ A_{l 1} + B_{l 1} & A_{l 2} + B_{l 2} & \dots & A_{l k} + B_{l k} \end{array}) \end{array}$
Si
$\begin{array}{r} A = (\begin{array}{c} A_{11} & A_{12} & \dots & A_{1 k} \\ A_{21} & A_{22} & \dots & A_{2 k} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ A_{l 1} & A_{l 2} & \dots & A_{l k} \end{array}) \end{array}$ y $\begin{array}{r} B = (\begin{array}{c} B_{11} & B_{12} & \dots & B_{1 r} \\ B_{21} & B_{22} & \dots & B_{2 r} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ B_{k 1} & B_{k 2} & \dots & B_{k r} \end{array}) \end{array}$
son de tamaño $m \times n$ y $n \times p$ respectivamente tal que $A_{i j}$ es de tamaño $m_{i} \times n_{j}$ y $B_{i j}$ de tamaño $n_{i} \times p_{j}$ , entonces
$\begin{array}{r} A B = (\begin{array}{c} C_{11} & C_{12} & \dots & C_{1 r} \\ C_{21} & C_{22} & \dots & C_{2 r} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ C_{l 1} & C_{l 2} & \dots & C_{l r} \end{array}) \end{array}$
donde
$\begin{array}{r} C_{i j} = \sum_{u = 1}^{k} A_{i u} B_{u j} . \end{array}$

Más adelante…

En unas cuantas entradas hablaremos del algoritmo de reducción gaussiana y lo usaremos para resolver sistemas de ecuaciones y encontrar inversas de matrices. Nos encontraremos con matrices de bloque muy específicas, por ejemplo, las que resultan de «pegarle» un vector columna a una matriz, por ejemplo

$\begin{array}{r} (\begin{array}{ccccc} - 3 & - 1 & 3 & - 11 & 0 \\ 8 & 3 & 0 & 2 & - 1 \\ 1 & - 5 & 0 & 0 & 0 \end{array}) . \end{array}$

y las que resultan de «pegarle» la matriz identidad a una matriz cuadrada, por ejemplo

$\begin{array}{r} (\begin{array}{cccccc} - 3 & - 1 & 3 & 1 & 0 & 0 \\ 8 & 3 & 0 & 0 & 1 & 0 \\ 1 & - 5 & 0 & 0 & 0 & 1 \end{array}) . \end{array}$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

¿Cómo se portan las matrices de bloques respecto a la transposición?
Escribe todas las formas en las que puedes dividir a la matriz $I_{3}$ para que quede como una matriz de bloques. Aquí hay algunas: $\begin{array}{r} (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}), (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}), (\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}) . \end{array}$
Demuestra que toda matriz diagonal puede verse como una matriz diagonal por bloques. Muestra que no toda matriz diagonal por bloques es una matriz diagonal.
Escribe todas las formas en las que puedes dividir a la matriz $I_{4}$ para que quede como una matriz diagonal por bloques.
¿Cómo es la inversa de una matriz diagonal por bloques?

Entradas relacionadas

Ir a Álgebra Lineal I
Entrada anterior del curso: Transposición de matrices, matrices simétricas y antisimétricas
Siguiente entrada del curso: Problemas de transpuesta de matriz y matrices de bloque

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Introducción

La función suma

Propiedades de la suma

La multiplicación

Definición de la multiplicación

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Intuición del producto de enteros y su definición formal

El producto en Z está bien definido

Propiedades del producto en Z

Divisores de cero y cancelación

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Una equivalencia del orden

El orden y las operaciones

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición del producto

Aprendiendo a multiplicar por uno

Aprendiendo a multiplicar por cero

La propiedad distributiva izquierda

El producto es conmutativo

El producto es asociativo

Ley de la cancelación

Resumen de las propiedades del producto

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición de matrices de bloques

Operaciones con matrices de bloques

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

El producto en $Z$ está bien definido

Propiedades del producto en $Z$