Introducción
En una entrada anterior definimos el conjunto $\mathbb{C}$ de los números complejos. Vimos que sus elementos tienen la forma $a+bi$, donde $a$ y $b$ son números reales. Definimos las operaciones de suma y producto, y vimos que, con estas operaciones, $\mathbb{C}$ es un campo. En esta entrada hablaremos acerca de la conjugación compleja.
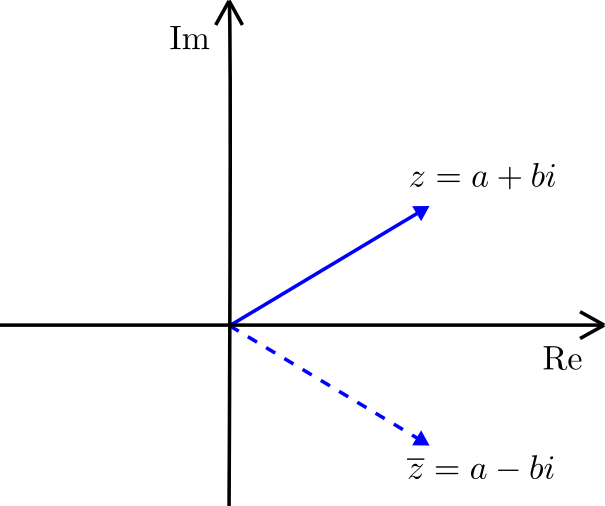
Definición. Sea $z=a+bi$ un número complejo. El conjugado de $z$ es el número complejo $a-bi$ que denotaremos como $\overline{z}$.
Ejemplo. Sea $z=5+8i$, entonces $\overline{z}=5-8i$. Si $z=\sqrt{3}-8\pi i $, entonces $\overline{z}=\sqrt{3}+8\pi i$.
En la entrada anterior justificamos que podíamos abandonar la notación de parejas, sin embargo en ocasiones seguirá siendo útil pensar al complejo $a+bi$ como el punto $(a,b)$ del plano. Si lo pensamos así, la conjugación compleja manda al punto $(a,b)$ en el punto $(a,-b)$, es decir, se comporta como una reflexión en el eje $x$.
Conjugación y operaciones complejas
La conjugación compleja «se comporta bien» con las operaciones definidas en $\mathbb{C}$. Este es el contenido de la siguiente proposición.
Proposición 1. Si $w$ y $z$ son números complejos, entonces:
- El conjugado de la suma es la suma de los conjugados, es decir, $\overline{w+z}=\overline{w}+\overline{z}$.
- El conjugado del producto es el producto de los conjugados, es decir, $\overline{wz}=\overline{w}\overline{z}$.
Demostración. Si escribimos a $w=a+bi$ y $z=c+di$ con $a,b,c,d$ números reales. Tenemos que
\begin{align*}
\overline{w+z}&=\overline{(a+c)+(b+d)i}\\
&=(a+c)-(b+d)i\\
&=(a-bi)+(c-di)\\
&=\overline{w}+\overline{z},
\end{align*} lo cual prueba la primera parte de la proposición. Por otro lado
\begin{align*}
\overline{wz}&=\overline{(ac-bd)+(ad+bc)i}\\
&=(ac-bd)-(ad+bc)i\\
&=(ac-(-b)(-d))+(a(-d)+b(-c))i\\
&=(a-bi)(c-di)\\
&=\overline{w}\overline{z},
\end{align*} lo cual prueba la segunda parte.
$\square$
Se pueden mostrar resultados análogos para la conjugación compleja de la resta y cociente. Esto se deja en la tarea moral.
Ejemplo. Considera los números complejos $5+4i$, $3+2i$ y $1-i$. Vamos a determinar el conjugado de su suma de dos formas distintas. Por un lado, si los sumamos obtenemos el complejo $$(5+3+1)+(4+2-1)i=9+5i,$$ cuyo conjugado es $9-5i$.
Por otro lado, podemos conjugar a cada uno de los números de manera independiente para obtener $5-4i$, $3-2i$ y $1+i$. Al hacer la suma de estos complejos, obtenemos $$(5+3+1)+(-4-2+1)i=9-5i.$$ En ambos casos obtenemos lo mismo.
$\triangle$
La conjugación compleja es autoinversa
Proposición 2. La operación «conjugar» es autoinversa, y por lo tanto es biyectiva.
Demostración. En efecto, si $z=a+bi$, entonces $$\overline{\overline{z}}=\overline{a-bi}=a+bi=z.$$
Para ver que conjugar es suprayectivo, tomemos $z$ en $\mathbb{C}$. Tenemos que $\overline{\overline{z}}=z$, de modo que $z$ está en la imagen de la operación conjugación.
Para ver que conjugar es inyectivo, tomemos $w$ y $z$ en $\mathbb{C}$ tales que $\overline{w}=\overline{z}$. Aplicando conjugación a esta igualdad, y usando la primer parte de la proposición, tenemos que $w=z$.
$\square$
Operaciones de un complejo con su conjugado
Sea $z=a+bi$ un número complejo, a $a$ le llamamos la parte real de $z$ y a $b$ le llamamos la parte imaginaria. Usamos la notación $a=\text{Re}(z)$ y $b=\text{Im}(z)$, respectivamente. Cuidado: la parte imaginaria es un número real. Se llama parte imaginaria porque es la que acompaña a $i$.
Si hacemos operaciones de un complejo con su conjugado, obtenemos valores especiales.
Proposición 3. Sea $z$ un número complejo. Entonces:
- $z+\overline{z}=2\text{Re}(z)$
- $z-\overline{z}=2\text{Im}(z) i$
- $z\overline{z}=\text{Re}(z)^2+\text{Im}(z)^2$
La demostración de la Proposición 3 es sencilla y se deja como tarea moral.
Ejemplo. Si tomamos el número complejo $3+4i$ y le sumamos su conjugado $3-4i$, obtenemos el número real $6$, que es dos veces la parte real de $3+4i$.
Si hacemos la multiplicación $(3+4i)(3-4i)$, obtenemos también un número real: $$3^2-(4i)^2=9-(-16)=25.$$
$\square$
Como corolario de la Proposición 3, obtenemos lo siguiente.
Corolario. Si $z=\overline{z}$, entonces $z$ es un número real.
Demostración. Por la primera parte de la Proposición 3, tenemos que $2z=z+\overline{z}=2\text{Re}(z)$, de modo que $z=\text{Re}(z)$ y por lo tanto $z$ es un número real.
$\square$
Ejercicio. Muestra que el complejo $$\left(\frac{1+\sqrt{5}}{2}+\frac{1-\sqrt{5}}{2} i \right) \left(\frac{1+\sqrt{5}}{2}-\frac{1-\sqrt{5}}{2} i \right)$$ es un número real.
Solución. Podríamos hacer las cuentas y verificar que la parte imaginaria es $0$. Sin embargo, basta con notar que la expresión es el producto de un complejo con su conjugado, es decir, es de la forma $z\overline{z}$. De manera directa, por la última parte de la Proposición 3 obtenemos que es un número real.
$\square$
La conjugación compleja es (casi) el único automorfismo que fija a los reales
En las secciones anteriores vimos que la conjugación compleja deja fijos a los reales y que respeta las operaciones. En esta sección veremos que es la única operación, en $\mathbb{C}$, que hace esto sin ser la identidad.
Teorema. Si $\eta:\mathbb{C}\to \mathbb{C}$ es una función biyectiva. tal que:
- $\eta$ no es la identidad.
- $\eta(a)=a$ para todo $a$ real.
- $\eta(w+z)=\eta(w)+\eta(z)$ para todo par de complejos $w$ y $z$.
- $\eta(wz)=\eta(w)\eta(z)$ para todo par de complejos $w$ y $z$.
Entonces $\eta$ es la conjugación compleja.
Demostración. Sea $z=a+bi$, tenemos que
\begin{align*}
\eta(a+bi)&=\eta(a)+\eta(bi)\\
&=\eta(a)+\eta(b)\eta(i)\\
&=a+b\eta(i),
\end{align*}
así que basta determinar quién es $\eta(i)$. Por otro lado, como $-1$ es real, tenemos también que
\begin{align*}
-1&=\eta(-1)\\
&=\eta(i\cdot i)\\
&=\eta(i)\eta(i)\\
&=\eta(i)^2,
\end{align*}
de modo que $\eta(i)$ es una raíz de $-1$ y por lo tanto es $i$ o $-i$. Si $\eta(i)=i$, tendríamos que $\eta$ es la identidad, lo cual contradice nuestras hipótesis. Así, $\eta(i)=-i$ y por lo tanto $\eta$ es la conjugación compleja.
$\square$
Más adelante…
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Considera los números complejos $w_j=5+(2-j)i$, en donde $j$ es un entero en $\lbrace 0,1,2,3,4\rbrace$. Encuentra el valor de la suma $w_0+w_1+w_2+w_3+w_4$ y del producto $w_0w_1w_2w_3w_4$.
- Toma los números complejos $w$ y $z$. Muestra que $\overline{w-z}=\overline{w}-\overline{z}$ y que si $z\neq 0$, entonces $\overline{w/z}=\overline{w}/ \overline{z}$.
- Haz la demostración de la Proposición 3.
- ¿Cuáles números complejos satisfacen que $z^2=\overline{z}$?
- Sea $z$ un número complejo distinto de $0$. ¿Qué obtienes cuando realizas la división $z/\overline{z}$?
En el blog hay una entrada acerca de aplicaciones de la aritmética de números complejos a la resolución de problemas en matemáticas. No formará parte de la evaluación del curso, pero puede ayudarte a entender más profundamente lo que estamos haciendo y a motivar la teoría que desarrollamos.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Problemas de operaciones en complejos
- Entrada siguiente del curso: Problemas de conjugación compleja
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
