Introducción

En la entrada anterior hablamos de las coordenadas rectangulares y polares de un número complejo. También, definimos la forma polar de un número complejo. En esta entrada hablaremos de cómo con la forma polar, de los elementos de $\mathbb{C}$, podemos entender fácilmente su multiplicación. Además, usaremos esto para demostrar la fórmula de De Moivre, que nos dice cómo encontrar las potencias de un complejo.

Como pequeño recordatorio, la forma polar del complejo $z=x+iy$ es $z=r(\cos \theta + i \sin \theta)$, en donde $r$ es la norma de $z$ y $\theta$ es el ángulo que hace con el eje real positivo, pensándolo como el punto $(x,y)$. Esto queda resumido por la siguiente figura:

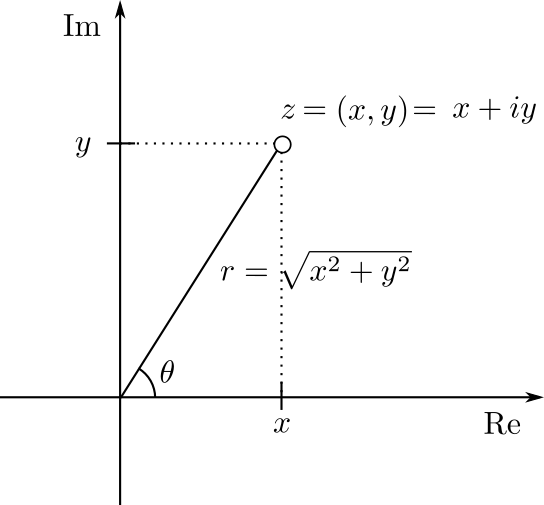
Forma polar, multiplicación y recordatorio trigonométrico

Para ver cómo la forma polar de los complejos nos ayuda a entender la multiplicación en $\mathbb{C}$, necesitamos recordar las siguientes fórmulas trigonométricas
\begin{align*}
\sin (\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha\\
\cos(\alpha+\beta) = \cos \alpha \cos \beta – \sin \beta \sin \alpha.
\end{align*}

Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r (\cos\alpha+ i \sin \alpha)\\
z&=s(\cos \beta + i \sin \beta)
\end{align*}

y los multiplicamos con la definición, su producto tendría parte real $$rs(\cos\alpha\cos \beta – \sin \alpha\sin \beta) = rs\cos (\alpha+\beta)$$ y parte imaginaria $$rs(\sin \alpha \cos \beta+ \sin\beta\cos\alpha)=rs\sin (\alpha+\beta).$$

Además, como la norma es multiplicativa, tenemos que la norma de $wz$ es $rs$. Con esto mostramos que la forma polar de $wz$ es exactamente $$wz=(rs)(\cos(\alpha+\beta)+i\sin(\alpha+\beta)).$$ Esto queda resumido en el siguiente resultado

Proposición. Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r \text{cis}(\alpha)\\
z&=s\text{cis}(\beta),
\end{align*} entonces la forma polar del producto es $$wz=rs\text{cis}(\alpha+\beta).$$

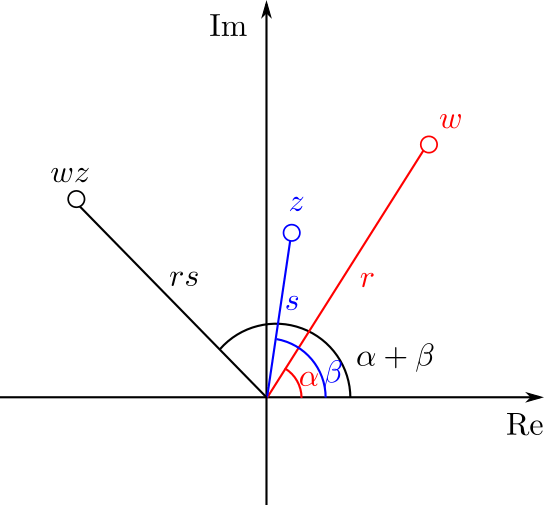
Otra forma de decirlo es que «al multiplicar complejos, multiplicamos normas y sumamos argumentos». Podemos también ver el resultado de forma geométrica mediante la siguiente figura, en donde marcamos con rojo y azul los factores, y con negro al producto.

Ejemplo. Vamos a encontrar la forma rectangular del producto de los complejos
\begin{align*}w& =7 \text{cis}\left( \frac{2\pi}{5} \right)\quad\text{y}\\ z&=2\text{cis}\left(\frac{3\pi}{5}\right).\end{align*}

Por la proposición anterior, el producto es exactamente el complejo
\begin{align*}
14 \text{cis}\left(\frac{2+3}{5}\pi \right)=14 \text{cis} (\pi).
\end{align*}

Esta es la forma polar del producto. Por un problema anterior, sabemos que $\text{cis}(\pi)=-1$, de modo que la forma rectangular del producto es $-14$.

Si tenemos un complejo no nulo en forma polar, podemos entender fácilmente su inverso multiplicativo. Esto está dado por la siguiente proposición, cuya demostración es sencilla y se deja como tarea moral.

Proposición. Sea $w\neq 0$ un complejo con forma polar $w=r\text{cis}(\theta)$. Su inverso multiplicativo es el complejo $r^{-1}\text{cis}(-\theta)$.

Ejemplo. Determinemos el inverso multiplicativo del complejo $$w=\sqrt{3}\text{cis}\left(\frac{3\pi}{7}\right).$$ Para ello, basta usar la proposición anterior, de donde $$w^{-1}=\frac{1}{\sqrt{3}} \text{cis}\left(-\frac{3\pi}{7}\right)=\frac{\sqrt{3}}{3}\text{cis}\frac{11\pi}{7}.$$

$\square$

Fórmula de De Moivre

La proposición para multiplicación de complejos se vuelve todavía más útil si la usamos iteradamente para hacer potencias de complejos.

Teorema (fórmula de De Moivre). Si $z$ es un complejo de norma $r$ y argumento $\theta$ y $n$ es un entero positivo, entonces $z^n$ es el complejo de norma $r^n$ y argumento $n\theta$. En otras palabras, si $z=r(\cos \theta + i \sin \theta)=r\text{cis}(\theta)$, entonces $$z^n=r^n (\cos (n\theta)+i\sin (n\theta))= r^n \text{cis} (n\theta).$$

Demostración. Procedemos por inducción sobre $n$. El caso $n=1$ es inmediato. Supongamos que el resultado es cierto para $n$, es decir, que $$z^n=r^n \text{cis} (n\theta).$$

Por hipótesis inductiva, tenemos entonces que la norma de $z^n$ es $r^n$, de modo que $z^{n+1}=z^n z$ tiene norma $r^nr=r^{n+1}$.

También por hipótesis inductiva, $z^n$ tiene argumento $n\theta$. Por cómo funciona la multiplicación compleja, el argumento de $z^{n+1}=z^n z$ es la suma de los argumentos de $z^n$ y $z$, es decir, $n\theta + \theta = (n+1)\theta$. Esto muestra que $$z^{n+1}=r^{n+1}\text{cis}((n+1)\theta),$$ y con esto acabamos el paso inductivo.

$\square$

Ejemplos de aplicación de fórmula de De Moivre

Ejemplo. Veremos quién es la décima potencia del complejo $$z=\sqrt{3}\text{cis} \left(\frac{4\pi}{5}\right).$$ Como este número ya está escrito en forma polar, podemos aplicarle directamente la fórmula de De Moivre:
\begin{align*}
z^{10}&=3^{10/2} \text{cis}\left(\frac{40\pi}{5}\right)\\
&=3^5 \text{cis} (8\pi)\\
&=3^5\\
&=243.
\end{align*}

$\square$

El ejemplo anterior nos dice que $z^{10}=243$. En otras palabras, $z$ es una raíz $10$-ésima de $243$. Pero existen otras raíces $10$-ésimas de 243, por ejemplo, tiene dos raíces reales $\sqrt[10]{243}$ y $-\sqrt[10]{243}$. ¿Cuántas raíces tiene entonces en total? ¿Quiénes son? Esto lo veremos en la siguiente entrada.

Veamos otro ejemplo en el que se aplica la fórmula de De Moivre.

Problema. Evalúa la expresión $(1+i)^{30}$, expresando el resultado final en forma rectangular.

Solución. Comenzamos expresando a $(1+i)$ en forma polar. Para ello, notamos que $\Vert 1+i \Vert = \sqrt{2}$, y que $1+i$ hace un ángulo de $\frac{\pi}{4}$ con el eje real positivo. Por el teorema de De Moivre, tenemos que

\begin{align*}
z^{30}&=\sqrt{2}^{30}\text{cis}\left(\frac{30\pi}{4}\right)\\
&=2^{15}\text{cis}\left(\frac{6\pi}{4} \right) \\
&=2^{15}\text{cis}\left(\frac{3\pi}{2} \right) \\
&=2^{15}(-i)\\
&=-2^{15}i.
\end{align*}

En la segunda igualdad usamos que $\frac{30\pi}{4}$ y $\frac{6\pi}{4}$ difieren en un múltiplo entero de $2\pi$. En la cuarta usamos la forma polar de $-i$.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que para un complejo $z\neq 0$ escrito en forma polar $z=r\text{cis}(\theta)$, su inverso multiplicativo tiene forma polar $r^{-1}\text{cis} (-\theta)$.
2. Evalúa la multiplicación $wz$, donde $w=2\text{cis}\left(\frac{5\pi}{7}\right)$ y $z=-5\text{cis}\left(\frac{7\pi}{5}\right)$. Expresa la respuesta forma polar.
3. Haz la multiplicación $wz$, donde $w=3\text{cis}\left(\frac{\pi}{2}\right)$ y $z=4\text{cis}\left(\frac{\pi}{3}\right)$. Expresa la respuesta en forma rectangular.
4. Sea $z=7\text{cis}\left(\frac{5\pi}{7}\right)$. Expresa $z^3$ en forma polar.
5. Sea $z=\sqrt[3]{5} \text{cis}\left(\frac{\pi}{3}\right)$. Expresa $z^9$ en forma rectangular.
6. Toma el complejo $z=-2+2i$. Evalúa la expresión $$1+z+\ldots+z^{29}.$$ Sugerencia: Usa primero la fórmula de suma de términos de una sucesión geométrica, y después la fórmula de De Moivre.

Puedes practicar más estos temas viendo los videos y haciendo los ejercicios de la página de Khan Academy, de su sección de números complejos.

Entradas relacionadas

• Ir a: Álgebra Superior II
• Entrada anterior del curso: Problemas de sistemas de ecuaciones complejos y forma polar
• Entrada siguiente del curso: Raíces de números complejos y raíces de la unidad

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»