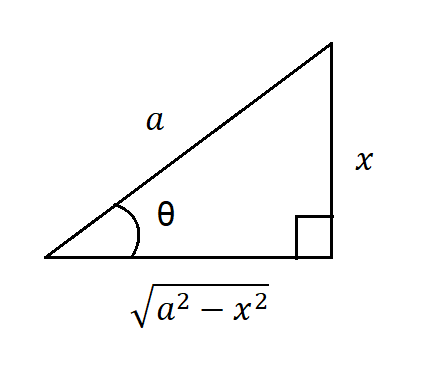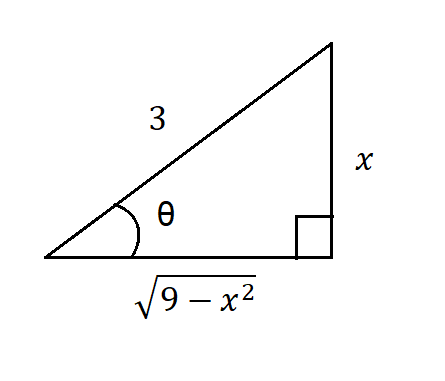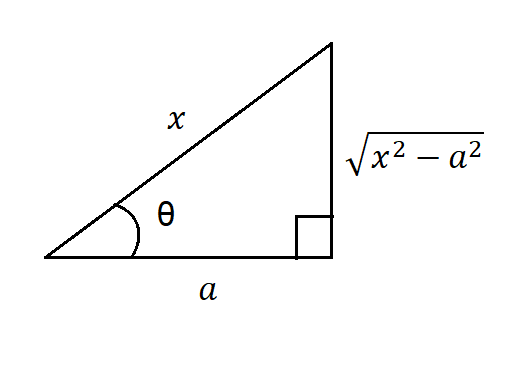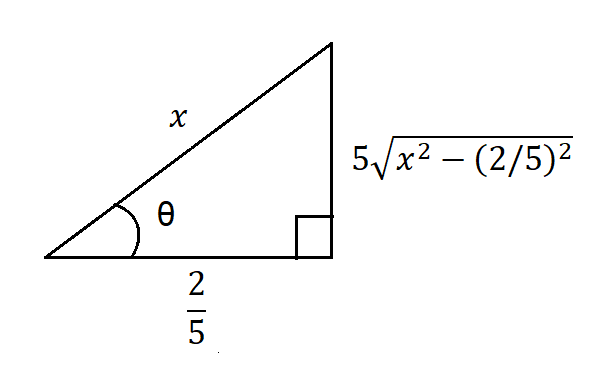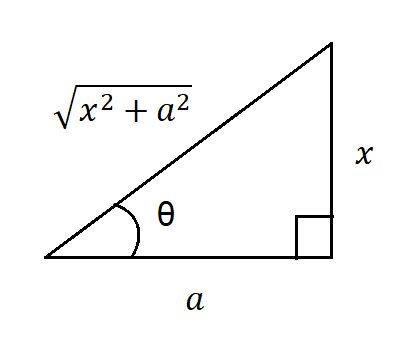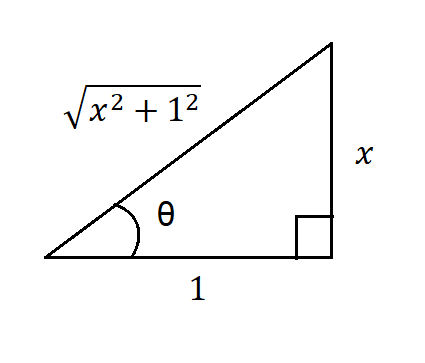Archivo de la etiqueta: funciones trigonométricas

Cálculo Diferencial e Integral II: Sustitución Trigonométrica

Por Miguel Ángel Rodríguez García

Introducción

En las últimas dos secciones anteriores vimos integrales trigonométricas que contiene producto de potencias de las funciones trigonométricas básicas, en esta sección veremos integrales que se resuelven con sustituciones utilizando las funciones trigonométricas, veamos como.

Método de sustitución trigonométrica

El método de sustitución trigonométrica consiste en resolver integrales que contienen términos de la forma:

$\sqrt{a^{2} - x^{2}}$
$\sqrt{x^{2} - a^{2}}$
$\sqrt{x^{2} + a^{2}}$

Para hacer estas sustituciones con las funciones trigonométricas básicas se debe ver cada caso según corresponda.

Caso 1: Integrales de la forma: $\sqrt{a^{2} - x^{2}}$

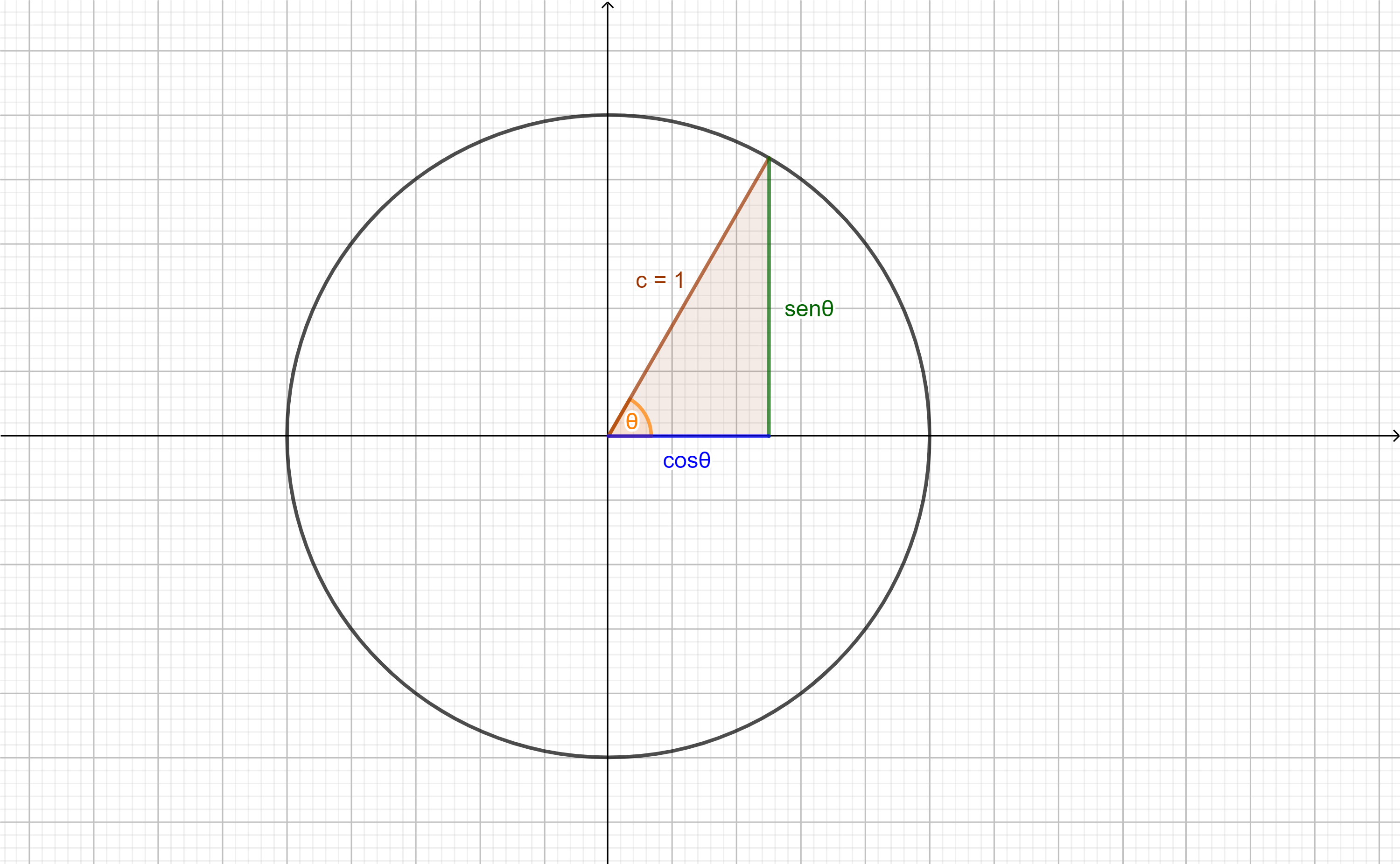
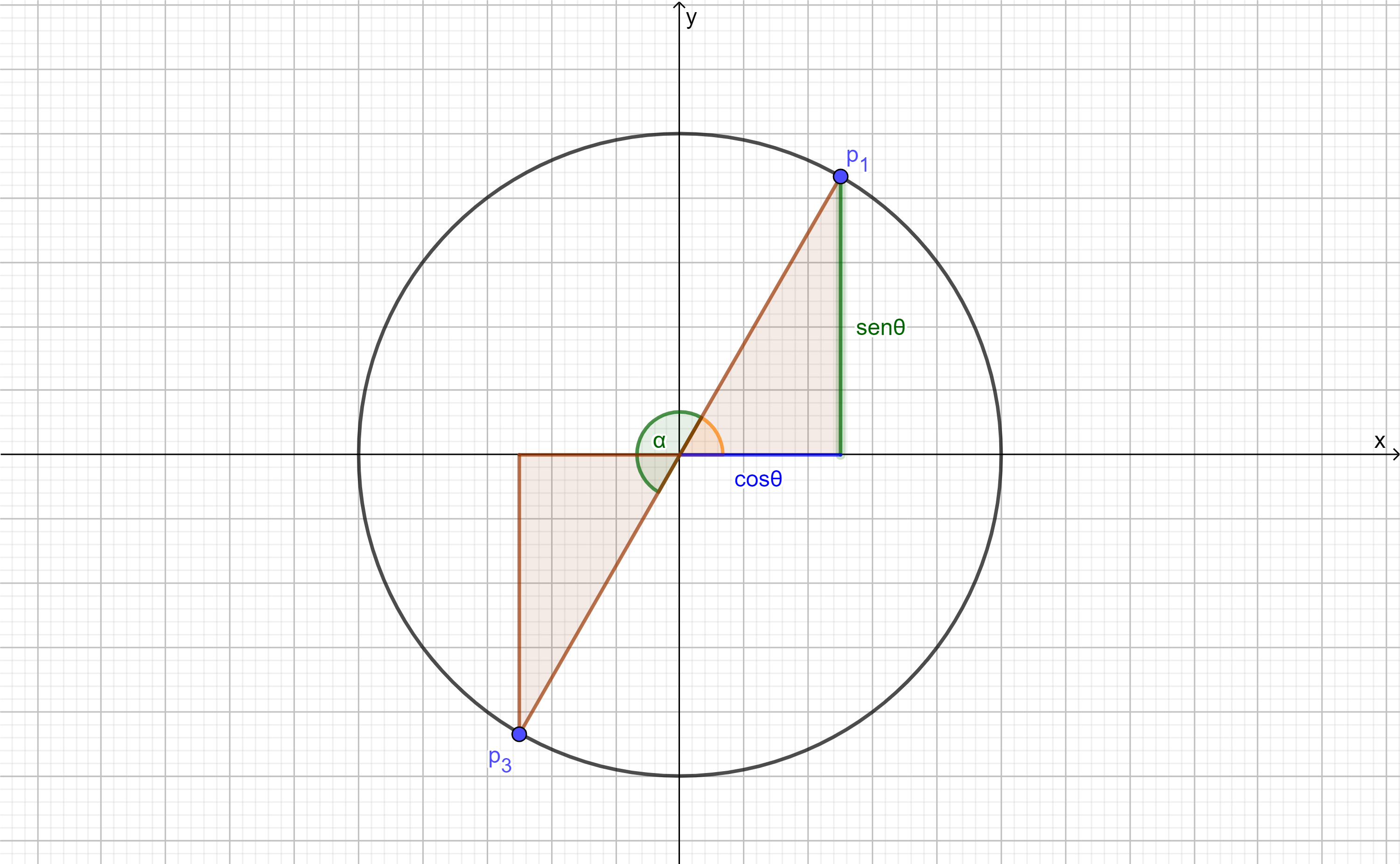
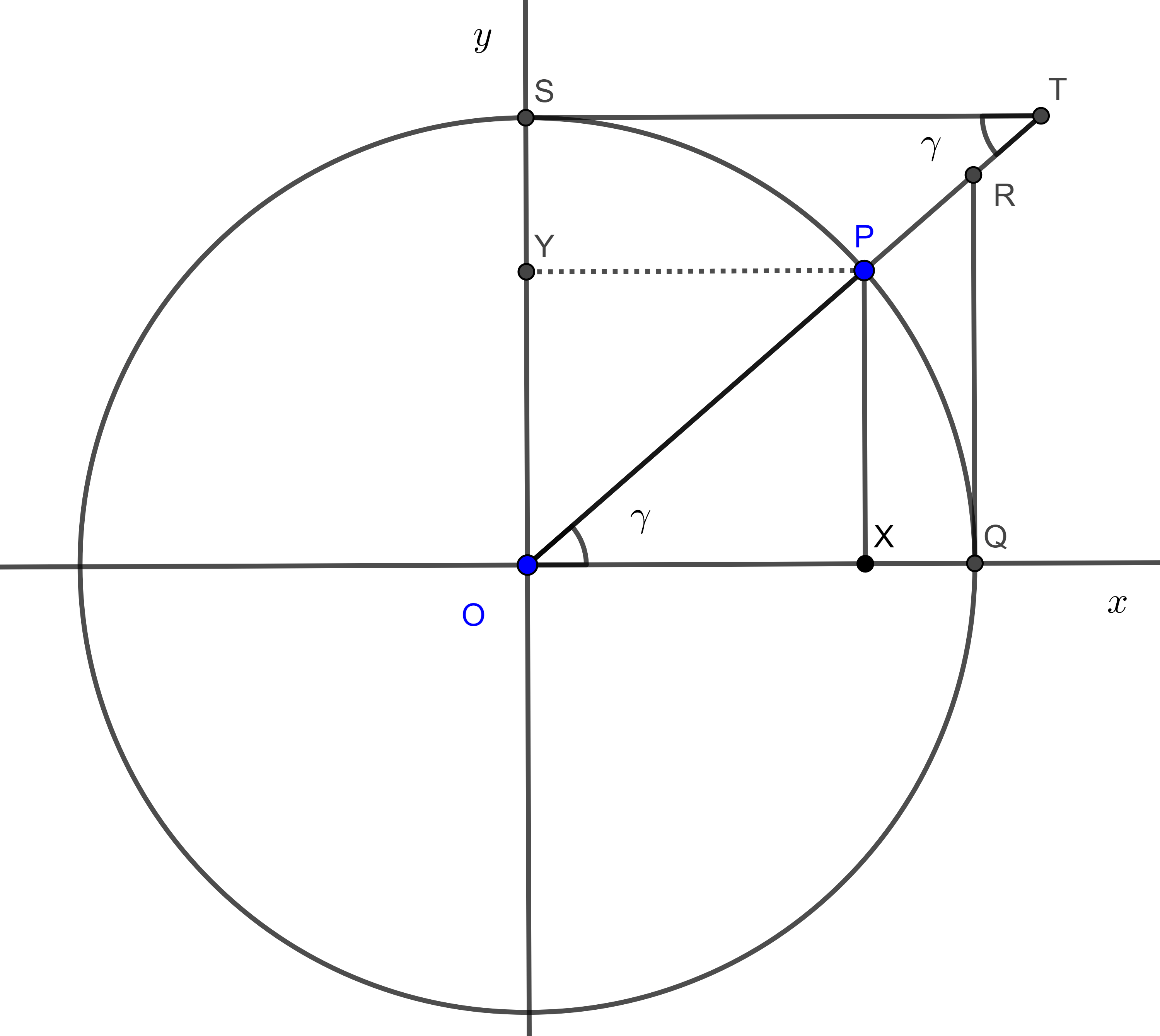
*Figura 1: Triángulo de referencia para la sustitución $x = a \sin (θ)$*

Podemos auxiliarnos con un triángulo rectángulo como vemos en la figura $(1)$ , y recordar un poco de trigonometría básica, recordemos que en un triángulo rectángulo:

$\sin (θ) = \frac{C a t e t o o p u e s t o}{H i p o t e n u s a} = \frac{x}{a} \Rightarrow a \cdot \sin θ = x$

Podemos hacer la sustitución:

$\begin{matrix} (1) & x = a \cdot \sin (θ) \end{matrix}$

Por otro lado:

$\begin{matrix} (2) & \cos (θ) = \frac{C a t e t o a d y a c e n t e}{H i p o t e n u s a} = \frac{\sqrt{a^{2} - x^{2}}}{a} \Rightarrow \sqrt{a^{2} - x^{2}} = a \cdot \cos (θ) \end{matrix}$

Estas son las sustituciones que debemos de hacer para integrales del tipo $\sqrt{a^{2} - x^{2}}$ , en este punto talvez pueda ser un poco confuso de utilizarlas, así que veamos el ejemplo siguiente.

$\int \frac{d x}{x^{2} \sqrt{9 - x^{2}}}$

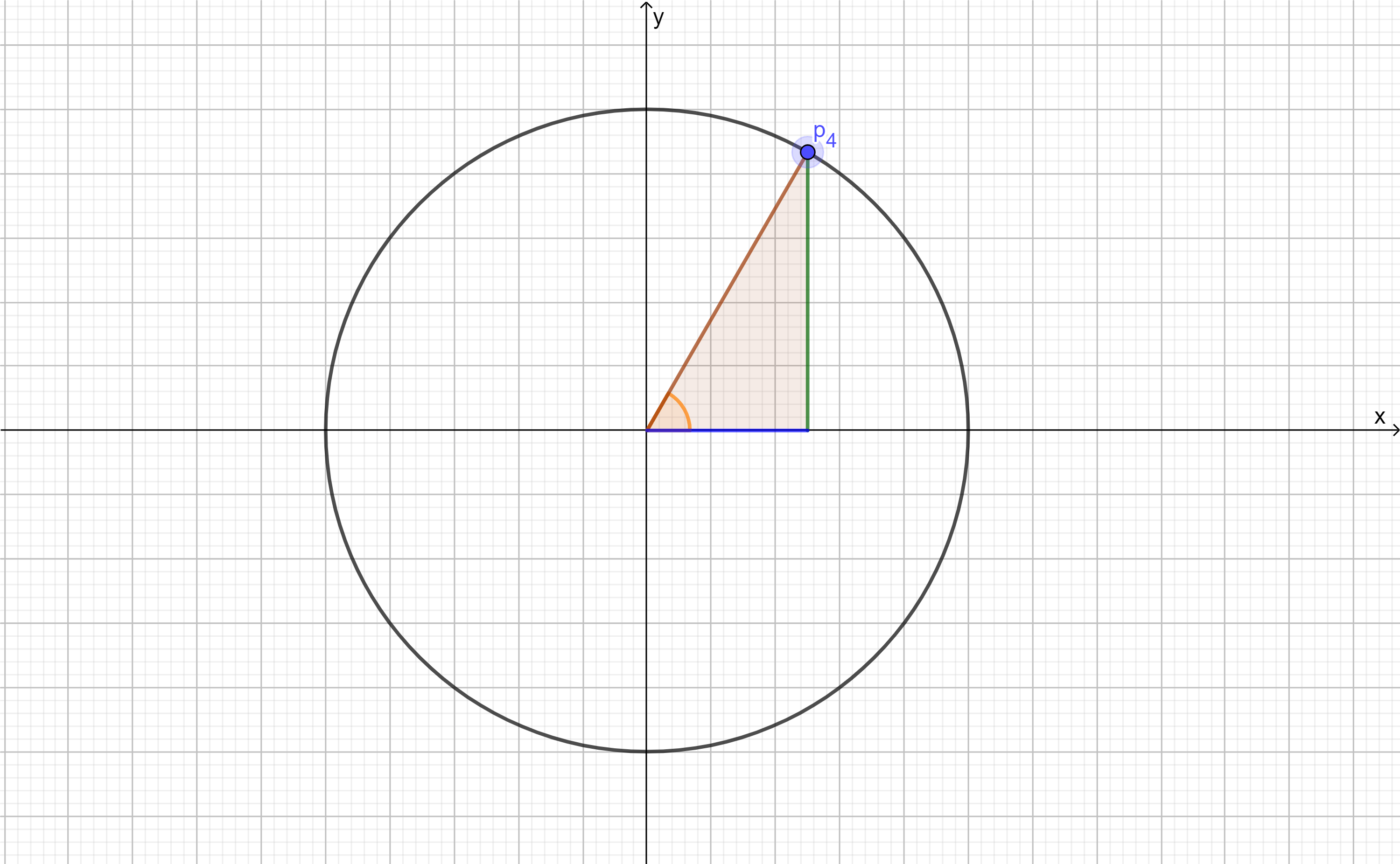
Vemos que lo que está adentro de la raíz es similar al del caso $(1)$ , por lo que podemos hacer la siguiente figura:

Figura 2: Triángulo para el ejercicio 1.

De la figura $(2)$ y de la relación $(1)$ , podemos escribir:

$\frac{x}{3} = \sin (θ) \Rightarrow x = 3 \sin (θ) \Rightarrow d x = 3 \cos (θ) d θ$

Elevamos al cuadrado la variable $x$ como:

$x^{2} = 9 \sin^{2} (θ)$

Por otro lado, utilizando la relación $(2)$ tenemos que:

$\frac{\sqrt{9 - x^{2}}}{3} = \cos (θ) \Rightarrow \sqrt{9 - x^{2}} = 3 \cos (θ)$

Así sustituimos estas variables en la integral obteniendo lo siguiente:

$\int \frac{d x}{x^{2} \sqrt{9 - x^{2}}} = \int \frac{3 \cos (θ) d θ}{9 \sin^{2} (θ) 3 \cos (θ)} = \frac{1}{9} \int \frac{1}{\sin^{2} (θ)} d θ = \frac{1}{9} \int c s c^{2} (θ) d θ$

La resolución de esta integral se utiliza los métodos de integrales trigonométricas vistos en esta entrada, por lo que:

$\frac{1}{9} \int \csc^{2} (θ) d θ = \frac{1}{9} (- \cot (θ)) + C$

Volvemos a la variable original $x$ , reescribimos a la función cotangente como: $\cot (θ) = \frac{\cos (θ)}{\sin (θ)}$

Con los cambios de variable que hicimos, tenemos que:

$\cot (θ) = \frac{\cos (θ)}{\sin (θ)} = \frac{\frac{\sqrt{9 - x^{2}}}{3}}{\frac{x}{3}} = \frac{\sqrt{9 - x^{2}}}{x}$

Así la resolución de la integral es:

$\int \frac{d x}{x^{2} \sqrt{9 - x^{2}}} = - \frac{1}{9} \frac{\sqrt{9 - x^{2}}}{x} + C$

Caso 2: Integrales de la forma $\sqrt{x^{2} - a^{2}}$

*Figura 3: Triángulo de referencia para la sustitución $x = a \sec (θ)$*

Análogamente, nos auxiliamos de un triángulo rectángulo como vemos en la figura $(3)$ , recordamos que:

$\sec (θ) = \frac{1}{\cos (θ)} = \frac{H i p o t e n u s a}{C a t e t o a d y a c e n t e} = \frac{x}{a}$

Podemos hacer la sustitución:

$\begin{matrix} (3) & x = a \cdot \sec (θ) \end{matrix}$

Por otro lado:

$\begin{matrix} (4) & \tan (θ) = \frac{C a t e t o o p u e s t o}{C a t e t o a d y a c e n t e} = \frac{\sqrt{x^{2} - a^{2}}}{a} \Rightarrow \sqrt{x^{2} - a^{2}} = a \cdot \tan (θ) \end{matrix}$

Por lo que estas son las sustituciones que debemos hacer en este caso, veamos un ejemplo.

$\int \frac{d x}{\sqrt{25 x^{2} - 4}}$

Nos fijamos en el radicando y notamos que es similar al caso $(2)$ , pero vemos que tenemos un problema con el número que va multiplicando $x^{2}$ , ya que se quiere que sea de la forma: $\sqrt{x^{2} - a^{2}}$ , por lo que podemos rescribir el radical como sigue: $\begin{matrix} (5) & \sqrt{25 x^{2} - 4} = \sqrt{25 (x^{2} - \frac{4}{25}}) = 5 \sqrt{x^{2} - {(\frac{2}{5})}^{2}} \end{matrix}$ .

Así podemos hacer la siguiente figura:

Figura 4: Triángulo para el ejercicio 2.

De la figura $(4)$ y de la relación $(3)$ , hacemos la sustitución:

$x = \frac{2}{5} \sec (θ) \Rightarrow d x = \frac{2}{5} \sec (θ) \tan (θ) d θ$

Por otro lado, utilizando la relación $(4)$ , tenemos que:

$\frac{\sqrt{x^{2} - (\frac{2}{5})^{2}}}{\frac{2}{5}} = \tan (θ) \Rightarrow \sqrt{x^{2} - {(\frac{2}{5})}^{2}} = \frac{2}{5} \tan (θ)$

Sustituyendo en la integral tenemos que:

$\int \frac{d x}{\sqrt{25 x^{2} - 4}} = \int \frac{\frac{2}{5} \sec (θ) \tan (θ)}{5 (\frac{2}{5} \tan (θ))} d θ = \frac{1}{5} \int \sec (θ) d θ$

Recordemos que el 5 que está multiplicando en el divisor viene de la relación $(5)$ .

Sabemos que la solución de esta integral está dada como:

$\int \sec (θ) d θ = l n | \sec (θ) + \tan (θ) | + C$

Por lo que:

$\frac{1}{5} \int \sec (θ) d θ = \frac{1}{5} l n | \sec (θ) + \tan (θ) | + C$

Volviendo a la variable original $x$ , el resultado de la integral es:

$\int \frac{d x}{\sqrt{25 x^{2} - 4}} = \frac{1}{5} l n | \frac{5 x}{2} + \frac{5 \sqrt{x^{2} - {(\frac{2}{5})}^{2}}}{2} | + C$

Caso 3: Integrales de la forma $\sqrt{x^{2} + a^{2}}$

*Figura 5: Triángulo de referencia para la sustitución $x = a \tan (θ)$*

Análogamente, nos auxiliamos de un triángulo rectángulo, como se muestra en la figura $(5)$ , sabemos que: $\tan (θ) = \frac{C a t e t o o p u e s t o}{C a t e t o a d y a c e n t e} = \frac{x}{a}$

Podemos hacer la sustitución:

$\begin{matrix} (6) & x = a \cdot \tan (θ) \end{matrix}$

Por otro lado:

$\begin{matrix} (7) & \sec (θ) = \frac{1}{\cos (θ)} = \frac{H i p o t e n u s a}{C a t e t o a d y a c e n t e} = \frac{\sqrt{x^{2} + a^{2}}}{a} \Rightarrow \sqrt{x^{2} + a^{2}} = a \cdot \sec (θ) \end{matrix}$

Veamos el siguiente ejemplo para ejemplar este caso.

$\int \frac{d x}{(x^{2} + 1)^{\frac{3}{2}}}$

Podemos expresar el integrando de la siguiente forma:

$\int \frac{d x}{(x^{2} + 1)^{\frac{3}{2}}} = \int \frac{d x}{(\sqrt{x^{2} + 1})^{3}}$

Figura 6: Triángulo para el ejercicio 3.

Vemos que es igual al caso $(3)$ , por lo que nos ayudamos de la figura $(6)$ y utilizando la relación $(6)$ , tenemos que:

$\frac{x}{1} = \tan (θ) \Rightarrow d x = \sec^{2} (θ) d θ$

Por otro lado, utilizando la relación $(7)$ , se tiene que:

$\frac{\sqrt{x^{2} + 1}}{1} = \sec (θ) \Rightarrow (\sqrt{x^{2} + 1})^{3} = \sqrt[3]{x^{2} + 1} = \sec^{3} (θ)$

Sustituyendo en la integral tenemos que:

$\int \frac{d x}{(x^{2} + 1)^{\frac{3}{2}}} = \int \frac{\sec^{2} (θ) d θ}{\sec^{3} (θ)} = \int \frac{1}{\sec (θ)} d θ = \int \cos (θ) d θ = \sin θ + C$

Para regresar a la variable $x$ volvemos a auxiliarnos de la figura $(6)$ , recordemos que:

$\sin (θ) = \frac{C a t e t o o p u e s t o}{H i p o t e n u s a} = \frac{x}{\sqrt{x^{2} + 1}}$

Así:

$\int \frac{d x}{(x^{2} + 1)^{\frac{3}{2}}} = \frac{x}{\sqrt{x^{2} + 1}} + C$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

Resolver las siguientes integrales:

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

$\int \frac{\sqrt{9 - x^{2}}}{x^{2}} d x$
$\int \frac{d x}{\sqrt{4 x^{2} + 1}} d x$
$\int \frac{\sqrt{x^{2} - 1}}{x} d x$
$\int \sqrt{x^{2} + x} d x$
$\int_{0}^{2 \sqrt{3}} \frac{x^{3}}{\sqrt{16 - x^{2}}} d x$
$\int_{\sqrt{3}}^{2} \frac{\sqrt{x^{2} - 3}}{x} d x$

Más adelante…

En esta sección vimos el método de sustitución trigonométrica viendo las condiciones para poder aplicar este método auxiliándonos con triángulos rectángulos en el cual nos ayuda a resolver integrales fácilmente, por lo que en esta entrada vimos que se pueden resolver integrales utilizando las funciones trigonométricas. En la siguiente sección veremos el método de fracciones parciales para poder integrar polinomios que tengan el grado del numerador menor que el del denominador.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral II.
Entrada anterior del curso: Cálculo Diferencial e Integral II: Integrales trigonométricas – Productos de potencias de tan(x) y sec(x) – El blog de Leo (nekomath.com)
Siguiente entrada del curso: Cálculo Diferencial e Integral II: Integración de funciones racionales por fracciones parciales – El blog de Leo (nekomath.com)

Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

Ahora que hemos comenzado a revisar las funciones trigonométricas de seno y coseno, en esta entrada veremos las funciones tangente, cotangente, secante y cosecante. De igual manera, revisaremos las funciones inversas y su representación gráfica.

Hablemos de la tangente y la cotangente

Recordemos de la entrada anterior las definiciones:

$\begin{aligned} t a n (θ) & = \frac{s e n (θ)}{c o s (θ)} & c o t (θ) & = \frac{c o s (θ)}{s e n (θ)} \end{aligned}$

Para la función tangente tenemos que su gráfica se vería como:

Observación: La tangente presenta asíntotas en los valores $x = \frac{k π}{2}$ con $k \in Z$ .

Y su rama principal la consideramos definida en el dominio:
$t a n : (- \frac{π}{2}, \frac{π}{2}) \to R$

Y para la función cotangente su gráfica sería:

Observación: La cotangente presenta asíntotas en los valores $x = k π$ con $k \in Z$ .

Para esta función consideraremos como su rama principal en el siguiente dominio:
$c o t : (0, π) \to R$ .

Ahora la secante y la cosecante

Ya vimos que están definidas como:
$\begin{aligned} s e c (θ) & = \frac{1}{c o s (θ)} & c s c (θ) & = \frac{1}{s e n (θ)} . \end{aligned}$

Comencemos con la gráfica para la función secante:

Observación: La secante presenta asíntotas en los valores $x = \frac{k π}{2}$ con $k \in Z$ .

Notemos que esta función se encuentra definida sobre cada cresta y por debajo de cada valle de la función $c o s (θ)$ :

Tomaremos como domino donde la función es invertible a:
$D = [0, \frac{π}{2}) \cup (\frac{π}{2}, π] .$

Para la función cosecante vemos que se encuentra definida sobre cada cresta y por debajo de cada valle de la función $s e n (θ)$ :

Observación: La cosecante presenta asíntotas en los valores $x = k π$ con $k \in Z$ .

Para esta función consideraremos al dominio donde es invertible a:
$D = [- \frac{π}{2}, 0) \cup (0, \frac{π}{2}] .$

¿Quiénes son las funciones inversas?

Para poder visualizar las gráficas de cada una de las funciones trigonométricas utilizaremos el método descrito previamente de reflejar la gráfica de la función respecto de la función identidad en el dominio donde es biyectiva o invertible.

Comenzaremos con la inversa de la función $f (x) = s e n (x)$ en el dominio $D_{f} = [- \frac{π}{2}, \frac{π}{2}]$ :

A $f^{- 1} (x)$ la llamaremos arcoseno de $x$ :
$f^{- 1} (x) = a r c s e n (x),$
geométricamente esta función nos da el arco cuyo seno es $x$ valor.

Procederemos de la misma manera con $g (x) = c o s (x)$ en el dominio $D_{g} = [0, π]$ :

Ahora a $g^{- 1}$ la llamaremos arcocoseno de $x$ :
$g^{- 1} (x) = a r c c o s (x)$
y su interpretación geométrica sería el arco cuyo coseno es el valor $x$ .

Dejaremos como ejercicio de Tarea moral realizar la gráfica para la función inversa de $h (x) = t a n (x)$ en el dominio $D_{h} = (- \frac{π}{2}, \frac{π}{2})$ :
$h^{- 1} (x) = a r c t a n (x),$
la función arcotangente nos da el arco cuya tangente es el valor $x$ .

Más adelante

En la siguiente entrada veremos al conjunto de funciones exponenciales y logarítmicas, sus representaciones gráficas, la relación que existe entre ellas y algunos resultados que cumplen, como las leyes de los exponentes y las leyes de los logaritmos.

Tarea moral

Obtener la gráfica de las siguientes funciones:
- $f (x) = - t a n (x)$
- $f (x) = - 2 s e c (x) + 1$
- $f (x) = a r c t a n (x)$
- $f (x) = 3 - c s c (x)$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 1)
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Funciones exponenciales y logarítmicas.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Funciones trigonométricas (Parte 1)

Por Karen González Cárdenas

Deja un comentario

Introducción

De las clases en el bachillerato recordarás las siguientes definiciones, utilizando el triángulo rectángulo de la imagen siguiente:

$\begin{aligned} s e n θ & = \frac{cat op}{hip} = \frac{b}{c} & c s c θ & = \frac{hip}{cat op} = \frac{c}{b} \\ c o s θ & = \frac{cat ad}{hip} = \frac{a}{c} & s e c θ & = \frac{hip}{cat ad} = \frac{c}{a} \\ t a n θ & = \frac{cat op}{cat ad} = \frac{b}{a} & c o t θ & = \frac{cat ad}{cat op} = \frac{a}{b} \end{aligned}$
donde:
cat op = cateto opuesto ; cat ad = cateto adyacente e hip= hipotenusa.

También recordemos que tenemos la siguiente equivalencia:

$360 °$ es equivalente a $2 π$ .

A lo largo de esta entrada veremos las principales características de este conjunto de funciones, sus gráficas y algunas identidades trigonométricas.

Identidades trigonométricas Pitagóricas

Si tomamos a la circunferencia unitaria y un triángulo rectángulo como en la imagen:

Observamos que al sustituir el valor hip $= 1$ en las definiciones anteriores para el $s e n θ$ y el $c o s θ$ tenemos:
$\begin{aligned} s e n θ & = \frac{cat op}{1} & c o s θ & = \frac{cat ad}{1} \\ = cat op & = cat ad \\ = b & = a \end{aligned}$

Dadas las igualdades obtenidas e hip $= 1$ al sustituir para el resto de las funciones tenemos:
$\begin{aligned} t a n θ & = \frac{s e n θ}{c o s θ} & c o t θ & = \frac{c o s θ}{s e n θ} \\ s e c θ & = \frac{1}{c o s θ} & c s c θ & = \frac{1}{s e n θ} \end{aligned}$

Recordemos el conocido Teorema de Pitágoras que nos da una relación entre los catetos y la hipotenusa de un triángulo rectángulo:
$a^{2} + b^{2} = c^{2} .$

Si lo aplicamos al triángulo rectángulo obtenido en la imagen anterior donde:
$\begin{aligned} a & = c o s θ & b & = s e n θ & c & = 1 \end{aligned}$
entonces tenemos la siguiente igualdad:
$\begin{matrix} (1) & c o s^{2} θ + s e n^{2} θ = 1. \end{matrix}$
Si dividimos $(1)$ entre $c o s^{2} θ$ obtenemos:
$\frac{c o s^{2} θ}{c o s^{2} θ} + \frac{s e n^{2} θ}{c o s^{2} θ} = \frac{1}{c o s^{2} θ} .$
Que simplificando sería:
$\begin{matrix} (2) & 1 + t a n^{2} θ = s e c^{2} θ . \end{matrix}$

Ahora bien si decidimos dividir $(1)$ entre $s e n^{2} θ$ :
$\frac{c o s^{2} θ}{s e n^{2} θ} + \frac{s e n^{2} θ}{s e n^{2} θ} = \frac{1}{s e n^{2} θ} .$
Que finalmente sería:
$\begin{matrix} (3) & c o t^{2} θ + 1 = c s c^{2} θ . \end{matrix}$

Las igualdades $(1)$ , $(2)$ y $(3)$ son llamadas Identidades Pitagóricas:
$\begin{aligned} c o s^{2} θ + s e n^{2} θ & = 1, \\ 1 + t a n^{2} θ & = s e c^{2} θ, \\ c o t^{2} θ + 1 & = c s c^{2} θ . \end{aligned}$

Otras identidades trigonométricas

Otras identidades trigonométricas que son de utilidad son las de suma de ángulos:
$\begin{aligned} c o s (α + β) & = c o s (α) c o s (β) - s e n (α) s e n (β), \\ s e n (α + β) & = c o s (α) s e n (β) + c o s (β) s e n (α) . \end{aligned}$
Para la resta de ángulos tendríamos un par similar:
$\begin{aligned} c o s (α - β) & = c o s (α) c o s (β) + s e n (α) s e n (β), \\ s e n (α - β) & = c o s (α) s e n (β) - c o s (β) s e n (α) . \end{aligned}$
Ahora veremos cómo obtener las identidades para los ángulos dobles:
$\begin{aligned} c o s (2 α) & = c o s (α + α) \\ = c o s (α) c o s (α) - s e n (α) s e n (α) \\ = c o s^{2} α - s e n^{2} α \end{aligned}$
Por lo tanto tendríamos para el coseno de $2 α$ :
$\begin{matrix} (4) & c o s (2 α) = c o s^{2} α - s e n^{2} α . \end{matrix}$
Si procedemos análogamente para el seno de $2 α$ :
$\begin{aligned} s e n (2 α) & = s e n (α + α) \\ = c o s (α) s e n (α) + c o s (α) s e n (α) \\ = 2 s e n (α) c o s (α) \end{aligned}$
Así concluimos que:
$\begin{matrix} (5) & s e n (2 α) = 2 s e n (α) c o s (α) . \end{matrix}$
También tenemos un par de identidades que relacionadas con el $s e n^{2} θ$ y el $c o s^{2} θ$ :
$\begin{aligned} s e n^{2} θ & = \frac{1}{2} (1 - c o s (2 θ)), & c o s^{2} θ & = \frac{1}{2} (1 + c o s (2 θ)) . \end{aligned}$
Se dejará como ejercicios en la Tarea moral obtener este par de igualdades.

Simetrías

Retomando la imagen anterior, si ahora reflejamos al triángulo respecto al eje $x$ , tenemos lo siguiente:

donde observamos los siguiente:
$\begin{aligned} β & = - θ & c_{2} & = 1 & b_{2} = s e n (- θ) \end{aligned}$

Así al considerar a los puntos $p_{1}$ y $p_{2}$ tenemos que estarían definidos de la siguiente manera:
$\begin{aligned} p_{1} & = (c o s (θ), s e n (θ)) & p_{2} & = (c o s (- θ), s e n (- θ)) \end{aligned}$
Resaltamos para $p_{2}$ que:
$p_{2} = (c o s (- θ), s e n (- θ)) = (c o s (θ), - s e n (θ)) .$
de esta igualdad podemos determinar si las funciones seno y coseno son pares o impares, este ejercicio formará parte de la Tarea moral.

Función periódica

Definición (función periódica): Decimos que una función $f$ es periódica si existe $N \in R$ tal que para todo $x \in D_{f}$ cumple que:
$f (x) = f (x + N)$
y $| N |$ se llama periodo de $f$ .
En la siguiente imagen observamos que $α = π$ por lo que tendríamos que el nuevo triángulo agregado es en realidad el original rotado:

Así tendríamos la siguiente definición para los puntos $p_{1}$ y $p_{3}$ :

$\begin{aligned} p_{1} & = (c o s (θ), s e n (θ)) & p_{3} & = (c o s (θ + π), s e n (θ + π)) \end{aligned}$

Si rotamos el triángulo ahora $α = 2 π$ tenemos que $p_{4}$ estaría definido como:
$p_{4} = (c o s (θ + 2 π), s e n (θ + 2 π)) .$

¡Y observamos que obtenemos el triángulo original! Consecuentemente tenemos las siguientes igualdades:
$\begin{aligned} s e n (θ) & = s e n (θ + 2 π), \\ c o s (θ) & = c o s (θ + 2 π) . \end{aligned}$
Aplicando la definición decimos que las funciones seno y coseno son periódicas con periodo $N = 2 π$ .
En las gráficas de las funciones observamos el comportamiento anterior, cada $2 π$ se comienzan a repetir los valores:

Observación: Vemos que para todo $x \in R$ ocurre:
$- 1 \leq s e n (x) \leq 1$
$- 1 \leq c o s (x) \leq 1$
por lo que las funciones seno y coseno son acotadas.

Consideraremos los siguientes dominios donde cada una de las funciones cumple ser inyectiva :
$\begin{array}{r} s e n : [- \frac{π}{2}, \frac{π}{2}] \to [- 1, 1] \end{array}$

$\begin{array}{r} c o s : [0, π] \to [- 1, 1] \end{array}$

Más adelante

En la próxima entrada, continuaremos con las definiciones de las funciones tangente, cotangente, secante y cosecante. Por lo tanto, realizaremos un análisis similar al dado para las funciones seno y coseno.

Tarea moral

Obtener las siguientes identidades trigonométricas:
- $s e n^{2} θ = \frac{1}{2} (1 - c o s (2 θ)) .$
- $c o s^{2} θ = \frac{1}{2} (1 + c o s (2 θ)) .$
- $t a n (α + β) = \frac{t a n (α) + t a n (β)}{- t a n (α) t a n (β)} .$
  Sugerencia.-Considera la igualdad:
  $t a n θ = \frac{s e n θ}{c o s θ}$
Determina si las siguientes funciones son pares, impares o ninguna de las opciones anteriores:
- $s e n (θ) .$
- $c o s (θ) .$
Obtén la gráfica de las siguientes funciones:
- $f (x) = s e n (x + \frac{π}{2}) .$
- $f (x) = - 2 c o s (x) + 1.$

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones polinomiales y racionales. Análisis geométrico de funciones.
Entrada siguiente del curso: Cálculo Diferencial e Integral I:Funciones trigonométricas (Segunda parte)
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Trigonometría

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada presentaremos las razones trigonométricas respecto de un ángulo agudo en un triángulo rectángulo, estas pueden ser vistas como funciones si consideramos el ángulo como una variable, veremos como extender estas funciones a ángulos de cualquier magnitud y algunas identidades trigonométricas.

Razones trigonométricas

Definiciones. Consideremos un triángulo rectángulo $△ A B C$ donde $A B$ es la hipotenusa y sea $α = ∠ B A C$ , decimos que $B C$ es el cateto opuesto a $α$ y $A C$ es el cateto adyacente a $α$ .

Definimos las razones trigonométricas respecto del ángulo $α$ como sigue:

El seno del ángulo $α$ como $\frac{c . o p u e s t o}{h i p o t e n u s a}$ y lo denotamos como $\sin α = \frac{B C}{A B}$ .
El coseno del ángulo $α$ como $\frac{c . a d y a c e n t e}{h i p o t e n u s a}$ y lo denotamos como $\cos α = \frac{A C}{A B}$ .
La tangente del ángulo $α$ como $\frac{c . o p u e s t o}{c . a d y a c e n t e}$ y lo denotamos como $\tan α = \frac{B C}{A C}$ .
La cosecante del ángulo $α$ como como $\frac{h i p o t e n u s a}{c . o p u e s t o}$ y lo denotamos como $\csc α = \frac{A B}{B C}$ .
La secante del ángulo $α$ como $\frac{h i p o t e n u s a}{c . a d y a c e n t e}$ y lo denotamos como $\sec α = \frac{A B}{A C}$ .
La cotangente del ángulo $α$ como $\frac{c . a d y a c e n t e}{c . o p u e s t o}$ y lo denotamos como $\cot α = \frac{A C}{B C}$ .

Si consideramos el ángulo complementario a $α$ , $β = ∠ C B A$ , entonces de las definiciones se siguen las siguientes relaciones:

$\sin α = \cos β$ , $\cos α = \sin β$ , $\tan α = \frac{\sin α}{\cos α}$ , $\tan α \tan β = 1$ .

$\csc α = \sec β$ , $\sec α = \csc β$ , $\cot α = \frac{\cos α}{\sin α}$ , $\cot α \cot β = 1$ .

Círculo trigonométrico

Consideremos $(O, 1)$ un círculo con centro en $O$ de radio $1$ , por $O$ trazamos dos rectas perpendiculares $x$ e $y$ , tomamos un punto $P \in (O, 1)$ en el cuadrante formado por el rayo derecho $O x$ y el rayo superior $O y$ y trazamos las proyecciones $X$ , $Y$ de $O$ a las rectas $x$ , $y$ respectivamente.

El triángulo $△ O P X$ es rectángulo y su hipotenusa $O P = 1$ , si consideramos el ángulo $∠ X O P = γ$ entonces
$\sin γ = P X$ y
$\cos γ = O X$ .

Tracemos la tangente a $(O, 1)$ por $Q$ , la intersección entre $x$ y $(O, 1)$ , tomemos $R$ como la intersección entre la tangente y $O P$ entonces $R Q ∥ P X$ y los triángulos $△ O P X$ y $△ O R Q$ son semejantes por lo tanto
$\tan γ = \frac{P X}{O X} = \frac{R Q}{O Q} = R Q$ y
$\sec γ = \frac{O P}{O X} = \frac{O R}{O Q} = O R$ .

Ahora trazamos la tangente a $(O, 1)$ por $S$ , la intersección de $y$ con $(O, 1)$ , tomamos $T$ como la intersección de la tangente con $O P$ entonces $S T ∥ x$ , por lo tanto $γ = ∠ S T O$ y así $△ O P X$ y $△ T O S$ son semejantes, por lo tanto,
$\csc γ = \frac{O P}{P X} = \frac{O T}{O S} = O T$ y
$\cot α = \frac{O X}{P X} = \frac{S T}{O S} = S T$ .

Con esta construcción podemos extender las definiciones de función trigonométrica para ángulos agudos a ángulos de cualquier magnitud trasladando el punto $P$ alrededor de la circunferencia $(O, 1)$ y tomando las proyecciones de $P$ , $X$ e $Y$ a las rectas $x$ e $y$ respectivamente que tomaremos como positivas si se encuentran en los rayos derecho y superior o negativas si se encuentran en los rayos izquierdos e inferior de las rectas $x$ , $y$ respectivamente.

De esta manera todas las razones trigonométricas quedan determinadas por el valor de $\sin γ = P X$ y $\cos γ = O X$ .

Teorema 1, identidad pitagórica. Sea $0 \leq γ < 2 π$ entonces, $\sin^{2} γ + \cos^{2} γ = 1$ .

Demostración. Aplicamos el teorema de Pitágoras al triángulo rectángulo $△ O P X$ , (figura 2).

$1 = P X^{2} + O X^{2} = \sin^{2} γ + \cos^{2} γ$ .

Ley extendida de senos

Teorema 2, ley extendida de los senos. Sean $△ A B C$ y $(O, R)$ su circuncírculo, etiquetemos $∠ B A C = α$ , $∠ C B A = β$ , $∠ A C B = γ$ y $a = B C$ , $b = A C$ , $c = A B$ las longitudes de sus lados, entonces
$\frac{\sin α}{a} = \frac{\sin β}{b} = \frac{\sin γ}{c} = \frac{1}{2 R}$ .

Demostración. Tracemos $D$ el punto diametralmente opuesto a $C$ , entonces $∠ B D C = α$ , pues subtienden el mismo arco.

$∠ C B D$ es un ángulo recto, pues $C D$ es diámetro, por lo tanto $\sin α = \sin ∠ B D C = \frac{a}{C D}$ .

Por lo tanto, $\frac{\sin α}{a} = \frac{1}{2 R}$ .

De manera análoga podemos ver que
$\sin β = \frac{b}{2 R}$ y
$\sin γ = \frac{c}{2 R}$ .

Por lo tanto, $\frac{\sin α}{a} = \frac{\sin β}{b} = \frac{\sin γ}{c} = \frac{1}{2 R}$ .

Corolario. El seno de un ángulo inscrito en una circunferencia de diámetro $1$ es igual a la cuerda que abarca dicho ángulo.

Demostración. Se sigue de sustituir $2 R = 1$ en el teorema anterior.

Ley de cosenos

Teorema 3, ley de cosenos. Sean $△ A B C$ , $∠ B A C = α$ , $∠ C B A = β$ , $∠ A C B = γ$ y $a = B C$ , $b = A C$ , $c = A B$ las longitudes de sus lados, entonces se da la siguiente igualdad:
$c^{2} = a^{2} + b^{2} - 2 a b \cos γ$ .

Demostración. Trazamos $D$ el pie de la perpendicular a $B C$ desde $A$ y aplicamos el teorema de Pitágoras a $△ A B D$ y $△ A D C,$ de donde obtenemos

$\begin{matrix} (6) & c^{2} = A D^{2} + (a - D C)^{2} = A D^{2} + a^{2} - 2 a (D C) + D C^{2}, \end{matrix}$
$b^{2} = A D^{2} + D C^{2}$
$\Leftrightarrow$ $\begin{matrix} (7) & A D^{2} = b^{2} - D C^{2} . \end{matrix}$

Sustituimos $(2)$ en $(1)$ y obtenemos $c^{2} = b^{2} + a^{2} - 2 a (D C)$ .

Por otro lado $\cos γ = \frac{D C}{b}$ $\Leftrightarrow$ $b \cos γ = D C$ .

Así que $c^{2} = a^{2} + b^{2} - 2 a b \cos γ$ .

De manera similar se puede ver que
$a^{2} = b^{2} + c^{2} - 2 b c \cos α$ y
$b^{2} = a^{2} + c^{2} - 2 a c \cos β$ .

El seno de la suma

Teorema 4, el seno de la suma de dos ángulos. Sean $α$ y $β$ ángulos agudos entonces $\sin (α + β) = \sin α \cos β + \sin β \cos α$ .

Demostración. Sea $A B C D$ cíclico tal que $B D = 1$ es diámetro del circuncírculo, $∠ D B A = α$ y $∠ C B D = β$ .

Como consecuencia del corolario tenemos que $A C = \sin (α + β)$ , ademas $△ B A D$ y $△ D C B$ son triángulos rectángulos pues $D B$ es diámetro.

Se sigue que
$A B = \cos α$ ,
$C D = \sin β$ ,
$A D = \sin α$ y
$B C = \cos β$ .

El teorema de Ptolomeo nos dice que
$\begin{matrix} (8) & A C \times B D = A B \times C D + B C \times A D . \end{matrix}$

Por lo tanto, $\sin (α + β) = \cos α \sin β + \sin α \cos β$ .

El coseno de la suma

Teorema 5, el coseno de la suma de dos ángulos. Sean $α \neq 0$ y $β$ ángulos agudos tales que $α + β < \frac{π}{2}$ entonces $\cos (α + β) = \cos α \cos β - \sin α \sin β$ .

Demostración. Sea $A B C D$ cíclico tal que $B C = 1$ es diámetro del circuncírculo, $∠ C B D = α$ y $∠ D B A = β$ .

Como $△ B A C$ y $△ B D C$ son triángulos rectángulos y $B C = 1$ tenemos que
$A C = \sin (α + β) = \sin α \cos β + \sin β \cos α$ (teorema 4),
$B D = \cos α$ ,
$A B = \cos (α + β)$ ,
$C D = \sin α$ ,
$A D = \sin ∠ D C A = \sin β$ (corolario).

Por el teorema de Ptolomeo $(3)$ , aplicado a $A B C D$ obtenemos:
$\cos (α + β) \sin α + \sin β$
$= (\sin α \cos β + \sin β \cos α) \cos α$
$= \sin α \cos β \cos α + \sin β \cos^{2} α$
$= \sin α \cos β \cos α + (\sin β) (1 - \sin^{2} α)$ (teorema 1)
$= \sin α \cos β \cos α - \sin β \sin^{2} α + \sin β$ .

$\Leftrightarrow$ $\cos (α + β) \sin α = \sin α \cos β \cos α - \sin β \sin^{2} α$ .

Por lo tanto, $\cos (α + β) = \cos β \cos α - \sin β \sin α$ .

Seno y coseno del ángulo medio

Teorema 6, el seno y el coseno del ángulo medio. Sea $α \neq 0$ un ángulo agudo entonces
$\sin \frac{α}{2} = \sqrt{\frac{1 - \cos α}{2}}$ y $\cos \frac{α}{2} = \sqrt{\frac{1 + \cos α}{2}}$ .

Demostración. Sea $A B C D$ cíclico tal que $B C = 1$ es diámetro y $∠ C B D = ∠ D B A = \frac{α}{2}$ .

Ya que $△ B A C$ y $△ B D C$ son triángulos rectángulos podemos ver que
$A C = \sin α$ ,
$B D = \cos \frac{α}{2}$ ,
$A B = \cos α$ ,
$C D = \sin \frac{α}{2}$ ,
$A D = \sin ∠ D C A = \sin \frac{α}{2}$ (corolario).

Aplicando Ptolomeo $(3)$ y el teorema 4 obtenemos:
$\cos α \sin \frac{α}{2} + \sin \frac{α}{2} = \sin α \cos \frac{α}{2}$
$= \sin (\frac{α}{2} + \frac{α}{2}) \cos \frac{α}{2} = 2 \sin \frac{α}{2} \cos^{2} \frac{α}{2}$ .

Por lo tanto, $2 \sin \frac{α}{2} \cos^{2} \frac{α}{2} = \sin \frac{α}{2} (\cos α + 1)$ $\Rightarrow$
$\begin{matrix} (9) & \cos^{2} \frac{α}{2} = \frac{\cos α + 1}{2} . \end{matrix}$

De donde se sigue que $\cos \frac{α}{2} = \sqrt{\frac{\cos α + 1}{2}}$ .

Ahora sustituimos la identidad pitagórica en la ecuación $(4)$ y obtenemos:
$1 - \sin^{2} \frac{α}{2} = \frac{\cos α + 1}{2}$
$\Leftrightarrow$
$\sin \frac{α}{2} = \sqrt{\frac{1 - \cos α}{2}}$ .

Más adelante…

En la siguiente entrada estudiaremos algunas propiedades relacionadas con el incírculo y los excÍrculos de un triángulo, así como también sobre sus centros y radios.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

$i)$ A partir de un triangulo equilátero deriva los valores de las seis razones trigonométricas para los ángulos $\frac{π}{3}$ y $\frac{π}{6}$ ,
$i i)$ A partir de un triángulo rectángulo isósceles deduce los valores de las seis razones trigonométricas para el ángulo $\frac{π}{4}$ .
Recordemos que consideramos la magnitud de un ángulo central como positiva, si recorremos el arco de circunferencia que subtiende dicho ángulo en el sentido contrario al de las manecillas del reloj y negativa en caso contraio, muestra que para cualquier valor de $α$ se cumple que:
$i)$ $\sin (- α) = - \sin α$ ,
$i i)$ $\cos (- α) = \cos α$ ,
$i i i)$ $\sin (π - α) = \sin α$ ,
$i v)$ $\cos (π - α) = - \cos α$ ,
$v)$ $\sec^{2} α = 1 + \tan^{2} α$ .
Sean $α$ y $β$ ángulos agudos tales que $α \geq β$ , muestra geométricamente:
$i)$ el seno de la diferencia de dos ángulos, $\sin (α - β) = \sin α \cos β - \sin β \cos α$ ,
$i i)$ el coseno de la diferencia de dos ángulos, $\cos (α - β) = \cos α \cos β + \sin α \sin β$ .
Sean $α$ y $β$ ángulos agudos prueba que:
$i)$ $\sin α \cos β = \frac{\sin (α + β) + \sin (α - β)}{2}$ ,
$i i)$ $\cos α \sin β = \frac{\sin (α + β) - \sin (α - β)}{2}$ .
Sea $△ A B C$ , por $A$ traza cualquier recta que corte a $B C$ en $L$ , muestra que $\frac{B L}{L C} = \frac{A B \sin ∠ B A L}{A C \sin ∠ L A C}$ .

Demuestra que si $\frac{\sin α}{\sin β} = \frac{\sin δ}{\sin γ}$ y $α + β = δ + γ < π$ entonces $α = δ$ y $β = γ$ .
Sea $△ A B C$ con $a = B C$ , $b = A C$ , $c = A B$ , $α = ∠ B A C$ , $β = ∠ C B A$ , $γ = ∠ A C B$ , demuestra las siguientes formulas para calcular el área de $△ A B C$ :
$i)$ $(△ A B C) = \frac{a c \sin β}{2} = \frac{a b \sin γ}{2} = \frac{b c \sin α}{2}$ ,
$i i)$ $(△ A B C) = \frac{a^{2} \sin β \sin γ}{2 \sin (β + γ)} = \frac{b^{2} \sin α \sin γ}{2 \sin (α + γ)} = \frac{c^{2} \sin α \sin β}{2 \sin (α + β)}$ .

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Teorema de Ptolomeo.
Siguiente entrada del curso: Circunferencias tritangentes.
Otros cursos.

Fuentes

Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 69-78.
Cárdenas, S., Notas de Geometría. México: Ed. Prensas de Ciencias, 2013, pp 55-62.
Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 89-95.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral: Límites de funciones trigonométricas

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores nos enfocamos en desarrollar el concepto de límite y revisamos diversos tipos de funciones, sin embargo, evitamos un tipo particular: las funciones trigonométricas. En esta entrada centraremos nuestra atención en la revisión de estos límites haciendo uso de toda la teoría revisada hasta este punto.

Límite de funciones trigonométricas cuando $x$ tiende a $x_{0}$

En los primeros ejemplos podrás visualizar la gráfica de la función con la finalidad de tener cierta intuición respecto a los límites, pero, en caso de requerirlo, puedes repasar las funciones trigonométricas.

Ejemplo 1. Prueba que $lim_{x \to 0} s e n (x) = s e n (0) .$

Demostración.

Para probar este límite, procederemos a calcular los límites laterales.

Sea $x \in (0, π / 2)$ . Usaremos que $0 < s e n (x) < x$ si $x \in (0, π / 2)$ .

Además, $lim_{x \to 0} = 0 y lim_{x \to 0} x = 0.$

Por el teorema del sándwich, podemos concluir que $\begin{matrix} (1) & lim_{x \to 0^{+}} s e n (x) = 0 = s e n (0) . \end{matrix}$

Si $x \in (- π / 2, 0)$ , entonces $- x \in (0, π / 2)$ . De esta forma, se obtiene que

$0 < s e n (- x) < - x .$

Como $s e n (- x) = - s e n (x)$ , se sigue que $0 < - s e n (x) < - x .$

Por lo tanto $x < s e n (x) < 0$

Nuevamente por el teorema del sándwich, se sigue que $\begin{matrix} (2) & lim_{x \to 0^{-}} s e n (x) = 0 = s e n (0) . \end{matrix}$

De $(1)$ y $(2)$ se concluye que $lim_{x \to 0} s e n (x) = s e n (0) .$

Ejemplo 2. Prueba que $lim_{x \to 0} c o s (x) = c o s (0) .$

Demostración.

Como $c o s^{2} (x) + s e n^{2} (x) = 1,$ se sigue que $| c o s (x) | = \sqrt{1 - s e n^{2} (x)} .$

Consideremos $x \in (- π / 2, π / 2)$ , entonces $c o s (x) > 0$ , y de la expresión anterior se sigue que $c o s (x) = \sqrt{1 - s e n^{2} (x)} .$

De esta manera, se tiene que

$\begin{aligned} lim_{x \to 0} c o s (x) & = lim_{x \to 0} \sqrt{1 - s e n^{2} (x)} \\ = \sqrt{1 - 0} \\ = 1 \\ = c o s (0) . \end{aligned}$

Por lo tanto

$lim_{x \to 0} c o s (x) = c o s (0) .$

Ejemplo 3. Prueba que el siguiente límite no existe $lim_{x \to 0} s e n (\frac{1}{x}) .$

Demostración.

Notemos que por la relación entre el límite de una función y el de una sucesión, basta dar dos sucesiones ${a_{n}}$ , ${b_{n}}$ tal que converjan a $x_{0} = 0$ y $a_{n}$ , $b_{n} \neq 0$ para todo $n \in N$ , pero que las sucesiones obtenidas de evaluar la función en los términos de ambas sucesiones, ${f (a_{n})}$ , ${f (b_{n})}$ converjan a valores distintos.

Definimos $f (x) = s e n (\frac{1}{x})$ y consideremos las sucesiones $a_{n} = (π n)^{- 1}$ y $b_{n} = (\frac{1}{2} π + 2 π n)^{- 1},$ donde $a_{n}$ , $b_{n} \neq 0$ para todo $n \in N .$

Veamos que
$\begin{aligned} lim_{n \to \infty} a_{n} = & lim_{n \to \infty} (π n)^{- 1} \\ = & lim_{n \to \infty} \frac{1}{π n} \\ = & 0. \end{aligned}$
$∴ lim_{n \to \infty} a_{n} = 0.$
Además,
$\begin{aligned} lim_{n \to \infty} b_{n} = & lim_{n \to \infty} {(\frac{1}{2} π + 2 π n)}^{- 1} \\ = & lim_{n \to \infty} \frac{1}{\frac{1}{2} π + 2 π n} \\ = & lim_{n \to \infty} \frac{1}{\frac{π + 4 π n}{2}} \\ = & lim_{n \to \infty} \frac{2}{π + 4 π n} \\ = & 0. \end{aligned}$
$∴ lim_{n \to \infty} b_{n} = 0.$
Es decir, las sucesiones ${a_{n}}$ y ${b_{n}}$ tienden a cero. Y notemos que $f (a_{n}) = s e n (n π) = 0$ y $f (b_{n}) = s e n (\frac{1}{2} π + 2 π n) = 1$ para todo $n \in N .$

De esta forma $lim_{n \to \infty} f (a_{n}) \neq lim_{n \to \infty} f (b_{n}) .$
Por tanto, podemos concluir que el límite no existe.

Ejemplo 4. Prueba que $lim_{x \to 0} x s e n (\frac{1}{x}) = 0.$

Demostración.

Haremos la demostración de este límite mediante la definición épsilon-delta.

Sea $ε > 0$ . Consideremos $δ = ε .$
Si $0 < | x - 0 | < δ$ , entonces
$\begin{matrix} | x | < δ = ε . \\ \Rightarrow & | x | < ε . \end{matrix}$
Además, sabemos que $- 1 < s e n (\frac{1}{x}) < 1$ para cualquier $x \neq 0.$ Entonces

$\begin{aligned} | f (x) - 0 | = & | x s e n (\frac{1}{x}) | \\ = & | x | | s e n (\frac{1}{x}) | \\ \leq & δ \cdot 1 \\ = & ε . \end{aligned}$
$∴ lim_{x \to 0} x s e n (\frac{1}{x}) = 0.$

El siguiente ejemplo es un límite que nos ayudará en diversas ocasiones, así que vale la pena ponerle particular atención.

Ejemplo 5. Prueba que $lim_{x \to 0} \frac{s e n (x)}{x} = 1.$

Demostración.

Como nos interesa revisar qué sucede cuando $x \to 0$ . Podemos considerar que $x \in (- \frac{π}{2}, \frac{π}{2})$ con $x \neq 0.$

De esta forma, se tiene que

Área $△ A B C = \frac{s e n (x) c o s (x)}{2}$ .
Área del sector circular $A D C = \frac{x r^{2}}{2} = \frac{x}{2}$ .
Área $△ A D E = \frac{1 \cdot t a n (x)}{2} = \frac{s e n (x)}{2 c o s (x)}$ .

Podemos notar que Área $△ A B C <$ Área del sector circular $A D C <$ Área $△ A D E$ .

Como $x \in (- \frac{π}{2}, \frac{π}{2})$ con $x \neq 0$ , entonces $s e n (x) \neq 0$ y $c o s (x) \neq 0$ . Así, se sigue que

$\begin{matrix} \frac{s e n (x) c o s (x)}{2} < \frac{x}{2} < \frac{s e n (x)}{2 c o s (x)} . \end{matrix}$

De donde se obtiene que $c o s (x) < \frac{x}{s e n (x)} < \frac{1}{c o s (x)} .$

Y se sigue que $c o s (x) < \frac{x}{s e n (x)} y \frac{x}{s e n (x)} < \frac{1}{c o s (x)} .$

Es decir, $\frac{s e n (x)}{x} < \frac{1}{c o s (x)} y c o s (x) < \frac{s e n (x)}{x} .$

$∴ c o s (x) < \frac{s e n (x)}{x} < \frac{1}{c o s (x)} .$

Además, $lim_{x \to 0} c o s (x) = 1$ y $lim_{x \to 0} \frac{1}{c o s (x)} = 1$ . Por el teorema del del sándwich se concluye que

$lim_{x \to 0} \frac{s e n (x)}{x} = 1.$

Ejemplo 6. Determina el siguiente límite $lim_{x \to 0} \frac{1 - c o s (x)}{x} .$

Si $0 < | x | < π$ , entonces

$\begin{aligned} \frac{1 - c o s (x)}{x} = & \frac{1 - c o s (x)}{x} \cdot \frac{1 + c o s (x)}{1 + c o s (x)} \\ = & \frac{1 - c o s^{2} (x)}{x (1 + c o s (x))} \\ = & \frac{s e n^{2} (x)}{x (1 + c o s (x))} \\ = & \frac{s e n (x)}{x} \frac{s e n (x)}{1 + c o s (x)} . \end{aligned}$

Así,
$\begin{aligned} lim_{x \to 0} \frac{1 - c o s (x)}{x} = & lim_{x \to 0} \frac{s e n (x)}{x} \cdot \frac{s e n (x)}{1 + c o s (x)} \\ = & lim_{x \to 0} \frac{s e n (x)}{x} \cdot lim_{x \to 0} \frac{s e n (x)}{1 + c o s (x)} \\ = & 1 \cdot \frac{0}{2} \\ = & 0. \end{aligned}$

$∴ lim_{x \to 0} \frac{1 - c o s (x)}{x} = 0.$

Ejemplo 7. Calcula el siguiente límite $lim_{x \to 0} \frac{x + s e n (x)}{x^{2} - s e n (x)} .$

$\begin{aligned} lim_{x \to 0} \frac{x + s e n (x)}{x^{2} - s e n (x)} = & lim_{x \to 0} \frac{x + s e n (x)}{x^{2} - s e n (x)} \cdot \frac{\frac{1}{x}}{\frac{1}{x}} \\ = & lim_{x \to 0} \frac{1 + \frac{s e n (x)}{x}}{x - \frac{s e n (x)}{x}} \\ = & \frac{1 + 1}{0 - 1} \\ = & - 2. \end{aligned}$
$∴ lim_{x \to 0} \frac{x + s e n (x)}{x^{2} - s e n (x)} = - 2.$

Ejemplo 8. Calcula $lim_{x \to 0} \frac{s e c (x) - 1}{x} .$

$\begin{aligned} lim_{x \to 0} \frac{s e c (x) - 1}{x} = & lim_{x \to 0} \frac{\frac{1}{c o s (x)} - 1}{x} \\ = & lim_{x \to 0} \frac{\frac{1 - c o s (x)}{c o s (x)}}{x} \\ = & lim_{x \to 0} \frac{1 - c o s (x)}{x c o s (x)} \\ = & lim_{x \to 0} \frac{1}{c o s (x)} \frac{1 - c o s (x)}{x} \\ = & 1 \cdot 0 \\ = & 0. \end{aligned}$
$∴ lim_{x \to 0} \frac{s e c (x) - 1}{x} = 0.$

Límite de funciones trigonométricas cuando $x$ tiende a infinito

Ahora procederemos a revisar algunos ejemplos de funciones trigonométricas cuando $x \to \infty$ , o bien, cuando $x \to - \infty .$

Ejemplo 9. Calcula el límite $lim_{x \to \infty} \frac{s e n (x)}{x} .$

Sabemos que $- 1 \leq s e n (x) \leq 1.$ De esta forma, si $x \neq 0$ , se tiene que $- \frac{1}{x} \leq \frac{s e n (x)}{x} \leq \frac{1}{x} .$

Además, $lim_{x \to \infty} - \frac{1}{x} = 0 = lim_{x \to \infty} \frac{1}{x} .$

Por el teorema del sándwich, se concluye que
$lim_{x \to \infty} s e n (x) = 0.$

Ejemplo 10. Calcula el límite $lim_{x \to \infty} \frac{x s e n (x)}{x^{2} + 5} .$
$\begin{aligned} lim_{x \to \infty} \frac{x s e n (x)}{x^{2} + 5} = & lim_{x \to \infty} \frac{x s e n (x)}{x^{2} + 5} \cdot \frac{\frac{1}{x^{2}}}{\frac{1}{x^{2}}} \\ = & lim_{x \to \infty} \frac{\frac{x s e n (x)}{x^{2}}}{\frac{x^{2} + 5}{x^{2}}} \\ = & lim_{x \to \infty} \frac{\frac{s e n (x)}{x}}{1 + \frac{5}{x^{2}}} \\ = & \frac{0}{1}, por lo visto en el ejemplo anterior \\ = & 0. \end{aligned}$
$∴ lim_{x \to \infty} \frac{x s e n (x)}{x^{2} + 5} = 0.$

Ejemplo 11. Determina si existe el siguiente límite $lim_{x \to \infty} \frac{x^{2} (1 + s e n^{2} (x))}{(x + s e n (x))^{2}} .$

El límite no existe. Considera las sucesiones generadas por $a_{n} = π n$ y $b_{n} = \frac{1}{2} π + 2 π n$ donde $a_{n}$ , $b_{n} \to \infty$ cuando $n \to \infty .$ Notemos que
$\begin{aligned} lim_{n \to \infty} f (a_{n}) = & lim_{n \to \infty} \frac{(π n)^{2} (1 + s e n^{2} (π n))}{(π n + s e n (π n))^{2}} \\ = & lim_{n \to \infty} \frac{(π n)^{2} (1 + 0)}{(π n + 0)^{2}} \\ = & lim_{n \to \infty} \frac{(π n)^{2}}{(π n)^{2}} \\ = & lim_{n \to \infty} 1 \\ = & 1. \end{aligned}$
$∴ lim_{n \to \infty} f (a_{n}) = 1.$
Por otro lado,
$\begin{aligned} lim_{n \to \infty} f (b_{n}) = & lim_{n \to \infty} \frac{(\frac{1}{2} π + 2 π n)^{2} (1 + s e n^{2} (\frac{1}{2} π + 2 π n))}{(\frac{1}{2} π + 2 π n + s e n (\frac{1}{2} π + 2 π n))^{2}} \\ = & lim_{n \to \infty} \frac{(\frac{1}{2} π + 2 π n)^{2} (1 + 1)}{(\frac{1}{2} π + 2 π n + 1)^{2}} \\ = & lim_{n \to \infty} \frac{2 (\frac{1}{2} π + 2 π n)^{2}}{(\frac{1}{2} π + 2 π n + 1)^{2}} \\ = & 2. \end{aligned}$
$∴ lim_{n \to \infty} f (b_{n}) = 2.$

Como $lim_{n \to \infty} f (a_{n}) \neq lim_{n \to \infty} f (b_{n}) .$
Podemos concluir que el límite $lim_{x \to \infty} \frac{x^{2} (1 + s e n^{2} (x))}{(x + s e n (x))^{2}}$ no existe.

Ejemplo 12. Determina el siguiente límite $lim_{x \to - \infty} \frac{3 x^{2} - s e n (5 x)}{x^{2} + 2} .$

Recordemos que $- 1 < s e n (5 x) < 1$ , de donde se sigue que $- 1 < - s e n (5 x) < 1$ , así
$\begin{matrix} 3 x^{2} - 1 < 3 x^{2} - s e n (5 x) < 3 x^{2} + 1. \end{matrix}$

Se sigue que
$\begin{matrix} \frac{3 x^{2} - 1}{x^{2} + 2} < \frac{3 x^{2} - s e n (5 x)}{x^{2} + 2} < \frac{3 x^{2} + 1}{x^{2} + 2}, pues x^{2} + 2 > 0. \end{matrix}$

Y notemos que

$\begin{aligned} lim_{x \to - \infty} \frac{3 x^{2} + 1}{x^{2} + 2} = & lim_{x \to - \infty} \frac{\frac{3 x^{2} + 1}{x^{2}}}{\frac{x^{2} + 2}{x^{2}}} \\ = & lim_{x \to - \infty} \frac{3 + \frac{1}{x^{2}}}{1 + \frac{2}{x^{2}}} \\ = & \frac{3}{1} \\ = & 3. \end{aligned}$

De forma similar, se obtiene que $lim_{x \to - \infty} \frac{3 x^{2} - 1}{x^{2} + 2} = 3.$

Por lo que se tiene que $lim_{x \to - \infty} \frac{3 x^{2} + 1}{x^{2} + 2} = 3 = lim_{x \to - \infty} \frac{3 x^{2} - 1}{x^{2} + 2} .$ Usando el teorema del sándwich podemos concluir que
$lim_{x \to - \infty} \frac{3 x^{2} - s e n (5 x)}{x^{2} + 2} = 3.$

Más adelante…

En la siguiente entrada revisaremos el concepto de asíntotas con lo que nos será posible analizar un comportamiento particular que llegan a tener las funciones, el cual es aproximarse a una recta en determinado momento; y, con esto, estaremos finalizando la unidad referente al límite de una función.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Halla los siguientes límites, justifica en caso de no alguno no exista.

$lim_{x \to 0} \frac{x^{2} (3 + s e n (x))}{(x + s e n (x))^{2}} .$
$lim_{x \to 1} \frac{s e n (x^{2} - 1)}{x - 1} .$
$lim_{x \to \infty} x^{2} s e n (\frac{1}{x}) .$
$lim_{x \to \infty} \frac{x + s e n^{3} (x)}{5 x + 6} .$
$lim_{x \to 0} \frac{t a n^{2} (x) + 2 x}{x + x^{2}} .$

Entradas relacionadas

Ir a Cálculo Diferencial e Integral I
Entrada anterior del curso: Límites infinitos
Siguiente entrada del curso: Asíntotas
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Introducción

Método de sustitución trigonométrica

Caso 1: Integrales de la forma: a2−x2

Caso 2: Integrales de la forma x2−a2

Caso 3: Integrales de la forma x2+a2

Tarea moral

Más adelante…

Entradas relacionadas

Introducción

Hablemos de la tangente y la cotangente

Ahora la secante y la cosecante

¿Quiénes son las funciones inversas?

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Identidades trigonométricas Pitagóricas

Otras identidades trigonométricas

Simetrías

Función periódica

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Razones trigonométricas

Círculo trigonométrico

Ley extendida de senos

Ley de cosenos

El seno de la suma

El coseno de la suma

Seno y coseno del ángulo medio

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Introducción

Límite de funciones trigonométricas cuando x tiende a x0

Límite de funciones trigonométricas cuando x tiende a infinito

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Caso 1: Integrales de la forma: $\sqrt{a^{2} - x^{2}}$

Caso 2: Integrales de la forma $\sqrt{x^{2} - a^{2}}$

Caso 3: Integrales de la forma $\sqrt{x^{2} + a^{2}}$

Límite de funciones trigonométricas cuando $x$ tiende a $x_{0}$

Límite de funciones trigonométricas cuando $x$ tiende a infinito