Archivo de la etiqueta: algebra

Seminario de Resolución de Problemas: Identidades algebraicas y binomio de Newton

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción a entradas de álgebra

Cuando en matemáticas hablamos de álgebra, se abarca una gran cantidad de ideas, que van desde el álgebra de secundaria, en la cual factorizamos, despejamos y usamos identidades algebraicas, hasta el álgebra abstracta, que estudia estructuras algebraicas más generales como grupos, anillos y campos. Todas estas ideas tienen amplias aplicaciones en la resolución de problemas. En esta entrada, y las que vendrán a continuación, veremos numerosos ejemplos de esto

Para empezar, hablaremos de álgebra en el sentido de secundaria y preparatoria. Veremos que estas ideas, aunque sencillas, son muy versátiles. Después hablaremos de polinomios y de dos resultados fundamentales en su teoría: el teorema de factorización única y el teorema de la identidad. Los polinomios abundan en las matemáticas, y un correcto entendimiento de ellos abre muchas puertas en la resolución de problemas. En una entrada final daremos algunas ideas de otras estructuras algebraicas como grupos, anillos y campos.

Más adelante en el curso hablaremos con detalle de otros dos temas relacionados con álgebra: desigualdades y álgebra lineal.

Como lo hemos hecho hasta ahora, la idea no es profundizar demasiado en el desarrollo de la teoría algebraica. Para eso, es más recomendable llevar buenos cursos de distintos tipos de álgebra a nivel superior. Aquí en el blog hay material de los cursos Álgebra Superior II y Álgebra Lineal I que imparto en la Facultad de Ciencias de la UNAM.

Identidades algebraicas

Comenzaremos hablando de identidades algebraicas. Una identidad algebraica es una igualdad que se satisface para ciertas variables, independientemente del valor que tomen. Algunos ejemplos son las igualdades que se aprenden a nivel secundaria y bachillerato:

\begin{gather*}
a^2-b^2=(a-b)(a+b),\\
a^2+2ab+b^2=(a+b)^2,\\
a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2,\\
a^n-b^n = (a-b)(a^{n-1}+a^{n-2}b+\ldots+ab^{n-2}+b^{n-1}).
\end{gather*}

Varias de las identidades algebraicas nos permiten desarrollar o factorizar una expresión. Factorizarla es bastante útil en problemas de teoría de números, en donde es importante conocer qué números dividen a la expresión. Desarrollarla a veces nos permite trabajar con una suma de términos simétricos, que podemos estudiar con técnicas de polinomios o con desigualdades.

Veamos algunos ejemplos.

Problema. Muestra que si $n$ es un entero, entonces $n^4-20n^2+4$ no es un número primo.

Sugerencia pre-solución. Intenta formular un problema equivalente al factorizar la expresión. Hay más de un camino por el que puedes proceder para factorizar, pero no todos te llevan a una solución. Intenta completar cuadrados de distintas formas y ve si encuentras un patrón.

Solución. Reescribimos la expresión como sigue:
\begin{align*}
n^4-20n^2+4&=n^4-4n^2+4-16n^2\\
&=(n^2-2)^2-(4n)^2\\
&=(n^2-4n-2)(n^2+4n-2).
\end{align*}

Para ver que la expresión no es un primo, basta con ver que ninguno de estos factores puede ser igual a $1$ o $-1$. Si $n^2-4n-2=1$ o $n^2+4n-2=1$, entonces $n^2=\pm 4n+3$. Trabajando módulo $4$, tendríamos $n^2\equiv 3 \pmod{4}$, lo cual es imposible.

Si $n^2-4n-2=-1$ o $n^2+4n-2=-1$, entonces sumando $6$ de ambos lados tenemos $$(n\pm 2)^2=n^2\pm 4n+4=5.$$ Esto es imposible pues $5$ no es el cuadrado de un entero. Así, $n^4-20n^2+4$ se puede factorizar en factores distintos de $1$ y $-1$ y por lo tanto no es primo.

$\square$

El siguiente problema fue parte de la 1a Olimpiada Mexicana de Teoría de Números. Veremos dos soluciones. Ambas usan ideas algebraicas, pero son distintas entre sí.

Problema. Sean $a,b,c,d$ enteros tales que

\begin{align*}
ab + bc + ca &= 1\\
ad + dc + ca &= 1\\
ab + bd + da &= 1.
\end{align*}

Determina todos los valores posibles que puede tomar $bc+cd+db$.

Sugerencia pre-solución 1. Hay varias formas de aprovechar la simetría del problema. Intenta manipular las ecuaciones para obtener información y recuerda que es importante usar que $a$, $b$, $c$ son enteros.

Solución 1. A partir de la primera y segunda ecuación, tenemos que $$ab+bc+ca=ad+dc+ca,$$

de donde $0=ad+dc-ab-bc=(a+c)(d-b)$. De aquí tenemos dos opciones: $a=-c$ o $b=d$. Si $a=-c$, de la segunda ecuación obtenemos $$1=ad+dc+ca=-c^2,$$ lo cual es imposible. Así, concluimos que $b=d$.

Por simetría, concluimos que $c=b$, así que $b=c=d$. Tras esto, las tres ecuaciones se reducen a una sola $$1=2ab+b^2=b(2a+b).$$ Las únicas factorizaciones de $1$ en enteros son $1=1\cdot 1$ o $1=(-1)(-1)$, de modo que $b=2a+b$, de donde $a=0$ y $b=\pm 1$. De cualquier forma, la expresión que buscamos es $bc+cd+db=3b^2=3$.

$\square$

Sugerencia pre-solución 2. Formula un problema equivalente sumando $a^2$ en ambos lados en cada una de las ecuaciones.

Solución 2. Sumando $a^2$ en ambos lados de la primer ecuación obtenemos $$a^2+1=a^2+ab+bc+ca=(a+b)(a+c).$$ Las otras dos ecuaciones dan expresiones simétricas. Multiplicando las tres, tenemos $$(a^2+1)(a^2+1)^2=(a+b)^2(b+c)^2(c+a)^2.$$

El lado derecho es el cuadrado de un entero, así que el izquierdo también debe serlo, de modo que $a^2+1$ debe ser el cuadrado de un entero. Pero los únicos cuadrados a distancia $1$ son $0$ y $1$, de donde $a^2+1=1$, y así $a=0$. Las ecuaciones se convierten entonces en $bc=dc=bd=1$, de donde la suma de las tres es $3$.

$\square$

Demostraciones del binomio de Newton

La siguiente es una de las identidades algebraicas más importantes.

Teorema (binomio de Newton). Para $a$ y $b$ números reales y $n$ un entero no negativo, se tiene que
\begin{align*}
(a+b)^n=\sum_{j=0}^n \binom{n}{j}a^{n-j}b^j
\end{align*}

El término de la derecha es $$a^n+\binom{n}{1}a^{n-1}b+\ldots+\binom{n}{n-1}ab^{n-1} + b^n.$$

Veamos algunas demostraciones del teorema de binomio de Newton, que usan ideas un poco distintas. La primera usa ideas combinatorias. La segunda, ideas más algebraicas. La tercera es menos general, pero usa ideas geométricas.

Demostración combinatoria

Demostración 1. Pensemos al lado izquierdo como el producto $$(a+b)(a+b)\ldots(a+b)(a+b).$$ ¿Cómo se obtienen factores al desarrollar esta expresión? En cada uno de los $n$ paréntesis hay que elegir o un $a$, o un $b$. Así, cada sumando es producto de $n$ letras.

Si elegimos $j$ veces $b$, entonces elegimos $n-j$ veces $a$. ¿De cuántas formas podemos elegir $j$ veces $b$? Tantas como subconjuntos de tamaño $j$ de un conjunto de $n$ elementos, es decir, $\binom{n}{j}$.Así, el término $a^{n-j}b^j$ aparece $\binom{n}{j}$ veces.

Para terminar, notemos que $j$ puede ir desde $0$ (no elegir ningún $b$), hasta $n$ (no elegir ningún $a$).

$\square$

La demostración anterior es combinatoria, pues está usando argumentos de conteo. Está contando de dos formas distintas los términos que aparecen en el producto desarrollado. Además, está usando la interpretación combinatoria de los coeficientes binomiales.

Demostración algebraica

Demostración 2. Si $b=0$, entonces en ambos lados tenemos $a^n$, ya que el único sumando en el que no aparece $b$ es el primero. Tenemos algo análogo si $a=0$. De otra forma, podemos asumir que $a$ y $b$ no son cero y dividir ambos lados de la igualdad que queremos entre $b^n$. Definiendo $x=a/b$, tenemos que mostrar que:

$$(x+1)^n= \sum_{j=0}^n \binom{n}{j}x^{n-j}.$$

Esta igualdad es claramente cierta para $n=0$, pues en ambos lados obtenemos $1$, y para $n=1$, pues en ambos lados obtenemos $x+1$. Procediendo por inducción (explicamos cada paso con un poco de detalles más abajo):

\begin{align*}
(x+1)^{n+1}&=(x+1)(x+1)^n\\
& = (x+1)\sum_{j=0}^n \binom{n}{j} x^{n-j}\\
&=\sum_{j=0}^n \binom{n}{j} x^{n-j+1}+\sum_{j=0}^n \binom{n}{j}x^{n-j}\\
& = \sum_{j=0}^{n+1} \binom{n}{j-1} x^{n-j}+\sum_{j=0}^{n+1} \binom{n}{j}x^{n-j}\\
&=\sum_{j=0}^{n+1}\left(\binom{n}{j-1}+\binom{n}{j}\right) x^{n-j}\\
&=\sum_{j=0}^{n+1}\binom{n+1}{j} x^{n-j}.
\end{align*}

El primer paso es claro. En el segundo usamos hipótesis inductiva. Luego, hacemos la multiplicación por $x+1$. El siguiente paso puede ser un poco confuso, pues parece que «agregamos términos», pero en la segunda suma sólo agregamos $\binom{n}{n+1}x^{-1}=0$. En la primer suma hicimos un shift o desfase: los términos que estaban antes para $j$ de $0$ a $n$, ahora están para $j$ de $1$ a $n+1$. Además, agregamos el término $\binom{n}{-1}x^{n}=0$. En el siguiente paso usamos la identidad de Pascal: $$\binom{n}{j-1}+\binom{n}{j}=\binom{n+1}{j},$$ que se puede demostrar combinatoriamente, o directamente de manera algebraica a partir de la fórmula para coeficientes binomiales.

Con esto termina la demostración por inducción.

$\square$

Esta segunda demostración es mucho más algebraica, es decir, usa ideas de cómo se manipulan las expresiones con variables. El primer paso, en el que reducimos el problema a cuando un término es $1$, se llama homogenización. En realidad no era estrictamente necesario hacerlo, pero simplifica la notación. En las sumas hicimos un shift, que es otra técnica que se usa al estudiar sumas y series.

Demostración geométrica

Daremos una última demostración del teorema del binomio de Newton, pero sólo para el caso $n=2$. Lo que tenemos que demostrar es simplemente la identidad $$(a+b)^2=a^2+2ab+b^2.$$ Para este caso, hay una bonita «demostración sin palabras»:

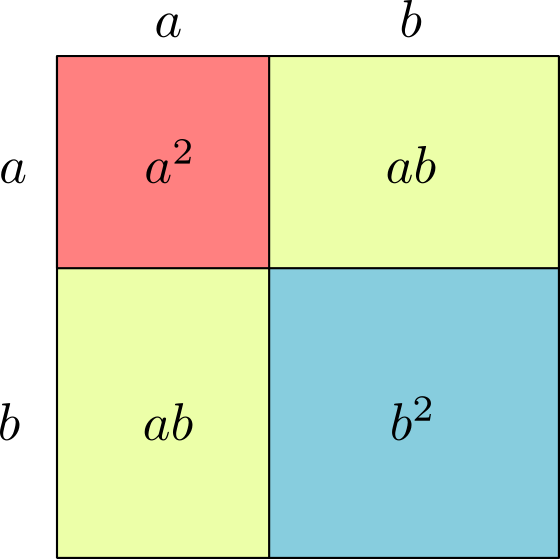
Binomio al cuadrado mostrado geométricamente
Demostración visual del binomio al cuadrado

Esta demostración es geométrica, pues estamos interpretando a la igualdad como una igualdad de áreas. Estamos usando una fórmula de área para cuadrados y rectángulos. Además, estamos usando que el área de una figura es aditiva, es decir, que es igual a la suma de áreas de figuras en las que queda subdividida.

Puedes elegir tu demostración favorita del binomio de Newton. Sin embargo, en resolución de problemas es importante saber proceder con varios acercamientos. Hay problemas en los que el acercamiento combinatorio, el algebraico o el geométrico es ventajoso, y por ello es mejor tener buena práctica en todos ellos.

Una aplicación del binomio de Newton en teoría de números

En entradas anteriores ya hemos usado el teorema del binomio de Newton en repetidas ocasiones, por ejemplo, en la entrada de aritmética de números complejos. Veamos un ejemplo más.

Problema. Sean $a$ y $b$ enteros primos relativos. Muestra que para todo entero positivo $n$, se tiene que $a^n$ y $b^n$ son primos relativos.

Sugerencia pre-problema. Hay varias formas de dar una solución de esto. Una es analizando a los enteros primo por primo. Sin embargo, existe una solución usando binomio de Newton y la caracterización en términos de combinaciones lineales enteras para primos relativos.

Solución. Como $a$ y $b$ son primos relativos, existe una combinación lineal entera de ellos que da $1$, digamos $$ax+by=1.$$ Elevando esta igualdad a la $2n-1$ tenemos $$1=1^{2n-1}=(ax+by)^{2n-1}.$$ Abriendo el último término con binomio de Newton queda
$$\sum_{j=0}^{n-1} \binom{2n-1}{j} a^{2n-1-j}b^j + \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^j,$$ y factorizando $a^n$ del primer sumando y $b^n$ del segundo,
$$a^n \sum_{j=0}^{n-1} \binom{2n-1}{j} a^{n-1-j}b^j + b^n \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^{j-n}.$$

Lo que queda a la derecha es una combinación lineal entera de $a^n$ y $b^n$ igual a $1$, y por lo tanto son primos relativos.

$\square$

Más problemas

En la siguiente entrada hablaremos de la identidad de Gauss para suma de cuadrados y de la identidad para $x^3+y^3+z^3-3xyz$, las cuales se usan frecuentemente en resolución de problemas. Además, puedes encontrar más problemas de identidades algebraicas en la Sección 4.1 del libro Problem Solving through Problems de Loren Larson.

Álgebra Superior II: Ecuaciones cuadráticas complejas

Por Leonardo Ignacio Martínez Sandoval

6 respuestas

Introducción

En entradas anteriores ya platicamos acerca de la construcción de los números complejos. Vimos que, con las operaciones de suma y resta que definimos, $\mathbb{C}$ es un campo. Además, introdujimos las nociones de conjugación compleja y de norma compleja. Como ya entendemos un poco de las operaciones que tenemos en $\mathbb{C}$, podemos empezar a hablar de otro de los temas que interesa al álgebra: resolver ecuaciones. Comenzaremos hablando acerca de ecuaciones cuadráticas complejas.

En entradas posteriores de este parcial, y del siguiente, veremos cómo resolver otro tipo de ecuaciones en los números complejos:

  • Sistemas de ecuaciones lineales complejos.
  • Ecuaciones de la forma $z^n=w$.
  • La ecuación cúbica $ax^3+bx^2+cx+d=0$.
  • La ecuación de grado 4 $ax^4+bx^3+cx^2+dx+e=0$.

En realidad, los números complejos son la estructura numérica correcta para resolver todo tipo de polinomios, es decir, expresiones como las de los últimos tres incisos anteriores. Esto se debe al teorema fundamental del álgebra, que dice lo siguiente.

Teorema (fundamental del álgebra). Sea $n$ un entero positivo y $a_0,\ldots,a_n$ en $\mathbb{C}$ con $a_n\neq 0$. La ecuación en números $$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0$$ tiene por lo menos una solución $x$ en $\mathbb{C}$.

La demostración de este teorema en el curso será optativa, y la veremos sólo si tenemos tiempo suficiente. Antes de poder hacer esto, tenemos que seguir discutiendo sobre los números complejos (en esta unidad) y a los polinomios (en la siguiente unidad). Si en algún momento llevas un curso de análisis complejo, también demostrarás el teorema fundamental del álgebra, con ideas un poco más profundas.

Otra aclaración. Si el teorema fundamental del álgebra dice que toda ecuación polinomial tiene solución, ¿por qué sólo estudiamos hasta la ecuación de grado cuatro? La razón es que para grados dos, tres y cuatro podemos dar las soluciones a estas ecuaciones de manera algebraica, es decir, podemos expresar las soluciones con una fórmula (de cierto tipo) en términos de los coeficientes de la ecuación. En el caso de que la ecuación sea de grado 5 en adelante, en cierto sentido matemático no se puede. La demostración de esto la puedes ver en un curso de álgebra moderna intermedio, en el que se discuta teoría de Galois.

Raíces cuadradas en los complejos

Las ecuaciones cuadráticas complejas se resuelven de una forma parecida a lo que hacemos en $\mathbb{R}$: usando la fórmula cuadrática. Es decir, si tenemos la ecuación $ax^2+bx+c=0$ con $a,b,c$ en $\mathbb{C}$ y $a\neq 0$, veremos más abajo que la podemos resolver mediante la fórmula $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}.$$

Esta expresión necesita que podamos encontrar la raíz cuadrada de un número complejo arbitrario. Vamos a mostrar que esto siempre es posible. Comencemos notando que el único complejo $z$ tal que $z^2=0$ es el $0$: si hubiera uno $z\neq 0$, multiplicando en ambos lados por $z^{-1}$ tendríamos que $z=0\cdot z^{-1}=0$, una contradicción.

Teorema. Sea $w\neq 0$ un número complejo. Entonces la ecuación $$z^2=w$$ tiene exactamente dos soluciones para $z$ en $\mathbb{C}$ y son inversos aditivos entre ellas.

Demostración. Tomemos $w=a+bi$ un número complejo. Supongamos que $z=x+yi$ es tal que $z^2=w=a+bi$. Tenemos que
\begin{align*}
a+bi=z^2=(x+iy)^2=(x^2-y^2)+2xyi,
\end{align*}

de donde $x^2-y^2=a$ y $2xy=b$. Elevando al cuadrado y sumando ambas ecuaciones, tenemos que
\begin{align*}
a^2+b^2&=(x^2-y^2)^2+(2xy)^2\\
&=(x^2+y^2)^2.
\end{align*}

Como $a$ y $b$ son números reales, tenemos que $a^2+b^2$ es un número real no negativo. Del mismo modo, $x^2+y^2$ es un real no negativo. De esta forma, sacando raíz cuadrada en la ecuación anterior, obtenemos que $$x^2+y^2=\sqrt{a^2+b^2}=\Vert w \Vert.$$

Sabemos además que $x^2-y^2=a=\text{Re}(w)$. Si sumamos ambas ecuaciones obtenemos $$x^2=\frac{\Vert w\Vert + \Rea(w)}{2}$$ y restándolas obtenemos $$y^2=\frac{\Vert w\Vert – \Rea(w)}{2}.$$

Recordemos que $\Vert w\Vert \geq |\Rea(w)|$ para todo complejo $w$, de modo que los términos del lado derecho de las igualdades anteriores son siempre positivos. Por esta razón, podemos sacar raíz de ambos lados. Pero ahora no hay nada que nos garantice que $x$ y $y$ sean positivos, así que hay que considerar dos casos en cada raíz, reflejados por el símbolo $\pm$ en las siguientes expresiones:

\begin{align*}
x&=\pm \sqrt{\frac{\Vert w\Vert + \Rea(w)}{2}}\\
y&=\pm \sqrt{\frac{\Vert w\Vert – \Rea(w)}{2}}.
\end{align*}

Hay que tener cuidado. No se valen las cuatro posibilidades de elecciones de signo. Notemos que de la ecuación $2xy=b$ tenemos que $xy$ tiene el mismo signo que $b=\Ima(w)$, así que si $\Ima(w)>0$ tienen que elegirse $x$ y $y$ con signos iguales y si $\Ima(w)<0$, tienen que elegirse con signos diferentes. Independientemente de la elección, las dos posibilidades dan dos soluciones para $z=x+iy$ que son inversas aditivas entre sí.

$\square$

Por notación. si tenemos un número complejo $w$, llamamos $\sqrt{w}$ a cualquiera de sus raíces cuadradas. Por el teorema anterior, su otra raíz es $-\sqrt{w}$.

Hay que tener cuidado. Para cuando $r$ es un real positivo, la notación $\sqrt{r}$ se refiere, por definición, a la raíz positiva. Cuando $w$ es un complejo arbitrario, no hay una forma «canónica» o «natural» de definir cuál de las dos raíces es «la correcta». Lo importante es que hay dos, y que son inversas aditivas entre sí.

Ejemplos de cómo obtener raíces cuadradas complejas

Antes de discutir cómo resolver ecuaciones cuadráticas complejas en general, veamos algunos ejemplos de cómo se usa el teorema anterior de manera práctica.

Problema 1. Encuentra las raíces cuadradas de $i$.

Solución. Tenemos que $\Vert i \Vert = 1$ y que $\Rea(i) = 0$, así que las soluciones $z=x+yi$ están dadas mediante

\begin{align*}
x&=\pm \sqrt{\frac{1}{2}}=\pm\frac{1}{\sqrt{2}}\\
y&=\pm \sqrt{\frac{1}{2}}=\pm\frac{1}{\sqrt{2}} .
\end{align*}

Como $\Ima(i)=1>0$, tenemos que elegir a $x$ y $y$ con los mismos signos entre sí, así que las soluciones son
\begin{align*}
z_1&=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}i\\
z_2&=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}i.
\end{align*}

$\triangle$

Problema 2. Encuentra las raíces cuadradas de $-21-20i$.

Solución. Tenemos que
\begin{align*}
\Vert -21-20i \Vert &= \sqrt{21^2+20^2}\\
&=\sqrt{841}\\
&=29,
\end{align*}

y que $\Rea(-21-20i)=-21$. Así, las soluciones $z=x+iy$ están dadas mediante

\begin{align*}
x&=\pm \sqrt{\frac{29-21}{2}}=\pm\sqrt{4}=\pm 2\\
y&=\pm \sqrt{\frac{29+21}{2}}=\pm\sqrt{25}=\pm 5.
\end{align*}

Como $\Ima(-21-20i)=-20<0$, debemos elegir $x$ y $y$ de distinto signo, de donde obtenemos las soluciones

\begin{align*}
z_1&=2-5i\\
z_2&=-2+5i.
\end{align*}

$\triangle$

Solución de ecuaciones cuadráticas complejas

Una vez que sabemos obtener la raíz cuadrada de un número complejo, tenemos todo lo necesario para resolver ecuaciones cuadráticas complejas en general. Consideremos $a,b$ y $c$ en $\mathbb{C}$ con $a\neq 0$. Veamos cómo resolver la ecuación $$ax^2+bx+c=0.$$

Para empezar, dividimos entre $a$ de ambos lados y restamos $\frac{c}{a}$, también, de ambos lados. Se obtiene que $$x^2+\frac{b}{a} x = -\frac{c}{a}.$$ El siguiente paso es un truco algebraico útil que se llama «completar el cuadrado». Pensamos a los términos del lado izquierdo como los primeros dos de un binomio cuadrado y nos preguntamos, ¿qué término faltaría? El término faltante es $\frac{b^2}{4a^2}$. Sumando este término en ambos lados, llegamos a $$x^2+\frac{b}{a} x + \frac{b^2}{4a^{2}} = \frac{b^2-4ac}{4a^2}.$$

La razón por la cual completamos el cuadrado es para poder escribir la expresión anterior como

$$(x+\frac{b}{2a})^2= \frac{b^2-4ac}{4a^2},$$

y aquí llegamos al punto en el que necesitamos obtener raíces cuadradas. Afortunadamente, ya sabemos que podemos hacer esto siempre en $\mathbb{C}$ y obtener $$x+\frac{b}{2a}=\pm\sqrt{ \frac{b^2-4ac}{4a^2}},$$ de donde concluimos que las soluciones son

$$x=-\frac{b}{2a}\pm\sqrt{ \frac{b^2-4ac}{4a^2}}.$$

Todos estos pasos son reversibles. Resumimos toda esta discusión en el siguiente resultado.

Teorema. Para $a,b,c$ en $\mathbb{C}$ y $a\neq 0$, la ecuación compleja $ax^2+bx+c=0$ tiene dos soluciones en $\mathbb{C}$ dadas por
\begin{align*}
x_1&=-\frac{b}{2a}+\sqrt{ \frac{b^2-4ac}{4a^2}}\\
x_2&=-\frac{b}{2a}- \sqrt{ \frac{b^2-4ac}{4a^2}}.
\end{align*}

Estas soluciones son iguales si y sólo si $b^2=4ac$ y en otro caso son distintas.

Ejemplos sobre resolución de ecuaciones cuadráticas complejas

Problema 1. Resuelve en $\mathbb{C}$ la ecuación $$x^2-5x+(7+i)=0.$$

Solución. Para usar la fórmula cuadrática, necesitaremos obtener la raíz $$\sqrt{\frac{25-4(7+i)}{4}}= \sqrt{-\frac{3}{4}-i}.$$

Como $$\left \lVert -\frac{3}{4}-i\right\lVert=\frac{\sqrt{25}}{4}=\frac{5}{4}$$ y $$\Rea\left(-\frac{3}{4}-i\right)=-\frac{3}{4},$$ las raíces $a+bi$ están dadas por

\begin{align*}
a=\pm\sqrt{\frac{\frac{5}{4}-\frac{3}{4}}{2}}=\pm\frac{1}{2}\\
b= \pm\sqrt{\frac{\frac{5}{4}+\frac{3}{4}}{2}}=\pm 1.
\end{align*}

Como $\Ima\left(-\frac{3}{4}-i\right)=-1<0$, para obtener las raíces tenemos que elegir signos distintos, es decir, que las raíces son \begin{align*}&\frac{1}{2} – i\\-&\frac{1}{2} +i.\end{align*}

Continuando con el problema original, concluimos, por la fórmula cuadrática, que las dos raíces son

\begin{align*}
x_1&=\frac{5}{2} + \frac{1}{2} – i = 3-i\\
x_2&=\frac{5}{2} – \frac{1}{2} + i =2+i.
\end{align*}

$\triangle$

La fórmula cuadrática funciona siempre para resolver ecuaciones cuadráticas complejas, pero a veces es demasiado. No hay que olvidar que tenemos toda el álgebra de $\mathbb{C}$ a nuestra disposición.

Problema 2. Resuelve en $\mathbb{C}$ la ecuación $$x^2-(3+8i)x=0.$$

Solución. En vez de usar la fórmula cuadrática, factorizamos la expresión del lado izquierdo para obtener que $$x(x-(3+8i))=0.$$

Para que un producto en $\mathbb{C}$ sea $0$, uno de los factores debe ser $0$. Así, $x=0$ ó $x-(3+8i)=0$, de donde las soluciones son \begin{align*}x_1&=0\\x_2&=3+8i.\end{align*}

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Verifica que los números complejos que obtuvimos en los ejemplos de raíces cuadráticas en efecto satisfacen que su cuadrado es el número original.
  2. Encuentra las raíces de $3+4i$, de $8-5i$, de $\frac{1}{2}-\frac{1}{3}i$ y de $2-\sqrt{5}i$.
  3. Verifica que las soluciones que obtuvimos en los ejemplos de ecuaciones cuadráticas complejas en efecto satisfacen la ecuación cuadrática dada.
  4. Resuelve la ecuación cuadrática compleja $$ix^2+7x-7-i=0.$$
  5. Si $w$ y $z$ son números complejos, ¿quienes son las raíces de $wz$? Las raíces cuadradas de $w$ son dos, las de $z$ son dos, y los posibles productos de ellas son cuatro números. ¿Por qué esto no contradice que $wz$ tiene dos raíces?

Puedes practicar este tema con los vídeos y ejercicios disponibles en la página de Khan Academy. Para ello, visita su sección de ecuaciones cuadráticas en los complejos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Construcción de números complejos

Por Leonardo Ignacio Martínez Sandoval

3 respuestas

Introducción

En una entrada anterior esbozamos las construcciones de los números racionales y los números reales. Es hora de construir los números complejos. Para ello, definiremos primero el conjunto, $\mathbb{C}$, sobre el que trabajaremos, después definiremos sus operaciones.

Una forma intuitiva de visualizar a $\mathbb{C}$ es tomar el conjunto de los números reales ($\mathbb{R}$) y en ellos introducir un nuevo elemento, $i$, el cual satisface que $i^2=-1$. Este es, realmente, un nuevo elemento, pues en $\mathbb{R}$ siempre se tiene que $x^2\geq 0$.

Una vez que introducimos a $i$, queremos que las operaciones de suma y producto estén definidas en $\mathbb{C}$ y que, además este conjunto, sea cerrado bajo estas operaciones. Es decir, es necesario que para cualquier número real $b$ se tenga $bi\in \mathbb{C}$ y que para cualesquiera números reales $a$ y $b$ tengamos, también, $a+bi\in \mathbb{C}$. Resulta que esto «es suficiente», en el sentido de que ya no hay que meter más números para que las operaciones estén bien definidas. Veamos como es esto, si tenemos los números de la forma $a+bi$ y $c+di$ con $a,b,c,d\in \mathbb{R}$ y los sumamos y multiplicamos como sigue: $$(a+bi)+(c+di)=(a+c)+(b+d)i$$, vemos que, la suma, «tiene la misma forma» (ya que $a+c$ y $b+d$ son números reales) así como su producto:
\begin{align*}
(a+bi)(c+di)&=ac+bci+adi+bdi^2\\
&=(ac-bd)+(ad+bc)i.
\end{align*}
Desde luego que lo anterior es soló una discusión informal. En las siguientes secciones veremos cómo formalizar estas ideas.

Los números complejos se comportan muy bien en términos algebraicos y en términos de análisis. En términos algebraicos, esto se comenzará a notar en la última parte del curso en donde veremos que cualquier polinomio tiene por lo menos una raíz compleja. En cursos posteriores, como el de álgebra lineal, verás otras de las propiedades algebraicas de los polinomios. Más adelante, si llevas un curso de variable compleja verás las bellas propiedades analíticas que tienen los números complejos.

El campo de los números complejos

La construcción del conjunto de números complejos es bastante sencilla. Para hacerla, simplemente consideraremos las parejas de números reales $$\mathbb{C}=\{(a,b): a,b\in \mathbb{R}\}.$$

Por el momento a cada $(a,b)$ lo puedes pensar de manera informal como el complejo $a+bi$. Lo interesante del conjunto de los números complejos no son sus elementos en sí, sino las siguientes operaciones que están definidas en él.

Definición. Para $(a,b)$ y $(c,d)$ en $\mathbb{C}$, definimos su suma como $$(a,b)+(c,d)=(a+c,b+d).$$

Recordemos que dentro del paréntesis se usa la suma de $\mathbb{R}$ ya que $a$, $b$, $c$ y $d$ son números reales.

Definición. Para $(a,b)$ y $(c,d)$ en $\mathbb{C}$, definimos su producto como $$(a,b)(c,d)=(ac-bd,ad+bc).$$

Igualmente dentro del paréntesis se usan la suma y producto de $\mathbb{R}$. La definición de producto está motivada por la discusión que hicimos en la introducción.

Teorema. El conjunto $\mathbb{C}$, junto con las operaciones de suma y producto que definimos, es un campo.

Demostración. La suma es conmutativa y asociativa ya que cada entrada pertenece a $\mathbb{R}$ y en $\mathbb{R}$ la suma es conmutativa y asociativa. El neutro es $(0,0)$ pues $$(a,b)+(0,0)=(a+0,b+0)=(a,b)$$ y para $(a,b)$ su inverso aditivo es $(-a,-b)$.

Veamos ahora el producto. Probemos que es conmutativo. Para dos complejos $(a,b)$ y $(c,d)$ tenemos que $$(a,b)(c,d)=(ac-bd,ad+bc)$$ y que $$(c,d)(a,b)=(ca-db,cb+da).$$

Ambos resultados son iguales ya que cada entrada pertenece a $\mathbb{R}$ y la suma y el producto son conmutativos en $\mathbb{R}$.

Probemos que el producto es asociativo. Para ello tomemos tres complejos $(a,b)$, $(c,d)$ y $(e,f)$. Tenemos que
\begin{align*}
[(a,b)(c,d)](e,f)&=(ac-bd,ad+bc)(e,f)\\
&=(ace-bde-adf-bcf,acf-bdf+ade+bce),
\end{align*} y que
\begin{align*}
(a,b)[(c,d)(e,f)]&=(a,b)(ce-df,cf+de)\\
&=(ace-adf-bcf-bde,acf+ade+bce-bdf),
\end{align*}

Ambas expresiones son iguales ya que cada entrada pertenece a $\mathbb{R}$ y la suma es conmutativa en $\mathbb{R}$.

El complejo $(1,0)$ actúa como neutro multiplicativo, pues $$(a,b)(1,0)=(a\cdot 1 – b\cdot 0, a\cdot 0 + b\cdot 1)=(a,b).$$ Además, si tomamos un complejo $(a,b)\neq (0,0)$ y lo multiplicamos por $\left(\frac{a}{a^2+b^2},\frac{-b}{a^2+b^2}\right)$ obtenemos \begin{align*}
(a,b)\left(\frac{a}{a^2+b^2},\frac{-b}{a^2+b^2}\right)&= \left(\frac{a^2+b^2}{a^2+b^2}, \frac{-ab}{a^2+b^2}+\frac{ba}{a^2+b^2}\right)\\ &= (1,0),
\end{align*} lo cual muestra que tenemos inversos multiplicativos.

Sólo falta demostrar la propiedad distributiva. Su verificación se deja como tarea moral.

$\square$

La copia de los reales en los números complejos

Dentro de $\mathbb{C}$ hay una copia de los números reales. Esta consiste en asociarle, a cada número real $a$, el número complejo $\varphi(a)=(a,0)$. Esta asociación es claramente biyectiva. Además, si $a$ y $b$ son números reales, tenemos que $$(a,0)+(b,0)=(a+b,0)=\varphi(a+b)$$ y
\begin{align*}
(a,0)(b,0) &= (ab-0\cdot 0, a\cdot 0 + b\cdot 0)\\
&= (ab,0) = \varphi(ab).
\end{align*}
Además los neutros se van a neutros y los inversos a inversos. Esto muestra que $\varphi$ es una asociación biyectiva entre $\mathbb{R}$ y los complejos de la forma $(a,0)$ y que respeta la estructura de campo de $\mathbb{R}$.

Por otro lado, notemos que $$(0,1) (0,1)= (0\cdot 0 – 1\cdot 1, 0\cdot 1 + 1\cdot 0)= (-1, 0).$$

En otras palabras, al elevar el complejo $(0,1)$ al cuadrado obtenemos el número $(-1,0)$, que es precisamente $\varphi(-1)$.

Tras toda esta discusión, estamos justificados entonces en llamar simplemente $1$ al complejo $(1,0)$, en llamar $i$ al complejo $(0,1)$, y por lo tanto en llamar $a+bi$ al complejo $(a,b)$. A partir de aquí ya podemos olvidar la notación de parejas y tratar a los números complejos como lo discutimos en la introducción.

Operaciones en la notación $a+bi$

La notación $a+bi$ para números complejos es bastante práctica. Podemos trabajar con los complejos «igualito que en $\mathbb{R}$, pero, además, con la propiedad de que $i^2=-1$».

Como $i^4=(-1)^2=1$, tenemos que las potencias de $i$ se ciclan cada cuatro: $$1, i, i^2, i^3, i^4, i^5, i^6, \ldots$$ son $$1,i, -1, -i, 1, i,\ldots .$$ Ya mencionamos en la introducción que para complejos $a+bi$ y $c+di$ se tiene que $$(a+bi)+(c+di)=(a+c)+(b+d)i$$ y que $$(a+bi)(c+di)=(ac-bd)+(ad+bc)i,$$ de modo que cualquier composición de sumas y productos de números complejos se puede simplificar a la forma $x+yi$ con $x$ y $y$ reales.

Ejemplo. Simplifica la expresión $$(1+i)(1-i)+(2+i)(3-4i).$$ Solución. Haciendo el producto del primer sumando tenemos $(1+i)(1-i)=1^2-i^2=1-(-1)=2$. Haciendo el producto del segundo sumando tenemos \begin{align*}
(2+i)(3-4i)&=6+3i-8i-4i^2\\
&=6-5i+4\\
&=10-5i.
\end{align*}
De esta forma, el resultado de la operación es $$2+(10-5i)=12-5i.$$

$\triangle$

En complejos también podemos usar expresiones fraccionales, como $\frac{3+2i}{5-i}$. Si queremos pasar estas expresiones a la forma $x+yi$ con $x$ y $y$ reales, tenemos que pensar a $\frac{1}{5-i}$ como «el inverso multiplicativo de $5-i$», que como vimos en la demostración de que $\mathbb{C}$ es un campo, es $$\frac{5}{5^2+(-1)^2}+\frac{1}{5^2+(-1)^2}i=\frac{5}{26}+\frac{1}{26} i.$$ Una vez hecho esto, tenemos que \begin{align*}
\frac{3+2i}{5-i}&=(3+2i)\left( \frac{5}{26}+\frac{1}{26} i \right)\\
&=\frac{13}{26} + \frac{13}{26} i\\
&=\frac{1}{2}+\frac{1}{2} i.
\end{align*}

Otra forma de pensarlo es que a una expresión de la forma $\frac{a+bi}{c+di}$ la podemos simplificar «multiplicando arriba y abajo» por $c-di$. De esta forma, obtenemos
\begin{align*}
\frac{a+bi}{c+di} \cdot \frac{c-di}{c-di} = \left(\frac{ac+bd}{c^2+d^2}\right) + \left(\frac{bc-ad}{c^2+d^2}\right)i.
\end{align*}

Ambos métodos dan el mismo resultado.

Más adelante…

Al tomar un número complejo $z=a+bi$ y calcular su inverso, aparecen de manera natural las expresiones $a-bi$ y $a^2+b^2$. Estas expresiones son fundamentales.

  • A $a-bi$ se le conoce como el conjugado de $z$, y se denota por $\overline{z}$.
  • A $\sqrt{a^2+b^2}$ se le conoce como la norma de $z$ y se denota por $|z|$.

En la siguiente ocasión hablaremos de las propiedades de estas dos operaciones y cómo están relacionadas entre sí. Más adelante veremos su utilidad al resolver ecuaciones cuadráticas en los números complejos.

Si quieres, puedes revisar esta entrada sobre aplicaciones interesantes de los números complejos en la resolución de problemas. Tiene teoría que no hemos visto, pero te puede servir de motivación para aprender lo que veremos a continuación.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que en los complejos se satisface la ley distributiva.
  2. Verifica que bajo la asociación $\varphi$ en efecto los neutros se van a los neutros y los inversos a inversos.
  3. Realiza la operación $(1+i)(2+i)(1+2i)(2+2i)$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.
  4. Realiza la operación $$\frac{3+5i}{2+i}-\frac{1+2i}{4-3i}$$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.
  5. Realiza la operación $$1+(1+i)+(1+i)^2+(1+i)^3+(1+i)^4$$ y expresa el resultado de la forma $x+yi$ con $x$ y $y$ reales.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Simplificación, suma y producto de complejos

Por Claudia Silva

Deja un comentario

Introducción

En una entrada de blog anterior, construimos el campo de los números complejos y definimos sus operaciones básicas. Ahora resolveremos algunos problemas de operaciones con complejos.

Haremos dos tipos de problemas. El primer tipo se trata de simplificar expresiones en números complejos para que se vuelvan de la forma $x+yi$ con $x$ y $y$ números reales. El segundo tipo es de realizar operaciones de suma, resta, producto y división de complejos, y luego simplificar.

Simplificación de expresiones complejas

Comenzamos con un vídeo de simplificar expresiones de números complejos.

Expresar en la forma $a+bi$ las expresiones…

Problemas de operaciones con complejos

Ahora vemos varios ejemplos de realizar sumas con números complejos.

Sumar números complejos

En todos los ejemplos del vídeo, realizamos sólo sumas de dos números, pero se podrían realizar sumas con cualquier cantidad de sumandos. Por ejemplo, podemos considerar la suma $$(5+2i)+(8+i)-(1-7i).$$ ¿Cuál sería el resultado de esta operación?

Finalmente, a continuación se muestra un vídeo en donde se realizan operaciones de productos y de divisiones de números complejos.

Productos y divisiones de números complejos

En el vídeo se define al conjugado del número complejo $z=a+bi$, que se denota por $\overline{z}$ y se obtiene de cambiarle el signo a la parte imaginaria. Por ejemplo, $\overline{4-5i}=4+5i$. Si multiplicas a un número complejo $a+bi$ por su conjugado, obtienes el real $a^2+b^2$. Esto es útil para quitar las partes imaginarias de los denominadores de expresiones fraccionales con complejos.

Más ejemplos y práctica extra

En otro curso, el Seminario de Resolución de Problemas, escribimos una entrada de cómo se pueden usar los números complejos para la resolución de problemas matemáticos. Ahí hay teoría más avanzada, pero puedes echarle un ojo para que veas lo que veremos más adelante en el curso.

En la página de Khan Academy en Español, puedes aprender más acerca de los números complejos, así como hacer muchos ejercicios de práctica.

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Generalizar el problema

Por Leonardo Ignacio Martínez Sandoval

1 respuesta

HeuristicasA veces tener un problema concreto es más difícil que tener un problema más general. En los problemas concretos puede haber números grandes, o un brinco muy difícil, o bien simplemente no existen herramientas para atacarlo por separado. Cuando generalizamos podemos aprovechar más teoría, por ejemplo el principio de inducción.

En estos videos veremos algunos ejemplos en los cuales es más fácil resolver un problema que aparentemente debería de ser más difícil.

Ir a los videos…