Identidades algebraicas y binomio de Newton

Introducción a entradas de álgebra

Cuando en matemáticas hablamos de álgebra, se abarca una gran cantidad de ideas, que van desde el álgebra de secundaria, en la cual factorizamos, despejamos y usamos identidades algebraicas, hasta el álgebra abstracta, que estudia estructuras algebraicas más generales como grupos, anillos y campos. Todas estas ideas tienen amplias aplicaciones en la resolución de problemas. En esta entrada, y las que vendrán a continuación, veremos numerosos ejemplos de esto

Para empezar, hablaremos de álgebra en el sentido de secundaria y preparatoria. Veremos que estas ideas, aunque sencillas, son muy versátiles. Después hablaremos de polinomios y de dos resultados fundamentales en su teoría: el teorema de factorización única y el teorema de la identidad. Los polinomios abundan en las matemáticas, y un correcto entendimiento de ellos abre muchas puertas en la resolución de problemas. En una entrada final daremos algunas ideas de otras estructuras algebraicas como grupos, anillos y campos.

Más adelante en el curso hablaremos con detalle de otros dos temas relacionados con álgebra: desigualdades y álgebra lineal.

Como lo hemos hecho hasta ahora, la idea no es profundizar demasiado en el desarrollo de la teoría algebraica. Para eso, es más recomendable llevar buenos cursos de distintos tipos de álgebra a nivel superior. Aquí en el blog hay material de los cursos Álgebra Superior II y Álgebra Lineal I que imparto en la Facultad de Ciencias de la UNAM.

Identidades algebraicas

Comenzaremos hablando de identidades algebraicas. Una identidad algebraica es una igualdad que se satisface para ciertas variables, independientemente del valor que tomen. Algunos ejemplos son las igualdades que se aprenden a nivel secundaria y bachillerato:

$\begin{gather*}a^2-b^2=(a-b)(a+b),\\a^2+2ab+b^2=(a+b)^2,\\a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2,\\a^n-b^n = (a-b)(a^{n-1}+a^{n-2}b+\ldots+ab^{n-2}+b^{n-1}).\end{gather*}$

Varias de las identidades algebraicas nos permiten desarrollar o factorizar una expresión. Factorizarla es bastante útil en problemas de teoría de números, en donde es importante conocer qué números dividen a la expresión. Desarrollarla a veces nos permite trabajar con una suma de términos simétricos, que podemos estudiar con técnicas de polinomios o con desigualdades.

Veamos algunos ejemplos.

Problema. Muestra que si $n$ es un entero, entonces $n^4-20n^2+4$ no es un número primo.

Sugerencia pre-solución. Intenta formular un problema equivalente al factorizar la expresión. Hay más de un camino por el que puedes proceder para factorizar, pero no todos te llevan a una solución. Intenta completar cuadrados de distintas formas y ve si encuentras un patrón.

Solución. Reescribimos la expresión como sigue:

$\begin{align*}n^4-20n^2+4&=n^4-4n^2+4-16n^2\\&=(n^2-2)^2-(4n)^2\\&=(n^2-4n-2)(n^2+4n-2).\end{align*}$

Para ver que la expresión no es un primo, basta con ver que ninguno de estos factores puede ser igual a $1$ o $-1$ . Si $n^2-4n-2=1$ o $n^2+4n-2=1$ , entonces $n^2=\pm 4n+3$ . Trabajando módulo $4$ , tendríamos $n^2\equiv 3 \pmod{4}$ , lo cual es imposible.

Si $n^2-4n-2=-1$ o $n^2+4n-2=-1$ , entonces sumando $6$ de ambos lados tenemos

$(n\pm 2)^2=n^2\pm 4n+4=5.$

Esto es imposible pues $5$ no es el cuadrado de un entero. Así, $n^4-20n^2+4$ se puede factorizar en factores distintos de $1$ y $-1$ y por lo tanto no es primo.

$\square$

El siguiente problema fue parte de la 1a Olimpiada Mexicana de Teoría de Números. Veremos dos soluciones. Ambas usan ideas algebraicas, pero son distintas entre sí.

Problema. Sean $a,b,c,d$ enteros tales que

$\begin{align*}ab + bc + ca &= 1\\ ad + dc + ca &= 1\\ ab + bd + da &= 1.\end{align*}$

Determina todos los valores posibles que puede tomar $bc+cd+db$ .

Sugerencia pre-solución 1. Hay varias formas de aprovechar la simetría del problema. Intenta manipular las ecuaciones para obtener información y recuerda que es importante usar que $a$ , $b$ , $c$ son enteros.

Solución 1. A partir de la primera y segunda ecuación, tenemos que

$ab+bc+ca=ad+dc+ca,$

de donde $0=ad+dc-ab-bc=(a+c)(d-b)$ . De aquí tenemos dos opciones: $a=-c$ o $b=d$ . Si $a=-c$ , de la segunda ecuación obtenemos

$1=ad+dc+ca=-c^2,$

lo cual es imposible. Así, concluimos que $b=d$ .

Por simetría, concluimos que $c=b$ , así que $b=c=d$ . Tras esto, las tres ecuaciones se reducen a una sola

$1=2ab+b^2=b(2a+b).$

Las únicas factorizaciones de $1$ en enteros son $1=1\cdot 1$ o $1=(-1)(-1)$ , de modo que $b=2a+b$ , de donde $a=0$ y $b=\pm 1$ . De cualquier forma, la expresión que buscamos es $bc+cd+db=3b^2=3$ .

$\square$

Sugerencia pre-solución 2. Formula un problema equivalente sumando $a^2$ en ambos lados en cada una de las ecuaciones.

Solución 2. Sumando $a^2$ en ambos lados de la primer ecuación obtenemos

$a^2+1=a^2+ab+bc+ca=(a+b)(a+c).$

Las otras dos ecuaciones dan expresiones simétricas. Multiplicando las tres, tenemos

$(a^2+1)(a^2+1)^2=(a+b)^2(b+c)^2(c+a)^2.$

El lado derecho es el cuadrado de un entero, así que el izquierdo también debe serlo, de modo que $a^2+1$ debe ser el cuadrado de un entero. Pero los únicos cuadrados a distancia $1$ son $0$ y $1$ , de donde $a^2+1=1$ , y así $a=0$ . Las ecuaciones se convierten entonces en $bc=dc=bd=1$ , de donde la suma de las tres es $3$ .

$\square$

Demostraciones del binomio de Newton

La siguiente es una de las identidades algebraicas más importantes.

Teorema (binomio de Newton). Para $a$ y $b$ números reales y $n$ un entero no negativo, se tiene que

$\begin{align*}(a+b)^n=\sum_{j=0}^n \binom{n}{j}a^{n-j}b^j\end{align*}$

El término de la derecha es

$a^n+\binom{n}{1}a^{n-1}b+\ldots+\binom{n}{n-1}ab^{n-1} + b^n.$

Veamos algunas demostraciones del teorema de binomio de Newton, que usan ideas un poco distintas. La primera usa ideas combinatorias. La segunda, ideas más algebraicas. La tercera es menos general, pero usa ideas geométricas.

Demostración combinatoria

Demostración 1. Pensemos al lado izquierdo como el producto

$(a+b)(a+b)\ldots(a+b)(a+b).$

¿Cómo se obtienen factores al desarrollar esta expresión? En cada uno de los $n$ paréntesis hay que elegir o un $a$ , o un $b$ . Así, cada sumando es producto de $n$ letras.

Si elegimos $j$ veces $b$ , entonces elegimos $n-j$ veces $a$ . ¿De cuántas formas podemos elegir $j$ veces $b$ ? Tantas como subconjuntos de tamaño $j$ de un conjunto de $n$ elementos, es decir, $\binom{n}{j}$ .Así, el término $a^{n-j}b^j$ aparece $\binom{n}{j}$ veces.

Para terminar, notemos que $j$ puede ir desde $0$ (no elegir ningún $b$ ), hasta $n$ (no elegir ningún $a$ ).

$\square$

La demostración anterior es combinatoria, pues está usando argumentos de conteo. Está contando de dos formas distintas los términos que aparecen en el producto desarrollado. Además, está usando la interpretación combinatoria de los coeficientes binomiales.

Demostración algebraica

Demostración 2. Si $b=0$ , entonces en ambos lados tenemos $a^n$ , ya que el único sumando en el que no aparece $b$ es el primero. Tenemos algo análogo si $a=0$ . De otra forma, podemos asumir que $a$ y $b$ no son cero y dividir ambos lados de la igualdad que queremos entre $b^n$ . Definiendo $x=a/b$ , tenemos que mostrar que:

$(x+1)^n= \sum_{j=0}^n \binom{n}{j}x^{n-j}.$

Esta igualdad es claramente cierta para $n=0$ , pues en ambos lados obtenemos $1$ , y para $n=1$ , pues en ambos lados obtenemos $x+1$ . Procediendo por inducción (explicamos cada paso con un poco de detalles más abajo):

$\begin{align*}(x+1)^{n+1}&=(x+1)(x+1)^n\\& = (x+1)\sum_{j=0}^n \binom{n}{j} x^{n-j}\\&=\sum_{j=0}^n \binom{n}{j} x^{n-j+1}+\sum_{j=0}^n \binom{n}{j}x^{n-j}\\& = \sum_{j=0}^{n+1} \binom{n}{j-1} x^{n-j}+\sum_{j=0}^{n+1} \binom{n}{j}x^{n-j}\\&=\sum_{j=0}^{n+1}\left(\binom{n}{j-1}+\binom{n}{j}\right) x^{n-j}\\&=\sum_{j=0}^{n+1}\binom{n+1}{j} x^{n-j}.\end{align}$

El primer paso es claro. En el segundo usamos hipótesis inductiva. Luego, hacemos la multiplicación por $x+1$ . El siguiente paso puede ser un poco confuso, pues parece que «agregamos términos», pero en la segunda suma sólo agregamos $\binom{n}{n+1}x^{-1}=0$ . En la primer suma hicimos un shift o desfase: los términos que estaban antes para $j$ de $0$ a $n$ , ahora están para $j$ de $1$ a $n+1$ . Además, agregamos el término $\binom{n}{-1}x^{n}=0$ . En el siguiente paso usamos la identidad de Pascal:

$\binom{n}{j-1}+\binom{n}{j}=\binom{n+1}{j},$

que se puede demostrar combinatoriamente, o directamente de manera algebraica a partir de la fórmula para coeficientes binomiales.

Con esto termina la demostración por inducción.

$\square$

Esta segunda demostración es mucho más algebraica, es decir, usa ideas de cómo se manipulan las expresiones con variables. El primer paso, en el que reducimos el problema a cuando un término es $1$ , se llama homogenización. En realidad no era estrictamente necesario hacerlo, pero simplifica la notación. En las sumas hicimos un shift, que es otra técnica que se usa al estudiar sumas y series.

Demostración geométrica

Daremos una última demostración del teorema del binomio de Newton, pero sólo para el caso $n=2$ . Lo que tenemos que demostrar es simplemente la identidad

$(a+b)^2=a^2+2ab+b^2.$

Para este caso, hay una bonita «demostración sin palabras»:

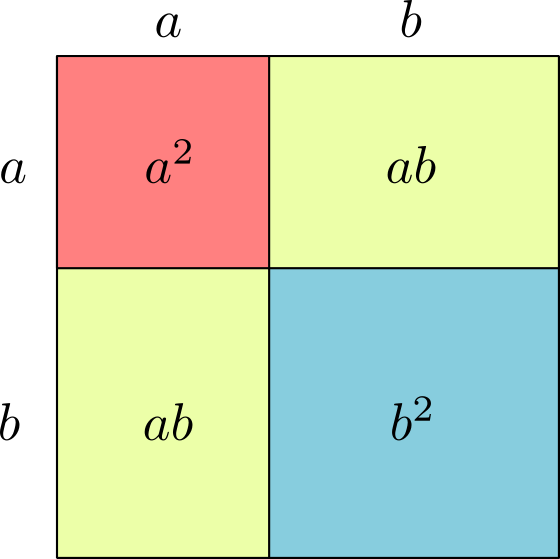
Binomio al cuadrado mostrado geométricamente — Demostración visual del binomio al cuadrado

Esta demostración es geométrica, pues estamos interpretando a la igualdad como una igualdad de áreas. Estamos usando una fórmula de área para cuadrados y rectángulos. Además, estamos usando que el área de una figura es aditiva, es decir, que es igual a la suma de áreas de figuras en las que queda subdividida.

Puedes elegir tu demostración favorita del binomio de Newton. Sin embargo, en resolución de problemas es importante saber proceder con varios acercamientos. Hay problemas en los que el acercamiento combinatorio, el algebraico o el geométrico es ventajoso, y por ello es mejor tener buena práctica en todos ellos.

Una aplicación del binomio de Newton en teoría de números

En entradas anteriores ya hemos usado el teorema del binomio de Newton en repetidas ocasiones, por ejemplo, en la entrada de aritmética de números complejos. Veamos un ejemplo más.

Problema. Sean $a$ y $b$ enteros primos relativos. Muestra que para todo entero positivo $n$ , se tiene que $a^n$ y $b^n$ son primos relativos.

Sugerencia pre-problema. Hay varias formas de dar una solución de esto. Una es analizando a los enteros primo por primo. Sin embargo, existe una solución usando binomio de Newton y la caracterización en términos de combinaciones lineales enteras para primos relativos.

Solución. Como $a$ y $b$ son primos relativos, existe una combinación lineal entera de ellos que da $1$ , digamos

$ax+by=1.$

Elevando esta igualdad a la $2n-1$ tenemos

$1=1^{2n-1}=(ax+by)^{2n-1}.$

Abriendo el último término con binomio de Newton queda

$\sum_{j=0}^{n-1} \binom{2n-1}{j} a^{2n-1-j}b^j + \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^j,$

y factorizando $a^n$ del primer sumando y $b^n$ del segundo,

$a^n \sum_{j=0}^{n-1} \binom{2n-1}{j} a^{n-1-j}b^j + b^n \sum_{j=n}^{2n-1} \binom{2n-1}{j} a^{2n-1-j}b^{j-n}.$

Lo que queda a la derecha es una combinación lineal entera de $a^n$ y $b^n$ igual a $1$ , y por lo tanto son primos relativos.

$\square$

Más problemas

En la siguiente entrada hablaremos de la identidad de Gauss para suma de cuadrados y de la identidad para $x^3+y^3+z^3-3xyz$ , las cuales se usan frecuentemente en resolución de problemas. Además, puedes encontrar más problemas de identidades algebraicas en la Sección 4.1 del libro Problem Solving through Problems de Loren Larson.

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Seminario de Resolución de Problemas: Identidades algebraicas y binomio de Newton

Introducción a entradas de álgebra

Identidades algebraicas

Demostraciones del binomio de Newton

Demostración combinatoria

Demostración algebraica

Demostración geométrica

Una aplicación del binomio de Newton en teoría de números

Más problemas

Deja una respuesta Cancelar la respuesta

Introducción a entradas de álgebra

Identidades algebraicas

Demostraciones del binomio de Newton

Demostración combinatoria

Demostración algebraica

Demostración geométrica

Una aplicación del binomio de Newton en teoría de números

Más problemas

Comparte esto:

Deja una respuesta Cancelar la respuesta