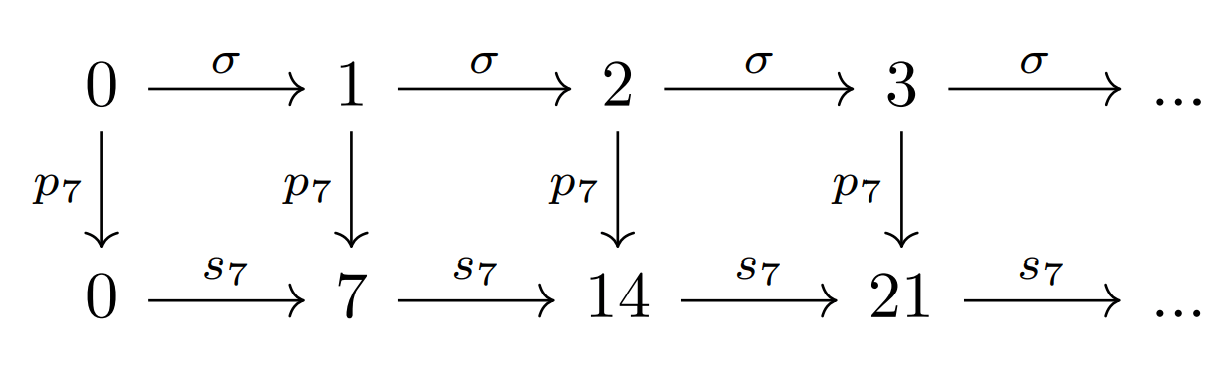Archivo de la etiqueta: inducción

Álgebra Superior I: Principio de inducción en los números naturales

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

En esta entrada vamos a hablar de el principio de inducción que se deriva del quinto axioma de Peano. Veremos cómo es que nos ayudará a un nuevo tipo de demostraciones, lo que significa en términos simples y algunos ejemplos de su uso.

El efecto dominó

Pensemos un poco en cómo funciona la inducción matemática viendo un ejemplo con las fichas de dominó. Imaginamos tenemos tres fichas de domino y las paramos una detrás de otra:

Si nosotros tiramos la primera ficha, las otras dos caerán:

Lo que se necesita para que se caigan las fichas será que la primera ficha caiga. Esto es cierto bajo ciertas condiciones. Deberemos saber que las fichas están suficientemente juntas para que una tire a la otra. Si por ejemplo, la última pieza estuviera muy lejos, la segunda pieza no la tiraría:

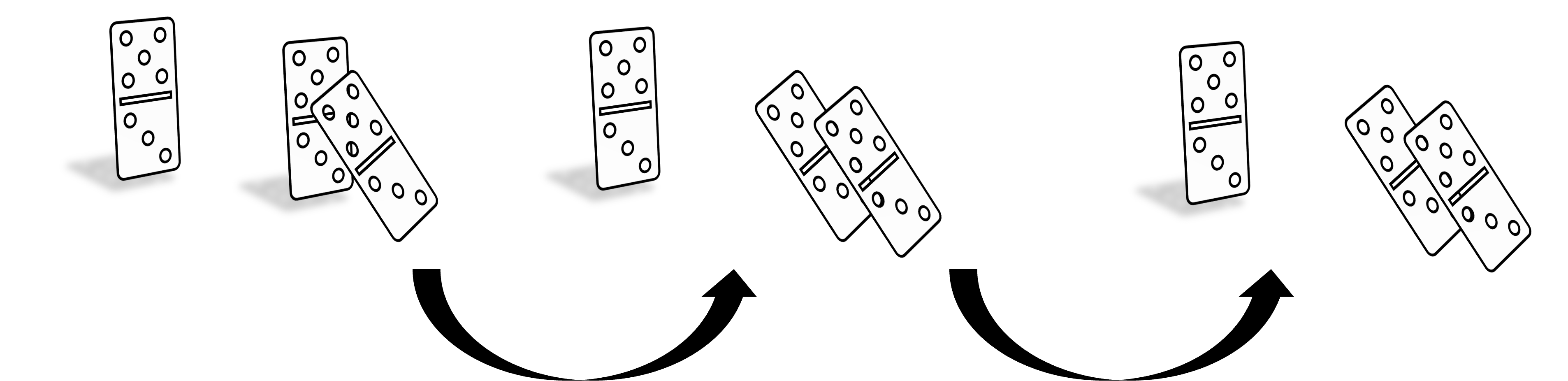
Con esto en mente, podríamos decir que todas las piezas de dominó se caen si:

  1. La primera pieza se cae.
  2. Cada vez que una pieza se cae, la pieza que sigue igual se cae.

Ahora, supongamos que tenemos una sucesión infinita de piezas de dominó, y enumeremos las piezas según los números naturales:

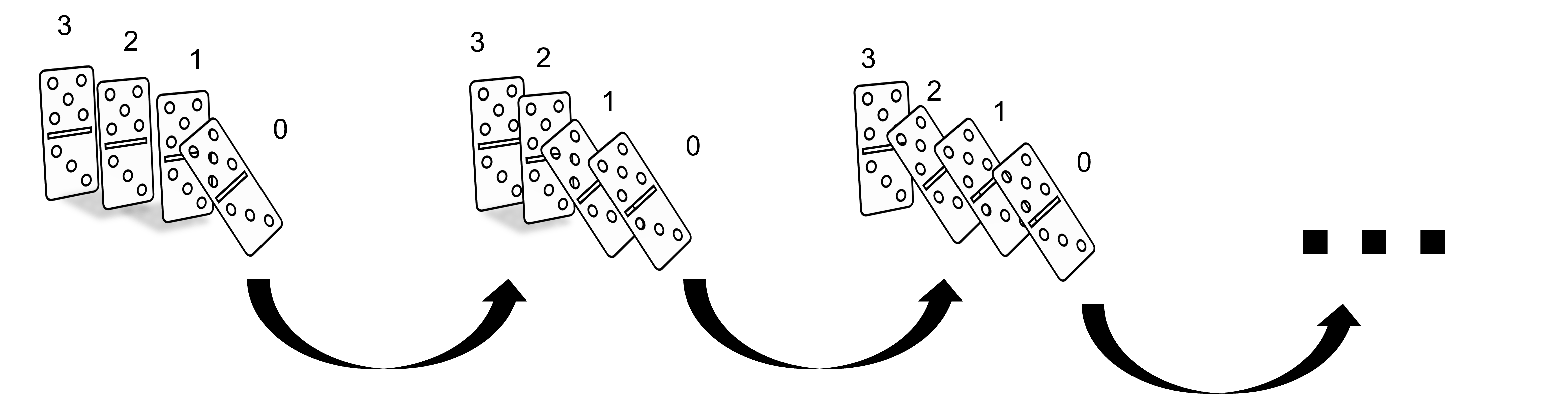
En el caso de que nuestras piezas estén bien colocadas, si tiramos la pieza $0$, esperaremos que se caiga la ficha $1$, seguido de la $2,$ la $3$ y así sucesivamente. De hecho si por algún momento dejáramos de ver las piezas y volteamos a ver en algún momento cualquier ficha cayendo, sabremos que la siguiente igual se cae. Es decir, imagina que nos distraemos después de tirar la primera ficha, al momento de volver a voltear a ver las fichas cayendo, estaremos viendo que alguna pieza se va cayendo tirando la que sigue. Digamos que nombramos a esta pieza la ficha $n$, entonces observaremos a la pieza $n+1$ caer enseguida:

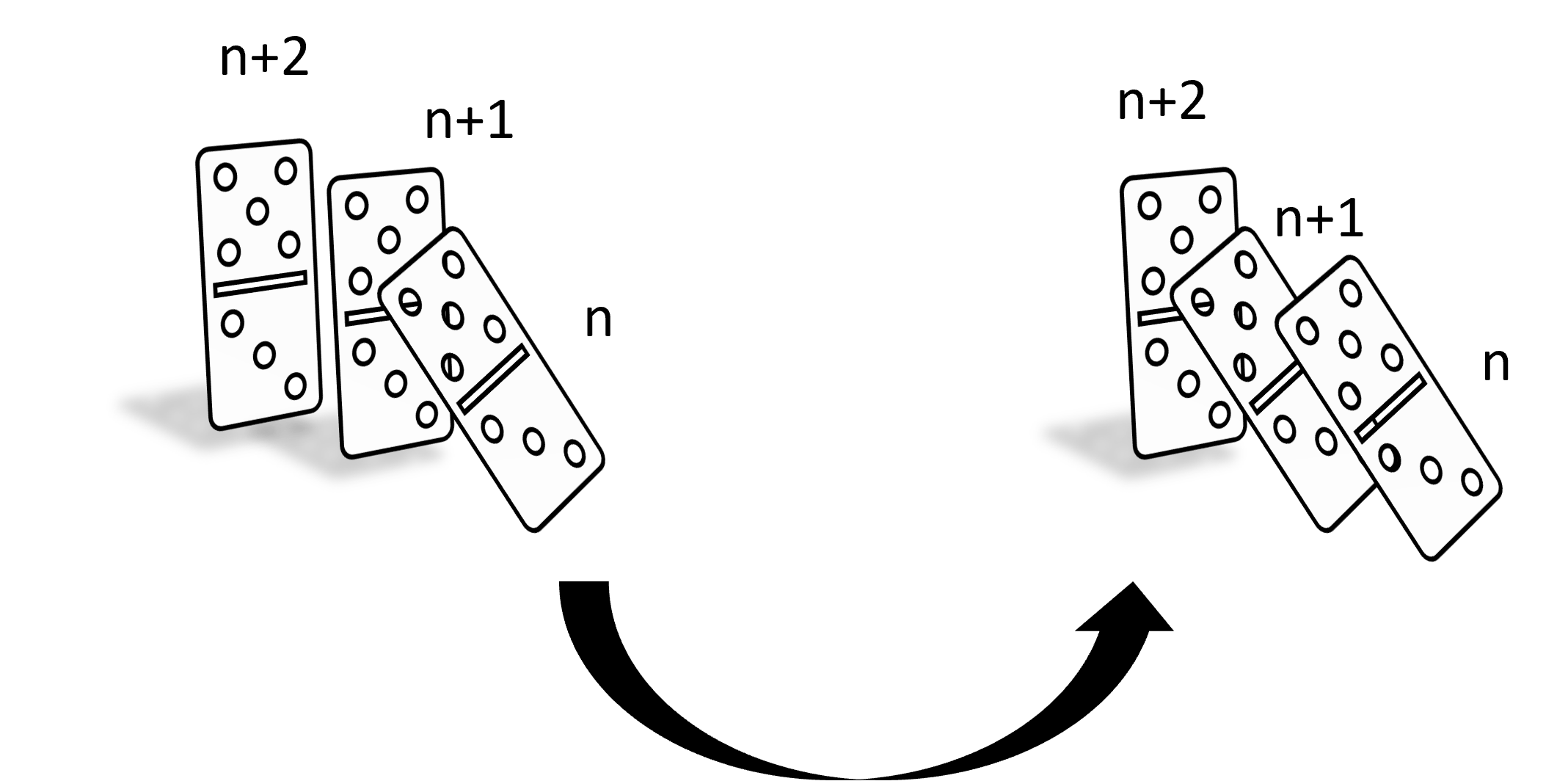
Lo que nos interesa para decir que todas las piezas se caen es que si una ficha se cae, la siguiente se cae. Es esta misma idea bajo las que se rige la inducción matemática, veamos la parte matemática de esta idea.

Sobre el quinto axioma de Peano

Veamos qué nos dice el último axioma que definimos con anterioridad:

Axioma 5 (Primer principio de inducción). Si $S$ es un subconjunto de $ \mathbb{N} $ tal que:

  1. $0 \in \mathbb{N}$
  2. Para cada número $n \in S$, sucede que $\sigma(n) \in S$

Entonces $S=\mathbb{N}$

Y veamos cómo es que esto se une con lo que hemos dicho sobre las fichas de dominó. La primera condición la podemos traducir como

1.Se cae la primera pieza.

Mientras que la segunda condición del axioma nos diría que:

2. Siempre que se cae una ficha, se cae la ficha que se encuentra delante.

Finalmente si se cumplen estas dos condiciones, nuestro axioma nos diría que el conjunto $S$ es el conjunto de los números naturales, pero recordemos que esto en términos del dominó significa que todas las piezas se caen. Entonces lo que nos dice el quinto axioma es que para verificar que un conjunto de números naturales es de hecho el conjunto de los números naturales, deberemos de ver que el primer número natural está y cada vez que veamos que un número natural está en el conjunto, su sucesor también deberá estar. La razón por la que intuitivamente esto funciona es por el principio del dominó.

Cuando nosotros tenemos una proposición matemática $P(n)$ para la cual queremos comprobar que cualquier número natural $n$ la cumple, la técnica de demostración por inducción será útil porque en lugar de probar que cada número individualmente la cumple, bastará demostrar que se satisfacen las condiciones del principio de inducción para argumentar que todos los números naturales la cumplen.

Algoritmo de demostraciones por inducción

Supongamos tenemos una proposición en el conjunto de los números naturales $P(n)$. El segundo axioma de los conjuntos garantiza la existencia de un conjunto 
$$S = \{n: P(n)\}$$.
Y el axioma 5 de Peano argumenta que si se cumplen las siguientes dos condiciones:

1. El $0$ pertenece al conjunto $S$ 
2. Si $n \in S$ entonces $n+1 \in X$

entonces $S = \mathbb{N}$. Es decir, todos los números naturales cumplen la condición $P(n)$
Veamos ahora estos dos pasos uno por uno:
1. Base inductiva: Probar que se cae la primera ficha. Este paso consistirá en demostrar que se cumple $P(0)$
2. Hipótesis de inducción: Suponer que un número $n$ cumple $P(n)$
3. Paso inductivo: Demostrar que la siguiente ficha se cae. En este paso debemos demostrar que se cumple también $P(n+1)$

Un ejemplo de inducción matemática

Proposición. La suma de los primeros $n$ números naturales es $\frac{n(n+1)}{2}$.

Esta proposición nos dice que si sumamos los primeros $n$ números n, el resultado será: $$ \sum_{i=0}^{n} i = 0+1+2+\dots+n-1+n = \frac{n(n+1)}{2}.$$ Para demostrar esto, seguiremos los pasos del algoritmo. Para ello, consideremos al conjunto $S=\{n \in \mathbb{N}: \sum_{i=0}^{n} i = \frac{n(n+1)}{2} \}$, es decir, $S$ es el conjunto de los números naturales $n$ para los cuales la suma de los primeros $n$ números naturales equivale a $ \frac{n(n+1)}{2} $. Lo que queremos demostrar es que este conjunto $S$ son todos los números naturales, es decir, que todos los números naturales cumplen esta condición. Para ello seguiremos los pasos del algoritmo.

Demostración. (por inducción sobre $n$).

Base inductiva. Demostraremos que $ \sum_{i=0}^{0} i = \frac{0(0+1)}{2} $. En efecto, notemos que $$ \sum_{i=0}^{0} i = 0= \frac{0(0+1)}{2} .$$ Así, ha quedado demostrada la base inductiva.

Hipótesis de inducción. Supongamos que $n \in \mathbb{N}$ es tal que $ \sum_{i=0}^{n} i = \frac{n(n+1)}{2} $.

Paso inductivo. Ahora demostraremos que $$ \sum_{i=0}^{n+1} i = \frac{(n+1)((n+1)+1)}{2}. $$ Para ello, basta notar que
$$\begin{align*}
\sum_{i=0}^{n+1} i &= \sum_{i=0}^{n} i + n+1 \\
&= \frac{n(n+1)}{2} + n+1 (\text{ esto por hipótesis de inducción}) \\
&= \frac{n(n+1)}{2} + \frac{2n+2}{2} \\
&= \frac{n(n+1)+2n+2}{2} \\
&= \frac{(n^2+n)+2n+2)}{2} \\
&= \frac{n^2+3n+2)}{2} \\
&= \frac{(n+1)(n+2)}{2} = \frac{(n+1)((n+1)+1)}{2} .
\end{align*}$$Quedando así demostrado el paso inductivo.

Así, hemos demostrado que el conjunto $S=\mathbb{N}$, es decir, que se cumple para todos los números naturales, quedando demostrada la proposición.

$\square$

Más adelante…

En la siguiente entrada daremos la definición de funciones recursivas que serán en pocas palabras, funciones en los números naturales las cuales son funciones que podemos definir solo diciendo cuánto valen en el $0$ y la evaluación en un término $\sigma(k)$ depende únicamente de la evaluación en $k$. También daremos un vistazo general al teorema de recursión.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra por inducción que la suma de los primeros $n$ números pares es $n(n+1)$.
  2. Encuentra una fórmula para la suma de los primeros $n$ números impares usando el ejercicio anterior junto al ejemplo demostrado en la entrada.
  3. Prueba que para cualquier número natural $n$, $$\sum_{i=1}^n(2i-1) = n^2 $$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Repaso. Inducción matemática

Por Karen González Cárdenas

4 respuestas

Introducción

En el curso de Álgebra Superior I se presenta al conjunto de los números naturales ($\mathbb{N}$). Posteriormente, en el curso de Álgebra Superior II se habla mucho más de ellos: se construyen a partir de teoría de conjuntos y se muestran desde los fundamentos muchas de sus propiedades.

Nosotros no nos enfocaremos en los aspectos anteriores, pero sí aprovecharemos que dicho conjunto posee una propiedad muy importante: el principio de inducción matemática. Como mencionamos en la entrada pasada, este método de demostración es aplicado frecuentemente en las pruebas en las que se desea probar que alguna propiedad se satisface para todos los números naturales.

En Cálculo Diferencial e Integral I haremos uso de la Inducción matemática constantemente, por lo que en esta entrada haremos una revisión a lo necesario para nuestro curso.

Efecto dominó

Imagina que te han regalado una cantidad infinita de fichas de dominó y que has decidido acomodarlas en una fila, una tras otra. Tu propósito al terminar de acomodarlas es dejar caer todas las fichas, por ello consideras empujar la primera ficha para que, al caer ésta, choque con la segunda provocando su caída, y así sucesivamente.

El riesgo del Efecto Dominó: Micro triangulaciones y sus ventajas en Trabajos de Investigación

Una vez que has decidido poner en marcha tu plan y empujas la ficha 1, te comienzas a preguntar: ¿Cómo puedo asegurar que la ficha 1,000 caerá si sólo he visto caer las primeras 50 fichas? ¿Y que hay de la ficha 1,000,000?

El Principio de Inducción es el que daría respuesta a tu pregunta. El razonamiento de este principio sustenta que si sabes que el procedimiento se ha cumplido para las primeras 50 fichas, en consecuencia cada ficha irá cayendo al final para cualquier ficha que consideres.

Ahora que tenemos una noción de su comportamiento, veremos la definición formal.

Principio de Inducción matemática

Cada autor decide si el conjunto de los números naturales considerará o no al cero como uno de sus elementos. En nuestro caso, tomaremos al cero como un número natural de aquí en adelante.

Definición: Sea $P$ una propiedad y $n\in \mathbb{N}$. Decimos que la propiedad $P$ es válida para todos los naturales si tenemos que:

  1. La propiedad $P$ se cumple para $0$.
  2. Si la propiedad $P$ se cumple para $n \Rightarrow$ la propiedad también se cumple para $n + 1$.

El punto número 1 es conocido como Base de Inducción. El antecedente del punto número 2 es llamado Hipótesis de Inducción y su consecuente Paso Inductivo. En algunos problemas basta con demostrar la afirmación únicamente cuando $n\geq 1$. En estos casos, la base de inducción debe de cumplirse para el natural $1$.

A continuación veremos un par de ejemplos para ver cómo funciona dicho principio.

Ejemplo: Demuestra utilizando Inducción matemática la siguiente fórmula.

$$1+2+ \ldots + n = \frac{n(n+1)}{2}, \quad \forall n\in \mathbb{N}$$

Observación: $\therefore$ se lee «por lo tanto» y $\forall$ significa «para todo».


Demostración: Haremos inducción sobre $n$.
Base de Inducción.- Verificamos que la fórmula se cumple cuando $n=1$

\begin{align*}
\frac{1(1+1)}{2}&= \frac{1(2)}{2}\\
&=\frac{2}{2}\\
&= 1
\end{align*}
Lo cual es cierto.

Hipótesis de Inducción.- Suponemos que la fórmula se cumple para cualquier $k\in \mathbb{N}$ así:
$$1+2+ \ldots + k = \frac{k(k+1)}{2}$$

Paso Inductivo.- Queremos probar que la fórmula se cumple para $k+1$, por lo que bastará probar la siguiente igualdad:
$$1+2+ \ldots + k+ (k+1) = \frac{(k+1)((k+1)+1)}{2}$$ es decir, $$1+2+ \ldots + k+ (k+1) = \frac{(k+1)(k+2)}{2}$$

Desarrollaremos el lado izquierdo de la igualdad sustituyendo lo que tenemos en la Hipótesis de Inducción, así queda lo siguiente:
\begin{align*}
1+2+ \ldots + k+ (k+1) &= \frac{k(k+1)}{2} + (k+1)\\
&= \frac{k(k+1)}{2}+ \frac{2(k+1)}{2}\\
&=\frac{k(k+1)+ 2(k+1)}{2}\\
&=\frac{(k+1)(k+2)}{2}
\end{align*}


$$\therefore 1+2+ \ldots + n = \frac{n(n+1)}{2}, \quad \forall n\in \mathbb{N}$$

$\square$

Ejemplo: Demuestra que

$2^{n} < n! \quad$ si $\quad n \geq 4$

Recordemos que $n!$ es llamado $n$ factorial y que está definido como: $n! = 1\cdot 2 \cdot \ldots \cdot (n-1)(n)$.


Demostración: Aplicando inducción sobre $n$, vemos que dada la condición de $n \geq 4$, bastaría probar que:
$$2^{n+3} < (n+3)!, \quad \forall n \in \mathbb{N}$$

La razón de considerar $n+3$ es porque queremos todos aquellos naturales mayores o iguales que 4, al sustituir valores para $n$:

\begin{align*}
n=1 &\Rightarrow 1+3\\
&\Rightarrow 4\\
\\
n=2 &\Rightarrow 2+3\\
&\Rightarrow 5\\
\\
n=3 &\Rightarrow 3+3\\
&\Rightarrow 6\\
&\vdots
\end{align*}
Notamos que los números que obtenemos lo cumplen, aún si continuáramos con dicha sustitución, por esa razón podemos proceder sin problemas.

Y ya que $n$ factorial está definido como: $n! = 1\cdot 2 \cdot \ldots \cdot (n-1)(n)$ tenemos que $4!= 4\cdot 3\cdot 2\cdot 1 =24$.

Base de Inducción.- Verificamos que la desigualdad se cumple para $n=1$. Así sustituyendo vemos:
$$2^{1+3} = 2^{4}=16$$ y que $$(1+3)! = 4! =24$$
Por lo que se cumple la desigualdad: $$2^{1+3} < (1+3)!$$

Hipótesis de Inducción.- Suponemos que la desigualdad se cumple para cualquier $k \in \mathbb{N}$.
$$2^{k+3} < (k+3)!$$

Paso Inductivo.- Queremos probar que la desigualdad se cumple para $k+1$, esto sería:
$$2^{(k+1)+3} < ((k+1)+3)!$$ que es lo mismo que, $$2^{k+4} < (k+4)!$$

Vemos que al reescribir la desigualdad anterior tenemos:
$$2\cdot 2^{k+3} < (k+3)! (k+4)$$
Por hipótesis de inducción sabemos se cumple $2^{k+3} < (k+3)!$, por lo que si se cumple la desigualdad $2< k+4$ terminamos.

$P.d:$ $$2< k+4,\quad \forall k\in \mathbb{N}$$
Demostración: Utilizaremos inducción sobre $k$.
Base Inducción.- Vemos para $k=1$ que $$2< 1+4 = 5$$ se cumple.

Hipótesis de Inducción.- Suponemos que es cierta la desigualdad $2< k+4$ para cualquier $k$.

Paso Inductivo.- Queremos probar que para $k+1$ se cumple la desigualdad $2< (k+1)+4$.
Observemos que $(k+1)+4= (k+4)+1$ que es el sucesor de $k+4$ por lo que cumple $k+4 < (k + 4)+1$.
Así haciendo uso de lo anterior y de la Hipótesis de Inducción se tiene lo siguiente:
$$2< k+4 < (k+4)+1 \quad \Rightarrow \quad2 < (k+4)+1$$
$$\therefore \quad 2 < (k+1)+4$$
$$\therefore \quad 2 < k+4 , \quad \forall k\in \mathbb{N}$$

$\square$

Por lo que ya podemos afirmar que $$2\cdot 2^{k+3} < (k+3)! (k+4).$$
Así concluimos: $$2^{n+3} < (n+3)!, \quad \forall n \in \mathbb{N}.$$

$\square$


Observación: $P.d.$ es una abreviación de «Por demostrar».

Principio de Inducción Fuerte

Existe otra forma de inducción, que debemos recordar por su utilidad, conocida como: Inducción Fuerte, que es consecuencia del Principio de Inducción que vimos antes.

Definición (Principio de Inducción fuerte): Consideremos $P$ una propiedad y $n , l \in \mathbb{N}$. Decimos que la propiedad $P$ es válida para todos los naturales si tenemos que:

  1. $P$ se cumple para $0$.
  2. Si $P$ se cumple para cualquier $l \leq n \Rightarrow P$ se cumple para $n+1$.

Ejemplo: Todos los números positivos $n >1$ son producto de primos.

Demostración: Utilizaremos Inducción fuerte sobre $n$.
Base de Inducción.- Como tenemos la condición $n>1$ consideraremos $n=2$.
Observamos que $2 = 2$ es un producto de primos ( 2 cumple la definición de ser primo).

Hipótesis de Inducción.- Supongamos que todos los números desde 2 hasta $k$ cumplen ser producto de números primos.

Paso Inductivo.- Queremos probar que $k+1$ es producto de números primos.
Recordemos que todo número es primo o compuesto, por lo que tenemos que considerar los siguientes casos.

Caso 1: $k+1$ es primo.
Como $k+1 = k+1$ se sigue que es producto de números primos y se cumple lo que queremos.

Caso 2: $k+1$ es compuesto.
Esto quiere decir que podemos expresar a $k+1$ como un producto de la siguiente manera:
$$k+1= a\cdot b$$ donde $k+1 > a \quad$ y $\quad b > 1$.
Observemos que las últimas desigualdades implican que $k \geq a,b \geq 2$, así por Hipótesis de Inducción $a$ y $b$ cumplen ser producto de números primos.
$\therefore \quad k+1$ es producto de primos.
$\therefore \quad$ Todos los números positivos $n >1$ son producto de primos.

$\square$

Más adelante

Ahora que hemos terminado con el repaso de Inducción matemática. En la siguiente entrada comenzaremos a ver un conjunto de números de suma importancia para el Cálculo: los reales.

Tarea moral

A continuación, encontrarás ejercicios en los que pondrás en práctica el Principio de Inducción matemática:

  1. Probar que: $n^{3} – n$ es un múltiplo de 6, $\forall n\in \mathbb{N}$.
  2. Utiliza inducción para probar la siguiente igualdad:
    $$1^{2}+2^{2}+\ldots + n^{2} = \frac{n(n+1)(2n+1)}{6}, \quad \forall n\in \mathbb{N}$$
  3. Demuestra que:
    $$1+3+5+7+\ldots +2n-1 = n^{2}, \quad \forall n\in \mathbb{N}$$
  4. Demuestra por inducción sobre $n$, con $r \neq 1$:
    $$1+r+r^{2}+ \ldots +r^{n} = \frac{1-r^{n+1}}{1-r}$$
  5. Utiliza inducción para probar la siguiente igualdad:
    $$2+5+8+ \ldots+ (3n-1)= \frac{n(3n+1)}{2}$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: La relación de orden en los naturales

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

Seguramente desde que construimos de forma intuitiva el conjunto de números naturales, te diste cuenta de que nuestra forma de generar nuevos números a través de la función sucesor, nos daba una jerarquía de qué número natural iba primero, y quien era el que inmediatamente le seguía. Así, el primer natural debería de ser el $0$, el cual debería ser menor a todos los demás. Después, seguiría $\sigma(0)=1$ el cual debería ser menor al sucesor de cualquier otro número. Este razonamiento podría seguir de forma inductiva para los demás números.

En esta entrada abordaremos el problema de cómo organizar el conjunto de naturales. Hay varias formas de definir esta relación. Pero el trabajo que realizamos en las dos entradas pasadas nos permitirá atacar dos problemas de manera sencilla: el de definir el orden en $\mathbb{N}$ y el de demostrar sus propiedades.

El orden parcial en $\mathbb{N}$

Recordemos que si $n$ es un número natural distinto de cero, entonces $n=\{0,1,…,n-1\}$. Entonces de forma intuitiva podemos afirmar que cada número natural tienen por elementos a todos los naturales «menores» a él. Usando esta idea, podemos dar las siguientes dos definiciones.

Definición. Si $n,m\in \mathbb{N}$, decimos que $n$ es menor que $m$, en símbolos, $n<m$ si $n\in m$.

Definición. Si $n,m\in \mathbb{N}$, decimos que $n$ es menor o igual que $m$, en símbolos $n\leq m$ si $n\in m$ o $n=m$.

Antes de lanzarnos a probar propiedades de estas relaciones, comenzaremos con verificar la segunda de ellas define un orden parcial.

Teorema. La relación $\leq$ es un orden parcial en $\mathbb{N}$.

Demostración. Recordemos que según la definición de orden parcial, debemos probar que $\leq$ es reflexiva, transitiva y antisimétrica, hagamos esto por pasos.

$\leq$ es reflexiva: Si $m$ es un natural, tenemos que $m=m$, por lo que por nuestra definición, podemos escribir que $m\leq m$.

$\leq$ es transitiva: Sean $n,m,l$ naturales tales que $n\leq m$ y $m\leq l$. Debemos demostrar que $n\leq l$. Si $n=m$ o $m=l$ la conclusión es inmediata de las hipótesis. En otro caso, tenemos que que $n\in m$ y $m\in l$. Como $l$ es un número natural, es un conjunto transitivo, entonces $n\in l$, por lo que $n\leq l$.

$\leq$ es antisimétrica: Si $n,m$ son naturales tales que $n\leq m$ y $m\leq n$, debemos demostrar que $n=m$. Para ver esto, procedamos por contradicción. Supongamos que no son iguales, entonces $n\in m$ y $m\in n$. Pero como ya hemos mencionado anteriormente, el hecho de que dos conjuntos pertenezcan mutuamente al otro es contradictorio con el axioma de regularidad. Entonces debe suceder que $n=m$ como queríamos.

$\square$

Propiedades del orden en los naturales

Ya mostramos que $\leq$ es un orden parcial en $\mathbb{N}$. Probemos otras propiedades que esperamos que satisfaga. Empezamos con la que mencionamos en la introducción de la entrada.

Teorema. $0\leq n$ para todo natural $n$

Demostración. Si $n=0$, el resultado se sigue de manera automática. Si $n\neq 0$, el resultado se sigue de que ya demostramos que $0$ está en cada natural distinto de $0$.

$\square$

La siguiente propiedad que probaremos es que la función sucesor sí preserva el orden que definimos.

Teorema. Si $n,m\in\mathbb{N}$ y $n<m$, entonces $\sigma(n)<\sigma(m)$

Demostración. Procedamos por inducción sobre $m$. Para el caso base debemos probar que la afirmación $n<0\Rightarrow\sigma(n)<0$, es verdadera. Sin embargo, el antecedente siempre es falso, ya que $n<0$ quiere decir que $n\in\emptyset$ lo cual es absurdo. Como el antecedente siempre es falso, entonces la base de inducción es verdadera.

Supongamos que para alguna $m$ se tiene que si $n<m$, entonces $\sigma(n)< \sigma(m)$. Debemos probar que el resultado es cierto para $\sigma(m)$. Supongamos entonces que $n<\sigma(m)$. Debemos probar que $\sigma(n)<\sigma( \sigma(m))$.

Como $n<\sigma(m)$, tenemos que $n\in \sigma(m)=m\cup \{m\}$, así que tenemos dos casos: $n\in m$ o $n\in\{m\}$.

Si $n\in m$, por hipótesis inductiva $\sigma(n)\in \sigma(m)$. Como $\sigma(m)\in \sigma(\sigma(m))$ y los naturales son transitivos, tenemos $\sigma(n)\in \sigma(\sigma(m))$, es decir, $\sigma(n)< \sigma(\sigma(m))$, como queríamos.

Finalmente, si $n\in \{m\}$, entonces $n=m$, pero así $\sigma(n)=\sigma(n)\in \sigma(\sigma(m))$, de modo que $\sigma(n)<\sigma(\sigma(m))$, como queríamos.

$\square$

El orden en los naturales es total

De entre los órdenes parciales hay un tipo de órdenes especiales: aquellos en los que cualesquiera dos elementos se pueden comparar. A estos se les conoce como órdenes totales. Los resultados de esta sección muestran que la relación $\leq$ en $\mathbb{N}$ es un orden total.

Un paso intermedio para demostrar esto es ver que si un número natural es menor que otro, entonces la función sucesor «no nos puede llevar muy lejos».

Teorema. Si $n,m$ son naturales tales que $m<n$, entonces se tiene que $\sigma(m)\leq n$.

Demostración. La hipótesis es imposible cuando $n=0$, pues no hay ningún natural menor a cero. Así, $n$ debe ser sucesor de algún otro natural, digamos $n=\sigma(k)$.

De $m<\sigma(k)$ tenemos que $m\in k\cup \{k\}$, así que $m\in k$, o $m=k$. Si $m\in k$, entonces $m<k$ y por el teorema anterior tenemos que $\sigma(m)<\sigma(k)=n$. Si $m=k$, entonces $\sigma(m)=\sigma(k)=n$. En cualquier caso tenemos $\sigma(m)\leq n$.

$\square$

El anterior teorema es equivalente a la afirmación siguiente.

Corolario. Si $n,m\in\mathbb{N}$, son tales que $m<n$ pero es falso que $\sigma(m)< n$, entonces $\sigma(m)=n$.

En estos momentos es conveniente regresar a leer las dos pruebas de los teoremas anteriores, y notar que en las demostraciones, cuando suponíamos que era falso que $n<m$ nunca supusimos que $n\geq m$. Sólo apelábamos directamente a la negación de la definición. Haber usado $n\geq m$ hubiera sido un error. En primer lugar, porque aún no hemos definido el símbolo $\geq$. Y en segundo lugar, porque aún no hemos descartado una cuarta posibilidad: que $n$ y $m$ no sean comparables. En realidad esto es imposible, pero hay que demostrarlo. En $\mathbb{N}$ el orden es total y de hecho satisface la propiedad de tricotomía que enunciamos a continuación.

Teorema. Para cualesquiera $n$ y $m$ naturales se cumple una y sólo una de las siguientes afirmaciones

  • $n=m$
  • $n< m$
  • $m< n$

Demostración. Ya hemos demostrado mediante el axioma de regularidad que estas proposiciones son mutuamente excluyentes. Sólo queda demostrar que siempre sucede por lo menos una de ellas. Demostraremos esto por inducción sobre $n$.

El caso base se reduce a probar que para cualquier $m$, se tiene que $0=m$, $0\in m$ o $m\in 0$. El primer teorema que probamos muestra que siempre se da la primera o la segunda opción.

Supongamos ahora que el resultado es cierto para alguna $n$. Debemos probarlo para $\sigma(n)$. Entonces sea $m\in\mathbb{N}$ arbitrario. Por hipótesis de inducción, $m$ es comparable con $n$, entonces podemos considerar tres casos:

$m=n$. Este caso es trivial porque entonces $m\in\sigma(n)$.

$m< n$. De nuevo tenemos que $m\in n\in \sigma(n)$, y por transitividad (del orden o de los conjuntos), tenemos que $m\in\sigma(n)$.

$n< m$. Por el teorema anterior, tenemos que en este caso, $\sigma(n)<m$ ó $\sigma(n)=m$.

De cualquier forma $\sigma(n)$ y $m$ son comparables. Esto termina la demostración.

$\square$

Para finalizar, hacemos la observación de que definir los símbolos $>$ y $\geq$ en $\mathbb{N}$ es sencillo. Simplemente, diremos que $n\geq m$ cuando $m\leq n$. Así mismo, diremos que $n>m$ cuando $m<n$.

Más adelante…

Ya empezamos a probar las propiedades del orden en $\mathbb{N}$. Sin embargo, falta ver una de las más importantes: el principio del buen orden. Esta lo veremos en la entrada siguiente. También veremos que, en cierto sentido, es equivalente al principio de inducción.

Otra cosa más que falta es ver que el orden que definimos «se comporta bien» con las operaciones de suma y producto en $\mathbb{N}$. Esto resultará de suma importancia para entradas posteriores.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que si $n\leq m$, entonces $n<\sigma(m)$.
  2. Prueba que $n\leq m$ si y sólo si $n\subseteq m$.
  3. Generaliza el teorema de que $\in$ define un orden en $\mathbb{N}$, a que $\in$ define un orden en cualquier conjunto transitivo.
  4. Demuestra que $\leq$, restringido a $n \times n$ es un orden total en el conjunto $n$.
  5. Encuentra un conjunto $A$ con tantos elementos como números naturales y una forma de ordenarlo linealmente, tal que $A$ tiene elemento máximo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Otras definiciones recursivas en los naturales (exponenciación y factorial)

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En las entradas pasadas hemos dado la definición recursiva de la suma y del producto usando el teorema de la recursión débil y probamos las propiedades elementales de estas operaciones usando el principio de inducción.

Continuando con esta línea de pensamiento, en esta entrada definiremos las funciones exponenciales usando las funciones producto; sin embargo, para definir estas funciones, también ocuparemos el teorema de recursión débil. Para ver que no enunciamos en vano la versión fuerte de este teorema, daremos como aplicación la definición de la función factorial, y de la misma forma a como lo hicimos antes, probaremos algunas de sus propiedades haciendo uso del principio de Inducción. Sin embargo, dejaremos algunas de las propiedades como ejercicio para que puedas practicar este tipo de pruebas una vez más.

Exponenciación en los naturales

Desde la educación elemental nos enseñan que «multiplicar es sumar repetidas veces» y que «exponenciar es multiplicar repetidas veces». Formalicemos esta intuición mediante el teorema de recursión.

Definición: Sea $m\in \mathbb{N}$. Definimos $\eta_{m}:\mathbb{N}\longrightarrow\mathbb(N),$ como la función que satisface las siguientes propiedades:

  1. $\eta_{m}(0)=1$
  2. $\eta_m(\sigma(n))=p_{m}(\eta_{m}(n)) $

Así como lo hemos hecho con la definición de producto y de suma, introduciremos la «notación usual» para hablar de esta función. En este caso, definimos $m^n:=\eta_m(n)$.

De este modo, en términos de las notaciones usuales, podemos suplir la propiedad (2) de la definición anterior como $m^{n+1}=m\cdot m^n$.

Las potencias de $0$ y de $1$

Así como lo hicimos con la suma y el producto, analizaremos de forma especial a las funciones $\eta_{0}$ y $\eta_{1}$.

Teorema: Tenemos que $\eta_{0}(0)=1$ y si $n\neq 0$, entonces $\eta_{0}(n)=0$.

La demostración queda como un ejercicio moral. La buena noticia es que hemos trabajado lo suficiente como para no tener que realizar una prueba por inducción. Cuando intentes demostrar esto por tu cuenta, recuerda qué sucede cuando multiplicamos por $0$.

Notemos que así como lo definimos, $0^0$ es $1$ en los números naturales. Sin embargo, como veremos más adelante y como posiblemente lo sabrás ya, la expresión $0^0$ no estará definida en otros sistemas numéricos como los números reales. Al igual que «$0$ es un natural», la definición de $0^0$ frecuentemente varía dependiendo del contexto.

Teorema: Tenemos que $\eta_{1}(n) =1$ para todo $n$ en los naturales.

Demostración. Para este resultado sí procederemos por inducción sobre $n$. Por la parte (1) de la definición de $\eta_{1}$, tenemos que $\eta_{1}(0)=1$. Esta es nuestra base de inducción.

Supongamos que $\eta_{1}(n)=1$. Queda demostrar que $\eta_{1}(\sigma(n))=1.$ Sin embargo esto se sigue ya que por definición, $\eta_{1}(\sigma(n))=1\cdot\eta_{1}(n)=1\cdot 1=1$. Te invitamos a identificar los argumentos que se ocuparon en cada paso.

$\square$

La exponencial no conmuta ni asocia

Como la notación que ocupamos para las funciones $\eta_{m}$ no es tan simétrica como la que ocupamos para el producto o para la suma, uno puede esperar que esta operación no sea en general conmutativa. En efecto esto es cierto, solo basta notar que

$0^1\neq1^0$

Así mismo la exponenciación no es en general asociativa, es decir que existen casos en que

$(n^m)^l\neq n^{(m^l)}$

Encontrar un contraejemplo queda como un ejercicio moral.

Le exponenciación y otras operaciones

Cuando estudiamos el producto de números naturales, vimos que esta operación se distribuye sobre la suma, entonces una buena pregunta es preguntarnos qué pasa cuando mezclamos la exponenciación con el producto y la suma. Quedará como ejercicio dar contraejemplos a todas las siguientes proposiciones:

  1. $n^{(l\cdot m)}=n^l\cdot n^l$
  2. $(l+m)^n=l^n+m^n$
  3. $n^{l+m}=n^l+n^m$

Sin embargo, probaremos dos teoremas conocidos usualmente como las leyes de los exponentes. El primero de ellos dice que por la izquierda, la exponenciación sí se distribuye sobre el producto.

Teorema: Si $a,b,n\in\mathbb{N}$, entonces $(a\cdot b)^n=a^n\cdot b^n$.

Demostración. Procedamos por inducción sobre $n$. De la definición de exponencial, tenemos que $(a\cdot b)^0=1=1\cdot 1= a^0\cdot b^0$, por lo que la base de inducción es cierta.

Supongamos que para algún $n$ se tiene que $(a\cdot b)^n=a^n\cdot b^n$ y probemos que $(a\cdot b)^{\sigma(n)}=a^{\sigma(n)}\cdot b^{\sigma(n)}$. Esto es cierto ya que

\begin{align*}
(a\cdot b)^{\sigma(n)}&=(a\cdot b)\cdot (a\cdot b)^n\\
&=(a\cdot b)\cdot (a^n\cdot b^n)\\
&=(a\cdot a^n)\cdot (b\cdot b^n)\\
&=a^{\sigma(n)}\cdot b^{\sigma(n)}
\end{align*}

A diferencia de las entradas anteriores ya ocupamos sin mención las propiedades ya demostradas o la hipótesis de inducción; sin embargo, sería bueno que detallaras las pruebas.

$\square$

Aunque vimos que en general no podemos hablar de que la exponencial se distribuya, sí hay importantes relaciones que notaremos en los siguientes dos teoremas.

Teorema: Si $a,b,n\in\mathbb{N}$, entonces $a^{b+n}=a^b\cdot a^n$.

Demostración. De nuevo procederemos por inducción sobre $n$. Si $n=0$, entonces $a^{b+0}=a^b =a ^b \cdot 1=a^b \cdot a^0$, con lo que probamos la base de inducción.

Supongamos entonces que para algún $n$ se tiene que $a^{b+n}=a^b\cdot a^n$, y demostremos el caso para $\sigma(n)$. Sabemos que

\begin{align*}
a^{b+ \sigma(n)}=&a^{\sigma(b+n)}\\
=&a\cdot a^{b+n}\\
=&a\cdot (a^b\cdot a^n)\\
=&a^b\cdot (a \cdot a^n)\\
=&a^b\cdot a^{\sigma(n)}
\end{align*}

Con esto termina la prueba.

$\square$

El siguiente teorema queda como ejercicio de la tarea moral, para que puedas practicar.

Teorema: Si $a,b,n\in\mathbb{N}$, entoces $(a^b)^n=a^{b\cdot n}$.

El factorial

Hasta ahora, sólo hemos ocupado el teorema de recursión débil a la hora de definir las operaciones. A pesar de que antes demostramos que ambas versiones del teorema son equivalentes, la siguiente definición mostrará la naturalidad que tiene el ocupar el teorema de Recursión Fuerte para algunas cosas.

Definición: Se define la función factorial, $f:\mathbb{N}\to \mathbb{N}$, como la única función dada por el teorema de recursión fuerte que cumple que

  • $f(0)=1$
  • $f(\sigma(n))=p_{\sigma(n)}(f(n))$

Usaremos la notación $n!:=f(n)$. Así, la primer parte de la definición dice que $0!=1$ y la segunda dice que $(n+1)!=(n+1)\cdot n!$.

Notemos que en la definición anterior es necesario ocupar el teorema de Recursión Fuerte ya que en cada paso damos una función distinta. En concreto, para dar la definición en $\sigma(n)$ usamos a la función $p_{\sigma(n)}$.

El factorial es una función que jugará un papel importante en varios temas que verás en la facultad. Tiene una fuerte relación con contar cosas, el cual es un tema que posiblemente hayas estudiado en Álgebra Superior II. Aparece al contar las permutaciones de objetos, pero también como parte de la fórmula para los coeficientes binomiales $\binom{n}{k}$. También, lo encontraremos en este curso a la hora de enunciar el teorema de Wilson de teoría de números, pero necesitamos definir más cosas antes de llegar ahí.

Sin embargo, algo que sí podemos hacer ahora es demostrar una propiedad interesante que satisface el factorial.

Proposición: Para todo $n\in \mathbb{N}$, se tiene que $0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+1=(n+1)!$

Demostración. Procederemos por inducción, el caso base es claro ya que $0\cdot 0!+1= 0+1=1!.$

Supongamos que el resultado es cierto para alguna $n$ y con esta suposición probemos que

$0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+(n+1)\cdot(n+1)!+1=(n+2)!$.

Sabemos por nuestra hipótesis de inducción que

\begin{align*}
&0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+(n+1)\cdot(n+1)!+1\\
=&(0\cdot 0!+1\cdot 1!+2\cdot 2!+…+n\cdot n!+1)+(n+1)\cdot(n+1)! \\
=&(n+1)!+ (n+1)\cdot(n+1)!\\
=&(n+1)!(1+n+1)\\
=&(n+1)!(n+2)\\
=&(n+2)!
\end{align*}

En la primer igualdad estamos usando la conmutatividad y asociatividad de la suma. En la segunda igualdad, la hipótesis de inducción. Para la tercer igualdad estamos factorizando el término $(n+1)!$. El resto de igualdades se siguen de las definiciones.

$\square$

Resumen de las propiedades de los exponentes

Para finalizar con la entrada, hacemos un repaso de las propiedades que demostramos, posiblemente las conozcas como las leyes de los exponentes

  • Para todo $n$ número natural, se tiene que $n^0=1$
  • Si $n\neq 0$,entonces $0^n=0$
  • Para todo $n$ número natural, se tiene que $n^1=n$
  • Para todo $n$ número natural, se tiene que $1^n=1$
  • Para $l,m,n$ naturales, se tiene que $(l\cdot m)^n=l\n\cdot m^n$
  • Para $l,m,n$ naturales, se tiene que $n^{l+m}=n^l\cdot n^m$
  • Para $l,m,n$ naturales, se tiene que $n^{l\cdot m}=(n^l)^m$

Más adelante…

Con esta entrada, acabamos con las definiciones de operaciones a través de los teoremas de Recursión; sin embargo, no podemos decir que no ocuparemos este teorema en futuras ocasiones, al menos de forma implícita, mucho menos nos olvidaremos del principio de Inducción, el cuál irá siempre adherido al concepto de número natural.

En las siguientes entradas, estudiaremos otro tipo de propiedades de los naturales, relacionadas con el orden y el tamaño que estos tienen. Sin embargo, aún ocuparemos las operaciones que definimos y las relacionaremos; por ejemplo, con el orden que les daremos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra los contraejemplos que faltaron en la entrada
  2. Da la demostración de que $0^n=0$, para toda $n$
  3. Prueba que para todos los naturales $a,b,n$, se tiene que $(a^b)^n=a^{b\cdot n}$
  4. El factorial consiste en «multiplicar los primeros enteros». ¿Qué pasa si queremos hacer algo análogo para sumar los primeros enteros? Da una definición recursiva de una función $S(n)=0+1+2+…+n$, ¿por qué en realidad no es necesario dar una definición recursiva de esta función?
  5. Demuestra que si $n,m$ son naturales tales que existe $k\in\mathbb{N}$ tal que $n\cdot k=n^k=m$, entonces $n^m=m^n$. El regreso de esta afirmación es también verdadero, pero para verlo formalmente, necesitamos desarrollar más teoría.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Definición del producto y sus propiedades básicas

Por Roberto Manríquez Castillo

Deja un comentario

Introducción

En la entrada anterior, nos dedicamos a buscar una definición apropiada para la suma de números naturales, y después nos dedicamos a probar las propiedades más elementales que esta operación satisface.

Ahora es el turno de la multiplicación o producto, que se definirá de forma similar a la suma, ya que ocuparemos el teorema de Recursión Débil, y para probar sus propiedades ocuparemos el principio de Inducción.

Te motivamos a releer la entrada anterior y pensar unos momentos en el ejercicio 5 de la entrada anterior.

Definición del producto

Así como con la suma, recurriremos a una definición recursiva, la cual existe en virtud del teorema de Recursión.

Definición. Sea $m\in\mathbb{N}$, defnimos la función $p_{m}:\mathbb{N}\longrightarrow\mathbb{N}$, como la función que satisface las propiedades siguientes:

  1. $p_{m}(0)=0$.
  2. $p_{m}(\sigma(n))=s_{m}((p_{m}(n))$.

Denotaremos a $p_{m}(n)$ como $m\cdot n$, o simplemente como $mn$

Ejemplo. Para aclarar la definición anterior, consideremos $p_{7}$ y realicemos el diagrama conmutativo correspondiente a su definición recursiva.

Recordemos que las flechas indican a donde es mandado cada elemento bajo cada función, entonces las flechas verticales, justamente son las que nos indican los valores de $p_{7}$ en cada número natural, observemos que estos valores coinciden con la conocida tabla del $7$.

$\triangle$

Aprendiendo a multiplicar por uno

En este momento, demostraremos las propiedades más importantes del producto. Tenemos la fortuna de que contamos con una buena cantidad de propiedades de las funciones $s_{n}$, las cuales ya podremos usar sin ningún problema, más aún, para simplificar la notación haremos uso de la notación $m+n$, en vez de la notación $s_{m}(n)$, cada vez que se pueda.

Siguiendo la idea anterior, mencionamos la siguiente identidad, que es solo una reformulación del punto (2) de la definición del producto, pero que nos servirá para esclarecer la mayor parte de las pruebas.

Observación. $a\cdot\sigma(n)=a+(a\cdot n)$.

Para referir a esta observación en una demostración ocuparemos el símbolo $\overset{*}{=}$.

Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{1}(n)=n$, es decir, $1\cdot n=n$

Demostración. Como se esperaba, la prueba es por inducción sobre $n$.

Base inductiva: Por la definición de $p_{1}$, tenemos que $p_{1}(0)=0$.

Hipótesis de inducción: Supongamos que para algún $n$, se tiene que $p_{1}(n)=n$

Paso inductivo: Debemos demostrar que $p_{1}(\sigma(n))=\sigma(n)$, esto se sigue por las siguientes igualdades

\begin{align*}
p_{1}(\sigma(n))&\overset{*}{=}1+(p_{1}(n))\\ &\overset{\text{H.I.}}{=}1+n=\sigma(n).
\end{align*}

Donde la última igualdad se da recordando que en la entrada anterior probamos que $s_{1}(n)=\sigma(n)$.

$\square$

Con esto hemos aprendido a multiplicar por $1$.

Aprendiendo a multiplicar por cero

Proposición. Para toda $n\in\mathbb{N}$, se tiene que $p_{0}(n)=0$.

Demostración. Procedamos por inducción sobre $n$, la base inductiva es directa de la definición, ya que $p_{0}(0)=0$.

Nuestra hipótesis de inducción consiste en suponer que para alguna $n$ se tiene que $p_{0}(n)=0$. Entonces queda demostrar que $p_{0}(\sigma(n))=0$. Esto se sigue de las siguientes igualdades.

\begin{align*}
p_{0}(\sigma(n))&\overset{*}{=}0+p_{0}(n)\\ &\overset{\text{H.I.}}{=}0+0=0
\end{align*}

$\square$

La propiedad distributiva izquierda

La siguiente propiedad es una de las más famosas, ya que nos permitirá relacionar la suma y el producto, además jugará un papel importante en la demostración de las siguientes propiedades.

Proposición (propiedad distributiva izquierda). Si $a,b,n$ son números naturales, entonces $p_{s_{a}(b)}(n)=s_{p_{a}(n)}(p_{b}(n))$, u ocupando la notación familiar $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.

Demostración. Procedamos por inducción, como podrás notar con todas estas demostraciones, la inducción será sobre la variable que aparezca más a la derecha de nuestras expresiones, es decir, la inducción será sobre $n$.

Base inductiva: Por la definición del producto tenemos que, $(a+b)\cdot 0=0$, y por las propiedades que demostramos para la suma, concluimos que $0=0+0$, sin embargo; de nuevo por la definición del producto, $0=(a\cdot n)$ y $0=(b\cdot n)$, uniendo todas estas igualdades concluimos que $(a+b)\cdot 0=(a\cdot n)+(b\cdot n)$, justo como queremos.

Hipótesis de inducción: Supongamos que para algún $n$ se tiene que $(a+b)\cdot n=(a\cdot n)+(b\cdot n)$.

Paso inductivo: Debemos probar que $(a+b)\cdot\sigma(n)=(a\cdot\sigma(n))+(b\cdot\sigma(n))$. Por la observación que hicimos, tenemos

\begin{align*}
(a+b)\cdot\sigma(n)&\overset{*}{=}(a+b)+((a+b)\cdot n)\\ &\overset{\text{H.I.}}{=}(a+b)+((a\cdot n)+(b\cdot n))
\end{align*}

A partir de aquí, el resultado se seguirá usando la asociatividad y la conmutatividad de la suma, en la siguiente cadena de igualades detallamos la demostración paso a paso ¿Puedes identificar cómo ocupamos las propiedades de la suma?.

\begin{align*}
(a+b)+((a\cdot n)+(b\cdot n))&=a+(b+((a\cdot n)+(b\cdot n)))\\
&=a+((b+(a\cdot n))+(b\cdot n))\\
&=a+(((a\cdot n)+b)+(b\cdot n))\\
&=a+((a\cdot n)+(b+(b\cdot n)))\\
&=(a+(a\cdot n))+(b+(b\cdot n))\\
&\overset{*}{=}(a\cdot \sigma (n))+(b\cdot \sigma (n))
\end{align*}

$\square$

Aunque la prueba anterior fue un poco más confusa que las anteriores, las consecuencias que tendrá esta proposición serán sumamente importantes.

El producto es conmutativo

Como mencionamos, la asociatividad y la conmutatividad, serán una consecuencia de las propiedades distributivas, por el momento veamos que en efecto el producto conmuta.

Proposición (conmutatividad). Si $m,n\in \mathbb{N}$, entonces $m\cdot n=n\cdot m$.

Demostración. Una vez más hagamos la prueba por inducción sobre $n$

Base inductiva: Por definición tenemos que $m\cdot 0 =0$, además $p_{0}(m)=0$ por lo demostrado antes, es decir que $m\cdot 0=0=0\cdot m$

Hipótesis de inducción: Supongamos que para alguna $n$, se tiene que $m\cdot n=n\cdot m$.

Paso inductivo: Debemos probar que $m\cdot\sigma(n)=\sigma(n)\cdot m$. Esto se sigue ya que

\begin{align*}
m\cdot\sigma(n)&\overset{*}{=}m+(m\cdot n)\\
&\overset{\text{H.I.}}{=}m+(n\cdot m)
\end{align*}

Pero ya demostramos que $m=1\cdot m$, usando esto y la propiedad ditributiva, podemos concluir que

\begin{align*}
m+(n\cdot m)&=(1\cdot m )+(n\cdot m)\\
&=(1+n)\cdot m=\sigma(n)\cdot m
\end{align*}

$\square$

Con la conmutatividad, podemos probar de manera inmediata el siguiente resultado

Corolario (propiedad distributiva derecha). Si $a,b,n$ son números naturales, entonces $a\cdot(b+ n)=(a\cdot b)+(a\cdot n)$.

La prueba queda como un ejercicio moral, en parte porque su prueba no requiere Inducción. Con este resultado, podemos probar la propiedad asociativa del producto.

El producto es asociativo

Con la propiedad distributiva derecha , podemos dar la demostración de la propiedad asociativa del producto.

Proposición (asociatividad). Si $a,b,n$ son números naturales, se tiene que $a\cdot(b\cdot n)=(a\cdot b)\cdot n$.

Demostración. De nuevo procedamos por inducción sobre $n$

Base inductiva: Notemos que por definición, para cualquier número natural $m$ se tiene que $0=p_{m}(0)=m\cdot 0$. Con esto en mente tenemos que, $(a\cdot b)\cdot(0)=0=a\cdot 0=a\cdot(b\cdot 0)$ que es justo la base de inducción.

Hipótesis de Inducción: Supongamos que para alguna $n\in \mathbb{N}$, tenemos que $(a\cdot b)\cdot n=a\cdot(b\cdot n)$

Paso Inductivo: Demostremos que $(a\cdot b)\cdot\sigma(n)=a\cdot(b\cdot \sigma(n))$. Como

\begin{align*}
(a\cdot b)\cdot\sigma(n)&\overset{*}{=}(a\cdot b)+(a\cdot b)\cdot n\\
&\overset{\text{H.I.}}{=}(a\cdot{b})+a\cdot(b\cdot n)\\
&=a\cdot (b+b\cdot n)\\
&\overset{*}{=}a\cdot(b\cdot \sigma (n))
\end{align*}

la igualdad que no está justificada es la aplicación de la propiedad distributiva.

$\square$

Ley de la cancelación

Para concluir con las propiedades del producto, enunciamos la propiedad de la cancelación del producto, recordemos que esta propiedad también es válida para la suma. Para hacer esta prueba necesitamos trabajar un poco.

Recordemos el ejercicio 2 de la Tarea moral de la entrada Principio de inducción y teoremas de recursión, el cual ya hemos ocupado anteriormente:

Si $n\neq0$, entonces existe $a\in \mathbb{N}$ tal que $n=\sigma(a)$

De la misma forma, el ejercicio 1 de la Tarea moral de la entrada pasada dice que:

Si $a,b\in\mathbb{N}$ son tales que $a+b=0$, entonces $a=b=0$

Con estos resultados en mente probamos el siguiente lema.

Lema. Si $n\neq 0$ y $m\in \mathbb{N}$ es tal que $m\cdot n=0$, entonces $m=0$.

Demostración. Como $n\neq0$, entonces existe $a\in \mathbb{N}$, tal que $n=\sigma(a)$, entonces tenemos que

\begin{align*}
0&=m\cdot n\\
&=m\cdot\sigma(a)\\
\overset{*}{=}m+(m\cdot a).
\end{align*}

Entonces tenemos que $m\cdot a=0$ y que $m=0$ que es lo que debíamos probar.

$\square$

Es común usar una equivalencia lógica del enunciado anterior, la cual dice:

Si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$

Proposición (ley de cancelación). Si $m,n$ son números naturales y $a\neq0$ y cumplen que $a\cdot n=a\cdot m$, entonces, $n=m$

Demostración. De nuevo, procedamos por inducción sobre $n$

Base inductiva: Supongamos que $n=0$ y $a\neq0$, entonces $a\cdot m=a\cdot n=a\cdot0 =0,$ por el Lema tenemos que $m=0=n$.

Hipótesis de inducción: Supongamos que para algún $n$, tenemos que si $a\neq0$ y $a\cdot n=a\cdot m$, entonces $n=m$.

Paso inductivo: Probemos para $\sigma(n)$, sea $a\neq 0$ y supongamos que $a\cdot\sigma(n)=a\cdot m$.

Como $\sigma(n)\neq 0$, y por hipótesis, $a\neq0$, entonces por la equivalencia del lema, concluimos que $a\cdot\sigma(n)\neq 0$, de donde $a\cdot m\neq 0$, esto implica que $m\neq 0$, por lo que existe $b$ tal que $m=\sigma(b)$, entonces podemos escribir

\begin{align*}
a+a\cdot n& \overset{*}{=}a\cdot\sigma(n)\\
&=a\cdot m\\
&=a\cdot\sigma(b)\\
&\overset{*}{=}a+a\cdot b
\end{align*}

Ocupando la ley de cancelación de la suma, tenemos que $a\cdot n=a\cdot b$.

Pero por hipótesis de inducción debemos de tener que $n=b$, esto quiere decir que $\sigma(n)=\sigma(b)=m$, justo como debíamos probar.

$\square$

Con esta prueba concluimos las propiedades más fundamentales del producto.

Resumen de las propiedades del producto

Para finalizar con la entrada, haremos un compendio de las propiedades que demostramos

  • Para todo $n$ natural, se tiene que $1\cdot n=n=n \cdot 1$
  • Para todo $n$ natural, se tiene que $0\cdot n=0=n \cdot 0$
  • Para $l,m,n$ naturales cualesquiera se tiene que $(l+m)\cdot n=(l\cdot n)+(m\cdot n)$
  • Para $m,n$ naturales se tiene que $m\cdot n=n\cdot m$
  • Para $l,m,n$ naturales cualesquiera se tiene que $l\cdot(m+n)=(l\cdot m)+(l\cdot n)$
  • Para $l,m,n$ naturales cualesquiera se tiene que $(l\cdot m)\cdot n=l\cdot(m\cdot n)$
  • Para $m,n$ naturales con $m\neq 0$, si $m\cdot n=0$, entonces $n=0$
  • Para $l,m,n$ naturales con $l\neq 0$, si $l\cdot n=l\cdot m$, entonces $n=m$

Más adelante…

Con las propiedades de la suma y del producto en nuestra bolsa de herramientas, tenemos ya una rica teoría que desarrollar; nos falta aún definir una relación muy familiar en el conjunto $\mathbb{N}$, el orden, al cual ya hemos apelado en la demostración del teorema de la Recursión Débil.

Por el momento estudiaremos con mayor detalle los conjuntos infinitos, donde veremos la importancia de los naturales dentro de esta clase de conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Prueba la Propiedad distributiva derecha.
  2. Usando únicamente la ley de cancelación el producto, demuestra el Lema previo a la demostración de la ley de cancelación.
  3. ¿Qué pasa si en el enunciado de la ley de la cancelación, no asumimos que $a\neq 0$?
  4. Demuestra usando el Lema previo a la demostración de la ley de cancelación que si $n,m\in \mathbb{N}\setminus\{0\}$, entonces $n\cdot m\in \mathbb{N}\setminus\{0\}$.
  5. Da una definición recursiva de las funciones $\eta_{m} (n)=m^n$ y prueba las leyes de los exponentes.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»