Introducción

Después de haber abordado a modo de repaso las herramientas que usaremos de álgebra lineal, estamos listos para estudiar la diferenciabilidad en funciones más generales. Ya estudiamos la diferenciabilidad en curvas (funciones $f:S\subseteq \mathbb{R}\to \mathbb{R}^m$) y en campos escalares (funciones $f:S\subseteq \mathbb{R}^n \to \mathbb{R}$). Ahora podemos estudiar la diferenciabilidad en campos vectoriales, que recuerda que ahora sí son funciones $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ para cualesquiera $m$ y $n$ enteros positivos.

Intuición de diferenciabilidad en campos vectoriales

Con anterioridad, hemos discutido la intuición geométrica de lo que quiere decir que un campo escalar $f:\mathbb{R}^n\to \mathbb{R}$ sea diferenciable. A grandes rasgos, estamos pidiendo que cerca de un punto $\bar{a}$ la función $f(\bar{a})$ cambie «como una función lineal». Esto quiere decir que la gráfica de la función se parece mucho a un hiperplano en $\mathbb{R}^{n+1}$ cerca del punto $\bar{a}$, tanto que de hecho podemos dar un hiperplano tangente a la gráfica en $\bar{a}$. Bajo suficiente regularidad, esta función lineal estaba dada por las derivadas parciales y estaba muy relacionada con el gradiente $\triangledown f$.

La situación para campos vectoriales es parecida. Si tenemos una función $f:\mathbb{R}^n\to \mathbb{R}^m$, entonces está dada por funciones coordenada que la expresan de la manera $f(\bar{x})=(f_1(\bar{x}),\ldots,f_m(\bar{x}))$ para cada $\bar{x}\in \mathbb{R}^n$. La diferenciabilidad que buscaremos ahora deberá suceder coordenada a coordenada, y por ello lo que pensaremos como derivada tendrá algo así como un gradiente por cada coordenada. Esto nos daría $m$ gradientes, pero una mejor forma de pensar en resumen a la derivada es como una transformación lineal $T:\mathbb{R}^n\to \mathbb{R}^m$ que nos diga con mucha precisión cuándo cambia la funciíon $f$ (cuando esto sea posible).

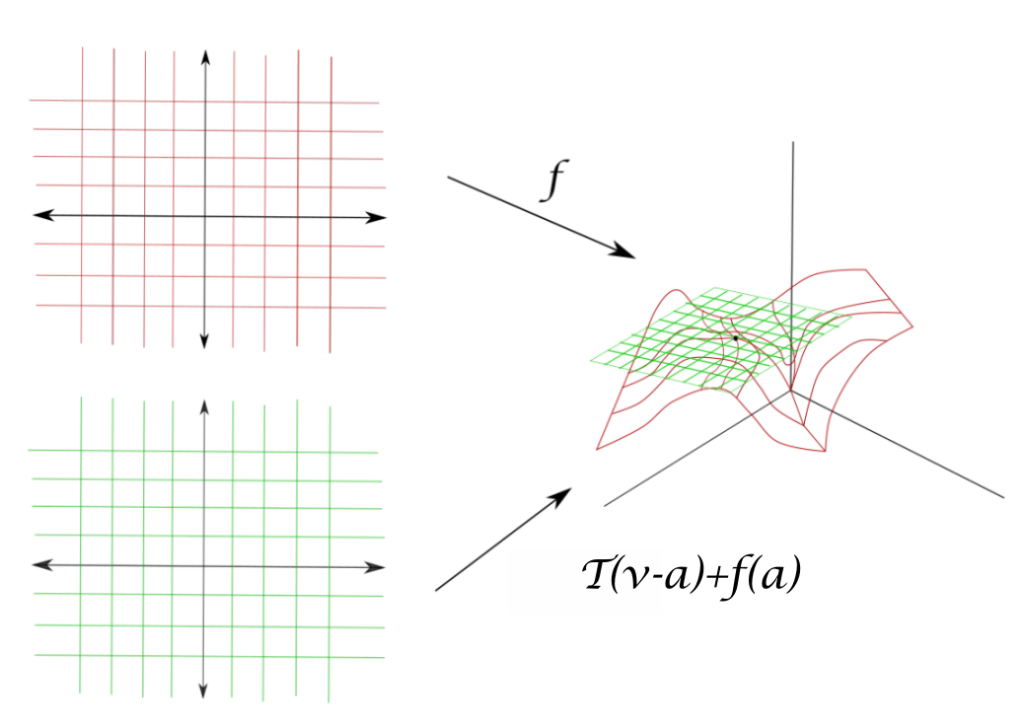
Para tener clara idea de lo que queremos hacer recordemos el ejemplo de campos escalares, y de aquí construiremos una generalización a campos vectoriales: Observa la Figura $1$. A la izquierda, hemos dibujado dos copias de $\mathbb{R}^n$ (pero que puedes pensar como $\mathbb{R}^2$). A la derecha, hemos dibujado la gráfica de dos funciones. Una es una función cualquiera $f:\mathbb{R}^{n}\rightarrow \mathbb{R}^m$. La otra es una transformación lineal $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^m$ que ha sido trasladada sobre el plano $xy$ y sobre el eje $z$ con la función $G(\bar{v})=T(\bar{v}-\bar{a})+f(\bar{a})$. Estas gráficas son objetos en $\mathbb{R}^n \times \mathbb{R}^m$ (ponemos un punto por cada pareja $(\bar{x},f(\bar{x}))$ con $\bar{x}\in \mathbb{R}^n$).

Como $T$ es lineal, cumple $T(\bar{0})=0$. Al hacer la traslación, obtenemos $G(\bar{a})=T(\bar{0})+f(\bar{a})=f(\bar{a})$. Así, $T$ traslada un subespacio $H$ de dimensión $n$ a un subespacio afín de dimensión $n$ que pasa por $f(\bar{a})$. Lo que buscaremos al pedir que la función $f$ sea diferenciable con derivada $T$ es que la gráfica de $f$ se parezca mucho a este subespacio $H+f(\bar{a})$, tanto que de hecho dicho subespacio lo podremos pensar como tangente a la gráfica en el punto $(\bar{a},f(\bar{a}))$.

Definición de diferenciabilidad para campos vectoriales

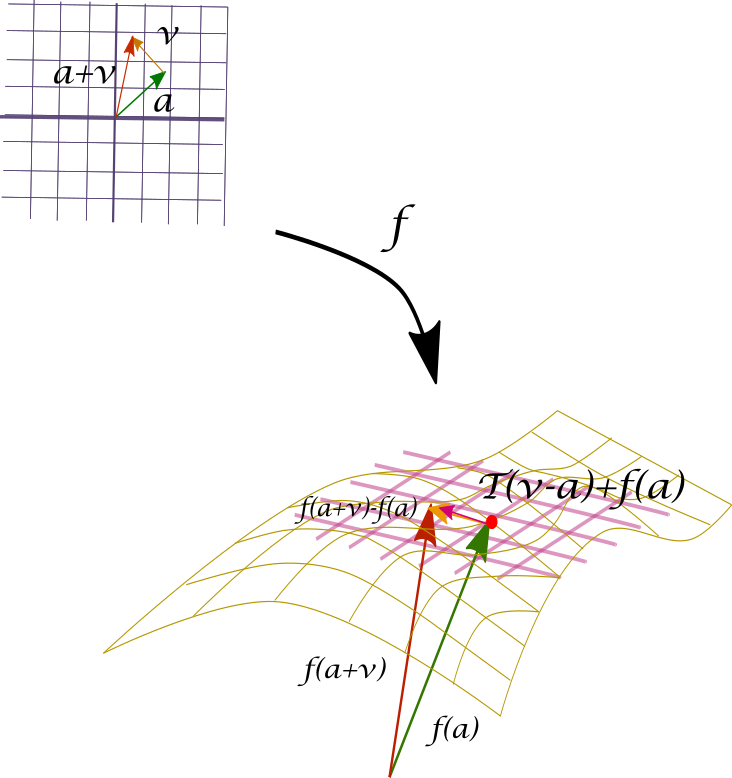
¿Cuál es la condición algebraica que pediremos? Será muy similar a lo que pasaba en campos escalares. Lo que queremos es que el cambio $f(\bar{a}+\bar{v})-f(\bar{a})$ se parezca mucho a $T(\bar{v})$ cuando $\bar{v}$ es pequeño. De hecho, tiene que parecerse tanto, tanto, que $f(\bar{a}+\bar{v})-f(\bar{a})$ debe parecerse a $T(\bar{v})$ más rápido de lo que $\bar{v}$ se va a $\bar{0}$. Esto nos lleva a plantear que la condición buscada sea la siguiente:

$$\lim_{\bar{v}\to \bar{0}}\frac{||(f(\bar{a}+\bar{v})-f(\bar{a}))-T(\bar{v})||}{||\bar{v}||}=0.$$ La Figura $2$ tiene un diagrama que ayuda a entender esto un poco mejor. Queremos que la flecha indicada en amarillo acabe muy cerca de $f(\bar{a}+\bar{v})$.

Por supuesto, la discusión que hemos tenido sólo aplica para cuando estamos trabajando cerca del punto $\bar{a}$, así que más bien la transformación lineal de la que estamos hablando dependerá del punto $\bar{a}$. Todo esto nos lleva a nuestra primera definición formal de diferenciabilidad.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Decimos que $f$ es diferenciable en $\bar{a}\in Int(S)$ si existe una transformación lineal $T_{\bar{a}}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ tal que

$$\lim_{\bar{v}\to \bar{0}}\frac{||f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})||}{||\bar{v}||}=0.$$

En este caso, a $T_{\bar{a}}$ le llamamos la derivada de $f$ en el punto $\bar{a}$.

Antes de empezar a demostrar propiedades de esta noción, nos conviene tener una versión alternativa y totalmente equivalente.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Decimos que $f$ es diferenciable en $\bar{a}\in Int(S)$ si existe una transformación lineal $T_{\bar{a}}:\mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ y una función $E:\mathbb{R}^n\times \mathbb{R}^n\to \mathbb{R}^m$ de manera que $$f(\bar{a}+\bar{v})=f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v})$$ con $$\lim_{||\bar{v}||\to 0}E(\bar{a};\bar{v})=0.$$

Esta definición es equivalente a la anterior pues si despejamos tenemos: \[E(\bar{a};\bar{v})=\frac{f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})}{||\bar{v}||},\] de donde se puede verificar que se cumple una definición si y sólo si se cumple la otra. Los detalles quedan como tarea moral.

Ejemplo. Consideremos la función $f(x,y)=(x^2y^2,xy)$ y tomemos el punto $a=(1,1)$. ¿Será $f$ diferenciable en $a$? Afirmamos que sí, que la función lineal $T_a(x,y)=(2x+2y, x+y)$ cumple con la definición de límite que se pide. Veamos esto en la primera versión de la definición. Tendríamos, usando $\bar{v}=(h,k)$, que

\begin{align*}
f((1,1)&+(h,k))-f(1,1)-T_a(h,k)\\
&=((h+1)^2(k+1)^2,(h+1)(k+1))-(1,1)-(2h+2k,h+k)\\
&=(h^2k^2+2h^2k+2hk^2+h^2+k^2+4hk,hk)
\end{align*}

Dividiendo entre $\sqrt{h^2+k^2}$ que es la norma de $v$, y haciendo manipulaciones algebraicas, se obtiene

$$\left(\frac{h^2k^2+2h^2k+2hk^2+h^2+k^2+4hk}{\sqrt{h^2+k^2}},\frac{hk}{\sqrt{h^2+k^2}}\right).$$

Por la desigualdad entre la media cuadrática y la media geométrica, $$\frac{|hk|}{\sqrt{h^2+k^2}}\leq \sqrt{\frac{|hk|}{2}},$$

de modo que cuando $(h,k)\to (0,0)$, la segunda coordenada del vector que nos interesa converge a cero. La primera coordenada también se puede ver que converge a cero: el primero, segundo, tercero y sexto sumandos se acotan de manera similar, pues tienen factores $h$ o $k$ adicionales. El cuarto y quinto sumando se acotan notando que $\frac{h^2+k^2}{\sqrt{h^2+k^2}}=\sqrt{h^2+k^2}$, que también converge a cero con $h$ y $k$. Los detalles quedan de tarea moral.

$\triangle$

Diferenciabilidad implica continuidad

En el caso de las funciones de una variable real teníamos claramente que diferenciabilidad implica continuidad. Como es de esperarse, lo mismo se cumple para campos vectoriales, ya que una función diferenciable es más «suave» que una continua.

Teorema. Supongamos $f:S\subseteq \mathbb{R}^n\to\mathbb{R}^m$ es un campo vectorial diferenciable en un punto $\bar{a}$ de $S$. Entonces $f$ es continuo en $\bar{a}$.

Demostración. Si $f$ es diferenciable en $\bar{a}$ entonces cumple con la ecuación \[f(\bar{a}+\bar{v})=f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v})\] con $E(\bar{a};\bar{v})$ una función tal que $\lim_{\bar{v}\to \bar{0}} E(\bar{a}; \bar{v})=0$ (¿Por qué es válida esta última afirmación?). Por ello:

\begin{align*}
\lim\limits_{\bar{v}\to \bar{0}}f(\bar{a}+\bar{v})&=\lim\limits_{\bar{v}\to \bar{0}}\left( f(\bar{a})+T_{\bar{a}}(\bar{v})+||\bar{v}||E(\bar{a};\bar{v}) \right)\\
&= \lim\limits_{\bar{v}\to \bar{0}}f(\bar{a})+\lim\limits_{\bar{v}\to \bar{0}}T_{\bar{a}}(\bar{v})+\lim\limits_{\bar{v}\to \bar{0}}||\bar{v}||E(\bar{a};\bar{v}).
\end{align*}

El primer sumando no depende de $\bar{v}$, así que es $f(\bar{a})$. El segundo se va a cero pues las transformaciones lineales son continuas. Finalmente, el tercer sumando se va a cero por lo que sabemos de $E(\bar{a},\bar{v})$. Así, $\lim\limits_{\bar{v}\to \bar{0}}f(\bar{a}+\bar{v})=f(\bar{a})$. Por lo tanto $f$ es continua.

$\square$.

Derivadas direccionales y derivadas parciales

Si bien tenemos dos definiciones de diferenciabilidad, aún no tenemos una manera muy práctica de encontrar o describir a la transformación lineal $T_{\bar{a}}$, que es la mejor aproximación lineal. En el ejemplo después de nuestra definición, nos dieron la transformación y funcionó, pero hasta donde hemos platicado, todavía es un misterio cómo obtenerla.

Nos gustaría tener una descripción más explícita pues queremos resolver problemas específicos como encontrar, por ejemplo, la ecuación de un hiperplano tangente. Este problema ya lo habíamos resuelto para campos escalares: si tenemos suficiente regularidad, entonces podemos construir la derivada a través de las derivadas parciales (que a su vez son derivadas direccionales). La teoría que ya desarrollamos prácticamente se puede copiar, considerando que ahora tendremos derivadas en cada función coordenada.

Lo primero que notaremos es que así como para campos escalares, para campos vectoriales también podemos definir la noción de derivadas direccionales. Pensemos en una función $f:S\subseteq \mathbb{R}^{n}\to \mathbb{R}^n$. Tomemos un vector fijo $\bar{a}\in Int=(S)$. Coloquemos una flecha que comience en $\bar{a}$ y tenga dirección dada por otro vector dado $\bar{y}\in \mathbb{R}^{n}$. Si multiplicamos a $\bar{y}$ por un escalar $h$ positivo, esto estira o encoge al vector $\bar{y}$, pero lo deja con la misma dirección. En el ejemplo de la Figura 3, al variar sobre todos los valores de $h$ se genera la recta $\bar{a}+h\bar{y}$. Si a los puntos de esta recta le aplicamos la función $f$, se obtiene un cierto lugar geométrico $$f(\bar{a}+h\bar{y})=(f_1(\bar{a}+h\bar{y}),\ldots,f_m(\bar{a}+h\bar{y})),$$ conforme se varían los valores de $h$. Lo que definiremos como derivada direccional nos permitirá hablar de un espacio afín tangente de dimensión $m$ a este lugar geométrico en el punto $f(\bar{a})$.

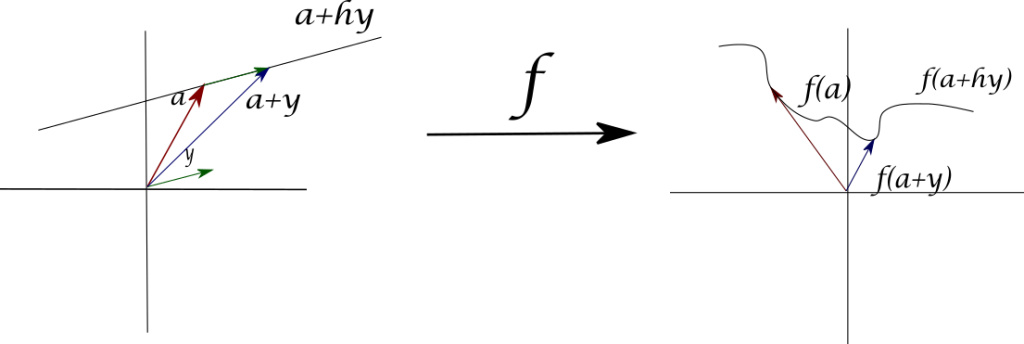
A continuación tenemos nuestra definición de derivada direccional para campos vectoriales.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Tomemos $\bar{a}\in Int(S)$, $\bar{y}\in \mathbb{R}^{n}$. Definimos la derivada direccional de $f$ en $\bar{a}$ en la dirección $\bar{y}$ como: \[ f'(\bar{a};\bar{y})=\lim\limits_{h\to 0}\frac{f(\bar{a}+h\bar{y})-f(\bar{a})}{h}, \] siempre y cuando el límite exista.

Notemos que $f'(\bar{a};\bar{y})$ es un vector de $\mathbb{R}^{m}$.

En los campos escalares teníamos derivadas parciales. En este caso también las tenemos y describen a las derivadas direccionales en el mismo sentido que en el caso escalar. Para formalizar las cosas, damos la definición a continuación.

Definición. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ un campo vectorial. Tomemos $\bar{a}\in Int(S)$, $\bar{y}\in \mathbb{R}^{n}$. Definimos la derivada direccional de $f$ en la coordenada $x_i$ en $a$ como la derivada parcial $f'(\bar{a};\hat{e}_i)$, donde $\hat{e}_i$ es el $i$-ésimo vector de la base canónica, siempre y cuando esta exista.

Como en el caso de los campos escalares, las derivadas direccionales pueden entenderse en términos de las derivadas parciales bajo suficiente regularidad. Tomemos $\hat{e}_1,\ldots,\hat{e}_n$ la base canónica de $\mathbb{R}^n$. Tomemos $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$. Pensemos que todas las derivadas parciales de $f$ existen en un punto dado $\bar{a}$ y que son continuas. Expresemos a $\bar{y}$ como $\bar{y}=\alpha_1\hat{e}_1+\alpha_2\hat{e}_2+\ldots+\alpha_n\hat{e}_n$ con $\hat{e}_1,\ldots,\hat{e}_n$ la base canónica de $\mathbb{R}^n$. En esta entrada discutiremos hacia el final que bajo estas condiciones tendremos que $f'(\bar{a};\bar{y})$ existe y de hecho que $$f'(\bar{a};\bar{y})=\sum_{i=1}^n \alpha_i f'(\bar{a};\bar{e}_i).$$

El tener derivadas parciales continuas resultará una hipótesis muy fuerte y de hecho implicará todavía más que la existencia de derivadas direccionales. De hecho, como en el caso de campos escalares, esta hipótesis implicará diferenciabilidad. Antes de discutir esto, veremos en la siguiente sección qué pasa componente a componente.

Si las derivadas parciales no son continuas, no deberíamos esperar que las derivadas direccionales existan: ¡hay muchas posibles direcciones y sólo sabemos que pasa en dos de ellas! Como tarea moral, puedes pensar en un contraejemplo de un campo escalar $f:\mathbb{R}^2\to \mathbb{R}^2$ con derivadas parciales en cierto punto $\bar{a}$, pero sin alguna (o algunas) derivadas direccionales en $\bar{a}$.

Derivadas por componente

Las derivadas direccionales pueden entenderse mediante las derivadas parciales, pero también, como en el caso de las trayectorias, pueden entenderse mediante las derivadas por componente. Para pensar en ello, tomemos $\hat{e}_1,\ldots,\hat{e}_m$ la base canónica de $\mathbb{R}^m$. Tomemos $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ con funciones coordenadas $f(\bar{x})=\left( f_{1}(\bar{x}),\dots ,f_{m}(\bar{x})\right)$. Pensemos que las derivadas direccionales de $f_1,\ldots, f_m$ en $\bar{a}$ en la dirección $\bar{y}$ existen.

Tenemos entonces:

\begin{align*} \lim\limits_{h\to 0}\frac{f(\bar{a}+h\bar{y})-f(\bar{a})}{h} &=\lim\limits_{h\to 0}\frac{\left( f_{1}(\bar{a}+h\bar{y}),\dots ,f_{m}(\bar{a}+h\bar{y})\right) -\left( f_{1}(\bar{a}),\dots ,f_{m}(\bar{a})\right)}{h}\\ &=\lim\limits_{h\to 0}\left( \frac{f_{1}(\bar{a}+h\bar{y})-f_{1}(\bar{a})}{h},\dots ,\frac{f_{m}(\bar{a}+h\bar{y})-f_{m}(\bar{a})}{h}\right)\\ &=\lim\limits_{h\to 0}\sum_{i=1}^{m}\frac{f_{i}(\bar{a}+h\bar{y})-f_{i}(\bar{a})}{h}{\hat{e}_{i}}\\
&=\sum_{i=1}^{m}\lim\limits_{h\to 0}\frac{f_{i}(\bar{a}+h\bar{y})-f_{i}(\bar{a})}{h}{\hat{e}_{i}}\\ &=\sum_{i=1}^{m}f_{i}'(\bar{a};\bar{y}){\hat{e}_{i}}. \end{align*}

En la última igualdad estamos usando la suposición de que las derivadas existen componente a componente. Como mostramos que el límite planteado inicialmente existe, obtenemos entonces que
\begin{equation} \label{eq:porcomponente} f'(\bar{a};\bar{y})=\sum_{i=1}^{m}f_{i}'(\bar{a};\bar{y}){\hat{e}_{i}} .\end{equation}

Lo que tenemos aquí es que la derivada direccional de $f$ en $\bar{a}$ en dirección de $\bar{y}$ es la suma vectorial de cada vector de la base escalado por la derivada direccional del campo escalar $f_{i}$ en $\bar{a}$ con respecto a la dirección de $\bar{y}$.

Diferenciabilidad implica derivadas direccionales

La noción de diferenciabilidad que dimos implica la diferenciabilidad de cada una de las funciones componente $f_i$ de una función $f:\mathbb{R}^n\to \mathbb{R}^m$. Es decir, si el campo vectorial es diferenciable, entonces cada uno de los campos escalares $f_1,\ldots,f_m$ componentes son también diferenciables, pues el límite $$\lim_{\bar{v}\to \bar{0}}\frac{||f(\bar{a}+\bar{v})-f(\bar{a})-T_{\bar{a}}(\bar{v})||}{||\bar{v}||}=0$$ se cumple, y por lo tanto se cumple componente a componente. En el caso de $T_{\bar{a}}$ el $i$-ésimo componente es precisamente hacer el producto interior del $i$-ésimo renglon de la matriz que representa a $T_{\bar{a}}$ con $\bar{v}$, y entonces la derivada $\triangledown f_i(\bar{a})$ del campo escalar $f_i$ está dada precisamente por dicho $i$-ésimo renglón.

A su vez, sabemos que si un campo escalar es diferenciable, entonces existen todas las derivadas parciales. Por lo que hemos platicado en unidades anteriores, si $\bar{y}\in \mathbb{R}^{n}$ se escribe en la base canónica como $\bar{y}=\sum_{j=1}^{n}y_{j}{\hat{e}_{j}}$, al aplicar $\triangledown f_i(\bar{a})$ obtenemos

\begin{align*}
\triangledown f_i(\bar{a})(\bar{y})&=\sum_{j=1}^n y_j\triangledown f_i(\bar{a})(\hat{e}_j)\\
&=\sum_{j=1}^n y_j \frac{\partial f_i}{\partial x_j}(\bar{a}),\\
\end{align*}

lo cual abreviamos como

$$f_i'(\bar{a};\bar{y})=\left(\frac{\partial f_i}{\partial x_1}(\bar{a}), \ldots, \frac{\partial f_i}{\partial x_n}(\bar{a})\right) \cdot \bar{y}.$$

Usando esta igualdad para cada $i$ y sustituyendo la ecuación \eqref{eq:porcomponente} que obtuvimos al analizar componente por componente, obtenemos entonces que

$$f^{\prime}(\bar{a};\bar{y})=\sum_{i=1}^m \left(\left(\frac{\partial f_i}{\partial x_1}(\bar{a}), \ldots, \frac{\partial f_i}{\partial x_n}(\bar{a})\right) \cdot \bar{y}\right)\hat{e}_i.$$

¡Pero esto se puede denotar de manera mucho más compacta mediante un producto matricial! Reflexiona un poco por qué la expresión anterior dice exactamente lo mismo que la siguiente:

$$f'(\bar{a};\bar{y})= \begin{pmatrix} \frac{\partial f_{1}}{\partial y_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial y_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix}.$$

Como tarea moral, tendrás que verificar que en un campo vectorial diferenciable en $\bar{a}$ se debe cumplir que $f'(\bar{a};\bar{y})=T_{\bar{a}}(\bar{y})$. Por lo discutido, debe pasar entonces para cada $y$ que \[ T_{\bar{a}}(\bar{y})=\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} y_{1} \\ \vdots \\ y_{n} \end{pmatrix}.\]

Esto precisamente nos está diciendo que si $f$ es diferenciable en $a$, entonces sus derivadas parciales deben existir y se debe cumplir que la forma matricial de $T_{\bar{a}}$ en las bases canónicas de $\mathbb{R}^n$ y $\mathbb{R}^m$ debe ser \begin{equation}\label{eq:jacobiana}\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}.\end{equation}

Matriz jacobiana

Toda la discusión anterior nos lleva a lo siguiente.

Definición. Dado un campo vectorial $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ diferenciable en un punto $\bar{a}\in Int(S)$ con derivada $T_{\bar{a}}$, a la matriz que representa a $T_{\bar{a}}$ en las bases canónicas la denotamos por $Df(\bar{a})$ y le llamamos la matriz jacobiana de $f$ en $\bar{a}$.

Por lo discutido en la sección anterior,

$$Df(\bar{a})=\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}.$$

Escribiremos $Df(\bar{a})(\bar{x})$ para referirnos al producto de la matriz $Df(\bar{a})$ con el vector (columna) $\bar{x}$, que precisamente coincide con $T_{\bar{a}}(\bar{x})$. Así, bajo la hipótesis de diferenciabilidad, hemos recuperado entonces lo que hace $T_{\bar{a}}$ como una multiplicación matricial, donde la matriz tiene como elementos a las derivadas parciales de las funciones coordenada en el punto $\bar{a}$.

Ejemplos de diferenciabilidad en campos vectoriales

Con todo lo discutido hasta ahora, obtenemos un método para obtener la derivada para campos vectoriales, lo que nos permitirá, por ejemplo, encontrar la transformación lineal de forma explícita y encontrar hiperplanos tangentes.

Ejemplo. Consideremos $f(x,y)=(x^{2},xy,y^{2}).$ Calculemos su diferencial en el punto $(1,-1)$. Las funciones coordenada son

\begin{align*}
f_{1}(x,y)&=x^{2}\\
f_{2}(x,y)&=xy\\
f_{3}(x,y)&=y^{2},
\end{align*}

de donde tenemos: \[ \frac{\partial f_{1}}{\partial x}(1,-1)=\left. 2x\right|_{_{(1,-1)}}=2;\hspace{3cm} \frac{\partial f_{1}}{\partial y}(1,-1)=0;\hspace{3cm}\frac{\partial f_{2}}{\partial x}(1,-1)=\left. y\right|_{_{(1,-1)}}=-1;\] \[ \frac{\partial f_{2}}{\partial y}(1,-1)=\left. x\right|_{_{(1,-1)}}=1;\hspace{3cm}\frac{\partial f_{3}}{\partial x}(1,-1)=0;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,-1)=\left. 2y\right|_{_{(1,-1)}}=-2.\] Así \[ Df(1,-1)=\begin{pmatrix} \frac{\partial f_{1}}{\partial x}(1,-1) & \frac{\partial f_{1}}{\partial y}(1,-1) \\ \frac{\partial f_{2}}{\partial x}(1,-1) & \frac{\partial f_{2}}{\partial y}(1,-1) \\ \frac{\partial f_{3}}{\partial x}(1,-1) & \frac{\partial f_{3}}{\partial y}(1,-1) \end{pmatrix}= \begin{pmatrix} 2 & 0 \\ -1 & 1 \\ 0 & -2 \end{pmatrix}.\]

$\triangle$

Ejemplo. Ahora obtengamos el plano tangente a una superficie dada en un punto dado. Sea $\mathcal{S}$ la superficie de $\mathbb{R}^{3}$ descrita por la imagen de la función $f(x,y)=(x,y,xy^{2})$. Vamos a determinar el plano tangente a dicha superficie en el punto $(1,1,1)$. Comencemos calculando $Df(1,1)$. En primer lugar calculemos las parciales: \[ \frac{\partial f_{1}}{\partial x}(1,1)=1;\hspace{3cm}\frac{\partial f_{1}}{\partial y}(1,1)=0;\hspace{3cm}\frac{\partial f_{2}}{\partial x}(1,1)=0 \] \[ \frac{\partial f_{2}}{\partial y}(1,1)=1;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,1)=1;\hspace{3cm}\frac{\partial f_{3}}{\partial y}(1,1)=2.\]

Por lo tanto \[ Df(1,1)=\begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 2 \end{pmatrix}.\]

Esta transformación manda al punto $(x,y)$ del plano $\mathbb{R}^2$ al punto\[ \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 2 \end{pmatrix}\begin{pmatrix} x \\ y \end{pmatrix}=\begin{pmatrix} x \\ y \\ x+2y \end{pmatrix}.\]

De modo que el plano centrado en el origen es el conjunto $$H=\{(x,y,x+2y)\in \mathbb{R}^{3}|(x,y)\in \mathbb{R}^{2}\}.$$

Pero este plano debemos todavía trasladarlo por el vector $(1,1,1)$ para que pase por el punto $f(1,1)$. Concluimos entonces que el plano tangente buscado es el conjunto

$$\{(x+1,y+1,x+2y+1)\in \mathbb{R}^{3}|(x,y)\in \mathbb{R}^{2}\}.$$

En la Figura 4 tenemos la en rojo la imagen del campo vectorial de este ejemplo y en verde la del plano tangente, el punto negro es el punto $(1,1,1)$.

$\triangle$

¿Y derivadas parciales implica diferenciabilidad?

Cuando un campo vectorial es diferenciable, existen todas las derivadas parciales de todos sus campos escalares coordenados. El regreso no es cierto. Sin embargo, sí se vale bajo una condición adicional de regularidad.

Definición. Diremos que un campo vectorial $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ es de clase $C^1$ (o simplemente es $C^1$) en un punto $\bar{a}\in S$ si todas las derivadas parciales de todas las funciones componentes de $f$ existen y son continuas en $\bar{a}$. Definimos de manera análoga lo que significa que $f$ sea de clase $C^1$ en todo $S$.

Teorema. Si $f:S\subseteq \mathbb{R}^n\to \mathbb{R}^m$ es un campo vectorial, $\bar{a}\in S$ y $f$ es $C^1$ en $\bar{a}$, entonces $f$ es diferenciable y su derivada $T_a$ tiene como forma matricial a la matriz jacobiana \eqref{eq:jacobiana}.

La prueba de este resultado se hace coordenada a coordenada, aplicando en cada una de ellas el teorema de diferenciabilidad y derivadas parciales para campos escalares que demostramos en la entrada del teorema del valor medio para campos escalares.

Más adelante…

En esta entrada introdujimos el concepto de diferenciabilidad, de derivadas parciales, direccionales y por componente. Además, mostramos que cuando una función es diferenciable, entonces su derivada tiene una forma matricial muy sencilla, dada por las derivadas parciales de las componentes. Esto es nuestra primera señal de que las derivadas y las matrices están muy relacionadas entre sí. Lo que veremos en la siguiente entrada es que esta conexión se sigue dando, y de hecho nos permitirá enunciar de manera muy elegante la regla de la cadena para campos vectoriales: ¡será una multiplicación de matrices!

Después de entender mejor la diferenciabilidad, presentaremos y demostraremos teoremas clásicos e importantes de campos vectoriales: el teorema de la función inversa, y el teorema de la función implícita.

Tarea moral

1. Completa los detalles faltantes del primer ejemplo que dimos de diferenciabilidad.
2. Calcula la matriz jacobiana de la función $g(x,y,z)=(xz,xy,x^{2}y^{2}z^{2})$. Úsala para encontrar la ecuación del espacio tangente a la gráfica en el punto $g(2,1,0)$.
3. Halla el campo vectorial cuya imagen es el plano tangente a la superficie dada por la ecuación $F(x,y)=x^{2}y^{2}+1$ en el punto $(1,1)$. Como ayuda al graficar $F$ en $\mathbb{R}^{3}$ nos dibuja la misma superficie que obtenemos de la imagen del campo vectorial $f(x,y)=(x,y,x^{2}y^{2}+1)$ que esta contenida en $\mathbb{R}^{3}$.
4. Verifica que en efecto las dos definiciones de diferenciabilidad que dimos son equivalentes.
5. Demuestra que si las parciales de cada componente de un campo vectorial existen, y son continuas, entonces la función es diferenciable. Tendrás que seguir la sugerencia dada en la última sección. Después, justifica la igualdad que dimos que escribe a las derivadas direccionales en términos de las parciales.
6. Explica a detalle por qué la expresión a la que llegamos para $f^{\prime}(\bar{a};\bar{y})$ en efecto se puede pensar como el producto matricial mencionado.
7. Encuentra un ejemplo de campo vectorial $f:\mathbb{R}^2\to \mathbb{R}^2$ en donde las derivadas parciales existen en algún punto $\bar{a}$, pero no todas las derivadas direccionales existen.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral III
• Entrada anterior del curso: Formas cuadráticas
• Entrada siguiente del curso: Regla de la cadena para campos vectoriales