Introducción
Gracias a las entradas anteriores ya hemos desarrollado un buen manejo de los números complejos. Sabemos cómo se construyen y cómo hacer operaciones básicas, incluyendo obtener conjugados, la forma polar, sacar normas y elevar a potencias. También hemos aprendido a resolver varias ecuaciones en los complejos: cuadráticas, sistemas lineales y raíces $n$-ésimas. Todo esto forma parte de los fundamentos algebraicos de $\mathbb{C}$. Ahora hablaremos un poco de la exponencial, el logaritmo y trigonometría en los complejos.
Aunque mencionaremos un poco de las motivaciones detrás de las definiciones, no profundizaremos tanto como con otros temas. Varias de las razones para elegir las siguientes definiciones tienen que ver con temas de ecuaciones diferenciales y de análisis complejo, que no se estudian sino hasta semestres posteriores.
Función exponencial compleja
Recordemos que, para un real $y$, definimos $\text{cis}(y)=\cos y + i \sin y$. La función $\text{cis}$ y la exponenciación en los reales nos ayudarán a definir la exponencial compleja.
Definición. Definimos la función $\exp:\mathbb{C}\to \mathbb{C}$ como $$\exp(x+yi)=e^x\text{cis}(y).$$
Ejemplo 1. Se tiene que $$\exp\left(1+\frac{\pi}{2} i\right) = e^1 \text{cis}\left(\frac{\pi}{2}\right) = ei.$$
$\triangle$
Ejemplo 2. Se tiene que $$\exp(\pi i) = e^0\text{cis}(\pi) = (1)(-1)=-1.$$ Como veremos más abajo, esto lo podemos reescribir como la famosa identidad de Euler $$e^{\pi i}+1=0.$$
$\triangle$
Ejemplo 3. Se tiene que $$\exp(2+3i)=e^2\text{cis}(3).$$ Como $\cos(3)$ y $\sin(3)$ no tienen ningún valor especial, esta es la forma final de la expresión.
$\triangle$
Propiedades de la función exponencial compleja
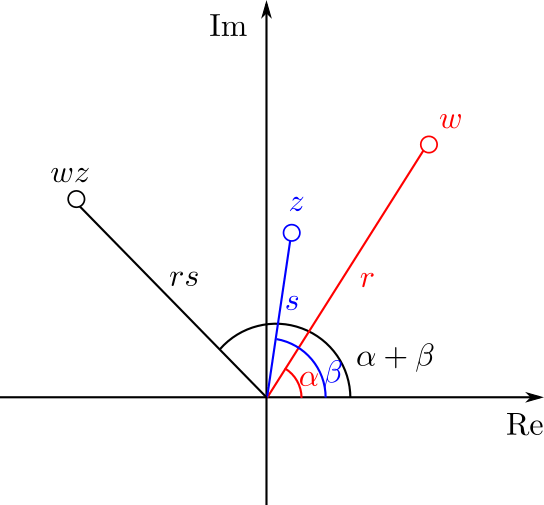
Una buena razón para definir la exponencial así es que si $y=0$, entonces la definición coincide con la definición en los reales: $$\exp(x)=e^x\text{cis}(0)=e^x.$$ Si $x=0$, tenemos que $\exp(iy)=\text{cis}(y)$, de modo que si $w$ tiene norma $r$ y argumento $\theta$, podemos reescribir su forma polar como $$w=r\exp(\theta i),$$ y una forma alternativa de escribir el teorema de De Moivre es $$w^n=r^n\exp(n\theta i).$$
Otra buena razón para definir la exponencial compleja como lo hicimos es que se sigue satisfaciendo que las sumas en la exponencial se abren en productos.
Proposición. Para $w$ y $z$ complejos se tiene que $$E(w+z)=E(w)E(z).$$
Demostración. Escribamos $w=a+bi$ y $z=c+di$ con $a,b,c$ y $d$ reales. Tenemos que
\begin{align*}
\exp(w+z)&=\exp((a+c)+(b+d)i)\\
&=e^{a+c}\text{cis}(b+d).
\end{align*}
Por propiedades de la exponencial en $\mathbb{R}$ tenemos que $e^{a+c}=e^ae^c$. Además, por cómo funciona la multiplicación compleja en términos polares, tenemos que $\text{cis}(b+d)=\text{cis}(b)\text{cis}(d)$. Usando estas observaciones podemos continuar con la cadena de igualdades,
\begin{align*}
&=e^ae^c\text{cis}(b)\text{cis}(d)\\
&=(e^a\text{cis}(b)) (e^c\text{cis}(d))\\
&=\exp(a+bi)\exp(c+di)\\
&=\exp(w)\exp(z).
\end{align*}
$\square$
Como $\exp$ extiende a la exponencial real y se vale abrir las sumas de exponentes en productos, puede ser tentador usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$. Hay que tener cuidado con esta interpretación, pues hasta ahora no hemos dicho qué quiere decir «elevar a una potencia». Cuando lo hagamos, veremos que usar la notación $e^{x+yi}$ sí tiene sentido, pero por el momento hay que apegarnos a la definición.
Hay otras buenas razones para definir la exponencial compleja como lo hicimos. Una muy importante es que es la solución a una ecuación diferencial muy natural. Más adelante, en tu formación matemática, verás esto.
Función logaritmo complejo
Con el logaritmo natural $\ln$ en $\mathbb{R}$ y la multifunción argumento podemos extender el logaritmo a $\mathbb{C}$.
Definición. Definimos la función $L:\mathbb{C}\setminus \{0\} \to \mathbb{C}$ como $$L(z)=\ln \Vert z \Vert + \arg(z) i.$$
Hay que ser un poco más precisos, pues $\arg(z)$ es una multifunción y toma varios valores. Cuando estamos trabajando con logaritmo, lo más conveniente por razones de simetría es que tomemos el argumento en el intervalo $(-\pi,\pi]$. En cursos posteriores hablarás de «otras» funciones logaritmo, y de por qué ésta es usualmente una buena elección.
Ejemplo. Los logaritmos de $i$ y de $-1$ son, respectivamente,
\begin{align*}
L(i)&=\ln \Vert i \Vert + \arg(i) i = \ln(1) + \frac{\pi}{2} i =\frac{\pi}{2} i\\
L(-1)&=\ln \Vert -1 \Vert + \arg(-1) i = \ln(1)+\pi i = \pi i.
\end{align*}
$\triangle$
Propiedades del logaritmo complejo
La función $\exp$ restringida a los números con parte imaginaria en $(-\pi,\pi]$ es invertible y su inversa es $L$. Esto justifica en parte la definición de logaritmo. Demostrar esto es sencillo y queda como tarea moral.
La función $L$ restringida a los reales positivos coincide con la función logaritmo natural, pues para $z=x+0i=x$, con $x>0$ se tiene que $\arg(x)=0$ y entonces $$L(z)=L(x)=\Vert x\Vert+\arg(x)i=x.$$
Como en el caso real, la función logaritmo abre productos en sumas, pero con un detalle que hay que cuidar.
Proposición. Para $w$ y $z$ complejos no $0$, se tiene que $L(wz)$ y $L(w)+L(z)$ difieren en un múltiplo entero de $2\pi i$.
Con la función logaritmo podemos definir potencias de números complejos.
Definición. Para $w,z$ en $\mathbb{C}$ con $w\neq 0$, definimos $$w^z=\exp(zL(w)).$$
Ejemplo. En particular, podemos tomar $w=e$, de donde \begin{align*}e^z&=\exp(zL(e))\\&=\exp(z\ln(e))\\&=\exp(z),\end{align*} de donde ahora sí podemos justificar usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$.
$\square$
Esta definición de exponenciación en $\mathbb{C}$ es buena, en parte, porque se puede probar que se satisfacen las leyes de los exponentes.
Proposición. Para $w, z_1, z_2$ en $\mathbb{C}$, con $w\neq 0$, se cumple que $$z^{w_1+w_2}=z^{w_1}z^{w_2}$$ y que $$(z^{w_1})^{w_2}=z^{w_1w_2}.$$
La demostración es sencilla y se deja como tarea moral.
Funciones trigonométricas complejas
Finalmente, definiremos las funciones trigonométricas en $\mathbb{C}$. Para ello, nos basaremos en la función exponencial que ya definimos.
Definición. Para $z$ cualquier complejo, definimos $$\cos(z)=\frac{e^{iz}+e^{-iz}}{2}$$ y $$\sin(z)=\frac{e^{iz}-e^{-iz}}{2}.$$
Una de las razones por las cuales esta definición es buena es que extiende a las funciones trigonométricas reales. En efecto, si $z=x+0i=x$ es real, entonces $\cos(z)$ es \begin{align*}
\frac{e^{iz}+e^{-iz}}{2}&=\frac{\text{cis}(x)+\text{cis}(-x)}{2}\\
&=\frac{2\cos(x)}{2}\\
&=\cos(x),
\end{align*} y de manera similar para $\sin(z)$.
Las funciones trigonométricas en $\mathbb{C}$ siguen cumpliendo varias propiedades que cumplían en $\mathbb{R}$.
Proposición. Para $w$ y $z$ complejos, se tiene que
\begin{align*}
\cos(w+z)=\cos(w)\cos(z)-\sin(w)\sin(z)\\
\sin(w+z)=\sin(w)\cos(z)+\sin(z)\cos(w).
\end{align*}
Demostración. Procedemos por definición. Tenemos que
\begin{align*}
4&\cos(w)\cos(z)\\
&=(e^{iw}+e^{-iw})(e^{iz}+e^{-iz})\\
&=(e^{i(w+z)}+e^{i(w-z)}+e^{i(z-w)}+e^{i(-z-w)})
\end{align*}
y que
\begin{align*}
4&\sin(w)\sin(z)\\
&=(e^{iw}-e^{-iw})(e^{iz}-e^{-iz})\\
&=(e^{i(w+z)}-e^{i(w-z)}-e^{i(z-w)}+e^{i(-z-w)}),
\end{align*}
de modo que
\begin{align*}
4(\cos(w)&\cos(z)-\sin(w)\sin(z))\\
&=2(e^{i(w+z)}+e^{-i(w+z)})\\
&=4\cos(w+z).
\end{align*}
Dividiendo entre $4$ ambos lados de la igualdad, obtenemos la primer identidad. La segunda se demuestra de manera análoga, y queda como tarea moral.
$\square$
Más adelante…
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Determina los valores de $\exp(3+\frac{3\pi}{4}i)$ y de $L(-i)$.
- Muestra que para $z$ con parte imaginaria en $(-\pi,\pi]$ se tiene que $L(\exp(z))=z$.
- Determina el valor de $(1+i)^{1+i}$.
- Muestra las leyes de los exponentes para la exponenciación en $\mathbb{C}$.
- Determina el valor de $\sin(i)$ y de $\cos(1+i)$.
- Muestra la identidad de seno de la suma de ángulos en $\mathbb{C}$.
- Investiga qué otras propiedades de las funciones trigonométricas reales se extienden al caso complejo.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Problemas de fórmula de De Moivre y raíces n-ésimas
- Entrada siguiente del curso: Problemas de exponencial, logaritmo y trigonometría en $\mathbb{C}$
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»