Introducción

En entradas anteriores de esta sección hablamos de propiedades aritméticas de números enteros. En esta entrada veremos varias de las propiedades aritméticas de los números complejos y cómo se pueden usar para resolver problemas, incluso aquellos en los que los números complejos no están mencionados de manera explícita en el enunciado.

Distintas formas de los números complejos

La forma más común en la que pensamos en números complejos es en su forma rectangular, en donde un complejo se escribe de la forma $z=a+bi$, en donde $a$ y $b$ son números reales y pensamos a $i$ como un número tal que $i^2=-1$. A $a$ le llamamos la parte real y a $b$ la parte imaginaria.

Podemos colocar al complejo $z=a+ib$ en el plano cartesiano, identificándolo con el punto $(a,b)$. De aquí, la forma polar del complejo es $z=r(\cos \theta +i\sin \theta )$, en donde $r$ es la norma $|z|:=\sqrt{a^2+b^2}$ y si $z\ne 0$, $\theta$ es el argumento, que es el ángulo en el sentido antihorario desde el origen entre el eje horizontal y el punto $(a,b)$. Si $z=0+i0=0$, no definimos el argumento.

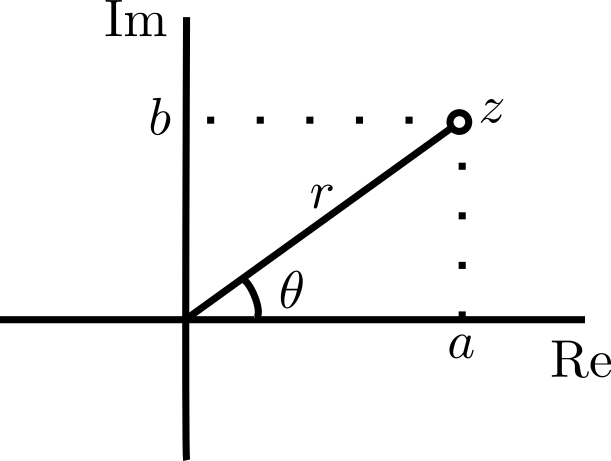
Así como le hacíamos en el caso de trabajar con módulos, a veces conviene pensar que el argumento es el único ángulo en $[0,2\pi )$ que cumple lo anterior. En otras ocasiones, conviene pensar al argumento como a veces que es la clase de todos los ángulos módulo $2\pi$.

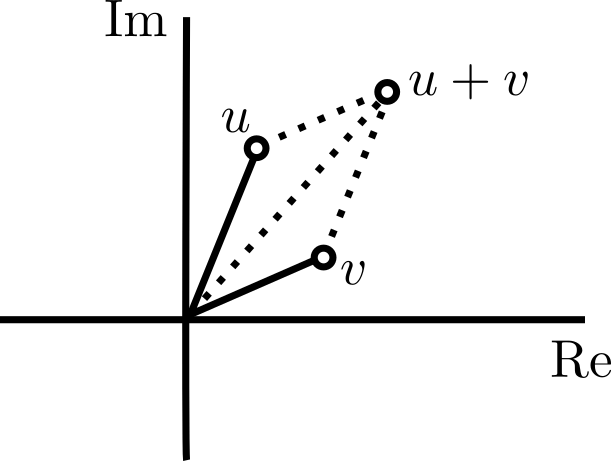
Cuando tenemos a complejos $w=a+ib$ y $z=c+id$ en forma rectangular, su suma $w+z=(a+c)+i(b+d)$ corresponde geométricamente a encontrar la diagonal del paralelogramo definido por $(a,b)$, $(c,d)$ y el origen, pues corresponde justo al punto $(a+c,b+d)$.

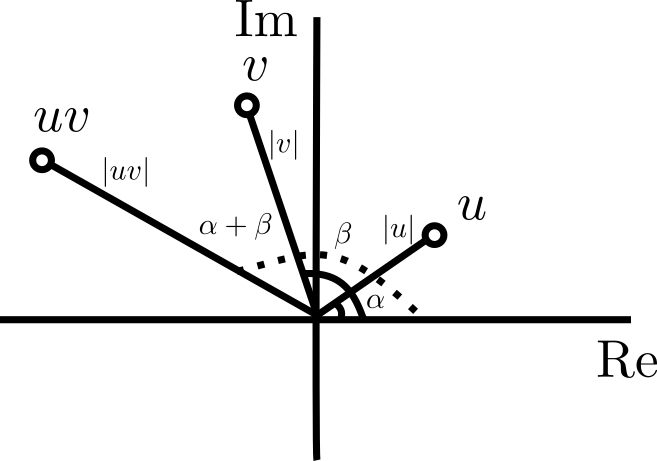
Su multiplicación $wz$ en forma rectangular es $(ac-bd)+(ad+bc)i$, que geométricamente no es tan claro que sea.

La forma exponencial $z=r{e}^{i\theta }$ es simplemente una forma de abreviar a la forma polar, pues por definición $e^{i\theta }=\cos \theta +i\sin \theta$. En forma exponencial, el producto es más sencillo de entender.

Ejercicio. Demuestra lo siguiente:

• Muestra que la norma es multiplicativa, es decir, que para complejos $r$ y $s$ se tiene que $|rs|=|r||s|$.
• Muestra que $e^{i\alpha }{e}^{i\beta }=e^{i(\alpha +\beta )}$.

Sugerencia. Para el primer punto, haz las cuentas usando la forma rectangular. Para el segundo punto, escribe las definiciones de todos los términos en forma polar. Haz las multiplicaciones en el lado izquierdo y usa las fórmulas trigonométricas para sumas de ángulos.

Por el ejercicio anterior, si tenemos a los complejos en forma polar $w=r{e}^{i\alpha }$, $z=s{e}^{i\beta }$, entonces el producto es $wz=rs{e}^{i(\alpha +\beta )}$, de modo que el producto corresponde al complejo con el producto de normas y suma de argumentos. En ocasiones esto nos permite plantear algunos problemas geométricos en términos de números complejos.

Aplicaciones de aritmética de complejos

Veamos dos aplicaciones de la teoría anterior a problemas que no mencionan en el enunciado a los números complejos.

Problema. Sean $a$ y $b$ enteros. Muestra que el número $(a^2+b^2{)}^n$ se puede expresar como la suma de los cuadrados de dos números enteros.

Podría ser tentador usar el binomio de Newton para elevar el binomio a la $n$-ésima potencia. Sugerimos que intentes esto para darte cuenta de las dificultades que presenta.

Sugerencia pre-solución. Escribe a $a^2+b^2$ como el cuadrado de la norma de un complejo y usa que es multiplicativa.

Solución. El número $r=a^2+b^2$ es la norma al cuadrado del número complejo $z=a+ib$. Entonces, el número $r^n=(a^2+b^2{)}^n$ es la norma al cuadrado del número complejo $z^n=(a+ib{)}^n$. Pero al desarrollar $(a+ib{)}^n$ obtenemos únicamente a $i$, potencias de $a$ y de $b$, y coeficientes binomiales. De modo que $z^n=(a+ib{)}^n=c+id$ con $c$ y $d$ enteros (aquí estamos usando notación adecuada: no es necesario saber quienes son, sólo que son enteros). Así, $r^n=c^2+d^2$ con $c$ y $d$ enteros.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Veamos ahora un ejemplo de geometría. Este problema es posible resolverlo de muchas formas, pero notemos que los números complejos nos dan una forma de hacerlo de manera algebraica de manera inmediata.

Problema. En la siguiente figura hay tres cuadrados de lado $1$ pegados uno tras otro. Determina la suma de los ángulos marcados con $\alpha$ y $\beta$.

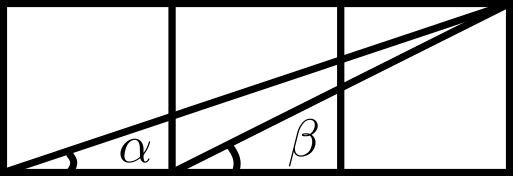
Sugerencia pre-solución. El problema pide determinar una suma de ángulos, así que conviene pensar esta suma de ángulos como el ángulo del producto de dos complejos. Haz tu propia figura, pero ahora sobre el plano complejo.

Solución. El ángulo $\alpha$ es igual al argumento del complejo $2+i$ y el ángulo $\beta$ es igual al argumento del complejo $3+i$. De esta forma, $\alpha +\beta$ es igual al argumento del complejo $(2+i)(3+i)=(6-1)+(2+3)i=5+5i$. Este complejo cae sobre la recta $\text{Re}(z)=\text{Im}(z)$, de modo que su argumento es $\pi /4$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Este problema también se puede resolver de (numerosas) maneras geométricas, que puedes consultar en este video.

Fórmula de De Moivre

El siguiente teorema se puede demostrar por inducción sobre $n$.

Teorema (fórmula de De Moivre). Para cualquier entero $n$ y ángulo $\theta$ se tiene que $$(\cos \theta +i\sin \theta {)}^n=\cos (n\theta )+i\sin (n\theta ).$$ Dicho de otra forma, en términos de la forma exponencial, se vale usar la siguiente ley de los exponentes $$(e^{\theta i}{)}^n=e^{(n\theta )i}.$$

La fórmula de De Moivre es otra herramienta que ayuda a resolver problemas de números reales enunciándolos en términos trigonométricos. El truco consiste en:

1. Tomar una expresión real que queramos entender.
2. Identificarla como la parte real o imaginaria de una expresión compleja.
3. Usar la aritmética de números complejos para entender la expresión compleja.
4. Regresar lo que entendamos a los reales.

Veamos un par de ejemplos, relacionados con funciones trigonométricas. Comenzamos con una fórma de encontrar la fórmula para el coseno de cinco veces un ángulo.

Problema. Sea $\theta \in [0,2\pi )$. Expresa a $\cos 5\theta$ en términos de $\cos \theta$.

Sugerencia pre-solución. Identifica a $\cos 5\theta$ como la parte real de un número complejo. Inspírate en la fórmula de De Moivre. Usa binomio de Newton.

Solución. Por la fórmula de De Moivre, $\cos 5\theta$ es la parte real del complejo $(\cos \theta +i\sin \theta {)}^5$, así que calculemos quién es exactamente este número usando binomio de Newton. Para simplificar la notación, definimos $a=\cos \theta$ y $b=\sin \theta$. Tenemos que

$$\begin{array}{rl}(a+ib{)}^5& =a^5+5a^4(bi)+10a^3(ib{)}^2+10a^2(ib{)}^3+5a(ib{)}^4+(ib{)}^5\\ & =(a^5-10a^3{b}^2+5a{b}^4)+(5a^{4}b-10a^2{b}^3+b^5)i.\end{array}$$

Además, por la identidad pitagórica recordemos que $a^2+b^2=1$, de donde $b^2=1-a^2$, de modo que la parte real de la expresión anterior es $$a^5-10a^3(1-a^2)+5a(1-2a^2+a^4),$$ que agrupando es $$16a^5-20a^3+5a.$$ Recordando que $a$ es $\cos \theta$, obtenemos la fórmula final $$\cos 5\theta =16{\cos }^5\theta –20{\cos }^3\theta +5\cos \theta .$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Raíces de la unidad

En muchos problemas se utilizan las raíces de la ecuación $x^n=1$.

Teorema. Sea $n\ge 1$ un entero. Las ecuación $x^n=1$ tiene $n$ soluciones complejas, que en el plano complejo forman los vértices del $n$-ágono regular con centro en $0$ y tal que uno de sus vértices es $1$. Si $\omega$ es la raíz de menor argumento positivo, entonces estas soluciones son $1,\omega ,{\omega }^2,\dots ,{\omega }^{n-1}$.

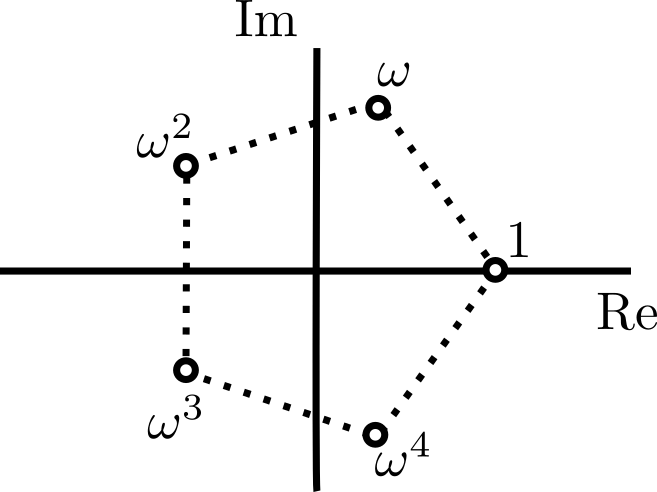
A estas soluciones les llamamos las raíces $n$-ésimas de la unidad. Notemos que ${\omega }^n=1$, y que en general si escribimos a un entero $m$ usando el algoritmo de la división como $m=qn+r$, entonces ${\omega }^m={\omega }^r$. ¡Los productos de raíces de la unidad se comportan como los elementos de ${\mathbb{Z}}_n$ bajo suma módulo $n$!

Proposición. Sea $n\ge 2$ un entero. La suma de las $n$ raíces $n$-ésimas de la unidad es $0$ y su producto es $1$.

La proposición anterior nos permite, en ocasiones, «filtrar» ciertas expresiones algebraicas. A continuación presentamos un ejemplo, que retomamos de los primeros ejemplos que vimos, cuando estábamos aprendiendo la heurística de encontrar un patrón.

Problema. Determina el valor de la suma $$(\genfrac{}{}{0ex}{}{100}{0})+(\genfrac{}{}{0ex}{}{100}{3})+(\genfrac{}{}{0ex}{}{100}{6})+\dots +(\genfrac{}{}{0ex}{}{100}{99}).$$

Sugerencia pre-solución. Si no recuerdas lo que debería salir, vuelve a experimentar con los primeros valores, para cuando en vez de usar $100$ se usan números más chiquitos. Para entender mejor el patron, generaliza el problema, y en vez de sólo tener múltiplos de $3$ abajo, explora también qué sucede cuando tienes los números que dejan residuo $0$, $1$ o $2$ módulo $3$.

Ya que recuerdes la fórmula que queremos, considera una raíz cúbica $\omega$ de la unidad distinta de $1$. Calcula $(1+1{)}^{100}$, $(1+\omega {)}^{100}$ y $(1+{\omega }^2{)}^{100}$ usando el binomio de Newton y aprovechando que toda potencia de $\omega$ es $1$, $\omega$ u ${\omega }^2$ para simplificar la notación.

Solución. Sea $\omega$ una raíz cúbica de la unidad distinta de $1$. Tenemos que ${\omega }^3=1$ y que $1+\omega +{\omega }^2=0$. De este modo, podemos usar $\omega$ y el binomio de Newton para calcular las siguientes expresiones

$$\begin{array}{rl}(1+1{)}^{100}& =(\genfrac{}{}{0ex}{}{100}{0})+(\genfrac{}{}{0ex}{}{100}{1})+(\genfrac{}{}{0ex}{}{100}{2})+(\genfrac{}{}{0ex}{}{100}{3})+\dots \\ (1+\omega {)}^{100}& =(\genfrac{}{}{0ex}{}{100}{0})+(\genfrac{}{}{0ex}{}{100}{1})\omega +(\genfrac{}{}{0ex}{}{100}{2}){\omega }^2+(\genfrac{}{}{0ex}{}{100}{3})+\dots \\ (1+{\omega }^2{)}^{100}& =(\genfrac{}{}{0ex}{}{100}{0})+(\genfrac{}{}{0ex}{}{100}{1}){\omega }^2+(\genfrac{}{}{0ex}{}{100}{2})\omega +(\genfrac{}{}{0ex}{}{100}{3})+\dots \end{array}$$

¿Qué sucede al sumar las tres expresiones? En el lado derecho, cada vez que $m$ es un múltiplo de $3$, tenemos $3(\genfrac{}{}{0ex}{}{100}{m})$, y cada vez que $m$ no es un múltiplo de $3$, tenemos $$(1+\omega +{\omega }^2)(\genfrac{}{}{0ex}{}{100}{m})=0.$$ ¡Se filtran exactamente los coeficientes binomiales con parte inferior múltiplo de $3$! Así, tres veces la suma que buscamos es igual a $$2^{100}+(1+\omega {)}^{100}+(1+{\omega }^2{)}^{100}.$$

Esta ya es una expresión suficientemente cerrada, pero podemos simplificar todavía más:

$$\begin{array}{rl}(1+\omega {)}^{100}& =(-{\omega }^2{)}^{100}={\omega }^{200}={\omega }^2\\ (1+{\omega }^2{)}^{100}& =(-\omega {)}^{100}=\omega \\ (1+\omega {)}^{100}+(1+{\omega }^2{)}^{100}& ={\omega }^2+\omega =-1.\end{array}$$

Así, la expresión que queremos es $\frac{2^{100}-1}{3}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más ejemplos

Puedes ver más ejemplos del uso de esta teoría en la Sección 3.5 del libro Problem Solving through Problems de Loren Larson.