Archivo de la etiqueta: imagen

Teoría de los Conjuntos I: Funciones

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

Esta sección estará dedicada a un tipo de relaciones a las que llamaremos funciones. Este tema será de gran importancia pues utilizaremos funciones con mucha frecuencia a partir de ahora, es por ello que dedicaremos una serie de entradas para tratarlas. En esta primera parte abordaremos la definición de función, algunas de sus propiedades y ejemplos.

¿Qué es una función?

La motivación de la definición de función es la siguiente. Tomemos $A$ y $B$ conjuntos. Queremos poder asignar a cualquier elemento de $A$ uno y sólo un elemento de $B$, de manera que inequívocamente para cada $a\in A$ podamos hablar del elemento que se le asignó en $B$. Las relaciones ayudan a emparejar elementos de $A$ y $B$, pero podemos tener dos problemas 1) Que no todo elemento de $A$ esté en alguna pareja de la relación o 2) Que algún elemento de $A$ quede emparejado con más de un elemento de $B$. Por ello, la definición de función queda establecida de la siguiente manera.

Definición. Sean $A$ y $B$ conjuntos. Una función $f$ de $A$ en $B$ es una relación $f\subseteq A\times B$ que satisface:

  1. Para cualquier $x\in A$, existe $y\in B$ tal que $(x,y)\in f$.
  2. Para cualesquiera $a\in A$ y $b,c\in B$, si $(a,b)\in f$ y $(a,c)\in f$, entonces $b=c$.

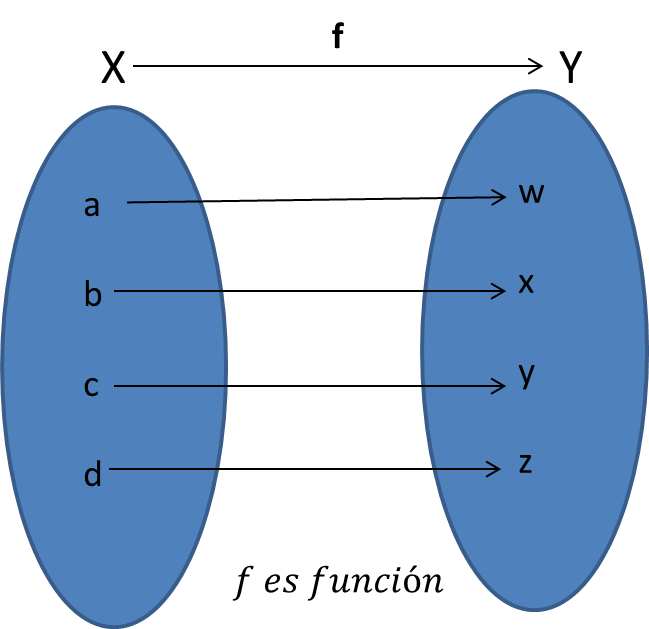
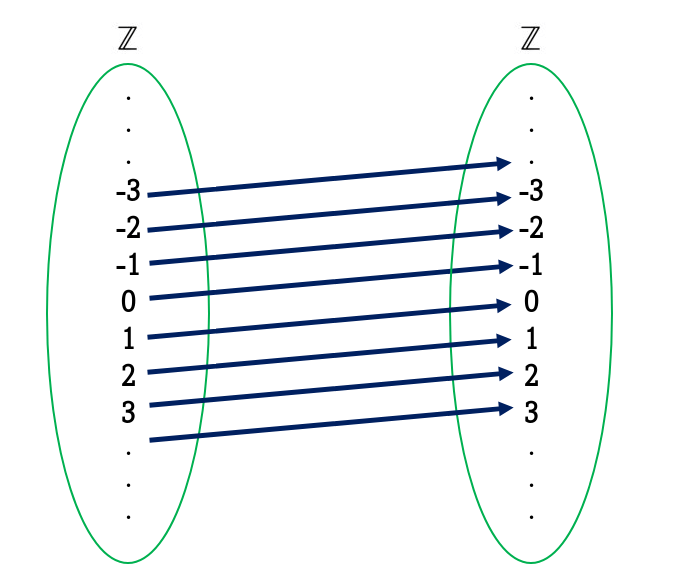
La definición anterior nos dice que dados dos conjuntos y una relación $R$ de $A$ en $B$, esta es una función si y sólo si cada elemento del $dom(R)$ esta relacionado con uno y sólo uno de $B$. Como se muestra en la siguiente imagen:

Para abordar la definición desde otra perspectiva revisaremos el siguiente ejemplo que nos muestra que no toda relación es función.

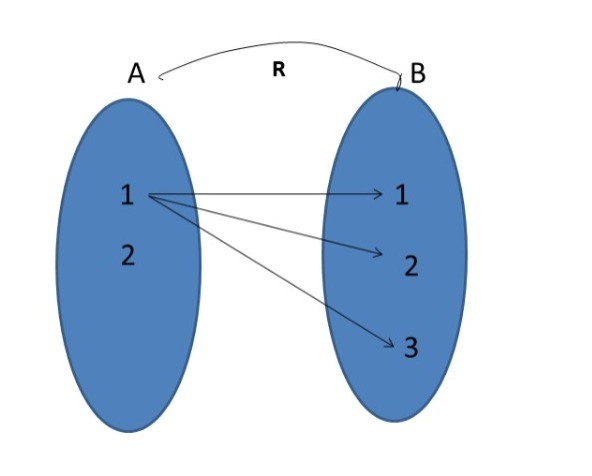
Ejemplo.

Sea $A=\set{1,2}$ y $B=\set{1,2,3}$. Sea $R$ una relación de $A$ en $B$ dada por $R=\set{(1,1), (1,2), (2,1)}$.

Resulta que $R$ no es función pues $(1,1)\in R$ y $(1,2)\in R$, sin embargo no es cierto que $1=2$.

$\square$

Ahora veamos el ejemplo de una relación que si es función.

Ejemplo.

Sea $A=\set{1,2,3}$ y $B=\set{1,2}$. Sea $f$ una relación de $A$ en $B$ dada por $f=\set{(1,1), (2,1), (3,1)}$.

En este ejemplo tenemos que $f$ es función pues cada elemento de $A$ está relacionado con uno y sólo uno de $B$, es decir, para cualesquiera $(a,b)\in f$ y $(a,c)\in f$ se cumple que $b=c$.

$\square$

Después de revisar estos ejemplos es importante mencionar que aunque no toda relación es función, siempre ocurrirá que una función es una relación, este último hecho se sigue de la definición de función.

Función vacía

Observa que si $X=\emptyset$ y $Y$ es un conjunto cualquiera, entonces el conjunto vacío es una función de $X$ en $Y$. En la sección de relaciones vimos que el conjunto vacío en efecto es una relación, nos resta ver que para cualesquiera $(a,b)\in f$ y $(a,c)\in f$ se cumple que $b=c$, sin embargo este enunciado se cumple por un argumento por vacuidad.

Por lo tanto, la relación vacía es función.

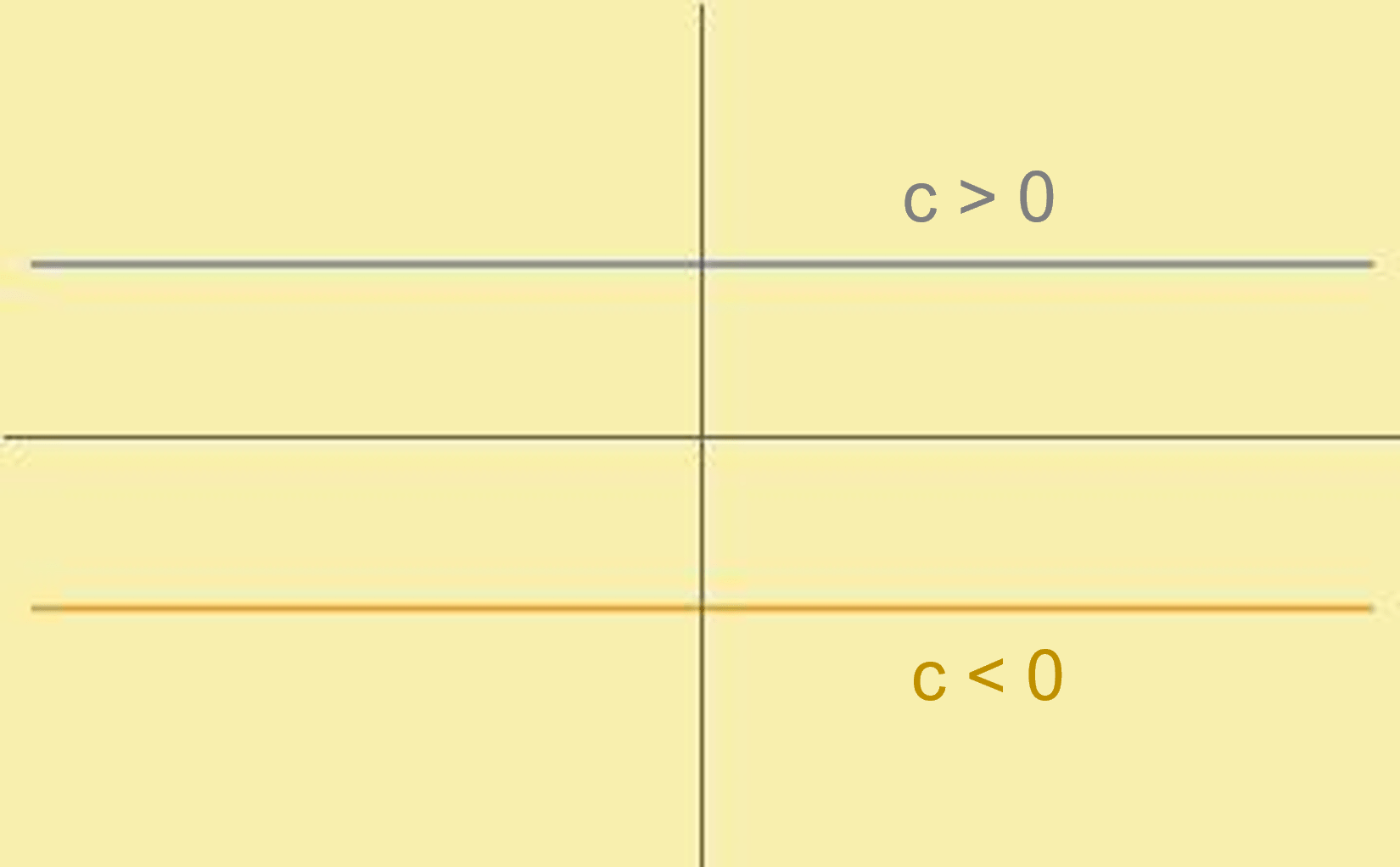
Función constante

Sean $X$, $Y$ conjuntos y $c\in Y$. Definimos la función $f_c$ de $X$ en $Y$ como $f_c=X\times \{c\}$. Nuestra función se verá de la siguiente forma:

Función identidad

Sea $X$ un conjunto, la relación identidad es función. Recordemos que la relación identidad $Id_X$ esta definida como sigue:

$Id_X=\set{(x,y)\in X\times Y: x=y}$

Dado que para cualesquiera $(x,y)\in Id_X$ y $(x,w)\in Id_X$ tenemos que $x=y$ y $x=w$ por definición de la relación $Id_X$, por lo tanto, $y=w$ y así concluimos que $Id_X$ es función.

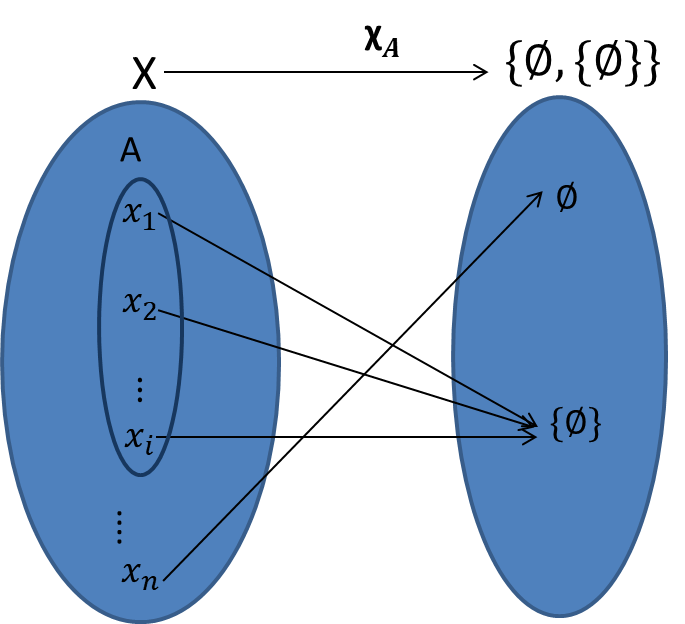
Función característica

Sean $A$ y $X$ conjuntos tales que $A\subseteq X$, definimos a la función característica $\chi_A$ de $A$ en $\set{\emptyset, \set{\emptyset}}$ como $\chi_A=\{(x, \{\emptyset\}):x\in A \}\cup \{(x, \emptyset):x\in X\setminus A\}$.

Función inclusión

Sea $X$ un conjunto cualquiera, definimos a la función inclusión como el siguiente conjunto:

$\iota_A= \set{(x,x):x\in A}$.

Debido a que las funciones serán recurrentes en las entradas subsecuentes, es necesario adoptar alguna notación para estos conceptos. Dada una relación $f$ de $A$ en $B$ utilizaremos la notación $f:A\to B$ para indicar que $f$ es una función. Ahora bien, si $f:A\to B$ y $x\in A$ y $y\in B$, escribiremos $f(x)=y$ si $(x,y)\in f$.

Dominio e imagen

De manera similar que con las relaciones trataremos las definiciones de dominio, imagen e imagen inversa, sin embargo ahora lo haremos para funciones.

Definición. Sea $f$ una función de A en B, definimos el dominio de la $f$ como:

$dom(f)=\set{x\in A:\exists y\in B(f(x)=y)}$.

Ejemplo.

Sea $A=\set{1,2,3,4}$ y $B=\set{1,2,3,4}$. Sea $f:A\to B$ una función dada por el conjunto $f=\set{(1,1), (2,2), (3,3), (4,4)}$.

Tenemos que,

$dom(f)=\set{x\in \set{1,2,3,4}:\exists y\in \set{1,2,3,4}(f(x)=y)}=\set{1,2,3,4}$.

$\square$

Definición. Sea $f$ una función de A en B, definimos la imagen de la función $r$ como:

$im(f)=\set{y\in B:\exists x\in A(f(x)=y)}$.

Ejemplo.

Sea $A=\set{1,2,3,4}$ y $B=\set{1}$. Sea $f:A\to B$ una función dada por $f(x)=1$ para todo $x\in A$.

Tenemos que,

$im(f)=\set{y\in B: \exists x(f(x)=y)}=\set{1}$.

$\square$

Definición. Sea $f$ una función de $A$ en $B$ y sea $D\subseteq A$. Definimos la imagen de $D$ bajo la función $f$ como el conjunto:

$f[D]=\set{f(x)\in B: \exists x\in D(f(x)=y)}$.

Ejemplo.

Sea $A=\set{1,2,3,4}$ y $B=\set{2,4,6,8}$. Sea $f:A\to B$ una función dada por $f(x)=2x$ para todo $x\in A$. Sea $A’=\set{2,4}\subseteq A$.

Tenemos que,

$f[A’]=\set{f(x)\in B: \exists x\in A'(f(x)=y)}=\set{4,8}$.

$\square$

Definición. Sea $f$ una función de $A$ en $B$ y sea $B’\subseteq B$. Definimos la imagen inversa de $B’$ bajo la función $f$ como el conjunto:

$f^{-1}[B’]=\set{x\in A: \exists y\in B'(f(x)=y)}$.

Ejemplo.

Sea $A=\set{1,2,3,4}$ y $B=\set{2,4,6,8}$. Sea $f:A\to B$ una función dada por $f(x)=2x$ para todo $x\in A$. Sea $B’=\set{2,4}\subseteq B$.

Tenemos que,

$f^{-1}[B’]=\set{x\in A: \exists y\in B'(f(x)=y)}=\set{1,2}$.

$\square$

Tarea moral

Los siguientes ejercicios te ayudarán a reforzar los conceptos de función, dominio e imagen.

  • Sea $f$ una función de $\set{1,2}$ en $\set{2.4,5}$ dada por $f=\set{(1,2), (2,4)}$. Describe al dominio y la imagen de $f$.
  • Sean $A=\set{1,2,3,4,5,6,7,8,9}$ y $B=\set{1,2,3,4,5,6,7}$ conjuntos. Responde si las siguientes relaciones son o no funciones:
    1. $f_1=\set{(1,1), (1,2), (2,1), (3,4)}$,
    2. $f_2=\set{(1,1), (2,2), (3,3), (4,4) (5,5)}$,
    3. $f_3=\set{(1,1), (2,1), (3,1), (4,1), (5,1)}$.

Más adelante…

La siguiente sección estará dedicada a hablar acerca de algunas de las propiedades que tiene la imagen de un conjunto bajo una función respecto a la unión, la intersección y la diferencia. Además hablaremos acerca de la composición de funciones, en esta parte retomaremos el concepto de composición de relaciones.

Entradas relacionadas

Teoría de los Conjuntos I: Relaciones

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

En esta nueva entrada veremos el concepto de relación, para lo cual es necesario tener fresco el concepto de producto cartesiano. Así mismo, definiremos nuevos conjuntos a partir de una relación, como lo son el dominio, la imagen de una relación, la imagen de un conjunto bajo una relación y el concepto de relación inversa. Concluiremos esta entrada definiendo a la imagen inversa de un conjunto bajo una relación.

Relación

Definición. Sean $A$ y $B$ conjuntos. Una relación $R$ de $A$ en $B$ es un subconjunto de $A\times B$. A $A$ le llamamos el dominio de la relación y a $B$ el codominio.

Si $A=B$ diremos que $R$ es una relación en $A$.

Ejemplo 1.

Sea $A=\set{\emptyset,\set{\emptyset}}$ y $B=\set{\emptyset, \set{\set{\emptyset}}}$ y definimos $R$ como:

$R=\set{(\emptyset, \emptyset), (\emptyset, \set{\set{\emptyset}})}$.

Dado que $A\times B=\set{(\emptyset,\emptyset), (\emptyset, \set{\set{\emptyset}}), (\set{\emptyset}, \emptyset), (\set{\emptyset}, \set{\set{\emptyset}})}$ y $R\subseteq A\times B$ decimos que $R$ es una relación de $A$ en $B$.

$\square$

Ejemplo 2.

Sea $A=\set{1,2}$ y $B=\set{1,2,3}$. Definimos $S=\set{(1,1), (1,2), (1,3)}$. Tenemos que $S$ es una relación de $A$ en $B$. En efecto, esto sucede pues $S=\set{(1,1), (1,2), (1,3)}\subseteq A\times B$, ya que $A\times B=\set{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)}$.

Podemos representar a $S$ mediante el siguiente diagrama. Del lado izquierdo hemos puesto al dominio $A$. Del lado derecho al codominio $B$. Para cada pareja $(a,b)$ de la relación, hemos puesto una flecha de $a$ a $b$.

Imagen de relación del ejemplo 2

$\square$

Definición. Si $(x,y)\in R$ con $R$ relación, decimos que $x$ está relacionado con $y$ mediante $R$ (o simplemente que $x$ está relacionado con $y$ si por el contexto es claro quién es $y$) y lo denotaremos como $xRy$.

Si retomamos el Ejemplo 1 podemos decir que $\emptyset R\emptyset$ y $\emptyset R\set{\set{\emptyset}}$.

A partir del Ejemplo 2 podemos decir que $1S1$, $1S2$ y $1S3$.

Relaciones relevantes

A continuación hablaremos de algunos ejemplos de relaciones que nos serán de utilidad más adelante.

  1. Relación vacía.
    Si $R=\emptyset$, entonces $R$ será llamada la relación vacía. Esto tiene sentido pues $\emptyset\subseteq A\times B$ para cualesquiera $A$ y $B$ conjuntos.
  2. Relación identidad.
    Sea $A$ un conjunto cualquiera. Definimos la relación identidad en $A$ como:
    $$Id_{A}=\set{(a,a):a\in A}.$$
    Notamos que $Id_{A}\subseteq A\times A$ pues para cualquier $(x,y)\in Id_{A}$ se tiene que $x=y$ con $x,y\in A$, lo que significa que $(x,y)\in A\times A$.
  3. Relación de pertenencia.
    Sea $A$ un conjunto. Definimos a la relación de pertenencia en $A$ como el siguiente conjunto:
    $$\in_{A}=\set{(a,b): a\in A,\ b\in A,\ a\in b}.$$
  4. Relación de contención.
    Sea $A$ un conjunto. Definimos a la relación de contención en $A$ como el siguiente conjunto:
    $$\subseteq_{A}=\set{(a,b): a\in A,\ b\in A,\ a\subseteq b}.$$

Dominio de una relación

Ya que hemos definido el concepto de relación, a continuación definiremos al dominio de una relación.

Definición. Sea $R$ una relación de $A$ en $B$. Definimos el dominio de la relación como:

$\text{dom}(R)=\set{x\in A:\exists y\in B( (x,y)\in R)}$.

Ejemplo.

Sean $A=B=\set{1,2}$. Definimos $R=\set{(1,2), (1,1), (2,2)}\subseteq A\times B$. Tenemos que $\text{dom}(R)=\set{1,2}$ pues para $1\in A$ existe, digamos, $1\in B$ tal que $(1,1)\in R$ y para $2\in A$ existe $2\in B$ tal que $(2,2)\in R$.

$\square$

Imagen de una relación

A continuación vamos a definir lo análogo al dominio activo, pero para el codominio. Le daremos un nombre al subconjunto de elementos del codominio que sí participan en la relación.

Definición. Sea $R$ una relación de $A$ en $B$. Definimos la imagen de $R$ como el conjunto

$\text{im}(R)=\set{y\in B:\exists x\in A( (x,y)\in R)}$.

Ejemplo.

Sean $A=B=\set{1,2}$. Definimos $R=\set{(1,2), (2,2)}\subseteq A\times B$.

Tenemos que $\text{im}(R)=\set{2}$ pues para $2\in B$ existe, digamos $2\in A$ tal que $(2,2)\in R$. Sin embargo, $1\not \in \text{im}(R)$ pues $R$ no tiene ninguna pareja de la forma $(x,1)$ con $x\in A$.

$\square$

Imagen de un conjunto bajo una relación

A veces queremos preguntarnos por los elementos del codominio que participan en la relación, pero sólamente con ciertos elementos del dominio. La siguiente definición establece esto.

Definición. Sea $R$ una relación de $A$ en $B$. Sea $C\subseteq A$. Definimos a la imagen de $C$ bajo $R$ como el el conjunto

$R[C]=\set{y\in B: \exists x\in C (xRy)}$.

Ejemplo.

Sean $A=\set{1,2}$ y $B=\set{1,2,3,4}$ conjuntos. Sea $R=\set{(1,1), (1,3), (2,1), (2,2), (2,4)}$, la cual es una relación de $A$ en $B$. Tomemos $C=\set{1}\subseteq A$. Tenemos que

$R[C]=\set{y\in \{1,2,3,4\}:\exists x\in\{1\}(xRy)}= \set{1,3}$.

$\square$

Relación inversa

Para cerrar esta entrada, introduciremos un concepto más: el de relación inversa.

Definición. Sean $A$ y $B$ conjuntos. Sea $R$ una relación de $A$ en $B$. Definimos la relación inversa de $R$ como la relación $R^{-1}$ de $B$ en $A$ definida como sigue:

$R^{-1}=\set{(b,a): (a,b)\in R}$.

Notemos que la relación inversa intercambia el orden de las entradas de las parejas ordenadas que son elementos de la relación $R$.

Ejemplo.

Sea $A=\set{\emptyset}$ y $B=\set{\emptyset, \set{\emptyset}}$ y definimos $R$ como:

$R=\set{(\emptyset, \emptyset), (\emptyset,\set{\emptyset})}.$

Tenemos que

$R^{-1}=\set{(\emptyset, \emptyset), (\set{\emptyset}, \emptyset)}.$

En efecto, como $(\emptyset, \emptyset)\in R$ tendremos que $(\emptyset, \emptyset)\in R^{-1}$ y como $(\set{\emptyset}, \emptyset)\in R$ tendremos que $(\emptyset, \set{\emptyset})\in R^{-1}$.

$\square$

Proposición. Sea $R$ una relación. Se cumple que $(R^{-1})^{-1}=R$.

Demostración.

Tenemos que

\begin{align*}
(R^{-1})^{-1}&=\set{(x,y): (y,x)\in R^{-1}}\\
&= \set{(x,y): (x,y)\in R}\\
&= R.
\end{align*}

$\square$

Imagen inversa de un conjunto bajo una relación

Definición. Sea $R$ una relación de $A$ en $B$. Sea $C\subseteq B$. Definimos a la imagen inversa de $C$ bajo $R$ como el el conjunto

$R^{-1}[C]=\set{x\in A: \exists y\in C (xRy)}$.

Ejemplo.

Sean $A=\set{1,2}$ y $B=\set{1,2,3,4}$ conjuntos. Si $R=\set{(1,1), (1,3), (2,1), (2,2), (2,4)}$ es una relación de $A$ en $B$, entonces $R^{-1}=\{(1,1), (1,2), (2,2), (3,1), (4,2)\}$. Tomemos $C=\set{1}\subseteq B$. Tenemos que

$R^{-1}[C]=\set{x\in \{1,2\}:\exists y\in\{1\}(xRy)}= \set{1,2}$.

$\square$

Tarea moral

La siguiente lista de ejercicios te permitira reforzar los conceptos de relación, dominio activo e imagen.

  1. Si $R$ es la relación vacía, encuentra el dominio activo y la imagen de $R$.
  2. Para $R$ es la relación identidad de $A$, encuentra el dominio y la imagen de $R$.
  3. Sea $R=\set{(1,2), (3,4)}$ una relación de $A=\set{1,2,3}$ en $B=\set{1,2,3,4}$. Encuentra el dominio y la imagen de $R$. Además, escribe al conjunto $R^{-1}$.
  4. Si $R$ es la relación identidad de $A$, describe quién es $R^{-1}$.

Más adelante…

En la siguiente entrada continuaremos con el tema de relaciones. Esta vez trataremos el tema de composición de relaciones. Definiremos a la composición de relaciones como una relación que se construye a partir de al menos dos relaciones cuyos dominios y codominios tienen ciertas propiedades en común.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición

Por Guillermo Oswaldo Cota Martínez

2 respuestas

Introducción

Habiendo hablado del producto cartesiano, ya tenemos los ingredientes para irnos acercando a la definición de función, pero antes de hablar de ellas, tenemos que hablar de relaciones y de algunos de sus conceptos. En esta entrada introduciremos el concepto de relación, dominio, codominio y composición entre relaciones.

Relaciones

Cuando estamos hablando de el producto cartesiano, estamos juntando las parejas posibles de elementos entre dos conjuntos. Pero quizá no nos interesen todas las parejas posibles, quizá a veces solo nos interesaría hablar de algún subconjunto de estas parejas. Por ejemplo, si tenemos los conjuntos de zapatos izquierdos y derechos denotados por $I,D$ entonces no siempre nos interesan todas las parejas posibles de zapatos, quizá solo nos interese combinar cada zapato izquierda con su par correspondiente. Para dar un ejemplo, imagina que hay tres zapatos $A,B,C$ y los conjuntos $I$ y $D$ contienen tres zapatos de cada uno de los zapatos que hay:

$I = \{I_A, I_B, I_C\} $

$D = \{D_A, D_B, D_C\} $

Si quisieramos unir cada zapato con su par, nos podemos fijar en su producto cartesiano $I \times D$, sin embargo hay elementos que sí nos van a interesar y otros que no. Por ejemplo, la pareja $(I_A,D_A)$ sí nos interesa, pues es el zapato izquierdo y derecho del zapato $A$. Por otro lado, la pareja $(I_A,D_C)$ no nos interesa, pues estamos juntando dos zapatos pero de modelos distintos. En particular, el subconjunto de $I \times D$ que describe a los tres zapatos es: $$R = \{(I_A,D_A),(I_B,D_B),(I_C,D_C)\}.$$ Este conjunto es una relación entre los conjuntos $I$ y $D$. Como podrás notar, $R \subset I \times D$, y para la definición de relación, basta con que el conjunto esté contenido en el producto cartesiano para que cumpla la definicón.

Definición. Sean $X$ y $Y$ dos conjuntos, una relación entre los conjuntos $X$ y $Y$ es un subconjunto $R$ del producto cartesiano $X \times Y$: $$R \subset X \times Y $$

Definición. Si $R$ es una relación de $X$ en $Y$, diremos que $x$ está relacionado con $y$ bajo la relación $R$ si la pareja $(x,y) \in X \times Y$ y $(x,y) \in R$.

Con esta última definición, podemos notar que el zapato izquierdo $A$ ($I_A$) está relacionado con el zapato derecho $A$ ($D_A$) bajo la relación $R$, pues la pareja $(I_A,D_A)$ pertenece a la relación $R$.

En nuestro ejemplo anterior, mostramos una relación entre $I$ y $D$. Otros ejemplos de relaciones entre $I$ y $D$ son los siguientes:

$\{(I_B,D_A),(I_C,D_B),(I_C,D_A)\},$
$\{(I_C,D_B)\}$
$\{(I_A,D_A),(I_C,D_B)\}$
$\emptyset$
$I \times D$

Dominio y codominio de relaciones

Vamos ahora a trabajar con el conjunto de los números enteros $\mathbb{Z}$. Y trabajaremos con el producto cartesiano $\mathbb{Z} \times \mathbb{Z}$. Llamemos a este producto cartesiano $\mathbb{Z}^2$ que es la forma en que comúnmente se le denota al producto cartesiano entre el mismo conjunto (en este caso $\mathbb{Z}$) en la literatura.

Ahora, consideremos la siguiente relación entre los conjuntos: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$

Y notemos que algunos ejemplos de elementos de esta relación son: $\{ (3,6),(0,0),(-3,-6),(3^{10},2*3^{10}) ,(-300,-600)\} \subset R$. Gráficamente, podemos ver la relación en la siguiente imagen:

Del lado izquierdo corresponden los elementos $x$ de las parejas $(x,y) \in R$ y del lado derecho los elementos $y$. Notemos que del lado izquierdo (los elementos $x$), no consideramos todos los elementos. Por ejemplo, los números $\{-5,-4,-2,-1,1,2,4,5\}$ no forman ninguna pareja, pues en la definición de nuestro conjunto, solo estamos considerando los múltiplos de $3$ del lado izquierdo de la relación. A estos números que sí forman parejas del lado izquierdo, les llamamos dominio.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El dominio de la relación $R$ es $$Dom(R) = \{x \in X: \exists y \in Y \text{ tal que } (x,y) \in R\}$$

Notemos que siempre pasará que $Dom(R)\subset X$, otra definición que no hay que confundir con la de dominio es la de contradominio, al que nos referimos como el conjunto $Y$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. El contradominio de $R$ es el conjunto $Y$.

En nuestro ejemplo anterior, $$Dom(R)=\{x \in X: x \text{ es múltiplo de 3}\}$$.

Esto es cierto, pues las parejas de la relación $R$ son aquellas parejas de la forma $(3n,6n)$, pues pedimos que del lado izquierdo estén los múltiplos de $3$ (todo múltiplo de $3$ puede escribirse como algún número entero $n$ multiplicado por $3$), y del lado izquierdo el doble del número que escribimos del otro lado (si del lado izquierdo está $3n$ entonces del derecho estará $2*3n=6n$). Así que el dominio son aquellos números que forman alguna pareja, es decir, los múltiplos de $3$.

Por otro lado, el contradominio es $\mathbb{Z}$. Ahora, podemos preguntarnos en un concepto análogo a la idea de los elementos $y$ para los cuales existe un elemento $x$ de forma que $(x,y)$ pertenezca a la relación, para eso, podemos observar que los únicos elementos de $Z$ que pertenecen a alguna pareja del lado derecho son $\{\dots,-12,-6,0,6,12,\dots\}$, es decir, los múltiplos de $6$, de manera que podríamos hablar de que este conjunto es la imagen de la relación $R$.

Definición. Sean $X,Y$ dos conjuntos y $R$ una relación de $X$ en $Y$. La imagen de $R$ es: $$Im(R) = \{y \in Y: \exists x \in X \text{ tal que } (x,y) \in R\}$$

Imagen Directa e Imagen Inversa

Ahora, tomemos a los conjuntos $A=\{0,2,3,5,6,7,8,9\}$ y $B=\{-6,-1,2,3,4,6,7,12,21\}$ veamos que $A \times B \subset \mathbb{Z}^2$ pues ambos son subconjuntos de números enteros. El siguiente concepto que vamos a presentar, va a ser la imagen directa e inversa. Para esto, consideremos nuevamente nuestra relación $R$ de la sección anterior. Veamos que los elementos de $A$ que pertenecen al dominio de $R$ son $\{0,3,6,9\}$ esto pues $\{(0,0),(3,6),(6,12),(9,18)\} \subset R$. Definamos la imagen directa de $A$ como los elementos en la imagen de $R$ con la restricción de que únicamente consideremos elementos de $A$ del lado izquierdo.

Definición. Sean $X,Y$ dos conjuntos, $A \subset X$ y $R$ una relación de $X$ en $Y$. La imagen directa de $A$ es el conjunto: $$Im[A]=\{y \in Y: \exists x \in A \text{ tal que }(x,y) \in R\}$$

Compara esta definición con la definición de imagen, lo único que estamos cambiando es el conjunto al que pertencen las $x$.

De manera similar, tenemos un concepto similar para $B$, en donde restringiremos ahora el dominio. Para esto, nota que las parejas de $R$ que tienen su imagen en $B$ son $\{(-3,-6),(3,6),(6,12)\}$. Y el concepto de imagen inversa, serán aquellos elementos del dominio de $R$ los cuales están relacionados con algún elemento de $B$.

Definición. Sean $X,Y$ dos conjuntos, $B\subset Y$ y $R$ una relación de $X$ en $Y$. La imagen inversa de $B$ es el conjunto: $$Im^{-1}[B]=\{x \in X: \exists y \in B \text{ tal que }(x,y) \in R\}$$

De esta, manera:

$$Im[A]=\{0,6,12,18\},$$ $$ Im^{-1}[B]=\{-3,3,6\}.$$

A continuación, vamos a introducir una última definición de esta entrada, que da la idea intuitiva de juntar distintas relaciones.

Composición de funciones

Ahora, veremos la siguiente relación entre el conjunto de zapatos izquierdos $I$ y conjunto de zapatos derechos $D$:

$$R = \{(x,y) \in I \times D: x \text{ es del mismo color que }y\} $$

Y la relación entre zapatos derechos y el conjunto $P$ de pantalones:

$$ T = \{(x,y) \in D \times P:x \text{ es del mismo color que }y\} $$

Estas relaciones solo nos están juntando colores de prendas, la primera nos junta zapatos del mismo color y la tercera relaciones el color de los zapatos derechos con el del pantalón.

Así que por si ejemplol tuvieramos los colores rojo, amarillo y azul entre zapatos izquierdos, derechos y pantalones, entonces la primera relación tendría al zapato izquierdo rojo $I_R$, el zapato derecho rojo $D_R$ y el pantalón rojo $P_R$, de manera que $(I_R,D_R) \in R \land (D_R,P_R) \in T$. ¿Podemos establecer la conexión entre los zapatos izquierdos y los pantalones? Pues con esta pareja, resulta que de alguna manera el zapato $D_R$ une a los dos elementos mediante dos relaciones distintas. La primera relación tiene como contradominio el conjunto $D$ mientras que la segunda lo tiene como dominio.

De la misma manera, podemos conectar el zapato izquierdo azul $I_A$ con algún pantalón de la siguiente manera:

  1. Notamos que $I_A$ está relacionado con el zapato derecho azul $D_A$ mediante la relación $R$.
  2. Observamos que a su vez el zapato $D_A$ está relacionado con el pantalón azul $P_A$ mediante $T$.

De esta manera, podemos encontrar alguna conexión del zapato $I_A$ al pantalón $P_A$ viendo que hay una relación entre $I_A$ con $D_A$ y de $D_A$ con $P_A$. Así que podríamos definir una relación entre los zapatos izquierdos y los pantalones a través de las relaciones $R$ y $T$. Definamos esta relación como $R \circ T$ de la siguiente manera:

$$T \circ R = \{(x,y) \in I \times P: \exists z \in D \text{ tal que }\big( (x,z) \in R \land (z,y) \in T\big) \} $$

Lo que queremos decir con esta expresión, es que los elementos de la relación $T \circ R$ son los elementos $(x,y)$ de tal forma que existe una forma de conectar $(x,y)$ mediante un elemento $z$ de tal forma que $x$ está relacionado con $y$ mediante la relación $T \circ R$ si existe un elemento $z$ que los conecta, es decir, si existe $z$ en $Im(R) \cap Dom(T)$ de tal forma que $(x,z) \in R$ y $(z,y) \in T$.

Definición. Sean $X,Z,Y$ tres conjuntos, $R$ una relación de $X$ en $Z$ y $T$ una relación de $Z$ en $Y$. La relación composición de $R$ con $T$ es la relación:
$$T \circ R = \{ (x,y) \in X \times Y: \exists z \in Z\big( (x,z) \in R \land (z,y) \in T\big)$$

Veamos ahora un ejemplo de nuevo con los número enteros. Considera la relación que ya habíamos visto anteriormente, dada por: $$R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $$ Nota ahora, que como dijimos anteriormente, estos son las parejas de la forma $(3n,6n)$ de manera que otra forma de escribir el conjunto es $$R = \{(3n,6n): n \in \mathbb{Z} \} $$.

Ahora considera la siguiente relación $T$:$$T = \{(x,y) \in \mathbb{Z}^2: x = y+1\}$$

Algunos elementos de esta relación son: $\{(3,2),(7,6),(1,0),(-9,-10)\}$. Gráficamente se ve de la siguiente manera:

Y si te das cuenta, únicamente son los números de la forma $(n+1,n)$. Por lo que podríamos escribir esta relación como $$T = \{(n+1,n): n \in \mathbb{Z} \} $$.

Ahora veamos cómo se ve la composición $T \circ R$. Para ello, tomemos un elemento de la relación $R$. Por ejemplo, $(3,6) \in R$. Ahora notemos que de igual forma, $(6,5)$ pertenece a la relación $T$. De manera que $(3,5) \in T \circ R$. En general, un elemento de la relación $R$ se escribe como $(3n,6n)$, y un elemento de la relación $T$, como dijimos al principio del párrafo, es de la forma $(n+1,n)$ o lo que es lo mismo, $(n,n-1)$. Y enseguida nota que si tomamos un número entero $n$, entonces $(3n,6n) \in R$ y $(6n,6n-1) \in T$. De esta manera, podemos escribir a la composición de $R$ con $T$ como el conjunto: $$ T \circ R = \{(3n,6n-1): n \in \mathbb{Z}\}$$

Más adelante…

En la siguiente entrada seguiremos hablando de las relaciones entre conjuntos y veremos algunos tipos de relaciones especiales que tendrán algunas propiedades interesantes. También hablaremos un poco más de relaciones de un conjunto en sí mismo, este tipo de relaciones ya las hemos visto, sin embargo, veremos más propiedades que pueden cumplir estas. Esto nos servirá para hablar después de órdenes entre conjuntos.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $$R=\{(x,y) \in \mathbb{Z}^2: x+y=0\}$$ y la relación$$T=\{(x,y) \in \mathbb{Z}^2: x-y=0\}.$$Encuentra:
    • $Dom(R)$
    • $Im(R)$
    • Escribe todos los elementos de $T \circ R$
    • Encuentra $Im[\{1,2,3,4,5\}]$ sobre la relación $R$
    • Encuentra $Im^{-1}[\{-1,-2,-3,-4,-5\}]$ sobre la relación $T$
  2. Demuestra que si $R = \{(x,y) \in \mathbb{Z}^2: (x \text{ es múltiplo de 3} )\land (y = 2x) \} $, entonces $$R = \{(3n,6n): n \in \mathbb{Z} \} $$
  3. La recta $\mathcal{L}$ con pendiente $m$ e intersección $b$ con el eje $y$ en los números enteros es el conjunto: $$\mathcal{L}=\{(x,y) \in \mathbb{Z}^2: mx+b=y\} $$ Encuentra $\mathcal{L_1}\cap \mathcal{L_2}$ donde $\mathcal{L_1}$ es la recta con $m=1,b=0$ y $\mathcal{L_2}$ es la recta con $m=-1,b=2$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Cálculo Diferencial e Integral I: Concepto de función

Por Karen González Cárdenas

Deja un comentario

Introducción

En la unidad anterior desarrollamos todo lo concerniente a los números reales, ahora comenzaremos a ver funciones. Para ello recordemos de nuestros cursos de álgebra cómo se define el producto cartesiano de un par de conjuntos $A$ y $B$:
$$ A\times B := \left\{ (a,b) : a \in A, b \in B \right\},$$
así vemos que sus elementos son pares ordenados.

Por lo que decimos que cualquier subconjunto $R \subseteq A\times B$, es llamado una relación entre $A$ y $B$.

Basándonos en este par de conceptos daremos la definición formal de función entre un par de conjuntos.

Definición de función

Definición (función): Una función $f$ entre los conjuntos $A$ y $B$ es una relación tal que:

  • Para todo $a \in A$ existe $b \in B$ donde $(a,b) \in f$.
  • Si $(a, b_{1}), (a, b_{2})$ entonces $b_{1}= b_{2}$.

Notación:

  • $f : A \rightarrow B$ es una función con dominio $A$ y codominio $B$.
  • $f(a)=b$ es llamada la regla de correspondencia de f.

En resumen, a una función $f : A \rightarrow B$ la conforman tres cosas:

  • Su dominio.
  • Su codominio.
  • Su regla de correspondencia.

El conjunto imagen de una función

Definición (Conjunto imagen): Sea $f : A \rightarrow B$ una función. La imagen de f se define como:
$$Im_{f}:= \left\{ b \in B : \exists a \in A (f(a) =b) \right\}.$$
Simplificado sería:
$$Im_{f}:= \left\{ f(a) \in B : a \in A \right\}.$$

Ejemplo: Sea $f: \r \rightarrow \r$. Si $f(x)=|x|$ entonces $Im_{f}=[0, \infty)$.

Demostración:
$\subseteq )$ Sea $x \in \r$. Vemos que $f(x)= |x|\geq 0$ por lo que $f(x) \in [0, \infty)$.

$\supseteq )$ Tomemos $y \in [0, \infty)$. Debemos probar que existe $x \in \r$ tal que $f(x)= y$.
Sea $x=y \in \r$ con $y \geq 0$. Así se sigue que $f(y)= |y|=y$ por lo que $f(y)=x$.

$\square$

Ejemplo

Encuentra el dominio y la imagen de la siguiente función:
$$f(x)= \sqrt{1-x^{2}}\quad \text{.}$$

Dominio:
Vemos que $y=\sqrt{1-x^{2}}$ está bien definido
\begin{align*}
&\Leftrightarrow 1-x^{2} \geq 0\\
&\Leftrightarrow 1 \geq x^{2}\\
&\Leftrightarrow 1 \geq |x|\\
\end{align*}
Así concluimos que el dominio es el conjunto:
$$D_{f}= [-1,1]\quad \text{.}$$
Imagen:
Como $x \in [-1,1]$ entonces
\begin{align*}
-1 \leq x \leq 1 &\Leftrightarrow 0 \leq x^{2} \leq 1\\
&\Leftrightarrow 0 \geq -x^{2} \geq -1\\
&\Leftrightarrow 1\geq 1-x^{2} \geq 1-1\\
&\Leftrightarrow 1\geq 1-x^{2} \geq 0\\
&\Leftrightarrow 1\geq \sqrt{1-x^{2}} \geq 0\\
\end{align*}

Por lo anterior tenemos:
$$Im_{f} = [0,1]\quad \text{.}$$

Ejercicio 1

Encuentra el dominio de la siguiente función:
\begin{equation*} f(x)= \frac{1}{4-x^{2}} \end{equation*}

Vemos que la función está bien definido si y sólo si:
\begin{align*}
4-x^{2} \neq 0 &\Leftrightarrow (2-x)(2+x) \neq 0\\
&\Leftrightarrow x \neq 2 \quad \text{y} \quad x\neq -2
\end{align*}
Por lo que su dominio sería:
$$D_{f}= \r – \left\{-2,2 \right\}\quad \text{.}$$
es decir, todos los reales quitando el $-2$ y el $2$.

Ejercicio 2

Encuentra el dominio de la siguiente función:
$$f(x)= \sqrt{x-x^{3}}\quad \text{.}$$

Dominio:
Vemos ahora que para $y=\sqrt{x-x^{3}}$ está bien definido
\begin{align*}
&\Leftrightarrow x-x^{3} \geq 0\\
&\Leftrightarrow x(1-x^{2}) \geq 0\\
&\Leftrightarrow x(1-x)(1+x) \geq 0\\
&\Leftrightarrow x \geq 0,\quad x\leq 1, \quad x \geq -1
\end{align*}

De las condiciones anteriores vemos que tenemos los siguientes posibles intervalos que cumplen la desigualdad inicial:

  • $(-\infty, -1]$
    Vemos que al sustituir $x= -1 \in (-\infty,-1]$ tenemos que:
    $$-1-(-1)^{3} = -1-(-1)= 0 \geq 0$$
    por lo que se cumple la desigualdad $x-x^{3} \geq 0$.
  • $(-1,0)$
    Tomando $x=-\frac{1}{2}$ vemos que:
    $$-\frac{1}{2} -\left(-\frac{1}{2} \right) ^{3} = -\frac{1}{2} + \frac{1}{8} = -\frac{3}{8}$$
    Por lo que no se cumple ser mayor o igual que cero.
  • $[1,0]$
    Ahora si tomamos $x=1$ observamos:
    $$1- 1^{3} =1-1 =0$$
    por lo que cumple la desigualdad.
  • $(1,\infty)$
    Por último si consideramos $x= 2$ ocurre que:
    $$2- (2)^{3} =2-8 =-6$$
    que no cumple la desigualdad.

Del análisis anterior vemos que los intervalos que cumplen con $x-x^{3} \geq 0$ son:
$$(-\infty, -1] \cup [1,0]\quad \text{.}$$
Por lo que el dominio de la función sería:
$$D_{f}=(-\infty, -1] \cup [1,0]\quad \text{.}$$

Gráfica de una función

Definición (gráfica): Sea $f:D_{f} \subseteq \r \rightarrow \r$ Definimos a la gráfica de f como el conjunto:
$$ Graf(f)= \left\{ (x,y)\in {\mathbb{R}}^2: x \in D_{f}, \quad y=f(x) \right\},$$
que es equivalente a decir:
$$Graf(f)= \left\{(x, f(x)): x \in D_{f} \right\}\quad \text{.}$$

Ejemplos

  • Para la función constante tenemos:
    $$f(x)=c ,$$
    donde $D_{f}= \r$ y $Im_{f}= {c}$.

    Por lo que su gráfica se vería como:
  • Para la función identidad tenemos:
    $$Id(x)=x ,$$
    donde $D_{f}= \r$ y $Im_{f}= \r$.

    Así su gráfica se vería:

Más adelante

En la próxima entrada veremos las definiciones relacionadas con las operaciones entre funciones: suma, producto, cociente y composición.

Tarea moral

A continuación encontrarás una serie de ejercicios que te ayudarán a repasar los conceptos antes vistos:

  • Sea $f: \r \rightarrow \r$. Demuestra que si $f(x)=x^{2}$ entonces $Im_{f}=[0, \infty).$
  • Encuentra el dominio de las siguientes funciones:
    • $\begin{multline*} f(x)= \sqrt{x+1} \end{multline*}$
    • $\begin{multline*} f(x)= x \sqrt{x^{2}-2} \end{multline*}$
    • $\begin{multline*} f(x)= \sqrt{-x}+ \frac{1}{\sqrt{x+2}} \end{multline*}$
    • $\begin{multline*} f(x)= \sqrt{2+x-x^{2}} \end{multline*}$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Ortogonalidad y transformación transpuesta

Por Leonardo Ignacio Martínez Sandoval

4 respuestas

Introducción

En entradas anteriores ya estudiamos la noción de espacio dual y la de ortogonalidad. También vimos cómo a partir de la ortogonalidad podemos definir subespacios como intersección de hiperplanos. Como veremos a continuación, la ortogonalidad también nos permite definir qué quiere decir que consideremos la «transformación transpuesta» de una transformación lineal.

Antes de comenzar, vale la pena recordar también que cada transformación lineal entre espacios de dimensión finita puede ser expresada mediante una matriz que depende de la elección de bases de los espacios vectoriales. Como tal vez te imaginarás, la transformación transpuesta tendrá como matriz a la matriz transpuesta de la transformación original.

Esta intuición nos dice que hay que tener cuidado. Supongamos que estamos trabajando sobre un campo $F$. Si tenemos espacios vectoriales $V$ de dimensión $n$, $W$ de dimensión $m$ y una tranformación lineal $T:V\to W$, recordemos que, tras elegir bases, $T$ está representada por una matriz $A$ en $M_{m,n}(F)$, es decir, con $m$ filas y $n$ columnas.

Pero la matriz transpuesta $^t A$ es de $n$ filas y $m$ columnas, así que típicamente no representará a una transformación de $V$ a $W$, pues las dimensiones no necesariamente coinciden. Podríamos intentar construir una transformación de $W$ a $V$ para que las dimensiones coincidan, pero resulta que esto no es «tan natural», por razones en las que no profundizaremos.

Lo que sí resulta muy natural y fácil de definir es una transformación de $W^\ast$ a $V^\ast$, lo cual tendrá sentido pues ya probamos que $\dim W^\ast = \dim W$ y $\dim V^\ast = \dim V$, así que será representada por una matriz en $M_{n,m}$. Es un poco más difícil conceptualmente, pero las consecuencias matemáticas son más bonitas y útiles. Sin decir más, comenzamos con la teoría.

Definición y ejemplo de transformación transpuesta

Para definir «transformación transpuesta», le hacemos como sigue.

Definición. Sean $V$ y $W$ espacios vectoriales sobre un campo $F$ y sea $T:V\to W$ una transformación lineal. Definimos la transformación transpuesta de $T$, como la transformación $^tT:W^\ast \to V^\ast$ tal que a cada forma lineal $l$ en $W^\ast$ la manda a la forma lineal $^tT(l)$ en $V^\ast$ para la cual $$(^tT(l))(v)=l(T(v)).$$

Otra forma de escribir a la definición es mediante la notación de emparejamiento canónico: $$\langle ^tT(l),v\rangle=\langle l, T(v)\rangle.$$

Veamos un ejemplo para entender mejor la definición.

Ejemplo. Considera a $V=M_{2}(\mathbb{R})$ y $W=\mathbb{R}^2$. Considera la transformación lineal $T:V\to W$ dada por $$T\begin{pmatrix} a& b\\ c&d\end{pmatrix}=(a+b,c+d).$$

La transformación $^t T$ va a mandar a una forma lineal $l$ de $W$ a una forma lineal $^tT(l)$ de $V$. Las formas lineales $l$ en $W$ se ven de la siguiente forma $$l(x,y)=rx+sy.$$ La forma lineal $^tT(l)$ en $V$ debe satisfacer que $^tT(l)=l\circ T$. En otras palabras, para cualquier matriz $\begin{pmatrix} a& b\\ c&d\end{pmatrix}$ se debe tener
\begin{align*}
(^t T(l)) \begin{pmatrix} a& b\\ c&d\end{pmatrix} &= l(a+b,c+d)\\
&=r(a+b)+s(c+d)\\
&=ra+rb+sc+sd.
\end{align*}

Si tomamos la base canónica $E_{11}$, $E_{12}$, $E_{21}$, $E_{22}$ de $V$ y la base canónica $e_1,e_2$ de $W$, observa que la transformación $T$ tiene como matriz asociada a la matriz $$\begin{pmatrix} 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 1\end{pmatrix}$$ (recuerda que se obtiene poniendo como columnas a los vectores coordenada de las imágenes de la base).

Por otro lado, los vectores de la base dual $e_1^\ast$ y $e_2^\ast$ «leen las coordenadas», de modo que $e_1^\ast(x,y)=x$ y $e_2^\ast(x,y)=y$. Por lo que vimos arriba, $(^t T)(e_1)$ es entonces la forma lineal $a+b$ y $(^t T)(e_2)$ es la forma lineal $c+d$. En términos de la base dual en $V^\ast$, estos son $E_{11}^\ast + E_{12}^\ast$ y $E_{21}^\ast+ E_{22}^\ast$ respectivamente. De esta forma, la transformación $^t T$ tiene matriz asociada $$\begin{pmatrix}1&0\\1&0\\0&1\\0&1\end{pmatrix}.$$

$\triangle$

Nota que en el ejemplo la transformación transpuesta tiene como matriz a la matriz transpuesta de la transformación original. Esto es algo que queremos que pase siempre, y más abajo lo demostramos.

Propiedades básicas de transformación transpuesta

Observa que la definición no necesita que $V$ y $W$ sean de dimensión finita. A continuación enunciamos y probamos algunos resultados que se valen también en el contexto de dimensión infinita.

Teorema 1. Tomemos $V$,$W$,$Z$ espacios vectoriales sobre un campo $F$ y $c$ en $F$. Sean $T_1,T_2: V \to W$ transformaciones lineales. Sea $T_3:W\to Z$ una transformación lineal. Se cumple todo lo siguiente:

  1. $^tT_1$ es una transformación lineal.
  2. $^t(T_1+cT_2)= {^tT_1} + c^tT_2$.
  3. $^t(T_3\circ T_1) = {^t T_1} \circ ^t T_3$.
  4. Si $V=W$ y $T_1$ es invertible, entonces $^t T_1$ también lo es y $(^t T_1)^{-1}= {^t (T_1^{-1})}$.

Para tener un poco más de intuición, observa cómo estas propiedades son análogas a las de transposición para matrices.

Demostración. Las partes 1 y 2 se demuestran usando cuidadosamente las definiciones. Haremos la demostración de $1$ y la demostración de $2$ queda como tarea moral. Para probar $1$, necesitamos probar que $^tT_1:W^\ast \to V^\ast$ es lineal, así que tomemos $l_1$, $l_2$ en $W^\ast$ y $a$ un escalar en $F$. Tenemos que demostrar que $$ ^tT_1(l_1+a l_2)= {^tT_1(l_1)}+ a ^tT_1(l_2).$$

Ésta es una igualdad de formas lineales en $V^\ast$, y para mostrar su validez tenemos que mostrar que se vale en cada $v\in V$. Por un lado,
\begin{align*}
^tT_1(l_1+a l_2)(v) &= (l_1+a l_2)(T_1(v))\\
&=l_1(T_1(v))+a l_2(T_1(v)).
\end{align*}

Por otro lado,
\begin{align*}
(^tT_1(l_1)+ a ^tT_1(l_2))(v)&= {^tT_1(l_1)(v)}+ a ^tT_1(l_2)(v)\\
&= l_1(T_1(v)) + a l_2(T_1(v)).
\end{align*}

En ambos casos obtenemos el mismo resultado, así que $^tT_1(l_1+a l_2)$ y $^tT_1(l_1)+ a ^tT_1(l_2)$ son iguales, mostrando que $^t T_1$ es lineal.

Pasemos a la parte 3. La igualdad $^t(T_3\circ T_1) = {^t T_1} \circ ^t T_3$ es una igualdad de transformaciones de $Z^\ast$ a $V^\ast$. Para verificar su veracidad, hay que ver que son iguales en cada elemento en su dominio. Tomemos entonces una forma lineal $l$ en $Z^\ast$. Queremos verificar la veracidad de $$ ^t(T_3\circ T_1)(l) = (^t T_1 \circ ^t T_3)(l),$$ que es una igualdad de formas lineales en $V^\ast$, de modo que tenemos que verificarla para cada $v$ en $V$. Por un lado,

\begin{align*}
^t(T_3\circ T_1)(l)(v)&=l((T_3\circ T_1)(v))\\&=l(T_3(T_1(v))),
\end{align*}

Por otro,
\begin{align*}
(^t T_1 \circ ^t T_3)(l)(v)&=(^tT_1(^t T_3 (l)))(v)\\&=(^t T_3 (l))(T_1(v))\\&=l(T_3(T_1(v))).
\end{align*}

En ambos casos obtenemos el mismo resultado.

Para la parte 4 basta notar que si $V=W$ y $T_1$ es invertible, entonces tiene una inversa $S:V\to V$, y por la parte $3$ tenemos que $$^t S\circ ^t T_1 = {^t(T_1\circ S)} = {^t \text{Id}_V} = \text{Id}_{V^\ast},$$

mostrando que $^t T_1$ tiene inversa $^tS$. Observa que estamos usando que la transpuesta de la transformación identidad es la identidad. Esto no lo hemos probado, pero lo puedes verificar como tarea moral.

$\square$

La matriz transpuesta es la matriz de la transformación transpuesta

Cuando estamos trabajando en espacios de dimensión finita, podemos mostrar que la matriz que le toca a la transformación transpuesta es precisamente la transpuesta de la matriz que le toca a la transformación original. Hacemos esto más preciso en el siguiente resultado.

Teorema 2. Sea $T:V\to W$ una transformación lineal entre espacios de dimensión finita y $B$ y $B’$ bases de $V$ y $W$ respectivamente. Si $A$ es la matriz de $T$ con respecto a $B$ y $B’$, entonces $^t A$ es la matriz de la transformación $^t T:W^\ast \to V^\ast$ con respecto a las bases duales $B’^\ast$ y $B^\ast$.

Demostración. Necesitamos definir algo de notación. Llamemos $n=\dim V$, $m=\dim W$, $B=\{b_1,\ldots, b_n\}$, $B’=\{c_1,\ldots, c_m\}$ y $A=[a_{ij}]$. Recordemos que la matriz $A$ está hecha por las coordenadas de las imágenes de la base $B$ en términos de la base $B’$, es decir, que por definición tenemos que para toda $j=1,\ldots, n$: \begin{equation}T(b_j)=\sum_{i=1}^{m} a_{ij} c_i.\end{equation}

La transformación $^t T:W^\ast \to V^\ast$ va de un espacio de dimensión $m$ a uno de dimensión $n$, así que en las bases $B’^\ast$ y $B^\ast$ se puede expresar como una matriz de $n$ filas y $m$ columnas. Afirmamos que ésta es la matriz $^t A$. Para ello, basta mostrar que las coordenadas de las imágenes de la base $B’^\ast$ en términos de la base $B^\ast$ están en las filas de $A$, es decir, que para todo $i=1, \ldots, m$ tenemos que $$^tT(c^\ast_i)=\sum_{j=1}^{n} a_{ij} b_j^\ast.$$

La anterior es una igualdad de formas lineales en $V^\ast$, de modo que para ser cierta tiene que ser cierta evaluada en todo $v$ en $V$. Pero por linealidad, basta que sea cierta para todo $b_j$ en la base $B$. Por un lado, usando (1),

\begin{align*}
^tT(c^\ast_i)(b_j)&=c^\ast_i(T(b_j))\\
&=c^\ast_i \left(\sum_{k=1}^{m} a_{kj} c_i\right)\\
&=\sum_{k=1}^{m} a_{kj} c^\ast_i(c_k)\\
&=a_{ij},
\end{align*}

en donde estamos usando que por definición de base dual $c_i^\ast (c_i)= 1$ y $c_j^\ast (c_i)=0$ si $i\neq j$. Por otro lado,

\begin{align*}
\left(\sum_{k=1}^{n} a_{ik} b_k^\ast\right)(b_j)&= \sum_{k=1}^{n} a_{ik} b_k^\ast(b_j)\\
&=a_{ij},
\end{align*}

en donde estamos usando linealidad y la definición de base dual para $B$.

Con esto concluimos la igualdad $$^tT(c^\ast_i)=\sum_{j=1}^{n} a_{ij} b_j^\ast,$$ que muestra que podemos leer las coordenadas de las evaluaciones de $^t T$ en $B’^\ast$ en términos de la base $B^\ast$ en las filas de $A$, por lo tanto podemos leerlas en las columnas de $^t A$. Esto muestra que $^t A$ es la matriz correspondiente a esta transformación en términos de las bases duales.

$\square$

Kernel e imagen de la transformación transpuesta

Finalmente, el siguiente resultado nos habla acerca de cómo están relacionadas las transformaciones transpuestas y la ortogonalidad.

Teorema 3. Sea $T:V\to W$ una transformación lineal entre espacios vectoriales de dimensión finita. Entonces

$$\ker (^t T) = (\Ima (T))^\bot,\quad \ker (T)=(\Ima (^t T))^\bot$$

y

$$\Ima (^t T) = (\ker(T))^\bot\,\quad \Ima (T)=(\ker(^t T))^\bot.$$

Demostración. Demostraremos la igualdad $\ker (^t T) = (\Ima (T))^\bot$. Notemos que $l \in \ker(^t T)$ si y sólo si $(^t T)(l)=0$, lo cual sucede si y sólo si $l\circ T = 0$. Pero esto último sucede si y sólo si para todo $v$ en $V$ se tiene que $l(T(v))=0$, que en otras palabras quiere decir que $l(w)=0$ para todo $w$ en $\Ima (T)$. En resumen, $l\in \ker(^t T)$ pasa si y sólo si $l$ se anula en todo $\Ima (T)$ es decir, si y sólo si está en $(\Ima (T))^\bot$.

El resto de las igualdades se demuestran de manera análoga, o alternativamente, usando la bidualidad canónica. Es un buen ejercicio hacerlo y se deja como tarea moral.

$\square$

Más adelante…

En esta entrada enunciamos un resultado muy importante: dada una transformación lineal $T$, su transformación transpuesta tiene como matriz asociada la matriz transpuesta de la matriz asociada de $T$. Este resultado nos permitirá calcular fácilmente la transpuesta de una transformación, como veremos en la entrada de problemas de este tema.

En la siguiente entrada del blog hablaremos por primera vez de formas bilineales: vamos a ver cómo nuestra discusión de transformaciones lineales facilitará mucho abordar este tema.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Muestra que la transpuesta de la transformación lineal $T:\mathbb{R}^2\to \mathbb{R}^2$ dada por $T(x,y)=T(7x+8y,6x+7y)$ es invertible. Encuentra a su transpuesta y a la inversa de la transpuesta explícitamente.
  • Muestra la parte $2$ del Teorema 1.
  • Muestra que la transpuesta de la transformación identidad es la identidad.
  • Demuestra el resto de las igualdades del Teorema 3.
  • Encuentra la transpuesta de la transformación traza que va de $M_n(\mathbb{R})$ a los reales. Recuerda que esta transformación manda a una matriz $A=[a_{ij}]$ a la suma de sus entradas en la diagonal principal, es decir $$A\mapsto a_{11}+a_{22}+\ldots+a_{nn}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»