Introducción

En esta entrada retomaremos el tema de relaciones que vimos anteriormente. Esta vez definiremos una nueva relación a partir de dos relaciones: la composición. Veremos si la composición de dos relaciones tiene propiedades como la conmutatividad o la asociatividad.

Definamos la composición

Definición. Sean $R_1$ y $R_2$ relaciones de $A$ en $B$ y de $C$ en $D$ respectivamente. Definimos a la composición de $R_1$ con $R_2$ como el siguiente conjunto:

$R_2\circ R_1=\{(a,c):\mathrm{\exists }b((a,b)\in R_{1}y(b,c)\in R_2)\}$.

En otros símbolos, si $a,b,c$ son elementos tales que $a{R}_{1}b$ y $b{R}_{2}c$, entonces se cumplirá que $a(R_2\circ R_1)c$.

Ejemplo.

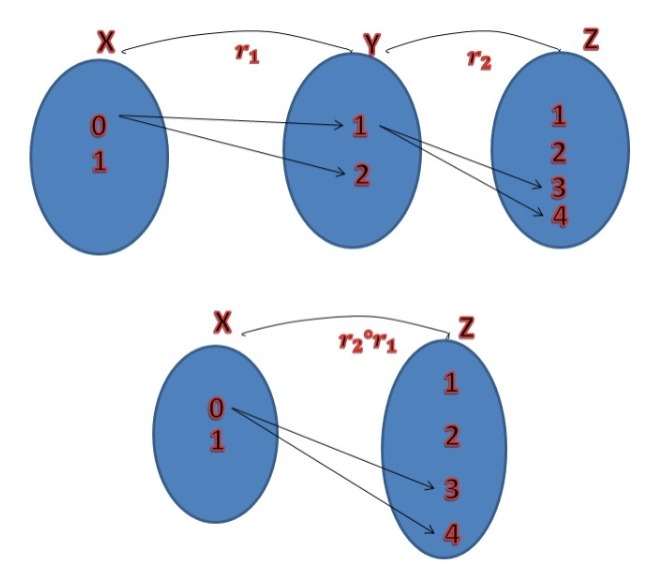
Sean $X=\{0,1\}$ y $Y=\{1,2\}$ y $Z=\{1,2,3,4\}$ conjuntos. Sean $R_1$ y $R_2$ relaciones de $X$ en $Y$ y de $Y$ en $Z$ definidas como sigue:

$R_1=\{(0,1),(0,2)\}y{R}_2=\{(1,3),(1,4)\}$.

Podemos hacer diagramas de ambas relaciones en una misma figura como sigue:

Luego, la composición de $R_2\circ R_1$ resulta ser el siguiente conjunto:

$R_2\circ R_1=\{(0,3),(0,4)\}$.

Para leerlo en el diagrama, podemos ver que hay un «camino» de $0$ a $3$ que usa las flechas de $0$ a $1$, y de $1$ a $3$. También hay un «camino» de $0$ a $4$ que usa las flechas de $0$ a $1$, y de $1$ a $4$.

Además de notarlo en el diagrama, podemos verificar mediante la definición. La pareja $(0,3)$ está pues $1\in Y$ tal que $(0,1)\in R_1$ y $(1,3)\in R_2$. Por su parte, la pareja $(0,4)$ está pues existe $1\in Y$ tal que $(0,1)\in R_1$ y $(1,4)\in R_2$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Algunos resultados

A continuación hablaremos de algunos resultados de la composición, la relación inversa y la relación identidad.

Proposición. Si $R$ es una relación en $A$, entonces $R\circ I{d}_A=R$.

Demostración.

Sea $R$ una relación en $A$. Veamos que $R\circ I{d}_A=R$.

$\subseteq$] Sea $(x,z)\in R\circ I{d}_A$, entonces existe $y$ tal que $(x,y)\in I{d}_A$ y $(y,z)\in R$.
Luego, como $(x,y)\in I{d}_A$ se sigue que $x=y$ y así $(y,z)=(x,z)\in R$.

$\supseteq$] Sea $(a,c)\in R$. Como $a,c\in A$, se sigue que $(a,a)\in I{d}_A$. Por lo que existe $a$ tal que $(a,a)\in I{d}_A$ y $(a,c)\in R$. Por lo tanto, $(a,c)\in R\circ I{d}_A$.

Por lo tanto, $R\circ I{d}_A=R$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Proposición. Si $R$ es una relación de $A$ en $B$, entonces $I{d}_{ImR}\subseteq R\circ R^{-1}$.

Demostración.

Sea $y\in Im(R)$. Como $y\in ImR$ existe $a\in A$ tal que $(a,y)\in R$, y por definición de relación inversa tenemos que $(y,a)\in R^{-1}$.

Encontramos $a\in A$ tal que $(y,a)\in R^{-1}$ y $(a,y)\in R$, esto es $(y,y)\in R\circ R^{-1}$. Así, $I{d}_{ImR}\subseteq R\circ R^{-1}$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Propiedades de la composición

Hemos dicho hasta ahora que la composición es una operación entre dos conjuntos que son relaciones. Por ello, podemos preguntarnos qué pasa con la conmutatividad y la asociatividad de dicha operación.

En general, no es cierto que $R_1\circ R_2=R_2\circ R_1$, es decir, la composición no es conmutativa.

Ejemplo.

Consideremos $X=\{1,2\}$. Sean $R_1=\{(1,1),(1,2)\}$ y $R_2=\{(1,2),(2,1)\}$ relaciones en $X$.

Por un lado tenemos que

$R_1\circ R_2=\{(2,1),(2,2)\}$

y por otro lado

$R_2\circ R_1=\{(1,2),(1,1)\}$.

De modo que $R_1\circ R_2\ne R_2\circ R_1$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

El segundo resultado que tenemos es que la asociatividad siempre se cumple.

Proposición. Si $R_1$, $R_2$ y $R_3$ son relaciones, entonces, $(R_3\circ R_2)\circ R_1=R_3\circ (R_2\circ R_1)$.

Demostración.

Sean $R_1$, $R_2$ y $R_3$ relaciones. Si $(x,z)\in (R_3\circ R_2)\circ R_1$, existe $y$ tal que $(x,y)\in R_1$ y $(y,z)\in R_3\circ R_2$. Luego, como $(y,z)\in R_3\circ R_2$, existe $w$ tal que $(y,w)\in R_2$ y $(w,z)\in R_3$. Así, dado que $(x,y)\in R_1$ y $(y,w)\in R_2$, $(x,w)\in R_2\circ R_1$, y como $(w,z)\in R_3$ entonces $(x,z)\in R_3\circ (R_2\circ R_1)$. Por tanto, $(R_3\circ R_2)\circ R_1\subseteq R_3\circ (R_2\circ R_1)$.
Ahora, si $(x,z)\in R_3\circ (R_2\circ R_1)$, existe $w$ tal que $(x,w)\in R_2\circ R_1$ y $(w,z)\in R_3$. Luego, existe $y$ tal que $(x,y)\in R_1$ y $(y,w)\in R_2$ y, por tanto, $(x,y)\in R_1$ y $(y,z)\in R_3\circ R_2$, por lo que $(x,z)\in (R_3\circ R_2)\circ R_1$. En consecuencia, $R_3\circ (R_2\circ R_1)\subseteq (R_3\circ R_2)\circ R_1$.

Por lo tanto, $(R_3\circ R_2)\circ R_1=R_3\circ (R_2\circ R_1)$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Hemos probado que la composición de relaciones es asociativa y a su vez concluimos que en general no conmuta.

Tarea moral

1. Demuestra que si $R$ es una relación arbitraria, $R\circ \mathrm{\varnothing }=\mathrm{\varnothing }=\mathrm{\varnothing }\circ R$.
2. Prueba que si $R$ es una relación en $A$, entonces $R=I{d}_A\circ R$.
3. Si $R$ y $S$ son relaciones, entonces $S\circ R\subseteq dom(R)\times im(S)$.
4. Sean $A=\{1,2,3\}$, $B=\{1,2\}$ y $C=\{1,2,3,4\}$. Sean $R_1=\{(1,2),(3,1)\}$ y $R_2=\{(1,4),(2,1),(2,3)\}$ relaciones de $A$ en $B$ y de $B$ en $C$ respectivamente. Calcula $R_2\circ R_1$.

Más adelante…

Ya hemos hablado de relaciones en general, y de cómo componerlas. A partir de ahora comenzaremos a pedirle más propiedades a nuestras relaciones para que se conviertan en algunos tipos de relaciones muy especiales: funciones, relaciones de equivalencia, órdenes, etc. Comenzaremos a hacer esto en la siguiente entrada, en donde veremos qué se le debe pedir a una relación para que sea una función. Así, todas las funciones son relaciones, sin embargo, no toda relación será función.

Entradas relacionadas

• Entrada relacionada: Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Relaciones
• Siguiente entrada: Teoría de los Conjuntos I: Funciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»