Introducción
En esta nueva entrada veremos el concepto de relación, para lo cual es necesario tener fresco el concepto de producto cartesiano. Así mismo, definiremos nuevos conjuntos a partir de una relación, como lo son el dominio, la imagen de una relación, la imagen de un conjunto bajo una relación y el concepto de relación inversa. Concluiremos esta entrada definiendo a la imagen inversa de un conjunto bajo una relación.
Relación
Definición. Sean $A$ y $B$ conjuntos. Una relación $R$ de $A$ en $B$ es un subconjunto de $A\times B$. A $A$ le llamamos el dominio de la relación y a $B$ el codominio.
Si $A=B$ diremos que $R$ es una relación en $A$.
Ejemplo 1.
Sea $A=\set{\emptyset,\set{\emptyset}}$ y $B=\set{\emptyset, \set{\set{\emptyset}}}$ y definimos $R$ como:
$R=\set{(\emptyset, \emptyset), (\emptyset, \set{\set{\emptyset}})}$.
Dado que $A\times B=\set{(\emptyset,\emptyset), (\emptyset, \set{\set{\emptyset}}), (\set{\emptyset}, \emptyset), (\set{\emptyset}, \set{\set{\emptyset}})}$ y $R\subseteq A\times B$ decimos que $R$ es una relación de $A$ en $B$.
$\square$
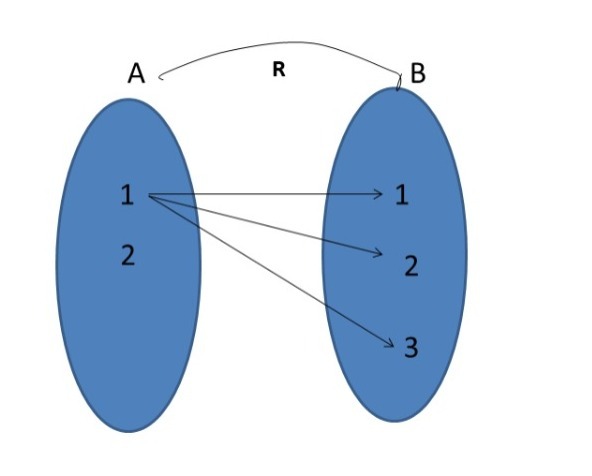
Ejemplo 2.
Sea $A=\set{1,2}$ y $B=\set{1,2,3}$. Definimos $S=\set{(1,1), (1,2), (1,3)}$. Tenemos que $S$ es una relación de $A$ en $B$. En efecto, esto sucede pues $S=\set{(1,1), (1,2), (1,3)}\subseteq A\times B$, ya que $A\times B=\set{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3)}$.
Podemos representar a $S$ mediante el siguiente diagrama. Del lado izquierdo hemos puesto al dominio $A$. Del lado derecho al codominio $B$. Para cada pareja $(a,b)$ de la relación, hemos puesto una flecha de $a$ a $b$.
$\square$
Definición. Si $(x,y)\in R$ con $R$ relación, decimos que $x$ está relacionado con $y$ mediante $R$ (o simplemente que $x$ está relacionado con $y$ si por el contexto es claro quién es $y$) y lo denotaremos como $xRy$.
Si retomamos el Ejemplo 1 podemos decir que $\emptyset R\emptyset$ y $\emptyset R\set{\set{\emptyset}}$.
A partir del Ejemplo 2 podemos decir que $1S1$, $1S2$ y $1S3$.
Relaciones relevantes
A continuación hablaremos de algunos ejemplos de relaciones que nos serán de utilidad más adelante.
- Relación vacía.
Si $R=\emptyset$, entonces $R$ será llamada la relación vacía. Esto tiene sentido pues $\emptyset\subseteq A\times B$ para cualesquiera $A$ y $B$ conjuntos. - Relación identidad.
Sea $A$ un conjunto cualquiera. Definimos la relación identidad en $A$ como:
$$Id_{A}=\set{(a,a):a\in A}.$$
Notamos que $Id_{A}\subseteq A\times A$ pues para cualquier $(x,y)\in Id_{A}$ se tiene que $x=y$ con $x,y\in A$, lo que significa que $(x,y)\in A\times A$. - Relación de pertenencia.
Sea $A$ un conjunto. Definimos a la relación de pertenencia en $A$ como el siguiente conjunto:
$$\in_{A}=\set{(a,b): a\in A,\ b\in A,\ a\in b}.$$ - Relación de contención.
Sea $A$ un conjunto. Definimos a la relación de contención en $A$ como el siguiente conjunto:
$$\subseteq_{A}=\set{(a,b): a\in A,\ b\in A,\ a\subseteq b}.$$
Dominio de una relación
Ya que hemos definido el concepto de relación, a continuación definiremos al dominio de una relación.
Definición. Sea $R$ una relación de $A$ en $B$. Definimos el dominio de la relación como:
$\text{dom}(R)=\set{x\in A:\exists y\in B( (x,y)\in R)}$.
Ejemplo.
Sean $A=B=\set{1,2}$. Definimos $R=\set{(1,2), (1,1), (2,2)}\subseteq A\times B$. Tenemos que $\text{dom}(R)=\set{1,2}$ pues para $1\in A$ existe, digamos, $1\in B$ tal que $(1,1)\in R$ y para $2\in A$ existe $2\in B$ tal que $(2,2)\in R$.
$\square$
Imagen de una relación
A continuación vamos a definir lo análogo al dominio activo, pero para el codominio. Le daremos un nombre al subconjunto de elementos del codominio que sí participan en la relación.
Definición. Sea $R$ una relación de $A$ en $B$. Definimos la imagen de $R$ como el conjunto
$\text{im}(R)=\set{y\in B:\exists x\in A( (x,y)\in R)}$.
Ejemplo.
Sean $A=B=\set{1,2}$. Definimos $R=\set{(1,2), (2,2)}\subseteq A\times B$.
Tenemos que $\text{im}(R)=\set{2}$ pues para $2\in B$ existe, digamos $2\in A$ tal que $(2,2)\in R$. Sin embargo, $1\not \in \text{im}(R)$ pues $R$ no tiene ninguna pareja de la forma $(x,1)$ con $x\in A$.
$\square$
Imagen de un conjunto bajo una relación
A veces queremos preguntarnos por los elementos del codominio que participan en la relación, pero sólamente con ciertos elementos del dominio. La siguiente definición establece esto.
Definición. Sea $R$ una relación de $A$ en $B$. Sea $C\subseteq A$. Definimos a la imagen de $C$ bajo $R$ como el el conjunto
$R[C]=\set{y\in B: \exists x\in C (xRy)}$.
Ejemplo.
Sean $A=\set{1,2}$ y $B=\set{1,2,3,4}$ conjuntos. Sea $R=\set{(1,1), (1,3), (2,1), (2,2), (2,4)}$, la cual es una relación de $A$ en $B$. Tomemos $C=\set{1}\subseteq A$. Tenemos que
$R[C]=\set{y\in \{1,2,3,4\}:\exists x\in\{1\}(xRy)}= \set{1,3}$.
$\square$
Relación inversa
Para cerrar esta entrada, introduciremos un concepto más: el de relación inversa.
Definición. Sean $A$ y $B$ conjuntos. Sea $R$ una relación de $A$ en $B$. Definimos la relación inversa de $R$ como la relación $R^{-1}$ de $B$ en $A$ definida como sigue:
$R^{-1}=\set{(b,a): (a,b)\in R}$.
Notemos que la relación inversa intercambia el orden de las entradas de las parejas ordenadas que son elementos de la relación $R$.
Ejemplo.
Sea $A=\set{\emptyset}$ y $B=\set{\emptyset, \set{\emptyset}}$ y definimos $R$ como:
$R=\set{(\emptyset, \emptyset), (\emptyset,\set{\emptyset})}.$
Tenemos que
$R^{-1}=\set{(\emptyset, \emptyset), (\set{\emptyset}, \emptyset)}.$
En efecto, como $(\emptyset, \emptyset)\in R$ tendremos que $(\emptyset, \emptyset)\in R^{-1}$ y como $(\set{\emptyset}, \emptyset)\in R$ tendremos que $(\emptyset, \set{\emptyset})\in R^{-1}$.
$\square$
Proposición. Sea $R$ una relación. Se cumple que $(R^{-1})^{-1}=R$.
Demostración.
Tenemos que
\begin{align*}
(R^{-1})^{-1}&=\set{(x,y): (y,x)\in R^{-1}}\\
&= \set{(x,y): (x,y)\in R}\\
&= R.
\end{align*}
$\square$
Imagen inversa de un conjunto bajo una relación
Definición. Sea $R$ una relación de $A$ en $B$. Sea $C\subseteq B$. Definimos a la imagen inversa de $C$ bajo $R$ como el el conjunto
$R^{-1}[C]=\set{x\in A: \exists y\in C (xRy)}$.
Ejemplo.
Sean $A=\set{1,2}$ y $B=\set{1,2,3,4}$ conjuntos. Si $R=\set{(1,1), (1,3), (2,1), (2,2), (2,4)}$ es una relación de $A$ en $B$, entonces $R^{-1}=\{(1,1), (1,2), (2,2), (3,1), (4,2)\}$. Tomemos $C=\set{1}\subseteq B$. Tenemos que
$R^{-1}[C]=\set{x\in \{1,2\}:\exists y\in\{1\}(xRy)}= \set{1,2}$.
$\square$
Tarea moral
La siguiente lista de ejercicios te permitira reforzar los conceptos de relación, dominio activo e imagen.
- Si $R$ es la relación vacía, encuentra el dominio activo y la imagen de $R$.
- Para $R$ es la relación identidad de $A$, encuentra el dominio y la imagen de $R$.
- Sea $R=\set{(1,2), (3,4)}$ una relación de $A=\set{1,2,3}$ en $B=\set{1,2,3,4}$. Encuentra el dominio y la imagen de $R$. Además, escribe al conjunto $R^{-1}$.
- Si $R$ es la relación identidad de $A$, describe quién es $R^{-1}$.
Más adelante…
En la siguiente entrada continuaremos con el tema de relaciones. Esta vez trataremos el tema de composición de relaciones. Definiremos a la composición de relaciones como una relación que se construye a partir de al menos dos relaciones cuyos dominios y codominios tienen ciertas propiedades en común.
Entradas relacionadas
- Entradas relacionadas:
Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición
Álgebra Superior I: Tipos de relaciones en conjuntos - Ir a: Teoría de los Conjuntos I
- Entrada anterior: Teoría de los Conjuntos I: Propiedades del producto cartesiano
- Siguiente entrada: Teoría de los Conjuntos I: Composición de relaciones
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»