Archivo de la etiqueta: composición

Cálculo Diferencial e Integral III: Regla de la cadena para campos vectoriales

Por Alejandro Antonio Estrada Franco

Introducción

Tenemos ya la definición de diferenciabilidad, y su versión manejable: la matriz jacobiana. Seguiremos construyendo conceptos y herramientas del análisis de los campos vectoriales muy importantes e interesantes. A continuación, enunciaremos una nueva versión de la regla de la cadena, que nos permitirá calcular las diferenciales de composiciones de campos vectoriales entre espacios de dimensión arbitraria. Esta regla tiene numerosas aplicaciones y es sorprendentemente fácil de enunciar en términos de producto de matrices.

Primeras ideas hacia la regla de la cadena

La situación típica de regla de la cadena es considerar dos funciones diferenciables que se puedan componer. A partir de ahí, buscamos ver si la composición también es diferenciable y, en ese caso, intentamos dar la derivada de la composición en términos de las derivadas de las funciones. Veamos qué pasa en campos vectoriales.

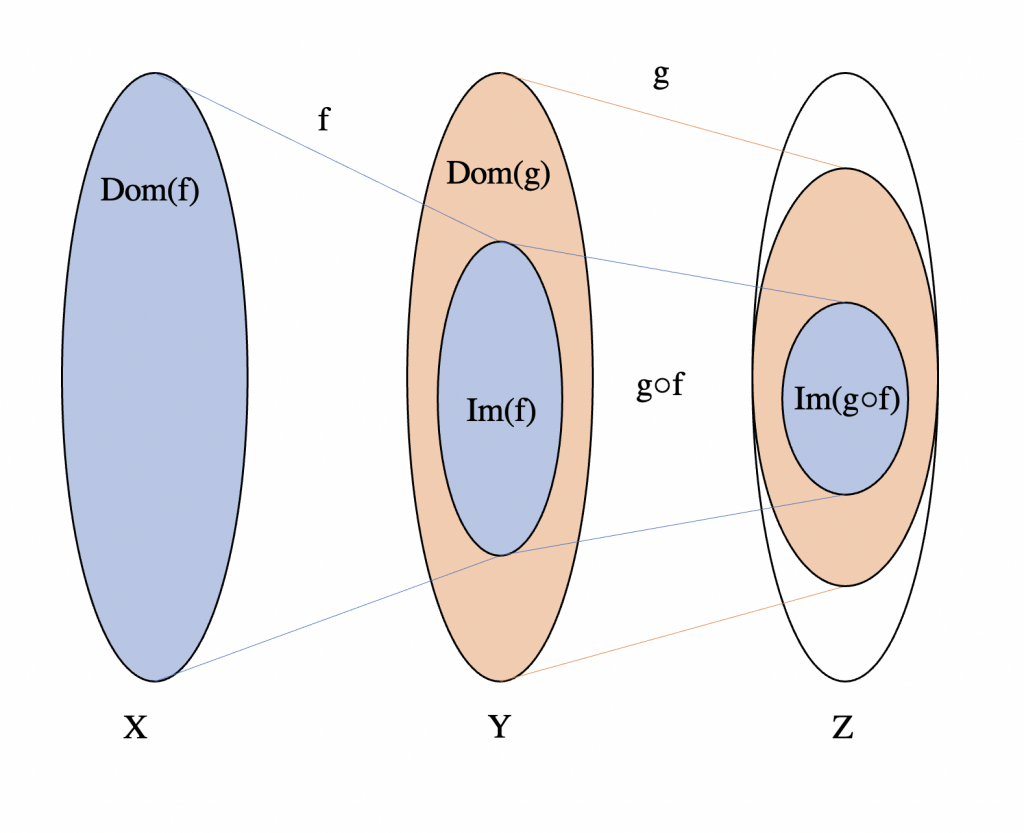
Pensemos en $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ y en su composición $h=f\circ g$ definida sobre alguna vecindad $V\subseteq S_g$ de $\bar{a}$ y tal que $g(V)\subseteq S_f$. Pensemos que $g$ es diferenciable en $\bar{a}$ con derivada $G_\bar{a}$ y que $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$.

Exploremos la diferenciabilidad de la composición $h$ en el punto $\bar{a}$. Para ello, tomemos un $\bar{y}\in \mathbb{R}^{l}$ tal que $\bar{a}+\bar{y}\in V$ y consideremos la siguiente expresión:

\begin{align*}
h(\bar{a}+\bar{y})-h(\bar{a})=f(g(\bar{a}+\bar{y}))-f(g(\bar{a})).
\end{align*}

Tomando $\bar{v}=g(\bar{a}+\bar{y})-g(\bar{a})$, tenemos $\bar{b}+\bar{v}=g(\bar{a})+\bar{v}=g(\bar{a}+\bar{y})$. De esta forma,

\begin{align*}
f(g(\bar{a}+\bar{y}))-f(g(\bar{a}))=f(\bar{b}+\bar{v})-f(\bar{b}).
\end{align*}

Por la diferenciabilidad de $g$ en $\bar{a}$, tenemos que podemos escribir

$$\bar{v}=G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}),$$ con $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$.

Usando la diferenciabilidad de $f$ en $\bar{b}$, y la linealidad de su derivada $F_\bar{b}$, tenemos entonces que:

\begin{align*}
f(\bar{b}+\bar{v})-f(\bar{b})&=F_\bar{b}(\bar{v})+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=F_\bar{b}(G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_f(\bar{b};\bar{v})\\
&=(F_{b}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||(F_{\bar{b}}\circ E_{g}(\bar{a};\bar{y}))+||\bar{v}||E_{f}(\bar{b};\bar{v}),
\end{align*}

con $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b};\bar{v})=0$.

Concatenando nuestras igualdades, podemos reescribir esto como

\[ h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),\] en donde hemos definido

\[ E_{h}(\bar{a};\bar{y})=(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})+\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b};\bar{v}).\] Si logramos demostrar que $\lim\limits_{\bar{y}\to \bar{0}}E_{h}(\bar{a};\bar{y})=0$, entonces tendremos la diferenciabilidad buscada, así como la derivada que queremos. Dejemos esto en pausa para enunciar y demostrar un lema auxiliar.

Un lema para acotar la norma de la derivada en un punto

Probemos el siguiente resultado.

Lema. Sea $\phi:S\subseteq \mathbb{R}^l\to \mathbb{R}^m$ un campo vectorial diferenciable en un punto $\bar{c}\in S$ y $T_\bar{c}$ su derivada. Entonces, para todo $\bar{v}\in \mathbb{R}^{l}$, se tiene:

$$||T_{\bar{c}}(\bar{v})||\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||.$$

Donde $\phi(\bar{v})=\left( \phi_{1}(\bar{v}),\dots ,\phi_{m}(\bar{v})\right)$

Demostración. Procedemos con desigualdad del triángulo como sigue:

\begin{align*}
||T_{\bar{c}}(\bar{v})||&=\left|\left|\sum_{k=1}^{m}(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_{k}\right|\right|\\
&\leq \sum_{k=1}^{m}||(\triangledown \phi_{k}(\bar{c})\cdot \bar{v})e_k||\\
&=\sum_{k=1}^{m}|\triangledown \phi_{k}(\bar{c})\cdot \bar{v}|
\end{align*}

y luego usamos la desigualdad de Cauchy-Schwarz en cada sumando para continuar como sigue

\begin{align*}
\leq \sum_{k=1}^{m}||\triangledown \phi_{k}(\bar{c})||||\bar{v}||,
\end{align*}

que es lo que buscábamos.

$\square$

Conclusión del análisis para regla de la cadena

Retomando el análisis para $E_{h}(\bar{a};\bar{y})$, dividamos el límite en los dos sumandos.

Primer sumando:

Como $F_{\bar{b}}$ es lineal, entonces es continua. También, sabemos que $\lim\limits_{\bar{y}\to \bar{0}}E_{g}(\bar{a};\bar{y})=0$. Así,

\begin{align*}
\lim\limits_{\bar{y}\to \bar{0}}(F_{\bar{b}}\circ E_{g})(\bar{a};\bar{y})&=F_{\bar{b}}\left(\lim\limits_{\bar{y}\to \bar{0}} E_{g}(\bar{a};\bar{y})\right)\\
&=F_\bar{b}(\bar{0})\\
&=0.
\end{align*}

Segundo sumando:

Retomando la definición de $\bar{v}$, aplicando desigualdad del triángulo y el lema que demostramos,

\begin{align*}
||\bar{v}||&=||G_{\bar{a}}(\bar{y})+||\bar{y}||E_{g}(\bar{a};\bar{y})||\\
&\leq ||G_{\bar{a}}(\bar{y})||+||\bar{y}||||E_{g}(\bar{a};\bar{y})||\\
&\leq \left(\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||||\bar{y}||\right)+||\bar{y}||||E_{g}(\bar{a};\bar{y})||.
\end{align*}

Dividiendo ambos lados entre $||\bar{y}||$, obtenemos entonces que

$$ \frac{||\bar{v}||}{||\bar{y}||}\leq \sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||+||E_{g}(\bar{a};\bar{y})||. $$

De aquí se ve que conforme $\bar{y}\to \bar{0}$, la expresión $\frac{||\bar{v}||}{||\bar{y}||}$ está acotada superiormente por la constante $A:=\sum_{k=1}^{m}||\triangledown g_{k}(\bar{a})||.$ Además, si $\bar{y}\to \bar{0}$, entonces $\bar{v}\to \bar{0}$. Así,

\[0\leq \lim\limits_{\bar{y}\to \bar{0}}\frac{||\bar{v}||}{||\bar{y}||}E_{f}(\bar{b},\bar{v})\leq A\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})=0 \] pues $\lim\limits_{\bar{y}\to \bar{0}}\bar{v}=\bar{0}$ implica $\lim\limits_{\bar{y}\to \bar{0}}E_{f}(\bar{b},\bar{v})$.

Hemos concluido que $$h(\bar{a}+\bar{y})-h(\bar{a})=(F_{\bar{b}}\circ G_{\bar{a}})(\bar{y})+||\bar{y}||E_{h}(\bar{a};\bar{y}),$$

con $\lim_{\bar{y}\to \bar{0}} E_h(\bar{a};\bar{y})=0$. Esto precisamente es la definición de $h=f\circ g$ es diferenciable en $\bar{a}$, y su derivada en $\bar{a}$ es la transformación lineal dada por la composición de transformaciones lineales $F_\bar{b}\circ G_\bar{a}$.

Recapitulación de la regla de la cadena

Recapitulamos toda la discusión anterior en el siguiente teorema.

Teorema (Regla de la cadena). Sean $f:S_{f}\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}^{n}$, $g:S_{g}\subseteq \mathbb{R}^{l}\rightarrow \mathbb{R}^{m}$ campos vectoriales. Supongamos que la composición $f\circ g$ está definida en todo un abierto $S\subseteq S_g$. Supongamos que $g$ es diferenciable en un punto $\bar{a}\in S$ con derivada $G_\bar{a}$ y $f$ es diferenciable en $\bar{b}:=g(\bar{a})$ con derivada $F_\bar{b}$. Entonces, $h$ es diferenciable en $\bar{a}$ con derivada $F_\bar{b}\circ G_\bar{a}$.

Dado que la representación matricial de la composición de dos transformaciones lineales es igual al producto de estas, podemos reescribir esto en términos de las matrices jacobianas como el siguiente producto matricial: $$Dh(\bar{a})=Df(\bar{b})Dg(\bar{a}).$$

Usos de la regla de la cadena

Hagamos algunos ejemplos de uso de regla de la cadena. En el primer ejemplo que veremos a continuación, la función $f$ es un campo escalar.

Ejemplo 1. Tomemos $g:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ campo vectorial, y $f:U\subseteq \mathbb{R}^{m}\rightarrow \mathbb{R}$ campo escalar. Consideremos $h=f\circ g$ y supongamos que se satisfacen las hipótesis del teorema de la regla de la cadena. Tenemos: \[ Df(\bar{b})=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix} \] y \[ Dg(\bar{a})=\begin{pmatrix}\frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix} . \]

Por la regla de la cadena tenemos $Dh(\bar{a})=Df(\bar{b})Dg(\bar{a})$ esto implica \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}=\begin{pmatrix} \frac{\partial f}{\partial x_{1}}(\bar{b}) & \dots & \frac{\partial f}{\partial x_{m}}(\bar{b}) \end{pmatrix}\begin{pmatrix} \frac{\partial g_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial g_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

Así \[ \begin{pmatrix} \frac{\partial h}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial h}{\partial x_{n}}(\bar{a}) \end{pmatrix}= \begin{pmatrix} \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{1}}(\bar{a}) & \dots & \sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{n}}(\bar{a}) \end{pmatrix}. \]

En otras palabras, tenemos las siguientes ecuaciones para calcular cada derivada parcial de $h$: \[ \frac{\partial h}{\partial x_{j}}(\bar{a})=\sum_{i=1}^{m}\frac{\partial f}{\partial x_{i}}(\bar{b})\frac{\partial g_{i}}{\partial x_{j}}(\bar{a}).\]

$\triangle$

Ejemplo 2. Sean $\bar{a}=(s,t)$ y $\bar{b}=(x,y)$ puntos en $\mathbb{R}^{2}$. Pensemos que las entradas de $\bar{b}$ están dadas en función de las entradas de $\bar{a}$ mediante las ecuaciones $x=g_{1}(s,t)$ y $y=g_{2}(s,t)$. Pensemos que tenemos un campo escalar $f:\mathbb{R}^2\to \mathbb{R}$, y definimos $h:\mathbb{R}^2\to \mathbb{R}$ mediante $$h(s,t)=f(g_{1}(s,t),g_{2}(s,t)).$$

Por el ejemplo anterior \[ \frac{\partial h}{\partial s}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial s} \] y \[ \frac{\partial h}{\partial t}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial t}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial t}. \] Como tarea moral queda que reflexiones qué significa $\partial x$ cuando aparece en el «numerador» y qué significa cuando aparece en el «denominador».

$\triangle$

Ejemplo 3. Para un campo escalar $f(x,y)$ consideremos un cambio de coordenadas $x=rcos\theta$, $y=rsen\theta$ es decir tomemos la función $\phi (r,\theta)=f(rcos\theta ,rsen\theta )$.

Por el ejemplo anterior tenemos \[ \frac{\partial \phi }{\partial r}=\frac{\partial f}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial r} \] y \[ \frac{\partial \phi }{\partial \theta }=\frac{\partial f}{\partial x}\frac{\partial x}{\partial \theta }+\frac{\partial f}{\partial y}\frac{\partial y}{\partial \theta } \] donde, haciendo las derivadas parciales tenemos: \[ \frac{\partial x}{\partial r}=cos\theta ,\hspace{1cm}\frac{\partial y}{\partial r}=sen\theta \] y \[ \frac{\partial x}{\partial \theta }=-rsen\theta,\hspace{1cm}\frac{\partial y}{\partial \theta }=-rcos\theta. \] Finalmente obtenemos: \[ \frac{\partial \phi }{\partial r }=\frac{\partial f }{\partial x }cos\theta +\frac{\partial f }{\partial y }sen\theta \] y \[ \frac{\partial \phi }{\partial \theta }=-\frac{\partial f }{\partial x }rsen\theta +\frac{\partial f }{\partial y }rcos\theta \] que son las derivadas parciales del cambio de coordenadas en el dominio de $f$.

$\triangle$

Mas adelante…

En la siguiente entrada comenzaremos a desarrollar la teoría para los importantes teoremas de la función inversa e implícita si tienes bien estudiada esta sección disfrutaras mucho de las siguientes.

Tarea moral

Considera el campo escalar $F(x,y,z)=x^{2}+y sen(z)$. Imagina que $x,y,z$ están dados por valores $u$ y $v$ mediante las condiciones $x=u+v$, $y=vu$, $z=u$. Calcula $\frac{\partial F}{\partial u}$, $\frac{\partial F}{\partial v}$.
Sea $g(x,y,z)=(xy,x)$, y $f(x,y)=(2x,xy^{2},y)$. Encuentra la matriz jacobiana del campo vectorial $g\circ f$. Encuentra también la matriz jacobiana del campo vectorial $f\circ g$.
En la demostración del lema que dimos, hay un paso que no justificamos: el primero. Convéncete de que es cierto repasando el contenido de la entrada anterior Diferenciabilidad.
Imagina que sabemos que la función $f:\mathbb{R}^n\to \mathbb{R}^n$ es invertible y derivable en $\bar{a}$ con derivada $T_\bar{a}$. Imagina que también sabemos que su inversa $f^{-1}$ es derivable en $\bar{b}=f(\bar{a})$ con derivada $S_\bar{b}$. De acuerdo a la regla de la cadena, ¿Qué podemos decir de $T_\bar{a}\circ S_\bar{b}$? En otras palabras, ¿Cómo son las matrices jacobianas entre sí, en términos de álgebra lineal?
Reflexiona en cómo todas las reglas de la cadena que hemos estudiado hasta ahora son un corolario de la regla de la cadena de esta entrada.

Entradas relacionadas

Ir a Cálculo Diferencial e Integral III
Entrada anterior del curso: Diferenciabilidad en campos vectoriales
Entrada siguiente del curso: Introducción al teorema de la función inversa

Álgebra Superior I: Funciones invertibles

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Anteriormente vimos el concepto de composición entre funciones, que nos permiten saltar entre varios conjuntos de manera sencilla, revisamos algunas de sus propiedades y dimos algunos ejemplos. Ahora nos toca profundizar un poco más en la composición de funciones analizando un caso particular de funciones: las invertibles. Que en términos simples nos permiten deshacer los efectos de las operaciones.

Revirtiendo las cosas.

Pensemos por un momento en un cubo rubik, hay distintas técnicas para armarlo, pero por ahora nos enfocaremos en sus movimientos. La forma en que se usa el cubo, es moviendo sus caras hasta que todas las caras tengan un solo color. Imagina que tienes un cubo en tus manos, si mueves la cara que está hasta arriba, tienes dos formas de hacerlo, girar en sentido de las manecillas del reloj y girar en sentido contrario a las manecillas del reloj. No pasa nada si no estás seguro de tu movimiento, pues siempre puedes deshacer un movimiento rotando la misma cara que volteaste en sentido contrario. Incluso si mueves varias caras, podrás regresar al estado original si recuerdas exactamente las caras que volteaste y la dirección, pues para deshacer los movimientos, tendrás que empezar por la última cara que volteaste y deberás girarla al sentido contrario al que le diste vuelta. Por ejemplo esta imagen indica dos movimientos a las caras y la forma de «deshacer» los movimientos.

En la imagen también marcamos los movimientos de mover las dos caras como $f$, por ahora imagínate que ese movimiento de girar las dos caras como lo muestra la imagen, se llama el movimiento $f$. Mientras que el movimiento de deshacerlas se llama $f^{-1}$. Entonces si realizamos primero el movimiento $f$, el movimiento $f^{-1}$ revierte lo que hizo la primera, volviendo al estado inicial. Así es como vamos a pensar en la reversibilidad de las funciones, una manera de «volver a armar» el cubo.

Funciones reversibles

Diremos que una función es reversible si existe una función $f^{-1}:Im(f) \rightarrow X$ tal que $f ^{-1}\circ f = Id$ donde $Id$ es la función i dentidad, es decir, es la única función que asigna a cada elemento a sí mismo, es decir $Id(x)=x$.

Algunas observaciones de las funciones invertibles. Sea $f:X \rightarrow Y$ una función invertible, entonces:

$f$ es inyectiva.

Demostración. Supongamos que no es inyectiva, entonces existen $x_1,x_2 \in X$ distintos tales que $f(x_1) = f(x_2)$. Como $f$ es invertible, entonces existe su función inversa $f^{-1}:Im(f) \rightarrow X$, en donde $$x_1 = f^{-1} \circ f(x_1) = f^{-1} \circ f(x_2) = x_2 $$ Siendo esta una contradicción, pues supusimos que eran distintos elementos. Así, la función es inyectiva.

$\square$

$f^{-1}$ es inyectiva.

Demostración. De manera similar a la demostración anterior, si $y_1,y_2 \in Dom(f^{-1})$ son tales que $f^{-1}(y_1) = f^{-1}(y_2)$, se tiene que al ser $f$ inyectiva, $$f(f^{-1}(y_1)) = f(f^{-1}(y_2)) \Rightarrow y_1=y_2$$ Llegando a que $f^{-1}$ es inyectiva.

$\square$

Así, te puedes dar una idea de lo que significan las funciones invertibles. Con estas proposiciones hemos probado además que la función $f^{-1}: Im(f) \rightarrow X$ es una biyección. ¿Te imaginas porqué? Pues resulta que la función $f^{-1}$ también es suprayectiva.

$f^{-1} \circ f = f \circ f^{-1}$

Demostración. Sabemos que $f^{-1} \circ f = Id$, entonces bastará demostrar que $f \circ f^{-1} = Id$. Para ello consideremos $y \in Dom(f^{-1})=Im(f) \subset Y$. Supongamos que $$f \circ f^{-1}(y)=w$$. Entonces $$f^{-1}(f \circ f^{-1}(y)) = f^{-1}(w). $$ Como la composición es asociativa, entonces: $$f^{-1}(f \circ f^{-1}(y)) = (f^{-1} \circ f) \circ f^{-1}(y) = f^{-1}(y) = f^{-1}(w)$$ Como $f^{-1}$ es inyectiva, entonces $y=w$.

$\square$

Sea $g:Im(f) \rightarrow Z$ una función invertible, entonces $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$ .

Demostración. Basta notar que por la asociatividad de las funciones:

$$ \begin{align*}
(g \circ f) \circ (f^{-1} \circ g^{-1}) &= g \circ (f \circ (f^{-1} \circ g^{-1})\\
&= g \circ ((f \circ f^{-1}) \circ g^{-1})\\
&= g \circ (Id \circ g^{-1}) \\
&= g \circ g^{-1} = Id
\end{align*}$$

$\square$

Más adelante…

Habiendo pasado por las funciones, su composición, sus propiedades y la inversa, utilizaremos estas definiciones para hablar de el tamaño de los conjuntos. Pues esta definición de funciones nos ayudan a decir «Cuántos elementos tiene un conjunto».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que $f^{-1}$ es suprayectiva.
Demuestra que $Dom(f^{-1})=Im(f)$.
Demuestra que $(f \circ (g \circ h))^{-1} = h^{-1} \circ (g^{-1} \circ f^{-1})$.
Da una condición suficiente para que una función no sea invertible.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Composición de funciones
Siguiente entrada del curso: Cardinalidad de conjuntos finitos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Superior I: Composición de funciones

Por Guillermo Oswaldo Cota Martínez

Deja un comentario

Introducción

Siguiendo la conversación de las funciones, esta vez hablaremos de la composición de funciones. Este es el concepto que nos permitirá combinar más de una función para crear nuevas funciones siempre que ciertas condiciones se cumplan.

Composiciones en relaciones

Anteriormente ya hemos mencionado que sobre tres conjuntos $X,Y,Z$ se puede definir una relación composición entre dos relaciones $R$ de $x$ en $Y$ y $T$ de $Y$ en $Z$. De manera que la relación $T \circ R$ es aquella que está compuesta de elementos de la forma $(x,z) \in X \times Z$ siempre y cuando exista alguna $y$ de manera que $(x,y) \in R$ y $(y,z) in T$. Así, la relación composición está formada de elementos que pueden ir de $X$ a $Y$ mediante la relación $R$ y de ahí pueden llegar a $Z$ mediante la relación $T$. Veremos a continuación cómo podemos traducir esto a las funciones.

Composiciones en funciones

La composición de funciones será una composición de relaciones, no cambiará la definición, pues las funciones siguen siendo relaciones y hemos establecido toda una base sobre lo que son las relaciones para llegar a hablar de las funciones de forma gradual.

Piensa en el siguiente ejemplo. Supongamos tenemos una máquina $f$ que transforma las horas en minutos y otra máquina $g$ que transforma los minutos en segundos. Cuando a la máquina $f$ le pasamos de entrada «$1$ hora», nos regresará «$60$ minutos». Mientras que cuando le pasamos la entrada «$1$ minuto» a la máquina $g$ esta nos devuelve «60 segundos». Ahora nos preguntamos ¿Hay una forma de convertir las horas en segundos? O dicho de otra forma, ¿Cómo podemos construir una máquina $h$ que convierta las horas en los segundos? Nota que no tenemos directamente la máquina que nos toma las horas y las convierte en segundos, pero sí tenemos una máquina que convierte las horas en minutos y después los minutos en segundos.

Supongamos que tenemos la entrada «1 hora» entonces con la máquina $f$ podemos saber que una hora equivale a $60$ minutos. Enseguida podemos usar la máquina $G$ para saber que que los $60$ minutos equivalen a $3600$ segundos, de manera que esa es la duración de una hora. A esta máquina $h$ le llamamos la composición de $f$ con $g$.

Pensemos a estas máquinas como funciones, si consideramos $H$ como al conjunto de número de horas a considerar ($H=\{1 hr, 2 hrs, 3 hrs, \dots\}$) a $M$ como el conjunto de los minutos ($M =\{1 min, 2 mins, 3 mins, \dots\}$) y a $S$ como el conjunto de los segundos a considerar ($S=\{1 seg, 2 segs, 3 segs, \dots\}$) entonces $f:H \rightarrow M$ y $g: M \rightarrow S$ son funciones que convierten una unidad de tiempo en otra. La función $h : H \rightarrow S$ buscada es justamente la composición de las funciones $g \circ f: H \rightarrow S$.

Nota que si queremos convertir un número de horas $n \in H$ a segundos entonces bastará con notar que $n$ horas son $f(n)$ minutos, y estos a su vez son $g(f(n))$ segundos. Veamos el primer ejemplo. Nota que $f(1 hr)=60 mins$. Entonces $g(f(1hr))=g(60min)=3600segs$. Por lo cual la función que convierte las horas a segundos es componer $f$ con $g$.

Composición de funciones

Gráficamente lo que significa la composición de funciones es la siguiente imagen:

Aquí podemos visualizar la función $g \circ f$ que es la función que va de $X$ a $Z$. En ella, vemos cómo es que la función $f$ va de X a Y, siendo que el dominio de $f$ queda dentro de $Y$, pues por definición, si la función $f$ va de $X$ a $Y$, entonces para cada elemento $x \in X$ sucede que existe $y \in Y$ tal que $f(x)=y$, significando que siempre $Im(f) \subset Y$ , y en nuestro caso en particular, $Y= Dom(g)$, siendo $g$ una función que va de $X$ a $Z$. Quizá lo que no es inmediato es la siguiente contención: $Im(g \circ f) \subset Im(g) \subset Z$.

Proposición. Si $f:X \rightarrow Y $ y $g: Y \rightarrow Z$ entonces $Im(g \circ f) \subset Im(g) \subset Z$

Demostración. Para esta demostración, consideremos $w \in Im(g \circ f) $ y veamos que $w \in Im(g)$. Para ello, notemos que por definición de la composición de funciones, si $w \in. Im(g \circ f)$ entonces existe $x \in X$ tal que $g \circ f(x) = w$. Es decir, $g(f(x))=w$ a su vez, como $f(x) \in Dom(g)$ entonces existe $y$ tal que $f(x)=y$ y $g(y)=w$. Ahora notemos que $y \in Dom(g)$ entonces $g(y) \in Im(g)$, es decir, $w=g(y) \in Dom(g)$. Por otro lado, por definición de función, la imagen de $g$ está contenida en $Z$. De esta manera, se tiene la contención buscada.

$\square$

Vamos a hacer algunas observaciones de esta composición de funciones.

Para componer funciones, la imagen de una función debe estar contenida en el dominio de la otra. Esto significa que si queremos componer $f$ con $g$, debemos saber que todo elemento convertido por $f$ puede ser pasado a $g$. Dicho de otra manera, si queremos convertir horas a segundos, la máquina $f$ convierte las horas a minutos, y la $g$ minutos a segundos, entonces siempre tiene que pasar que $f$ devuelva minutos para poder componerse con $g$, pues acepta nada más minutos como entrada, si $f$ convirtiera horas a días, $g$ lo rechazaría, pues un día no está expresado en términos de minutos.
La composición de funciones es asociativa, es decir, $(g\circ f) \circ h = g \circ (f \circ h)$.

Demostración. Consideremos $f : X \rightarrow Y$, $g : Y \rightarrow Z$ y $h : W \rightarrow X$. Para demostrar que la función es asociativa, deberíamos demostrar que apra algún $x$ arbitrario en el dominio de la composición $(W)$, se cumple que

$$ (g\circ f) \circ h(x) = g \circ (f \circ h)(x) $$

Para ello, llamemos $f \circ h = F$, $g \circ f = G$,$h(x)=y$ y $f(y)=z$. Ahora, nota por un lado que $$ g \ circ (f \circ h)(x) = g \circ F(x) = g(F(x)) = g(z)$$

Por otro lado, $(g \circ f) \circ h(x) = G \circ h(x) = G(y) = g \circ f(y) = g(z)$

Llegando a los mismos resultados, lo que debe significar que las funciones son iguales para $x$, pudiéndose generalizar para cada elemento del dominio de la composición.

$\square$

Más adelante…

Habiendo visto la composición de funciones, estamos listos para dar el siguiente paso y encontrar una clase muy particular de funciones: funciones invertibles, que serán aquellas funciones que podemos «deshacer».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Demuestra que si $f$ es suprayectiva, entonces $Im(g \circ f) = Im(g)$.
Sea $f: \mathbb{R} \ rightarrow \mathbb{R}$ dada por $f(x)=\frac{3x+1}{2}$:
1. Encuentra $g: \mathbb{R} \ rightarrow \mathbb{R}$ tal que $g \circ f (x)= x$
2. Demuestra que $g \circ f = f \circ g$
Da condiciones suficientes y necesarias para que $g \circ f$ sea biyectiva.

Entradas relacionadas

Ir a Álgebra Superior I
Entrada anterior del curso: Funciones inyectivas, suprayectivas y biyectivas
Siguiente entrada del curso: Cardinalidad de conjuntos finitos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Teoría de los Conjuntos I: Composición de relaciones

Por Gabriela Hernández Aguilar

Deja un comentario

Introducción

En esta entrada retomaremos el tema de relaciones que vimos anteriormente. Esta vez definiremos una nueva relación a partir de dos relaciones: la composición. Veremos si la composición de dos relaciones tiene propiedades como la conmutatividad o la asociatividad.

Definamos la composición

Definición. Sean $R_1$ y $R_2$ relaciones de $A$ en $B$ y de $C$ en $D$ respectivamente. Definimos a la composición de $R_1$ con $R_2$ como el siguiente conjunto:

$R_2\circ R_1=\set{(a,c): \exists b\ tal\ que\ (a,b)\in R_1\ y\ (b,c)\in R_2}$.

En otros símbolos, si $a,b,c$ son elementos tales que $aR_1b$ y $bR_2c$, entonces se cumplirá que $a (R_2\circ R_1) c$.

Ejemplo.

Sean $X=\set{0,1}$ y $Y=\set{1,2}$ y $Z=\set{1,2,3,4}$ conjuntos. Sean $R_1$ y $R_2$ relaciones de $X$ en $Y$ y de $Y$ en $Z$ definidas como sigue:

$R_1=\set{(0,1), (0,2)}\ y\ R_2=\set{(1,3), (1,4)}$.

Podemos hacer diagramas de ambas relaciones en una misma figura como sigue:

Luego, la composición de $R_2\circ R_1$ resulta ser el siguiente conjunto:

$R_2\circ R_1=\set{(0, 3), (0,4)}$.

Para leerlo en el diagrama, podemos ver que hay un «camino» de $0$ a $3$ que usa las flechas de $0$ a $1$, y de $1$ a $3$. También hay un «camino» de $0$ a $4$ que usa las flechas de $0$ a $1$, y de $1$ a $4$.

Además de notarlo en el diagrama, podemos verificar mediante la definición. La pareja $(0,3)$ está pues $1\in Y$ tal que $(0,1)\in R_1$ y $(1,3)\in R_2$. Por su parte, la pareja $(0,4)$ está pues existe $1\in Y$ tal que $(0,1)\in R_1$ y $(1,4)\in R_2$.

$\square$

Algunos resultados

A continuación hablaremos de algunos resultados de la composición, la relación inversa y la relación identidad.

Proposición. Si $R$ es una relación en $A$, entonces $R\circ Id_{A}=R$.

Demostración.

Sea $R$ una relación en $A$. Veamos que $R\circ Id_{A}=R$.

$\subseteq$] Sea $(x,z)\in R\circ Id_{A}$, entonces existe $y$ tal que $(x,y)\in Id_{A}$ y $(y,z)\in R$.
Luego, como $(x,y)\in Id_{A}$ se sigue que $x=y$ y así $(y,z)=(x,z)\in R$.

$\supseteq$] Sea $(a,c)\in R$. Como $a,c\in A$, se sigue que $(a,a)\in Id_{A}$. Por lo que existe $a$ tal que $(a,a)\in Id_{A}$ y $(a,c)\in R$. Por lo tanto, $(a,c)\in R\circ Id_{A}$.

Por lo tanto, $R\circ Id_{A}=R$.

$\square$

Proposición. Si $R$ es una relación de $A$ en $B$, entonces $Id_{Im\ R}\subseteq R\circ R^{-1}$.

Demostración.

Sea $y\in Im(R)$. Como $y\in Im\ R$ existe $a\in A$ tal que $(a,y)\in R$, y por definición de relación inversa tenemos que $(y,a)\in R^{-1}$.

Encontramos $a\in A$ tal que $(y,a)\in R^{-1}$ y $(a,y)\in R$, esto es $(y,y)\in R\circ R^{-1}$. Así, $Id_{Im\ R}\subseteq R\circ R^{-1}$.

$\square$

Propiedades de la composición

Hemos dicho hasta ahora que la composición es una operación entre dos conjuntos que son relaciones. Por ello, podemos preguntarnos qué pasa con la conmutatividad y la asociatividad de dicha operación.

En general, no es cierto que $R_1\circ R_2=R_2\circ R_1$, es decir, la composición no es conmutativa.

Ejemplo.

Consideremos $X=\set{1,2}$. Sean $R_1=\set{(1,1), (1,2)}$ y $R_2=\set{(1,2),(2,1)}$ relaciones en $X$.

Por un lado tenemos que

$R_1\circ R_2=\set{(2,1), (2,2)}$

y por otro lado

$R_2\circ R_1=\set{(1,2),(1,1)}$.

De modo que $R_1\circ R_2\not=R_2\circ R_1$.

$\square$

El segundo resultado que tenemos es que la asociatividad siempre se cumple.

Proposición. Si $R_1$, $R_2$ y $R_3$ son relaciones, entonces, $(R_3\circ R_2)\circ R_1=R_3\circ (R_2\circ R_1)$.

Demostración.

Sean $R_1$, $R_2$ y $R_3$ relaciones, tenemos que $(x,z)\in (R_3\circ R_2)\circ R_1$ si y sólo si existe $y$ tal que $(x,y)\in R_1$ y $(y,z)\in R_3\circ R_2$ si y sólo si $(x,y)\in R_1$ y existe $w$ tal que $(y,w)\in R_2$ y $(w,z)\in R_3$ para algún $y$ si y sólo si existe $w$ tal que $(x,w)\in R_2\circ R_1$ y $(w,z)\in R_3$ si y sólo si $(x,z)\in R_3\circ(R_2\circ R_1)$.

Por lo tanto, $(R_3\circ R_2)\circ R_1=R_3\circ (R_2\circ R_1)$.

$\square$

Hemos probado que la composición de relaciones es asociativa y a su vez concluimos que en general no conmuta.

Tarea moral

Demuestra que si $R$ es una relación arbitraria, $R\circ \emptyset=\emptyset=\emptyset\circ R$.
Prueba que si $R$ es una relación en $A$, entonces $R=Id_{A}\circ R$.
Sea $R$ una relación de $A$ en $B$. Demuestra que $Id_{\text{DomAct} R}\subseteq R^{-1}\circ R$.
Sean $A= \set{1,2,3}$, $B=\set{1,2}$ y $C=\set{1,2,3,4}$. Sean $R_1=\set{(1,2), (3,1)}$ y $R_2=\set{(1,4), (2,1), (2,3)}$ relaciones de $A$ en $B$ y de $B$ en $C$ respectivamente. Calcula $R_2\circ R_1$.

Más adelante…

Ya hemos hablado de relaciones en general, y de cómo componerlas. A partir de ahora comenzaremos a pedirle más propiedades a nuestras relaciones para que se conviertan en algunos tipos de relaciones muy especiales: funciones, relaciones de equivalencia, órdenes, etc. Comenzaremos a hacer esto en la siguiente entrada, en donde veremos qué se le debe pedir a una relación para que sea una función. Así, todas las funciones son relaciones, sin embargo, no toda relación será función.

Entradas relacionadas

Entrada relacionada: Álgebra Superior I: Relaciones en conjuntos: dominio, codominio y composición
Ir a Teoría de los Conjuntos I
Entrada anterior: Teoría de los Conjuntos I: Relaciones
Siguiente entrada: Teoría de los Conjuntos I: Funciones

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Geometría Analítica I: Grupos de transformaciones

Por Paola Berenice García Ramírez

Deja un comentario

Introducción

En la primera entrada de esta unidad [1a entrada] indicamos que serán muy importantes tanto las propiedades de los vectores como los lugares geométricos vistos en las primeras dos unidades, pues serán de vital apoyo para comprender los tipos de transformaciones que estaremos viendo.

En la entrada anterior [2a entrada] contemplamos los conceptos necesarios de las funciones que nos ayudaron a definir formalmente a una transformación. En ésta entrada vamos a comenzar por dos conjuntos: $\Delta_{2}$ y $\Delta_{3}$, las propiedades que cumplen y que nos ayudarán a comprender la definición de un grupo. Ambos conjuntos son los ejemplos más representativos de los grupos de transformaciones: los grupos simétricos de orden n. Pretendemos dar a conocer el tema en éste primer curso de Geometría Analítica de forma introductoria; pero puede profundizarse en asignaturas más avanzadas de la carrera universitaria, una de ellas es Álgebra Moderna en la Teoría de Grupos.

El conjunto $\Delta_{2}$

Antes que nada nos pondremos de acuerdo en la notación que vamos a usar: $x \mapsto y$ nos indicará que al elemento $x$ le corresponde el elemento $y$ bajo la función correspondiente.

El primero conjunto que conoceremos tiene dos elementos $\{ 0,1 \}$, a quien identificaremos por $\Delta_{2}$ y se lee «delta-dos». ¿Cuáles son las funciones de $\Delta_{2}$ en sí mismas? Primero tenemos a

\begin{align*}
0 & \xmapsto{id} 0\\
1 & \mapsto 1\\
\end{align*}

a quien llamaremos por $id$ (identidad de $\Delta_{2}$); porque al elemento $0$ le corresponde él mismo y al elemento $1$ le corresponde él mismo. La siguiente función es

\begin{align*}
0 & \xmapsto{\rho} 1\\
1 & \mapsto 0\\
\end{align*}

que denotamos por $\rho$. ¿Qué ocurre si recurrimos a la función composición $\rho \circ \rho$? Si comenzamos con $0$ sabemos bajo $\rho$ que $\rho (0) = 1$, por ello

\begin{align*}
(\rho \circ \rho)(0) &= \rho [\rho (0)]\\
& = \rho (1) = 0.\\
\end{align*}

Y si comenzamos con $\rho (1)$, en forma análoga obtendremos $(\rho \circ \rho)(1) = 1$. Podemos darnos cuenta que $\rho$ es su propio inverso, pues $(\rho \circ \rho = id)$.

Otra forma en que podemos trabajar la composición de funciones es siguiendo los elementos mediante una tablita. Vamos a ver que $\rho \circ \rho = id$ como sigue:

\begin{align*}
0 & \xmapsto{p} 1 \xmapsto{p} 0\\
1 & \mapsto 0 \mapsto 1\\
\end{align*}

donde colocamos la función correspondiente sobre cada flecha entre los elementos y nos damos cuenta que los elementos iniciales coinciden con las imágenes finales bajo la composición. Entonces concluimos que se cumple $\rho \circ \rho = id$.

Tenemos otras dos funciones:

\begin{align*}
0 & \xmapsto{C_{0}} 0 \hspace{0.2cm} & 0 \xmapsto{C_{1}} 1\\
1 & \mapsto 0 \hspace{0.18cm} &1 \mapsto 1\\
\end{align*}

e independientemente del elemento inicial, bajo $C_{0}$ corresponde el elemento $0$ y bajo $C_{1}$ corresponde el elemento $1$. Tanto $C_{0}$ como $C_{1}$ se consideran funciones constantes; mientras que las únicas transformaciones que contemplaremos de $\Delta_{2}$ son $ id $ y $ \rho $.

El conjunto $\Delta_{3}$

Ahora consideremos al conjunto $\Delta_{3} := \{ 0,1,2 \}$ e indicaremos las funciones de $\Delta_{3}$ en sí mismo bajo la notación

\begin{align*}
0 & \mapsto x\\
1 & \mapsto y\\
2 & \mapsto z
\end{align*}

donde $x, y, z \in \Delta_{3}$. Como $x, y, z \in \Delta_{3}$ son imágenes arbitrarias, habrán $3^3 = 27$ funciones, pero sólo 6 serán transformaciones. Vamos a explicar porqué sólo 6 transformaciones: puesto que queremos biyectividad, al elegir a $0$ y corresponderle su imagen, entonces al $1$ le podrán corresponder sólo $2$ opciones y a su vez, cuando llegamos al $2$, ya sólo le podrá corresponder $1$ opción. En resumen, en la primera posición hay $3$ opciones, en la segunda hay $2$ opciones y en la tercera sólo $1$ y el número de transformaciones será de $3 \times 2 \times 1 = 6$.

Las primeras 3 transformaciones que veremos son:

\begin{align*}
&0 \xmapsto{id} 0 &0 \xmapsto{\rho_{1}} 1& \hspace{0.2cm} &0 \xmapsto{\rho_{2}} 2\\
&1 \mapsto 1 &1 \mapsto 2 & \hspace{0.2cm} &1 \mapsto 0\\
&2 \mapsto 2 &2 \mapsto 0 & \hspace{0.2cm} &2 \mapsto 1
\end{align*}

De hecho a las 6 transformaciones las visualizaremos como las «simetrías» de un triángulo equilátero. Las primeras 3 corresponden a rotaciones (la identidad es quien rota $0$ grados). Diremos que $\rho_{1}$ y $\rho_{2}$ son inversas, pues $\rho_{1} \circ \rho_{2} = \rho_{2} \circ \rho_{1} = id$ (vamos a dejar esta relación como ejercicio de la tarea moral, para practicar). Es decir, con cualquier elemento inicial, la imagen de la composición será el mismo elemento inicial. Esto quiere decir que una rotación rotará $120°$ en una dirección y al aplicar la segunda rotación rota $120°$ pero en dirección contraria. Los triángulos correspondientes son:

También se cumple que $\rho_{1} \circ \rho_{1} = \rho_{2}$, pues

\begin{align*}
0 & \xmapsto{\rho_{1}} 1 \xmapsto{\rho_{1}} 2\\
1 & \mapsto 2 \mapsto 0 \\
2 & \mapsto 0 \mapsto 1
\end{align*}

Entonces decimos que cumple la siguiente definición:

Definición. Sea $f$ cualquier transformación, decimos que

\begin{equation*}
f^{n} = f \circ f \circ \cdots \circ f,
\end{equation*}

es decir, $f^{n}$ es $f$ compuesta consigo misma n veces.

En nuestro ejemplo, escribiremos que se cumple entonces la relación $\rho_{1}^{2} = \rho_{2}$. Por otro lado, para $\Delta_{3}$ tenemos otras 3 transformaciones llamadas transposiciones que geométricamente las visualizamos como reflexiones y son:

\begin{align*}
&0 \xmapsto{\alpha} 0 & 0 \xmapsto{\beta} 2 & \hspace{0.2cm} & 0 \xmapsto{\gamma} 1\\
&1 \mapsto 2 &1 \mapsto 1 & \hspace{0.2cm} &1 \mapsto 0\\
&2 \mapsto 1 &2 \mapsto 0 & \hspace{0.2cm} &2 \mapsto 2
\end{align*}

El triángulo que representa a estas transformaciones es:

Las direcciones de la flecha dependerán de cada transformación. Ahora vamos a probar una relación que cumple $ \alpha, $ la cual es:

Demostrar que se cumple $\alpha^{2} = id$.

Demostración. En efecto, recordemos que $ \alpha^{2} = \alpha \circ \alpha$, así que desarrollaremos el seguimiento de elementos a través de la composición $\alpha \circ \alpha$ como sigue:

\begin{align*}
0 & \xmapsto{\alpha} 0 \xmapsto{\alpha} 0\\
1 & \mapsto 2 \mapsto 1 \\
2 & \mapsto 1 \mapsto 2
\end{align*}

y observemos que al final de la composición obtuvimos $\alpha^2 (0)=0$, $\alpha^2 (1)=1$, $\alpha^2 (2)=2$ y con ello vemos que $\alpha^{2}=id.$

$\square$

En la sección de tarea moral dejaremos unos ejercicios de práctica sobre más relaciones que cumplen $\alpha$, $\beta$ y $\gamma$; como son $\alpha^2 = \beta^2 = \gamma^2 = id$, $\alpha \circ \beta = \rho_{1}$ y que $\alpha \circ \beta \circ \alpha = \beta \circ \alpha \circ \beta = \gamma$.

A continuación vamos a definir a un conjunto de transformaciones que cumplen ciertas propiedades interesantes y para ejemplificar a dicho conjunto retomaremos uno de los conjuntos vistos en esta entrada.

Grupos de transformaciones

Definición. A un conjunto $G$ de transformaciones de un conjunto $A$ le llamaremos un grupo de transformaciones de $A$ si cumple:

$id_{A} \in G$
$f,g \in G \longrightarrow g \circ f \in G$
$f \in G \longrightarrow f^{-1} \in G$

Como ejemplos, tomemos a $A$ como $A = \Delta_{3}$. Sabemos que tiene 6 elementos, pero un grupo de transformaciones es el de las rotaciones ya que contiene a la identidad $(1)$, es cerrado bajo la composición $(2)$ y es cerrado bajo inversas $(3)$.

Otro grupo de transformaciones de $A=\Delta_{3}$ es el de las transposiciones (o reflexiones) junto con la identidad.

Definición. Dado un conjunto cualquiera de transformaciones de $A$, el grupo que genera es el grupo de transformaciones obtenido de todas las posibles composiciones con elementos de él o sus inversos.

Como ejemplo de un grupo que genera tenemos a $\alpha$ y $\beta$ ya que generan todas las transformaciones de $\Delta_{3}$.

También $\rho_{1}$ genera el grupo de rotaciones de $\Delta_{3}$ ( porque $\rho^{3} = id$, $\rho_{1}$ y $\rho^{2} = \rho_{2}$).

Para terminar con esta entrada daremos un concepto adicional. Si te llamaron la atención los conjuntos $\Delta_{2}$ y $\Delta_{3}$ y quieres saber más de ellos o si hay más conjuntos similares, la respuesta es sí. Pertenecen a un conjunto de transformaciones, el cual definiremos a continuación:

Definición. Al conjunto de todas las transformaciones de un conjunto con $n$ elementos $\Delta_{n} := \{ 0, 1, \cdots, n-1 \}$ se le llama grupo simétrico de orden $n$ y se le denota $S_{n}$. Dicho grupo tiene $n! = n \times (n-1) \times (n-2 ) \cdots \times 2 \times 1$ ($n$ factorial) elementos a los cuales se le llaman permutaciones.

Tarea moral

Considerando el conjunto $\Delta_{3}$ y sus transformaciones $id$, $\rho_{1}$ y $\rho_{2}$ que vimos en esta entrada, demostrar que $\rho_{1}$ y $\rho_{2}$ son inversas, es decir:
1. $\rho_{1} \circ \rho_{2} = \rho_{2} \circ \rho_{1} = id$
Considerando el conjunto $\Delta_{3}$ y sus transformaciones $id$, $\alpha$, $\beta$ y $\gamma$ que vimos en esta entrada, demostrar que se cumplen las relaciones siguientes:
1. $\alpha^2 = \beta^2 = \gamma^2 = id$. [Sugerencia: Hacer cada composición por separado].
2. $\alpha \circ \beta = \rho_{1}$
3. $\alpha \circ \beta \circ \alpha = \beta \circ \alpha \circ \beta = \gamma$.
Demuestren que $\rho_{1}$ genera el grupo de rotaciones de $\Delta_{3}$. [Sugerencia: Demuestren que se cumplen las relaciones $\rho^{3} = id$, y $\rho^{2} = \rho_{2}$), porque $\rho_{1}$ es un elemento de dicho grupo de rotaciones].

Más adelante

En esta entrada vimos que en el conjunto $\Delta_{3}$ hay dos posibles grupos de transformaciones: el de las rotaciones y el de las transposiciones junto con la identidad. Mediante triángulos pudimos visualizar el comportamiento que hay en los elementos iniciales y sus imágenes; con ello se comprende porque están en cada grupo.

En la siguiente entrada continuaremos con un primer grupo de transformaciones en los \mathbb{R}, que es de las transformaciones afines, que tiene una muy buena relación con un lugar geométrico que ya hemos visto: las rectas. La entrada [Rectas en forma paramétrica] de la Unidad 1 nos podrá ayudar como repaso si lo requerimos.

Enlaces

Página principal del curso:
Entrada anterior del curso:
Siguiente entrada del curso: