Introducción

En esta nueva entrada demostraremos algunas de las propiedades del producto cartesiano. Discutiremos sobre si esta operación en conjuntos es conmutativa o asociativa. Para algunos de nuestros ejemplos usaremos los conjuntos $0,1,2,3,4$ que recuerda que definimos en la entrada de axioma de la unión y axioma del par.

Producto cartesiano

Recordemos la definición de producto cartesiano.

Definición. Sean $A$ y $B$ conjuntos cualesquiera, definimos el producto cartesiano de $A$ y $B$, como:

$A\times B=\set{(a,b): a\in A\ y\ b\in B}$.

Ejemplo.

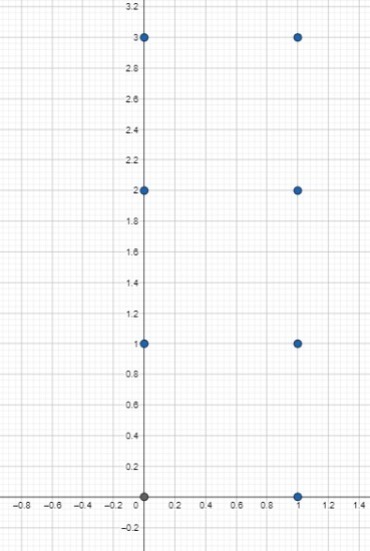
Consideremos los conjuntos $A=\set{0,1}$ y $B=\set{0,1,2,3}$. Tenemos que $A\times B=\set{(0,0),(0,1), (0,2), (0,3), (1,0), (1,1), (1,2), (1,3)}$. De hecho, podemos representar geométricamente a este conjunto como se muestra en la siguiente imagen:

Por supuesto, esta representación es un poco informal pues estamos usando la recta numérica con números reales (que no hemos dicho qué son) y estamos asumiendo cierto orden (del cuál no hemos hablado). Por el momento, piensa que esta representación es sólo para conectar la idea de producto cartesiano con conceptos que has visto en otros cursos.

$\square$

Conmutatividad del producto cartesiano

En general el producto cartesiano no es conmutativo, es decir, si $A$ y $B$ son conjuntos, no necesariamente es cierto que $A\times B=B\times A$.

Ejemplo.

Sean $A=\set{\emptyset}$ y $B=\set{\set{\emptyset}}$, tenemos que:

$A\times B=\set{(\emptyset, \set{\emptyset})}$.

Por otro lado,

$B\times A=\set{(\set{\emptyset},\emptyset)}$.

Dado que tanto $A\times B$ y $B\times A$ sólo tienen un elemento, para que pase que $A\times B=B\times A$, tendría que ocurrir que $(\emptyset,\set{\emptyset})=(\set{\emptyset}, \emptyset)$. Usando el teorema que vimos en la entrada pasada tendríamos que $\emptyset=\set{\emptyset}$ y $\set{\emptyset}=\emptyset$, lo cual no ocurre. Por lo tanto, $A\times B\not=B\times A$.

$\square$

Veamos ahora bajo qué condición el producto cartesiano sí conmuta.

Proposición. Sean $A$ y $B$ conjuntos nos vacíos. Tenemos que $A\times B=B\times A$ si y sólo si $A=B$.

Demostración.

$\rightarrow$] Supongamos que $A$ y $B$ son conjuntos no vacíos tales que $A\times B=B\times A$. Veamos que $A=B$.

Sea $x\in A$. Como $B\not=\emptyset$, existe $y\in B$ y así la pareja $(x,y)\in A\times B$. Por hipótesis $A\times B=B\times A$, por lo que $(x,y)\in B\times A$, esto es $x\in B$ y $y\in A$. En particular, $x\in B$ y por lo tanto, $A\subseteq B$.

Para ver que $B\subseteq A$ seguimos un argumento análogo al anterior. Por lo tanto, $A=B$.

$\leftarrow$] Supongamos ahora que $A=B$. Tenemos que $A\times B=B\times A$.

$\square$

Asociatividad del producto cartesiano

Además de preguntarnos acerca de la conmutatividad podemos preguntarnos si el producto cartesiano es asociativo. Para tratar la asociatividad de una operación son necesarios tres conjuntos, sin embargo, no hemos visto la definición de producto cartesiano para más de dos conjuntos.

Para el producto cartesiano de tres conjuntos, necesitamos definir primero qué es una terna ordenada.

Definición. Sean $a,b,c$ conjuntos, definimos la terna ordenada $(a,b,c)$ como:

$(a,b,c)=((a,b),c)$.

Ejemplo.

\begin{align*}
(\emptyset, \emptyset,\emptyset) &=((\emptyset, \emptyset),\emptyset)\\
&=(\set{\set{\emptyset},\set{\emptyset,\emptyset}},\emptyset)\\
&=(\set{\set{\emptyset}},\emptyset)\\
&=\set{\set{\set{\set{\emptyset}}},\set{\set{\set{\emptyset}},\emptyset}}.
\end{align*}

$\square$

En la definición anterior ponemos en la primera coordenada una pareja. Existe otra manera de proceder, colocando la pareja en la segunda coordenada.

Definición. Sean $a,b,c$ conjuntos, definimos $(a,b,c)_2$ como:

$(a,b,c)_2=(a,(b,c))$.

Ejemplo.

\begin{align*}
(\emptyset, \emptyset,\emptyset)_2 &=(\emptyset, (\emptyset,\emptyset))\\
&=(\emptyset,\set{\set{\emptyset},\set{\emptyset,\emptyset}})\\
&=(\emptyset, \set{\set{\emptyset}})\\
&=\set{\set{\emptyset}, \set{\emptyset, \set{\set{\emptyset}}}}.
\end{align*}

$\square$

Aun cuando $(a,b,c)_2$ también nos permitiría definir el concepto de terna ordenada, es importante usar sólo una pues no son iguales. Los conjuntos que nos resultan son diferentes. Si revisamos con detalle los ejemplos anteriores, tenemos que $((\emptyset,\emptyset),\emptyset)\not=(\emptyset,(\emptyset,\emptyset))$ pues $\set{\set{\set{\emptyset}}}\not=\set{\emptyset}$ dado que sus elementos no son iguales, es decir, $\emptyset\not=\set{\set{\emptyset}}$.

A partir de los conceptos anteriores tenemos que el producto cartesiano también podría definirse de dos maneras diferentes.

Definición. Sean $A,B$ y $C$ conjuntos. Definimos el producto cartesiano de $A$, $B$ y $C$ como:

$A\times B\times C=(A\times B)\times C=\set{((x,y),z): (x,y)\in A\times B\ y\ z\in C}$.

Ejemplo.

Sean $A=B=C=\set{\emptyset}$. Tenemos que:

\begin{align*}
A\times B\times C&=(A\times B)\times C\\
&=(\set{\emptyset}\times\set{\emptyset})\times\set{\emptyset}\\
&= \set{(\emptyset,\emptyset)}\times\set{\emptyset}\\
&=\set{((\emptyset, \emptyset), \emptyset)}.
\end{align*}

$\square$

Una manera alternativa de hacer lo anterior es con las ternas del estilo $(x,y,z)_2$.

Definición. Sean $A,B$ y $C$ conjuntos. Definimos

$(A\times B\times C)_2=A\times (B\times C)=\set{(x,(y,z)): x\in A\ y\ (y,z)\in B \times C}$.

Ejemplo.

Sean $A=B=C=\set{\emptyset}$ conjuntos,

\begin{align*}
A\times (B\times C)&=\set{\emptyset}\times (\set{\emptyset}\times\set{\emptyset})\\
&=\set{\emptyset}\times \set{(\emptyset, \emptyset)}\\
&= \set{(\emptyset,(\emptyset,\emptyset))}.
\end{align*}

$\square$

Revisando los dos ejemplos anteriores tenemos que $A\times(B\times C)\not=(A\times B)\times C)$ pues $(\emptyset,(\emptyset,\emptyset))\in A\times (B\times C)$ y $((\emptyset, \emptyset), \emptyset)\in (A\times B)\times C$ son tales que $(\emptyset, (\emptyset, \emptyset))\not=((\emptyset, \emptyset), \emptyset)$. Concluimos que las definiciones de $A\times B\times C$ y $(A\times B\times C)_2$ son distintas, y en cierto sentido, concluimos que el producto cartesiano no es asociativo.

Tarea moral

• Demuestra que para $a,b,c$ conjuntos se tiene que $(a,b,c)$ es conjunto, y que para $A,B,C$ conjuntos se tiene que $A\times B \times C$ también es conjunto.
• Prueba que $(a,b,c)=(d,e,f)$ si y sólo si $a=d$, $b=e$ y $c=f$.
• Prueba que si $A\not=\emptyset$, entonces $(A\times A)\times A\not=A\times (A\times A)$.
• Demuestra que $A\times B=\emptyset$ si y sólo si $A=\emptyset$ o $B=\emptyset$.
• Muestra que si $C\times D\not=\emptyset$ entonces $C\times D\subseteq A\times B$ si y sólo si $C\subseteq A$ y $D\subseteq B$.

Más adelante…

En la siguiente entrada veremos cómo se comporta el producto cartesiano con las operaciones que tratamos en secciones anteriores como la unión, la intersección y la diferencia. Esto lo podremos hacer pues, como vimos, el producto cartesiano es un conjunto cuyos elementos son parejas ordenadas.

Entradas relacionadas

• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Parejas ordenadas y producto cartesiano
• Siguiente entrada: Teoría de los Conjuntos I: Propiedades del producto cartesiano (parte II)

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»