Archivo de la etiqueta: multiplicación

Álgebra Superior II: Exponencial, logaritmo y trigonometría en los complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Gracias a las entradas anteriores ya hemos desarrollado un buen manejo de los números complejos. Sabemos cómo se construyen y cómo hacer operaciones básicas, incluyendo obtener conjugados, la forma polar, sacar normas y elevar a potencias. También hemos aprendido a resolver varias ecuaciones en los complejos: cuadráticas, sistemas lineales y raíces $n$-ésimas. Todo esto forma parte de los fundamentos algebraicos de $\mathbb{C}$. Ahora hablaremos un poco de la exponencial, el logaritmo y trigonometría en los complejos.

Aunque mencionaremos un poco de las motivaciones detrás de las definiciones, no profundizaremos tanto como con otros temas. Varias de las razones para elegir las siguientes definiciones tienen que ver con temas de ecuaciones diferenciales y de análisis complejo, que no se estudian sino hasta semestres posteriores.

Función exponencial compleja

Recordemos que, para un real $y$, definimos $\text{cis}(y)=\cos y + i \sin y$. La función $\text{cis}$ y la exponenciación en los reales nos ayudarán a definir la exponencial compleja.

Definición. Definimos la función $\exp:\mathbb{C}\to \mathbb{C}$ como $$\exp(x+yi)=e^x\text{cis}(y).$$

Ejemplo 1. Se tiene que $$\exp\left(1+\frac{\pi}{2} i\right) = e^1 \text{cis}\left(\frac{\pi}{2}\right) = ei.$$

$\triangle$

Ejemplo 2. Se tiene que $$\exp(\pi i) = e^0\text{cis}(\pi) = (1)(-1)=-1.$$ Como veremos más abajo, esto lo podemos reescribir como la famosa identidad de Euler $$e^{\pi i}+1=0.$$

$\triangle$

Ejemplo 3. Se tiene que $$\exp(2+3i)=e^2\text{cis}(3).$$ Como $\cos(3)$ y $\sin(3)$ no tienen ningún valor especial, esta es la forma final de la expresión.

$\triangle$

Propiedades de la función exponencial compleja

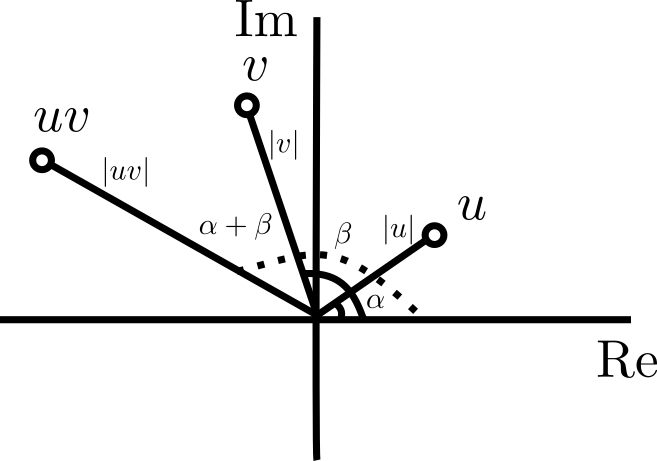
Una buena razón para definir la exponencial así es que si $y=0$, entonces la definición coincide con la definición en los reales: $$\exp(x)=e^x\text{cis}(0)=e^x.$$ Si $x=0$, tenemos que $\exp(iy)=\text{cis}(y)$, de modo que si $w$ tiene norma $r$ y argumento $\theta$, podemos reescribir su forma polar como $$w=r\exp(\theta i),$$ y una forma alternativa de escribir el teorema de De Moivre es $$w^n=r^n\exp(n\theta i).$$

Otra buena razón para definir la exponencial compleja como lo hicimos es que se sigue satisfaciendo que las sumas en la exponencial se abren en productos.

Proposición. Para $w$ y $z$ complejos se tiene que $$E(w+z)=E(w)E(z).$$

Demostración. Escribamos $w=a+bi$ y $z=c+di$ con $a,b,c$ y $d$ reales. Tenemos que
\begin{align*}
\exp(w+z)&=\exp((a+c)+(b+d)i)\\
&=e^{a+c}\text{cis}(b+d).
\end{align*}

Por propiedades de la exponencial en $\mathbb{R}$ tenemos que $e^{a+c}=e^ae^c$. Además, por cómo funciona la multiplicación compleja en términos polares, tenemos que $\text{cis}(b+d)=\text{cis}(b)\text{cis}(d)$. Usando estas observaciones podemos continuar con la cadena de igualdades,

\begin{align*}
&=e^ae^c\text{cis}(b)\text{cis}(d)\\
&=(e^a\text{cis}(b)) (e^c\text{cis}(d))\\
&=\exp(a+bi)\exp(c+di)\\
&=\exp(w)\exp(z).
\end{align*}

$\square$

Como $\exp$ extiende a la exponencial real y se vale abrir las sumas de exponentes en productos, puede ser tentador usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$. Hay que tener cuidado con esta interpretación, pues hasta ahora no hemos dicho qué quiere decir «elevar a una potencia». Cuando lo hagamos, veremos que usar la notación $e^{x+yi}$ sí tiene sentido, pero por el momento hay que apegarnos a la definición.

Hay otras buenas razones para definir la exponencial compleja como lo hicimos. Una muy importante es que es la solución a una ecuación diferencial muy natural. Más adelante, en tu formación matemática, verás esto.

Función logaritmo complejo

Con el logaritmo natural $\ln$ en $\mathbb{R}$ y la multifunción argumento podemos extender el logaritmo a $\mathbb{C}$.

Definición. Definimos la función $L:\mathbb{C}\setminus \{0\} \to \mathbb{C}$ como $$L(z)=\ln \Vert z \Vert + \arg(z) i.$$

Hay que ser un poco más precisos, pues $\arg(z)$ es una multifunción y toma varios valores. Cuando estamos trabajando con logaritmo, lo más conveniente por razones de simetría es que tomemos el argumento en el intervalo $(-\pi,\pi]$. En cursos posteriores hablarás de «otras» funciones logaritmo, y de por qué ésta es usualmente una buena elección.

Ejemplo. Los logaritmos de $i$ y de $-1$ son, respectivamente,
\begin{align*}
L(i)&=\ln \Vert i \Vert + \arg(i) i = \ln(1) + \frac{\pi}{2} i =\frac{\pi}{2} i\\
L(-1)&=\ln \Vert -1 \Vert + \arg(-1) i = \ln(1)+\pi i = \pi i.
\end{align*}

$\triangle$

Propiedades del logaritmo complejo

La función $\exp$ restringida a los números con parte imaginaria en $(-\pi,\pi]$ es invertible y su inversa es $L$. Esto justifica en parte la definición de logaritmo. Demostrar esto es sencillo y queda como tarea moral.

La función $L$ restringida a los reales positivos coincide con la función logaritmo natural, pues para $z=x+0i=x$, con $x>0$ se tiene que $\arg(x)=0$ y entonces $$L(z)=L(x)=\Vert x\Vert+\arg(x)i=x.$$

Como en el caso real, la función logaritmo abre productos en sumas, pero con un detalle que hay que cuidar.

Proposición. Para $w$ y $z$ complejos no $0$, se tiene que $L(wz)$ y $L(w)+L(z)$ difieren en un múltiplo entero de $2\pi i$.

Con la función logaritmo podemos definir potencias de números complejos.

Definición. Para $w,z$ en $\mathbb{C}$ con $w\neq 0$, definimos $$w^z=\exp(zL(w)).$$

Ejemplo. En particular, podemos tomar $w=e$, de donde \begin{align*}e^z&=\exp(zL(e))\\&=\exp(z\ln(e))\\&=\exp(z),\end{align*} de donde ahora sí podemos justificar usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$.

$\square$

Esta definición de exponenciación en $\mathbb{C}$ es buena, en parte, porque se puede probar que se satisfacen las leyes de los exponentes.

Proposición. Para $w, z_1, z_2$ en $\mathbb{C}$, con $w\neq 0$, se cumple que $$z^{w_1+w_2}=z^{w_1}z^{w_2}$$ y que $$(z^{w_1})^{w_2}=z^{w_1w_2}.$$

La demostración es sencilla y se deja como tarea moral.

Funciones trigonométricas complejas

Finalmente, definiremos las funciones trigonométricas en $\mathbb{C}$. Para ello, nos basaremos en la función exponencial que ya definimos.

Definición. Para $z$ cualquier complejo, definimos $$\cos(z)=\frac{e^{iz}+e^{-iz}}{2}$$ y $$\sin(z)=\frac{e^{iz}-e^{-iz}}{2}.$$

Una de las razones por las cuales esta definición es buena es que extiende a las funciones trigonométricas reales. En efecto, si $z=x+0i=x$ es real, entonces $\cos(z)$ es \begin{align*}
\frac{e^{iz}+e^{-iz}}{2}&=\frac{\text{cis}(x)+\text{cis}(-x)}{2}\\
&=\frac{2\cos(x)}{2}\\
&=\cos(x),
\end{align*} y de manera similar para $\sin(z)$.

Las funciones trigonométricas en $\mathbb{C}$ siguen cumpliendo varias propiedades que cumplían en $\mathbb{R}$.

Proposición. Para $w$ y $z$ complejos, se tiene que
\begin{align*}
\cos(w+z)=\cos(w)\cos(z)-\sin(w)\sin(z)\\
\sin(w+z)=\sin(w)\cos(z)+\sin(z)\cos(w).
\end{align*}

Demostración. Procedemos por definición. Tenemos que
\begin{align*}
4&\cos(w)\cos(z)\\
&=(e^{iw}+e^{-iw})(e^{iz}+e^{-iz})\\
&=(e^{i(w+z)}+e^{i(w-z)}+e^{i(z-w)}+e^{i(-z-w)})
\end{align*}

y que
\begin{align*}
4&\sin(w)\sin(z)\\
&=(e^{iw}-e^{-iw})(e^{iz}-e^{-iz})\\
&=(e^{i(w+z)}-e^{i(w-z)}-e^{i(z-w)}+e^{i(-z-w)}),
\end{align*}

de modo que
\begin{align*}
4(\cos(w)&\cos(z)-\sin(w)\sin(z))\\
&=2(e^{i(w+z)}+e^{-i(w+z)})\\
&=4\cos(w+z).
\end{align*}

Dividiendo entre $4$ ambos lados de la igualdad, obtenemos la primer identidad. La segunda se demuestra de manera análoga, y queda como tarea moral.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Determina los valores de $\exp(3+\frac{3\pi}{4}i)$ y de $L(-i)$.
  2. Muestra que para $z$ con parte imaginaria en $(-\pi,\pi]$ se tiene que $L(\exp(z))=z$.
  3. Determina el valor de $(1+i)^{1+i}$.
  4. Muestra las leyes de los exponentes para la exponenciación en $\mathbb{C}$.
  5. Determina el valor de $\sin(i)$ y de $\cos(1+i)$.
  6. Muestra la identidad de seno de la suma de ángulos en $\mathbb{C}$.
  7. Investiga qué otras propiedades de las funciones trigonométricas reales se extienden al caso complejo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Multiplicación en forma polar y fórmula de De Moivre

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

En la entrada anterior hablamos de las coordenadas rectangulares y polares de un número complejo. También, definimos la forma polar de un número complejo. En esta entrada hablaremos de cómo con la forma polar, de los elementos de $\mathbb{C}$, podemos entender fácilmente su multiplicación. Además, usaremos esto para demostrar la fórmula de De Moivre, que nos dice cómo encontrar las potencias de un complejo.

Como pequeño recordatorio, la forma polar del complejo $z=x+iy$ es $z=r(\cos \theta + i \sin \theta)$, en donde $r$ es la norma de $z$ y $\theta$ es el ángulo que hace con el eje real positivo, pensándolo como el punto $(x,y)$. Esto queda resumido por la siguiente figura:

Complejo en forma rectangular y polar
Complejo en forma rectangular y polar

Forma polar, multiplicación y recordatorio trigonométrico

Para ver cómo la forma polar de los complejos nos ayuda a entender la multiplicación en $\mathbb{C}$, necesitamos recordar las siguientes fórmulas trigonométricas
\begin{align*}
\sin (\alpha+\beta) = \sin \alpha \cos \beta + \sin \beta \cos \alpha\\
\cos(\alpha+\beta) = \cos \alpha \cos \beta – \sin \beta \sin \alpha.
\end{align*}

Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r (\cos\alpha+ i \sin \alpha)\\
z&=s(\cos \beta + i \sin \beta)
\end{align*}

y los multiplicamos con la definición, su producto tendría parte real $$rs(\cos\alpha\cos \beta – \sin \alpha\sin \beta) = rs\cos (\alpha+\beta)$$ y parte imaginaria $$rs(\sin \alpha \cos \beta+ \sin\beta\cos\alpha)=rs\sin (\alpha+\beta).$$

Además, como la norma es multiplicativa, tenemos que la norma de $wz$ es $rs$. Con esto mostramos que la forma polar de $wz$ es exactamente $$wz=(rs)(\cos(\alpha+\beta)+i\sin(\alpha+\beta)).$$ Esto queda resumido en el siguiente resultado

Proposición. Si tenemos dos números complejos en forma polar
\begin{align*}
w&=r \text{cis}(\alpha)\\
z&=s\text{cis}(\beta),
\end{align*} entonces la forma polar del producto es $$wz=rs\text{cis}(\alpha+\beta).$$

Otra forma de decirlo es que «al multiplicar complejos, multiplicamos normas y sumamos argumentos». Podemos también ver el resultado de forma geométrica mediante la siguiente figura, en donde marcamos con rojo y azul los factores, y con negro al producto.

Interpretación geométrica de la multiplicación en los complejos
Interpretación geométrica de la multiplicación en los complejos

Ejemplo. Vamos a encontrar la forma rectangular del producto de los complejos
\begin{align*}w& =7 \text{cis}\left( \frac{2\pi}{5} \right)\quad\text{y}\\ z&=2\text{cis}\left(\frac{3\pi}{5}\right).\end{align*}

Por la proposición anterior, el producto es exactamente el complejo
\begin{align*}
14 \text{cis}\left(\frac{2+3}{5}\pi \right)=14 \text{cis} (\pi).
\end{align*}

Esta es la forma polar del producto. Por un problema anterior, sabemos que $\text{cis}(\pi)=-1$, de modo que la forma rectangular del producto es $-14$.

Si tenemos un complejo no nulo en forma polar, podemos entender fácilmente su inverso multiplicativo. Esto está dado por la siguiente proposición, cuya demostración es sencilla y se deja como tarea moral.

Proposición. Sea $w\neq 0$ un complejo con forma polar $w=r\text{cis}(\theta)$. Su inverso multiplicativo es el complejo $r^{-1}\text{cis}(-\theta)$.

Ejemplo. Determinemos el inverso multiplicativo del complejo $$w=\sqrt{3}\text{cis}\left(\frac{3\pi}{7}\right).$$ Para ello, basta usar la proposición anterior, de donde $$w^{-1}=\frac{1}{\sqrt{3}} \text{cis}\left(-\frac{3\pi}{7}\right)=\frac{\sqrt{3}}{3}\text{cis}\frac{11\pi}{7}.$$

$\triangle$

Fórmula de De Moivre

La proposición para multiplicación de complejos se vuelve todavía más útil si la usamos iteradamente para hacer potencias de complejos.

Teorema (fórmula de De Moivre). Si $z$ es un complejo de norma $r$ y argumento $\theta$ y $n$ es un entero positivo, entonces $z^n$ es el complejo de norma $r^n$ y argumento $n\theta$. En otras palabras, si $z=r(\cos \theta + i \sin \theta)=r\text{cis}(\theta)$, entonces $$z^n=r^n (\cos (n\theta)+i\sin (n\theta))= r^n \text{cis} (n\theta).$$

Demostración. Procedemos por inducción sobre $n$. El caso $n=1$ es inmediato. Supongamos que el resultado es cierto para $n$, es decir, que $$z^n=r^n \text{cis} (n\theta).$$

Por hipótesis inductiva, tenemos entonces que la norma de $z^n$ es $r^n$, de modo que $z^{n+1}=z^n z$ tiene norma $r^nr=r^{n+1}$.

También por hipótesis inductiva, $z^n$ tiene argumento $n\theta$. Por cómo funciona la multiplicación compleja, el argumento de $z^{n+1}=z^n z$ es la suma de los argumentos de $z^n$ y $z$, es decir, $n\theta + \theta = (n+1)\theta$. Esto muestra que $$z^{n+1}=r^{n+1}\text{cis}((n+1)\theta),$$ y con esto acabamos el paso inductivo.

$\square$

Ejemplos de aplicación de fórmula de De Moivre

Ejemplo. Veremos quién es la décima potencia del complejo $$z=\sqrt{3}\text{cis} \left(\frac{4\pi}{5}\right).$$ Como este número ya está escrito en forma polar, podemos aplicarle directamente la fórmula de De Moivre:
\begin{align*}
z^{10}&=3^{10/2} \text{cis}\left(\frac{40\pi}{5}\right)\\
&=3^5 \text{cis} (8\pi)\\
&=3^5\\
&=243.
\end{align*}

$\triangle$

El ejemplo anterior nos dice que $z^{10}=243$. En otras palabras, $z$ es una raíz $10$-ésima de $243$. Pero existen otras raíces $10$-ésimas de 243, por ejemplo, tiene dos raíces reales $\sqrt[10]{243}$ y $-\sqrt[10]{243}$. ¿Cuántas raíces tiene entonces en total? ¿Quiénes son? Esto lo veremos en la siguiente entrada.

Veamos otro ejemplo en el que se aplica la fórmula de De Moivre.

Problema. Evalúa la expresión $(1+i)^{30}$, expresando el resultado final en forma rectangular.

Solución. Comenzamos expresando a $(1+i)$ en forma polar. Para ello, notamos que $\Vert 1+i \Vert = \sqrt{2}$, y que $1+i$ hace un ángulo de $\frac{\pi}{4}$ con el eje real positivo. Por el teorema de De Moivre, tenemos que

\begin{align*}
z^{30}&=\sqrt{2}^{30}\text{cis}\left(\frac{30\pi}{4}\right)\\
&=2^{15}\text{cis}\left(\frac{6\pi}{4} \right) \\
&=2^{15}\text{cis}\left(\frac{3\pi}{2} \right) \\
&=2^{15}(-i)\\
&=-2^{15}i.
\end{align*}

En la segunda igualdad usamos que $\frac{30\pi}{4}$ y $\frac{6\pi}{4}$ difieren en un múltiplo entero de $2\pi$. En la cuarta usamos la forma polar de $-i$.

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que para un complejo $z\neq 0$ escrito en forma polar $z=r\text{cis}(\theta)$, su inverso multiplicativo tiene forma polar $r^{-1}\text{cis} (-\theta)$.
  2. Evalúa la multiplicación $wz$, donde $w=2\text{cis}\left(\frac{5\pi}{7}\right)$ y $z=-5\text{cis}\left(\frac{7\pi}{5}\right)$. Expresa la respuesta forma polar.
  3. Haz la multiplicación $wz$, donde $w=3\text{cis}\left(\frac{\pi}{2}\right)$ y $z=4\text{cis}\left(\frac{\pi}{3}\right)$. Expresa la respuesta en forma rectangular.
  4. Sea $z=7\text{cis}\left(\frac{5\pi}{7}\right)$. Expresa $z^3$ en forma polar.
  5. Sea $z=\sqrt[3]{5} \text{cis}\left(\frac{\pi}{3}\right)$. Expresa $z^9$ en forma rectangular.
  6. Toma el complejo $z=-2+2i$. Evalúa la expresión $$1+z+\ldots+z^{29}.$$ Sugerencia: Usa primero la fórmula de suma de términos de una sucesión geométrica, y después la fórmula de De Moivre.

Puedes practicar más estos temas viendo los videos y haciendo los ejercicios de la página de Khan Academy, de su sección de números complejos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Forma polar y cambios de coordenadas de un complejo

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En las entradas anteriores comenzamos a hablar acerca de cómo resolver algunas ecuaciones en $\mathbb{C}$. Platicamos de ecuaciones cuadráticas y la fórmula general. Luego, vimos sistemas de ecuaciones lineales y varios métodos para resolverlos. Lo siguiente que haremos será resolver ecuaciones de la forma $z^n=w$, en donde $w$ en $\mathbb{C}$ y $n$ en $\mathbb{N}$ están dados y $z$ es la variable a determinar. Antes de resolver esta ecuación, necesitamos entender mejor la multiplicación en $\mathbb{C}$, y para ello vamos a estudiar la forma polar de un complejo.

En esta entrada comenzaremos recordando las coordenadas rectangulares de un número complejo, además definiremos sus coordenadas polares. Veremos cómo pasar de coordenadas rectangulares a polares de manera biyectiva, con lo cual podremos definir qué es la forma polar.

Más adelante, la forma polar nos ayudará a entender mejor la geometría de la multiplicación y exponenciación en $\mathbb{C}$. Esto será muy útil cuando queramos «sacar raíces $n$-ésimas», lo cual necesitaremos para resolver ecuaciones del estilo $z^n=w$.

De coordenadas rectangulares a coordenadas polares

Tomemos un número complejo $z=x+yi$ y pensémoslo como un punto del plano complejo, es decir, como el punto $(x,y)$ . Diremos que $(x,y)$ son las coordenadas rectangulares de $z$. Es recomendable recordar la siguiente figura, y regresar a ella frecuentemente.

Complejo en forma rectangular y polar
Complejo en forma rectangular y polar

El número complejo $z$ tiene norma $r=\sqrt{x^2+y^2}$. Además, si $z\neq 0$, tenemos que $z$ define un ángulo $\theta$ con el eje real positivo, medido en el sentido contrario al avance de las manecillas del reloj a partir del eje real positivo, al cual le llamaremos el argumento de $z$ y lo denotaremos por $\text{arg}(z)$. Todos los ángulos que manejamos están en radianes.

Sin embargo, este ángulo no es único. El complejo $z$ define al ángulo $\theta$ pero, por ejemplo, también define al ángulo $\theta+2\pi$, pues la suma de $2\pi$ corresponde a dar una vuelta completa alrededor del origen. Por ello, pensaremos que el argumento de $z$ toma todos los valores $$\{\theta+2k\pi:k\in \mathbb{Z}\}.$$ Así, $\text{arg}(z)$ es una multifunción, algo así como una función, pero que toma varios valores. Cuando digamos que un complejo tiene argumento $\theta$, nos referiremos a $\theta$ o cualquier otro ángulo que difiera un múltiplo entero de $2\pi$ Más adelante hablaremos de esto con detalle.

Aunque haya varios ángulos que le correspondan a $z$, hay uno único en el intervalo $[0,2\pi)$.

Definición. Definimos las coordenadas polares de un número complejo $z=x+yi$ como sigue:

  • Si $z=0$, sus coordenadas polares son $(0,0)$.
  • Si $z\neq 0$, entonces tomamos $r=\Vert z \Vert = \sqrt{x^2+y^2}$ y $\theta$ el único ángulo en $[0,2\pi)$ que hace $z$ con el eje real positivo. Las coordenadas polares de $z$ son $(r,\theta)$.

Observa que $r$ siempre es no negativo y es cero si y sólo si $z=0$. Además por trigonometría para el ángulo $\theta$ se cumple que \begin{align*}\sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r},\end{align*} lo cual nos da la siguiente forma práctica para encontrar $\theta$:

  • Calculamos $\frac{y}{r}$ o $\frac{x}{r}$ (el que parezca más sencillo).
  • Aplicamos una función trigonométrica inversa para reducir el problema a dos opciones.
  • Elegimos la opción correcta de acuerdo al signo de $x$ o $y$.

Ejemplo. Tomemos al complejo $z=3-3\sqrt{3}i$. Vamos a pasarlo a forma polar. Su norma es $\sqrt{9+27}=\sqrt{36}=6$. Para determinar el ángulo $\theta$ que define con el eje real, podemos notar que $$\cos{\theta}=\frac{3}{6}=\frac{1}{2},$$ así que $\theta = \frac{\pi}{3}$ ó $\theta= 2\pi-\frac{\pi}{3}=\frac{5\pi}{3}$, pues son los únicos ángulos en $[0,2\pi)$ con ese coseno. Como la parte imaginaria es negativa, se da el segundo caso. Por lo tanto, las coordenadas polares de $z$ son $\left(6,\frac{5\pi}{3}\right)$.

$\triangle$

De coordenadas polares a coordenadas rectangulares

También hay una forma de pasar de coordenadas polares a coordenadas rectangulares. En efecto, tomemos un real no negativo $r$ y consideremos la pregunta ¿quienes son los números complejos de norma $r$?

Por un lado, si $r=0$, necesitamos que $x^2+y^2=0^2=0$, de donde $x=y=0$, así que las coordenadas rectangulares deben ser $(0,0)$. Por otro lado, si $r>0$, se necesita que $$x^2+y^2=r^2,$$ lo cual, por el teorema de Pitágoras, define una circunferencia de radio $r$ con centro en el origen.

Circunferencia de complejos de norma r.
Circunferencia de complejos de norma $r$

Si además elegimos un ángulo, $\theta$ en $[0,2\pi)$, que el complejo haga con el eje real, entonces queda determinado de manera única. Supongamos que este complejo es $z=x+yi$

Por trigonometría, tenemos que
\begin{align*}x&=r\cos \theta\\ y &= r\sin \theta.\end{align*}

Problema. Determina en la forma $x+yi$ al número complejo cuyas coordenadas polares son $\left(7,\frac{3\pi}{4}\right)$.

Solución. Usamos las fórmulas obtenidas arriba. Tenemos que

\begin{align*}\\
x&=7\cos \frac{3\pi}{4}=7\cdot \left(-\frac{1}{\sqrt{2}}\right)=-\frac{7}{\sqrt{2}}\\
y &= 7\sin \frac{3\pi}{4}= 7\cdot \frac{1}{\sqrt{2}}=\frac{7}{\sqrt{2}}.
\end{align*}

De este modo, el complejo buscado es el $$-\frac{7}{\sqrt{2}}+\frac{7}{\sqrt{2}}.$$

$\square$

Los cambios de coordenadas son inversos entre sí

La primer sección explica cómo de coordenadas rectangulares podemos pasar a coordenadas polares. La anterior dice cómo pasar de coordenadas polares a rectangulares. Resulta que estas operaciones son inversas la una de la otra como veremos en la siguiente:

Proposición. Si tomamos coordenadas polares $(r,\theta)$ de un complejo, las pasamos a coordenadas rectangulares $(x,y)$ y luego éstas las pasamos a coordenadas polares $(r’,\theta’)$ de nuevo, tenemos que $$(r,\theta)=(r’,\theta’).$$

Demostración. En el caso $r=0$, sólo definimos coordenadas polares con $\theta=0$. Al ir a coordenadas rectangulares vamos al punto $(0,0)$, que de nuevo regresa a polares $(0,0)$. Podemos suponer entonces que $r>0$.

Como mencionamos en la segunda sección, las coordenadas rectangulares correspondientes a $(r,\theta)$ son exactamente $$(x,y)=(r\cos \theta,r\sin \theta).$$ Pasemos este complejo a coordenadas polares $(r’,\theta’)$. Usando la identidad pitagórica $\cos ^2\theta + \sin^2 \theta = 1$, la norma de este complejo es
\begin{align*}
\sqrt{r^2\cos^2\theta+r^2\sin^2 \theta} &= r\sqrt{\cos ^2\theta +\sin^2 \theta}\\
&=r\sqrt{1}\\
&=r,
\end{align*}

lo que prueba $r=r’$. Además, como discutimos en la primer sección, tenemos que
\begin{align*}
\sin \theta’ = \frac{r\sin \theta}{r} = \sin \theta\\
\cos \theta’ = \frac{r\cos \theta}{r}=\cos \theta.
\end{align*}

De esta forma, $\theta$ y $\theta’$ son ángulos en $[0,2\pi)$ con el mismo seno y coseno, lo cual implica $\theta=\theta’$.

$\square$

Corolario. El cambio de coordenadas rectangulares a polares , visto como una función de $$\mathbb{R}\times \mathbb{R}$$ a $$(\mathbb{R}^+\times [0,2\pi))\cup \{(0,0)\}$$ es biyectivo.

La forma polar de un número complejo

En las secciones anteriores pensamos a los complejos como parejas ordenadas. Podemos regresar los resultados obtenidos a la forma $x+yi$ de los complejos para justificar la siguiente definición.

Definición. La forma polar de un número complejo $z=x+yi$ es $z=r(\cos \theta + i\sin \theta)$, donde $(r,\theta)$ son las coordenadas polares de $(x,y)$.

Por costumbre, en la forma polar se pone $i$ antes de $\sin \theta$, a diferencia de la forma rectangular, en donde se pone $i$ después de $y$. A veces en expresiones como las de la forma polar aparecen ángulos $\theta$ fuera del rango $[0,2\pi)$. Podemos hacer las cuentas que necesitemos fuera de este rango sin problema. Al final podemos sumar o restar un múltiplo entero de $2\pi$ para caer en el rango $[0,2\pi)$. Esto no cambia el seno ni coseno del ángulo, por lo que no cambia al número complejo.

Como la expresión $ \cos \theta + i\sin \theta$ se usa mucho, usualmente se abrevia.

Definición. Para un ángulo $\theta$ definimos $\text{cis}(\theta) = \cos \theta + i \sin \theta$.

Problema. Determina la forma polar de los complejos $1$, $-1$, $i$ y $-i$.

Solución. Todos estos números tienen norma $1$. Además, hacen ángulos $0, \pi, \frac{\pi}{2}, \frac{3\pi}{2}$ con el eje real positivo, respectivamente. De esta forma, sus coordenadas polares son
\begin{align*}
(1,0)\quad (1,\pi)\quad\left(1,\frac{\pi}{2}\right)\quad \left(1,\frac{3\pi}{2}\right),
\end{align*}

respectivamente.

De esta forma, la forma polar de cada uno es:
\begin{align*}
1&=\cos 0+i \sin 0=\text{cis} (0)\\
-1&=\cos \pi + i \sin \pi = \text{cis} (\pi) \\
i&=\cos \frac{\pi}{2} + i \sin \frac{\pi}{2} = \text{cis} \left(\frac{\pi}{2}\right)\\
-i&= \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2} = \text{cis} \left( \frac{3\pi}{2}\right).
\end{align*}

$\triangle$

Una aclaración muy importante es que la forma polar de $z=x+yi$ no es $r+\theta i$. La forma polar es exactamente el mismo número complejo que el original, simplemente escrito de manera diferente.

Si la forma polar de un complejo es exactamente el mismo número que el original, ¿de qué nos sirve tenerlo en coordenadas polares? Resulta que la multiplicación compleja se entiende mucho mejor en términos de la forma polar. En la siguiente entrada veremos esto y cómo lo podemos usar para encontrar potencias de números complejos fácilmente.

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Determina la forma polar de los siguientes complejos: $7-7i$ y $-2+2\sqrt{3}i$.
  2. Determina la forma rectangular de los complejos con coordenadas polares $\left(2,\frac{\pi}{3}\right)$ y $\left(1, \frac{11\pi}{6}\right)$.
  3. Si la forma polar del complejo $z$ es $r\text{cis} \theta$, ¿quién es la forma polar del conjugado?
  4. ¿Cuáles son aquellos números complejos que se obtienen al variar $\theta$ en la forma polar $3\text{cis}(\theta)$?
  5. ¿Qué figura en el plano definen aquellos números complejos que se obtienen al variar $r$ en la forma polar $r\text{cis}(\pi)$?

Puedes practicar más estos temas viendo los videos y haciendo los ejercicios de la página de Khan Academy, de su sección de números complejos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Sistemas de ecuaciones lineales complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En la entrada anterior comenzamos a hablar acerca de resolver, en los complejos, ecuaciones de distintos tipos. Además, profundizamos en cómo resolver las ecuaciones cuadráticas complejas. En esta entrada platicaremos acerca de los sistemas de ecuaciones lineales complejos.

Resolveremos a detalle el caso de dos variables y dos ecuaciones. Después, hablaremos un poco acerca de sistemas de ecuaciones con más variables. Un estudio cuidadoso de los sistemas de ecuaciones lineales con más variables se hace en los cursos de álgebra lineal. Un muy buen texto para aprender estos temas es el libro Essential Linear Algebra de Titu Andreescu.

Sistemas de ecuaciones lineales complejos con dos incógnitas

Si $a,b$ son elementos de $\mathbb{C}$ y $a\neq 0$, la ecuación lineal $$ax=b$$ tiene una única solución, dada por $x=\frac{b}{a}$, la cual está bien definida pues todo complejo distinto de $0$ tiene inverso multiplicativo.

Si tenemos los números complejos $a,b,c,d,e$ y $f$, el sistema de ecuaciones lineales en los complejos

\begin{align*}
ax+by &= c\\
dx+ey&=f
\end{align*}

puede comportarse de tres formas distintas:

  • Su solución existe y es única.
  • Tiene una infinidad de soluciones.
  • No tiene solución.

Si tiene al menos soluciones distintas, tenemos entonces que tiene una infinidad. Cuando la solución del sistema es única, el sistema se puede resolver por los métodos básicos con los que se resuelve un sistema en $\mathbb{R}$:

  • Por substitución: de la primera ecuación se despeja la variable $x$ y su valor se pone en la segunda ecuación. De ahí, obtenemos una ecuación en $y$. Se despeja $y$ para obtener su valor y con ello se obtiene el valor de $x$.
  • Igualando coeficientes: multiplicamos la primer ecuación por $d$ y la segunda por $-a$. Al sumar ambas ecuaciones resultantes, queda una ecuación lineal en $y$.

Ejemplos de sistemas de ecuaciones lineales complejos

Ejemplo 1. Determina todas las soluciones del sistema
\begin{align*}
2x+iy&= 3+4i\\
ix+5y&= 9 – 4i.
\end{align*}

Solución. Para empezar, multiplicamos la segunda ecuación por $2i$, de donde obtenemos el sistema
\begin{align*}
2x+iy&= 3+4i\\
-2x+10iy&=8+18i.
\end{align*}

Sumando ambas ecuaciones, obtenemos que $11iy=11+22i$. Multiplicando por $-\frac{i}{11}$ de ambos lados, obtenemos $$y=2-i.$$

Substituyendo en la segunda ecuación, notamos que $$2x=3+4i-i(2-i)=2+2i,$$ de donde $x=1+i$. De aquí, la única solución puede ser $x=1+i$ y $y=2-i$, que se puede verificar que en efecto satisfacen la ecuación.

$\triangle$

Ejemplo 2. Determina todas las soluciones del sistema
\begin{align*}
(3+2i)x+iy&= 3+3i\\
(-4+6i)x-2y&= -6 + 6i.
\end{align*}

Solución. Multiplicando la primer ecuación por $2i$ obtenemos que es equivalente a la ecuación $$(-4i+6i)x-2y=-6+6i,$$ es decir, ambas ecuaciones difieren sólo por un factor $2i$, así que son la misma. Si elegimos cualquier valor de $y$, podemos encontrar un valor de $x$ que cumpla con la ecuación. Por ejemplo, tomando $y=1$, de la ecuación obtenemos que $x=1$. Así, esta ecuación tiene una infinidad de soluciones, dadas por elegir un $y$ y definir $x=\frac{3+3i-iy}{3+2i}.$

$\triangle$

Ejemplo 3. Determina todas las soluciones del sistema
\begin{align*}
(1+2i)x+(-2+i)y&= 3+6i\\
3x+3iy&= 8.
\end{align*}

Solución. Supongamos que existe alguna solución para $x$ y $y$. Multipliquemos la primer ecuación por $3$ y la segunda por $1+2i$. Obtenemos que
\begin{align*}
(3+6i)x+(-6+3i)y&= 9+18i\\
(3+6i)x+(-6+3i)y&= 8+16i.
\end{align*}

De aquí, $9+18i=8+16i$, lo cual es una contradicción. Así, esta ecuación no tiene soluciones.

$\triangle$

Método del determinante

Un método más general para resolver sistemas de ecuaciones lineales complejos con dos incógnitas, que nos dice todo lo que puede suceder, es el siguiente. De hecho, exactamente el mismo teorema funciona para $\mathbb{R}$.

Teorema. Sean $a,b,c,d,e$ y $f$ en $\mathbb{C}$. Para el sistema \begin{align*}
ax+by &= c\\
dx+ey&=f
\end{align*}

definimos a su determinante como el número complejo $ae-bd$. Entonces:

  • Si el determinante es distinto de $0$, el sistema tiene una solución única para $x$ y $y$ dada por
    \begin{align*}
    x&=\frac{ce-bf}{ae-bd}\\
    y&=\frac{af-cd}{ae-bd}.
    \end{align*}
  • Si el determinante es $0$, entonces el sistema no tiene solución, o tiene una infinidad.

Demostración. Cuando el determinante no es $0$, resolvemos el sistema por igualación de coeficientes. Multiplicando la primer ecuación por $-d$, la segunda por $a$ y sumando, obtenemos que $$(ae-bd)y=af-cd.$$ Como el determinante no es cero, $$y=\frac{af-cd}{ae-bd}.$$ Así mismo, multiplicando la primer ecuación por $e$, la segunda por $-b$ y sumando, obtenemos de manera análoga que $$x=\frac{ce-bf}{ae-bd}.$$ Así, si existe una solución, debe tener estos valores. Queda como tarea moral verificar que estos valores cumplen.

Cuando el determinante es $0$, tenemos que $ae=bd$. Si $a=b=e=d=0$, para que exista una solución se necesita forzosamente que $c=f=0$, y de hecho en este caso cualquier pareja $x,y$ funciona. Si en este caso alguno de $c$ o $f$ no es $0$, el sistema no tiene solución.

Así, continuando el análisis podemos suponer sin pérdida de generalidad que $a\neq 0$. De este modo, $e=\frac{bd}{a}$, por lo que la segunda ecuación es equivalente a $$dx+\frac{bd}{a}y=f,$$ que es $adx+bdy=af$.

Si $d=0$, tenemos, de la ecuación anterior, que $af=0$ y del determinante que $ae=bd=0$. Como $a\neq 0$, se necesita que $e=f=0$, de modo que en realidad sólo tenemos una ecuación, la primera. Como $a\neq 0$, podemos elegir cualquier valor de $y$ y de ahí despejar el valor de $x$, obteniendo una infinidad de soluciones.

Si $d\neq 0$, entonces la ecuación $adx+bdy=af$ es equivalente a la ecuación $ax+by=\frac{af}{d}$. La primer ecuación y esta implican que si hay solución, entonces $\frac{af}{d}=c$. De ser así ,sólo tenemos una ecuación, pero repetida. Por el mismo argumento de arriba, hay una infinidad de soluciones.

$\square$

Sistemas de ecuaciones lineales complejos con más incógnitas

Los sistemas lineales complejos con más incógnitas se pueden resolver con las mismas técnicas que aquellos en los reales. En cursos como álgebra lineal verás cómo resolver un sistema lineal en general y cómo saber cómo se ven todas sus soluciones. Sin embargo, puedes aprovechar lo que ya sabes del álgebra de los complejos para resolver distintos sistemas lineales.

Problema 1. Resuelve en los complejos el sistema de ecuaciones

\begin{align*}
3a+(2+i)b+(1+2i)c&=1+i\\
3b+(2+i)c&=2+2i\\
3c&=3+3i.
\end{align*}

Solución. Resolvemos el sistema por substitución. Nos conviene empezar con la tercer ecuación, que tiene únicamente una variable. De ella obtenemos que $c=1+i$. Substituyendo en la segunda ecuación, obtenemos que $$3b+(2+i)(1+i)=2+2i,$$ de donde $$3b+1+3i=2+2i,$$ así que $$3b=1-i,$$ entonces $$b=\frac{1}{3}-\frac{1}{3}i.$$

Con los valores de $b$ y $c$ podemos substituir en la primer ecuación. Notando que
\begin{align*}
(2+i)\left(\frac{1}{3}-\frac{1}{3}i\right)=1-\frac{1}{3}i\\
(1+2i)(1+i)=-1+3i\\
(1+i)-\left(1-\frac{1}{3}i\right)-(-1+3i)=1-\frac{5}{3}i,
\end{align*}

obtenemos que $$a=\frac{1}{3}-\frac{5}{9}i.$$

En resumen,
\begin{align*}
a&=\frac{1}{3}-\frac{5}{9}i\\
b&=\frac{1}{3}-\frac{1}{3}i\\
c&=1+i
\end{align*}

es la única posible solución, y se puede mostrar que en efecto satisface las tres ecuaciones.

$\triangle$

Problema 2. Resuelve en los complejos el sistema de ecuaciones

\begin{align*}
(1+5i)a+b+c+d+e&=2\\
a+(1+5i)b+c+d+e&=2\\
a+b+(1+5i)c+d+e&=2\\
a+b+c+(1+5i)d+e&=2\\
a+b+c+d+(1+5i)e&=2.
\end{align*}

Solución. Sumando todas las ecuaciones, tenemos que $$(5+5i)(a+b+c+d+e)=10,$$ de donde obtenemos que
\begin{align*}
a+b+c+d+e&=\frac{2}{1+i}\\
&=1-i.
\end{align*}

De la primera ecuación, obtenemos que \begin{align*}2&=(a+b+c+d+e)+5ia\\&=1-i+5ia,\end{align*} por lo que $$a=\frac{1+i}{5i}=\frac{1}{5}-\frac{1}{5}i.$$ Por simetría, el resto de las variables también tiene este valor, de modo que $$a=b=c=d=e= \frac{1}{5}-\frac{1}{5}i$$ es la única solución.

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Verifica que las soluciones de los ejemplos de sistemas de ecuaciones lineales complejos de dos variables en efecto son soluciones.
  2. Resuelve en los complejos el sistema de ecuaciones \begin{align*}2x+(1+i)y &= 4\\ (5-i)x+(3+2i)y &=0.\end{align*}
  3. En el teorema del método del determinante, cuando el determinante no es cero, encontramos una solución. Verifica que en efecto satisface el sistema original.
  4. Verifica que las soluciones de los ejemplos en varias variables en efecto satisfacen el sistema original.
  5. Resuelve en los complejos el sistema de ecuaciones \begin{align*} x+(1+i)y &= 4\\ y+(2+i)z &= 5\\ z + (3+i)x &= 6.\end{align*}

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: Aritmética de números complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En entradas anteriores de esta sección hablamos de propiedades aritméticas de números enteros. En esta entrada veremos varias de las propiedades aritméticas de los números complejos y cómo se pueden usar para resolver problemas, incluso aquellos en los que los números complejos no están mencionados de manera explícita en el enunciado.

Distintas formas de los números complejos

La forma más común en la que pensamos en números complejos es en su forma rectangular, en donde un complejo se escribe de la forma $z=a+bi$, en donde $a$ y $b$ son números reales y pensamos a $i$ como un número tal que $i^2=-1$. A $a$ le llamamos la parte real y a $b$ la parte imaginaria.

Podemos colocar al complejo $z=a+ib$ en el plano cartesiano, identificándolo con el punto $(a,b)$. De aquí, la forma polar del complejo es $z=r(\cos \theta + i \sin \theta)$, en donde $r$ es la norma $|z|:=\sqrt{a^2+b^2}$ y si $z\neq 0$, $\theta$ es el argumento, que es el ángulo en el sentido antihorario desde el origen entre el eje horizontal y el punto $(a,b)$. Si $z=0+i0=0$, no definimos el argumento.

Forma polar y rectangular de un complejo
Forma polar y rectangular de un complejo.

Así como le hacíamos en el caso de trabajar con módulos, a veces conviene pensar que el argumento es el único ángulo en $[0,2\pi)$ que cumple lo anterior. En otras ocasiones, conviene pensar al argumento como a veces que es la clase de todos los ángulos módulo $2\pi$.

Cuando tenemos a complejos $w=a+ib$ y $z=c+id$ en forma rectangular, su suma $w+z=(a+c) + i(b+d)$ corresponde geométricamente a encontrar la diagonal del paralelogramo definido por $(a,b)$, $(c,d)$ y el origen, pues corresponde justo al punto $(a+c,b+d)$.

Suma de números complejos
Suma de números complejos.

Su multiplicación $wz$ en forma rectangular es $(ac-bd)+(ad+bc)i$, que geométricamente no es tan claro que sea.

La forma exponencial $z=re^{i\theta}$ es simplemente una forma de abreviar a la forma polar, pues por definición $e^{i\theta}=\cos \theta + i \sin \theta$. En forma exponencial, el producto es más sencillo de entender.

Ejercicio. Demuestra lo siguiente:

  • Muestra que la norma es multiplicativa, es decir, que para complejos $r$ y $s$ se tiene que $|rs|=|r||s|$.
  • Muestra que $e^{i\alpha}e^{i\beta}=e^{i(\alpha+\beta)}$.

Sugerencia. Para el primer punto, haz las cuentas usando la forma rectangular. Para el segundo punto, escribe las definiciones de todos los términos en forma polar. Haz las multiplicaciones en el lado izquierdo y usa las fórmulas trigonométricas para sumas de ángulos.

Por el ejercicio anterior, si tenemos a los complejos en forma polar $w=re^{i\alpha}$, $z=se^{i\beta}$, entonces el producto es $wz=rse^{i(\alpha+\beta)}$, de modo que el producto corresponde al complejo con el producto de normas y suma de argumentos. En ocasiones esto nos permite plantear algunos problemas geométricos en términos de números complejos.

Producto de números complejos.
Multiplicación de números complejos.


Aplicaciones de aritmética de complejos

Veamos dos aplicaciones de la teoría anterior a problemas que no mencionan en el enunciado a los números complejos.

Problema. Sean $a$ y $b$ enteros. Muestra que el número $(a^2+b^2)^n$ se puede expresar como la suma de los cuadrados de dos números enteros.

Podría ser tentador usar el binomio de Newton para elevar el binomio a la $n$-ésima potencia. Sugerimos que intentes esto para darte cuenta de las dificultades que presenta.

Sugerencia pre-solución. Escribe a $a^2+b^2$ como el cuadrado de la norma de un complejo y usa que es multiplicativa.

Solución. El número $r=a^2+b^2$ es la norma al cuadrado del número complejo $z=a+ib$. Entonces, el número $r^n=(a^2+b^2)^n$ es la norma al cuadrado del número complejo $z^n=(a+ib)^n$. Pero al desarrollar $(a+ib)^n$ obtenemos únicamente a $i$, potencias de $a$ y de $b$, y coeficientes binomiales. De modo que $z^n=(a+ib)^n=c+id$ con $c$ y $d$ enteros (aquí estamos usando notación adecuada: no es necesario saber quienes son, sólo que son enteros). Así, $r^n=c^2+d^2$ con $c$ y $d$ enteros.

$\square$

Veamos ahora un ejemplo de geometría. Este problema es posible resolverlo de muchas formas, pero notemos que los números complejos nos dan una forma de hacerlo de manera algebraica de manera inmediata.

Problema. En la siguiente figura hay tres cuadrados de lado $1$ pegados uno tras otro. Determina la suma de los ángulos marcados con $\alpha$ y $\beta$.

Problema de suma de ángulos
Determinar el valor de la suma $\alpha+\beta$.

Sugerencia pre-solución. El problema pide determinar una suma de ángulos, así que conviene pensar esta suma de ángulos como el ángulo del producto de dos complejos. Haz tu propia figura, pero ahora sobre el plano complejo.

Solución. El ángulo $\alpha$ es igual al argumento del complejo $2+i$ y el ángulo $\beta$ es igual al argumento del complejo $3+i$. De esta forma, $\alpha+\beta$ es igual al argumento del complejo $(2+i)(3+i)=(6-1)+(2+3)i=5+5i$. Este complejo cae sobre la recta $\text{Re}(z)=\text{Im}(z)$, de modo que su argumento es $\pi / 4$.

$\square$

Este problema también se puede resolver de (numerosas) maneras geométricas, que puedes consultar en este video.

Fórmula de De Moivre

El siguiente teorema se puede demostrar por inducción sobre $n$.

Teorema (fórmula de De Moivre). Para cualquier entero $n$ y ángulo $\theta$ se tiene que $$(\cos \theta + i \sin \theta)^n=\cos (n\theta) + i \sin (n\theta).$$ Dicho de otra forma, en términos de la forma exponencial, se vale usar la siguiente ley de los exponentes $$(e^{\theta i})^n=e^{(n\theta) i}.$$

La fórmula de De Moivre es otra herramienta que ayuda a resolver problemas de números reales enunciándolos en términos trigonométricos. El truco consiste en:

  1. Tomar una expresión real que queramos entender.
  2. Identificarla como la parte real o imaginaria de una expresión compleja.
  3. Usar la aritmética de números complejos para entender la expresión compleja.
  4. Regresar lo que entendamos a los reales.

Veamos un par de ejemplos, relacionados con funciones trigonométricas. Comenzamos con una fórma de encontrar la fórmula para el coseno de cinco veces un ángulo.

Problema. Sea $\theta\in [0,2\pi)$. Expresa a $\cos 5\theta$ en términos de $\cos \theta$.

Sugerencia pre-solución. Identifica a $\cos 5\theta$ como la parte real de un número complejo. Inspírate en la fórmula de De Moivre. Usa binomio de Newton.

Solución. Por la fórmula de De Moivre, $\cos 5\theta$ es la parte real del complejo $(\cos \theta + i \sin \theta)^5$, así que calculemos quién es exactamente este número usando binomio de Newton. Para simplificar la notación, definimos $a=\cos \theta$ y $b=\sin \theta$. Tenemos que

\begin{align*}
(a+ib)^5&=a^5+5a^4(bi)+10a^3(ib)^2+10a^2(ib)^3+5a(ib)^4+(ib)^5\\
&=(a^5-10a^3b^2+5ab^4) + (5a^4b-10a^2b^3+b^5) i.
\end{align*}

Además, por la identidad pitagórica recordemos que $a^2+b^2=1$, de donde $b^2=1-a^2$, de modo que la parte real de la expresión anterior es $$a^5-10a^3(1-a^2)+5a(1-2a^2+a^4),$$ que agrupando es $$16a^5-20a^3+5a.$$ Recordando que $a$ es $\cos \theta$, obtenemos la fórmula final $$\cos 5\theta = 16\cos^5 \theta – 20 \cos^3 \theta + 5\cos \theta.$$

$\square$

Raíces de la unidad

En muchos problemas se utilizan las raíces de la ecuación $x^n=1$.

Teorema. Sea $n\geq 1$ un entero. Las ecuación $x^n=1$ tiene $n$ soluciones complejas, que en el plano complejo forman los vértices del $n$-ágono regular con centro en $0$ y tal que uno de sus vértices es $1$. Si $\omega$ es la raíz de menor argumento positivo, entonces estas soluciones son $1,\omega, \omega^2,\ldots,\omega^{n-1}$.

Raíces de la unidad en los números complejos
Raíces $n$-ésimas de la unidad para $n=5$.

A estas soluciones les llamamos las raíces $n$-ésimas de la unidad. Notemos que $\omega^{n}=1$, y que en general si escribimos a un entero $m$ usando el algoritmo de la división como $m=qn+r$, entonces $\omega^m=\omega^r$. ¡Los productos de raíces de la unidad se comportan como los elementos de $\mathbb{Z}_n$ bajo suma módulo $n$!

Proposición. Sea $n\geq 2$ un entero. La suma de las $n$ raíces $n$-ésimas de la unidad es $0$ y su producto es $1$.

La proposición anterior nos permite, en ocasiones, «filtrar» ciertas expresiones algebraicas. A continuación presentamos un ejemplo, que retomamos de los primeros ejemplos que vimos, cuando estábamos aprendiendo la heurística de encontrar un patrón.

Problema. Determina el valor de la suma $$\binom{100}{0}+\binom{100}{3}+\binom{100}{6}+\ldots+\binom{100}{99}.$$

Sugerencia pre-solución. Si no recuerdas lo que debería salir, vuelve a experimentar con los primeros valores, para cuando en vez de usar $100$ se usan números más chiquitos. Para entender mejor el patron, generaliza el problema, y en vez de sólo tener múltiplos de $3$ abajo, explora también qué sucede cuando tienes los números que dejan residuo $0$, $1$ o $2$ módulo $3$.

Ya que recuerdes la fórmula que queremos, considera una raíz cúbica $\omega$ de la unidad distinta de $1$. Calcula $(1+1)^{100}$, $(1+\omega)^{100}$ y $(1+\omega^2)^{100}$ usando el binomio de Newton y aprovechando que toda potencia de $\omega$ es $1$, $\omega$ u $\omega^2$ para simplificar la notación.

Solución. Sea $\omega$ una raíz cúbica de la unidad distinta de $1$. Tenemos que $\omega^3=1$ y que $1+\omega+\omega^2=0$. De este modo, podemos usar $\omega$ y el binomio de Newton para calcular las siguientes expresiones

\begin{align*}
(1+1)^{100}&=\binom{100}{0}+\binom{100}{1}+\binom{100}{2}+ \binom{100}{3}+ \ldots\\
(1+\omega)^{100}&= \binom{100}{0}+\binom{100}{1}\omega+\binom{100}{2}\omega^2+\binom{100}{3}+\ldots\\
(1+\omega^2)^{100}&= \binom{100}{0}+\binom{100}{1}\omega^2+\binom{100}{2}\omega+ \binom{100}{3}+\ldots
\end{align*}

¿Qué sucede al sumar las tres expresiones? En el lado derecho, cada vez que $m$ es un múltiplo de $3$, tenemos $3\binom{100}{m}$, y cada vez que $m$ no es un múltiplo de $3$, tenemos $$(1+\omega+\omega^2)\binom{100}{m}=0.$$ ¡Se filtran exactamente los coeficientes binomiales con parte inferior múltiplo de $3$! Así, tres veces la suma que buscamos es igual a $$2^{100}+(1+\omega)^{100}+(1+\omega^2)^{100}.$$

Esta ya es una expresión suficientemente cerrada, pero podemos simplificar todavía más:

\begin{align*}
(1+\omega)^{100}&=(-\omega^2)^{100}=\omega^{200}=\omega^2\\
(1+\omega^2)^{100}&=(-\omega)^{100}=\omega\\
(1+\omega)^{100}+(1+\omega^2)^{100}&=\omega^2+\omega=-1.
\end{align*}

Así, la expresión que queremos es $\frac{2^{100}-1}{3}$.

$\square$

Más ejemplos

Puedes ver más ejemplos del uso de esta teoría en la Sección 3.5 del libro Problem Solving through Problems de Loren Larson.