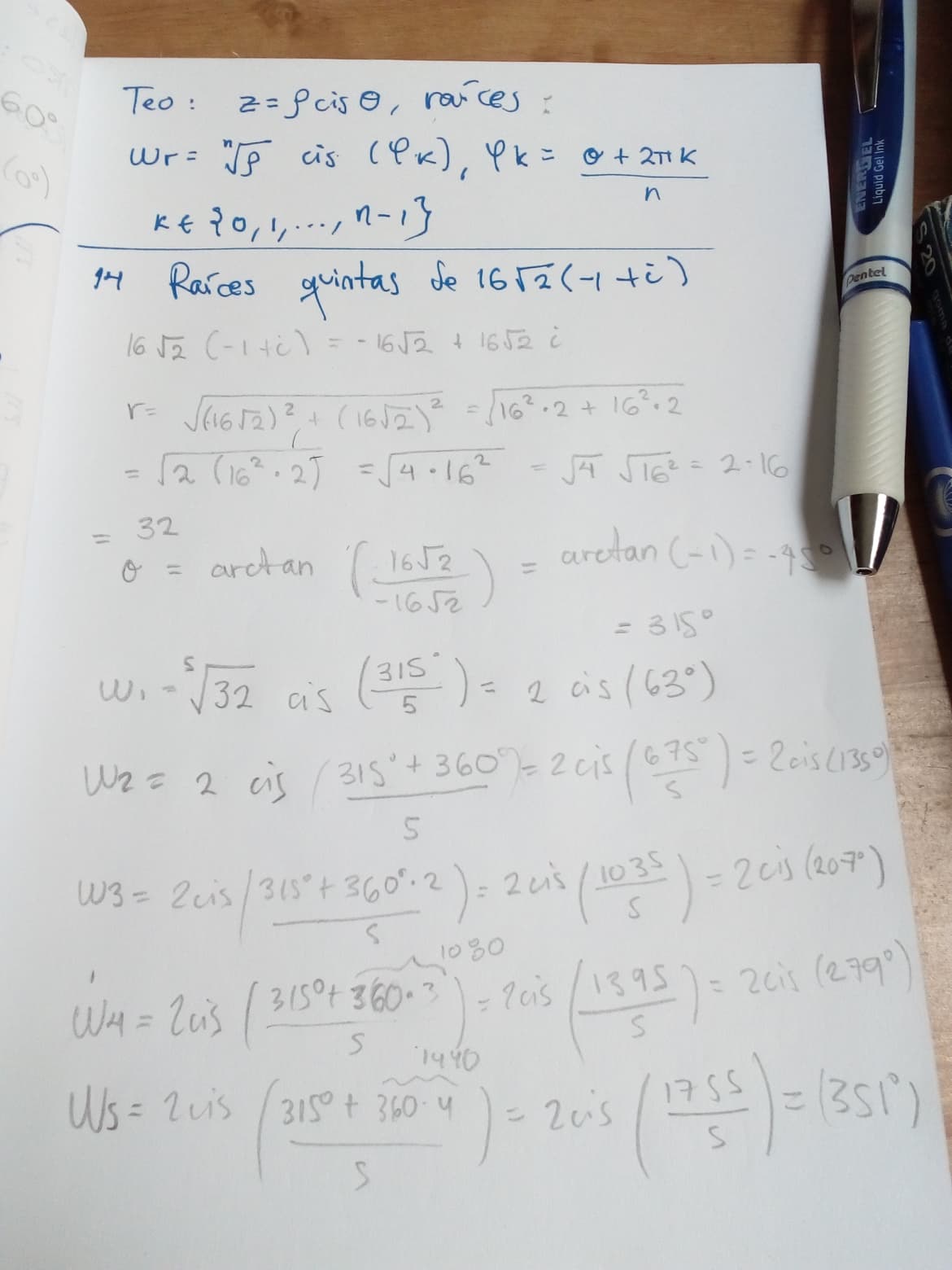Archivo de la etiqueta: complejos

Álgebra Superior II: Inmersión de R en R[x], grado y evaluación de polinomios

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En esta entrada comenzaremos mostrando que podemos usar «la notación de siempre» para los polinomios, usando un símbolo $x$ y potencias. Después de eso, hablaremos del grado de un polinomio y de cómo se comporta con las operaciones que hemos definido. Finalmente, haremos una distinción importante entre los polinomios, y las funciones que inducen.

Como recordatorio, en la entrada anterior definimos a los polinomios y sus operaciones de suma y multiplicación. Para ello, construimos a los polinomios como sucesiones en las que casi todos los términos son $0$. Vimos que bajo estas operaciones se obtiene un dominio entero, es decir, un anillo conmutativo con unidad multiplicativa en donde se vale la regla de cancelación.

Regresando a la notación con $x$ y potencias

Ya dimos cimientos sólidos para construir al anillo de polinomios con coeficientes reales y sus operaciones. Es momento de regresar a la «notación usual» usando $x$ y sus potencias, pues será más práctica en lo que viene.

Para empezar, notemos que a cada real $r$ podemos asociarle el polinomio $(r,\overline{0})$. Esta es una asociación en la que las operaciones de suma y producto de $\mathbb{R}$ se corresponden con las de $\mathbb{R}[x]$.

Observa además que tras esta asociación, el real $0$ es el polinomio $(\overline{0})$ y el real $1$ es el polinomio $(1,\overline{0})$, así que la asociación respeta los neutros de las operaciones. De manera similar se puede mostrar que la asociación respeta inversos aditivos y multiplicativos.

Por esta razón, para un real $r$ podemos simplemente usar el símbolo $r$ para el polinomio $(r,\overline{0})$, y todas las operaciones siguen siendo válidas. Para expresar a cualquier otro polinomio, nos bastará con introducir un símbolo más, y potencias.

Definición. Definimos $x$ como el polinomio $\{0,1,\overline{0}\}$. Para cada natural $n$ definimos $x^n$ como el polinomio $\{a_n\}$ tal que $a_j=1$ si $j=n$ y $a_j=0$ para $j\neq n$.

Ejemplo 1. La definición de arriba implica $x^0=1$ y $x^1=x$. El polinomio $x^3$ es el polinomio $$(0,0,0,1,\overline{0}).$$

$\triangle$

Ejemplo 2. Hagamos la multiplicación de los polinomios $x^2$ y $x^3$. Estos son, por definición, $(0,0,1,\overline{0})$ y $(0,0,0,1,\overline{0})$. Hagamos esta multiplicación con el método de la tabla:

$0$$0$$1$
$0$$0$$0$$0$
$0$$0$$0$$0$
$0$$0$$0$$0$
$1$$0$$0$$1$
Multiplicación de $x^2$ y $x^3$.

El producto es el polinomio $(0,0,0,0,0,1,\overline{0})$, que por definición es el polinomio $x^5$.

$\triangle$

En general, para $m$ y $n$ enteros no negativos se tiene que $x^mx^n = x^{m+n}$, como puedes verificar de tarea moral.

Ya que tenemos al símbolo $x$ y sus potencias, necesitaremos también agregar coeficientes para poder construir cualquier polinomio.

Definición. Dados un polinomio $a:=\{a_n\}$ y un real $r$, definimos al polinomio $ra$ como la sucesión $$ra:=\{ra_n\},$$ es decir, aquella obtenida de multiplicar cada elemento de $a$ por $r$.

Ejemplo 3. Si tomamos al polinomio $$a=\left(0,\frac{1}{2},0,\frac{1}{3},\overline{0}\right)$$ y al real $r=6$, tenemos que $$6a=\left(0,3,0,2,\overline{0}\right).$$

Observa que $3x$ es el polinomio $(0,3,\overline{0})$, que $2x^3$ es el polinomio $(0,0,0,2,\overline{0})$ y que la suma de los dos es precisamente el polinomio $6a$, de modo que podemos escribir $$6a=3x+2x^3.$$

Si tomamos cualquier polinomio $a$ y al real $ 0$, tenemos que $$0a=\{0,0,0,0,\ldots\}=(\overline{0}),$$ es decir, $0a$ es el polinomio cero.

$\triangle$

La siguiente proposición es sencilla y su demostración queda como tarea moral.

Proposición. Para cualquier polinomio $a=\{a_n\}$ en $\mathbb{R}[x]$, los reales $a_0,a_1,\ldots$ son los únicos reales tales que $$a=a_0+a_1x+a_2x^2+a_3x^3+\ldots.$$

Todo lo que hemos discutido en esta sección permite que ahora sí identifiquemos formalmente al polinomio $$(a_0, a_1, a_2, a_3, a_4, a_5, \ldots),$$ con la expresión $$a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+\ldots$$

y que realicemos las operaciones en $\mathbb{R}[x]$ «como siempre», es decir, sumando coeficientes de términos iguales y multiplicando mediante la distribución y reagrupamiento. Así, a partir de ahora ya no usaremos la notación de sucesiones y simplemente escribiremos a los polinomios con la notación de $x$ y sus potencias. También, favoreceremos llamarles a los polinomios $p(x),q(x),r(x),\ldots$ en vez de $a,b,c,\ldots$.

Ejercicio. Realiza la operación $6(\frac{1}{2}+x)(1+3x^2)$.

Solución. Por asociatividad, podemos hacer primero la primer multiplicación, que da $3+6x$. Luego, multiplicamos este polinomio por el tercer término. Podemos usar las propiedades de anillo para distribuir y agrupar, o bien, podemos seguir usando el método de la tabla.

Cuando hacemos lo primero, queda
\begin{align*}
(3+6x)(1+3x^2)&=3+9x^2+6x+18x^3\\
&=3+6x+9x^2+18x^3.
\end{align*}

Si hacemos lo segundo, tendríamos que hacer la siguiente tabla (¡cuidado con dejar el cero correspondiente al término $x$ del segundo factor!)

$3$$6$
$1$$3$$6$
$0$$0$$0$
$3$$9$$18$
Multiplicación de dos polinomios

Leyendo por diagonales, el resultado es $$3+6x+9x^2+18x^3,$$ tal y como calculamos con el primer método.

$\triangle$

Grado de polinomios

Vamos a definir «grado» para todo polinomio que no sea el polinomio $0$. Es muy importante recordar que el polinomio $0$ no tiene grado.

Definición. Un polinomio $p(x)$ en $\mathbb{R}[x]$ es de grado $n$ si es de la forma $$p(x)=a_0+a_1x+\ldots+a_nx^n,$$ para reales $a_0,\ldots,a_n$ y $a_n\neq 0$. Al grado de $p(x)$ lo denotamos por $\deg(p(x))$.

Por la discusión de la sección anterior, el grado está bien definido. En términos de la sucesión correspondiente al polinomio, su grado es el mayor entero que sea subíndice de una entrada no cero.

Ejemplo 1. El grado del polinomio $p(x)=3$ es $0$. De hecho, todo polinomio que viene de un real tiene grado $0$. Excepto el polinomio $0$.

El grado del polinomio $q(x)=1+2x^3+3x^7$ es $7$.

Sin embargo, el polinomio $r(x)=0$ no tiene grado, pues es el polinomio $0$.

Notemos que el polinomio $s(x)=2+4x$ se escribe como $(2,4,\overline{0})$ en notación de sucesión. La entrada $0 $ es $2$, la entrada $1$ es $4$ y el resto de las entradas son $0$. El grado de $s(x)$ es $1$, que es precisamente la posición de la última entrada distinta de $0$ en su notación de sucesión.

$\triangle$

El siguiente resultado habla de cómo interactúa el grado con operaciones de polinomios.

Proposición. Si $p(x)$ y $q(x)$ son polinomios en $\mathbb{R}[x]$ distintos de cero, entonces:

  • El grado del producto cumple $$\deg(p(x)q(x)) = \deg(p(x))+\deg(q(x)).$$
  • El grado de la suma cumple $$\deg(p(x)+q(x))\leq \max(\deg(p(x)),\deg(q(x))).$$
  • Si $\deg(p(x))>\deg(q(x))$, entonces $$\deg(p(x)+q(x))=\deg(p(x)).$$

Demostración. Supongamos que los grados de $p(x)$ y $q(x)$ son, respectivamente, $m$ y $n$, y que $p(x)$ y $q(x)$ son
\begin{align*}
p(x)&=a_0+a_1x+\ldots+a_mx^m\\
q(x)&=b_1+b_1x+\ldots+b_nx^n.
\end{align*}
La demostración de la primera parte ya la hicimos en la entrada anterior. En la notación que estamos usando ahora, vimos que el coeficiente de $x^{m+n}$ en $p(x)q(x)$ es justo $a_mb_n\neq 0$, y que este es el término de mayor exponente.

Para la segunda y tercera partes, podemos asumir que $m\geq n$. Tenemos que $p(x)+q(x)$ es $$\left(\sum_{i=0}^n (a_i+b_i)x^i\right) + a_{n+1}x^{n+1}+\ldots+a_mx^m.$$ De aquí, se ve que el máximo exponente que podría aparecer es $m$, lo cual prueba la segunda parte.

Para la tercer parte, cuando $m>n$ tenemos que el coeficiente de $x^m$ es $a_m\neq 0$, y que es el término con mayor exponente. Así, el grado de la suma es $m$.

$\square$

La hipótesis adicional del tercer punto es necesaria, pues en la suma de dos polinomios del mismo grado, es posible que «se cancele» el término de mayor grado.

Ejemplo 2. El producto de los polinomios $1+x+x^2+x^3$ y $1-x$ es $1-x^4$. Esto concuerda con lo que esperábamos de sus grados. El primero tiene grado $3$, el segundo grado $1$ y su producto grado $4=3+1$.

La suma de los polinomios $1+\pi x^3 + \pi^2 x^5$ y $1-\pi x^3$ es $2+\pi^2x^5$, que es un polinomio de grado $5$, como esperaríamos por la tercer parte de la proposición.

La suma de los polinomios $4x^5+6x^7$ y $6x^5+4x^7$ es $10x^5+10x^7$. Es de grado $7$, como esperaríamos por la segunda parte de la proposición.

Sin embargo, en la suma de polinomios el grado puede disminuir. Por ejemplo, los polinomios $1+x^3-x^7$ y $1+x^2+x^7$ tienen grado $7$, pero su suma es el polinomio $2+x^2+x^3$, que tiene grado $3$.

$\triangle$

Evaluación de polinomios e introducción a raíces

Es importante entender que hay una diferencia entre un polinomio, y la función que induce. Por la manera en que definimos a los polinomios, «en el fondo» son sucesiones, incluso con la nueva notación de $x$ y potencias. Sin embargo, cualquier polinomio define una función.

Definición. Si tenemos un polinomio $$p(x)=a_0+a_1x+\ldots+a_nx^n$$ en $\mathbb{R}$, éste define una función aplicar $p$ que es una función $f_p:\mathbb{R}\to \mathbb{R}$ dada por $$f_p(r)=a_0+a_1r+a_2r^2+\ldots+a_nr^n$$ para todo $r\in \mathbb{R}$.

Ejemplo 1. El polinomio $p(x)=3x^2+4x^3$ induce a la función $f_p:\mathbb{R}\to \mathbb{R}$ tal que $f_p(r)=3r^2+4r^3$. Tenemos, por ejemplo, que $$f_p(1)=3\cdot 1^2 + 4\cdot 1^3 = 7$$ y que $$f_p(2)=3\cdot 2^2 + 4\cdot 2^3=44.$$

$\triangle$

Como las reglas de los exponentes y la multiplicación por reales funciona igual en $\mathbb{R}$ que en $\mathbb{R}[x]$, la evaluación en un real $r$ obtiene exactamente lo mismo a que si simplemente reemplazamos $x$ por $r$ y hacemos las operaciones. Por ello, usualmente no distinguimos entre $p(x)$ y $f_p$, su función evaluación, y para un real $r$ usamos simplemente $p(r)$ para referirnos a $f_p(r)$.

De manera totalmente análoga, podemos pensar a $p(x)$ como una función $p:\mathbb{C}\to \mathbb{C}$. También, como comentamos al inicio, podemos definir a los polinomios con coeficientes complejos, es decir a $\mathbb{C}[x]$, y pensarlos como funciones.

Es momento de introducir una definición clave para lo que resta del curso.

Definición. Sea $p(x)$ un polinomio en $\mathbb{R}[x]$ o $\mathbb{C}[x]$ y sea $r$ un real o complejo. Decimos que $r$ es una raíz de $p(x)$ si $p(r)=0$.

Ejemplo 2. El polinomio $p(x)=3$ no tiene raíces, pues para cualquier real o complejo $r$ se tiene $p(r)=3\neq 0$. Por otro lado, cualquier real o complejo es raíz del polinomio $z(x)=0$.

El polinomio $q(x)=x^2+1$ no tiene raíces en $\mathbb{R}$ pues $q(r)\geq 1$ para cualquier real $r$. Pero sí tiene raíces en $\mathbb{C}$, pues $$q(i)=i^2+1=-1+1=0.$$

El polinomio $s(x)=x(x-1)(x-1)=x^3-2x^2+x$ tiene como únicas raíces a $ 0$ y $1$, lo cual se puede verificar fácilmente antes de hacer la multiplicación. Esto debería darnos la intuición de que conocer a las raíces de un polinomio nos permite factorizarlo y viceversa. Esta intuición es correcta y la formalizaremos más adelante.

$\triangle$

Cuando hablamos de los números complejos, vimos cómo obtener las raíces de los polinomios de grado $2$, y de los polinomios de la forma $x^n-a$ en $\mathbb{C}$. La mayor parte de lo que haremos de aquí en adelante en el curso será entender a las raíces reales y complejas de más tipos de polinomios.

Más adelante…

Ya que hemos formalizado la notación estándar que conocemos de los polinomios, su estudio podrá ser más cómodo, hacemos énfasis en que casi todas las definiciones que dimos en esta sección se apoyaros simplemente en un uso adecuado de la notación; por lo que no hay que perder de vista que en el fondo, los polinomios siguen siendo sucesiones de números, y que el símbolo $x$ solo es una forma de representar la sucesión $(0,1,\overline{0})$.

Aun así, hemos justificado que este cambio de notación no tiene nada que envidiar a la notación original, por lo que en las siguientes entradas, ocuparemos la notación más familiar, lo cual será una pieza clave, para hacer más legibles las demostraciones en las siguientes entradas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Pasa el polinomio $(0,0,0,0,4,0,3,\overline{0})$ a notación con $x$ y potencias. Luego, pasa el polinomio $1-x^3+x^6-x^9$ a notación de sucesión. Suma ambos polinomios y exprésalos en notación con $x$. Multiplícalos usando distribución y agrupamiento. Multiplícalos usando una tabla.
  2. Prueba usando la definición de multiplicación y de $x^n$ que para $m$ y $n$ enteros no negativos se tiene que $x^{m+n}= x^m x^n$.
  3. Toma $P_1(x),\ldots,P_m(x)$ polinomios en $\mathbb{R}[x]$ de grado $n_1,\ldots,n_m$ respectivamente. ¿Cuál es el grado de $P_1(x)+\ldots+P_m(x)$? ¿Y el grado de $P_1(x)\cdot \ldots \cdot P_m(x)$?
  4. Usando distribución y agrupamiento, muestra que para cada entero positivo $n$ se cumple que $$(1-x)(1+x+x^2+\ldots+x^{n-1})=1-x^n.$$
  5. Justifica que si $r(x)$ es un polinomio y $f_r$ es la función aplicar $r$, entonces para cualesquiera polinomios $p(x)$ y $q(x)$, se tiene que $f_p+f_q=f_{p+q}$ y que $f_pf_q=f_{pq}$.

Para practicar la aritmética de polinomios, puedes ir a la sección correspondiente de Khan Academy.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Problemas de exponencial, logaritmo y trigonometría en los complejos

Por Claudia Silva

Deja un comentario

Introducción

En entradas anteriores, vimos la construcción de los números complejos, sus operaciones y varias de sus características algebraicas. Conociendo ya las funciones exponencial y logaritmo, así como las funciones trigonométricas seno y coseno, vamos a iniciar con un breve análisis geométrico de la función exponencial. Posteriormente pasaremos a hacer unos ejercicios simples de operar dichas funciones en números complejos concretos.

Geometría de la exponencial compleja

Para empezar, estudiamos qué le hace la función exponencial al plano complejo de manera geométrica. Para hacer esto, tomamos varias rectas en el plano complejo para entender en qué se transforman tras aplicarles la función exponencial.

A grandes rasgos, cuando tomamos una recta vertical, la imagen de esta le da la vuelta al origen repetidamente. Cuando tomamos una recta horizontal, su imagen es un rayo que emana del origen (sin tocarlo).

En este video se explican estas ideas de manera visual.

Calcular una exponencial compleja

Lo siguiente que haremos es resolver un ejercicio de calcular la exponencial de un número complejo. Recuerda que, por definición, se tiene que $$e^{x+iy}=e^x\text{cis}(y).$$

Ejercicio. Expresa $e^{4+\frac{\pi}{6}i}$ en la forma $x+iy$.

Problema de logaritmo complejo

Recuerda que el logaritmo complejo funciona como inverso de la función exponencial. Para que esto sea cierto, tenemos que restringir la exponencial a una franja del plano complejo.

Por definición, tenemos que $$L(z)=\ln \norm{z} + \text{arg}(z)i.$$ Para que la definición funcione bien, es necesario que tomemos el argumento en el intervalo $(-\pi,\pi]$.

Resolveremos el siguiente ejercicio.

Ejercicio. Calcula $L\left(\frac{1}{2}+\frac{\sqrt{3}}{2} i\right)$.

Problema de trigonometría compleja

Por último, haremos un ejercicio de calcular una función trigonométrica compleja. Sólo necesitaremos la definición de la función coseno, pero por conveniencia, a continuación recordamos tanto la definición de seno, como la de coseno.

\begin{align*}
\cos(z)=\frac{e^{zi}+e^{-zi}}{2},
\sin(z)=\frac{e^{zi}-e^{-zi}}{2}.
\end{align*}

Con esto en mente, resolveremos el siguiente ejercicio.

Ejercicio. Calcula $\cos\left(\frac{\pi}{2}+\frac{\pi}{2} i\right)$.

Más tarde les subo fotos por si alguien tiene dificultades para ver los videos.

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Problemas de fórmula de De Moivre y raíces n-ésimas

Por Claudia Silva

2 respuestas

Introducción

En una entrada anterior, vimos cómo se comporta la multiplicación en forma polar y cómo podemos aprovechar esto para hacer potencias. Concretamente, el teorema de De Moivre es muy útil para elevar complejos a potencias sin tener que hacer gran cantidad de productos.

Los primeros dos videos son ejercicios que ejemplifican lo anterior. Después, usamos lo que aprendimos en la entrada de raíces $n$-ésimas para resolver dos problemas más.

Al final, compartimos un enlace en el que puedes practicar más con operaciones de números complejos.

Problemas de fórmula de De Moivre

Para empezar, vemos dos problemas de exponenciación completa. El primero es una aplicación directa de la fórmula de De Moivre.

Problema. Usa el teorema de De Moivre para elevar a la potencia indicada $$\left(\sqrt{3}(\cos 25^\circ + i \sin 25^\circ\right)^6.$$

En algunos problemas es posible que sea necesario primero obtener la forma polar de un complejo antes de poder usar la fórmula de De Moivre. El segundo problema es un ejemplo de esto.

Problema. Encuentra el valor de $(\sqrt{3}-i)^{12}$.

Problemas de raíces $n$-ésimas

Si ahora, en vez de querer elevar a cierta potencia, queremos obtener raíces $n$-ésimas, con el uso de un poderoso teorema que dedujimos a partir de la fórmula de De Moivre, sabemos que son exactamente $n$ raíces, y podemos calcularlas explícitamente. A continuación, vemos dos ejercicios que ejemplifican lo anterior.

Problema. Obtén las raíces cúbicas del complejo $3+4i$.

Problema. Obtén las raíces quintas del complejo $16\sqrt{2}(-1+i)$.

Ojo. En algún momento del siguiente video se encuentra que el ángulo es $360^\circ – 45^\circ$. Sin embargo, debe decir $180^\circ – 45^\circ$, pues se debe estar en el cuadrante 2, ya que la parte real es negativa y la compleja es positiva.

Fotos de los ejercicios de hoy

Finalmente, les dejo fotos de lo resuelto en los vídeos, para quienes tengan dificultades para ver los vídeos. En la tercera foto no están tan desarrolladas las cuentas como en el vídeo.

Problemas de fórmula de De Moivre, 1
Problemas de fórmula de De Moivre y de raíces
Problemas de raíces n-ésimas.

Más material de De Moivre y raíces

Puedes practicar más acerca de exponenciación y raíces complejas con los videos y ejercicios del tema en Khan Academy.

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Exponencial, logaritmo y trigonometría en los complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Gracias a las entradas anteriores ya hemos desarrollado un buen manejo de los números complejos. Sabemos cómo se construyen y cómo hacer operaciones básicas, incluyendo obtener conjugados, la forma polar, sacar normas y elevar a potencias. También hemos aprendido a resolver varias ecuaciones en los complejos: cuadráticas, sistemas lineales y raíces $n$-ésimas. Todo esto forma parte de los fundamentos algebraicos de $\mathbb{C}$. Ahora hablaremos un poco de la exponencial, el logaritmo y trigonometría en los complejos.

Aunque mencionaremos un poco de las motivaciones detrás de las definiciones, no profundizaremos tanto como con otros temas. Varias de las razones para elegir las siguientes definiciones tienen que ver con temas de ecuaciones diferenciales y de análisis complejo, que no se estudian sino hasta semestres posteriores.

Función exponencial compleja

Recordemos que, para un real $y$, definimos $\text{cis}(y)=\cos y + i \sin y$. La función $\text{cis}$ y la exponenciación en los reales nos ayudarán a definir la exponencial compleja.

Definición. Definimos la función $\exp:\mathbb{C}\to \mathbb{C}$ como $$\exp(x+yi)=e^x\text{cis}(y).$$

Ejemplo 1. Se tiene que $$\exp\left(1+\frac{\pi}{2} i\right) = e^1 \text{cis}\left(\frac{\pi}{2}\right) = ei.$$

$\triangle$

Ejemplo 2. Se tiene que $$\exp(\pi i) = e^0\text{cis}(\pi) = (1)(-1)=-1.$$ Como veremos más abajo, esto lo podemos reescribir como la famosa identidad de Euler $$e^{\pi i}+1=0.$$

$\triangle$

Ejemplo 3. Se tiene que $$\exp(2+3i)=e^2\text{cis}(3).$$ Como $\cos(3)$ y $\sin(3)$ no tienen ningún valor especial, esta es la forma final de la expresión.

$\triangle$

Propiedades de la función exponencial compleja

Una buena razón para definir la exponencial así es que si $y=0$, entonces la definición coincide con la definición en los reales: $$\exp(x)=e^x\text{cis}(0)=e^x.$$ Si $x=0$, tenemos que $\exp(iy)=\text{cis}(y)$, de modo que si $w$ tiene norma $r$ y argumento $\theta$, podemos reescribir su forma polar como $$w=r\exp(\theta i),$$ y una forma alternativa de escribir el teorema de De Moivre es $$w^n=r^n\exp(n\theta i).$$

Otra buena razón para definir la exponencial compleja como lo hicimos es que se sigue satisfaciendo que las sumas en la exponencial se abren en productos.

Proposición. Para $w$ y $z$ complejos se tiene que $$E(w+z)=E(w)E(z).$$

Demostración. Escribamos $w=a+bi$ y $z=c+di$ con $a,b,c$ y $d$ reales. Tenemos que
\begin{align*}
\exp(w+z)&=\exp((a+c)+(b+d)i)\\
&=e^{a+c}\text{cis}(b+d).
\end{align*}

Por propiedades de la exponencial en $\mathbb{R}$ tenemos que $e^{a+c}=e^ae^c$. Además, por cómo funciona la multiplicación compleja en términos polares, tenemos que $\text{cis}(b+d)=\text{cis}(b)\text{cis}(d)$. Usando estas observaciones podemos continuar con la cadena de igualdades,

\begin{align*}
&=e^ae^c\text{cis}(b)\text{cis}(d)\\
&=(e^a\text{cis}(b)) (e^c\text{cis}(d))\\
&=\exp(a+bi)\exp(c+di)\\
&=\exp(w)\exp(z).
\end{align*}

$\square$

Como $\exp$ extiende a la exponencial real y se vale abrir las sumas de exponentes en productos, puede ser tentador usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$. Hay que tener cuidado con esta interpretación, pues hasta ahora no hemos dicho qué quiere decir «elevar a una potencia». Cuando lo hagamos, veremos que usar la notación $e^{x+yi}$ sí tiene sentido, pero por el momento hay que apegarnos a la definición.

Hay otras buenas razones para definir la exponencial compleja como lo hicimos. Una muy importante es que es la solución a una ecuación diferencial muy natural. Más adelante, en tu formación matemática, verás esto.

Función logaritmo complejo

Con el logaritmo natural $\ln$ en $\mathbb{R}$ y la multifunción argumento podemos extender el logaritmo a $\mathbb{C}$.

Definición. Definimos la función $L:\mathbb{C}\setminus \{0\} \to \mathbb{C}$ como $$L(z)=\ln \Vert z \Vert + \arg(z) i.$$

Hay que ser un poco más precisos, pues $\arg(z)$ es una multifunción y toma varios valores. Cuando estamos trabajando con logaritmo, lo más conveniente por razones de simetría es que tomemos el argumento en el intervalo $(-\pi,\pi]$. En cursos posteriores hablarás de «otras» funciones logaritmo, y de por qué ésta es usualmente una buena elección.

Ejemplo. Los logaritmos de $i$ y de $-1$ son, respectivamente,
\begin{align*}
L(i)&=\ln \Vert i \Vert + \arg(i) i = \ln(1) + \frac{\pi}{2} i =\frac{\pi}{2} i\\
L(-1)&=\ln \Vert -1 \Vert + \arg(-1) i = \ln(1)+\pi i = \pi i.
\end{align*}

$\triangle$

Propiedades del logaritmo complejo

La función $\exp$ restringida a los números con parte imaginaria en $(-\pi,\pi]$ es invertible y su inversa es $L$. Esto justifica en parte la definición de logaritmo. Demostrar esto es sencillo y queda como tarea moral.

La función $L$ restringida a los reales positivos coincide con la función logaritmo natural, pues para $z=x+0i=x$, con $x>0$ se tiene que $\arg(x)=0$ y entonces $$L(z)=L(x)=\Vert x\Vert+\arg(x)i=x.$$

Como en el caso real, la función logaritmo abre productos en sumas, pero con un detalle que hay que cuidar.

Proposición. Para $w$ y $z$ complejos no $0$, se tiene que $L(wz)$ y $L(w)+L(z)$ difieren en un múltiplo entero de $2\pi i$.

Con la función logaritmo podemos definir potencias de números complejos.

Definición. Para $w,z$ en $\mathbb{C}$ con $w\neq 0$, definimos $$w^z=\exp(zL(w)).$$

Ejemplo. En particular, podemos tomar $w=e$, de donde \begin{align*}e^z&=\exp(zL(e))\\&=\exp(z\ln(e))\\&=\exp(z),\end{align*} de donde ahora sí podemos justificar usar la notación $e^{x+yi}$ en vez de $\exp(x+yi)$.

$\square$

Esta definición de exponenciación en $\mathbb{C}$ es buena, en parte, porque se puede probar que se satisfacen las leyes de los exponentes.

Proposición. Para $w, z_1, z_2$ en $\mathbb{C}$, con $w\neq 0$, se cumple que $$z^{w_1+w_2}=z^{w_1}z^{w_2}$$ y que $$(z^{w_1})^{w_2}=z^{w_1w_2}.$$

La demostración es sencilla y se deja como tarea moral.

Funciones trigonométricas complejas

Finalmente, definiremos las funciones trigonométricas en $\mathbb{C}$. Para ello, nos basaremos en la función exponencial que ya definimos.

Definición. Para $z$ cualquier complejo, definimos $$\cos(z)=\frac{e^{iz}+e^{-iz}}{2}$$ y $$\sin(z)=\frac{e^{iz}-e^{-iz}}{2}.$$

Una de las razones por las cuales esta definición es buena es que extiende a las funciones trigonométricas reales. En efecto, si $z=x+0i=x$ es real, entonces $\cos(z)$ es \begin{align*}
\frac{e^{iz}+e^{-iz}}{2}&=\frac{\text{cis}(x)+\text{cis}(-x)}{2}\\
&=\frac{2\cos(x)}{2}\\
&=\cos(x),
\end{align*} y de manera similar para $\sin(z)$.

Las funciones trigonométricas en $\mathbb{C}$ siguen cumpliendo varias propiedades que cumplían en $\mathbb{R}$.

Proposición. Para $w$ y $z$ complejos, se tiene que
\begin{align*}
\cos(w+z)=\cos(w)\cos(z)-\sin(w)\sin(z)\\
\sin(w+z)=\sin(w)\cos(z)+\sin(z)\cos(w).
\end{align*}

Demostración. Procedemos por definición. Tenemos que
\begin{align*}
4&\cos(w)\cos(z)\\
&=(e^{iw}+e^{-iw})(e^{iz}+e^{-iz})\\
&=(e^{i(w+z)}+e^{i(w-z)}+e^{i(z-w)}+e^{i(-z-w)})
\end{align*}

y que
\begin{align*}
4&\sin(w)\sin(z)\\
&=(e^{iw}-e^{-iw})(e^{iz}-e^{-iz})\\
&=(e^{i(w+z)}-e^{i(w-z)}-e^{i(z-w)}+e^{i(-z-w)}),
\end{align*}

de modo que
\begin{align*}
4(\cos(w)&\cos(z)-\sin(w)\sin(z))\\
&=2(e^{i(w+z)}+e^{-i(w+z)})\\
&=4\cos(w+z).
\end{align*}

Dividiendo entre $4$ ambos lados de la igualdad, obtenemos la primer identidad. La segunda se demuestra de manera análoga, y queda como tarea moral.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Determina los valores de $\exp(3+\frac{3\pi}{4}i)$ y de $L(-i)$.
  2. Muestra que para $z$ con parte imaginaria en $(-\pi,\pi]$ se tiene que $L(\exp(z))=z$.
  3. Determina el valor de $(1+i)^{1+i}$.
  4. Muestra las leyes de los exponentes para la exponenciación en $\mathbb{C}$.
  5. Determina el valor de $\sin(i)$ y de $\cos(1+i)$.
  6. Muestra la identidad de seno de la suma de ángulos en $\mathbb{C}$.
  7. Investiga qué otras propiedades de las funciones trigonométricas reales se extienden al caso complejo.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Raíces en los complejos y raíces de la unidad.

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En esta entrada veremos cómo resolver, en $\mathbb{C}$, la ecuación $w^n=z$, en donde $z$ es un complejo y $n$ es un entero positivo. Puedes pensar esto como que aprenderemos a obtener raíces en los complejos, pero sólo para $n$ entero. Más adelante hablaremos de la función exponencial compleja que nos permitirá elevar a otro tipo de exponentes.

Nuestra herramienta principal será la fórmula de De Moivre, que ya demostramos en una entrada anterior. Encontrar raíces $n$-ésimas es una herramienta más en nuestra caja para trabajar con números complejos, que hasta el momento ya incluye resolver ecuaciones cuadráticas complejas y sistemas de ecuaciones lineales complejos.

Introducción a raíces en los complejos

Pensemos en un ejemplo sencillo. ¿Cuáles son los complejos $w$ tales que $w^4=1$? En $\mathbb{R}$ tenemos dos de ellos: $1$ y $-1$. Como $$(-i)^4=i^4=(-1)^2=1,$$ en $\mathbb{C}$ tenemos otras dos soluciones: $i$ y $-i$. Así que tenemos $4$ soluciones en $\mathbb{C}$: $1$, $-1$, $i$ y $-i$.

Para mostrar que son las únicas en este sencillo caso, podemos hacer lo siguiente. Expresamos $1$ en forma polar $1=\text{cis}(0)$ y también, en forma polar, una solución $w=s\text{cis}(\alpha)$, con $\theta$ en $[0,2\pi)$. Por el teorema de De Moivre, tenemos que $$1=w^4=s^4\text{cis}(4\alpha).$$

Así, la norma $s$ de $w$ debe satisfacer $s^4=1$, y además $\text{cis}(4\alpha)$ debe ser $1$, por lo que $4\alpha$ debe ser un múltiplo entero de $2\pi$. La norma es un real positivo, así que la única solución para $s$ es $1$. Ahora, ¿cuántos argumentos $\alpha$ en $[0,2\pi)$ hacen que $4\alpha$ sea un múltiplo entero de $2\pi$?

Para determinar esto, notemos que $4\alpha$ está en $[0,8\pi)$, y ahí hay exactamente cuatro múltiplos enteros de $2\pi$, que son $$0,2\pi, 4\pi, 6\pi.$$ Esto es justo lo que limita las soluciones a que sean a lo más $4$.

Podemos continuar para verificar que en efecto son las soluciones que ya encontramos. Las soluciones para $\alpha$ en cada caso son $$0,\frac{\pi}{2},\pi,\frac{3\pi}{2}.$$ Concluimos entonces que las soluciones complejas de $w^4=1$ son, en forma polar,
\begin{align*}
w_1&=\text{cis}(0)\\
w_2&=\text{cis}\left(\frac{\pi}{2}\right)\\
w_3&=\text{cis}\left(\pi\right)\\
w_4&=\text{cis}\left(\frac{3\pi}{2}\right),
\end{align*}

que son exactamente $1,i,-1,-i$.

$\triangle$

El teorema de raíces en los complejos

La discusión anterior funciona en general para cualquier entero positivo $n$ y para cualquier complejo $\mathbb{C}$. Siempre tenemos exactamente $n$ soluciones y sabemos cómo se ven en forma polar.

Teorema. Sea $z=r\text{cis}(\theta)$ un número complejo, distinto de cero, dado en forma polar y $n$ un entero positivo. Existen exactamente $n$ elementos distintos de $\mathbb{C}$ tales que $w^n = z$. Están dados en forma polar por $$w_j=r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)$$ para $j=0,1,2\ldots,n-1$.

Demostración. Tomemos una solución $w$ y la escribimos en forma polar $w=s\text{cis}(\alpha)$, con $\alpha$ en $[0,2\pi)$. Usando que $w$ es solución y la fórmula de De Moivre, obtenemos que $$r\text{cis}(\theta)=s^n\text{cis}(n\alpha).$$ Como $s$ tiene que ser real positivo, obtenemos que $s=r^{1/n}$ (aquí estamos usando la raíz $n$-ésima en los reales).

El ángulo $n\alpha$ está en el intervalo $[0,2n\pi)$, y debe diferir en un múltiplo entero de $2\pi$ del ángulo $\theta$. Como $\theta$ está en $[0,2\pi)$, las únicas posibilidades para $n\alpha$ pueden ser los $n$ valores $$\theta, \theta+2\pi,\ldots, \theta+2(n-1)\pi,$$ de donde las soluciones para $\alpha$ son $$\frac{\theta}{n},\frac{\theta}{n}+\frac{2\pi}{n}, \ldots, \frac{\theta}{n} + (n-1)\frac{2\pi}{n},$$ respectivamente. Como son ángulos distintos en $[0,2\pi)$, obtenemos las posibles soluciones distintas $$r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)\quad \text{para $j=0,\ldots,n-1$}.$$

Verificar que en efecto son soluciones es sencillo, ya sea revirtiendo los pasos que hicimos, o usando directamente la fórmula de De Moivre. Esta verificación queda como tarea moral.

$\square$

Observa que el teorema dice que para obtener una raíz podemos empezar del complejo de norma $r^{1/n}$ y argumento $\frac{\theta}{n}$, y de ahí obtener el resto de las raíces en los complejos «rotando repetidamente $\frac{2\pi}{n}$ en el plano complejo». Esto muestra que las raíces forman los vértices de un $n$-ágono regular.

Nos costó un poco de trabajo mostrar que teníamos a lo más $n$ soluciones. En realidad, cualquier ecuación polinomial de grado $n$, es decir, de la forma $$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0$$ tiene a lo más $n$ soluciones. Esto lo veremos con toda generalidad en la última unidad, cuando hablemos de polinomios.

Ejemplos de obtener raíces en los complejos

Ejemplo. Encontremos todas las raíces séptimas del complejo $128\text{cis}\left(\frac{14\pi}{13}\right)$. Para empezar, notemos que $128^{1/7}=2$, de modo que todas las raíces tienen norma $2$.

Una de las raíces tiene argumento $\frac{14\pi}{7\cdot 13}=\frac{2\pi}{13}$ y el argumento del resto difiere en múltiplos enteros de $\frac{2\pi}{7}$. De esta forma, las raíces son

\begin{align*}
w_1&=2\text{cis}\left(\frac{2\pi}{13}\right)\\
w_2&=2\text{cis}\left(\frac{2\pi}{13}+\frac{2\pi}{7}\right)=2\text{cis}\left(\frac{40\pi}{91}\right)\\
w_3&=2\text{cis}\left(\frac{2\pi}{13}+\frac{4\pi}{7}\right)=2\text{cis}\left(\frac{66\pi}{91}\right)\\
w_4&=2\text{cis}\left(\frac{2\pi}{13}+\frac{6\pi}{7}\right)=2\text{cis}\left(\frac{92\pi}{91}\right)\\
w_5&=2\text{cis}\left(\frac{2\pi}{13}+\frac{8\pi}{7}\right)=2\text{cis}\left(\frac{118\pi}{91}\right)\\
w_6&=2\text{cis}\left(\frac{2\pi}{13}+\frac{10\pi}{7}\right)=2\text{cis}\left(\frac{144\pi}{91}\right)\\
w_7&=2\text{cis}\left(\frac{2\pi}{13}+\frac{12\pi}{7}\right)=2\text{cis}\left(\frac{170\pi}{91}\right).
\end{align*}

$\triangle$

Problema. Sabemos que $(2-3i)^4=-119+120i$. Encuentra las otras raíces cuartas de $-119+120i$.

Solución. Podríamos pasar $-119+120i$ a forma polar y usar el método anterior. Esto funciona y dará una solución. Pero veamos una solución alternativa más corta, que nos ayuda a entender mejor el teorema de raíces en los complejos.

De acuerdo con lo que probamos, las raíces varían únicamente en argumento, al que se le va sumando $\frac{\pi}{2}$. Es decir, si tenemos una raíz en el plano complejo, las demás se obtienen de ir rotando $\frac{\pi}{2}$ (recuerda que esto es $90^\circ$) desde el origen. Al ir rotando el punto $(2,-3)$ en el plano complejo en este ángulo, obtenemos los puntos $(-3,-2)$, $(-2,3)$ y $(3,2)$, de modo que las otras tres raíces son $-3-2i$, $-2+3i$ y $3+2i$.

Otra forma más de pensarlo es la siguiente. Si ya tenemos una raíz cuarta $w$ de un complejo $z$, entonces todas las raíces se obtienen multplicando por $1,i,-1, -i$. En efecto, por ejemplo, $$(iw)^4=i^4w^4=w^4=1.$$ Así, para el problema que nos interesa, las soluciones son

\begin{align*}w_1&=2-3i\\w_2&=i(2-3i)=3+2i\\w_3&=-(2-3i)=-2+3i\\w_4&=-i(2-3i)=-3-2i,\end{align*}
lo cual coincide con lo que habíamos encontrado antes.

$\triangle$

Raíces $n$-ésimas de la unidad

Un caso particular importante de la teoría desarrollada en la sección anterior es cuando $z$ es $1$. Sea $n$ un entero positivo y $w$ un complejo tal que $w^n=1$. A $w$ se le conoce como una raíz $n$-ésima de la unidad.

Teorema (de las raíces $n$-ésimas de la unidad). Sea $n$ un entero positivo. Existen exactamente $n$ raíces $n$-ésimas de la unidad distintas. Si $\omega$ es la que tiene el menor argumento positivo, entonces dichas raíces son $$1,\omega, \omega^2,\ldots, \omega^{n-1}.$$

La demostración se sigue fácilmente del teorema de raíces $n$-ésimas y queda como tarea moral. Cualquier raíz $n$-ésima $\omega$ tal que sus primeras potencias generen todas las raíces $n$-ésimas de la unidad se le conoce como una raíz primitiva.

Las raíces $n$-ésimas de la unidad tienen una interpretación geométrica bonita. Forman los vértices del $n$-ágono regular con $n$ vértices, sobre la circunferencia unitaria, donde uno de los vértices es $1$.

Ejemplo. Obtengamos las raíces quintas de la unidad. Primero, obtengamos la de menor argumento positivo, que por el teorema de raíces en los complejos, es $$\omega = \text{cis}\left(\frac{2\pi}{5}\right).$$ El resto de las raíces son entonces $\omega^2$, $\omega^3$, $\omega^4$ y $1$. Las podemos encontrar en el plano complejo como vértices del siguiente pentágono regular:

Ejemplo de raíces en los complejos: raíces quintas de la unidad
Raíces quintas de la unidad

Cualquiera de $\omega$, $\omega^2$, $\omega^3$ y $\omega^4$ son raíces primitivas, pero $1$ no es raíz primitiva pues sus potencias sólo son él mismo.

$\triangle$

Las raíces $n$-ésimas de la unidad se utilizan en muchos contextos. Aunque se puede trabajar con ellas de forma explícita, muchas veces se utilizan sólo las propiedades algebraicas que cumplen. A continuación enunciamos algunas.

Teorema. Sea $\omega$ una raíz primitiva $n$-ésima de la unidad. Las raíces $n$-ésimas de la unidad $$\omega_i = \omega^i $$ para $i=0,\ldots,n-1$ satisfacen las siguientes propiedades:

  • Para $n>1$, se tiene que $\omega_0+\ldots+\omega_{n-1}=0$.
  • Para $k=0,1,\ldots,n-1$, se tiene que $$(\omega_k)^{-1}=\overline{\omega_k}=\omega_{n-k}.$$
  • Se tiene que $\omega_0\cdot\ldots\cdot \omega_{n-1} = (-1)^{n+1}$.

Demostración. Empezamos con el primer inciso. Si $n>1$, tenemos que $1$ no es raíz primitiva, así que para el primer inciso sabemos que $\omega\neq 1$. Usamos la fórmula para suma de términos en una progresión geométrica:
\begin{align*}
\omega_0+\omega_1&+\ldots+\omega_{n-1}\\
&= 1+\omega+\ldots+\omega^{n-1}\\
&=\frac{1-\omega^n}{1-\omega}\\
&=\frac{1-1}{1-\omega}\\
&=0.
\end{align*}

Para la segunda parte, notemos que $$\omega_k\omega_{n-k}=\omega^k\omega^{n-k}=\omega^n=1,$$ lo cual prueba una de las igualdades. La otra igualdad se sigue del hecho general que el inverso de un complejo de norma $1$ es su conjugado, cuya demostración queda como tarea moral.

La tercera parte se sigue de la propiedad anterior. Al multiplicar todas las raíces de la unidad, podemos emparejar a cada raíz con su conjugado para obtener producto $1$. Las únicas excepciones es cuando emparejamos a un complejo consigo mismo, es decir, para cuando $\omega_k=\overline{\omega_k}$, lo cual sucede sólo cuando $\omega_k$ es real. Las únicas posibilidades son $1$ ó $-1$. El $1$ no tiene problema pues colabora con un factor $1$. Si $n$ es impar, $-1$ no es raíz $n$-ésima, así que no contribuye al producto. Si $n$ es par sí. Esto muestra lo que queremos pues $(-1)^{n+1}$ es $1$ si $n$ es impar y $-1$ si es par.

$\square$

Para un entero positivo $n$, llamemos $(U_n,\cdot)$ al conjunto de raíces $n$-ésimas de la unidad equipadas con el producto complejo.

Teorema. Para cada entero positivo $n$, se tiene que $(U_n,\cdot)$ es un grupo y es isomorfo a $(\mathbb{Z}_n,+)$.

Demostración. El producto de cualesquiera dos raíces $n$-ésimas es también una raíz $n$-ésima. Por el teorema anterior, los inversos multiplicativos de las raíces $n$-ésimas también son raíces $n$-ésimas. Esto basta para mostrar que se forma un grupo.

Para la segunda parte, notamos que ambos grupos son el grupo cíclico de $n$ elementos. Una correspondencia entre ellos está dada por mandar $[1]_n$ a cualquier raíz primitiva.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra las raíces cúbicas de $8-8i$ y dibújalas en el plano complejo.
  2. Verifica que las soluciones obtenidas en el teorema de raíces $n$-ésimas en efecto son soluciones.
  3. Muestra el teorema de las raíces $n$-ésimas de la unidad.
  4. Prueba que si $z$ es un complejo de norma $1$, entonces su inverso es su conjugado.
  5. Sea $\omega$ una raíz $n$-ésima primitiva de la unidad. Muestra que $w^k$ es una raíz primitiva si y sólo si $n$ y $k$ son primos relativos, es decir, $\MCD{n,k}=1$. Sugerencia: Usa lo que sabemos de soluciones a ecuaciones diofantinas lineales.
  6. Encuentra de manera explícita la parte real y la parte imaginaria de todas las raíces quintas de la unidad.
    Sugerencia: La ecuación $w^5-1=0$ se puede factorizar como $$(w-1)(w^4+w^3+w^2+w+1)$$ y $w^4+w^3+w^2+w+1$ se puede factorizar como $$\left(w^2+\frac{1+\sqrt{5}}{2}w+1\right)\left(w^2+\frac{1-\sqrt{5}}{2}w+1\right).$$ Usa lo que sabemos de resolver ecuaciones cuadráticas cojmplejas.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»