Introducción
En una entrada anterior, vimos cómo se comporta la multiplicación en forma polar y cómo podemos aprovechar esto para hacer potencias. Concretamente, el teorema de De Moivre es muy útil para elevar complejos a potencias sin tener que hacer gran cantidad de productos.
Los primeros dos videos son ejercicios que ejemplifican lo anterior. Después, usamos lo que aprendimos en la entrada de raíces $n$-ésimas para resolver dos problemas más.
Al final, compartimos un enlace en el que puedes practicar más con operaciones de números complejos.
Problemas de fórmula de De Moivre
Para empezar, vemos dos problemas de exponenciación completa. El primero es una aplicación directa de la fórmula de De Moivre.
Problema. Usa el teorema de De Moivre para elevar a la potencia indicada $$\left(\sqrt{3}(\cos 25^\circ + i \sin 25^\circ\right)^6.$$
En algunos problemas es posible que sea necesario primero obtener la forma polar de un complejo antes de poder usar la fórmula de De Moivre. El segundo problema es un ejemplo de esto.
Problema. Encuentra el valor de $(\sqrt{3}-i)^{12}$.
Problemas de raíces $n$-ésimas
Si ahora, en vez de querer elevar a cierta potencia, queremos obtener raíces $n$-ésimas, con el uso de un poderoso teorema que dedujimos a partir de la fórmula de De Moivre, sabemos que son exactamente $n$ raíces, y podemos calcularlas explícitamente. A continuación, vemos dos ejercicios que ejemplifican lo anterior.
Problema. Obtén las raíces cúbicas del complejo $3+4i$.
Problema. Obtén las raíces quintas del complejo $16\sqrt{2}(-1+i)$.
Ojo. En algún momento del siguiente video se encuentra que el ángulo es $360^\circ – 45^\circ$. Sin embargo, debe decir $180^\circ – 45^\circ$, pues se debe estar en el cuadrante 2, ya que la parte real es negativa y la compleja es positiva.
Fotos de los ejercicios de hoy
Finalmente, les dejo fotos de lo resuelto en los vídeos, para quienes tengan dificultades para ver los vídeos. En la tercera foto no están tan desarrolladas las cuentas como en el vídeo.


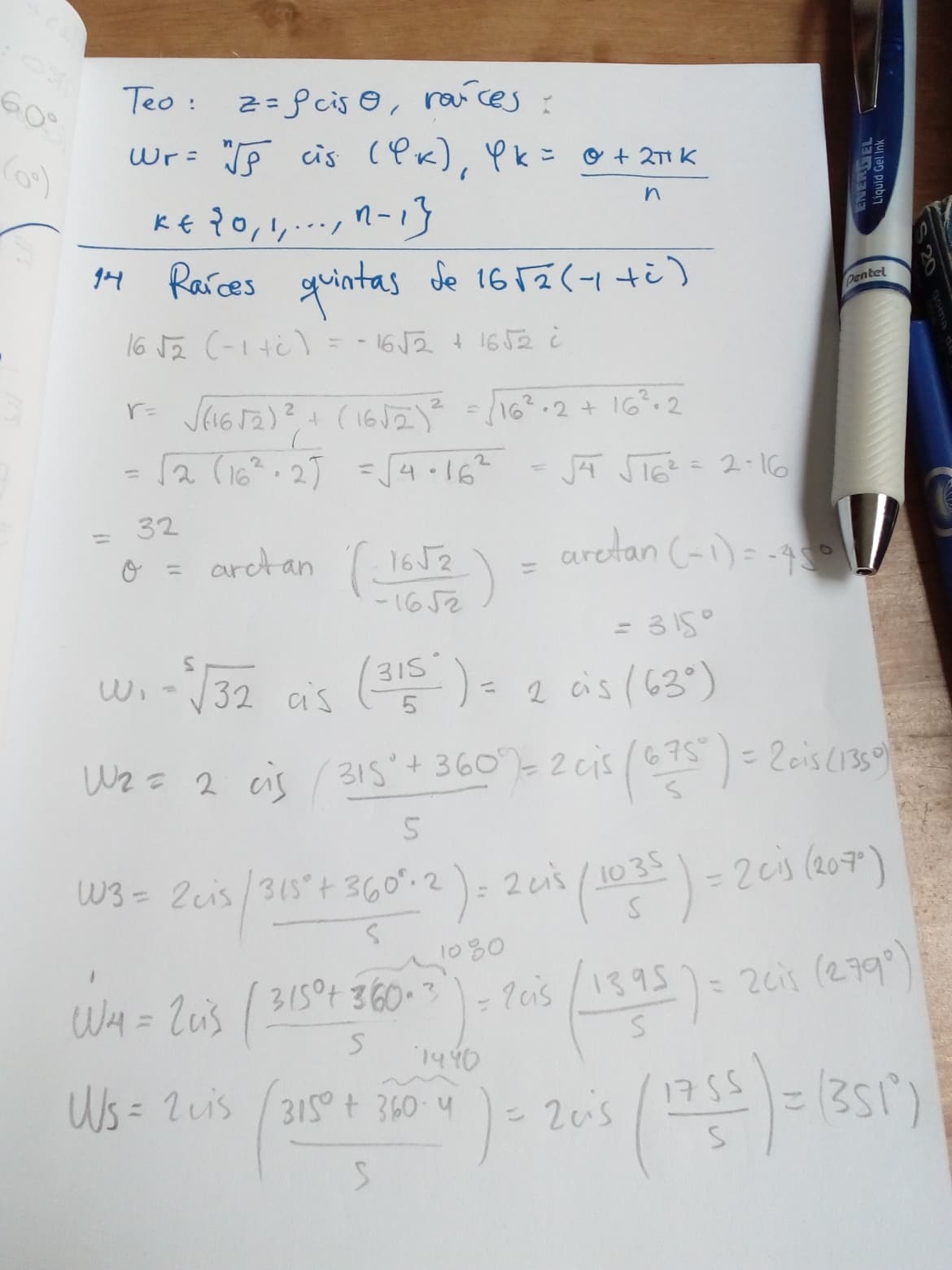
Más material de De Moivre y raíces
Puedes practicar más acerca de exponenciación y raíces complejas con los videos y ejercicios del tema en Khan Academy.
Más adelante…
Tarea moral
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Raíces de números complejos y raíces de la unidad
- Entrada siguiente del curso: Exponencial, logaritmo y trigonometría en los complejos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»


