Introducción

En esta semana veremos algunas herramientas para resolver problemas de geometría. Como con otros temas que hemos visto, sería imposible tratar a profundidad el área. En vez de eso, lo que haremos es ver un poco de varias de las herramientas que se pueden usar en la solución de problemas geométricos, comenzando con geometría euclideana. Veremos ideas de lo siguiente:

• Geometría triángulos y circunferencias
• Geometría analítica
• Vectores en geometría
• Números complejos en geometría
• Geometría discreta

En esta entrada comenzaremos con la parte de geometría euclideana. Más adelante hablaremos de las demás ideas.

Geometría euclideana

Cuando en geometría nos referimos a una solución por geometría euclideana o geometría sintética nos referimos a un argumento que no use parametrizaciones de los objetos del plano en términos de coordenadas, vectores o complejos. Simplemente usamos conceptos geométricos como ángulos, distancias, semejanza, congruencia, etc. Todas estas se pueden pensar como propiedades que se mantienen invariantes bajo movimientos rígidos del plano. Dentro de los resultados más versátiles del área tenemos los siguientes.

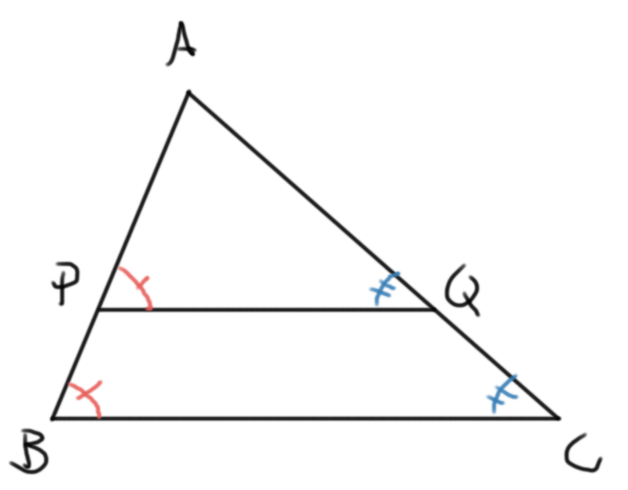
Teorema (de Tales). Tomemos puntos $P$ y $Q$ sobre los lados $AB$ y $AC$ de $\triangle ABC$. Se tiene que $AP/AQ = AB/AC$ si y sólo si la recta $PQ$ es paralela a la recta $BC$.

Teorema (criterios de congruencia). Sean $\triangle ABC$ y $\triangle DEF$ triángulos. Cualquiera de las siguientes condiciones (o sus simétricos) implican que $\triangle ABC$ y $\triangle DEF$ son congruentes:

• (LLL) $AB=DE$, $BC=EF$ y $CA=FD$
• (LAL) $AB=DE$, $\angle BAC = \angle EDF$ y $CA=FD$
• (ALA) $\angle BAC = \angle EDF$, $CA=FD$ y $\angle BCA – \angle EFD$.

Teorema (criterios de semejanza). Sean $\triangle ABC$ y $\triangle DEF$ triángulos. Cualquiera de las siguientes condiciones (o sus simétricos) implican que $\triangle ABC$ y $\triangle DEF$ son semejantes.

• (LLL) $\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}$.
• (LAL) $\frac{AB}{DE}=\frac{CA}{FD}$ y $\angle BAC = \angle EDF$.
• (AA) $\angle BAC = \angle EDF$ y $\angle BCA – \angle EFD$.

Veamos un ejemplo en el que se usan estos hechos básicos.

Problema. Sobre los lados $AB$ y $AC$ de un triángulo $ABC$ se construyen cuadrados $ABPQ$ y $ACRS$ como en la figura. Muestra que $CQ=BS$.

Sugerencia pre-solución. En geometría es típico modificar un problema. En vez de intentar medir los segmentos requeridos, es útil preguntarse si forman parte de triángulos que sean congruentes, o que sea pueda ver que son congruentes por algún criterio. Por supuesto, en todo problema de geometría es útil hacer muchas figuras.

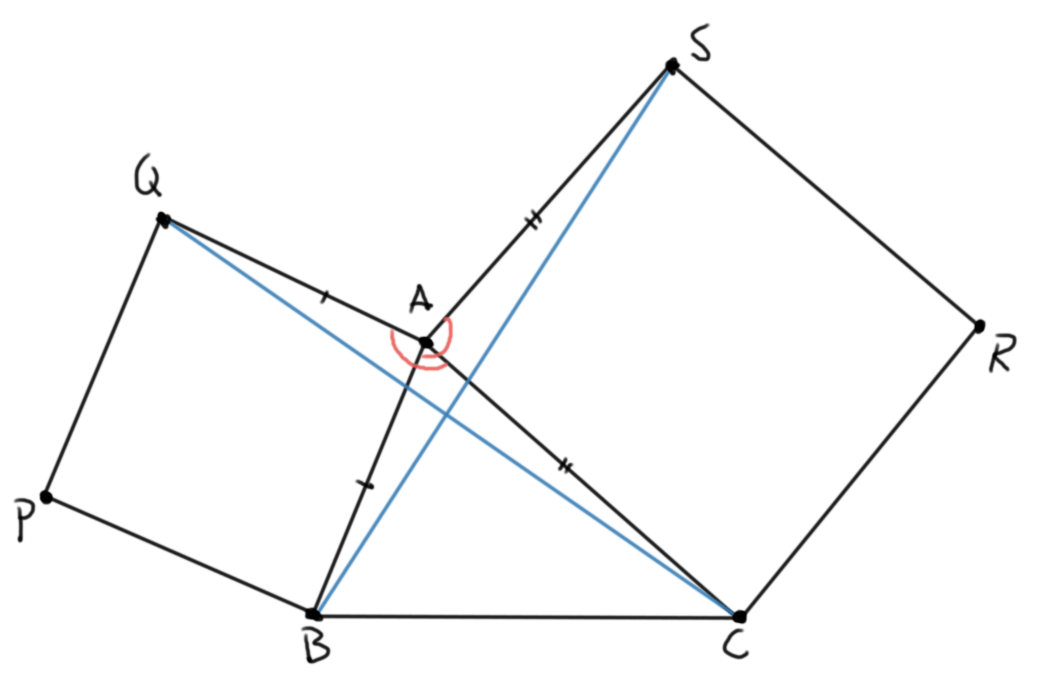
Solución. Consideremos los triángulos $ABS$ y $AQC$. Tenemos que $AB=AQ$ pues ambos son lados del cuadrado $ABPQ$. De manera similar, $AC=AS$. Finalmente, tenemos que $\angle BAS = \angle QAC$, pues ambos ángulos son iguales a $$90^\circ + \angle BAC.$$

Por esta razón, podemos usar el criterio de congruencia $LAL$ en estos triángulos para concluir que son congruentes. De aquí se concluye que $CQ=BS$, como queríamos.

$\square$

Recordatorio de puntos notables en triángulos

Otro tema relevante para la geometría euclideana es la geometría de triángulos. Tomemos un triángulo $\triangle ABC$. Hay algunos puntos y rectas notables en el triángulo, que se usan en varios problemas. A continuación enunciamos las más importantes.

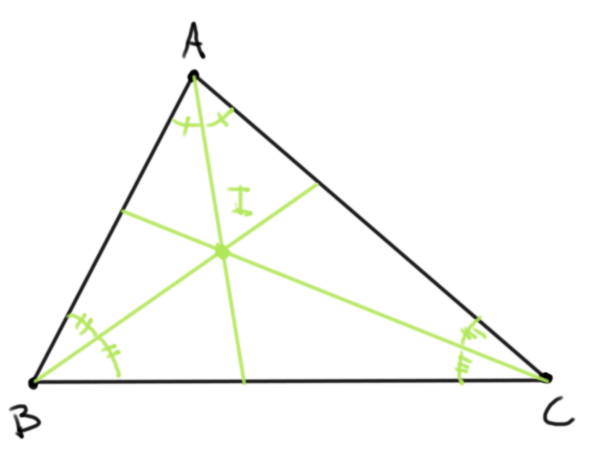
• Si $L$, $M$ y $N$ son los puntos medios de $BC$, $CA$ y $AB$, respectivamente, entonces a cada una de las rectas $AL$, $BM$ y $CN$ se le conoce como una mediana. Las medianas de un triángulo concurren en un punto llamado el gravicentro o baricentro, que usualmente se denota por $G$.

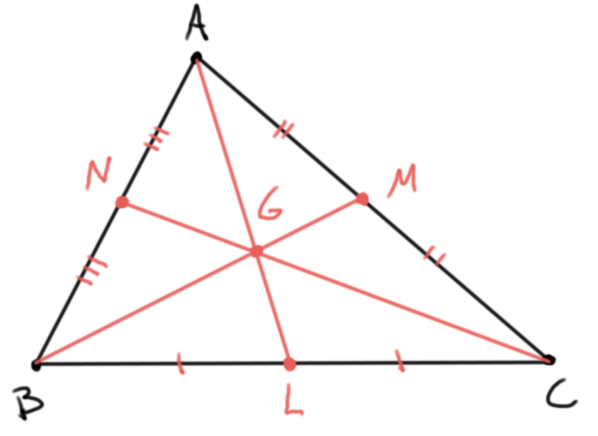
• Si $D$, $E$ y $F$ son las proyecciones desde $A$, $B$, $C$ a los lados $BC$, $CA$ y $AB$ respectivamente, entonces a cada una de las rectas $AD$, $BE$ y $CF$ se le conoce como una altura. Las alturas de un triángulo concurren en un punto llamado el ortocentro, que usualmente se denota por $H$.

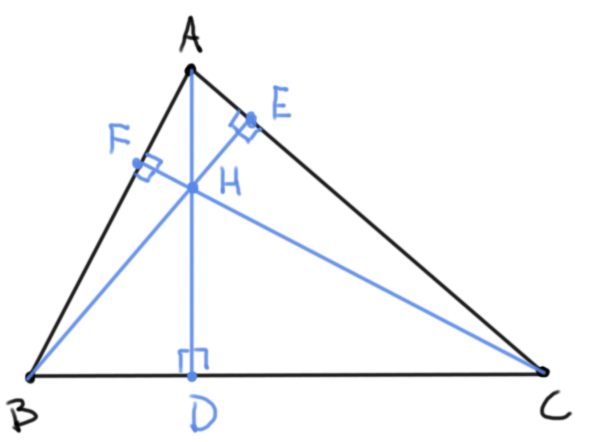
• Las rectas que cortan a la mitad a cada uno de los ángulos internos de $\triangle ABC$ se les conoce como las bisectrices internas del triángulo. Concurren en un punto llamado el incentro, usualmente denotado por $I$. El incentro sirve como centro para la única circunferencia que es tangente a los segmentos $AB$, $BC$ y $CA$.

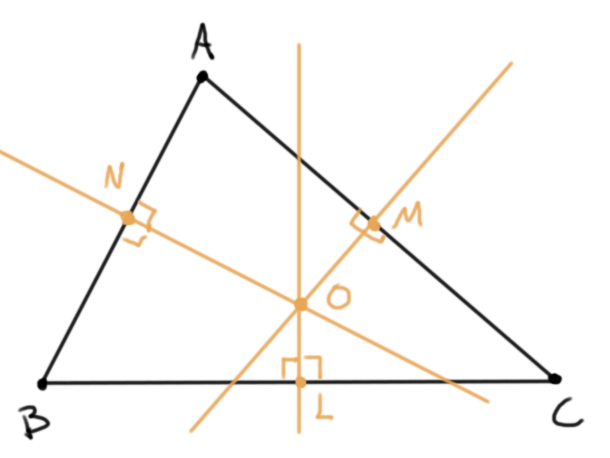
• Las rectas perpendiculares a los lados del triángulo y que pasan por sus puntos medios se les llama mediatrices y concurren en un punto llamado el circuncentro, que se suele denotar $O$. Este punto sirve como centro de la única circunferencia que pasa por los tres vértices $A$, $B$ y $C$.

Veamos las demostraciones de algunas de estas afirmaciones, para repasar algunos argumentos geométricos.

Una idea útil es caracterizar a una recta como el conjunto de puntos que satisfacen cierta propiedad. Por ejemplo, probemos primero la siguiente caracterización de las mediatrices.

Proposición. La recta perpendicular $\ell$ a un segmento $BC$ que pasa por su punto medio $L$ consiste exactamente de los puntos $P$ tales que $PB=PC$.

Demostración. Para ver que cualquier punto en $\ell$ satisface esto, se puede usar el criterio LAL de congruencia en los triángulos $PBL$ y $PCL$, usando el ángulo recto que comparten. Para ver que cualquier punto tal que $PB=PC$ está en $\ell$, se usa que $\angle PBC = \angle PCB$ (por el triángulo isósceles $PBC$), y entonces al bajar la perpendicular desde $P$ a $BC$ a un punto $L’$, los triángulos $PBL’$ y $PCL’$ comparten dos ángulos (y por lo tanto los tres), de donde se puede usar de nuevo el criterio LAL para concluir que $L=L’$.

$\square$

Demostrar que las mediatrices concurren es entonces muy sencillo. Si $P$ es la intersección de la mediatriz en $BC$ y en $CA$, entonces por el resultado anterior tenemos $PB=PC=PA$, y entonces también por el resultado anterior se tiene que $P$ está en la mediatriz de $AB$. De manera análoga se puede mostrar que una bisectriz consiste de los puntos que equidistan de los lados que la definen, y con ello mostrar que las bisectrices internas de un triángulo concurren.

Veamos ahora un problema de geometría euclideana que involucra a las alturas y a las medianas. Es el Problema 1 del Concurso Nacional de la Olimpiada Mexicana de Matemáticas de 2009.

Problema. Sea $ABC$ un triángulo y $D$ el pie de la altura desde $A$. Con centro en $D$ se traza una circunferencia de radio $DA$. Esta circunferencia corta a los lados $AB$ y $AC$ del triángulo en puntos $P$ y $Q$ respectivamente. Muestra que los triángulos $AQP$ y $ABC$ son semejantes.

Sugerencia pre-solución. Para mostrar que estos triángulos son semejantes, basta con mostrar que tienen ángulos iguales.

Solución. Tracemos además los pies de altura $E$ y $F$ desde $B$ y $C$ respectivamente.

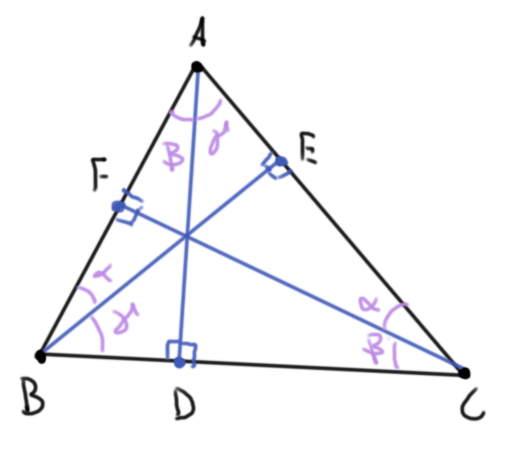
Observemos que $\triangle ABD$ y $\triangle CBF$ comparten los ángulos rectos y el ángulo en $B$, de modo que son semejantes y por lo tanto su tercer ángulo es igual. Este y argumentos análogos muestran que
\begin{align*}
\alpha&:=\angle ABE = \angle ACF\\
\beta&:=\angle BAD = \angle BCF\\
\gamma&:= \angle CBE = \angle CAD.
\end{align*}

De esta forma, los ángulos internos de $\triangle ABC$ miden $\angle A= \beta+\gamma$, $\angle B = \gamma+\alpha$ y $\angle C = \alpha+\beta$. Ya que la suma interna de los ángulos de un triángulo es $180^\circ$, concluimos que $\alpha+\beta+\gamma = 90^\circ$.

Ahora, usando los triángulos isósceles $\triangle ADP$ y $\triangle ADQ$ del problema, tenemos que
\begin{align*}
\angle DPA &= \angle DAP = \beta\\
\angle DQA &= \angle DAQ = \gamma.
\end{align*}

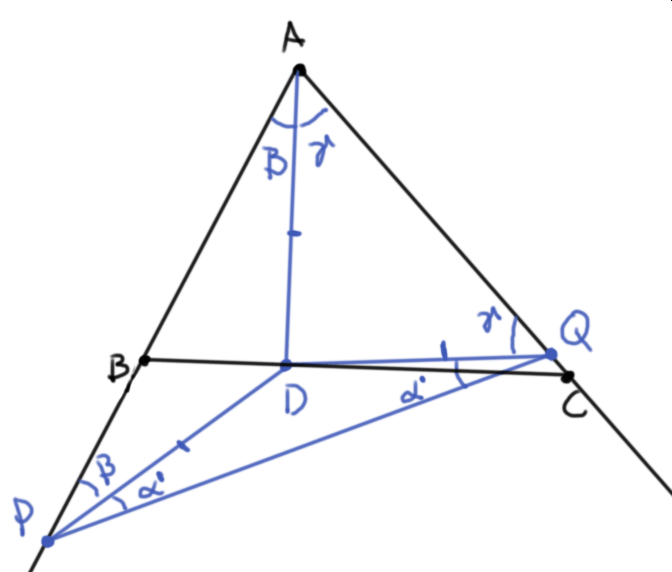
Como $\triangle PDQ$ también es isósceles con $PD=DQ$, tenemos que $$\alpha’=:\angle DPQ = \angle DQP.$$ Por la suma de ángulos en el triángulo $APQ$, tenemos que $\alpha’+\beta + \gamma = 90^\circ$. Así, $\alpha = \alpha’$. Concluimos entonces que en el $\triangle PAQ$ los ángulos internos son $\angle A = \beta+ \gamma$, $\angle P = \alpha+\beta$ y $\angle Q = \gamma + \alpha$.

De esta forma, los triángulos $ABC$ y $AQP$ son semejantes por el criterio AA.

$\square$

Otra técnica útil para resolver problemas de geometría consiste en mostrar que un punto está en dos rectas notables (por ejemplo, en las medianas $AL$ y $BM$), deducir que entonces es el punto notable correspondiente (en este caso el gravicentro $G$), y usar la información de que entonces la recta por el tercer vértice y el punto es la tercer recta notable (que en el ejemplo diría que $CG$ es la mediana).

Recordatorio de geometría del círculo

Un tercer ingrediente básico para la geometría euclideana es entender qué pasa con las circunferencias. Tomemos una circunferencia $\Gamma$ y dos puntos fijos $A$ y $B$ sobre ella. Tomemos $C$ y $D$ otros dos puntos sobre $\Gamma$ distintos de $A$ y $B$ sobre el mismo arco definido por $A$ y $B$ y sea $E$ otro punto sobre $\Gamma$, en el arco opuesto. Entonces

• Los ángulos $\angle ACB$ y $\angle ADB$ son iguales.
• Los ángulos $\angle ACB$ y $\angle AEB$ son suplementarios, es decir, suman $180^\circ$.

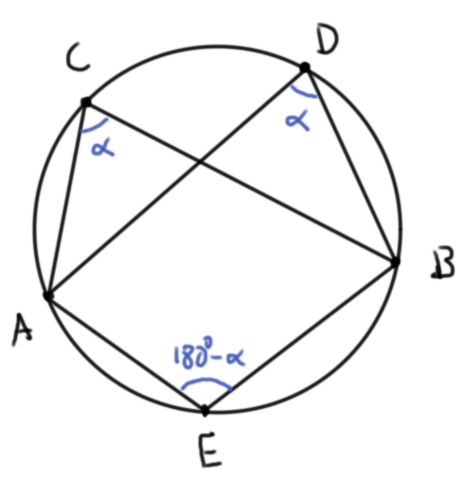
De hecho, este resultado es un si y sólo si. Para $A$, $B$, $C$, $D$ puntos distintos en el plano:

• Si $\angle ACB$ y $\angle ADB$ son iguales, entonces $A$, $B$, $C$, $D$ son puntos sobre una circunferencia y $C$ y $D$ están en el mismo arco definido por $A$ y $B$ y
• Si los ángulos $\angle ACB$ y $\angle ADB$ son suplementarios, entonces $A$, $B$, $C$, $D$ son puntos sobre una circunferencia y $C$ y $D$ están en arcos opuestos definidos por $A$ y $B$.

Cuando $A$, $B$, $C$ y $D$ son puntos distintos que yacen sobre una misma circunferencia, en ese orden, decimos que $ABCD$ es un cuadrilátero cíclico.

Teorema (potencia de un punto). Sea $P$ un punto y $\Gamma$ una circunferencia. Tomemos dos rectas por $P$ que corten a la circunferencia en puntos $A$, $B$, $C$ y $D$ como en alguna de las figuras. Entonces $PA\cdot PB = PC \cdot PD$.

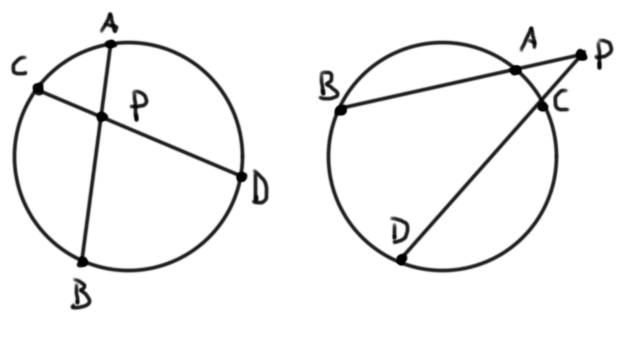
Veamos un problema de la Olimpiada Matemática de la Cuenca del Pacífico en donde confluyen algunas de estas ideas. Es el problema 1 de la edición de 2016.

Problema. Un triángulo $ABC$ es grandioso si para cualquier punto $D$ en el lado $BC$, cuando se toman los pies de las perpendiculares $P$ y $Q$ de $D$ a las rectas $AB$ y $AC$, respectivamente, sucede que la reflexión de $D$ en la recta $PQ$ cae sobre el circuncírculo del triángulo $ABC$.

Muestra que un triángulo $ABC$ es grandioso si y sólo si $\angle A = 90^\circ$ y $AB=AC$.

Sugerencia pre-solución. El problema dice que cierta condición se debe cumplir para todo punto $D$ en el lado $BC$. Considera algunos casos extremos de lo que puede ser $D$, de los que puedas obtener información de cómo debe ser el triángulo.

Solución. Para cualquier punto $D$ en el lado $BC$, vamos a llamar $D’$ a la reflexión de $D$ en la recta $PQ$. Primero veremos que si $ABC$ es grandioso, entonces es isósceles y con ángulo recto en $A$.

Como la hipótesis se cumple para cualquier punto $D$, en particular se cumple para cuando elegimos $D$ como el punto donde la bisectriz desde $A$ intersecta a $BC$. Nota que $P$ y $Q$ están en los rayos $AB$ y $AC$. Además, $P$ y $Q$ son reflexiones entre sí con respecto a la recta $AD$, de modo que $PQ$ es perpendicular a $AD$. Por esto, se tiene que $D’$ está en la recta $AD$, así que o es $A$, o es el segundo punto de intersección de la bisectriz en $A$ con el circuncírculo del triángulo. Como además $APDQ$ es un cuadrilátero cíclico, se tiene que $AD$ intersecta a $PQ$ y por lo tanto $D’=A$.

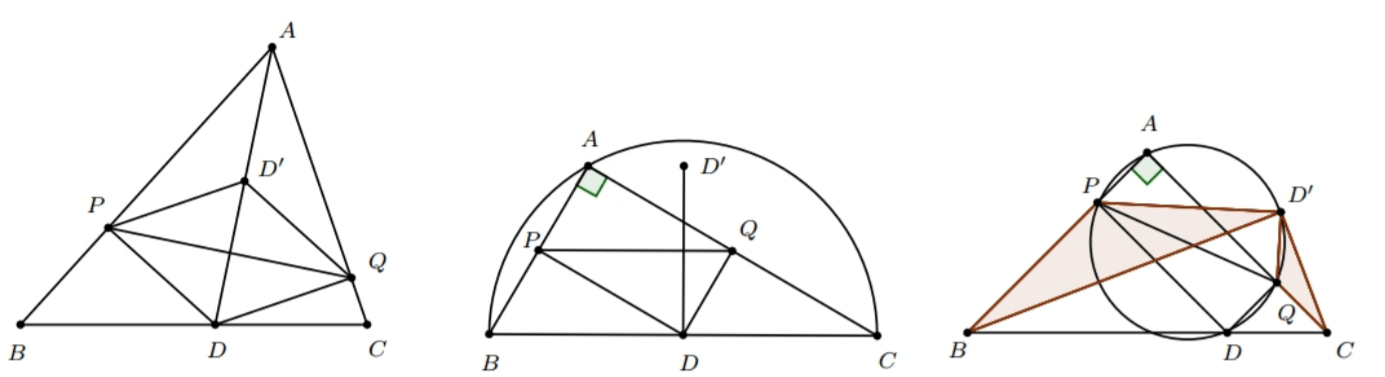
Tenemos entonces las igualdades de ángulos
\begin{align*}
\angle BAC &= \angle PD’Q \\
&= \angle PDQ \\
&= 180^\circ – \angle BAC.
\end{align*}

Concluimos entonces que $\angle BAC = 90^\circ$, que muestra que el triángulo es rectángulo en $A$.

Ahora tomamos a $D$ como el punto medio de $BC$, lo cual hace que $P$ y $Q$ sean los puntos medios de $AB$ y $AC$ respectivamente. Pero entonces $PQ$ es paralelo a $BC$ y por lo tanto $DD’$ es perpendicular a $BC$. La distancia de $D’$ a $BC$ es igual al circunradio del triángulo (pues $D’$ debe caer en el circuncírculo), y es igual a la distancia de $A$ a $BC$. Esto sólo puede suceder cuando $ABC$ es isósceles y con ángulo recto en $A$, como queríamos.

Veamos ahora que si $ABC$ es isósceles y de ángulo recto en $A$, entonces se cumple la propiedad para todo punto $D$ en $BC$. Como $D$ es la reflexión en $PQ$, tendríamos $D’P=DP=BP$. De manera similar, $D’Q=DQ=CQ$.

El cuadrilátero $APDQD’$ es cíclico de diámetro $PQ$, pues todos los ángulos $\angle PAQ$, $\angle PD’Q$ y $\angle PDQ$ son de $90^\circ$. De aquí, $\angle APD’= \angle AQD’$, de donde obtenemos que $\angle BPD’= \angle CQD’$. Con esto concluimos que $\triangle D’PB$ y $\triangle D’QC$ son semejantes. De aquí se sigue que

\begin{align*}
\angle PD’Q &= \angle PD’C+ \angle CD’Q\\
&=\angle PD’C + \angle BD’P\\
&= \angle BD’C.
\end{align*}

Como además tenemos $\frac{D’P}{D’Q}= \frac{D’B}{D’C}$, concluimos que también $\triangle D’PQ$ y $\triangle D’BC$ son semejantes. Pero como $\triangle DPQ$ y $\triangle D’PQ$ son congruentes, se obtiene que $$\angle BD’C=\angle PD’Q = \angle PDQ = 90^\circ.$$ Con esto concluimos que $D’$ yace en la circunferencia de diámetro $BC$, que es precisamente el circuncírculo de $\triangle ABC$.

$\square$

Más problemas

Puedes encontrar más problemas de geometría euclideana en la sección 8.1 del libro Problem Solving through Problems de Loren Larson. Para tener buenos fundamentos en geometría euclideana, se pueden revisar algunos textos en el área, como los cuadernos de la Olimpiada Mexicana de Matemáticas de Geometría y de Geometría: Ejercicios y problemas.