Introducción
En esta entrada veremos cómo resolver, en $\mathbb{C}$, la ecuación $w^n=z$, en donde $z$ es un complejo y $n$ es un entero positivo. Puedes pensar esto como que aprenderemos a obtener raíces en los complejos, pero sólo para $n$ entero. Más adelante hablaremos de la función exponencial compleja que nos permitirá elevar a otro tipo de exponentes.
Nuestra herramienta principal será la fórmula de De Moivre, que ya demostramos en una entrada anterior. Encontrar raíces $n$-ésimas es una herramienta más en nuestra caja para trabajar con números complejos, que hasta el momento ya incluye resolver ecuaciones cuadráticas complejas y sistemas de ecuaciones lineales complejos.
Introducción a raíces en los complejos
Pensemos en un ejemplo sencillo. ¿Cuáles son los complejos $w$ tales que $w^4=1$? En $\mathbb{R}$ tenemos dos de ellos: $1$ y $-1$. Como $$(-i)^4=i^4=(-1)^2=1,$$ en $\mathbb{C}$ tenemos otras dos soluciones: $i$ y $-i$. Así que tenemos $4$ soluciones en $\mathbb{C}$: $1$, $-1$, $i$ y $-i$.
Para mostrar que son las únicas en este sencillo caso, podemos hacer lo siguiente. Expresamos $1$ en forma polar $1=\text{cis}(0)$ y también, en forma polar, una solución $w=s\text{cis}(\alpha)$, con $\theta$ en $[0,2\pi)$. Por el teorema de De Moivre, tenemos que $$1=w^4=s^4\text{cis}(4\alpha).$$
Así, la norma $s$ de $w$ debe satisfacer $s^4=1$, y además $\text{cis}(4\alpha)$ debe ser $1$, por lo que $4\alpha$ debe ser un múltiplo entero de $2\pi$. La norma es un real positivo, así que la única solución para $s$ es $1$. Ahora, ¿cuántos argumentos $\alpha$ en $[0,2\pi)$ hacen que $4\alpha$ sea un múltiplo entero de $2\pi$?
Para determinar esto, notemos que $4\alpha$ está en $[0,8\pi)$, y ahí hay exactamente cuatro múltiplos enteros de $2\pi$, que son $$0,2\pi, 4\pi, 6\pi.$$ Esto es justo lo que limita las soluciones a que sean a lo más $4$.
Podemos continuar para verificar que en efecto son las soluciones que ya encontramos. Las soluciones para $\alpha$ en cada caso son $$0,\frac{\pi}{2},\pi,\frac{3\pi}{2}.$$ Concluimos entonces que las soluciones complejas de $w^4=1$ son, en forma polar,
\begin{align*}
w_1&=\text{cis}(0)\\
w_2&=\text{cis}\left(\frac{\pi}{2}\right)\\
w_3&=\text{cis}\left(\pi\right)\\
w_4&=\text{cis}\left(\frac{3\pi}{2}\right),
\end{align*}
que son exactamente $1,i,-1,-i$.
$\triangle$
El teorema de raíces en los complejos
La discusión anterior funciona en general para cualquier entero positivo $n$ y para cualquier complejo $\mathbb{C}$. Siempre tenemos exactamente $n$ soluciones y sabemos cómo se ven en forma polar.
Teorema. Sea $z=r\text{cis}(\theta)$ un número complejo, distinto de cero, dado en forma polar y $n$ un entero positivo. Existen exactamente $n$ elementos distintos de $\mathbb{C}$ tales que $w^n = z$. Están dados en forma polar por $$w_j=r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)$$ para $j=0,1,2\ldots,n-1$.
Demostración. Tomemos una solución $w$ y la escribimos en forma polar $w=s\text{cis}(\alpha)$, con $\alpha$ en $[0,2\pi)$. Usando que $w$ es solución y la fórmula de De Moivre, obtenemos que $$r\text{cis}(\theta)=s^n\text{cis}(n\alpha).$$ Como $s$ tiene que ser real positivo, obtenemos que $s=r^{1/n}$ (aquí estamos usando la raíz $n$-ésima en los reales).
El ángulo $n\alpha$ está en el intervalo $[0,2n\pi)$, y debe diferir en un múltiplo entero de $2\pi$ del ángulo $\theta$. Como $\theta$ está en $[0,2\pi)$, las únicas posibilidades para $n\alpha$ pueden ser los $n$ valores $$\theta, \theta+2\pi,\ldots, \theta+2(n-1)\pi,$$ de donde las soluciones para $\alpha$ son $$\frac{\theta}{n},\frac{\theta}{n}+\frac{2\pi}{n}, \ldots, \frac{\theta}{n} + (n-1)\frac{2\pi}{n},$$ respectivamente. Como son ángulos distintos en $[0,2\pi)$, obtenemos las posibles soluciones distintas $$r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)\quad \text{para $j=0,\ldots,n-1$}.$$
Verificar que en efecto son soluciones es sencillo, ya sea revirtiendo los pasos que hicimos, o usando directamente la fórmula de De Moivre. Esta verificación queda como tarea moral.
$\square$
Observa que el teorema dice que para obtener una raíz podemos empezar del complejo de norma $r^{1/n}$ y argumento $\frac{\theta}{n}$, y de ahí obtener el resto de las raíces en los complejos «rotando repetidamente $\frac{2\pi}{n}$ en el plano complejo». Esto muestra que las raíces forman los vértices de un $n$-ágono regular.
Nos costó un poco de trabajo mostrar que teníamos a lo más $n$ soluciones. En realidad, cualquier ecuación polinomial de grado $n$, es decir, de la forma $$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0$$ tiene a lo más $n$ soluciones. Esto lo veremos con toda generalidad en la última unidad, cuando hablemos de polinomios.
Ejemplos de obtener raíces en los complejos
Ejemplo. Encontremos todas las raíces séptimas del complejo $128\text{cis}\left(\frac{14\pi}{13}\right)$. Para empezar, notemos que $128^{1/7}=2$, de modo que todas las raíces tienen norma $2$.
Una de las raíces tiene argumento $\frac{14\pi}{7\cdot 13}=\frac{2\pi}{13}$ y el argumento del resto difiere en múltiplos enteros de $\frac{2\pi}{7}$. De esta forma, las raíces son
\begin{align*}
w_1&=2\text{cis}\left(\frac{2\pi}{13}\right)\\
w_2&=2\text{cis}\left(\frac{2\pi}{13}+\frac{2\pi}{7}\right)=2\text{cis}\left(\frac{40\pi}{91}\right)\\
w_3&=2\text{cis}\left(\frac{2\pi}{13}+\frac{4\pi}{7}\right)=2\text{cis}\left(\frac{66\pi}{91}\right)\\
w_4&=2\text{cis}\left(\frac{2\pi}{13}+\frac{6\pi}{7}\right)=2\text{cis}\left(\frac{92\pi}{91}\right)\\
w_5&=2\text{cis}\left(\frac{2\pi}{13}+\frac{8\pi}{7}\right)=2\text{cis}\left(\frac{118\pi}{91}\right)\\
w_6&=2\text{cis}\left(\frac{2\pi}{13}+\frac{10\pi}{7}\right)=2\text{cis}\left(\frac{144\pi}{91}\right)\\
w_7&=2\text{cis}\left(\frac{2\pi}{13}+\frac{12\pi}{7}\right)=2\text{cis}\left(\frac{170\pi}{91}\right).
\end{align*}
$\triangle$
Problema. Sabemos que $(2-3i)^4=-119+120i$. Encuentra las otras raíces cuartas de $-119+120i$.
Solución. Podríamos pasar $-119+120i$ a forma polar y usar el método anterior. Esto funciona y dará una solución. Pero veamos una solución alternativa más corta, que nos ayuda a entender mejor el teorema de raíces en los complejos.
De acuerdo con lo que probamos, las raíces varían únicamente en argumento, al que se le va sumando $\frac{\pi}{2}$. Es decir, si tenemos una raíz en el plano complejo, las demás se obtienen de ir rotando $\frac{\pi}{2}$ (recuerda que esto es $90^\circ$) desde el origen. Al ir rotando el punto $(2,-3)$ en el plano complejo en este ángulo, obtenemos los puntos $(-3,-2)$, $(-2,3)$ y $(3,2)$, de modo que las otras tres raíces son $-3-2i$, $-2+3i$ y $3+2i$.
Otra forma más de pensarlo es la siguiente. Si ya tenemos una raíz cuarta $w$ de un complejo $z$, entonces todas las raíces se obtienen multplicando por $1,i,-1, -i$. En efecto, por ejemplo, $$(iw)^4=i^4w^4=w^4=1.$$ Así, para el problema que nos interesa, las soluciones son
\begin{align*}w_1&=2-3i\\w_2&=i(2-3i)=3+2i\\w_3&=-(2-3i)=-2+3i\\w_4&=-i(2-3i)=-3-2i,\end{align*}
lo cual coincide con lo que habíamos encontrado antes.
$\triangle$
Raíces $n$-ésimas de la unidad
Un caso particular importante de la teoría desarrollada en la sección anterior es cuando $z$ es $1$. Sea $n$ un entero positivo y $w$ un complejo tal que $w^n=1$. A $w$ se le conoce como una raíz $n$-ésima de la unidad.
Teorema (de las raíces $n$-ésimas de la unidad). Sea $n$ un entero positivo. Existen exactamente $n$ raíces $n$-ésimas de la unidad distintas. Si $\omega$ es la que tiene el menor argumento positivo, entonces dichas raíces son $$1,\omega, \omega^2,\ldots, \omega^{n-1}.$$
La demostración se sigue fácilmente del teorema de raíces $n$-ésimas y queda como tarea moral. Cualquier raíz $n$-ésima $\omega$ tal que sus primeras potencias generen todas las raíces $n$-ésimas de la unidad se le conoce como una raíz primitiva.
Las raíces $n$-ésimas de la unidad tienen una interpretación geométrica bonita. Forman los vértices del $n$-ágono regular con $n$ vértices, sobre la circunferencia unitaria, donde uno de los vértices es $1$.
Ejemplo. Obtengamos las raíces quintas de la unidad. Primero, obtengamos la de menor argumento positivo, que por el teorema de raíces en los complejos, es $$\omega = \text{cis}\left(\frac{2\pi}{5}\right).$$ El resto de las raíces son entonces $\omega^2$, $\omega^3$, $\omega^4$ y $1$. Las podemos encontrar en el plano complejo como vértices del siguiente pentágono regular:
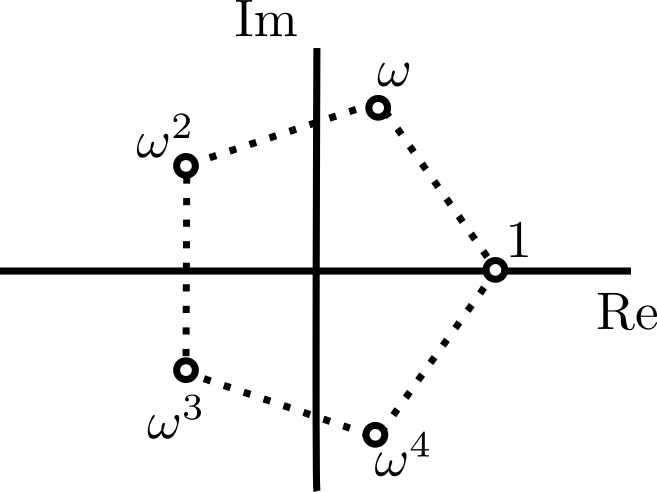
Cualquiera de $\omega$, $\omega^2$, $\omega^3$ y $\omega^4$ son raíces primitivas, pero $1$ no es raíz primitiva pues sus potencias sólo son él mismo.
$\triangle$
Las raíces $n$-ésimas de la unidad se utilizan en muchos contextos. Aunque se puede trabajar con ellas de forma explícita, muchas veces se utilizan sólo las propiedades algebraicas que cumplen. A continuación enunciamos algunas.
Teorema. Sea $\omega$ una raíz primitiva $n$-ésima de la unidad. Las raíces $n$-ésimas de la unidad $$\omega_i = \omega^i $$ para $i=0,\ldots,n-1$ satisfacen las siguientes propiedades:
- Para $n>1$, se tiene que $\omega_0+\ldots+\omega_{n-1}=0$.
- Para $k=0,1,\ldots,n-1$, se tiene que $$(\omega_k)^{-1}=\overline{\omega_k}=\omega_{n-k}.$$
- Se tiene que $\omega_0\cdot\ldots\cdot \omega_{n-1} = (-1)^{n+1}$.
Demostración. Empezamos con el primer inciso. Si $n>1$, tenemos que $1$ no es raíz primitiva, así que para el primer inciso sabemos que $\omega\neq 1$. Usamos la fórmula para suma de términos en una progresión geométrica:
\begin{align*}
\omega_0+\omega_1&+\ldots+\omega_{n-1}\\
&= 1+\omega+\ldots+\omega^{n-1}\\
&=\frac{1-\omega^n}{1-\omega}\\
&=\frac{1-1}{1-\omega}\\
&=0.
\end{align*}
Para la segunda parte, notemos que $$\omega_k\omega_{n-k}=\omega^k\omega^{n-k}=\omega^n=1,$$ lo cual prueba una de las igualdades. La otra igualdad se sigue del hecho general que el inverso de un complejo de norma $1$ es su conjugado, cuya demostración queda como tarea moral.
La tercera parte se sigue de la propiedad anterior. Al multiplicar todas las raíces de la unidad, podemos emparejar a cada raíz con su conjugado para obtener producto $1$. Las únicas excepciones es cuando emparejamos a un complejo consigo mismo, es decir, para cuando $\omega_k=\overline{\omega_k}$, lo cual sucede sólo cuando $\omega_k$ es real. Las únicas posibilidades son $1$ ó $-1$. El $1$ no tiene problema pues colabora con un factor $1$. Si $n$ es impar, $-1$ no es raíz $n$-ésima, así que no contribuye al producto. Si $n$ es par sí. Esto muestra lo que queremos pues $(-1)^{n+1}$ es $1$ si $n$ es impar y $-1$ si es par.
$\square$
Para un entero positivo $n$, llamemos $(U_n,\cdot)$ al conjunto de raíces $n$-ésimas de la unidad equipadas con el producto complejo.
Teorema. Para cada entero positivo $n$, se tiene que $(U_n,\cdot)$ es un grupo y es isomorfo a $(\mathbb{Z}_n,+)$.
Demostración. El producto de cualesquiera dos raíces $n$-ésimas es también una raíz $n$-ésima. Por el teorema anterior, los inversos multiplicativos de las raíces $n$-ésimas también son raíces $n$-ésimas. Esto basta para mostrar que se forma un grupo.
Para la segunda parte, notamos que ambos grupos son el grupo cíclico de $n$ elementos. Una correspondencia entre ellos está dada por mandar $[1]_n$ a cualquier raíz primitiva.
$\square$
Más adelante…
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Encuentra las raíces cúbicas de $8-8i$ y dibújalas en el plano complejo.
- Verifica que las soluciones obtenidas en el teorema de raíces $n$-ésimas en efecto son soluciones.
- Muestra el teorema de las raíces $n$-ésimas de la unidad.
- Prueba que si $z$ es un complejo de norma $1$, entonces su inverso es su conjugado.
- Sea $\omega$ una raíz $n$-ésima primitiva de la unidad. Muestra que $w^k$ es una raíz primitiva si y sólo si $n$ y $k$ son primos relativos, es decir, $\MCD{n,k}=1$. Sugerencia: Usa lo que sabemos de soluciones a ecuaciones diofantinas lineales.
- Encuentra de manera explícita la parte real y la parte imaginaria de todas las raíces quintas de la unidad.
Sugerencia: La ecuación $w^5-1=0$ se puede factorizar como $$(w-1)(w^4+w^3+w^2+w+1)$$ y $w^4+w^3+w^2+w+1$ se puede factorizar como $$\left(w^2+\frac{1+\sqrt{5}}{2}w+1\right)\left(w^2+\frac{1-\sqrt{5}}{2}w+1\right).$$ Usa lo que sabemos de resolver ecuaciones cuadráticas cojmplejas.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Multiplicación en forma polar y fórmula de De Moivre
- Entrada siguiente del curso: Problemas de fórmula de De Moivre y raíces n-ésimas
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»