Archivo de la etiqueta: triángulo

Geometría analítica I: Aplicaciones a geometría del triángulo

Por Elsa Fernanda Torres Feria

Introducción

En esta entrada usaremos la forma normal de la recta para demostrar dos teoremas conocidos como teoremas de concurrencia de líneas.

Medianas y baricentro

Cerremos la entrada con la enunciación y la demostración del siguiente teorema.

Teorema. Dado un triángulo PQR, sus tres medianas concurren en un punto que divide al segmento dentro del triángulo (de cada mediana) en proporción 1:2.

Demostración.

Para empezar la demostración, construimos un triángulo PQR.

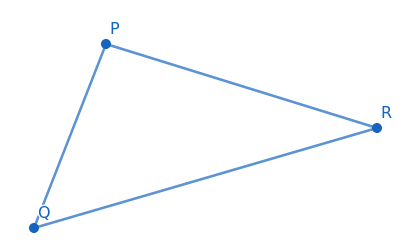
Para construir las medianas, primero localizamos los puntos medios de cada segmento (A, B, C) cuyas coordenadas baricéntricas están dadas por

$\begin{aligned} A & = \frac{1}{2} P + \frac{1}{2} Q \\ B & = \frac{1}{2} Q + \frac{1}{2} R \\ C & = \frac{1}{2} R + \frac{1}{2} P \end{aligned}$

Ya que queremos que se encuentren justo en el punto medio de cada segmento.

Al trazar la mediana del segmento $P Q$ tenemos lo siguiente

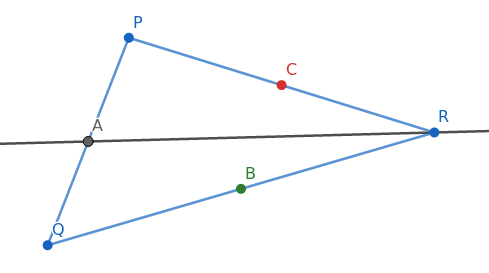
La manera en la que procederemos a partir de ahora, es que localizaremos el punto en el segmento de cada mediana que lo divide en proporción 1:2 esperando llegar a que los tres puntos son el mismo.

Comencemos con el punto $G$ que divide al segmento $A R$ en proporción 1:2, esto es que $G$ sea:

$G = \frac{1}{3} R + \frac{2}{3} A$

AL sustituir el valor de $A$ , tenemos como resultado
$\begin{aligned} G & = \frac{1}{3} R + \frac{2}{3} (\frac{1}{2} P + \frac{1}{2} Q) \\ = \frac{1}{3} R + \frac{1}{3} P + \frac{1}{3} Q \end{aligned}$

Lo que puede ser replicado para cada segmento. Para el $B P$ se tiene

$\begin{aligned} G^{'} & = \frac{1}{3} P + \frac{2}{3} B \\ = \frac{1}{3} P + \frac{2}{3} (\frac{1}{2} Q + \frac{1}{2} R) \\ = \frac{1}{3} P + \frac{1}{3} Q + \frac{1}{3} R \\ = \frac{1}{3} R + \frac{1}{3} P + \frac{1}{3} Q \end{aligned}$

Y para el $C Q$

$\begin{aligned} G » & = \frac{1}{3} Q + \frac{2}{3} C \\ = \frac{1}{3} Q + \frac{2}{3} (\frac{1}{2} R + \frac{1}{2} P) \\ = \frac{1}{3} Q + \frac{1}{3} R + \frac{1}{3} P \\ = \frac{1}{3} R + \frac{1}{3} P + \frac{1}{3} Q \end{aligned}$

$∴$ $G = G^{'} = G »$

Acabamos de demostrar que los puntos que dividen a cada mediana en una proporción 1:2 son el mismo para cada una, por lo que las tres medianas concurren en este punto.

A este punto $G$ se le conoce como el baricentro del triángulo, y podrás imaginar después de que discutimos la idea física de estas coordenadas, que $G$ corresponde al centro de masa o punto de equilibrio del triángulo.

Utiliza el siguiente interactivo para asegurarte de que esto es válido con cualquier triángulo, puedes mover los puntos P,Q y R y aún existirá el punto $G$ de intersección de las 3 medianas. Si te da curiosidad, puedes usar la herramienta de distancia de GeoGebra para medir la longitud de cada segmento de la mediana y verificar que efectivamente, está en una relación 1:2 con respecto al punto $G$ .

Teoremas de concurrencia

Para poder realizar las demostraciones, definiremos a la altura de un triángulo como la recta que pasa por uno de sus vértices y es ortogonal al lado opuesto. Ahora, enunciemos y demostremos el primer teorema.

Teorema 1. Las alturas de un triángulo son concurrentes.

Demostración

Comencemos esta demostración con un interactivo que ilustre un triángulo y sus alturas.

Las rectas verdes son las alturas del triángulo y en el interactivo es bastante evidente que concurren en un punto y que esto pasa para cualquier triángulo (para comprobarlo puedes mover con tu cursor los vértices para modificar el triángulo). Sin embargo en este curso de geometría analítica, queremos demostrarlo de manera algebraica.

Para esta demostración algebraica, notemos que los vértices del triángulo son $A$ , $B$ , y $C$ y las alturas asociadas a cada vértice son $a$ , $b$ y $c$ respectivamente. Escribamos la forma normal de cada una de estas rectas (alturas). Para $a$ tenemos

$a$ : $(C - B) \cdot x = (C - B) \cdot A$

pues la recta $a$ es ortogonal al lado del triángulo que pasa por los vértices $C$ y $B$ , por lo que este lado tiene dirección $(C - B)$ y pasa por el punto $A$ . De manera análoga, sabemos que $b$ es perpendicular a la recta que pasa por $A$ y $C$ con dirección $A - C$ y pasa también por el punto $B$ , así

$b$ : $(A - C) \cdot x = (A - C) \cdot B$

Y de la misma forma para $c$ tenemos

$c$ : $(B - A) \cdot x = (B - A) \cdot C$

Nota que si sumamos las dos primeras ecuaciones, obtendremos la ecuación negativa de $c$ :

$\begin{aligned} (C - B) \cdot x + (A - C) \cdot x & = (C - B) \cdot A + (A - C) \cdot B \\ (C - B + A - C) \cdot x & = C \cdot A - B \cdot A + A \cdot B - C \cdot B \\ (- B + A) \cdot x & = C \cdot A - A \cdot B + A \cdot B - C \cdot B \\ (- B + A) \cdot x & = C \cdot A - C \cdot B \\ (- B + A) \cdot x & = (A - B) \cdot C \end{aligned}$

Esto es importante, pues si tomamos un elemento en la intersección de las alturas $a$ y $b$ ( $x \in a \cap b$ ), entonces también está en la suma y está última nos da como resultado el negativo de la ecuación de la recta $c$ , por lo tanto $x \in c$ .

De manera análoga, si sumamos $b$ y $c$ obtenemos

$(B - C) \cdot x = (B - C) \cdot A$

que corresponde a la ecuación negativa de $a$ , por lo que si $x \in b \cap c$ , entonces $x$ está en la suma de las ecuaciones y por tanto está en $a$ .

Para completar la demostración, deberíamos realizar el mismo procedimiento al sumar las ecuaciones de $c$ y $a$ y confirmar que un punto en su intersección está en $b$ .

$∴$ si dos de las alturas se intersectan, entonces la tercera recta también y en el mismo punto.

$s q u a r e$

Teorema 2.

Demuestra que las tres mediatrices de un triángulo son concurrentes.

Demostración

Para comenzar la demostración, recordemos que la mediatriz de un segmento es la recta que es ortogonal a este y pasa por su punto medio.

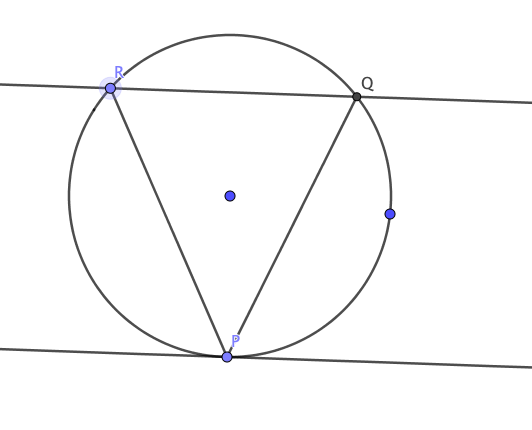
De nuevo, es claro que las tres mediatrices del triángulo con vértices $D$ , $E$ y $F$ concurren en un punto. Denominamos a los puntos medios de cada lado como $a$ , $b$ y $c$ , que es por donde pasan las mediatrices.

Ahora, para comenzar la parte algebraica de la demostración, definamos en su forma normal la primera miediatriz $i$ . Siguiendo la idea de la demostración pasada, $i$ es ortogonal a $(E - F)$ y pasa por el punto $a$ por lo que

$i$ : $(E - F) \cdot x = (E - F) \cdot a$

De la misma manera, $j$ es ortogonal a $(D - E)$ y pasa por $b$ , así

$j$ : $(D - E) \cdot x = (D - E) \cdot b$

Y para $k$ tenemos

$k$ : $(F-D) \cdot x = (F-D) \cdot c

Sigamos la intuición de la demostración anterior y sumemos las expresiones de $i$ y $j$

$\begin{aligned} (E - F) \cdot x + (D - E) \cdot x & = (E - F) \cdot a + (D - E) \cdot b \\ E \cdot x - F \cdot x + D \cdot x - E \cdot x & = E \cdot a - F \cdot a + D \cdot b - E \cdot b \\ D \cdot x - F \cdot x & = E \cdot a - F \cdot a + D \cdot b - E \cdot b \end{aligned}$

Para seguir avanzando con nuestra demostración, debemos recordar que $a,$ , $b$ y $c$ son los puntos medios de cada lado del triángulo, por lo que podemos expresarlos en términos de los vértices de la siguiente manera

$a = \frac{F + E}{2}$ , $b = \frac{E + D}{2}$ Y $c = \frac{D + F}{2}$

Con esto en mente, podemos sustituir $a$ y $b$ en la ecuación anterior y desarrollar

$D \cdot x - F \cdot x = E \cdot (\frac{F + E}{2}) - F \cdot (\frac{F + E}{2}) + D \cdot (\frac{E + D}{2}) - E \cdot (\frac{E + D}{2})$

Al realizar todo el desarrollo obtenemos que

$D \cdot x - F \cdot x = \frac{1}{2} (D \cdot D - F \cdot F)$

Ahora, en la demostración pasada queríamos llegar a algún múltiplo de $k$ para demostrar que las 3 rectas se intersectaban, siguiendo con esa lógica, desarrollemos el lado derecho de $k$ tomando en cuenta a $c$ como punto medio de un lado

$\begin{aligned} (F - D) \cdot c & = (F - D) \cdot \frac{D + F}{2} \\ = \frac{1}{2} (F - D) \cdot (D + F) \\ = \frac{1}{2} (F \cdot D + F \¢ d o t F - D \cdot D - F \cdot D) \\ = \frac{1}{2} (F \cdot F - D \cdot D) \end{aligned}$

Que es justamente el negativo de lo que obtuvimos arriba, por lo que al sumar las expresiones de $i$ y $j$ obtenemos el negativo de la expresión de $k$ . Así, si un punto $x$ está en $i \cap j$ , entonces está en la suma y por lo tanto está en $k$ .

El procedimiento es análogo para cada uno de los casos faltantes.

Para concluir esta entrada, denotaremos al punto en el que concurren las mediatrices como circuncentro.

Más adelante…

En las próximas entradas discutiremos la forma normal de un elemento geométrico en el espacio $R^{3}$ que no será la recta y hablaremos de la norma de un vector, que de cierta manera apareció en nuestras demostraciones pero no lo hemos discutido con formalidad hasta ahora.

Tarea moral

Completa los casos faltantes en la demostración del primer teorema.
Completa los casos faltantes en la demostración del segundo teorema.
Encuentra el circuncentro del triángulo que tiene como vértices los puntos $(5, 3)$ , $(2, - 1)$ y $(8, 0)$ .

Geometría Analítica I: Rectas en forma baricéntrica

Por Elsa Fernanda Torres Feria

Deja un comentario

Introducción

En esta entrada daremos una descripción alternativa de rectas: la forma baricéntrica. Esta manera de pensar nos ayuda a construir de manera muy rápida una recta que pase por dos puntos dados, o bien el segmento que une a dos puntos. Además, a través de ella podemos entender a las rectas desde un punto de vista más físico

Rectas en forma baricéntrica

En la forma paramétrica de una recta por $P$ con dirección $Q$ , tenemos que $P$ y $Q$ juegan papeles diferentes. En la forma que exploraremos ahora, se tendrá que juegan papeles iguales. De manera intuitiva, la forma que definiremos a continuación nos ayuda a construir fácilmente rectas que pasen por dos puntos dados.

Definición. Sean $P$ y $Q$ dos puntos distintos en $R^{2}$ . La recta en forma baricéntrica por $P$ y $Q$ es el conjunto

$l := {r P + s Q : r, s \in R y r + s = 1} .$

Ahora tenemos dos parámetros $r$ y $s$ que nos ayudan a ubicar un punto en la recta en cualquiera de las dos direcciones. Puedes pensar que la restricción $r + s = 1$ es la que hace que nos quedemos en la recta. Además, podemos pensar a $r$ y $s$ como «pesos» que nos dicen qué tan cerca estamos de $P$ y de $Q$ . Intuitivamente si $s > r$ , entonces el punto $X$ de la recta se encuentra más cerca del punto $Q$ y viceversa, si $r > s$ , entonces el punto $X$ de la recta está más cercano a $P$ . Esto es sólo intuitivo pues aún no tenemos una definición formal de distancia, pero más adelante retomaremos esto para formalizarlo.

Utiliza el siguiente interactivo para variar los valores de la coordenada baricéntrica $s$ de la recta (recuerda que r=1-s) y ubicar el punto $X$ en la recta que depende de estos valores.

Interpretación física

Ya que definimos las coordenadas baricéntricas, hablemos un poco de la interpretación física de esta con la cuál la idea de «peso» que le asignamos a estas coordenadas toma más sentido. Pensemos a la recta como una barra rígida sobre la cual está distribuida una masa unitaria (esto es que la masa en total es 1). El punto de equilibrio estará dado por las coordenadas baricéntricas correspondientes a las masas.

Ahora que estamos hablando de masas, resulta que podemos asociarle una fuerza a cada una para comprender mejor esta interpretación física. Retomando lo de hace unos párrafos, si $s > r$ , entonces la fuerza asociada a $s$ será mayor a la asociada a $r$ ( $F_{s} > F_{r}$ ) y si tenemos una de nuestras coordenadas baricéntricas negativas, podemos pensar entonces en una fuerza que va en sentido contrario a la positiva. Si pensamos en la fuerza gravitacional, un signo menos en nuestras coordenadas se podría visualizar como algo jalando hacia arriba.

Apoyate del interactivo anterior para comprender mejor esta idea y analiza el siguiente ejemplo:

Ejemplo: Sea $s = 0.3$ y $r = 0.7$ , nota que el punto está más cercano de $P$ .

Relación entre rectas paramétricas y rectas baricéntricas

En nuestro modelo ya definimos dos «tipos» de rectas: las rectas paramétricas y las rectas baricéntricas. Sería muy mala noticia que hayamos definido objetos geométricos diferentes, es decir, que hubiera algún objeto geométrico que sí fuera recta paramétrica pero que no fuera recta baricéntrica. O viceversa. Afortunadamente esto no es así. Todas las rectas paramétricas se pueden expresar de manera baricéntrica y todas las rectas baricéntricas se pueden expresar de manera paramétrica.

Demostrar esto formalmente nos lleva a argumentos de teoría de conjuntos. Veamos un ejemplo.

Proposición. Toda recta en forma paramétrica se puede expresar en forma baricéntrica.

Demostración. Tomemos la recta con forma paramétrica por $P$ y dirección $Q$ :

$ℓ = {P + r Q : r \in R} .$

Tenemos que encontrar una manera de expresarla en forma baricéntrica. Recordemos que la intuición de la forma baricéntrica es que pasa por dos puntos que le demos, así que nos conviene proponer dos puntos en $ℓ$ . Uno de ellos es $P$ (con $r = 0$ ) y otro es $P + Q$ (con $r = 1$ ). Ya tenemos entonces nuestra línea baricéntrica candidata:

$m = {r P + s (P + Q) : r, s \in R y r + s = 1} .$

Debemos demostrar que $ℓ = m$ . Esta es una afirmación de igualdad de dos conjuntos, así que hay que hacer una doble contención.

Un punto en $ℓ$ es de la forma $P + r Q$ , que se puede reescribir como $(1 - r) P + r (P + Q)$ . Aquí tanto $1 - r$ como $r$ son reales y suman $1$ , así que este punto está en $m$ . Esto muestra que $l \subseteq m$ .

Ahora tomemos un punto en $m$ . Es de la forma $r P + s (P + Q)$ en donde $r, s$ son reales de suma $1$ . De esta manera, $s = 1 - r$ , de modo que podemos reescribir:

$r P + s (P + Q) = r P + (1 - r) (P + Q) = P + (1 - r) Q .$

Esto es justo una de las expresiones que está en $ℓ$ . Concluimos que $m \subseteq ℓ$ y por lo tanto que $ℓ = m$ .

Una demostración similar muestra que toda recta en forma baricéntrica se puede expresar en forma paramétrica.

Segmentos y rayos

Hay algunas cosas que es más cómodo trabajar usando una forma de las rectas u otra. Por ejemplo, la definición de segmentos es muy fácil de dar pensando en forma baricéntrica.

Definición. El segmento entre dos puntos $P$ y $Q$ del plano es el conjunto:

$\overset{―}{P Q} := {r P + s Q : r \geq 0, s \geq 0 y r + s = 1} .$

La definición es prácticamente igual a la de recta en forma baricéntrica, pero limitando los valores de $r$ y $s$ a números no negativos.

Por otro lado, la definición de rayo es más fácil darla pensando en forma paramétrica.

Definición. El rayo desde un punto $P$ en dirección $Q$ es el conjunto:

$\vec{P Q} := {P + r Q : r \geq 0} .$

En este caso tenemos prácticamente la definición de recta en forma paramétrica, pero limitando el parámetro $r$ a números no negativos.

Postulados 1 y 3 de Euclides

Si recuerdas, en entradas anteriores se habló de que con esta «nueva» construcción de la geometría (la forma analítica), los postulados de Euclides podían ser demostrados. Ha llegado el momento en el que demostraremos una proposición que fusiona a los postulados 1 y 3.

Proposición. Para cualesquiera dos puntos $P$ y $Q$ , se puede trazar el segmento de recta que los une y este segmento se puede prolongar indefinidamente a una recta.

Demostración. Ya dimos una definición de segmento. Notemos que en esta definición tenemos que sus extremos se dan precisamente con $r = 0, s = 1$ , que corresponde al punto $Q$ y con $r = 1, s = 0$ , que corresponde al punto $P$ . Además, dicho segmento se queda contenido en la recta baricéntrica por $P$ y $Q$ , pues en ella se permiten $r$ y $s$ arbitrarios de suma $1$ , mientras que en el segmento sólo se permiten los no negativos.

De esta manera, la recta baricéntrica por $P$ y $Q$ es justo la prolongación del segmento que buscamos. Se prolonga indefinidamente al tomar valores de $r > 1$ y valores de $r < 0$ tan lejanos como queramos (y la $s$ correspondiente para que sume $1$ ). Al igual que en el caso paramétrico, se puede mostrar que todos estos puntos son distintos para valores distintos de $r$ .

Más adelante…

Hasta ahora hemos avanzado lo suficiente para hablar en entradas próximas de algo que se asomaba desde los postulados de Euclides, la intersección de rectas y las rectas paralelas.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

A partir de la forma baricéntrica de una recta, muestra cómo proponer su forma paramétrica $l = {Q + r (P - Q) : r \in R}$ . Haz una demostración por doble contención de que esas rectas son iguales.
Considera la siguiente recta en forma paramétrica: $L = {(5, 3) + r (- 7, 2) : r \in R}$ . Da una forma baricéntrica para $L$ .
Para asegurarte que entendiste la interpretación física, realiza los siguientes ejercicios:
- Imagina que tienes una barra rígida de 2 metros de longitud sobre la cuál tienes colgadas dos masas (una en cada extremo), una de 40 kg y otra de 10 gk. ¿cuáles son las coordenadas baricéntricas del punto de apoyo o de equilibrio de esta barra?
- Si ahora sabes que el punto de apoyo se encuentra en uno de los extremos de la barra rígida y quieres levantar los 40 kg con la fuerza de otra masa de 10 kg, ¿dónde debes colocar la masa para que esto sea posible? Realiza un dibujo.
Dado dos puntos $X$ y $Y$ se define su punto medio como el punto $\frac{X + Y}{2}$ . Considera los puntos $A = (- 2, 9)$ , $B = (7, - 1)$ y $C = (3, 5)$ . Encuentra el punto medio $L$ de $B$ y $C$ . Encuentra el punto medio $M$ de $C$ y $A$ . Encuentra el punto medio $N$ de $A$ y $B$ . Da expresiones paramétricas y baricéntricas para las rectas $A L$ , $B M$ y $C N$ .
Para los puntos del problema anterior encuentra ecuaciones para todos los segmentos y rayos que puedas definir.

Seminario de Resolución de Problemas: Coeficientes binomiales

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Los coeficientes binomiales aparecen en muchos problemas de matemáticas, y por ello es útil conocerlos bien y saber sus propiedades básicas. En esta entrada hablaremos de varios aspectos de los coeficientes binomiales: algebraicos, combinatorios y de teoría de números. Aunque resolvamos un problema con una técnica en particular, te recomendamos intentar usar las distintas herramientas en otros problemas, para conocer sus alcances y limitaciones.

Antes de empezar, ponemos una figura con un hecho curioso acerca de los coeficientes binomiales:

Coeficientes binomiales, Pascal y Fibonacci — «Las sumas de las diagonales del triángulo de Pascal dan los números de Fibonacci»

Definición algebraica de coeficientes binomiales

Como recordatorio, para $n \geq 0$ un entero, definimos $n!$ recursivamente como $0! = 1$ y $n! = n (n - 1)!$ . En otras palabras, para $n \geq 1$ tenemos $n! = 1 \cdot 2 \cdot \dots \cdot n .$

Definimos para $n \geq 0$ un entero y $k$ un entero en ${0, \dots, n}$ al coeficiente binomial $n$ en $k$ como $(\binom{n}{k}) := \frac{n!}{k! (n - k)!} .$ Si $n$ es un entero negativo o $k$ es un entero fuera del rango ${0, \dots, n}$ es conveniente definir $(\binom{n}{k}) = 0$ .

A partir de la definición, es claro que $(\binom{n}{n}) = (\binom{n}{0}) = 1$ para todo entero positivo $n$ . Lo que no es inmediato a partir de la definición es que $(\binom{n}{k})$ siempre sea un entero. Veremos eso en la siguiente sección.

Mientras tanto, veamos algunas propiedades de los coeficientes binomiales que se pueden verificar sin mostrar que $(\binom{n}{k})$ es entero.

Propiedad (simetría). $(\binom{n}{k}) = (\binom{n}{n - k}) .$

Propiedad (fórmula de Pascal). $(\binom{n + 1}{k + 1}) = (\binom{n}{k}) + (\binom{n}{k + 1}) .$

Propiedad (propiedad de entrada-salida). $(\binom{n + 1}{k + 1}) = \frac{n + 1}{k + 1} (\binom{n}{k}) .$

El siguiente problema se puede resolver usando estas identidades.

Propiedad (suma cambiando arriba). Muestra que para $n$ y $k$ enteros positivos se tiene que $\sum_{j = 0}^{k} (\binom{n + j}{n}) = (\binom{n + k + 1}{n + 1}) .$

Sugerencia pre-solución. Primero, formula un problema equivalente usando la propiedad de simetría. Luego, procede por inducción y usa otra de las propiedades de coeficientes binomiales mencionada arriba.

Solución. Usando la propiedad de simetría de coeficientes binomiales, el problema es equivalente a demostrar que $\sum_{j = 0}^{k} (\binom{n + j}{j}) = (\binom{n + k + 1}{k}) .$ Fijemos un entero $n \geq 0$ y hagamos inducción sobre $k$ . Para $k = 0$ , la identidad es cierta pues $(\binom{n}{0}) = 1 = (\binom{n + 1}{0}) .$

Para $k = 1$ , tenemos que mostrar que $(\binom{n}{0}) + (\binom{n + 1}{1}) = (\binom{n + 2}{1})$ . El primer término se puede escribir como $(\binom{n + 1}{0})$ , pues ambos son $1$ . Así, lo que hay que mostrar es $(\binom{n + 1}{0}) + (\binom{n + 1}{1}) = (\binom{n + 2}{1}),$ que es cierto por la fórmula de Pascal.

Suponiendo el resultado cierto para una $k$ dada, mostraremos que es cierto para $k + 1$ . Esto se sigue de la siguiente cadena de igualdades, en donde en la segunda igualdad usamos la hipótesis inductiva, y en la tercera la fórmula de Pascal:

$\begin{aligned} \sum_{j = 0}^{k + 1} (\binom{n + j}{j}) & = \sum_{j = 0}^{k} (\binom{n + j}{j}) + (\binom{n + k + 1}{k + 1}) \\ = (\binom{n + k + 1}{k}) + (\binom{n + k + 1}{k + 1}) \\ = (\binom{n + k + 2}{k + 1}) . \end{aligned}$

Esto termina la inducción.

Existen otras formas de demostrar identidades con coeficientes binomiales, y de hecho una misma identidad se puede mostrar de varias formas. Veamos más técnicas.

Aspectos combinatorios de los coeficientes binomiales

El coeficiente binomial $(\binom{n}{k})$ cuenta la cantidad de subconjuntos de tamaño $k$ de un conjunto de tamaño $n$ . Argumentar esto es relativamente fácil, usando un argumento de doble conteo. Supongamos que dicha cantidad de subconjuntos es igual a $A$ .

Respondamos la pregunta, ¿cuántos vectores de $k$ entradas existen, tales que las entradas son distintas y vienen de un conjunto de $n$ elementos? La pregunta es un poco distinta, pues como tenemos vectores, aquí sí importa el orden de los elementos. Supongamos que la respuesta es $B$ .

Una forma de responder la pregunta es la siguiente. Primero, elegimos cuál subconjunto de tamaño $k$ conformará las entradas. Esto se puede hacer de $A$ formas (que aunque no sepamos cuánto vale, lo podemos usar). Luego, hay que ordenar las $k$ entradas elegidas, que se puede hacer de $k!$ maneras. Así, esto muestra que $B = k! A$ .

Otra forma de responder la pregunta es la siguiente. Elegimos el primer elemento, que se puede hacer de $n$ formas. Luego el segundo, de entre los $n - 1$ restantes, que se puede hacer de $n - 1$ formas. Siguiendo de esta manera, el último de los $k$ hay que elegirlo entre $n - k + 1$ restantes. Así, esta otra forma de contar dice que $B = n \cdot (n - 1) \cdot \dots \cdot (n - k + 1) = \frac{n!}{(n - k)!} .$

Como ambas formas de contar son válidas, tenemos que $k! A = B = \frac{n!}{(n - k)!}$ , de donde $A = \frac{n!}{k! (n - k)!} = (\binom{n}{k})$ .

Hay problemas que de lejos parecen preguntar algo de álgebra, pero que pueden ser interpretados en términos combinatorios para dar una solución.

Problema. Para $n$ un entero positivo, muestra que $\sum_{k = 1}^{n} k (\binom{n}{k}) = n 2^{n - 1} .$

Sugerencia pre-solución. Construye un problema de conteo cuya respuesta se pueda poner tanto en términos del lado izquierdo, como en términos del lado derecho.

Solución. Preguntémonos, ¿de cuántas formas se puede elegir un subconjunto de un conjunto de $n$ elementos en el que uno de sus elementos está pintado de azul?

Por un lado, primero se puede elegir qué elemento va a ser el azul. Hay $n$ formas de hacer esta elección, y ésta forza a que el elemento en azul esté en el subconjunto. Luego, de los $n - 1$ elementos restantes hay que elegir un subconjunto para completar la elección, lo cual se puede hacer de $2^{n - 1}$ formas posibles. Así, una forma de contar da $n 2^{n - 1}$ .

Por otro lado, primero se puede decidir de qué tamaño $k$ va a ser el subconjunto. Como hay un elemento especial, el tamaño $k$ va de $1$ a $n$ . Ya elegido $k$ , hay $(\binom{n}{k})$ formas de elegir cuál será el subconjunto. Ya elegido el subconjunto, hay $k$ formas de elegir cuál será el elemento pintado de azul. Así, otra posible respuesta, también correcta, es $\sum_{k = 1}^{n} k (\binom{n}{k})$ .

Como estamos contando lo mismo con ambas expresiones, concluimos la igualdad del problema.

A este método de resolver problemas se le conoce como contar de dos formas distintas y funciona no sólo con coeficientes binomiales, sino también con cualquier otra expresión algebraica que tenga términos que se puedan interpretar de manera combinatoria. Hay otro ejemplo en el blog, en donde vemos cómo aparecen los números de Fibonacci en el triángulo de Pascal. En esa entrada también hablamos de cómo aparecen los coeficientes binomiales en el triángulo de Pascal.

Coeficientes binomiales y binomio de Newton

La interpretación combinatoria de los coeficientes binomiales nos da una demostración para la fórmula del binomio de Newton, que ya vimos en una entrada anterior. Aquí enunciamos la fómula como recordatorio.

Teorema (binomio de Newton). Para $a$ y $b$ números reales y $n$ un entero no negativo, se tiene que
$\begin{array}{r} (a + b)^{n} = \sum_{j = 0}^{n} (\binom{n}{j}) a^{n - j} b^{j} . \end{array}$

Si en el binomio de Newton ponemos $a = b = 1$ , obtenemos $(\binom{n}{0}) + (\binom{n}{1}) + \dots + (\binom{n}{n}) = (1 + 1)^{n} = 2^{n} .$ Otra forma de probar esta identidad es simplemente notar que tanto la suma de la izquierda como el término de la derecha cuentan la cantidad de subconjuntos de un conjunto de $n$ elementos: la de la izquierda los cuenta por tamaño, y el de la derecha decidiendo para cada elemento si está o no.

Si ponemos $a = 1$ , $b = - 1$ , obtenemos que $(\binom{n}{0}) - (\binom{n}{1}) + \dots + (- 1)^{n} (\binom{n}{n}) = 0,$ o bien $(\binom{n}{0}) + (\binom{n}{2}) + \dots = (\binom{n}{1}) + (\binom{n}{3}) + \dots .$

Se obtienen otras identidades de coeficientes binomiales interesantes si se usan raíces $n$ -ésimas de la unidad, como ya vimos en la entrada de aritmética compleja.

Hay otras formas de usar el binomio de Newton para probar identidades de coeficientes binomiales.

Problema. Muestra que ${(\binom{n}{0})}^{2} + {(\binom{n}{1})}^{2} + \dots + {(\binom{n}{n})}^{2} = (\binom{2 n}{n}) .$

Sugerencia pre-solución. Considera el polinomio $(1 + x)^{2 n}$ .

Solución. Consideremos el polinomio $(1 + x)^{2 n}$ y determinemos el coeficiente de su término $x^{n}$ .

Usando el binomio de Newton directamente, tenemos que $(1 + x)^{2 n} = \sum_{j = 0}^{2 n} (\binom{2 n}{j}) x^{j},$ de modo que el coeficiente de $x^{n}$ es $(\binom{2 n}{n})$ .

Por otro lado, podemos escribir $(1 + x)^{2 n} = (1 + x)^{n} (1 + x)^{n}$ . Usando el binomio de Newton, tenemos $(1 + x)^{n} = \sum_{j = 0}^{n} (\binom{n}{j}) x^{j} .$ Al multiplicar esta expresión consigo misma, los términos que quedan de grado $n$ son cuando, para cada $j$ , elegimos en un paréntesis al término que tiene $x^{j}$ (que tiene coeficiente $(\binom{n}{j})$ ) y en el otro al que tiene a $x^{n - j}$ (que tiene coeficiente $(\binom{n}{n - j})$ ).

De esta forma, el coeficiente del término de grado $n$ es $\sum_{j = 0}^{n} (\binom{n}{j}) (\binom{n}{n - j}) .$ Usando la identidad de simetría, podemos cambiar $(\binom{n}{n - j})$ por $(\binom{n}{j})$ , para obtener $\sum_{j = 0}^{n} {(\binom{n}{j})}^{2} .$ Igualando ambas formas de encontrar el coeficiente, obtenemos la identidad deseada.

Hay otras técnicas que usan herramientas de integrales o derivadas. Vimos un ejemplo de esto en una entrada anterior.

Coeficientes binomiales y teoría de números

El hecho de que los coeficientes binomiales son la respuesta a un problema de conteo, implica que son enteros no negativos. Alternativamente, esto se puede demostrar por inducción usando la identidad de Pascal.

Este hecho nos puede ayudar a resolver problemas de teoría de números. Veamos un ejemplo clásico.

Problema. Muestra que el producto de $n$ enteros consecutivos siempre es divisible entre $n!$ .

Sugerencia pre-solución. Haz una división en casos para ver si se incluye al cero, si son sólo negativos o sólo positivos. Reduce el caso de negativos a positivos y usa notación adecuada para escribir al producto de dichos enteros usando un coeficiente binomial.

Solución. Si alguno de los enteros es $0$ , entonces el producto es $0$ , que es divisible entre cualquier número. Si son $n$ enteros negativos, entonces podemos cambiar el signo a todos y su producto diferirá, quizás, en un factor $- 1$ que no afecta la divisibilidad, y habremos obtenido un problema con $n$ enteros positivos consecutivos. De esta manera, podemos enfocarnos en el caso de $n$ enteros positivos consecutivos.

Llamemos al primero $k + 1$ , para $k \geq 0$ . Los demás son entonces $k + 2, \dots, k + n$ . Su producto es
$\begin{aligned} (k + 1) (k + 2) \dots (k + n) & = \frac{k!}{k!} (k + 1) (k + 2) \dots (k + n) \\ = \frac{(n + k)!}{k!} \\ = n! (\binom{n + k}{k}) . \end{aligned}$

Como $(\binom{n + k}{k})$ es un entero, tenemos que el lado derecho es un múltiplo de $n!$ , como queríamos.

Otro tipo de técnicas hablan de la divisibilidad de un coeficiente binomial. Por ejemplo si tenemos un primo $p$ , sabemos que todos los siguiente coeficientes binomiales son enteros $(\binom{p}{1}), (\binom{p}{2}), \dots, (\binom{p}{p}) .$ Por su expresión en términos de factoriales, todos tienen a $p$ en el numerador, pero no tienen ningún divisor de $p$ distinto de $1$ en el denominador, pues $p$ es primo. Así, todos ellos son enteros divisibles entre $p$ . Eso puede ayudar en problemas como el siguiente.

Problema. Muestra que si $p$ es un número primo, entonces $p^{2}$ divide a $(\binom{2 p}{p}) - 2$ .

Sugerencia pre-solución. Formula un problema equivalente usando un resultado anterior.

Solución. Por un problema anterior, $(\binom{2 p}{p}) = {(\binom{p}{0})}^{2} + {(\binom{p}{1})}^{2} + \dots + {(\binom{p}{p})}^{2} .$

Por la discusión previa, para $j = 1, \dots, p - 1$ tenemos que $p ∣ (\binom{p}{j})$ , así que $p^{2} ∣ {(\binom{p}{j})}^{2}$ . De esta forma, trabajando módulo $2 p$ tenemos $\begin{aligned} (\binom{2 p}{p}) & \equiv {(\binom{p}{0})}^{2} + {(\binom{p}{p})}^{2} \\ \equiv 1 + 1 \equiv 2 (\mod p^{2}) . \end{aligned}$

Esto es justo lo que queríamos mostrar.

Más problemas

Puedes encontrar más problemas de coeficientes binomiales en la sección 5.1 del libro Problem Solving through Problems de Loren Larson.

Seminario de Resolución de Problemas: El teorema del valor extremo

Por Fabian Ferrari

Deja un comentario

Introducción

En una entrada anterior, acerca de funciones continuas, mencionamos dos teoremas fundamentales que estas funciones satisfacen: el teorema del valor intermedio y el teorema del valor extremo. Ya hablamos acerca del teorema del valor intermedio en una entrada anterior. El objetivo de esta entrada es mencionar aplicaciones del teorema del valor extremo.

Como recordatorio, el teorema del valor extremo o teorema de los valores extremos nos dice que si una función $f (x)$ es continua en un intervalo cerrado $[a, b]$ , entonces existen valores $c$ y $d$ en $[a, b]$ tales que $f (c) \leq f (x) \leq f (d)$ para toda $x$ en el intervalo $[a, b]$ .

En otras palabras, lo que nos dice el teorema es que si una función es continua en un intervalo cerrado, tenemos que la función debe alcanzar un valor máximo y un valor mínimo dentro del intervalo.

Dos teoremas para funciones derivables

Aprovecharemos para mencionar dos teoremas importantes que se ocuparán más adelante. Las demostraciones de dichos teoremas tienen que ver con la aplicación del teorema del valor extremo, estos teoremas son el teorema de Rolle y el teorema del valor medio (no confundir con el teorema del valor intermedio).

Teorema de Rolle. Sean $a < b$ reales y $f : [a, b] \to R$ una función continua en el intervalo $[a, b]$ y derivable en $(a, b)$ . Se tiene que si $f (a) = f (b)$ , entonces existe $c$ en $(a, b)$ tal que $f^{'} (c) = 0$ .

Sugerencia pre-demostración. Por el teorema del valor extremo, la función debe alcanzar un máximo y un mínimo en el intervalo. Divide en casos de acuerdo a dónde están estos valores, si en los extremos o no.

Demostración: Como $f (x)$ es una función continua en $[a, b]$ , por el teorema del valor extremo tenemos que $f (x)$ alcanza un valor máximo y un valor mínimo en el intervalo $[a, b]$ . Tenemos entonces los siguientes casos.

Caso i: Si el valor máximo y mínimo se encuentran en los extremos del intervalo, tenemos que la función $f (x)$ tiene que ser constante dado que $f (a) = f (b)$ . y se tiene que $f^{'} (c) = 0$ para todo $c$ en $[a, b]$ .

Caso ii: Si el valor mínimo o máximo no están en los extremos. Sean $c_{1}$ y $c_{2}$ en $(a, b)$ , los valores en los que la función alcanza su mínimo y máximo respectivamente. Alguno de estos no está en los extremos. Como $f (x)$ es derivable en $(a, b)$ , tenemos que también va a ser derivable en alguno de los puntos $c_{1}$ y $c_{2}$ , teniendo que $f^{'} (c_{1}) = 0$ o $f^{'} (c_{2}) = 0$ , así que basta con tomar $c = c_{1}$ o $c = c_{2}$ .

Teorema del valor medio. Sean $a < b$ reales y $f : [a, b] \to R$ una función continua en $[a, b]$ y diferenciable en $(a, b)$ . Entonces existe un número $c$ en $(a, b)$ tal que

$\frac{f (b) - f (a)}{b - a} = f^{'} (c)$ .

Demostración: Consideremos la siguiente función auxiliar:

$g (x) = (f (b) - f (a)) x - (b - a) f (x)$

Tenemos que $g (x)$ es continua en $[a, b]$ y además es derivable en $(a, b)$ . La derivada de $g (x)$ está dada por

$g^{'} (x) = f (b) - f (a) - (b - a) f^{'} (x)$

Como $g (x)$ es continua en $[a, b]$ , tenemos que por el teorema del valor extremo, la función alcanza un máximo y un mínimo en el intervalo $[a, b]$ . Haciendo las cuentas, $g (a) = g (b)$ , de modo que si el máximo y mínimo ocurren en los extremos, entonces $g$ es constante y toda $c \in (a, b)$ satisface $g^{'} (c) = 0$

En otro caso, sea $c \in (a, b)$ el valor en donde $g (x)$ alcanza su mínimo o su máximo. Tenemos que $g^{'} (c) = 0$ .

Así, como $g^{'} (c) = f (b) - f (a) - (b - a) f^{'} (c)$ , tenemos que:

$0 = f (b) - f (a) - (b - a) f^{'} (c)$

$(b - a) f^{'} (c) = f (b) - f (a)$

$f^{'} (c) = \frac{f (b) - f (a)}{b - a}$

Alternativamente, en la función anterior pudimos haber aplicado el teorema de Rolle directamente a la función $g$ . En las siguientes entradas veremos aplicaciones de estos resultados a problemas concretos.

Aplicación del teorema del valor extremo a un problema

Problema. Se tiene un circulo de radio $r$ , y una tangente $L$ que pasa por un punto $P$ de la circunferencia. De un punto cualquiera $R$ en la circunferencia se traza una paralela a $L$ que corta a la circunferencia en $Q$ . Determina el área máxima que puede tener el triángulo $P Q R$ .

Sugerencia pre-solución. Antes que nada, haz una figura. Usa el teorema del valor extremo para asegurar la existencia del valor máximo. Para ello, necesitarás construir una función continua cuyo valor sea el área buscada. Puedes usar argumentos de simetría para conjeturar cuándo se alcanza el valor máximo.

Solución. Hacemos el siguiente diagrama para entender mejor el problema.

Fijémonos que las condiciones de la altura y la base del triángulo $P Q R$ se pueden describir mediante la siguiente figura:

Condiciones para la altura y base del triángulo

Notemos que la altura del triángulo está dada por $r + h$ , donde $h$ puede variar entre $- r$ y $r$ . Este dibujo también nos es de ayuda para determinar el valor de la base. Por el teorema de Pitágoras y sabiendo que la distancia del centro $C$ a los puntos $R$ y $Q$ es igual a $r$ , tenemos que la base del triángulo es igual a $2 \sqrt{r^{2} - h^{2}}$ .

Así, el área del triángulo está dada por $(\sqrt{r^{2} - h^{2}}) (r + h)$ , pero como $h$ varía, nos conviene ver el área en función de $h$ .

$A (h) = \sqrt{r^{2} - h^{2}} (r + h),$

La función $A (h)$ es una función continua en el intervalo $[- r, r]$ .

Notemos que cuando $h$ toma los valores de $- r$ y $r$ , el valor del área es nulo, es decir que en estos valores alcanza el mínimo, lo cual quiere decir que por el teorema del valor extremo, el valor máximo lo alcanza en algún valor en $(- r, r)$ .

Si derivamos la función $A (h)$ , tenemos

$A^{'} (h) = \frac{r^{2} - r h - 2 h^{2}}{\sqrt{r^{2} - h^{2}}} .$

Como sabemos que hay un máximo en el intervalo $(- r, r)$ y la derivada en este punto máximo debe ser igual a cero, hacemos $A^{'} (h) = 0$ .

Así,

$\frac{r^{2} - r h - 2 h^{2}}{\sqrt{r^{2} - h^{2}}} = 0.$

Resolviendo la ecuación tenemos que

$h = \frac{r}{2} .$

Así, el área máxima del triángulo $P Q R$ es $A = \sqrt{r^{2} - {(\frac{r}{2})}^{2}} (r + \frac{r}{2}) = \frac{3 \sqrt{3} r^{2}}{4} .$

Más ejemplos

Se pueden encontrar más problemas de aplicación del teorema del vaalor extremo en la Sección 6.4 del libro Problem Solving through Problems de Loren Larson.

Elegir notación efectiva

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Para que las matemáticas realmente simplifiquen las cosas y no las compliquen más, una de las cosas que se necesita es tener una notación adecuada.

En esta serie de videos veremos algunos ejemplos en los cuales elegir variables adecuadas o una representación adecuada del problema puede ayudar en la solución del problema o bien simplifica algunas cuentas.

Ir a los videos…

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Archivo de la etiqueta: triángulo

Geometría analítica I: Aplicaciones a geometría del triángulo

Introducción

Medianas y baricentro

Teoremas de concurrencia

Más adelante…

Tarea moral

Geometría Analítica I: Rectas en forma baricéntrica

Introducción

Rectas en forma baricéntrica

Interpretación física

Relación entre rectas paramétricas y rectas baricéntricas

Segmentos y rayos

Postulados 1 y 3 de Euclides

Más adelante…

Tarea moral

Seminario de Resolución de Problemas: Coeficientes binomiales

Introducción

Definición algebraica de coeficientes binomiales

Aspectos combinatorios de los coeficientes binomiales

Coeficientes binomiales y binomio de Newton

Coeficientes binomiales y teoría de números

Más problemas

Seminario de Resolución de Problemas: El teorema del valor extremo

Introducción

Dos teoremas para funciones derivables

Aplicación del teorema del valor extremo a un problema

Más ejemplos

Elegir notación efectiva