Archivo de la etiqueta: ortogonalidad

Geometría Moderna II: Circunferencias ortogonales

Por Armando Arzola Pérez

Deja un comentario

Introducción

En esta entrada introduciremos un nuevo concepto: el de circunferencias ortogonales. Veremos cómo se relaciona este concepto con el de eje radical, que estudiamos en la entrada anterior.

Circunferencias ortogonales

La definición que nos interesa estudiar ahora es la siguiente.

Definición. Dos circunferencias $\mathcal{C_1}$ y $\mathcal{C_2}$ que se intersecan en un punto $P$ son ortogonales si sus tangentes en $P$ forman un ángulo recto.

Hagamos algunas observaciones de esta definición. Primero, dos circunferencias tangentes no pueden ser ortogonales pues si el punto de tangencia es $P$, entonces tienen la misma tangente en $P$. Así, las circunferencias deben intersectarse en al menos dos puntos $P$ y $Q$. Por simetría, las tangentes en $P$ son ortogonales si y sólo si las tangentes en $Q$ lo son.

Además, si los centros son $O_1$ y $O_2$, respectivamente, entonces sabemos que $O_1P$ es ortogonal a la tangente a $\mathcal{C}_1$ por $P$ y análogamente $O_2P$ es ortogonal a la tangente a $\mathcal{C}_2$ por $P$. Así, las tangentes son ortogonales si y sólo si los radios $O_1P$ y $O_2P$ lo son.

Algunas conexiones entre circunferencias ortogonales y eje radical

Veamos un primer resultado que relaciona circunferencias ortogonales y el eje radical.

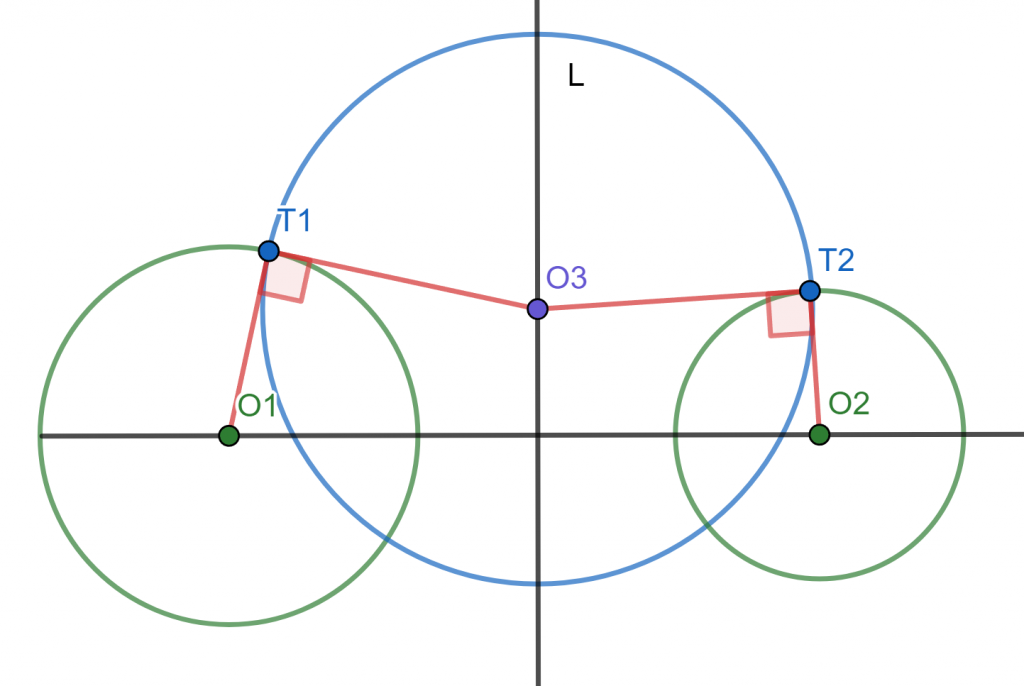
Teorema. Sean $\mathcal{C_1}$ y $\mathcal{C_2}$ circunferencias de centros distintos. Si $\mathcal{C}_3$ es ortogonal a ambas circunferencias, entonces su centro $O_3$ se encuentra en el eje radical de ambas.

Demostración. Denotaremos por $T_1$ a uno de los puntos de intersección de $\mathcal{C}_1$ y $\mathcal{C}_3$, y por $T_2$ a uno de los puntos de intersección de $\mathcal{C}_2$ y $\mathcal{C}_3$ (ver la figura a continuación). Debemos mostrar que $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$, es decir, que $$\text{Pot}(O_3,\mathcal{C}_1)=\text{Pot}(O_3,\mathcal{C}_2).$$

Circunferencias Ortogonales del primer teorema.

Como $O_3T_2$ y $O_3T_1$ son radios de $\mathcal{C}_3$, entonces $$O_3T_1^2=O_3T_2^2.$$

En la entrada de potencia de un punto vimos que podemos calcular la potencia en términos de la longitud de una tangente como sigue: $$\text{Pot}(O_3,\mathcal{C}_1)=O_3T_1^2=O_3T_2^2=\text{Pot}(O_3,\mathcal{C}_2).$$

Así, concluimos lo que queríamos, que $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$.

$\square$

El siguiente resultado es similar, y en cierto sentido es un «regreso» del anterior.

Teorema. Sean $\mathcal{C_1}$ y $\mathcal{C_2}$ circunferencias de centros distintos. Sea $\mathcal{C}_3$ una circunferencia cuyo centro $O_3$ está en el eje radical de las dos circunferencias dadas. Si $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_2$, entonces también es ortogonal a $\mathcal{C}_1$.

Demostración. Tomaremos como referencia la figura anterior. A partir de las hipótesis, queremos demostrar que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$. Sea $r_1$ el radio de $\mathcal{C}_1$. Por el teorema de Pitágoras, lo que queremos sucede si y sólo si $$O_3O_1^2-r_1^2= O_3T_1^2.$$

Dado que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_2$, el triángulo $\triangle O_3T_2O_2$ es rectángulo. Por el teorema de Pitágoras se cumple entonces que $O_3O_2^2-r_2^2= O_3T_2^2$. Como $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$, y por cómo se calcula la potencia en términos de la distancia al centro y del radio, tenemos que: $$O_3O_2^2 – r_2^2=\text{Pot}(O_2,\mathcal{C}_3)=\text{Pot}(O_2,\mathcal{C}_2)=O_3O_1^2-r_1^2.$$

De este modo, $$O_3T_1^2=O_3T_2^2=O_3O_2^2-r_2^2=O_3O_1^2-r_1^2.$$

Esto es justo lo que necesitábamos para concluir que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$.

$\square$

Posición de una circunferencia ortogonal a dos dadas con respecto a su eje radical

Veamos un resultado más, que nos habla acerca de la posición de una circunferencia en relación a otras dos a las que es tangente.

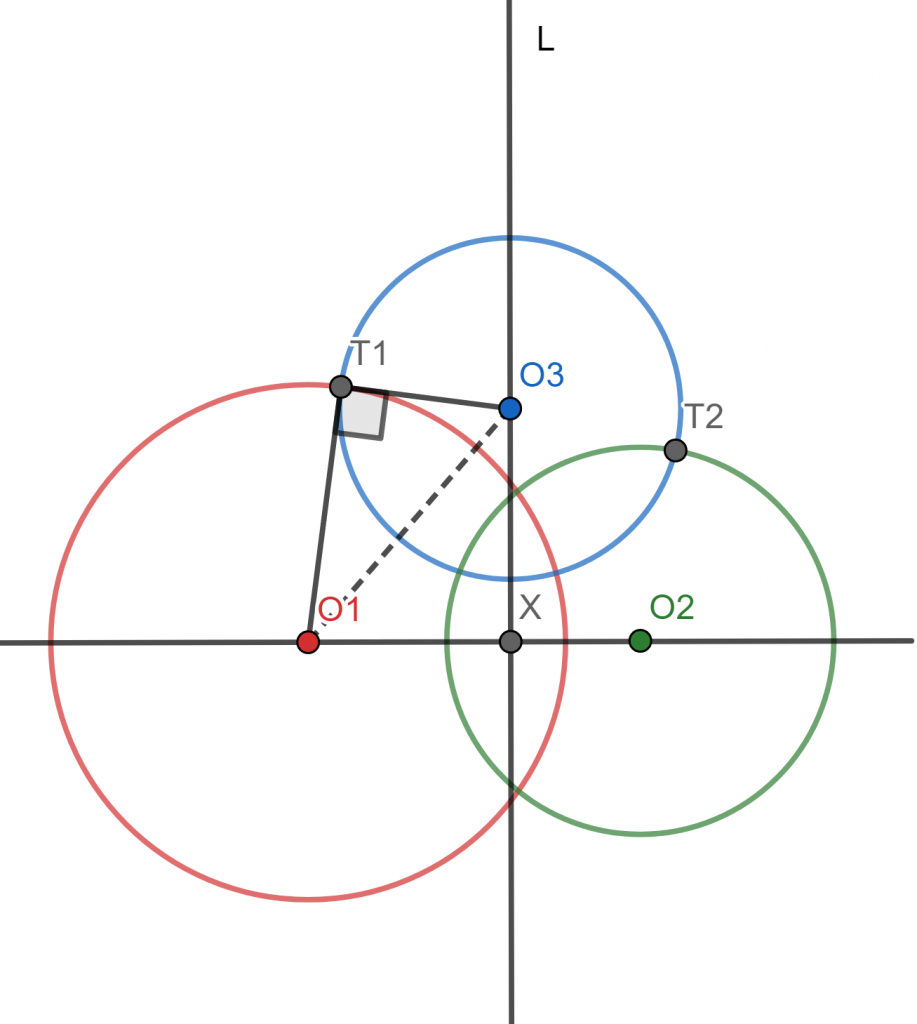
Teorema. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias de centros distintos $O_1$ y $O_2$. Sea $\mathcal{C}_3$ una circunferencia ortogonal a $\mathcal{C}_1$ y $\mathcal{C}_2$. La circunferencia $\mathcal{C}_3$ está posicionada con respecto a la línea de los centros $O_1O_2$ de acuerdo a los siguientes tres casos:

  1. Si $\mathcal{C}_1$ y $\mathcal{C}_2$ se intersectan en dos puntos, entonces $\mathcal{C}_3$ no intersecta a $O_1O_2$.
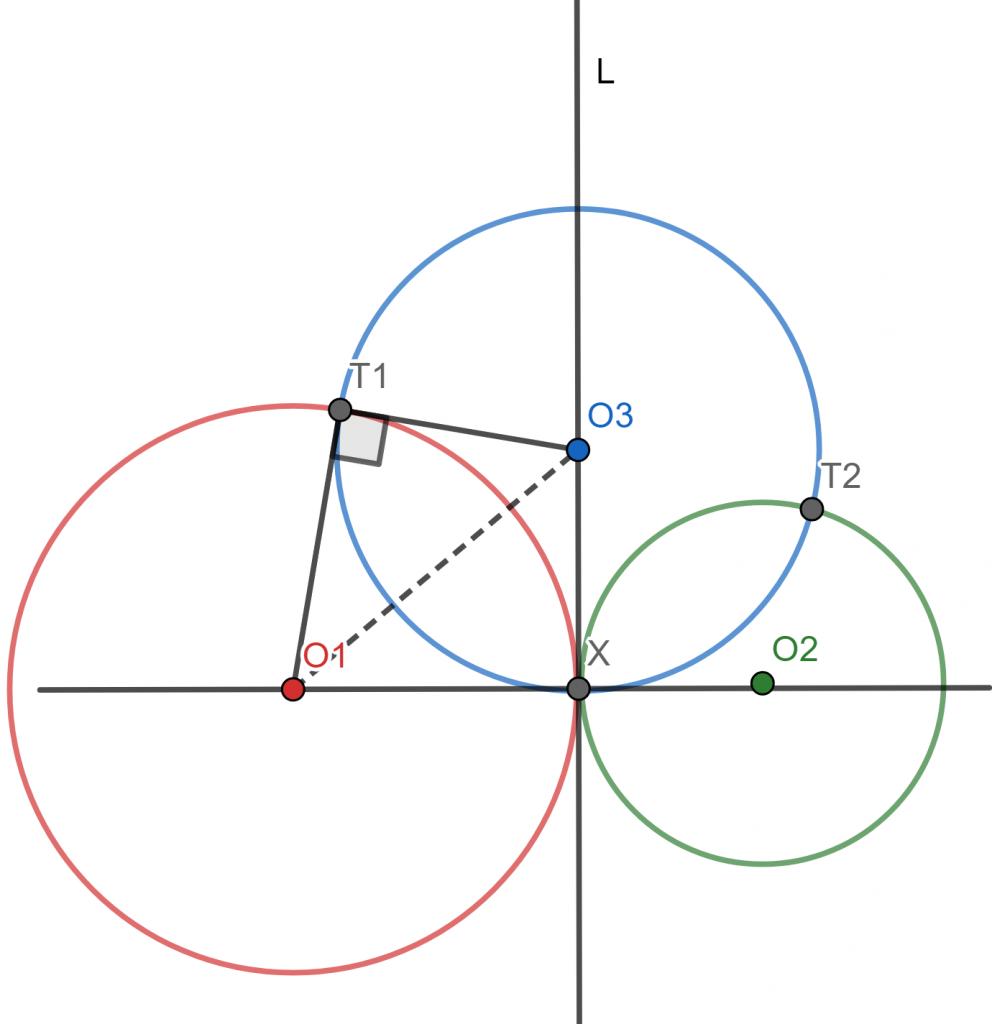
  2. Si $\mathcal{C}_1$ y $\mathcal{C}_2$ son tangentes, entonces $\mathcal{C}_3$ es tangente a $O_1O_2$.
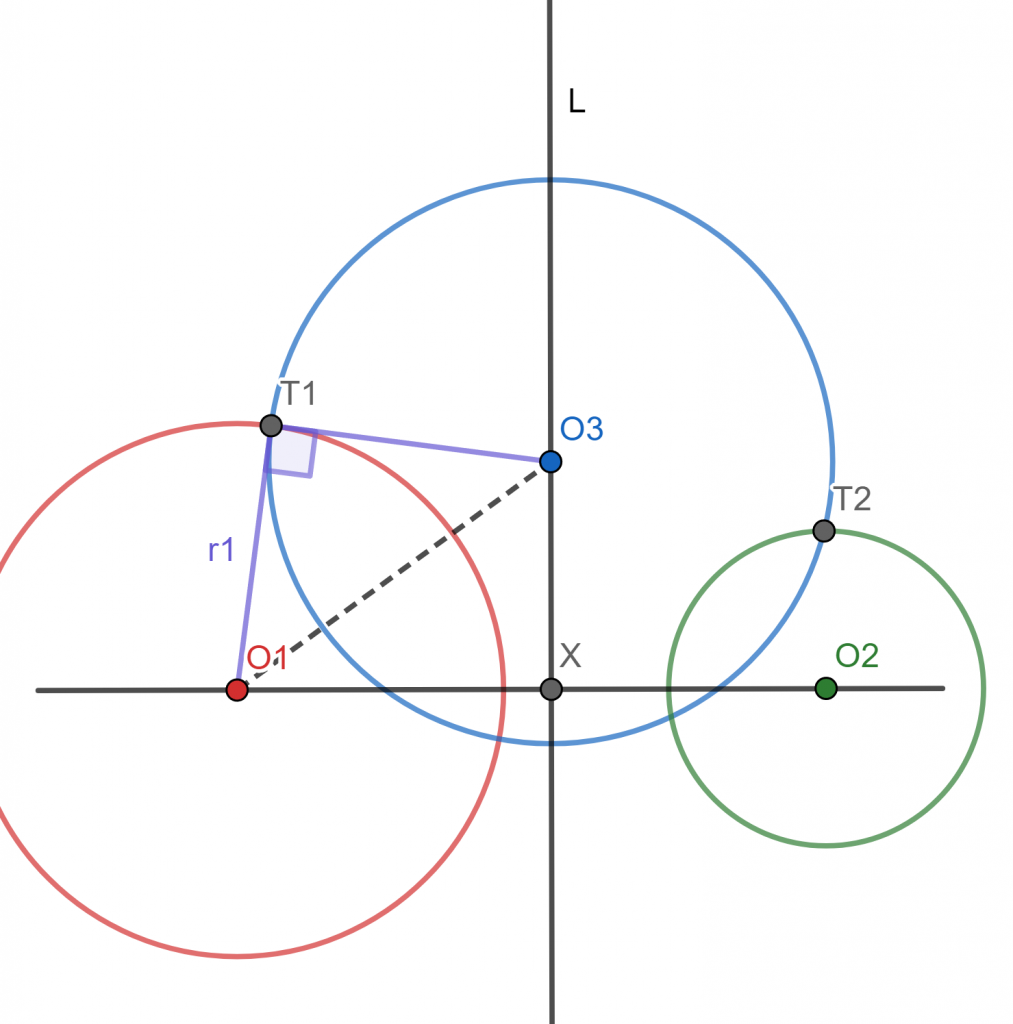
  3. Si $\mathcal{C}_1$ y $\mathcal{C}_2$ no se intersectan, entonces $\mathcal{C}_3$ intersecta a $O_1O_2$ en dos puntos.

Demostración. Sea $\mathcal{C}_3$ una circunferencia ortogonal a dos circunferencias dadas $\mathcal{C}_1$ y $\mathcal{C}_2$. Sean $r_1$, $r_2$, $r_3$ los radios de $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$, respectivamente. Sea $X$ la intersección de $O_1O_2$ con el eje radical $l$ de las circunferencias $\mathcal{C}_1$ y $\mathcal{C}_2$. Sea $T_1$ un punto de intersección de $O_3$ con $O_1$ y $T_1$ un punto de intersección de $O_3$ con $O_2$. La figura a continuación muestra el dibujo para el primer caso.

Circunferencias Ortogonales

Dado que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$ y $\mathcal{C}_2$, se tienen dos triángulos rectángulos: $$\triangle O_3T_1O_1 \quad \text{y} \quad \triangle O_3XO_1.$$

Por el teorema de Pitágoras, tenemos que $$O_3T_1^2+r_1^2=O_3O_1^2=O_1X^2+O_3X^2,$$

de donde $r_1^2-O_1X^2=O_3X^2-r_3^2$. Tratemos ahora sí cada caso por separado.

Caso 1. Supongamos que $\mathcal{C}_1$ y $\mathcal{C}_2$ se intersectan en dos puntos. Mostraremos que $\mathcal{C}_3$ no intersecta a $O_1O_2$.

Como las circunferencias se intersectan en dos puntos, el eje radical es la recta que une las intersecciones. Por ello, $r_1>|O_1X|$. Usando las cuentas de arriba:

\begin{align*}
& r_1>|O_1X|\\
\Rightarrow &r_1^2>O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 >0\\
\Rightarrow & O_3X^2-r_3^2>0\\
\Rightarrow & O_3X^2>r_3^2.
\end{align*}

Esto último sucede si y sólo si $|O_3X|>r_3$. Esto nos dice que $X$ está fuera de la circunferencia $\mathcal{C}_3$ y entonces dicha circunferencia no intersecta a $O_1O_2$.

Caso 2. Supongamos ahora que $\mathcal{C}_1$ y $\mathcal{C}_2$ son tangentes. Debemos demostrar que $\mathcal{C}_3$ es tangente a $O_1O_2$. En este caso, $r_1=|O_1X|$. Y entonces tenemos la siguiente cadena de implicaciones:

\begin{align*}
& r_1>=O_1X|\\
\Rightarrow &r_1^2=O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 =0\\
\Rightarrow & O_3X^2-r_3^2=0\\
\Rightarrow & O_3X^2=r_3^2.
\end{align*}

Esto, junto con el hecho de que $O_3X$ es perpendicular a $O_1O_2$, implica que $O_1O_2$ es tangente a $\mathcal{C}_3$.

Caso 3. Finalmente, supongamos que $\mathcal{C}_1$ y $\mathcal{C}_2$ no se intersectan. Debemos mostrar que $\mathcal{C}_3$ sí intersecta a $O_1O_2$ en dos puntos. Para ello basta mostrar que $|O_3X|<r_3$. La suposición de que las circunferencias no se intersectan implica que $r_1<|O_1X|$.

Circunferencias Ortogonales

Una vez más procedemos con las siguientes implicaciones:

\begin{align*}
& r_1<|O_1X|\\
\Rightarrow &r_1^2<O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 <0\\
\Rightarrow & O_3X^2-r_3^2<0\\
\Rightarrow & O_3X^2<r_3^2.
\end{align*}

Por ello, $|O_3X|<r_3$, como queríamos.

$\square$

Más adelante…

Hemos abordado algunos resultados de circunferencias ortogonales. Lo que haremos en la siguiente entrada es estudiar a las familiar coaxiales de circunferencias. Sabemos que cualesquiera dos circunferencias tienen un eje radical pero, ¿qué sucede tenemos más de dos circunferencias que comparten eje radical?

Entradas relacionadas

Álgebra Lineal II: Ortogonalidad en espacios euclideanos

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

Anteriormente, cuando hablamos del espacio dual de un espacio vectorial, definimos qué quería decir que una forma lineal y un vector fueran ortogonales. Esa noción de ortogonalidad nos ayudó a definir qué era un hiperplano de un espacio vectorial y a demuestra que cualquier subespacio de dimensión $k$ de un espacio de dimensión $n$ podía ponerse como intersección de $n-k$ hiperplanos.

Hay otra noción de ortogonalidad en álgebra lineal que también ya discutimos en el primer curso: la ortogonalidad de parejas de vectores con respecto a un producto interior. En el primer curso vimos esta noción muy brevemente. Lo que haremos ahora es profundizar en esta noción de ortogonalidad. De hecho, gracias a las herramientas que hemos desarrollado podemos conectar ambas nociones de ortogonalidad.

Esta teoría la veremos de manera explícita en el caso real en la entrada. El caso en $\mathbb{C}$ queda esbozado en los ejercicios.

Definición de ortogonalidad

Comenzamos con las siguientes definiciones.

Definición. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ y $b$ una forma bilineal de $V$. Diremos que dos vectores $x,y$ en $V$ son ortogonales (con respecto a $b$) si $b(x,y)=0$.

Definición. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ y $b$ una forma bilineal de $V$. Sea $S$ un subconjunto de vectores de $V$. El conjunto ortogonal de $S$ (con respecto a $b$) consiste de todos aquellos vectores en $V$ que sean ortogonales a todos los vectores de $S$. En símbolos:

$$S^{\bot}:=\{v \in V : \forall s \in S, b(s,v)=0\}.$$

Es un buen ejercicio verificar que $S^\bot$ siempre es un subespacio de $V$. Finalmente, definimos la ortogonalidad de conjuntos.

Definición. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ y $b$ una forma bilineal de $V$. Diremos que dos subconjuntos $S$ y $T$ son ortogonales (con respecto a $b$) si $S \subseteq T^{\bot}$.

En otras palabras, estamos pidiendo que todo vector de $S$ sea ortogonal a todo vector de $T$.

Observación. Si tenemos un espacio vectorial con producto interior $\langle \cdot, \cdot \rangle$ de norma $\norm{\cdot}$, entonces tenemos la fórmula $$\norm{x+y}^2=\norm{x}^2+2\langle x,y\rangle +\norm{y}^2.$$

De esta forma, $x$ y $y$ son ortogonales si y sólo si $$\norm{x+y}^2= \norm{x}^2+\norm{y}^2.$$ Podemos pensar esto como una generalización del teorema de Pitágoras.

Descomposición en un subespacio y su ortogonal

Comenzamos esta sección con un resultado auxiliar.

Teorema. Sea $V$ un espacio euclideano y $W$ un subespacio de $V$. Entonces $$V=W\oplus W^\bot.$$

Demostración. Sea $\langle \cdot,\cdot \rangle$ el producto interior de $V$. Para demostrar la igualdad que queremos, debemos mostrar que $W$ y $W^\bot$ están en posición de suma directa y que $V=W+W^\bot$.

Para ver que $W$ y $W^\bot$ están en posición de suma directa, basta ver que el único elemento en la intersección es el $0$. Si $x$ está en dicha intersección, entonces $\langle x, x \rangle =0$, pues por estar en $W^\bot$ debe ser ortogonal a todos los de $W$, en particular a sí mismo. Pero como tenemos un producto interior, esto implica que $x=0$.

Tomemos ahora un vector $v\in V$ cualquiera. Definamos la forma lineal $f:W\to \mathbb{R}$ tal que $f(u)=\langle u, v \rangle$. Por el teorema de representación de Riesz aplicado al espacio vectorial $W$ y a su forma lineal $f$, tenemos que existe un (único) vector $x$ en $W$ tal que $f(u)=\langle u, x \rangle$ para cualquier $u$ en $W$.

Definamos $y=v-x$ y veamos que está en $W^\bot$. En efecto, para cualquier $u$ en $W$ tenemos:

\begin{align*}
\langle u, y\rangle &= \langle u, v-x \rangle\\
&=\langle u, v \rangle – \langle u , x \rangle\\
&=f(u)-f(u)\\
&=0.
\end{align*}

De esta manera, podemos escribir $v=x+y$ con $x\in W$ y $y\in W^\bot$.

$\square$

En particular, el teorema anterior nos dice que la unión disjunta de una base de $W$ y una base de $W^\bot$ es una base de $V$. Por ello, tenemos el siguiente corolario.

Corolario. Sea $V$ un espacio euclideano y $W$ un subespacio de $V$. Entonces $$\dim{W}+\dim{W^\bot}=\dim{V}.$$

Tenemos un corolario más.

Corolario. Sea $V$ un espacio euclideano y $W$ un subespacio de $V$. Entonces $$(W^\bot)^\bot=W.$$

Demostración. Tanto $W$ como $(W^\bot)^\bot$ son subespacios de $V$. Tenemos que $W\subseteq (W^\bot)^\bot$ pues cualquier elemento de $W$ es ortogonal a cualquier elemento de $W^\bot$. Además, por el corolario anterior tenemos:

\begin{align*}
\dim{W}+\dim{W^\bot}&=\dim{V}\\
\dim{W^\bot}+\dim{(W^\bot)^\bot}&=\dim{V}.
\end{align*}

De aquí se sigue que $\dim{W} = \dim{(W^\bot)^\bot}$. Así, la igualdad que queremos de subespacios se sigue si un subespacio está contenido en otro de la misma dimensión, entonces deben de ser iguales.

$\square$

Proyecciones ortogonales

Debido al teorema anterior, podemos dar la siguiente definición.

Definición. Sea $V$ un espacio euclideano y $W$ un subespacio de $V$. La proyección ortogonal hacia $W$ es la transformación lineal $p_W:V\to W$ tal que a cada $v$ en $V$ lo manda al único vector $p_W(v)$ tal que $x-p_W(v)$ está en $W^\bot$.

Dicho en otras palabras, para encontrar a la proyección de $v$ en $W$ debemos escribirlo de la forma $v=x+y$ con $x\in W$ y $y\in W^\bot$ y entonces $p_W(v)=x$.

Distancia a subespacios

Cuando definimos la distancia entre conjuntos que tienen más de un punto, una posible forma de hacerlo es considerando los puntos más cercanos en ambos conjuntos, o en caso de no existir, el ínfimo de las distancias entre ellos. Esto da buenas propiedades para la distancia. En particular, cuando queremos definir la distancia de un punto $x$ a un conjunto $S$ hacemos lo siguiente.

Definición. Sea $V$ un espacio vectorial real con producto interior $\langle \cdot, \cdot \rangle$ de norma $\norm{\cdot}$. Sea $S$ un subconjunto de $V$ y $v$ un vector de $V$. Definimos la distancia de $v$ a $S$ como la menor posible distancia de $v$ hacia algún punto de $S$. En símbolos:

$$d(v,S):=\inf_{s\in S} d(v,s).$$

En general, puede ser complicado encontrar el punto que minimiza la distancia de un punto a un conjunto. Sin embargo, esto es más sencillo de hacer si el conjunto es un subespacio de un espacio con producto interior: se hace a través de la proyección al subespacio. Esto queda reflejado en el siguiente resultado.

Proposición. Sea $V$ un espacio euclideano con producto interior $\langle \cdot, \cdot \rangle$ de norma $\norm{\cdot}$. Sea $W$ un subespacio de $V$ y sea $v$ un vector en $V$. Entonces $$d(v,W)=\norm{v-p_W(v)}.$$

Más aún, $p_W(v)$ es el único punto en $W$ para el cual se alcanza la distancia mínima.

Demostración. Por el teorema de descomposición en un subespacio y su ortogonal, sabemos que podemos escribir $v=x+y$ con $x$ en $W$ y con $y$ en $W^\bot$.

Tomemos cualquier elemento $w$ en $W$. Tenemos que $x-w$ está en $W$ y que $y$ está en $W^\bot$. Así, usando el teorema de Pitágoras tenemos que:

\begin{align*}
\norm{v-w}^2&=\norm{y+(x-w)}^2\\
&=\norm{y}^2+\norm{x-w}^2\\
&\geq \norm{y}^2\\
&=\norm{v-x}^2.
\end{align*}

Esto muestra que $\norm{v-w}\geq \norm{v-x}$. Como $x\in W$, esto muestra que la distancia de $v$ a $W$ en efecto se alcanza con $x=p_W(v)$, pues cualquier otra distancia es mayor o igual.

La igualdad en la cadena anterior de alcanza si y sólo si $\norm{x-w}^2=0$, lo cual sucede si y sólo si $x=w$, como queríamos.

$\square$

Más adelante…

En la siguiente entrada recordaremos varias de las ventajas que tiene contar con una base de un espacio vectorial en la que cualesquiera dos vectores sean ortogonales entre sí. Y en la entrada después de esa, recordaremos algunas hipótesis bajo las cuales podemos garantizar encontrar una de esas bases.

Tarea moral

  1. Resuelve los siguientes ejercicios:
    1. Sea $\mathbb{R}^3$ con el producto interno canónico y $W=\{(0,0,a_3) : a_3 \in \mathbb{R} \}$. Encuentra a $W^{\bot}$ y define la proyección ortogonal $p_W$ hacia $W$.
    2. Encuentra el vector en $\text{Span}((1,2,1), (-1,3,-4))$ que sea el más cercano (respecto a la norma euclidiana) al vector $(-1,1,1)$.
  2. Sea $V$ un espacio euclidiano y $T : V \to V $ una transformación lineal tal que $T^2=T$. Prueba que T es una proyección ortogonal si y solo si para cualesquiera $x$ y $y$ en $V$ se tiene que $$\langle T(x),y\rangle =\langle x,T(y)\rangle.$$
  3. Resuelve los siguientes ejercicios:
    1. Demuestra que una proyección ortogonal reduce la norma, es decir, que si $T$ es una proyección ortogonal, entonces $\norm{T(v)}\leq \norm{v}$.
    2. Prueba que una proyección ortogonal únicamente puede tener como eigenvalores a $0$ ó a $1$.
  4. Demuestra que la composición de dos proyecciones ortogonales no necesariamente es una proyección ortogonal.
  5. En el teorema de descomposición, ¿es necesaria la hipótesis de tener un producto interior? ¿Qué sucede si sólo tenemos una forma bilineal, simétrica y positiva?

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Dualidad y representación de Riesz en espacios euclideanos

Por Diego Ligani Rodríguez Trejo

Deja un comentario

Introducción

En Álgebra Lineal I introdujimos el concepto de espacio dual, a grandes rasgos, era el espacio vectorial donde estaban todas las formas lineales de un espacio hacia su campo. Por otro lado, en entradas recientes hicimos un recordatorio de qué era un producto interior. Lo que haremos ahora es relacionar ambos conceptos. Esta relación no debería ser tan inesperada, pues un producto interior es una forma bilineal, y al fijar una entrada de este obtenemos una forma lineal.

Lo primero que haremos es ver cómo conectar la matriz que representa a una forma bilineal con una matriz que envía vectores a formas lineales. Después, veremos una versión particular de un resultado profundo: el teorema de representación de Riesz. Veremos que, en espacios euclideanos, toda forma lineal se puede pensar «como hacer producto interior con algún vector».

Nos enfocaremos únicamente a los resultados en el caso real. Los casos en el caso complejo son muy parecidos, y se exploran en los ejercicios.

La matriz de una transformación que «crea» formas lineales

Sea $V$ un espacio vectorial real con una forma bilineal $b$. A partir de $b$ podemos construir muchas formas lineales, a través de la función $\varphi_b:V\to V^\ast$ que asigna a cada vector $y$ de $V$ a la forma lineal $\varphi_b(y):=b(\cdot,y)$.

Podemos pensar a $\varphi_b$ como «una maquinita que genera formas lineales» que depende del vector $b$. Claramente $\varphi_b(y)$ es lineal, pues $b$ es lineal en su primera entrada. Y también claramente $\varphi_b$ es lineal, pues $b$ es lineal en su segunda entrada. En cierto sentido, la matriz correspondiente a la forma bilineal $b$ coincide con la matriz correspondiente a $\varphi_b$.

Proposición. Sea $\beta$ una base de un espacio vectorial $V$ de dimensión finita sobre los reales. Sea $\beta^\ast$ su base dual. Tomemos $b$ una forma bilineal en $V$. La matriz de $\varphi_b$ con respecto a las bases $\beta$ y $\beta’$ es igual a la matriz de $b$ con respecto a la base $\beta$.

Demostración. Llamemos a los elementos de la base $\beta$ como $u_1,\ldots,u_n$ y a los de la base $\beta^ \ast$ como $l_1,\ldots,l_n$. Para encontrar la $j$-ésima columna de la matriz de $\varphi_b$ con respecto a $\beta$ y $\beta^\ast$, debemos expresar a cada $\varphi_b(u_j)$ como combinación lineal de los elementos $l_1,\ldots,l_n$. Para hacer esto, es más sencillo ver cómo es $\varphi_b(u_j)(x)$ para cada $x\in V$ y usar que los $l_i$ «leen» las coordenadas en la base $\beta$.

Para ello, tomemos $x=\sum_{i=1}^nu_ix_i$. Tenemos lo siguiente:

\begin{align*}
\varphi_b(u_j)(x)&=b(\sum_{i=1}^nu_ix_i,u_j)\\
&= \sum_{i=1}^nx_ib(u_i,u_j)\\
&= \sum_{i=1}^n l_i(x) b(u_i,u_j).
\end{align*}

Como esto sucede para cada vector $x$, tenemos entonces que $$\varphi_b(u_j)=\sum_{i=1}^n b(u_i,u_j) l_i.$$

Pero esto es justo lo que queremos. Las entradas de la $j$-ésima columna de la matriz que representa a $\varphi_b$ son entonces los coeficientes $b(u_1,u_j),b(u_2,u_j),\ldots,b(u_n,u_j)$. Pero esas son justo las entradas de la $j$-ésima columna de la matriz que representa a $b$ en la base $\beta$.

$\square$

Teorema de representación de Riesz

La sección anterior explica cómo de una forma bilineal $b$ podemos obtener una «máquinita» que genera formas lineales $\varphi_b$. Si $b$ es mucho más especial (un producto interior), entonces esta maquinita es «más potente», en el sentido de que puede generar cualquier forma lineal del espacio. A este resultado se le conoce como el teorema de representación de Riesz. Aunque sus versiones más generales incluyen ciertos espacios de dimensión infinita, y el enunciado dice algo más general, en este curso nos limitaremos a enunciar y demostrar la versión en espacios vectoriales de dimensión finita.

Teorema (teorema de representación de Riesz). Sea $V$ un espacio euclidiano con producto interno $\langle \cdot, \cdot \rangle$. La función $\varphi_{\langle \cdot, \cdot \rangle}: V \rightarrow V^\ast$ es un isomorfismo.

Demostración. Debemos probar que $\varphi_{\langle \cdot, \cdot \rangle}$ es una transformación lineal biyectiva hacia $V^\ast$. Como mencionamos en la sección anterior, cada $\varphi_{\langle \cdot, \cdot \rangle}(y)$ es una forma lineal pues el producto interior es lineal en su primera entrada. Además, $\varphi_{\langle \cdot, \cdot \rangle}$ es una transformación lineal pues el producto interior es lineal en su segunda entrada.

Por los resultados que se vieron en el curso de Álgebra Lineal I, se tiene que $\dim V = \dim V^\ast$. De esta manera, basta ver que $\varphi_{\langle\cdot,\cdot \rangle}$ es inyectiva. Y para ello, basta ver que el único vector $y$ tal que $\varphi_{\langle \cdot, \cdot \rangle}(y)$ es la forma lineal cero es $y=0$.

Supongamos entonces que $\varphi_{\langle \cdot, \cdot \rangle}(y)$ es la forma lineal cero. Si este es el caso, entonces para cualquier $x$ en $V$ tendríamos que $\langle x, y \rangle = 0$. En particular, esto sería cierto para $x=y$, de modo que $\langle y, y \rangle =0$. Pero como el producto interior es positivo definido, esto implica que $y=0$.

Esto muestra que $\varphi_{\langle \cdot, \cdot \rangle}$ es inyectiva. Como es transformación lineal entre espacios de la misma dimensión, entonces es biyectiva.

$\square$

Ejemplo de representación de Riesz

Las operaciones que se hacen para calcular una forma lineal no siempre son sencillas. Lo que nos dice el teorema de representación de Riesz es que podemos tomar un «vector representante» de una forma lineal para que evaluarla corresponda «simplemente» a hacer un producto interior. Si es fácil hacer ese producto interior, entonces podemos simplificar la evaluación de la forma lineal.

Ejemplo. Tomemos $V$ el espacio vectorial de polinomios con coeficientes reales y grado a lo más $2$. Hemos visto con anterioridad que $\langle \cdot, \cdot \rangle: V\times V \to \mathbb{R}$ dado por: $$\langle p, q \rangle = p(0)q(0)+p(1)q(1)+p(2)q(2) $$ es un producto interior.

Hemos visto también que $I:V\to \mathbb{R}$ dada por $I(p)=\int_0^1 p(x)\, dx$ es una forma lineal. El teorema de representación de Riesz nos garantiza que $I$, que es una integral definida, debería poder «representarse» como el producto interior con un polinomio especial $q$. Esto parecen ser buenas noticias: para $I(p)$ necesitamos hacer una integral. Para hacer el producto interior, sólo son unas multiplicaciones y sumas.

El polinomio «mágico» que funciona en este caso es el polinomio $q(x)=-\frac{x^2}{2}+\frac{3}{4}x+\frac{5}{12}$. Puedes verificar que:

\begin{align*}
q(0)&=\frac{5}{12}\\
q(1)&=\frac{2}{3}\\
q(2)&=-\frac{1}{12}.
\end{align*}

De esta manera, si hacemos el producto interior con cualquier otro polinomio $p(x)=ax^2+bx+c$ obtenemos:

\begin{align*}
\langle p, q \rangle &= p(0)q(0) + p(1)q(1)+p(2)q(2)\\
&= c\cdot \frac{5}{12} + (a+b+c)\cdot \frac{2}{3} + (4a+2b+c) \cdot \left(-\frac{1}{12}\right)\\
&=\frac{a}{3}+\frac{b}{2}+c.
\end{align*}

Si por otro lado hacemos la integral, obtenemos:

\begin{align*}
\int_0^1 ax^2 + bx + c \, dx &= \left. \left(\frac{ax^3}{3}+\frac{bx^2}{2}+cx \right)\right|_0^1\\
&=\frac{a}{3}+\frac{b}{2}+c.
\end{align*}

En ambos casos se obtiene lo mismo.

$\triangle$

Se podría tener una discusión más profunda para explicar cómo se obtuvo el polinomio $q$ del ejemplo anterior. Sin embargo, dejaremos la experimentación de esto para los ejercicios. Por ahora, la mayor ventaja que le encontraremos al teorema de representación de Riesz es la garantía teórica de que dicho vector que representa a una forma lineal dado un producto interior siempre existe en los espacios euclideanos.

Más adelante…

Hemos enunciado y demostrado una versión del teorema de Riesz para espacios euclieanos. Este teorema tiene versiones más generales en el contexto de espacios de Hilbert. Así mismo, una versión más extensa del teorema de Riesz nos dice cómo es la norma del vector que representa a un producto interior. Estos resultados son muy interesantes, pero quedan fuera del alcance de este curso. Es posible que los estudies si llevas un curso de análisis funcional.

Un poco más adelante, en la Unidad 3, usaremos el teorema de representación de Riesz para definir a las transformaciones adjuntas, a las simétricas y a las ortogonales. Por ahora, nos enfocaremos en estudiar más definiciones y propiedades en espacios euclideanos. La siguiente definición que repasaremos es la de ortogonalidad para vectores y para espacios vectoriales. Es un concepto que se estudia por encima en Álgebra Lineal I, pero ahora tenemos herramientas para poder decir más.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso. Sin embargo, sirven de ayuda para repasar los conceptos vistos en esta entrada.

  1. ¿Podemos definir a $\varphi_b: V \rightarrow V^*$ en la otra entrada? Es decir, como la función tal que $\varphi_b(x)=b(x,\cdot)$? Si hacemos esto, ¿cambian en algo los resultados que vimos?
  2. Considera el espacio vectorial de matrices en $M_n(\mathbb{R})$. Anteriormente vimos que $b(A,B)=\text{tr}(\text{ }^t A B)$ es un producto interior y que sacar traza es una forma lineal. De acuerdo al teorema de representación de Riesz, debe haber una matriz $T$ que representa a la traza, es decir, tal que $\text{tr}(A)=b(A,T)$. ¿Quién es esta matriz $T$? Ahora, si tomamos la transformación que manda una matriz $A$ a la suma de las entradas en su antidiagonal, esto también es una forma lineal. ¿Quién es la matriz que representa a esta forma lineal con el producto interior dado?
  3. Enuncia y demuestra un teorema de igualdad de formas matriciales para el caso de formas sesquilineales. ¿Necesitas alguna hipótesis adicional?
  4. Enuncia y demuestra un teorema de representación de Riesz para espacios hermitianos. Deberás tener cuidado, pues el vector que representa a una forma lineal tendrá que estar en la coordenada que conjuga escalares. ¿Por qué?
  5. ¿Será cierto el teorema de representación de Riesz si la forma bilineal no es un producto interior? Identifica dónde falla la prueba que dimos. Luego, construye un contraejemplo para ver que la hipótesis de que $b$ sea positiva definida es fundamental. Es decir, encuentra un espacio vectorial $V$ real con una forma bilineal simétrica y positiva $b$, en donde exista una forma lineal $l$ tal que sea imposible encontrar un vector $y$ tal que para todo $x$ en $V$ se tenga que $l(x)=b(x,y)$. Sugerencia. Parace que hay muchos cuantificadores. Intenta dar un contraejemplo lo más sencillo posible, por ejemplo, en $\mathbb{R}^2$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal I: Problemas de bases ortogonales, Fourier y proceso de Gram-Schmidt

Por Blanca Radillo

2 respuestas

Introducción

Durante las últimas clases hemos visto problemas y teoremas que nos demuestran que las bases ortogonales son extremadamente útiles en la práctica, ya que podemos calcular fácilmente varias propiedades una vez que tengamos a nuestra disposición una base ortogonal del espacio que nos interesa. Veamos más problemas de bases ortogonales y otros resultados que nos permitirán reforzar estas ideas.

Problemas resueltos de bases ortogonales y proyecciones

Para continuar con este tema, veremos que las bases ortogonales nos permiten encontrar de manera sencilla la proyección de un vector sobre un subespacio. Primero, recordemos que si $V=W\oplus W_2$, para todo $v\in V$ podemos definir su proyección en $W$, que denotamos $\pi_W(v)$, como el único elemento en $W$ tal que $v-\pi_W(v) \in W_2$.

Debido a las discusiones sobre bases ortogonales, no es difícil ver que si $\langle w,u \rangle =0$ para todo $w\in W$, entonces $u\in W_2$. Como consecuencia de esto, tenemos el siguiente resultado:

Teorema. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ con producto interior $\langle \cdot , \cdot \rangle$, y sea $W$ un subespacio de $V$ de dimensión finita. Sea $v_1,\cdots,v_n$ una base ortogonal de $W$. Entonces para todo $v\in V$ tenemos que

$\pi_W(v)=\sum_{i=1}^n \frac{\langle v,v_i \rangle}{\norm{v_i}^2} v_i .$

Demostración. Escribimos $v$ como $v=\pi_W(v)+u$ con $u\in W_2$. Por la observación previa al teorema, $\langle u,v_i \rangle =0$ para todo $i$. Además existen $a_1,\cdots,a_n$ tales que $\pi_W(v)=a_1 v_1+\cdots+a_n v_n$. Entonces

\begin{align*}
0 &= \langle u,v_i \rangle =\langle v,v_i \rangle – \langle \pi_W(v),v_i \rangle \\
&= \langle v,v_i \rangle – \sum_{j=1}^n a_j \langle v_j,v_i \rangle \\
&= \langle v,v_i \rangle – a_i \langle v_i,v_i \rangle,
\end{align*}

porque $v_1,\cdots,v_n$ es una base ortogonal. Por lo tanto, para todo $i$, obtenemos

$a_i=\frac{\langle v,v_i \rangle}{\norm{v_i}^2}.$

$\square$

Distancia de un vector a un subespacio y desigualdad de Bessel

En la clase de ayer, vimos la definición de distancia entre dos vectores. También se puede definir la distancia entre un vector y un subconjunto como la distancia entre el vector y el vector «más cercano» del subconjunto, en símbolos:

$d(v,W)=\min_{x\in W} \norm{x-v}.$

Dado que $x\in W$, $x-\pi_W(v) \in W$, y por definición de proyección $v-\pi_W(v) \in W_2$, entonces

\begin{align*}
\norm{x-v}^2 &=\norm{(x-\pi_W(v))+(\pi_W(v)-v)}^2 \\
&= \norm{x-\pi_W(v)}^2+2\langle x-\pi_W(v),\pi_W(v)-v \rangle+\norm{\pi_W(v)-v}^2 \\
&= \norm{x-\pi_W(v)}^2+\norm{\pi_W(v)-v}^2\\
&\geq \norm{\pi_W(v)-v}^2.
\end{align*}

Y dado que la proyección pertenece a $W$, la desigualdad anterior muestra que la proyección es precisamente el vector en $W$ con el que $v$ alcanza la distancia a $W$. En conclusión, $$d(v,W)=\norm{\pi_W(v)-v}.$$

Teorema. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ con producto interior $\langle \cdot , \cdot \rangle$, y sea $W$ un subespacio de $V$ de dimensión finita. Sea $v_1,\ldots,v_n$ una base ortonormal de $W$. Entonces para todo $v\in V$ tenemos que

$\pi_W(v)=\sum_{i=1}^n \langle v,v_i \rangle v_i,$

y

\begin{align*}
d(v,W)^2&=\norm{v-\sum_{i=1}^n \langle v,v_i \rangle v_i }^2\\
&=\norm{v}^2-\sum_{i=1}^n \langle v,v_i \rangle^2.
\end{align*}

En particular

$\sum_{i=1}^n \langle v,v_i \rangle^2\leq \norm{v}^2.$

A esta última desigualdad se le conoce como desigualdad de Bessel.

Demostración. Por el teorema anterior y dado que $v_1,\cdots,v_n$ es una base ortonormal, obtenemos la primera ecuación. Ahora, por Pitágoras,

$d(v,W)^2=\norm{v-\pi_W(v)}^2=\norm{v}^2-\norm{\pi_W(v)}^2.$

Por otro lado, tenemos que

\begin{align*}
\norm{\pi_W(v)}^2 &=\norm{\sum_{i=1}^n \langle v,v_i \rangle v_i}^2 \\
&= \sum_{i,j=1}^n \langle \langle v,v_i \rangle v_i, \langle v,v_j \rangle v_j \rangle \\
&= \sum_{i,j=1}^n \langle v,v_i \rangle \langle v,v_j \rangle \langle v_i,v_j \rangle \\
&=\sum_{i=1}^n \langle v,v_i \rangle^2.
\end{align*}

Por lo tanto, se cumple la igualdad de la distancia. Finalmente como $d(v,W)^2 \geq 0$, inmediatamente tenemos la desigualdad de Bessel.

$\square$

Veamos ahora dos problemas más en los que usamos la teoría de bases ortonormales.

Aplicación del proceso de Gram-Schmidt

Primero, veremos un ejemplo más del uso del proceso de Gram-Schmidt.

Problema. Consideremos $V$ como el espacio vectorial de polinomios en $[0,1]$ de grado a lo más $2$, con producto interior definido por $$\langle p,q \rangle =\int_0^1 xp(x)q(x) dx.$$

Aplica el algoritmo de Gram-Schmidt a los vectores $1,x,x^2$.

Solución. Es fácil ver que ese sí es un producto interior en $V$ (tarea moral). Nombremos $v_1=1, v_2=x, v_3=x^2$. Entonces

$$e_1=\frac{v_1}{\norm{v_1}}=\sqrt{2}v_1=\sqrt{2},$$

ya que $$\norm{v_1}^2=\int_0^1 x \, dx=\frac{1}{2}.$$

Sea $z_2=v_2-\langle v_2,e_1 \rangle e_1$. Calculando, $$\langle v_2,e_1 \rangle=\int_0^1 \sqrt{2}x^2 dx=\frac{\sqrt{2}}{3}.$$ Entonces $z_2=x-\frac{\sqrt{2}}{3}\sqrt{2}=x-\frac{2}{3}.$ Esto implica que

$e_2=\frac{z_2}{\norm{z_2}}=6\left(x-\frac{2}{3}\right)=6x-4.$

Finalmente, sea $z_3=v_3-\langle v_3,e_1\rangle e_1 -\langle v_3,e_2 \rangle e_2$. Haciendo los cálculos obtenemos que

$z_3=x^2-\left(\frac{\sqrt{2}}{4}\right)\sqrt{2}-\left(\frac{1}{5}\right)(6x-4)$

$z_3=x^2-\frac{6}{5}x+\frac{3}{10}.$

Por lo tanto

$e_3=\frac{z_3}{\norm{z_3}}=10\sqrt{6}(x^2-\frac{6}{5}x+\frac{3}{10}).$

$\triangle$

El teorema de Plancherel y una fórmula con $\pi$

Finalmente, en este ejemplo, usaremos técnicas de la descomposición de Fourier para solucionar un problema bonito de series.

Problema. Consideremos la función $2\pi-$periódica $f:\mathbb{R}\rightarrow \mathbb{R}$ definida como $f(0)=f(\pi)=0,$ $f(x)=-1-\frac{x}{\pi}$ en el intervalo $(-\pi,0)$, y $f(x)=1-\frac{x}{\pi}$ en el intervalo $(0,\pi)$.

Problemas de bases ortogonales: Aplicando el teorema de Plancherel para una fórmula que involucra a pi.
Gráfica de la función $f$.

Usa el teorema de Plancherel para deducir las identidades de Euler

\begin{align*}
\sum_{n=1}^\infty \frac{1}{n^2} &= \frac{\pi^2}{6},\\
\sum_{n=0}^\infty \frac{1}{(2n+1)^2} & = \frac{\pi^2}{8}.
\end{align*}

Solución. Notemos que no sólo es $2\pi-$periódica, también es una función impar, es decir, $f(-x)=-f(x)$. Por lo visto en la clase del miércoles pasado tenemos que calcular

$a_0(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) dx,$

$a_k(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) cos(kx) dx,$

$b_k(f)=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x)sen(kx) dx.$

Para no hacer más larga esta entrada, la obtención de los coeficientes de Fourier se los dejaremos como un buen ejercicio de cálculo. Para hacer las integrales hay que separar la integral en cada uno de los intervalos $[-\pi,0]$ y $[0,\pi]$ y en cada uno de ellos usar integración por partes.

El resultado es que para todo $k\geq 1$, $$a_0=0, a_k=0, b_k=\frac{2}{k\pi}.$$

Entonces por el teorema de Plancherel,

\begin{align*}
\sum_{k=1}^\infty \frac{4}{k^2\pi^2} &=\frac{1}{\pi} \int_{-\pi}^{\pi} f^2(x) dx \\
&= \frac{1}{\pi} \left( \int_{-\pi}^0 \left(1+\frac{x}{\pi}\right)^2 dx + \int_0^\pi \left(1-\frac{x}{\pi}\right)^2 dx \right) \\
&= \frac{2}{3},
\end{align*}

teniendo que $$\sum_{k=1}^\infty \frac{1}{k^2} =\frac{2}{3}\frac{\pi^2}{4}=\frac{\pi^2}{6}.$$

Ahora para obtener la otra identidad de Euler, notemos que

\begin{align*}
\sum_{n=0}^\infty \frac{1}{(2n+1)^2} &= \sum_{n=1}^\infty \frac{1}{n^2} – \sum_{n=1}^\infty \frac{1}{(2n)^2} \\
&= \frac{\pi^2}{6}-\frac{\pi^2}{4\cdot6}= \frac{\pi^2}{8}.
\end{align*}

$\triangle$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Proceso de Gram-Schmidt

Por Blanca Radillo

4 respuestas

Introducción

Durante esta semana hemos introducido el concepto de bases ortogonales y ortonormales, así como algunas propiedades especiales. Para poder aplicar los resultados que hemos visto, es necesario insistir en que las bases sean de este tipo (ortonormales). Ahora veremos cómo encontrar bases ortonormales usando algo llamado el proceso de Gram-Schmidt.

Recordando todos los problemas anteriores de este curso, decíamos que una base es un conjunto de vectores linealmente independientes y que el número de vectores coincide con la dimensión del espacio. Pero hasta este momento no nos interesó determinar si las bases eran ortonormales o no. Si nos pusiéramos a ver si lo eran, es probable que muy pocas lo sean. Entonces surgen dos preguntas, ¿será difícil encontrar una base ortonormal de un espacio vectorial? y ¿habrá alguna manera de construir una base ortonormal?

Proceso de Gram-Schmidt

La respuesta a la primera pregunta es «no, no es difícil», y justo la respuesta de la segunda pregunta es la justificación. Dada una base cualquiera del espacio vectorial, podemos construir una base ortonormal de ese mismo espacio gracias al siguiente teorema.

Teorema (Gram-Schmidt). Sean $v_1,v_2,\cdots,v_d$ vectores linealmente independientes en un espacio vectorial $V$ sobre $\mathbb{R}$ (no necesariamente de dimensión finita), con producto interior $\langle \cdot , \cdot \rangle$. Entonces existe una única familia de vectores ortonormales $e_1,e_2,\ldots,e_d$ en $V$ con la propiedad de que para todo $k=1,2,\ldots,d$, tenemos que

\begin{align*}
\text{span}(e_1,e_2,\cdots,e_k)&=\text{span}(v_1,v_2,\cdots,v_k), \quad \text{y} \quad\\
\langle e_k,v_k \rangle&>0.
\end{align*}

Demostración. Lo haremos por inducción sobre $d$, la cantidad de vectores con la que empezamos.

La base inductiva es cuando $d=1$. Tomamos un vector $e_1\in \text{span}(v_1)$, entonces podemos escribirlo como $e_1=\lambda v_1$ para cierta $\lambda$. Si queremos que $0<\langle e_1,v_1 \rangle=\lambda\norm{v_1}^2$, entonces $\lambda>0$. Además queremos que $e_1$ tenga norma igual a 1, entonces $$1=\norm{e_1}^2=\langle e_1,e_1 \rangle=\lambda^2\norm{v_1}^2,$$ lo cual es posible si $\lambda=\frac{1}{\norm{v_1}}$. Como $e_1$ es un múltiplo escalar de $v_1$, se tiene que $\text{span}(e_1)=\text{span}(v_1)$. Además, la construcción forzó a que $e_1=\frac{1}{\norm{v_1}} v_1$ sea el único vector que satisface las condiciones del teorema.

Hagamos ahora el paso inductivo. Tomemos un entero $d\geq 2$, y supongamos que el teorema es cierto para $d-1$. Sean $v_1,v_2,\cdots,v_d$ vectores en $V$ linelmente independientes. Por hipótesis, sabemos que existe una única familia de vectores ortonormales $e_1,\cdots,e_{d-1}$ que satisfacen las condiciones del teorema respecto a la familia $v_1,\cdots,v_{d-1}$. Es suficiente con probar que existe un único vector $e_d$ tal que $e_1,\cdots,e_d$ satisface el teorema con respecto a $v_1,\cdots,v_d$, esto es
\begin{align*}
\norm{e_d}&=1,\\
\langle e_d,e_i \rangle&=0 \quad \forall 1\leq i\leq d-1,\\
\langle e_d, v_d \rangle &> 0,
\end{align*}

y

$\text{span}(e_1,\cdots,e_d)=\text{span}(v_1,\cdots,v_d),$

ya que, por hipótesis, los casos de $k<d$ se cumplen.

La idea para construir $e_d$ es tomarlo de $\text{span}(v_1,\cdots,v_d)$, expresarlo como combinación lineal de estos y encontrar condiciones necesarias y suficientes sobre los coeficientes de $e_d$ para que satisfaga las conclusiones del teorema. Hagamos esto.

Sea $e_d$ un vector tal que $e_d\in\text{span}(v_1,\cdots,v_d)$. Por ser linealmente independientes y por hipótesis $$\text{span}(v_1,\cdots,v_d)=\text{span}(e_1,\cdots,e_{d-1})+\text{span}(v_d),$$ entonces podemos escribir $e_d$ como

$e_d=\lambda v_d +\sum_{i=1}^{d-1} a_i e_i$

para algunos $\lambda,a_1,\cdots,a_{d-1}$. Si resulta que $\lambda\neq 0$, esto también implicará que $\text{span}(e_1,\cdots,e_d)=\text{span}(v_1,\cdots,v_d)$.

Ahora, dado que $e_d$ debe formar una familia ortonormal con el resto de los vectores, para todo $j=1,\cdots,d-1$, tenemos que


\begin{align*}
0&=\langle e_d,e_j \rangle\\
&=\lambda\langle v_d,e_j\rangle + \sum_{i=1}^{d-1} a_i\langle e_i,e_j \rangle\\
&=\lambda\langle v_d,e_j \rangle +a_j,
\end{align*}

entonces $a_j=-\lambda\langle v_d,e_j \rangle$. Si logramos mostrar que hay un único $\lambda$ con el que se pueda satisfacer la conclusión del teorema, el argumento anterior muestra que también hay únicos $a_1,\ldots,a_{d-1}$ y por lo tanto que hay un único vector $e_d$ que satisface el teorema.

Sustituyendo los coeficientes anteriores, obtenemos que

$e_d=\lambda\left(v_d-\sum_{i=1}^{d-1} \langle v_d,e_i\rangle e_i \right).$

Notemos que si $z:=v_d-\sum_{i=1}^{d-1} \langle v_d,e_i\rangle e_i$ es cero, $v_d$ estaría en $$\text{span}(e_1,\cdots,e_{d-1}) = \text{span}(v_1,\cdots,v_{d-1}),$$ contradiciendo que los vectores $v_i$’s son linealmente independientes, entonces $z\neq 0$.

Ahora como queremos que $1=\norm{e_d}=|\lambda| \norm{z}$, esto implica que $|\lambda|=\frac{1}{\norm{z}}$.

Como además queremos que $\langle e_d,v_d \rangle >0$ y

$\langle e_d,v_d\rangle =\left\langle e_d,\frac{e_d}{\lambda}+\sum_{i=1}^{d-1} \langle v_d,e_i\rangle e_i \right\rangle=\frac{1}{\lambda},$

se deduce que $\lambda$ es único y está determinado por $\lambda=\frac{1}{\norm{z}}.$ Por lo tanto existe (y es único) el vector $e_d$ que satisface el teorema.

$\square$

Este proceso de construcción es mejor conocido como el proceso de Gram-Schmidt. La demostración da a la vez un algoritmo que nos permite encontrar bases ortogonales (y de hecho ortonormales). Veremos ejemplos de esto en la siguiente sección. Antes de eso, enunciaremos formalmente una de las conclusiones más importantes del teorema anterior.

Recuerda que un espacio Euclideano es un espacio vectorial de dimensión finita sobre $\mathbb{R}$ y con un producto interior. Podemos aplicar el proceso de Gram-Schmidt a cualquier base $v_1,\ldots,v_d$ de un espacio Euclideano $V$ y al final obtendremos una familia $e_1,\ldots,e_d$ de vectores ortonormales. Como sabemos que las familias de vectores ortonormales son linealmente independientes, y tenemos $d$ vectores, concluimos que $e_1,\ldots,e_d$ es una base ortonormal. En resumen, tenemos el siguiente resultado.

Corolario. Todo espacio Euclideano tiene una base ortonormal.

Ejemplos de aplicación del proceso de Gram-Schmidt

A continuación veremos algunos ejemplos que nos ayuden a clarificar más este algoritmo.

Ejemplo 1. Sean $v_1,v_2,v_3$ vectores en $\mathbb{R}^3$ (con el producto interior estándar) definidos por

$v_1=(1, 1, 0), \quad v_2=( 1, 1, 1), \quad v_3=( 1, 0, 1)$.

Es fácil ver que estos vectores son linealmente independientes. Entonces construyamos según el proceso de Gram-Schmidt la familia ortonormal de vectores $e_1,e_2,e_3$. Tenemos que

$e_1=\frac{v_1}{\norm{v_1}}=\frac{v_1}{\sqrt{2}}=\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right)$.

Ahora, tomando $z_2=v_2-\langle v_2,e_1\rangle e_1$, tenemos que $e_2$ está definido como $\frac{z_2}{\norm{z_2}}$, entonces

\begin{align*}
z_2&=(1,1,1)-\left[(1,1,1)\cdot \left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right)\right]\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right) \\
&=(1,1,1)-\left[\frac{2}{\sqrt{2}}\right]\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\right) \\
&=(1,1,1)-(2/2,2/2,0)\\
&=(1,1,1)-(1,1,0)=(0,0,1).
\end{align*}

Esto implica que $e_2=\frac{1}{1}(0,0,1)=(0,0,1)$. Finalmente tomando $z_3=v_3-\langle v_3,e_1 \rangle e_1 – \langle v_3,e_2 \rangle e_2$, sabemos que $e_3=\frac{z_3}{\norm{z_3}}$. Entonces

\begin{align*}
z_3&=v_3-\langle v_3,e_1 \rangle e_1 – \langle v_3,e_2 \rangle e_2 \\
&=(1,0,1)-\left(\frac{1}{2},\frac{1}{2},0\right)-(0,0,1) \\
&=\left(\frac{1}{2},-\frac{1}{2},0\right).
\end{align*}

Por lo tanto

$e_3=\frac{1}{\sqrt{1/2}}\left(\frac{1}{2}, -\frac{1}{2},0\right)=\left(\frac{1}{\sqrt{2}},\frac{-1}{\sqrt{2}},0\right).$

$\triangle$

Ejemplo 2. Sea $V$ el espacio de polinomios en $[0,1]$ con coeficientes reales de grado a lo más 2, con el producto interior

$\langle p,q \rangle =\int_0^1 p(x)q(x) dx.$

Sean $v_1=1$, $v_2=1+x$, $v_3=1+x^2$ vectores en $V$ que claramente son linealmente independientes. Encontraremos los vectores que nos da el proceso de Gram-Schmidt.

Primero calculemos

$\norm{v_1}^2=\int_0^1 1 dx= 1$,

entonces $e_1=\frac{v_1}{\norm{v_1}}=v_1=1$. Ahora calculemos $z_2$:

\begin{align*}
z_2&=v_2-\langle v_2,e_1 \rangle e_1 \\
&=1+x- \int_0^1 (1+x)dx=1+x-\left(1+\frac{1}{2}\right) \\
&=x-\frac{1}{2}.
\end{align*}

Haciendo la integral $$\int_0^1 \left(x-\frac{1}{2}\right)^2 dx$$ se obtiene que $\norm{z_2}=\sqrt{\frac{1}{12}}$, entonces $e_2=\sqrt{12}\left(x-\frac{1}{2}\right)$.

Por último, hay que calcular $z_3$ así como su norma. Primero,

\begin{align*}
z_3&=v_3-\langle v_3,e_1 \rangle e_1 – \langle v_3,e_2 \rangle e_2 \\
&=(1+x^2)-\int_0^1 (1+x^2)dx – 12\left(x-\frac{1}{2}\right)\int_0^1 (1+x^2)\left(x-\frac{1}{2}\right)dx \\
&=1+x^2-\left(1+\frac{1}{3}\right)-12\left(x-\frac{1}{2}\right)\left(\frac{1}{12}\right) \\
&=x^2-\frac{1}{3}-x+\frac{1}{2} \\
&=x^2-x+\frac{1}{6},
\end{align*}

y luego, con la integral $$\int_0^1 \left(x^2-x+\frac{1}{6}\right)^2 dx$$ se calcula que $\norm{z_3}=\frac{1}{6\sqrt{5}}$, por lo tanto $e_3=6\sqrt{5}\left(x^2-x+\frac{1}{6}\right)$.

$\triangle$

Aunque no es un proceso muy eficiente, nos garantiza que podemos encontrar una base ortonormal para cualquier espacio vectorial (con producto interior). Ya con una base ortonormal, podemos usar la descomposición de Fourier de la cual hablamos la entrada anterior y con ella todas las consecuencias que tiene.

Si quieres ver muchos más ejemplos del proceso en $\mathbb{R}^n$, puedes usar una herramienta en línea que te permite ver el proceso paso a paso en el conjunto de vectores que tu elijas. Una posible página es el Gram-Schmid Calculator de eMathHelp.

Más adelante…

En esta última entrada teórica de la unidad 3, vimos el método de Gram-Schmidt para construir una base ortonormal, que es un proceso algorítmico que parte de tener una base de un espacio y al final calcula una base ortonormal. También se vieron algunos ejemplos de la aplicación de este proceso para espacios vectoriales finitos como $\mathbb{R}^3$ y el espacio de polinomios en [0,1] de grado a lo más 2. Aunque no es una manera muy eficaz para encontrar una base ortonormal, sí te garantiza que lo que construye es una.

En la próxima entrada veremos ejercicios resueltos de los temas que hemos estado estudiando a lo largo de esta semana. 

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Verifica que con el valor $\lambda$ que se encontró en la demostración del teorema de Gram-Schmidt en efecto se obtiene un vector $e_d$ que satisface todas las conclusiones que se desean.
  • Revisa que los vectores que se obtuvieron en los ejemplos de aplicación del proceso de Gram-Schmidt en efecto son bases ortogonales de los espacios correspondientes.
  • Aplica el proceso de Gram-Schmidt a los polinomios $1$, $x$, $x^2$ en el espacio Euclideano de los polinomios reales de grado a lo más dos y producto interior $$\langle p, q \rangle = p(0)q(0)+p(1)q(1)+p(2)q(2).$$
  • Aplica el proceso de Gram-Schmidt a los vectores \begin{align*}(1,1,1,1)\\ (0,1,1,1)\\ (0,0,1,1)\\ (0,0,0,1)\end{align*} de $\mathbb{R}^4$ con el producto interior canónico (el producto punto).
  • Usa el Gram-Schmidt Calculator de eMathHelp para ver paso a paso cómo se aplica el proceso de Gram-Schmidt a los vectores \begin{align*}(1,2,1,1,-1)\\ (0,0,1,0,0)\\ (2,0,0,1,1)\\ (0,2,0,0,1)\\ (-3,0,0,1,0)\end{align*} de $\mathbb{R}^5$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»