(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
INTRODUCCIÓN
El primero de los teoremas en esta entrada es uno de los más importantes del curso. Este teorema nos simplifica cálculos, ya que en ocasiones nos permite calcular la dimensión de ciertos subespacios sin necesidad de hacer una descripción explícita de una de sus bases.
El segundo de los teoremas resulta también muy útil ya que nos da otra manera de estudiar si una transformación lineal es o no inyectiva.
Teorema: Sean $K$ un campo y $V,W$ $K$-espacios vectoriales, $T\in\mathcal{L}(V,W)$.
Si $V$ es de dimensión finita, entonces se cumple que:
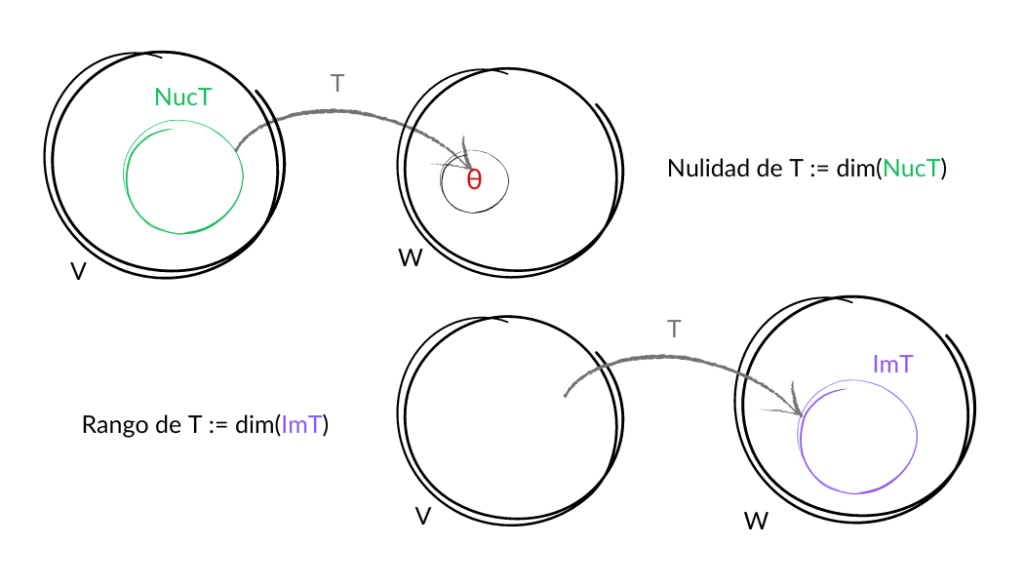
a) $Núc\,T$ es de dimensión finita
b) $Im\,T$ es de dimensión finita
c) $dim_K Núc\,T+dim_KIm\,T=dim_KV.$
Demostración: Supongamos que $V$ es de dimensión finita, digamos $dim_K\,V=n$.
a) Como $Núc\,T\subseteq V$ y $V$ es de dimensión finita, entonces $Núc\,T$ también es de dimensión finita, digamos que $dim_KNúc\,T=m$.
b) Consideremos $\Delta =\{v_1,v_2,…,v_m\}$ una base de $Núc\,T$.
Como es un conjunto linealmente independiente en $V,$ podemos completar $\Delta$ a una base de $V,$ digamos $\beta =\{v_1,v_2,…,v_m,v_{m+1},…,v_n\}$.
Veamos que $\Gamma = \{ T(v_{m+1}),T(v_{m+2}),…,T(v_{n})\}$ es una base de $Im\,T$ con $n-m$ elementos.
- P.D. $T(v_{m+1}),T(v_{m+2}),…,T(v_n)$ es una lista l.i.
Sean $\lambda_{m+1},\lambda_{m+2},…,\lambda_n\in K$ tales que $\sum_{i=m+1}^n \lambda_i T(v_i)=\theta_W$.
Como $T$ es lineal $T \left( \sum_{i=m+1}^n \lambda_iv_i \right) =\sum_{i=m+1}^n \lambda_i T(v_i)=\theta_W$.
Por lo cual, $\sum_{i=m+1}^n \lambda_iv_i\in Núc\,T$.
Como $\Delta =\{v_1,v_2,…,v_m\}$ es base de $Núc\,T$, existen $\mu_1,\mu_2,…,\mu_m\in K$ tales que $\sum_{i=m+1}^n \lambda_iv_i=\sum_{j=1}^m \mu_jv_j$.
De donde $- \sum_{j=1}^m \mu_jv_j + \sum_{i=m+1}^n \lambda_iv_i =\theta_W$.
Tenemos igualada a $\theta_W$ una combinación lineal de elementos de $\beta =\{v_1,v_2,…,v_m,v_{m+1},…,v_n\}$ que es linealmente independiente.
Por lo tanto, todos los coeficientes de esta combinación lineal son $0_K$ y en particular llegamos a que $\lambda_{m+1}=\lambda_{m+2}=…=\lambda_n=0_K$.
Concluimos que $T(v_{m+1}),T(v_{m+2}),…,T(v_n)$ es una lista l.i., en consecuencia el conjunto $\{T(v_{m+1}),T(v_{m+2}),…,T(v_n)\}$ es l.i. y tiene $n-m$ elementos.
- P.D. $\langle\Gamma\rangle =Im\,T$
Sabemos que $\Gamma\subseteq Im\,T$ y que $Im\,T$ es un espacio vectorial. Por lo tanto, $\langle\Gamma\rangle\subseteq Im\,T$.
Ahora bien, sea $w\in Im\,T$. Por definición de $Im\,T$, existe $v\in V$ tal que $T(v)=w$.
Como $\beta =\{v_1,v_2,…,v_n\}$ es base de $V$, entonces existen $\lambda_1,\lambda_2,…,\lambda_n\in K$ tales que $v=\sum_{i=1}^n \lambda_iv_i$.
Así, obtenemos que $w=T(v)=T\left( \sum_{i=1}^n \lambda_iv_i\right)$.
Y como $T$ es lineal, podemos concluir de las igualdades anteriores que $w=\sum_{i=1}^n \lambda_iT(v_i)$.
Tenemos que $\Delta =\{v_1,v_2,…,v_m\}$ es base de $Núc\,T$ y por lo tanto $\Delta\subseteq Núc(T)$. Es decir, $T(v_1)=T(v_2)=…=T(v_m)=\theta_W$.
Así, $w=\sum_{i=1}^n \lambda_iT(v_i)=\sum_{i=1}^m \lambda_iT(v_i)+\sum_{i={m+1}}^n \lambda_iT(v_i)$$=\sum_{i=1}^m \lambda_i\theta_W+\sum_{i={m+1}}^n \lambda_iT(v_i)=\theta_W+\sum_{i={m+1}}^n \lambda_iT(v_i)$$=\sum_{i={m+1}}^n \lambda_iT(v_i)$.
Obtuvimos a $w$ expresado como una combinación lineal de términos de $\Gamma =\{T(v_{m+1}),T(v_{m+2}),…,T(v_n)\}$. Por lo tanto, $Im\,T\subseteq\Gamma$.
Concluimos que $\Gamma$ es base de $Im\,T$.
Como $|\Gamma|=n-m$, entonces $Im\,T$ es de dimensión finita y $dim_KIm\,T=n-m.$
c) Tenemos por el inciso anterior que $dim_KNúc\,T=m$, $dim_KIm\,T=n-m$ y $dim_K\,V=n$.
Así, $dim_KV-dim_KNúc\,T=n-m=dim_KIm\,T$, lo que implica que $dim_KV=dim_KNúc\,T+dim_KIm\,T$.
Teorema: Sean $K$ un campo y $V,W$ $K$-espacios vectoriales y $T\in\mathcal{L}(V,W)$.
Entonces $T$ es inyectiva si y sólo si $Núc\,T=\{\theta_V\}.$
Demostración: Veamos ambas implicaciones.
$\Longrightarrow$ Supongamos que $T$ es inyectiva.
P.D. $Núc\,T=\{\theta_V\}$.
Dado que $\theta_V\in Núc\,T$ se tiene que $\{\theta_V\}\subseteq Núc\,T$ por lo que basta en realidad verificar la otra contención.
Sea $v\in Núc\,T$.
Por definición de núcleo tenemos que $T(v)=\theta_W$.
Además, sabemos que $T(\theta_V)=\theta_W$.
Así, tenemos que $T(v)=T(\theta_V)$ con $T$ inyectiva.
Por lo tanto, $v=\theta_V$.
Llegamos a que el único elemento del núcleo de $T$ es $\theta_V$.
$\Longleftarrow$ Supongamos que $Núc\,T=\{\theta_V\}$.
P.D. $T$ es inyectiva.
Sean $u,v\in V$ tales que $T(u)=T(v)$.
Entonces $T(u)-T(v)=\theta_W$.
Como $T$ es lineal, tenemos que $T(u-v)=T(u)-T(v)$.
Así que $T(u-v)=\theta_W$ y por lo tanto, $u-v\in Núc\,T$ donde (por hipótesis) el único elemento que existe es $\theta_V$.
Así, $u-v=\theta_V$ y concluimos que $u=v$.
Partiendo de que $T(u)=T(v)$ llegamos a que $u$ debe ser igual a $v$ y por lo tanto, $T$ es inyectiva.
Corolario: Sean $K$ un campo y $V,W$ $K$-espacios vectoriales, $T\in\mathcal{L}(V,W)$. Si $V,W$ son de dimensión finita y de la misma dimensión, entonces $T$ es inyectiva si y sólo si $T$ es suprayectiva.
Demostración: Supongamos que $V,W$ son $K$-espacios vectoriales de dimensión finita y $dim_KV=dim_KW.$
Tenemos por el teorema anterior que $T$ es inyectiva si y sólo si $Núc\,T=\{\theta_V\}$.
Podemos utilizar este resultado porque nuestras nuevas hipótesis no afectan.
Observemos además que $Núc\,T=\{\theta_V\}$ si y sólo si $dim_KNúc\,T=0$ porque el único conjunto que no tiene elementos es el conjunto vacío, que es una base del espacio trivial.
Por el teorema de la dimensión tenemos que $dim_KNúc\,T+dim_hIm\,T=dim_KV$.
Así, que $dim_KNúc\,T=0$ si y sólo si $dim_KIm\,T=dim_KV$.
Como tenemos por hipótesis que $dim_KV=dim_KW$, entonces $dim_KIm\,T=dim_KV$ si y sólo si $dim_KIm\,T=dim_KW$.
Recordando que $Im\,T\leqslant W$ se cumple que $dim_KIm\,T=dim_KW$ si y sólo si $Im\,T=W$.
Y dentro de las equivalencias de que $T$ sea suprayectiva está que $Im\,T=W$.
Por la cadena de dobles implicaciones concluimos que, bajo nuestras hipótesis, $T$ es inyectiva si y sólo si $T$ es suprayectiva.
Tarea Moral
- Para la transformación lineal $T:\mathbb{R}^3\longrightarrow \mathbb{R}^2$ con $T(a_1,a_2,a_3)=(a_1 + 2a_2, 2a_3 – a_1)$ verifica que se cumple el primer teorema de esta entrada y determina si $T$ es inyectiva o suprayectiva.
- Si $T:\mathbb{R}^2\longrightarrow\mathbb{R}^2$ es lineal y sabemos que $T(1,0)=(2,4)$ y $T(1,1)=(8,5)$. ¿Es $T$ inyectiva?
Más adelante…
El último ejercicio de la Tarea Moral en la entrada anterior, 2.1. TRANSFORMACIÓN LINEAL: definición y ejemplos, pregunta la existencia de una transformación lineal de acuerdo a dos valores dados y a continuación veremos cómo podemos plantear y resolver este problema de manera más general.
Entradas relacionadas
- Ir a Álgebra Lineal I
- Entrada anterior del curso: 2.2. NÚCLEO, NULIDAD, IMAGEN Y RANGO: definiciones, ejemplos y propiedades
- Siguiente entrada del curso: 2.4. TRANSFORMACIÓN LINEAL: descripción a partir de su efecto en una base