Archivo de la etiqueta: determinante

Álgebra Lineal I: Técnicas básicas de cálculo de determinantes

Por Leonardo Ignacio Martínez Sandoval

8 respuestas

Introducción

Ya definimos a los determinantes para vectores, para transformaciones y para matrices. Además, mostramos algunas propiedades básicas de determinantes y las usamos para resolver varios problemas. Como hemos discutido, los determinantes guardan información importante sobre una transformación lineal o sobre una matriz. También ayudan a implementar la técnica de diagonalización la cual introdujimos hace algunas entradas y en la cual profundizaremos después. Es por esta razón que es importante tener varias técnicas para el cálculo de determinantes.

Fuera de este curso, los determinantes sirven en muchas otras áreas de las matemáticas. Cuando se hace cálculo de varias variables ayudan a enunciar el teorema del cambio de variable. En combinatoria ayudan a calcular el número de árboles generadores de una gráfica. Más adelante en tu formación matemática es probable que te encuentres con otros ejemplos.

Calculo de determinantes de $2\times 2$

Como ya discutimos anteriormente, una matriz en $M_2(F)$, digamos $A=\begin{pmatrix}a&b\\ c&d\end{pmatrix}$ tiene determinante $ad-bc$.

Problema. Calcula el determinante de la matriz $$\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}^8.$$

Solución. Por la fórmula para el determinante de las matrices de $2\times 2$, se tiene que $\begin{vmatrix} 0 & 1\\ 1 & 1\end{vmatrix} = 0\cdot 1 – 1\cdot 1 = -1.$

Como el determinante es multiplicativo, $\det(A^2)=\det(A)\det(A)=(\det(A))^2$, e inductivamente se puede mostrar que para todo entero positivo $n$ se tiene que $\det(A^n)=(\det(A))^n$. De esta forma, el determinante que buscamos es $(-1)^8=1$.

$\triangle$

Observa que hubiera tomado más trabajo elevar la matriz a la octava potencia. Aunque esto usualmente no es recomendable, en este problema hay algo interesante que sucede con esta matriz. Llamémosla $A=\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}$. Haciendo las cuentas para las primeras potencias, se tiene que
\begin{align*}
A&=\begin{pmatrix} 0 & 1\\ 1 & 1\end{pmatrix}\\
A^2&=\begin{pmatrix} 1 & 1\\ 1 & 2\end{pmatrix}\\
A^3&=\begin{pmatrix} 1 & 2\\ 2 & 3\end{pmatrix}\\
A^4&=\begin{pmatrix} 2 & 3\\ 3 & 5\end{pmatrix}\\
A^5&=\begin{pmatrix} 3 & 5\\ 5 & 8\end{pmatrix}
\end{align*}

Aquí aparece la sucesión de Fibonacci, dada por $F_0=0$, $F_1=1$ y $F_{n+2}=F_{n+1}+F_n$ para $n\geq 0$, cuyos primeros términos son $$0,1,1,2,3,5,8,13,21,\ldots.$$ De hecho se puede probar por inducción que $$A^n=\begin{pmatrix} F_{n-1} & F_n\\ F_n & F_{n+1}\end{pmatrix}.$$

Así, por un lado el determinante de la matriz $A^n$ es $F_{n-1}F_{n+1}-F_n^2$, usando la fórmula de determinante de $2\times 2$. Por otro lado, es $(-1)^n$, por el argumento del problema. Con esto hemos demostrado que para cualquier entero $n$ tenemos la siguiente identidad para los números de Fibonacci: $$F_{n-1}F_{n+1}-F_n^2 = (-1)^n.$$

Cálculo de determinantes de $3\times 3$

Para calcular el determinante de una matriz en $M_3(F)$ por definición, digamos de $A=\begin{pmatrix}a&b&c\\ d&e&f\\ g&h&i\end{pmatrix}$, tenemos que hacer una suma de $3!=6$ términos. Si se hacen las cuentas de manera explícita, el valor que se obtiene es $$aei+bfg+cdh-ceg-afh-bdi.$$

Esto se puede recordar mediante el siguiente diagrama, en el cual se ponen la primera y la segunda columna de nuevo, a la derecha. Las diagonales hacia abajo son términos positivos y las diagonales hacia arriba son términos negativos.

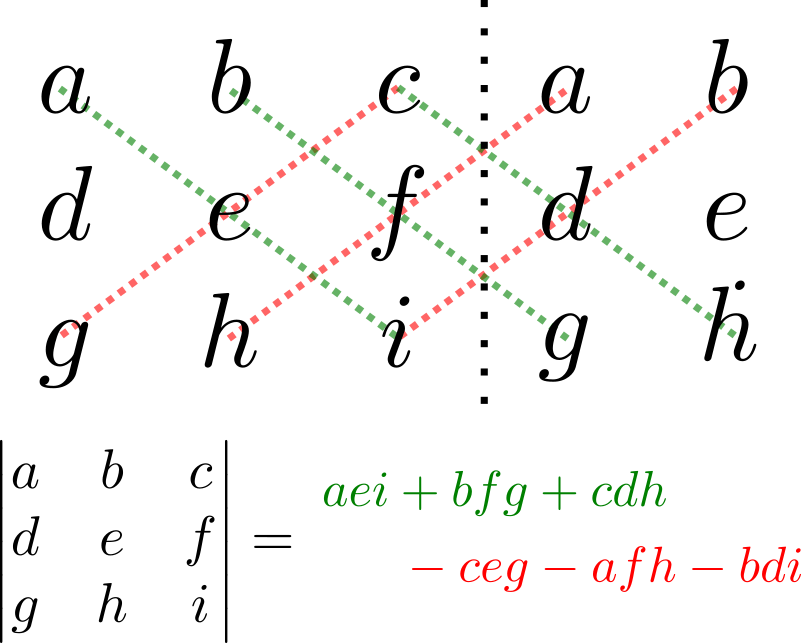
Cálculo de determinantes de matrices de 3x3
Cálculo de determinantes de $3\times 3$

Veamos un ejemplo de un problema en el que se puede aprovechar esta técnica.

Problema. Determina para qué reales $a,b,c$ se tiene que los vectores $(a,b,0)$, $(a,0,b)$ y $(0,a,b)$ son una base de $\mathbb{R}^3$.

Solución. Para que estos vectores sean una base de $\mathbb{R}^3$, basta con que sean linealmente independientes, pues son $3$. Como hemos visto en entradas anteriores, para que sean linealmente independientes, es necesario y suficiente que el determinante de la matriz $\begin{pmatrix}a&b&0\\ a&0&b\\ 0&a&b\end{pmatrix}$ sea distinto de cero.

Usando la técnica de arriba, hacemos siguiente diagrama:

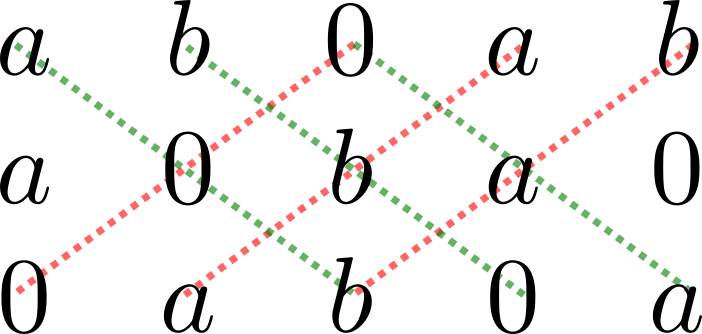
De aquí, vemos que el determinante es $$0+0+0-0-a^2b-ab^2=-ab(a+b).$$ Esta expresión es igual a cero si $a=0$, si $b=0$ o si $a+b=0$. En cualquier otro caso, el determinante no es cero, y por lo tanto los vectores forman una base.

$\triangle$

Ten mucho cuidado. Esta técnica no funciona para matrices de $4\times 4$ o más. Hay una forma sencilla de convencerse de ello. Por ejemplo, el determinante de una matriz de $4\times 4$ debe tener $4!=24$ sumandos. Si intentamos copiar la técnica de arriba, tendremos solamente $8$ sumandos ($4$ en una diagonal y $4$ en otra). Para cuando tenemos matrices de $4\times 4$ o más, tenemos que recurrir a otras técnicas.

Reducción gaussiana para determinantes

Cuando vimos el tema de sistemas de ecuaciones hablamos del algoritmo de reducción gaussiana, y vimos que este siempre lleva una matriz en $M_{m,n}(F)$ a su forma escalonada reducida mediante operaciones elementales. Cuando aplicamos el algoritmo a matrices en $M_n(F)$, siempre llegamos a una matriz triangular, en donde sabemos fácilmente calcular el determinante: es simplemente el producto de las entradas en la diagonal. Nota cómo lo anterior también se cumple para las matrices diagonales, pues son un caso particular de matrices triangulares.

Por esta razón, es fundamental para el cálculo de determinantes saber qué le hacen las operaciones elementales al determinante de una matriz.

Teorema. Las operaciones elementales tienen el siguiente efecto en el determinante de una matriz $A$:

  1. Si todos los elementos de un renglón o columna de $A$ se multiplican por $\lambda$, entonces el determinante se multiplica por $\lambda$.
  2. Cuando se intercambian dos renglones o columnas de $A$, el determinante se multiplica por $-1$.
  3. Si a un renglón de $A$ se le suma un múltiplo escalar de otro renglón, entonces el determinante no cambia. Sucede algo análogo para columnas.

Demostración. El punto $1$ ya lo demostramos en la entrada anterior, en donde vimos que el determinante es homogéneo.

Para los puntos $2$ y $3$, usemos que si $e_1,\ldots e_n$ es la base canónica de $F^n$, el determinante de una matriz con renglones $R_1,\ldots,R_n$ es $$\det_{(e_1,\ldots,e_n)}(R_1,\ldots,R_n).$$

Intercambiar los renglones $i$ y $j$ es hacer $\det_{(e_1,\ldots,e_n)}(R_{\sigma(1)},\ldots,R_{\sigma(n)})$ para la transposición $\sigma$ que intercambia $i$ y $j$. Como el determinante es antisimétrico y $\sigma$ tiene signo $-1$, obtenemos la conclusión.

Hagamos ahora el tercer punto. Tomemos $i\neq j$ y un escalar $\lambda$. Si al $i$-ésimo renglón de $A$ le sumamos $\lambda$ veces el $j$-ésimo renglón de $A$, esto es lo mismo que multiplicar a $A$ por la izquierda por la matriz $B$ que tiene unos en la diagonal y $\lambda$ en la entrada $(i,j)$. La matriz $B$ es triangular, de modo que su determinante es el producto de las entradas, que es $1$. De esta forma, $$\det(BA)=\det(B)\det(A)=\det(A).$$

$\square$

Así, una estrategia para calcular el determinante de una matriz es hacer reducción gaussiana hasta llegar a una matriz diagonal (incluso es suficiente que sea triangular superior) de determinante $\Delta$. Si en el camino se hicieron $r$ intercambios de renglones y se multiplicaron los renglones por escalares $\lambda_1,\ldots,\lambda_s$, entonces el determinante de $A$ será $$\frac{(-1)^r \Delta}{\lambda_1\cdot\ldots\cdot \lambda_s}.$$

Otras propiedades para calcular determinantes

Aquí recolectamos otras propiedades de determinantes que pueden ayudar a calcularlos. Ya mostramos todas ellas, salvo la número $2$. Esta la mostramos después de la lista.

  1. Si se descompone una columna de una matriz como suma de dos columnas, entonces el determinantes es la suma de los determinantes en los que ponemos cada columna en vez de la original.
  2. Si $A$ es una matriz en $M_n(\mathbb{C})$, entonces el determinante de la matriz conjugada $\overline{A}$ es el conjugado del determinante de $A$.
  3. El determinante es multiplicativo.
  4. Si $A$ es una matriz en $M_n(F)$, el determinante de $\lambda A$ es $\lambda^n$ veces el determinante de $A$.
  5. El determinante de una matriz triangular es el producto de sus entradas en la diagonal.
  6. El determinante de una matriz invertible es el inverso multiplicativo del determinante de la matriz.
  7. Una matriz tiene el mismo determinante que su transpuesta.

Proposición. Si $A$ es una matriz en $M_n(\mathbb{C})$, entonces el determinante de la matriz conjugada $\overline{A}$ es el conjugado del determinante de $A$.

Demostración. La conjugación compleja abre sumas y productos. Aplicando esto repetidas veces obtenemos la siguiente cadena de igualdades:

\begin{align*}
\overline{\det(A)}&=\overline{\sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}}\\
&=\sum_{\sigma \in S_n} \overline{\text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}}\\
&=\sum_{\sigma \in S_n} \text{sign}(\sigma)\overline{a_{1\sigma(1)}}\cdot\ldots\cdot \overline{a_{n\sigma(n)}}\\
&=\det(\overline{A}).
\end{align*}

$\square$

Hay una última técnica que es fundamental para el cálculo de determinantes: la expansión de Laplace. En algunos textos incluso se usa para definir el determinante. Probablemente la conoces: es la que consiste en hacer el determinante «con respecto a una fila o columna» y proceder de manera recursiva. Hablaremos de ella más adelante y veremos por qué funciona.

Dos problemas de cálculo de determinantes

Problema 1. Considera la matriz $$A=\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ -1 & -3 & 0 & 1\end{pmatrix}.$$ Calcula los siguientes determinantes:

  • $\det A$
  • $\det(^t A)$
  • $\det(A^{-1})$
  • $\det(^t A A)$
  • $\det(-2A)$

Solución. Hagamos primero el determinante de la matriz $A$. Para ello, haremos operaciones elementales como sigue
\begin{align*}
&\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ -1 & -3 & 0 & 1\end{pmatrix}\\
\to&\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & -\frac{14}{5} & \frac{2}{5} & 1\end{pmatrix}\\
\to &\begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & 0 & -\frac{12}{5} & \frac{33}{5}\end{pmatrix}\\
\to& \begin{pmatrix}5& 1 & 2& 0 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 5 & 2\\ 0 & 0 & 0 & \frac{189}{25}\end{pmatrix}.
\end{align*}

En el primer paso sumamos $1/5$ veces el primer renglón al último. Luego, sumamos $14/5$ veces el segundo renglón al último. Finalmente, sumamos $12/25$ veces el tercer renglón al último. De esta forma, nunca cambiamos el determinante de la matriz. Así, del determinante de $A$ es el mismo que el de la matriz final, que por ser triangular superior es el producto de las entradas en su diagonal. De este modo, $$\det(A) = 5\cdot 1 \cdot 5 \cdot \frac{189}{5} = 189.$$

El determinante de una matriz es igual al de su transpuesta, así que $\det(^t A)=\det(A)$. El determinante $\det(A^{-1})$ es el inverso multiplicativo de $\det(A)$, así que es $\frac{1}{189}$.

Como el determinante es multiplicativo, $$\det({^tA}A)=\det({^tA})\det(A)=189\cdot 189=35721.$$

Finalmente, usando que el determinante es homogéneo y que estamos en $M_4(\mathbb{R})$, tenemos que
\begin{align*}
\det(-2A)&=(-2)^4\det(A)\\
&=16\cdot 189\\
&=3024.
\end{align*}

$\triangle$

Problema 2. Sean $a,b,c$ números complejos. Calculando el determinante de la matriz $$A=\begin{pmatrix}a&b&c\\ c&a&b\\ b&c&a\end{pmatrix}$$ en $M_3(\mathbb{C})$ de dos formas distintas, muestra que $$a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca).$$

Solución. Usando la técnica para determinantes de $3\cdot 3$ tenemos que por un lado,
\begin{align*}
\det(A) &= a^3 + b^3 + c^3 – abc – bca – cab\\
&=a^3+b^3+c^3-3abc.
\end{align*}

Por otro lado, el determinante no cambia si al primer renglón le sumamos los otros dos, así que el determinante de $A$ también es $$\begin{vmatrix}a+b+c&a+b+c&a+b+c\\ c&a&b\\ b&c&a\end{vmatrix}.$$ Como el determinante es homogéneo, podemos factorizar $a+b+c$ de la primera entrada para obtener que $$\det(A)=(a+b+c)\begin{vmatrix}1&1&1\\ c&a&b\\ b&c&a\end{vmatrix}.$$

Aplicando de nuevo la fórmula de determinantes de $3\times 3$, tenemos que $$\begin{vmatrix}1&1&1\\ c&a&b\\ b&c&a\end{vmatrix} = a^2+b^2+c^2-ab-bc-ca.$$

Concluimos entonces que $$\det(A)=(a+b+c)(a^2+b^2+c^2-ab-bc-ca).$$ Igualando ambas expresiones para $\det(A)$ obtenemos la identidad deseada.

$\triangle$

Más adelante…

En esta entrada vimos varias formas para calcular el determinante de una matriz. Cuando nos enfrentemos con un problema que requiere el cálculo de un determinante, tenemos que elegir la que más nos convenga (o la que requiera menos pasos). La mejor forma de desarrollar un poco de «intuición» al momento de elegir el mejor método para calcular determinantes es haciendo ejercicios.

A continuación pondremos en práctica lo que aprendimos en esta entrada haciendo varios ejercicios de cálculo de determinantes.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Sea $\alpha$ un número real. Encuentra el determinante de la matriz $$\begin{pmatrix}\sin \alpha & \cos \alpha \\ -\cos \alpha & \sin \alpha \end{pmatrix}.$$
  • Determina para qué valores de $a$ la matriz $$\begin{pmatrix} a & 0 & a & 0 & a \\0 & a & 0 & a & 0 \\ 0 & 0 & a & 0 & 0 \\ 0 & a & 0 & a & 0 \\ a & 0 & a & 0 & a \end{pmatrix}$$ es invertible.
  • Encuentra el determinante de la matriz $$\begin{pmatrix} 2 & 1 & 0 & 0 & 0 \\0 & 2 & 1 & 0 & 0 \\ 0 & 0 & 2 & 1 & 0 \\ 0 & 0 & 0 & 2 & 1 \\ 1 & 0 & 0 & 0 & 2 \end{pmatrix}.$$
  • Sea $x$ un número complejo. Muestra que el determinante de la matriz $$\begin{pmatrix}3x^2-6x+5&2x^2-4x+2&x^2-2x\\ 2x^2-4x+2&2x^2+2x+1&x^2-x\\ x^2-2x&x^2-x&x^2\end{pmatrix}$$ es $x^6$. Sugerencia. Hay una solución simple, factorizando a la matriz como el producto de dos matrices triangulares, una superior y una inferior, una transpuesta de la otra.
  • Muestra que si $A=\begin{pmatrix}0& 1 \\ 1 & 1\end{pmatrix}$, entonces $$A^n=\begin{pmatrix} F_{n-1} & F_n\\ F_n & F_{n+1}\end{pmatrix},$$ donde $\{F_n\}$ es la sucesión de Fibonacci. Muestra que para los números de Fibonacci se satisface que $$F_{2n}=F_n(F_{n+1}+F_{n-1}).$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Determinantes de matrices y transformaciones lineales

Por Leonardo Ignacio Martínez Sandoval

6 respuestas

Introducción

En la entrada anterior dimos la definición de determinante para ciertos vectores con respecto a una base. En esta entrada continuamos con la construcción de determinantes. Primero, basados en la teoría que desarrollamos anteriormente, definiremos determinantes de transformaciones lineales. Luego, mediante la cercanía entre transformaciones lineales y matrices, definimos determinantes de matrices.

Determinantes de transformaciones lineales

Ahora definiremos el determinante para transformaciones lineales. Antes de esto, necesitamos hacer algunas observaciones iniciales y demostrar un resultado.

Si tomamos un espacio vectorial $V$ de dimensión finita $n\geq 1$ sobre un campo $F$, una transformación lineal $T:V\to V$ y una forma $n$-lineal $f:V^n\to F$, se puede mostrar que la transformación $$T_f:V^n\to F$$ dada por $$T_f(x_1,\ldots,x_n)=f(T(x_1),\ldots,T(x_n))$$ también es una forma $n$-lineal. Además, se puede mostrar que si $f$ es alternante, entonces $T_f$ también lo es. Mostrar ambas cosas es relativamente sencillo y queda como tarea moral.

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n\geq 1$ sobre el campo $F$. Para cualquier transformación lineal $T:V\to V$ existe un único escalar $\det T$ en $F$ tal que $$f(T(x_1),\ldots,T(x_n))=\det T\cdot f(x_1,\ldots, x_n)$$ para cualquier forma $n$-lineal alternante $f:V^n\to F$ y cualquier elección $x_1,\ldots,x_n$ de vectores en $V$.

Demostración. Fijemos una base $B=(b_1,\ldots,b_n)$ cualquiera de $V$. Llamemos $g$ a la forma $n$-lineal alternante $\det_{(b_1,\ldots,b_n)}$. Por la discusión de arriba, la asignación $T_g:V^n\to F$ dada por $$(x_1,\ldots,x_n)\mapsto g(T(x_1),\ldots,T(x_n))$$ es una forma $n$-lineal y alternante.

Por el teorema que mostramos en la entrada de determinantes de vectores, se debe cumplir que $$T_g = T_g(b_1,\ldots,b_n) \cdot g.$$ Afirmamos que $\det T:= T_g(b_1,\ldots, b_n)$ es el escalar que estamos buscando.

En efecto, para cualquier otra forma $n$-lineal alternante $f$, tenemos por el mismo teorema que $$f=f(b_1,\ldots,b_n) \cdot g.$$ Usando la linealidad de $T$ y la igualdad anterior, se tiene que

\begin{align*}
T_f &= f(b_1,\ldots,b_n)\cdot T_g\\
&=f(b_1,\ldots,b_n) \cdot \det T \cdot g\\
&= \det T \cdot f.
\end{align*}

Con esto se prueba que $\det T$ funciona para cualquier forma lineal $f$. La unicidad sale eligiendo $(x_1,\ldots,x_n)=(b_1,\ldots,b_n)$ y $f=g$ en el enunciado del teorema, pues esto forza a que $$\det T = g(T(b_1),\ldots,T(b_n)).$$

$\square$

Ahora sí, estamos listos para definir el determinante de una transformación lineal.

Definición. El escalar $\det T$ del teorema anterior es el determinante de la transformación lineal $T$.

Para obtener el valor de $\det T$, podemos entonces simplemente fijar una base $B=(b_1,\ldots,b_n)$ y el determinante estará dado por $$\det T = \det_{(b_1,\ldots,b_n)}(T(b_1),\ldots, T(b_n)).$$ Como el teorema también prueba unicidad, sin importar que base $B$ elijamos este número siempre será el mismo.

Ejemplo 1. Vamos a encontrar el determinante de la transformación lineal $T:\mathbb{R}^3 \to \mathbb{R}^3$ dada por $$T(x,y,z)=(2z,2y,2x).$$ Para ello, usaremos la base canónica de $\mathbb{R}^3$. Tenemos que
\begin{align*}
T(1,0,0)&=(0,0,2)=2e_3\\
T(0,1,0)&=(0,2,0)=2e_2\\
T(0,0,1)&=(2,0,0)=2e_1.
\end{align*}

De acuerdo al teorema anterior, podemos encontrar al determinante de $T$ como $$\det T = \det_{(e_1,e_2,e_3)}(2e_3,2e_2,2e_1).$$

Como el determinante (para vectores) es antisimétrico, al intercambiar las entradas $1$ y $3$ su signo cambia en $-1$. Usando la $3$-linealidad en cada entrada, podemos sacar un factor $2$ de cada una. Así, tenemos:
\begin{align*}
\det T &= \det_{(e_1,e_2,e_3)}(2e_3,2e_2,2e_1)\\
&= -\det_{(e_1,e_2,e_3)}(2e_1,2e_2,2e_3)\\
&=-8\det_{(e_1,e_2,e_3)}(e_1,e_2,e_3)\\
&=-8.
\end{align*}

Concluimos entonces que el determinante de $T$ es $-8$.

$\triangle$

Ejemplo 2. Vamos ahora a encontrar el determinante de la transformación $T:\mathbb{R}_n[x]\to \mathbb{R}_n[x]$ que deriva polinomios, es decir, tal que $T(p)=p’$. Tomemos $q_0=1,q_1=x,\ldots,q_n=x^n$ la base canónica de $\mathbb{R}_n[x]$.

Notemos que, $T(1)=0$, de modo que los vectores $T(1),\ldots,T(x^n)$ son linealmente dependientes. Así, sin tener que hacer el resto de los cálculos, podemos deducir ya que $$\det_{(q_0,\ldots,q_n)}(T(q_0),\ldots,T(q_n))=0.$$ Concluimos entonces que $\det T = 0$.

$\triangle$

Determinantes de matrices

La expresión $$\det T = \det_{(b_1,\ldots,b_n)}(T(b_1),\ldots, T(b_n))$$ para una transformación lineal $T$ también nos permite poner al determinante en términos de las entradas de la matriz de $T$ con respecto a la base $B$. Recordemos que dicha matriz $A_T=[a_{ij}]$ tiene en la columna $i$ las coordenadas de $b_i$ en la base $B$. En otras palabras, para cada $i$ se cumple que $$T(b_i)=\sum_{j=1}^n a_{ji}b_i.$$

Usando esta notación, obtenemos que $$\det T = \sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)},$$ de manera que podemos expresar a $\det T$ en términos únicamente de su matriz en la base $B$.

Esto nos motiva a definir el determinante de una matriz en general.

Definición. Para una matriz $A$ en $M_n(F)$ de entradas $A=[a_{ij}]$, el determinante de $A$ es $$\det A = \sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}.$$ A $\det A$ también lo escribimos a veces en notación de «matriz con barras verticales» como sigue:

\begin{align*}
\det A = \begin{vmatrix}
a_{11} & a_{12} & \ldots & a_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & & \ddots & \vdots\\
a_{n1} & a_{n2} & \ldots & a_{nn}.
\end{vmatrix}
\end{align*}

Ejemplo. Si queremos calcular el determinante de una matriz en $M_2(F)$, digamos $$A=\begin{pmatrix} a & b \\ c & d \end{pmatrix},$$ debemos considerar dos permutaciones: la identidad y la transposición $(1,2)$.

La identidad tiene signo $1$ y le corresponde el sumando $ad$. La transposición tiene signo $-1$ y le corresponde el sumando $bc$. Así, $$\begin{vmatrix} a & b \\ c & d \end{vmatrix} = ad-bc.$$

$\triangle$

Retomando la discusión antes de la definición, tenemos entonces que $\det T = \det A_T$, en donde a la izquierda hablamos de un determinante de transformaciones lineales y a la derecha de uno de matrices. La matriz de $T$ depende de la base elegida, pero como vimos, el determinante de $T$ no. Esta es una conclusión muy importante, y la enunciamos como teorema en términos de matrices.

Teorema. Sean $A$ y $P$ matrices en $M_n(F)$ con $P$ invertible. El determinante de $A$ y el de $P^{-1}AP$ son iguales.

Determinantes de matrices triangulares

Terminamos esta entrada con un problema que nos ayudará a repasar la definición y que más adelante servirá para calcular determinantes.

Problema. Muestra que el determinante de una matriz triangular superior o triangular inferior es igual al producto de las entradas de su diagonal.

Solución. En una matriz triangular superior tenemos que $a_{ij}=0$ si $i>j$. Vamos a estudiar la expresión $$\sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}.$$

Si una permutación $\sigma$ no es la identidad, entonces hay un entero $i$ que no deja fijo, digamos $\sigma(i)\neq i$. Tomemos a $i$ como el mayor entero que $\sigma$ no deja fijo. Notemos que $\sigma(i)$ tampoco queda fijo por $\sigma$ pues $\sigma(\sigma(i))=\sigma(i)$ implica $\sigma(i)=i$, ya que $\sigma$ es biyectiva, y estamos suponiendo $\sigma(i)\neq i$. Por la maximalidad de $i$, concluimos que $\sigma(i)<i$.Entonces el sumando correspondiente a $\sigma$ es $0$ pues tiene como factor a la entrada $a_{i\sigma(i)}=0$.

En otras palabras, la única permutación a la que le puede corresponder un sumando no cero es la identidad, cuyo signo es $1$. De esta forma,
\begin{align*}
\det(A) &= \sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}\\
&=a_{11}\cdot \ldots \cdot a_{nn}.
\end{align*}

$\square$

Más adelante…

En esta entrada planteamos cómo se define el concepto de matriz para transformaciones lineales y cómo esta definición se extiende naturalmente a la definición del determinante de una matriz, recordando que a cada transformación lineal se le puede asociar una matriz y viceversa.

En las siguientes entradas vamos a ver qué propiedades que cumplen los determinantes y aprenderemos diferentes técnicas para calcularlos. A lo largo de la unidad, desarrollaremos bastante práctica en el cálculo y la manipulación de los determinantes, ya sea el determinante de un conjunto de vectores, de una transformación lineal o de una matriz.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Muestra que la transformación $T_f$ definida en la entrada es $n$-lineal y alternante.
  • Usando la definición de determinante para transformaciones lineales, encuentra el determinante de la transformación lineal $T:\mathbb{R}^n \to \mathbb{R}^n$ dada por $$T(x_1,x_2,\ldots,x_n)=(x_2,x_3,\ldots,x_1).$$
  • Calcula por definición el determinante de las matrices $$\begin{pmatrix} 3 & 2 \\ 4 & 1\end{pmatrix}$$ y $$\begin{pmatrix} 1 & 2 & 4 \\ 1 & 3 & 9 \\ 1 & 4 & 16 \end{pmatrix}.$$
  • Calcula por definición el determinante de la matriz $$\begin{pmatrix} 1 & 1 & 1 \\ 2 & 3 & 4 \\ 4 & 9 & 16\end{pmatrix}$$ y compáralo con el de la matriz de $3\times 3$ del inciso anterior. ¿Qué notas?
  • Completa el argumento para mostrar que el determinante de una matriz triangular inferior es el producto de las entradas en su diagonal.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Determinantes de vectores e independencia lineal

Por Leonardo Ignacio Martínez Sandoval

4 respuestas

Introducción

En este cuarto y último bloque del curso comenzamos hablando de transformaciones multilineales y de permutaciones. Luego, nos enfocamos en las transformaciones multilineales antisimétricas y alternantes. Con la teoría que hemos desarrollado hasta ahora, estamos listos para definir determinantes de vectores, de transformaciones lineales y de matrices.

En esta entrada comenzaremos con la definición de determinantes de vectores. En la siguiente entrada hablaremos acerca de determinantes de matrices y de transformaciones lineales. Después de definir determinantes, probaremos varias de las propiedades que satisfacen. Posteriormente, hablaremos de varias técnicas que nos permitirán calcular una amplia variedad de determinantes para tipos especiales de matrices.

Determinantes de vectores

Para empezar, definiremos qué es el determinante de un conjunto de vectores en un espacio de dimensión finita con respecto a una base.

Definición. Sea $B=(b_1,\ldots,b_n)$ una base de un espacio vectorial $V$ de dimensión finita $n$ y $x_1,\ldots,x_n$ vectores de $V$. Cada uno de los $x_i$ se puede escribir como $$x_i=\sum_{j=1}^n a_{ji}b_j.$$

El determinante de $x_1,\ldots,x_n$ con respecto a $(b_1,\ldots,b_n)$ es $$\sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)},$$ y lo denotamos por $\det_{(b_1,\ldots,b_n)} (x_1,\ldots,x_n)$.

Observa que estamos sumando tantos términos como elementos en $S_n$. Como existen $n!$ permutaciones de un conjunto de $n$ elementos, entonces la suma de la derecha tiene $n!$ sumandos.

Ejemplo. Consideremos la base $b_1=1$, $b_2=1+x$ y $b_3=1+x+x^2$ del espacio vectorial $\mathbb{R}_2[x]$ de polinomios con coeficientes reales y grado a lo más $2$. Tomemos los polinomios $v_1=1$, $v_2=2x$ y $v_3=3x^2$. Vamos a calcular el determinante de $v_1, v_2, v_3$ con respecto a la base $(b_1,b_2,b_3)$.

Para hacer eso, lo primero que tenemos que hacer es expresar a $v_1, v_2, v_3$ en términos de la base. Hacemos esto a continuación:
\begin{align*}
v_1&= 1\cdot b_1 + 0 \cdot b_2 + 0 \cdot b_3\\
v_2&= -2\cdot b_1 + 2 \cdot b_2 + 0 \cdot b_3\\
v_3&= 0 \cdot b_1 – 3 \cdot b_2 +3 b_3.
\end{align*}

De aquí, obtenemos
\begin{align*}
a_{11}&=1, a_{21}=0, a_{31}=0,\\
a_{12}&=-2, a_{22}=2, a_{32}=0,\\
a_{13}&=0, a_{23}=-3, a_{33}=3.
\end{align*}

Si queremos calcular el determinante, tenemos que considerar las $3!=3\cdot 2 \cdot 1 = 6$ permutaciones en $S_3$. Estas permutaciones son

\begin{align*}
\sigma_1 &= \begin{pmatrix}1 & 2 & 3 \\ 1 & 2 & 3\end{pmatrix}\\
\sigma_2 &= \begin{pmatrix}1 & 2 & 3 \\ 1 & 3 & 2\end{pmatrix}\\
\sigma_3 &= \begin{pmatrix}1 & 2 & 3 \\ 2 & 1 & 3\end{pmatrix}\\
\sigma_4 &= \begin{pmatrix}1 & 2 & 3 \\ 2 & 3 & 1\end{pmatrix}\\
\sigma_5 &= \begin{pmatrix}1 & 2 & 3 \\ 3 & 2 & 1\end{pmatrix}\\
\sigma_6 &= \begin{pmatrix}1 & 2 & 3 \\ 3 & 1 & 2\end{pmatrix}.
\end{align*}

Los signos de $\sigma_1,\ldots,\sigma_6$ son, como puedes verificar, $1$, $-1$, $-1$, $1$, $-1$ y $1$, respectivamente.

El sumando correspondiente a $\sigma_1$ es
\begin{align}
\text{sign}(\sigma_1) &a_{1\sigma_1(1)}a_{2\sigma_1(2)}a_{3\sigma_1(3)}\\
&= 1 \cdot a_{11}a_{22}a_{33}\\
&=1\cdot 1\cdot 2 \cdot 3 = 6.
\end{align}

El sumando correspondiente a $\sigma_2$ es
\begin{align}
\text{sign}(\sigma_2) &a_{1\sigma_2(1)}a_{2\sigma_2(2)}a_{3\sigma_2(3)}\\
&= (-1) \cdot a_{11}a_{23}a_{32}\\
&=(-1) \cdot 1\cdot (-3) \cdot 0 = 0.
\end{align}

Continuando de esta manera, se puede ver que los sumandos correspondientes a $\sigma_1,\ldots,\sigma_6$ son $$+6,-0,-0,+0,-0,+0,$$ respectivamente de modo que el determinante es $6$.

$\triangle$

La expresión de determinante puede parecer algo complicada, pero a través de ella podemos demostrar fácilmente algunos resultados. Consideremos como ejemplo el siguiente resultado.

Proposición. Sea $B=(b_1,\ldots,b_n)$ una base de un espacio vectorial $V$ de dimensión finita $n$. El determinante de $B$ con respecto a sí mismo es $1$.

Demostración. Cuando escribimos a $b_i$ en términos de la base $b$, tenemos que $$b_i=\sum_{j=1}^n a_{ji} b_j.$$ Como la expresión en una base es única, debemos tener $a_{ii}=1$ y $a_{ji}=0$ si $j\neq i$. Ahora, veamos qué le sucede al determinante $$\sum_{\sigma \in S_n} \text{sign}(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}.$$

Si $\sigma$ es una permutación tal que $\sigma(i)\neq i$ para alguna $i$, entonces en el producto del sumando correspondiente a $\sigma$ aparece $a_{i\sigma(i)}=0$, de modo que ese sumando es cero. En otras palabras, el único sumando no cero es cuando $\sigma$ es la permutación identidad.

Como el signo de la identidad es $1$ y cada $a_{ii}$ es $1$, tenemos que el determinante es
\begin{align*}
\sum_{\sigma \in S_n} \text{sign}&(\sigma)a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)} \\
&=a_{11}\cdot\ldots\cdot a_{nn}\\
&= 1\cdot\ldots\cdot 1 \\
& = 1.
\end{align*}

$\square$

El determinante es una forma $n$-lineal alternante

La razón por la cual hablamos de transformaciones $n$-lineales antisimétricas y alternantes antes de hablar de determinantes es que, en cierto sentido, los determinantes de vectores son las únicas transformaciones de este tipo. Los siguientes resultados formalizan esta intuición.

Teorema. Sea $B=(b_1,\ldots,b_n)$ una base de un espacio vectorial $V$ sobre $F$. Entonces la transformación $\det_{(b_1,\ldots,b_n)}:V^n \to F$ es una forma $n$-lineal y alternante.

Demostración. La observación clave para demostrar este resultado es que $\det_{(b_1,\ldots,b_n)}$ se puede reescribir en términos de la base dual $b_1^\ast, \ldots, b_n^\ast$. En efecto, recuerda que $b_i^\ast$ es la forma lineal que «lee» la coordenada de un vector $v$ escrito en la base $B$. De esta forma,

\begin{align*}
\det_{(b_1,\ldots,b_n)}&(v_1,\ldots,v_n)\\
&=\sum_{\sigma\in S_n}\left(\text{sign}(\sigma) \prod_{j=1}^n b_j^\ast(v_{\sigma(j)})\right)\\
\end{align*}

Para cada permutación $\sigma$, el sumando correspondiente es una forma $n$-lineal, pues es producto de $n$ formas lineales evaluadas en los distintos vectores. Así que $\det_{(b_1,\ldots,b_n)}$ es suma de formas $n$-lineales y por lo tanto es forma $n$-lineal.

Para mostrar que el determinante es alternante, tenemos que mostrar que es igual a $0$ cuando algún par de sus entradas son iguales. Supongamos que $i\neq j$ y que $v_i=v_j$. Tomemos $\tau$ a la transposición que intercambia a $i$ y a $j$. Cuando se compone una permutación con una transposición, su signo cambia. Así, para cualquier permutación $\sigma$, tenemos que $\sigma\tau$ tiene signo diferente.

Además, para cualquier $\sigma$ tenemos que $$a_{1\sigma(1)}\cdot\ldots\cdot a_{n\sigma(n)}$$ y $$a_{1\sigma\tau(1)}\cdot\ldots\cdot a_{n\sigma\tau(n)}$$ son iguales, pues $v_i=v_j$. Combinando ambas ideas, podemos emparejar a cada sumando del determinante con otro con el cual sume cero. Esto muestra que el determinante es $0$.

$\square$

Usando la teoría que desarrollamos en la entrada anterior, tenemos el siguiente corolario.

Corolario. La forma $n$-lineal $\det_{(b_1,\ldots,b_n)}$ es antisimétrica.

Los determinantes de vectores son las «únicas» formas $n$-lineales alternantes

Ya vimos que el determinante es una forma $n$-lineal alternante. Veamos ahora por qué decimos que es «la única». El siguiente resultado dice que cualquier otra forma $n$-lineal alternante varía de $\det_{(b_1,\ldots,b_n)}$ únicamente por un factor multiplicativo.

Teorema. Sea $B=(b_1,\ldots,b_n)$ una base de un espacio vectorial $V$. Si $f:V^n \to F$ es cualquier forma $n$-lineal y alternante, entonces $$f=f(b_1,\ldots,b_n)\det_{(b_1,\ldots,b_n)}.$$

Demostración. Para mostrar la igualdad del teorema, que es una igualdad de transformaciones, tenemos que ver que es cierta al evaluar en cualesquiera vectores $x_1,\ldots,x_n$. Escribamos a cada $x_i$ en términos de la base $B$: $$x_i=\sum_{j=1}^n a_{ij}b_j.$$

Usando la $n$-linealidad de $f$ en cada una de las entradas, tenemos que
\begin{align*}
f(x_1,\ldots,x_n)&=\sum_{i=1}^n a_{1i} f(b_i,x_2,\ldots,x_n)\\
&=\sum_{i,j=1}^n a_{1i}a_{2i} f(b_i,b_j,x_3,\ldots,x_n)\\
&=\ldots\\
&=\sum_{i_1,\ldots,i_n = 1}^n a_{1i_1}\ldots a_{ni_n} f(b_{i_1},\ldots,b_{i_n}).
\end{align*}

Aquí hay muchos términos, pero la mayoría de ellos son $0$. En efecto, si $b_{i_k}=b_{i_l}$, como $f$ es alternante tendríamos que ese sumando es $0$. Así, los únicos sumandos que pueden ser no cero son cuando la elección de subíndices es una permutación, es decir cuando existe $\sigma$ en $S_n$ tal que para $i_k=\sigma(k)$.

Por lo tanto, podemos simplificar la expresión anterior a
$$f(x_1,\ldots,x_n)=\sum_{\sigma \in S_n}a_{1 \sigma(1)}\ldots a_{n\sigma(n)} f(b_{\sigma(1)},\ldots,b_{\sigma(n)}).$$

Como $f$ es alternante, entonces es antisimétrica. De este modo, podemos continuar la igualdad anterior como
\begin{align*}
&=\sum_{\sigma \in S_n} \text{sign}(\sigma) a_{1 \sigma(1)}\ldots a_{n\sigma(n)} f(b_1,\ldots,b_n)\\
&=f(b_1,\ldots,b_n) \det_{(b_1,\ldots,b_n)}(x_1,\ldots, x_n).
\end{align*}

Esto es justo lo que queríamos probar.

$\square$

Los determinantes de vectores caracterizan bases

Como consecuencia del último teorema de la sección anterior, los determinantes de vectores caracterizan totalmente a los conjuntos de vectores que son bases. A continuación enunciamos esto formalmente.

Corolario. En un espacio vectorial $V$ de dimensión $n$ son equivalentes las siguientes tres afirmaciones para vectores $x_1,\ldots,x_n$ de $V$:

  1. El determinante de $x_1,\ldots,x_n$ con respecto a toda base es distinto de $0$.
  2. El determinante de $x_1,\ldots,x_n$ con respecto a alguna base es distinto de $0$.
  3. $x_1,\ldots,x_n$ es una base de $V$.

Demostración. La afirmación (1) es más fuerte que la (2) y por lo tanto la implica.

Ahora, probemos que la afirmación (2) implica la afirmación (3). Como $x_1,\ldots,x_n$ son $n$ vectores y $n$ es la dimensión de $V$, para mostrar que forman una base basta mostrar que son linealmente independientes. Anteriormente, vimos que cualquier forma alternante manda vectores linealmente dependientes a $0$. Como la hipótesis de (2) es que existe alguna forma alternante que no se anula en $x_1,\ldots, x_n$, entonces deben ser linealmente independientes y por lo tanto formar una base.

Finalmente, probemos que (3) implica (1). Tomemos $B=(b_1,\ldots,b_n)$ otra base de $V$. Como $\det_{(x_1,\ldots,x_n)}$ es una forma $n$-lineal, podemos aplicar el teorema anterior y evaluar en $x_1,\ldots,x_n$ para concluir que
\begin{align*}
\det_{(x_1,\ldots,x_n)}&(x_1,\ldots,x_n)&\\
&=\det_{(x_1,\ldots,x_n)}(b_1,\ldots,b_n) \det_{(b_1,\ldots,b_n)}(x_1,\ldots,x_n).
\end{align*}

El término de la izquierda es igual a $1$, de modo que ambos factores a la derecha deben ser distintos de $0$.

$\square$

Ejemplo. En el ejemplo que dimos de polinomios vimos que el determinante de $1$, $2x$ y $3x^2$ con respecto a la base $1$, $1+x$ y $1+x+x^2$ es igual a $6$. De acuerdo al teorema anterior, esto implica que $1$, $2x$ y $3x^2$ es un conjunto linealmente independiente de polinomios, y de hecho una base.

Además, el teorema anterior también implica que sin importar que otra base $B$ de $\mathbb{R}_2[x]$ tomemos, el determinante de $1$, $2x$ y $3x^2$ con respecto a $B$ también será distinto de $0$.

$\triangle$

Más adelante…

A lo largo de esta entrada estudiamos la definición de determinantes para un conjunto de vectores y enunciamos sus principales propiedades. En las siguientes entradas vamos a hablar cómo se define el determinante para matrices y para transformaciones lineales. Después de las definiciones, pasaremos a estudiar cómo se calculan los determinantes y veremos cómo se aplican a diferentes problemas de álgebra lineal.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • ¿Cuántos sumandos tendrá el determinante de $5$ vectores en un espacio vectorial de dimensión $5$ con respecto a cualquier base? Da el número de manera explícita.
  • Verifica que en el primer ejemplo de determinantes de esta entrada, en efecto los sumandos correspondientes a $\sigma_1,\ldots,\sigma_6$ son los que se enuncian.
  • Encuentra el determinante de los vectores $(3,1)$ y $(2,4)$ con respecto a la base $((5,1), (2,3))$ de $\mathbb{R}^2$.
  • Muestra que los vectores $(1,4,5,2)$, $(0,3,2,1)$, $(0,0,-1,4)$ y $(0,0,0,1)$ son linealmente independientes calculando por definición su determinante con respecto a la base canónica de $\mathbb{R}^4$.
  • Usa un argumento de determinantes para mostrar que los vectores $(1,4,3)$, $(2,-2,9)$, $(7,8,27)$ de $\mathbb{R}^3$ no son linealmente independientes. Sugerencia. Calcula su determinante con respecto a la base canónica.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Seminario de Resolución de Problemas: Identidad de Gauss e identidad de suma de cubos

Por Leonardo Ignacio Martínez Sandoval

1 respuesta

[latexpage]

Introducción

En la entrada anterior comenzamos a platicar acerca de identidades algebraicas útiles en la resolución de problemas matemáticos. Vimos algunas identidades básicas y platicamos acerca del teorema del binomio de Newton. En esta entrada veremos dos identidades más: la identidad de Gauss para suma de cuadrados y la identidad para factorizar $a^3+b^3+c^3-3abc$. Damos más de una demostración de cada una de ellas para seguir explorando ideas algebraicas.

Identidad de cuadrados de Gauss

Proposición. Para $a,b,c,d$ números reales se cumple que $$(a^2+b^2)(c^2+d^2)=(ac-bd)^2+(ad+bc)^2.$$

Demostración 1. Simplemente desarrollamos. Por un lado,
\begin{align*}
(a^2+b^2)(c^2+d^2) = a^2c^2+a^2d^2+b^2c^2+b^2d^2.
\end{align*}

Por otro lado, $ (ac-bd)^2+(ad+bc)^2$ es
\begin{align*}
&a^2c^2-2abcd+b^2d^2+a^2d^2+2abcd+b^2c^2\\
= &a^2c^2+a^2d^2+b^2c^2+b^2d^2.
\end{align*}

$\square$

La siguiente demostración nos ayuda a entender un poco mejor la identidad y tiene una idea que se puede aplicar en varios contextos.

Demostración 2. Vamos a dar un pequeño brinco a los números complejos, pues ahí podemos hacer la factorización $x^2+y^2=(x+yi)(x-yi)$.

Usando esa identidad:
\begin{align*}
&(a^2+b^2)(c^2+d^2) \\
=&(a+bi)(a-bi)(c+di)(c-di)\\
=&(a+bi)(c+di)(a-bi)(c-di)\\
=&((ac-bd)+(ad+bc)i) ((ac-bd)-(ad+bc)i)\\
=&(ac-bd)^2+(ad+bc)^2.
\end{align*}

$\square$

La idea que se puede recuperar de la demostración anterior es la siguiente: a veces una identidad no se puede factorizar en los números reales (racionales, enteros, etc), pero sí en los números complejos (otro sistema numérico más grande). Aunque el problema hable de números reales, es posible que podamos ir a los complejos y regresar a los reales con información.

Problema ejemplo para identidad de Gauss

Problema. Muestra que si tienes un número $x$ de la forma $r^2+7s^2$, con $r$ y $s$ números enteros, entonces el número $x^{2020}$ también es de esa forma.

Sugerencia pre-solución. Aquí, el exponente $2020$ es sospechoso, y sugiere que en realidad el problema debe ser más general. Haz algunos casos pequeños para buscar un patrón de cómo se comporta el producto de dos números de esa forma. Después, para estudiar las potencias, usa el principio de inducción.

Solución. Notemos que $$x=r^2+7s^2=(r+\sqrt{7}si)(r-\sqrt{7}si)$$ Tomemos otro número de esa forma, digamos $$y=t^2+7u^2= (t+\sqrt{7}ui)(t-\sqrt{7}ui).$$ Al hacer el producto de $x$ y $y$, aparecerá un factor $$ (r+\sqrt{7}si)(t+\sqrt{7}ui)=((rt-7su)+(ru+st)\sqrt{7}i)$$ y un factor $$ (r-\sqrt{7}si)(t-\sqrt{7}ui)=((rt-7su)-(ru+st)\sqrt{7}i),$$ que multiplicados son iguales a $$(rt-7su)^2+7(ru+st)^2.$$ Con todo esto, concluimos que el producto de cualesquiera dos números de la forma buscada, también es de la forma buscada. De aquí, $x^2$ es de la forma buscada, e inductivamente $x^n$ es de la forma buscada para todo entero $n\geq 1$. En particular, $x^{2020}$ es de la forma que se quiere.

$\square$

Identidad para $a^3+b^3+c^3-3abc$

Proposición. Para $a,b,c$ números reales, se tiene que $$a^3+b^3+c^3-3abc$$ es igual a $$(a+b+c)(a^2+b^2+c^2-ab-bc-ca).$$

Esta identidad también tiene varias demostraciones, que en conjunto guardan varias ideas. Veamos dos de ellas.

Demostración 1. Simplemente hacemos el producto de la segunda expresión para verificar que nos de la primera. Claramente aparece un único $a^3$ y por simétría aparecen $b^3$ y $c^3$ exactamente una vez. También, claramente aparece tres veces la expresión $-abc$. Todas las expresiones que aparecen son cúbicas y ya contamos las «de la forma» $x^3$ y $xyz$, así que por simetría basta ver qué pasa con cada expresión de la forma $x^2y$. Estas se obtienen ya sea de elegir $x$ en la primera y $-xy$ en la segunda, o bien $y$ en la primera y $x^2$ en la segunda, de modo que todas ellas se cancelan.

Sólo para asegurarnos que hicimos todo bien, deberíamos haber contado $3\cdot 6=18$ monomios. Hay tres de la forma $x^3$, tres de la forma $xyz$ y cada uno de los seis la forma $x^2y$ ya lo encontramos $2$ veces, una vez positivo y una vez negativo. Así, nuestra cuenta abarca $3+3+6\cdot 3= 18$ monomios, así que ya contamos todos los términos.

$\square$

Hay una segunda demostración, que usa ideas de álgebra lineal. Daremos la idea general, y más adelante, cuando hablemos de matrices y determinantes, platicaremos de estas ideas más a detalle.

Demostración. Calculemos el determinante $D$ de la matriz $$\begin{pmatrix} a & b & c \\ c & a & b \\ b & c & a\end{pmatrix}$$ de dos formas distintas. Por un lado, podemos sumar los renglones $2$ y $3$ al primer renglón sin que cambie el determinante, así, $$D=\begin{vmatrix} a+b+c & a+b+c & a+b+c\\ c & a & b \\ b & c & a\end{vmatrix}.$$ De aquí, podemos factorizar $a+b+c$ pues está en cada entrada del primer renglón $$D=(a+b+c)\begin{vmatrix} 1 & 1 & 1\\ c & a & b \\ b & c & a\end{vmatrix}.$$

Finalmente, desarrollando el determinante que queda usando el primer renglón, tenemos que
\begin{align*}
D&=(a+b+c)((a^2-bc)-(ca-b^2)+(c^2-ab))\\
&=(a+b+c)(a^2+b^2+c^2-ab-bc-ca).
\end{align*}

Por otro lado, usando el truco para desarrollar un determinante de $3\times 3$ por diagonales,
\begin{align*}
D&=a^3+b^3+c^3-abc-abc-abc\\
&= a^3+b^3+c^3-3abc.
\end{align*}

Igualando ambas expresiones para $D$, obtenemos la identidad deseada.

$\square$

Problema ejemplo de factorización de $a^3+b^3+c^3-3abc$

Problema. Sean $a,b,c$ números reales. Muestra que $a^3+b^3+c^3=3abc$ si y sólo si $a+b+c=0$ o $a=b=c$.

Sugerencia pre-solución. Necesitarás la identidad anterior y un análisis de casos. También, para uno de los casos necesitarás usar la factorización de $x^2-2xy+y^2$ algunas veces.

Solución. De acuerdo a la identidad de la sección anterior, $a^3+b^3+c^3=3abc$ si y sólo si $$(a+b+c)(a^2+b^2+c^2-ab-bc-ca)=0.$$

Notemos que $$a^2+b^2+c^2-ab-bc-ca=\frac{(a-b)^2+(b-c)^2+(c-a)^2}{2},$$ que siempre es mayor o igual que cero y es igual a $0$ si y sólo si $a-b=b-c=c-a=0$, si y sólo si $a=b=c$.

Así, $a^3+b^3+c^3=3abc$ si y sólo si alguno de los factores que lo conforman es cero, lo cual pasa si y sólo si $a+b+c=0$ o $a=b=c$.

$\square$

Más problemas

Puedes ver más problemas que usan identidades algebraicas en la entrada anterior de este tema. Además, puedes encontrar más problemas de identidades algebraicas en la Sección 4.1 del libro Problem Solving through Problems de Loren Larson.

Álgebra Superior II: Sistemas de ecuaciones lineales complejos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En la entrada anterior comenzamos a hablar acerca de resolver, en los complejos, ecuaciones de distintos tipos. Además, profundizamos en cómo resolver las ecuaciones cuadráticas complejas. En esta entrada platicaremos acerca de los sistemas de ecuaciones lineales complejos.

Resolveremos a detalle el caso de dos variables y dos ecuaciones. Después, hablaremos un poco acerca de sistemas de ecuaciones con más variables. Un estudio cuidadoso de los sistemas de ecuaciones lineales con más variables se hace en los cursos de álgebra lineal. Un muy buen texto para aprender estos temas es el libro Essential Linear Algebra de Titu Andreescu.

Sistemas de ecuaciones lineales complejos con dos incógnitas

Si $a,b$ son elementos de $\mathbb{C}$ y $a\neq 0$, la ecuación lineal $$ax=b$$ tiene una única solución, dada por $x=\frac{b}{a}$, la cual está bien definida pues todo complejo distinto de $0$ tiene inverso multiplicativo.

Si tenemos los números complejos $a,b,c,d,e$ y $f$, el sistema de ecuaciones lineales en los complejos

\begin{align*}
ax+by &= c\\
dx+ey&=f
\end{align*}

puede comportarse de tres formas distintas:

  • Su solución existe y es única.
  • Tiene una infinidad de soluciones.
  • No tiene solución.

Si tiene al menos soluciones distintas, tenemos entonces que tiene una infinidad. Cuando la solución del sistema es única, el sistema se puede resolver por los métodos básicos con los que se resuelve un sistema en $\mathbb{R}$:

  • Por substitución: de la primera ecuación se despeja la variable $x$ y su valor se pone en la segunda ecuación. De ahí, obtenemos una ecuación en $y$. Se despeja $y$ para obtener su valor y con ello se obtiene el valor de $x$.
  • Igualando coeficientes: multiplicamos la primer ecuación por $d$ y la segunda por $-a$. Al sumar ambas ecuaciones resultantes, queda una ecuación lineal en $y$.

Ejemplos de sistemas de ecuaciones lineales complejos

Ejemplo 1. Determina todas las soluciones del sistema
\begin{align*}
2x+iy&= 3+4i\\
ix+5y&= 9 – 4i.
\end{align*}

Solución. Para empezar, multiplicamos la segunda ecuación por $2i$, de donde obtenemos el sistema
\begin{align*}
2x+iy&= 3+4i\\
-2x+10iy&=8+18i.
\end{align*}

Sumando ambas ecuaciones, obtenemos que $11iy=11+22i$. Multiplicando por $-\frac{i}{11}$ de ambos lados, obtenemos $$y=2-i.$$

Substituyendo en la segunda ecuación, notamos que $$2x=3+4i-i(2-i)=2+2i,$$ de donde $x=1+i$. De aquí, la única solución puede ser $x=1+i$ y $y=2-i$, que se puede verificar que en efecto satisfacen la ecuación.

$\triangle$

Ejemplo 2. Determina todas las soluciones del sistema
\begin{align*}
(3+2i)x+iy&= 3+3i\\
(-4+6i)x-2y&= -6 + 6i.
\end{align*}

Solución. Multiplicando la primer ecuación por $2i$ obtenemos que es equivalente a la ecuación $$(-4i+6i)x-2y=-6+6i,$$ es decir, ambas ecuaciones difieren sólo por un factor $2i$, así que son la misma. Si elegimos cualquier valor de $y$, podemos encontrar un valor de $x$ que cumpla con la ecuación. Por ejemplo, tomando $y=1$, de la ecuación obtenemos que $x=1$. Así, esta ecuación tiene una infinidad de soluciones, dadas por elegir un $y$ y definir $x=\frac{3+3i-iy}{3+2i}.$

$\triangle$

Ejemplo 3. Determina todas las soluciones del sistema
\begin{align*}
(1+2i)x+(-2+i)y&= 3+6i\\
3x+3iy&= 8.
\end{align*}

Solución. Supongamos que existe alguna solución para $x$ y $y$. Multipliquemos la primer ecuación por $3$ y la segunda por $1+2i$. Obtenemos que
\begin{align*}
(3+6i)x+(-6+3i)y&= 9+18i\\
(3+6i)x+(-6+3i)y&= 8+16i.
\end{align*}

De aquí, $9+18i=8+16i$, lo cual es una contradicción. Así, esta ecuación no tiene soluciones.

$\triangle$

Método del determinante

Un método más general para resolver sistemas de ecuaciones lineales complejos con dos incógnitas, que nos dice todo lo que puede suceder, es el siguiente. De hecho, exactamente el mismo teorema funciona para $\mathbb{R}$.

Teorema. Sean $a,b,c,d,e$ y $f$ en $\mathbb{C}$. Para el sistema \begin{align*}
ax+by &= c\\
dx+ey&=f
\end{align*}

definimos a su determinante como el número complejo $ae-bd$. Entonces:

  • Si el determinante es distinto de $0$, el sistema tiene una solución única para $x$ y $y$ dada por
    \begin{align*}
    x&=\frac{ce-bf}{ae-bd}\\
    y&=\frac{af-cd}{ae-bd}.
    \end{align*}
  • Si el determinante es $0$, entonces el sistema no tiene solución, o tiene una infinidad.

Demostración. Cuando el determinante no es $0$, resolvemos el sistema por igualación de coeficientes. Multiplicando la primer ecuación por $-d$, la segunda por $a$ y sumando, obtenemos que $$(ae-bd)y=af-cd.$$ Como el determinante no es cero, $$y=\frac{af-cd}{ae-bd}.$$ Así mismo, multiplicando la primer ecuación por $e$, la segunda por $-b$ y sumando, obtenemos de manera análoga que $$x=\frac{ce-bf}{ae-bd}.$$ Así, si existe una solución, debe tener estos valores. Queda como tarea moral verificar que estos valores cumplen.

Cuando el determinante es $0$, tenemos que $ae=bd$. Si $a=b=e=d=0$, para que exista una solución se necesita forzosamente que $c=f=0$, y de hecho en este caso cualquier pareja $x,y$ funciona. Si en este caso alguno de $c$ o $f$ no es $0$, el sistema no tiene solución.

Así, continuando el análisis podemos suponer sin pérdida de generalidad que $a\neq 0$. De este modo, $e=\frac{bd}{a}$, por lo que la segunda ecuación es equivalente a $$dx+\frac{bd}{a}y=f,$$ que es $adx+bdy=af$.

Si $d=0$, tenemos, de la ecuación anterior, que $af=0$ y del determinante que $ae=bd=0$. Como $a\neq 0$, se necesita que $e=f=0$, de modo que en realidad sólo tenemos una ecuación, la primera. Como $a\neq 0$, podemos elegir cualquier valor de $y$ y de ahí despejar el valor de $x$, obteniendo una infinidad de soluciones.

Si $d\neq 0$, entonces la ecuación $adx+bdy=af$ es equivalente a la ecuación $ax+by=\frac{af}{d}$. La primer ecuación y esta implican que si hay solución, entonces $\frac{af}{d}=c$. De ser así ,sólo tenemos una ecuación, pero repetida. Por el mismo argumento de arriba, hay una infinidad de soluciones.

$\square$

Sistemas de ecuaciones lineales complejos con más incógnitas

Los sistemas lineales complejos con más incógnitas se pueden resolver con las mismas técnicas que aquellos en los reales. En cursos como álgebra lineal verás cómo resolver un sistema lineal en general y cómo saber cómo se ven todas sus soluciones. Sin embargo, puedes aprovechar lo que ya sabes del álgebra de los complejos para resolver distintos sistemas lineales.

Problema 1. Resuelve en los complejos el sistema de ecuaciones

\begin{align*}
3a+(2+i)b+(1+2i)c&=1+i\\
3b+(2+i)c&=2+2i\\
3c&=3+3i.
\end{align*}

Solución. Resolvemos el sistema por substitución. Nos conviene empezar con la tercer ecuación, que tiene únicamente una variable. De ella obtenemos que $c=1+i$. Substituyendo en la segunda ecuación, obtenemos que $$3b+(2+i)(1+i)=2+2i,$$ de donde $$3b+1+3i=2+2i,$$ así que $$3b=1-i,$$ entonces $$b=\frac{1}{3}-\frac{1}{3}i.$$

Con los valores de $b$ y $c$ podemos substituir en la primer ecuación. Notando que
\begin{align*}
(2+i)\left(\frac{1}{3}-\frac{1}{3}i\right)=1-\frac{1}{3}i\\
(1+2i)(1+i)=-1+3i\\
(1+i)-\left(1-\frac{1}{3}i\right)-(-1+3i)=1-\frac{5}{3}i,
\end{align*}

obtenemos que $$a=\frac{1}{3}-\frac{5}{9}i.$$

En resumen,
\begin{align*}
a&=\frac{1}{3}-\frac{5}{9}i\\
b&=\frac{1}{3}-\frac{1}{3}i\\
c&=1+i
\end{align*}

es la única posible solución, y se puede mostrar que en efecto satisface las tres ecuaciones.

$\triangle$

Problema 2. Resuelve en los complejos el sistema de ecuaciones

\begin{align*}
(1+5i)a+b+c+d+e&=2\\
a+(1+5i)b+c+d+e&=2\\
a+b+(1+5i)c+d+e&=2\\
a+b+c+(1+5i)d+e&=2\\
a+b+c+d+(1+5i)e&=2.
\end{align*}

Solución. Sumando todas las ecuaciones, tenemos que $$(5+5i)(a+b+c+d+e)=10,$$ de donde obtenemos que
\begin{align*}
a+b+c+d+e&=\frac{2}{1+i}\\
&=1-i.
\end{align*}

De la primera ecuación, obtenemos que \begin{align*}2&=(a+b+c+d+e)+5ia\\&=1-i+5ia,\end{align*} por lo que $$a=\frac{1+i}{5i}=\frac{1}{5}-\frac{1}{5}i.$$ Por simetría, el resto de las variables también tiene este valor, de modo que $$a=b=c=d=e= \frac{1}{5}-\frac{1}{5}i$$ es la única solución.

$\triangle$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Verifica que las soluciones de los ejemplos de sistemas de ecuaciones lineales complejos de dos variables en efecto son soluciones.
  2. Resuelve en los complejos el sistema de ecuaciones \begin{align*}2x+(1+i)y &= 4\\ (5-i)x+(3+2i)y &=0.\end{align*}
  3. En el teorema del método del determinante, cuando el determinante no es cero, encontramos una solución. Verifica que en efecto satisface el sistema original.
  4. Verifica que las soluciones de los ejemplos en varias variables en efecto satisfacen el sistema original.
  5. Resuelve en los complejos el sistema de ecuaciones \begin{align*} x+(1+i)y &= 4\\ y+(2+i)z &= 5\\ z + (3+i)x &= 6.\end{align*}

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»