Archivo de la etiqueta: invertible

Álgebra Superior I: Determinante de matrices y propiedades

Por Eduardo García Caballero

Deja un comentario

Introducción

Uno de los conceptos más importantes en el álgebra lineal es la operación conocida como determinante. Si bien este concepto se extiende a distintos objetos, en esta entrada lo revisaremos como una operación que se puede aplicar a matrices cuadradas. Como veremos, el determinante está muy conectado con otros conceptos que hemos platicado sobre matrices

Definición para matrices de $2\times 2$

A modo de introducción, comenzaremos hablando de determinantes para matrices de $2\times 2$. Aunque este caso es sencillo, podremos explorar algunas de las propiedades que tienen los determinantes, las cuales se cumplirán de manera más genera. Así, comencemos con la siguiente definición.

Definición. Para una matriz $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$, definimos su determinante como
\[
\operatorname{det}(A) = ad – bc.
\]

Basándonos en esta definición, podemos calcular los determinantes
\[
\operatorname{det}
\begin{pmatrix} 9 & 3 \\ 5 & 2 \end{pmatrix}=9\cdot 2 – 3\cdot 5 = 3
\]
y
\[
\operatorname{det}
\begin{pmatrix} 4 & -3 \\ 12 & -9 \end{pmatrix}
=
4\cdot (-9)-(-3)\cdot 12= 0.
\]

Otra notación que podemos encontrar para determinantes es la notación de barras. Lo que se hace es que la matriz se encierra en barras verticales, en vez de paréntesis. Así, los determinantes anteriores también se pueden escribir como
\[
\begin{vmatrix} 9 & 3 \\ 5 & 2 \end{vmatrix} = 3
\qquad
\text{y}
\qquad
\begin{vmatrix} 4 & -3 \\ 12 & -9 \end{vmatrix} = 0.
\]

Primeras propiedades del determinante

El determinante de una matriz de $2\times 2$ ayuda a detectar cuándo una matriz es invertible. De hecho, esto es algo que vimos previamente, en la entrada de matrices invertibles. En ella, dijimos que una matriz $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ es invertible si y sólo si se cumple que $ad – bc \ne 0$. ¡Aquí aparece el determinante! Podemos reescribir el resultado de la siguiente manera.

Teorema. Una matriz de la forma $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ es invertible si y sólo si $\det(A) \ne 0$. Cuando el determinante es distinto de cero, la inversa es $A^{-1} = \frac{1}{\det(A)}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$.

Otra propiedad muy importante que cumple el determinante para matrices de $2\times 2$ es la de ser multiplicativo; es decir, para matrices $A$ y $B$ se cumple que $\operatorname{det}(AB) = \operatorname{det}(A) \operatorname{det}(B)$. La demostración de esto se basa directamente en las definiciones de determinante y de producto de matrices. Hagamos las cuentas a continuación para matrices $A=\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}$ y $B=\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}.$

Tenemos que:
\begin{align*}
\operatorname{det}(AB)
&=
\operatorname{det}
\left(
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\right)
\\[5pt]
&=
\operatorname{det}
\begin{pmatrix}
a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\
a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22}
\end{pmatrix}
\\[5pt]
&=
(a_{11}b_{11} + a_{12}b_{21})(a_{21}b_{12} + a_{22}b_{22})-(a_{11}b_{12} + a_{12}b_{22})(a_{21}b_{11} + a_{22}b_{21})
\\[5pt]
&=
a_{11}a_{22}b_{11}b_{22} – a_{12}a_{21}b_{11}b_{22} – a_{11}a_{22}b_{12}b_{21} + a_{12}a_{21}b_{12}b_{21}
\\[5pt]
&=
(a_{11}a_{22} – a_{12}a_{21})(b_{11}b_{22} – b_{12}b_{21})
\\[5pt]
&=
\operatorname{det}
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\operatorname{det}
\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\\[5pt]
&=
\operatorname{det}(A)\operatorname{det}(B).
\end{align*}

Interpretación geométrica del determinante de $2\times 2$

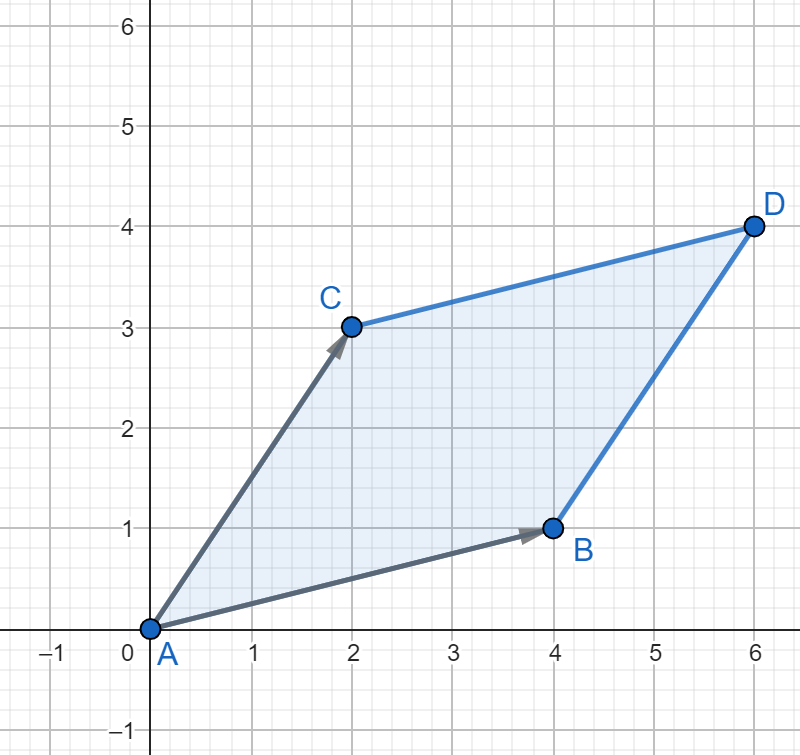
El determinante también tiene una interpretación geométrica muy interesante. Si tenemos una matriz de $2\times 2$, entonces podemos pensar a cada una de las columnas de esta matriz como un vector en el plano. Resulta que el determinante es igual al área del paralelogramo formado por estos vectores.

Por ejemplo, si consideramos la matriz
\[
\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix},
\]
podemos ver que el vector asociado a su primera columna es el vector $(4,1)$, mientras que el vector asociado a su segunda columna es $(2,3)$:

Así, el paralelogramo $ABDC$ de la figura anterior formado por estos dos vectores tiene área igual a
\[
\operatorname{det}
\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}
= 4\cdot 3 – 2\cdot 1 = 10.
\]

No daremos la demostración de este hecho, pues se necesita hablar más sobre la geometría del plano. Sin embargo, las ideas necesarias para este resultado pueden consultarse en un curso de Geometría Analítica I.

Definición recursiva

También nos interesa hablar de determinantes de matrices más grandes. De hecho, nos interesa hablar del determinante de cualquier matriz cuadrada. La definición formal requiere de varios conocimientos de Álgebra Lineal I. Sin embargo, por el momento podemos platicar de cómo se obtienen los determinantes de matrices recursivamente. Con esto queremos decir que para calcular el determinante de matrices de $3\times 3$, necesitaremos calcular varios de matrices de $2\times 2$. Así mismo, para calcular el de matrices de $4\times 4$ requeriremos calcular varios de matrices de $3\times 3$ (que a su vez requieren varios de $2\times 2$).

Para explicar cómo es esta relación de poner determinantes de matrices grandes en términos de matrices más pequeñas, primeramente definiremos la función $\operatorname{sign}$, la cual asigna a cada pareja de enteros positivos $(i,j)$ el valor
\[
\operatorname{sign}(i,j) = (-1)^{i+j}.
\]
A partir de la función $\operatorname{sign}$ podemos hacer una matriz cuya entrada $a_{ij}$ es $\operatorname{sign}(i,j)$. Para visualizarla más fácilmente, podemos pensar que a la entrada $a_{11}$ (la cual se encuentra en la esquina superior izquierda) le asigna el signo “$+$”, y posteriormente va alternando los signos del resto de entradas. Por ejemplo, los signos correspondientes a las entradas de la matriz de $3 \times 3$
\[
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
\]
serían
\[
\begin{pmatrix}
+ & – & + \\
– & + & – \\
+ & – & +
\end{pmatrix},
\]
mientras que los signos correspondientes a las entradas de la matriz de $4 \times 4$
\[
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{pmatrix}
\]
serían
\[
\begin{pmatrix}
+ & – & + & – \\
– & + & – & + \\
+ & – & + & – \\
– & + & – & +
\end{pmatrix}.
\]

Ya que entendimos cómo se construyen estas matrices, el cálculo de determinantes se realiza como sigue.

Estrategia. Realizaremos el cálculo de determinante de una matriz de $n \times n$ descomponiéndola para realizar el cálculo de determinantes de matrices de $(n-1) \times (n-1)$. Eventualmente llegaremos al calcular únicamente determinantes de matrices de $2 \times 2$, para las cuales ya tenemos una fórmula. Para esto, haremos los siguientes pasos repetidamente.

  1. Seleccionaremos una fila o columna arbitraria de la matriz original (como en este paso no importa cuál fila o columna seleccionemos, buscaremos una que simplifique las operaciones que realizaremos; generalmente nos convendrá seleccionar una fila o columna que cuente en su mayoría con ceros).
  2. Para cada entrada $a_{ij}$ en la fila o columna seleccionada, calculamos el valor de
    \[
    \operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{ij}),
    \]
    donde $A_{ij}$ es el la matriz que resulta de quitar la fila $i$ y la columna $j$ a la matriz original.
  3. El determinante de la matriz será la suma de todos los términos calculados en el paso anterior.

Veamos algunos ejemplos de cómo se utiliza la estrategia recién descrita.

Ejemplo con matriz de $3\times 3$

Consideremos la matriz de $3 \times 3$
\[
\begin{pmatrix}
3 & 1 & -1 \\
6 & -1 & -2 \\
4 & -3 & -2
\end{pmatrix}.
\]

A primera vista no hay alguna fila o columna que parezca simplificar los cálculos, por lo cual podemos proceder con cualquiera de estas; nosotros seleccionaremos la primera fila.
\[
\begin{pmatrix}
\fbox{3} & \fbox{1} & \fbox{-1} \\
6 & -1 & -2 \\
4 & -3 & -2
\end{pmatrix}.
\]

Para cada término de la primera fila, calculamos el producto
\[
\operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{i,j}),
\]
obteniendo
\begin{align*}
\operatorname{sign}(1,1) \cdot (a_{11}) \cdot \operatorname{det}(A_{11})
&= +(3)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
\blacksquare & -1 & -2 \\
\blacksquare & -3 & -2
\end{pmatrix}
\\[5pt]
&= +(3)\operatorname{det} \begin{pmatrix} -1 & -2 \\ -3 & -2 \end{pmatrix}
\\[5pt]
&= +(3)[(-1)(-2) – (-2)(-3)]
\\[5pt]
&= +(3)(-4)
\\[5pt]
&= -12,
\\[10pt]
\operatorname{sign}(1,2) \cdot (a_{12}) \cdot \operatorname{det}(A_{12})
&= -(1)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
6 & \blacksquare & -2 \\
4 & \blacksquare & -2
\end{pmatrix}
\\[5pt]
&= -(1)\operatorname{det}
\begin{pmatrix} 6 & -2 \\ 4 & -2 \end{pmatrix}
\\[5pt]
&=-(1)[(6)(-2) – (-2)(4)]
\\[5pt]
&=-(1)(-4)
\\[5pt]
&=4,
\\[10pt]
\operatorname{sign}(1,3) \cdot (a_{13}) \cdot \operatorname{det}(A_{13})
&= +(-1)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
6 & -1 & \blacksquare \\
4 & -3 & \blacksquare
\end{pmatrix}
\\[5pt]
&= +(-1)\operatorname{det} \begin{pmatrix} 6 & -1 \\ 4 & -3 \end{pmatrix}
\\[5pt]
&= +(-1)[(6)(-3) – (-1)(4)]
\\[5pt]
&= +(-1)(-14)
\\[5pt]
&= 14.
\end{align*}

Finalmente, el determinante de nuestra matriz original será la suma de los términos calculados; es decir,
\[
\begin{pmatrix}
3 & 1 & -1 \\
6 & -1 & -2 \\
4 & -3 & -1
\end{pmatrix}
=
(-12) + (4) + (14) = 6.
\]

Ejemplo con matriz de $4\times 4$

En el siguiente ejemplo veremos cómo el escoger una fila o columna en específico nos puede ayudar a simplificar mucho los cálculos.

Consideremos la matriz
\[
\begin{pmatrix}
4 & 0 & 2 & 2 \\
-1 & 3 & -2 & 5 \\
-2 & 0 & 2 & -3 \\
1 & 0 & 4 & -1
\end{pmatrix}.
\]

Observemos que el valor de tres de las entradas de la segunda columna es $0$. Por esta razón, seleccionaremos esta columna para descomponer la matriz:
\[
\begin{pmatrix}
4 & \fbox{0} & 2 & 2 \\
-1 & \fbox{3} & -2 & 5 \\
-2 & \fbox{0} & 2 & -3 \\
1 & \fbox{0} & 4 & -1
\end{pmatrix}.
\]

El siguiente paso será calcular el producto
\[
\operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{ij}),
\]
para cada entrada de esta columna. Sin embargo, por la elección de columna que hicimos, podemos ver que el valor de $a_{ij}$ es 0 para tres de las entradas, y por tanto también lo es para el producto que deseamos calcular. De este modo, únicamente nos restaría calcular el producto
\begin{align*}
\operatorname{sign}(2,2) \cdot a_{22} \cdot \operatorname{det}(A_{22})
&=
+(3)\operatorname{det}
\begin{pmatrix}
4 & \blacksquare & 2 & 2 \\
\blacksquare & \blacksquare & \blacksquare & \blacksquare \\
-2 & \blacksquare & 2 & -3 \\
1 & \blacksquare & 4 & -1
\end{pmatrix}
\\[5pt]
&= +(3)\operatorname{det}
\begin{pmatrix}
4 & 2 & 2 \\
-2 & 2 & -3 \\
1 & 4 & -1
\end{pmatrix}.
\end{align*}
Se queda como ejercicio al lector concluir que el resultado de este último producto es 30.

De este modo, obtenemos que
\[
\operatorname{det}
\begin{pmatrix}
4 & 0 & 2 & 2 \\
-1 & 3 & -2 & 5 \\
-2 & 0 & 2 & -3 \\
1 & 0 & 4 & -1
\end{pmatrix}
= 0 + 30 + 0 + 0 = 30.
\]

Aunque esta definición recursiva nos permite calcular el determinante de una matriz cuadrada de cualquier tamaño, rápidamente se vuelve un método muy poco práctico (para obtener el determinante de una matriz de $6 \times 6$ tendríamos que calcular hasta 60 determinantes de matrices de $2 \times 2$). En el curso de Álgebra Lineal I se aprende otra definición de determinante a través de permutaciones, de las cuales se desprenden varios métodos más eficientes para calcular determinante. Hablaremos un poco de estos métodos en la siguiente entrada.

Las propiedades de $2\times 2$ también se valen para $n\times n$

Las propiedades que enunciamos para matrices de $2\times 2$ también se valen para determinantes de matrices más grandes. Todo lo siguiente es cierto, sin embargo, en este curso no contamos con las herramientas para demostrar todo con la formalidad apropiada:

  • El determinante es multiplicativo: Si $A$ y $B$ son matrices de $n\times n$, entonces $\operatorname{det}(AB) = \operatorname{det}(A)\operatorname{det}(B)$.
  • El determinante detecta matrices invertibles: Una matriz $A$ de $n\times n$ es invertible si y sólo si su determinante es distinto de $0$.
  • El determinante tiene que ver con un volumen: Los vectores columna de una matriz $A$ de $n\times n$ hacen un paralelepípedo $n$-dimensional cuyo volumen $n$-dimensional es justo $\det{A}$.

Más adelante…

En esta entrada conocimos el concepto de determinante de matrices, vimos cómo calcularlo para matrices de distintos tamaños y revisamos cómo se interpreta cuando consideramos las matrices como transformaciones de flechas en el plano. En la siguiente entrada enunciaremos y aprenderemos a usar algunas de las propiedades que cumplen los determinantes.

Tarea moral

  1. Calcula los determinantes de las siguientes matrices:
    • $\begin{pmatrix} 5 & 8 \\ 3 & 9 \end{pmatrix}, \begin{pmatrix} 10 & 11 \\ -1 & 9 \end{pmatrix}, \begin{pmatrix} 31 & 38 \\ 13 & -29 \end{pmatrix}$
    • $\begin{pmatrix} 1 & 5 & 2 \\ 3 & -1 & 8 \\ 0 & 2 & 5 \end{pmatrix}, \begin{pmatrix} 1 & 8 & 4 \\ 0 & 5 & -3 \\ 0 & 0 & -1 \end{pmatrix}, \begin{pmatrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 3 & 3 & 3 \end{pmatrix}$
    • $\begin{pmatrix} 5 & 7 & -1 & 2 \\ 3 & 0 & 1 & 0 \\ 2 & -2 & 2 & -2 \\ 5 & 1 & 1 & 0 \end{pmatrix}, \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{pmatrix}$
  2. Demuestra que para una matriz $A$ y un entero positivo $n$ se cumple que $\det(A^n)=\det(A)^n$.
  3. Sea $A$ una matriz de $3\times 3$. Muestra que $\det(A)=\det(A^T)$.
  4. Sea $A$ una matriz invertible de $2\times 2$. Demuestra que $\det(A)=\det(A^{-1})^{-1}$.
  5. ¿Qué le sucede al determinante de una matriz $A$ cuando intercambias dos filas? Haz algunos experimentos para hacer una conjetura, y demuéstrala.

Entradas relacionadas

Álgebra Superior I: Cálculo de determinantes

Por Eduardo García Caballero

Deja un comentario

Introducción

En la entrada anterior introdujimos el concepto de determinante de matrices cuadradas. Dimos la definición para matrices de $2\times 2$. Aunque no dimos la definición en general (pues corresponde a un curso de Álgebra Lineal I), dijimos cómo se pueden calcular los determinantes de manera recursiva. Pero, ¿hay otras herramientas para hacer el cálculo de determinantes más sencillo?

En esta entrada hablaremos de más propiedades de los determinantes. Comenzaremos viendo que si en una matriz tenemos dos filas o columnas iguales, el determinante se hace igual a cero. Luego, veremos que los determinantes son lineales (por renglón o columna), que están muy contectados con las operaciones elementales y platicaremos de algunos determinantes especiales.

Linealidad por filas o columnas

El determinante «abre sumas y saca escalares», pero hay que ser muy cuidadosos, pues no lo hace para toda una matriz, sino sólo renglón a renglón, o columna a columna. Enunciemos esto en las siguientes proposiciones.

Proposición. El determinante saca escalares renglón por renglón o columna por columna. Por ejemplo, pensemos en sacar escalares por renglón. Si $k$ es un número real y tenemos una matriz de la forma
\[
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & & \vdots \\
ka_{i1} & ka_{i2} & \cdots & ka_{in} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix},
\]
entonces
\[
\operatorname{det}
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & & \vdots \\
ka_{i1} & ka_{i2} & \cdots & ka_{in} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}
=
k\operatorname{det}
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
\vdots & \vdots & & \vdots \\
a_{i1} & a_{i2} & \cdots & a_{in} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}.
\]

No podemos dar la demostración muy formalmente, pues necesitamos de más herramientas. Pero puedes convencerte de que esta proposición es cierta pensando en lo que sucede cuando se calcula el determinante recursivamente en la fila $i$. En la matriz de la izquierda, usamos los coeficientes $ka_{i1},\ldots,ka_{in}$ para acompañar a los determinantes de las matrices de $(n-1)\times (n-1)$ que van saliendo. Pero entonces en cada término aparece $k$ y se puede factorizar. Lo que queda es $k$ veces el desarrollo recursivo de la matriz sin las $k$’s en el renglón $i$.

Ejemplo. Calculemos el determinante de la matriz $A=\begin{pmatrix} 2 & 2 & -1 \\ 0 & 2 & 3 \\ -3 & 2 & 1\end{pmatrix}$. En la primera columna hay un $0$, así que nos conviene usar esta columna para encontrar el determinante. Aplicando la regla recursiva, obtenemos que:

\begin{align*}
\det(A)=\begin{vmatrix} 2 & 2 & -1 \\ 0 & 2 & 3 \\ -3 & 2 & 1\end{vmatrix} &= (2) \begin{vmatrix} 2 & 3 \\ 2 & 1 \end{vmatrix} – (0) \begin{vmatrix} 2 & -1 \\ 2 & 1 \end{vmatrix} + (-3) \begin{vmatrix} 2 & -1 \\ 2 & 3 \end{vmatrix}\\
&=2(2\cdot 1 – 3 \cdot 2) – 0 (2 \cdot 1 – (-1)\cdot 2) – 3 (2\cdot 3 – (-1)\cdot 2)\\
&=2(-4)-0(4)-3(8)\\
&=-32.
\end{align*}

¿Qué sucedería si quisiéramos ahora el determinante de la matriz $B=\begin{pmatrix} 2 & 1 & -1 \\ 0 & 1 & 3 \\ -3 & 1 & 1\end{pmatrix}$? Podríamos hacer algo similar para desarrollar en la primera fila. Pero esta matriz está muy relacionada con la primera. La segunda columna de $B$ es $1/2$ veces la segunda columna de $A$. Por la propiedad que dijimos arriba, tendríamos entonces que $$\det(B)=\frac{1}{2}\det(A)=\frac{-32}{2}=-16.$$

$\triangle$

Ejemplo. Hay que tener mucho cuidado, pues el determinante no saca escalares con el producto escalar de matrices. Observa que si $A=\begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}$, entonces $\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} = 2\cdot 1 – 1\cdot 1 = 1$. Sin embargo, $$\det(2A)=\begin{vmatrix} 4 & 2 \\ 2 & 2 \end{vmatrix}=4\cdot 2 – 2 \cdot 2 = 4\neq 2\det(A).$$

En vez de salir dos veces el determinante, salió cuatro veces el determinante. Esto tiene sentido de acuerdo a la propiedad anterior: sale un factor $2$ pues la primera fila es el doble, y sale otro factor $2$ porque la segunda fila también es el doble.

$\square$

Proposición. El determinante abre sumas renglón por renglón, o columa por columna. Por ejemplo, veamos el caso para columnas. Si tenemos una matriz de la forma
\[
\begin{pmatrix}
a_{11} & \cdots & a_{1i} + b_{1i} & \cdots & a_{1n} \\
a_{21} & \cdots & a_{2i} + b_{2i} & \cdots & a_{2n} \\
\vdots & & \vdots & & \vdots \\
a_{n1} & \cdots & a_{ni} + b_{ni} & \cdots & a_{nn}
\end{pmatrix},
\]
entonces este determinante es igual a
\begin{align*}
\operatorname{det}
\begin{pmatrix}
a_{11} & \cdots & a_{1i} & \cdots & a_{1n} \\
a_{21} & \cdots & a_{2i} & \cdots & a_{2n} \\
\vdots & & \vdots & & \vdots \\
a_{n1} & \cdots & a_{ni} & \cdots & a_{nn}
\end{pmatrix}
+
\operatorname{det}
\begin{pmatrix}
a_{11} & \cdots & b_{1i} & \cdots & a_{1n} \\
a_{21} & \cdots & b_{2i} & \cdots & a_{2n} \\
\vdots & & \vdots & & \vdots \\
a_{n1} & \cdots & b_{ni} & \cdots & a_{nn}
\end{pmatrix}.
\end{align*}

Una vez más, no podemos dar una demostración muy formal a estas alturas. Pero como en el caso de sacar escalares, también podemos argumentar un poco informalmente qué sucede. Si realizamos el cálculo de determinantes en la columna $i$, entonces cada término de la forma $a_{ji}+b_{ji}$ acompaña a un determinante $D_{ji}$ de una matriz de $(n-1)\times (n-1)$ que ya no incluye a esa columna. Por ley distributiva, cada sumando es entonces $(a_{ji}+b_{ji})D_{ji}=a_{ji}D_{ji}+b_{ji}D_{ji}$ (acompañado por un $+$ o un $-$). Agrupando en un lado los sumandos con $a_{ji}$’s y por otro los sumandos con $b_{ji}$’s obtenemos la identidad deseada.

Ejemplo. Las matrices $\begin{pmatrix} 5 & 2 \\ 2 & 1 \end{pmatrix}$ y $\begin{pmatrix} 2 & 5 \\ 2 & 1 \end{pmatrix}$ tienen determinantes $1$ y $-8$ respectivamente (verifícalo). De acuerdo a la propiedad anterior, el determinante de la matriz $$\begin{pmatrix} 5 + 2 & 2 + 5 \\ 2 & 1 \end{pmatrix} = \begin{pmatrix} 7 & 7 \\ 2 & 1 \end{pmatrix}$$

debería ser $1 + (-8) = -7$. Y sí, en efecto $7\cdot 1 – 2 \times 7 = -7$.

$\triangle$

Hay que tener mucho cuidado, pues en esta propiedad de la suma las dos matrices tienen que ser iguales en casi todas las filas (o columnas), excepto en una. En esa fila (o columna) es donde se da la suma. En general, no sucede que $\det(A+B)=\det(A)+\det(B)$.

Ejemplo. Puedes verificar que las matrices $A=\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1\end{pmatrix}$ y $B=\begin{pmatrix} -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1\end{pmatrix}$ tienen ambas determinante $1$. Sin embargo, su suma es la matriz de puros ceros, que tiene determinante $0$. Así, $$\det(A)+\det(B)=2\neq 0 = \det(A+B).$$

$\triangle$

El determinante y operaciones elementales

El siguiente resultado nos dice qué sucede al determinante de una matriz cuando le aplicamos operaciones elementales.

Teorema. Sea $A$ una matriz cuadrada.

  • Si $B$ es una matriz que se obtiene de $A$ al reescalar un renglón con el escalar $\alpha$, entonces $\det(B)=\alpha\det(A)$.
  • Si $B$ es una matriz que se obtiene de $A$ al intercambiar dos renglones, entonces $\det(B)=-\det(A)$.
  • Si $B$ es una matriz que se obtiene de $A$ al hacer una transvección, entonces $\det(B)=\det(A)$.

No nos enfocaremos mucho en demostrar estas propiedades, pues se demuestran con más generalidad en el curso de Álgebra Lineal I. Sin embargo, a partir de ellas podemos encontrar un método de cálculo de determinantes haciendo reducción gaussiana.

Teorema. Sea $A$ una matriz cuadrada. Supongamos que para llevar $A$ a su forma escalonada reducida $A_{red}$ se aplicaron algunas transvecciones, $m$ intercambios de renglones y $k$ reescalamientos por escalares no cero $\alpha_1,\ldots,\alpha_k$ (en el orden apropiado). Entonces $$\det(A)=\frac{(-1)^m\det(A_{red})}{\alpha_1\alpha_2\cdots\alpha_k}.$$ En particular:

  • Si $A_{red}$ no es la identidad, entonces $\det(A_{red})=0$ y entonces $\det(A)=0$.
  • Si $A_{red}$ es la identidad, entonces $\det(A_{red})=1$ y entonces $$\det(A)=\frac{(-1)^m}{\alpha_1\alpha_2\cdots\alpha_k}.$$

Veamos un ejemplo.

Ejemplo. Calculemos el determinante de la matriz $A=\begin{pmatrix} 2 & 2 & -2 \\ 0 & 2 & 3 \\ -3 & 2 & 1\end{pmatrix}$ usando reducción gaussiana. Multiplicamos la primera fila por $\alpha_1=1/2$ y la sumamos tres veces a la última (transvección no cambia el determinante):

$$\begin{pmatrix} 1 & 1 & -1 \\ 0 & 2 & 3 \\ 0 & 5 & -2\end{pmatrix}$$

Multiplicamos por $\alpha_2=1/5$ la segunda fila y la intercambiamos con la tercera (va $m=1$).

$$\begin{pmatrix} 1 & 1 & -1 \\ 0 & 1 & -\frac{2}{5} \\ 0 & 2 & 3\end{pmatrix}.$$

Restamos dos veces la segunda fila a la tercera (transvección no cambia el determinante)

$$\begin{pmatrix} 1 & 1 & -1 \\ 0 & 1 & -\frac{2}{5} \\ 0 & 0 & \frac{19}{5}\end{pmatrix},$$

y multiplicamos la tercera fila por $\alpha_3=5/19$:

$$\begin{pmatrix} 1 & 1 & -1 \\ 0 & 1 & -\frac{2}{5}\\ 0 & 0 & 1\end{pmatrix}.$$

Hacemos transvecciones para hacer cero las entradas arriba de la diagonal principal (transvecciones no cambian el determinante): $$\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{pmatrix}.$$

Ya llegamos a la identidad. Los reescalamientos fueron por $1/2$, $1/5$ y $5/19$ y usamos en total $1$ intercambio. Así, $$\det(A)=\frac{(-1)^1}{(1/2)(1/5)(5/19)}=-38.$$

$\triangle$

Es recomendable que calcules el determinante del ejemplo anterior con la regla recursiva de expansión por menores para que verifiques que da lo mismo.

Algunos determinantes especiales

A continuación enunciamos otras propiedades que cumplen los determinantes. Todas estas puedes demostrarlas suponiendo propiedades que ya hemos enunciado.

Proposición. Para cualquier entero positivo $n$ se cumple que la matriz identidad $\mathcal{I}_n$ tiene como determinante $\operatorname{det}(\mathcal{I}_n) = 1$.

Este resultado es un caso particular de una proposición más general.

Proposición. El determinante de una matriz diagonal es igual al producto de los elementos de su diagonal; es decir,
\[
\operatorname{det}
\begin{pmatrix}
a_{11} & 0 & \cdots & 0 \\
0 & a_{22} & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & a_{nn}
\end{pmatrix}
=
a_{11} a_{12} \cdots a_{nn}.
\]

Para probar esta proposición, puedes usar la regla recursiva para hacer la expansión por la última fila (o columna) y usar inducción.

Proposición. $\operatorname{det}(A^T) = \operatorname{det}(A)$.

Este resultado también sale inductivamente. Como los determinantes se pueden expandir por renglones o columnas, entonces puedes hacer una expansión en alguna fila de $A$ y será equivalente a hacer la expansión por columnas en $A^T$.

Proposición. Si $A$ es una matriz invertible, entonces $\operatorname{det}(A^{-1}) = \dfrac{1}{\operatorname{det}(A)}$.

Para demostrar este resultado, se puede usar la proposición del determinante de la identidad, y lo que vimos la entrada pasada sobre que $\det(AB)=\det(A)\det(B)$.

Los argumentos que hemos dado son un poco informales, pero quedará en los ejercicios de esta entrada que pienses en cómo justificarlos con más formalidad.

Ejemplos interesantes de cálculo de determinantes

Las propiedades anteriores nos permiten hacer el cálculo de determinantes de varias maneras (no sólo expansión por menores). A continuación presentamos dos ejemplos que usan varias de las técnicas discutidas arriba.

Ejemplo. Calculemos el siguiente determinante:

$$\begin{vmatrix} 1 & 5 & 3 \\ 2 & 9 & 1 \\ 5 & 4 & 3 \end{vmatrix}.$$

Como aplicar transvecciones no cambia el determinante, podemos restar la primera fila a la segunda, y luego cinco veces la primera fila a la tercera y el determinante no cambia. Así, este determinante es el mismo que

$$\begin{vmatrix} 1 & 5 & 3 \\ 0 & -1 & -5 \\ 0 & -21 & -12 \end{vmatrix}.$$

Multiplicar la segunda fila por $-1$ cambia el determinante en $-1$. Y luego multiplicar la tercera por $-1$ lo vuelve a cambiar en $-1$. Entonces haciendo ambas operaciones el determinante no cambia y obtenemos que el determinante es igual a

$$\begin{vmatrix} 1 & 5 & 3 \\ 0 & 1 & 5 \\ 0 & 21 & 12 \end{vmatrix}.$$

En esta matriz podemos expandir por la primera columna en donde hay dos ceros. Por ello, el determinante es

$$\begin{vmatrix} 1 & 5 \\ 21 & 12 \end{vmatrix}= (1\cdot 12) – (5 \cdot 21) = -93.$$

$\triangle$

Ejemplo. Calculemos el siguiente determinante:

$$\begin{vmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ 3 & 4 & 1 & 2 \\ 4 & 1 & 2 & 3 \end{vmatrix}.$$

Hacer transvecciones no cambia el determinante, entonces podemos sumar todas las filas a la última sin alterar el determinante. Como $1+2+3+4=10$, obtenemos:

$$\begin{vmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ 3 & 4 & 1 & 2 \\ 10 & 10 & 10 & 10 \end{vmatrix}.$$

Ahora, la última fila tiene un factor $10$ que podemos factorizar:

$$10\cdot \begin{vmatrix} 1 & 2 & 3 & 4 \\ 2 & 3 & 4 & 1 \\ 3 & 4 & 1 & 2 \\ 1 & 1 & 1 & 1 \end{vmatrix}.$$

Ahora, podemos restar la primera columna a todas las demás, sin cambiar el determinante:

$$10\cdot \begin{vmatrix} 1 & 1 & 2 & 3 \\ 2 & 1 & 2 & -1 \\ 3 & 1 & -2 & 1 \\ 1 & 0 & 0 & 0 \end{vmatrix}.$$

Luego, podemos sumar la segunda fila a la tercera sin cambiar el determinante:

$$10\cdot \begin{vmatrix} 1 & 1 & 2 & 3 \\ 2 & 1 & 2 & -1 \\ 5 & 2 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{vmatrix}.$$

Expandiendo por la última fila:

$$-10\cdot \begin{vmatrix} 1 & 2 & 3 \\ 1 & 2 & -1 \\ 2 & 0 & 0 \end{vmatrix}.$$

Expandiendo nuevamente por la última fila:

$$-10 \cdot 2 \cdot \begin{vmatrix} 2 & 3 \\ 2 & -1 \end{vmatrix}.$$

El determinante de $2\times 2$ que queda ya sale directo de la fórmula como $2\cdot (-1)-3\cdot 2 = -8$. Así, el determinante buscado es $(-10)\cdot 2 \cdot (-8)=160$.

$\triangle$

Más adelante…

Los determinantes son una propiedad fundamental de las matrices. En estas entradas apenas comenzamos a platicar un poco de ellos. Por un lado, son muy importantes algebraicamente pues ayudan a decidir cuándo una matriz es invertible. Se pueden utilizar para resolver sistemas de $n$ ecuaciones lineales en $n$ incógnitas con algo conocido como la regla de Cramer. Por otro lado, los determinantes también tienen una interpretación geométrica que es sumamente importante en geometría analítica y en cálculo integral de varias variables. En cursos posteriores en tu formación matemática te los seguirás encontrando.

Tarea moral

  1. Calcula el siguiente determinante: $$\begin{vmatrix} 1 & 1 & 1 & 1 \\ 2 & 0 & 2 & 2 \\ 0 & 3 & 3 & 0 \\ 0 & 0 & 4 & 0 \end{vmatrix}.$$ Intenta hacerlo de varias formas, aprovechando todas las herramientas que hemos discutido en esta entrada.
  2. También se pueden obtener determinantes en matrices en donde hay variables en vez de escalares. Encuentra el determinante de la matriz $$\begin{pmatrix} a & b & c \\ b & c & a \\ c & a & b \end{pmatrix}.$$
  3. Encuentra todas las matrices $A$ de $2\times 2$ que existen tales que $$\det(A+I_2)=\det(A)+1.$$
  4. Demuestra todas las propiedades de la sección de «Algunos determinantes especiales». Ahí mismo hay sugerencias de cómo puedes proceder.
  5. Revisa las entradas Álgebra Lineal I: Técnicas básicas de cálculo de determinantes y Seminario de Resolución de Problemas: Cálculo de determinantes para conocer todavía más estrategias y ejemplos de cálculo de determinantes.

Entradas relacionadas

Cálculo Diferencial e Integral III: Introducción al teorema de la función inversa

Por Alejandro Antonio Estrada Franco

Deja un comentario

Introducción

Estamos a punto de entrar a discutir dos de los resultados principales de nuestro curso: el teorema de la función inversa y el teorema de la función implícita. Repasemos un poco qué hemos hecho hasta ahora. En las dos entradas anteriores introdujimos la noción de diferenciabilidad, la cual cuando sucede para una función $f:\mathbb{R}^n\to \mathbb{R}^m$, nos dice que $f$ se parece mucho a una función lineal en un punto dado. Vimos que esta noción implica continuidad y que tiene una regla de la cadena relacionada con el producto de matrices. También, hemos discutido cómo esta noción se relaciona con la existencia de espacios tangentes a gráficas multidimensionales.

Ahora queremos entender todavía mejor a las funciones diferenciables. Hay dos teoremas que nos permiten hacer eso. Uno es el teorema de la función inversa y el otro es el teorema de la función implícita. En esta entrada hablaremos del primero, y en un par de entradas más introduciremos el segundo resultado. El propósito del teorema de la función inversa es dar una condición bajo la cual una función es invertible, por lo menos localmente. De hecho, la mayoría de las veces sólo se puede garantizar la invertibilidad localmente, pues las funciones usualmente no son inyectivas y esto da comportamientos globales más difíciles de manejar.

Enunciar el teorema y entenderlo requiere de cierto esfuerzo. Y demostrarlo todavía más. Por esta razón, en esta entrada nos enfocaremos sólo en dar el teorema y presentar herramientas preliminares que necesitaremos para hacer su demostración.

Enunciado del teorema de la función inversa

Supongamos que tenemos $f:\mathbb{R}^n\to \mathbb{R}^n$ y que es diferenciable en el punto $\bar{a}$. Entonces, $f$ se parece mucho a una función lineal en $\bar{a}$, más o menos $f(\bar{x})\approx f(\bar{a}) + T_{\bar{a}}(\bar{x}-\bar{a})$. Así, si $T_{\bar{a}}$ es invertible, suena a que «cerquita de $\bar{a}$» la función $f(\bar{x})$ debe de ser invertible. El teorema de la función inversa pone estas ideas de manera formal.

Teorema (de la función inversa). Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el abierto $S$. Si la matriz $Df(\bar{a})$ es invertible, entonces, existe $\delta >0$ tal que:

  1. $B_{\delta}(\bar{a})\subseteq S$ y $f$ es inyectiva en $B_{\delta}(\bar{a})$.
  2. $f^{-1}:f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ es continua en $f(B_{\delta}(\bar{a}))$.
  3. $f(B_{\delta}(\bar{a}))\subseteq \mathbb{R}^{n}$ es un conjunto abierto.
  4. $f^{-1}$ es de clase $C^{1}$ en $f(B_{\delta}(\bar{a}))$ y además, si $\bar{x}=f(\bar{v})\in f(B_{\delta}(\bar{a}))$, entonces, $Df^{-1}(\bar{x})=Df^{-1}(f(\bar{v}))=(Df(\bar{v}))^{-1}$.

Veamos qué nos dice de manera intuitiva cada una de las conclusiones del teorema.

  1. Tendremos una bola $B_\delta(\bar{a})$ dentro de la cual $f$ será inyectiva, y por lo tanto será biyectiva hacia su imagen. Así, $f$ restringida a esta bola será invertible. Es importante que sea una bola abierta, porque entonces sí tenemos toda una región «gordita» en donde pasa la invertibilidad (piensa que si fuera un cerrado, a lo mejor sólo es el punto $\bar{a}$ y esto no tiene chiste).
  2. La inversa $f^{-1}$ que existirá para $f$ será continua. Esto es lo mínimo que podríamos esperar, aunque de hecho el punto $4$ garantiza algo mucho mejor.
  3. La imagen de $f$ en la bola $B_\delta(\bar{a})$ será un conjunto abierto.
  4. Más aún, se tendrá que $f^{-1}$ será de clase $C^1$ y se podrá dar de manera explícita a su derivada en términos de la derivada de $f$ con una regla muy sencilla: simplemente la matriz que funciona para derivar $f$ le sacamos su inversa como matriz y esa funciona al evaluarla en el punto apropiado.

El teorema de la función inversa es profundo pues tanto su enunciado como su demostración combina ideas de topología, álgebra y cálculo. Por esta razón, para su demostración necesitaremos recopilar varias de las herramientas de álgebra lineal que hemos repasado en la Unidad 2 y la Unidad 5. Así mismo, necesitaremos ideas topológicas de las que hemos visto en la Unidad 3. Con ellas desarrollaremos algunos resultados auxiliares que en la siguiente entrada nos permitirán concluir la demostración.

Un criterio para campos vectoriales $C^1$

El teorema de la función inversa es para funciones de clase $C^1$. Nos conviene entender esta noción mejor. Cuando una función $f$ es de clase $C^1$, entonces es diferenciable. Pero el regreso no es cierto y hay contraejemplos. ¿Qué le falta a una función diferenciable para ser de clase $C^1$? A grandes rasgos, que las funciones derivadas $T_\bar{a}$ y $T_\bar{b}$ hagan casi lo mismo cuando $\bar{a}$ y $\bar{b}$ son cercanos. En términos de matrices, necesitaremos que la expresión $||(Df(\bar{a})-Df(\bar{b}))(\bar{x})||$ sea pequeña cuando $\bar{a}$ y $\bar{b}$ son cercanos entre sí.

El siguiente teorema será importante en nuestro camino hacia el teorema de la función inversa. Intuitivamente, para lo que lo usaremos es para aproximar una función $f$ localmente, con «cuadritos» que corresponden a los planos tangentes, porque «muy cerquita» estos planos varían muy poco si pedimos que $f$ sea de clase $C^1$. Es decir si $\bar{a}$ y $\bar{b}$ son dos puntos en el dominio de una función diferenciable, y estos están muy cerca uno del otro, sus planos tangentes serán casi el mismo. Esto nos invita a cambiar localmente a una superficie por cuadritos como más adelante se explicará con detalle.

Figura 1. En azul y en rojo dos planos que corresponden a las derivadas $T_{\bar{a}}$ y $T_{\bar{b}}$. Este cambio calculado es distintos puntos cercanos es «suave», esto se expresará con la ecuación $||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\leq \epsilon ||\bar{x}||$ ya con las diferenciales para todo $\bar{x}$.

El teorema concreto que nos interesa demostrar es la siguiente equivalencia para que una función sea de clase $C^1$.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{m}$ una función diferenciable en $S$. Se tiene que $f$ es de clase $C^{1}$ en $S$ si y sólo si para todo $\bar{a}\in S$ y para cada $\varepsilon >0$ existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y si $\bar{b}\in B_{\delta}(\bar{a})$ se tiene $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq \varepsilon ||\bar{x}||$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. $\Rightarrow).$ Supongamos que $f$ es de clase $C^1$ en $S$, es decir, todas sus funciones componentes tienen derivadas parciales en $S$ y son continuas. Sea $\varepsilon>0$. Veremos que se puede encontrar una $\delta$ como en el enunciado.

Tomemos $\bar{a}$ y $\bar{b}$ en $S$. Expresamos a $(Df(\bar{b})-Df(\bar{a}))(\bar{x})$ como

\begin{align*}
\begin{pmatrix} \frac{\partial f_{1}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{1}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{n}}(\bar{a}) \\ \vdots & \ddots & \dots \\ \frac{\partial f_{m}}{\partial x_{1}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{1}}(\bar{a}) & \dots & \frac{\partial f_{m}}{\partial x_{n}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{n}}(\bar{a}) \end{pmatrix}\begin{pmatrix} x_{1} \\ \vdots \\ x_{n}\end{pmatrix}
\end{align*}

o equivalentemente como

\begin{align*}
\begin{pmatrix} \left( \triangledown f_{1}(\bar{b})-\triangledown f_{1}(\bar{a})\right) \cdot \bar{x} \\ \vdots \\ \left( \triangledown f_{m}(\bar{b})-\triangledown f_{m}(\bar{a})\right) \cdot \bar{x} \end{pmatrix}.
\end{align*}

De tal manera que por Cauchy-Schwarz:

\begin{align*}
||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2&=\sum_{i=1}^m (\left( \triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})\right)\cdot \bar{x})^2\\
&\leq \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2||\bar{x}||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m ||\triangledown f_{i}(\bar{b})-\triangledown f_{i}(\bar{a})||^2\\
&=||\bar{x}||^2 \sum_{i=1}^m \sum_{j=1}^{n}\left( \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a})\right) ^{2}
\end{align*}

En este punto se ve la importancia de que las parciales sean continuas. Podemos encontrar una $\delta$ que nos garantice que $B_\delta\subseteq S$ y que si $||\bar{b}-\bar{a}||<\delta$, entonces $$\left| \frac{\partial f_{i}}{\partial x_{j}}(\bar{b})-\frac{\partial f_{i}}{\partial x_{j}}(\bar{a}) \right| < \frac{\varepsilon}{\sqrt{mn}}.$$ En esta situación, podemos seguir acotando $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||^2$ como sigue:
\begin{align*}
&\leq ||\bar{x}|| \sum_{i=1}^m \sum_{j=1}^{n}\frac{\varepsilon^2}{mn}\\
&=\varepsilon^2||\bar{x}||^2.
\end{align*}

Al sacar raiz cuadrada, obtenemos la desigualdad $$||(Df(\bar{b})-Df(\bar{a}))(x)||\leq \varepsilon||\bar{x}||$$ buscada.

$\Leftarrow).$ Supongamos ahora que para cada $\varepsilon$ existe una $\delta$ como en el enunciado del teorema. Debemos ver que todas las derivadas parciales de todas las componentes son continuas. Podemos aplicar la desigualdad $||(Df(\bar{b})-Df(\bar{a}))(\bar{x})||\leq ||\bar{x}||\varepsilon$ tomando como $\bar{x}$ cada vector $\hat{e}_i$ de la base canónica. Esto nos dice que

\[ ||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||< \varepsilon||\hat{e}_i|| =\varepsilon.\]

Por nuestro desarrollo anterior, para cada $i$ tenemos

\begin{align*}
\varepsilon&>||Df(\bar{b})(\hat{e}_i)-Df(\bar{a})(\hat{e}_i)||\\
&=||\left( \triangledown f_{1}(\bar{b})\cdot \hat{e}_i-\triangledown f_{1}(\bar{a})\cdot \hat{e}_i,\dots ,\triangledown f_{m}(\bar{b})\cdot \hat{e}_i-\triangledown f_{m}(\bar{a})\cdot \hat{e}_i\right)||\\
&=\left| \left|\left( \frac{\partial f_{1}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{1}}{\partial x_{i}}(\bar{a}),\dots ,\frac{\partial f_{m}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{m}}{\partial x_{i}}(\bar{a})\right) \right| \right|\\
&= \sqrt{\sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right)^{2}}.
\end{align*}

Elevando al cuadrado,

\[ \sum_{j=1}^{m}\left(\frac{\partial f_{j}}{\partial x_{i}}(b)-\frac{\partial f_{j}}{\partial x_{i}}(a)\right)^{2}<\varepsilon ^{2}.\]

Como todos los términos son no negativos, cada uno es menor a $\epsilon^2$. Así, para cada $i,j$ tenemos

\[ \left|\frac{\partial f_{j}}{\partial x_{i}}(\bar{b})-\frac{\partial f_{j}}{\partial x_{i}}(\bar{a})\right|<\varepsilon.\]

Esto es precisamente lo que estábamos buscando: si $\bar{b}$ está lo suficientemente cerca de $\bar{a}$, cada derivada parcial en $\bar{b}$ está cerca de su correspondiente en $\bar{a}$.

$\square$

Invertibilidad de $Df(\bar{a})$ en todo un abierto

En esta sección demostraremos lo siguiente. Si $f:\mathbb{R}^n\to \mathbb{R}^n$ es un campo vectorial diferenciable en $\bar{a}$ y $Df(\bar{a})$ es invertible, entonces $Df(\bar{x})$ será invertible para cualquier $\bar{x}$ alrededor de cierta bola abierta alrededor de $\bar{a}$. Los argumentos en esta ocasión están un poco más relacionados con el álgebra lineal.

Será útil que recuerdes que una transformación lineal $T:\mathbb{R}^n \to \mathbb{R}^n$ es invertible si el único $\bar{x}\in \mathbb{R}^n$ tal que $T(\bar{x})=\bar{0}$ es $\bar{x}=\bar{0}$. El siguiente criterio es otra caracterización de invertibilidad en términos de lo que le hace $T$ a la norma de los vectores.

Teorema. Sea $T:\mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una transformación lineal. La transformación $T$ es invertible si y sólo si existe $\varepsilon >0$ tal que $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. $\left. \Rightarrow \right)$ Como $T$ es invertible, para todo $\bar{x}\neq \bar{0}$ sucede que $T(\bar{x})\neq \bar{0}$. En particular, esto sucede para todos los vectores en $S^{n-1}$ (recuerda que es la esfera de radio $1$ y dimensión $n-1$ centrada en $\bar{0}$). Esta esfera es compacta y consiste exactamente de los $\bar{x}\in \mathbb{R}^n$ de norma $1$.

Sabemos que las transformaciones lineales y la función norma son continuas. Por la compacidad de $S^{n-1}$, la expresión $||T(\bar{x})||$ tiene un mínimo digamos $\varepsilon$, que alcanza en $S^{n-1}$. Por el argumento del párrafo anterior, $\varepsilon>0$.

Tomemos ahora cualquier vector $\bar{x}\in \mathbb{R}^n$. Si $\bar{x}=\bar{0}$, entonces $$||T(\bar{0})||=||\bar{0}||=0\geq \varepsilon ||\bar{0}||.$$ Si $\bar{x}\neq \bar{0}$, el vector $\frac{\bar{x}}{||\bar{x}||}$ está en $S^{n-1}$, de modo que $$\left|\left|T\left(\frac{\bar{x}}{||\bar{x}||}\right)\right|\right| \geq \varepsilon.$$ Usando linealidad para sacar el factor $||\bar{x}||$ y despejando obtenemos $$||T(\bar{x})||\geq \varepsilon ||\bar{x}||,$$ como estábamos buscando.

$\left. \Leftarrow \right)$ Este lado es más sencillo. Si existe dicha $\varepsilon >0$, entonces sucede que para $\bar{x}$ en $\mathbb{R}^n$, con $\bar{x}\neq \bar{0}$ tenemos $$||T(\bar{x})||\geq \varepsilon||\bar{x}||>0.$$ Por lo tanto, $T(\bar{x})\neq \bar{0}$ y así $T$ es invertible.

$\square$

Obtengamos una consecuencia del teorema de clasificación de la sección anterior que está muy relacionada con este resultado que acabamos de demostrar.

Teorema. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ de clase $C^{1}$ en el conjunto abierto $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces existen $\delta >0$ y $m>0$ tales que $B_{\delta}(\bar{a})\subseteq S$ y $||Df(\bar{b})(\bar{x})||\geq m||\bar{x}||$, para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.

Demostración. Como $Df(\bar{a})$ es invertible, por el teorema que acabamos de demostrar existe $\varepsilon’>0$ tal que $$||Df(\bar{a})(\bar{x})||\geq \varepsilon’||\bar{x}||$$ para todo $\bar{x}\in \mathbb{R}^{n}$.

Por nuestra caracterización de funciones $C^1$, Ahora como $f\in C^{1}$ en $S$ (abierto) para $\varepsilon =\frac{\varepsilon’}{2}>0$, existe $\delta >0$ tal que $B_{\delta}(\bar{a})\subseteq S$, y $||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\leq \frac{\varepsilon’}{2}||\bar{x}||$ para todo $\bar{b}\in B_{\delta}(\bar{a})$ y para todo $\bar{x}\in \mathbb{R}^{n}$.

Por la desigualdad del triángulo, \[ ||Df(\bar{a})(\bar{x})-Df(\bar{b})(\bar{x})||+||Df(\bar{b})(\bar{x})||\geq ||Df(\bar{a})(\bar{x})||,\]

de donde

\begin{align*}
||Df(\bar{b})(\bar{x})||&\geq ||Df(\bar{a})(\bar{x})||-||Df(\bar{b})(\bar{x})-Df(\bar{a})(\bar{x})||\\
&\geq \varepsilon’||\bar{x}||-\frac{\varepsilon’}{2}||\bar{x}||\\
&= \frac{\varepsilon’}{2} ||\bar{x}||.
\end{align*}

De esta manera, el resultado es cierto para la $\delta$ que dimos y para $m=\frac{\varepsilon’}{2}$.

$\square$

El siguiente corolario es consecuencia inmediata de lo discutido en esta sección y está escrito de acuerdo a la aplicación que haremos más adelante en la demostración del teorema de la función inversa.

Corolario. Sea $f:S\subseteq \mathbb{R}^{n}\rightarrow \mathbb{R}^{n}$ una función de clase $C^{1}$ en $S$ y $\bar{a}\in S$. Si $Df(\bar{a})$ es invertible, entonces, existe $\delta > 0$ tal que $B_{\delta}(\bar{a})\subseteq S$ y $Df(\bar{b})$ es invertible para todo $\bar{b}\in B_{\delta}(\bar{a})$.

Queda como tarea moral responder por qué este corolario es consecuencia inmediata del teorema anterior.

Un poco de intuición geométrica

Dejamos esta entrada hasta aquí, la naturaleza densamente teórica de lo que estamos haciendo puede hacer pesadas las exposiciones. Lo que hasta aquí demostramos es que para un campo vectorial $C^1$ si su derivada en $\bar{a}$ es invertible, entonces lo es en toda una vecindad que tiene a $\bar{a}$. Imaginemos al pedacito de superficie $f(B_{\delta}(\bar{a}))$ cubierto con pequeños rectángulos. En cada punto, las imágenes de estos rectángulos están muy cerquita, casi pegados a la superficie. Esto nos garantizaría la invertibilidad de $f$ en esta vecindad.

Figura 2

En la Figura 2 vemos ilustrado esto. El círculo inferior corresponde a la vecindad $B_{\delta}(\bar{a})$ en el dominio de $f$. La función $f$ levanta una porción del plano en la sabana delineada con negro arriba del círculo. En el círculo tenemos al punto $\bar{a}$ en verde agua. Sobre la sábana de arriba tenemos con el mismo color a $f(\bar{a})$. Los puntos negros pequeños dentro de la vecindad alrededor de $\bar{a}$ son alzados por $f$ a puntos negros sobre la sabana. Sobre de cada punto negro en la sabana tenemos un cuadrito rojo que representa al cachito de plano tangente cerca de la imagen de cada punto. La imagen esta llena de estos pequeños cuadritos, todos ellos representan diferenciales invertibles, esto nos permitirá asegurar la invertibilidad de $f$ en al menos una vecindad.

Más adelante…

En la siguiente entrada demostraremos el teorema de la función inversa, inciso por inciso. Es importante que estes familiarizado con los resultados de esta entrada, pues serán parte importante de la demostración.

Tarea moral

  1. ¿Qué diría el teorema de la función inversa para campos vectoriales $f:\mathbb{R}^2\to \mathbb{R}^2$? ¿Se puede usar para $$f(r,\theta)=(r\cos(\theta),r\sin(\theta))?$$ Si es así, ¿para qué valores de $r$ y $\theta$? ¿Qué diría en este caso explícitamente?
  2. Explica por qué el corolario que enunciamos en efecto se deduce de manera inmediata de lo discutido en la sección correspondiente.
  3. Revisa todas las desigualdades que usamos en esta entrada. ¿Qué resultado estamos usando? ¿Cuándo se darían estas igualdades?
  4. Demuestra que el determinante de una matriz es una función continua en términos de las entradas de la matriz. Usa esto para demostrar que si $A\in M_n(\mathbb{R})$ es una matriz y $B$ es una matriz muy cercana a $A$, entonces $B$ también es invertible.
  5. Demuestra que si una transformación $T$ es diagonalizable, entonces en el teorema de caracterización de invertibilidad se puede usar como $\epsilon$ al mínimo de la expresión $|\lambda|$ variando sobre todos los eigenvalores $\lambda$ de $T$.

Entradas relacionadas

Álgebra Superior I: Funciones invertibles

Por Guillermo Oswaldo Cota Martínez

1 respuesta

Introducción

Anteriormente vimos el concepto de composición entre funciones, que nos permiten saltar entre varios conjuntos de manera sencilla, revisamos algunas de sus propiedades y dimos algunos ejemplos. Ahora nos toca profundizar un poco más en la composición de funciones analizando un caso particular de funciones: las invertibles. Que en términos simples nos permiten deshacer los efectos de las operaciones.

Revirtiendo las cosas.

Pensemos por un momento en un cubo rubik, hay distintas técnicas para armarlo, pero por ahora nos enfocaremos en sus movimientos. La forma en que se usa el cubo, es moviendo sus caras hasta que todas las caras tengan un solo color. Imagina que tienes un cubo en tus manos, si mueves la cara que está hasta arriba, tienes dos formas de hacerlo, girar en sentido de las manecillas del reloj y girar en sentido contrario a las manecillas del reloj. No pasa nada si no estás seguro de tu movimiento, pues siempre puedes deshacer un movimiento rotando la misma cara que volteaste en sentido contrario. Incluso si mueves varias caras, podrás regresar al estado original si recuerdas exactamente las caras que volteaste y la dirección, pues para deshacer los movimientos, tendrás que empezar por la última cara que volteaste y deberás girarla al sentido contrario al que le diste vuelta. Por ejemplo esta imagen indica dos movimientos a las caras y la forma de «deshacer» los movimientos.

En la imagen también marcamos los movimientos de mover las dos caras como $f$, por ahora imagínate que ese movimiento de girar las dos caras como lo muestra la imagen, se llama el movimiento $f$. Mientras que el movimiento de deshacerlas se llama $f^{-1}$. Entonces si realizamos primero el movimiento $f$, el movimiento $f^{-1}$ revierte lo que hizo la primera, volviendo al estado inicial. Así es como vamos a pensar en la reversibilidad de las funciones, una manera de «volver a armar» el cubo.

Funciones reversibles

Diremos que una función es reversible si existe una función $f^{-1}:Im(f) \rightarrow X$ tal que $f ^{-1}\circ f = Id$ donde $Id$ es la función identidad, es decir, es la única función que asigna a cada elemento a sí mismo, es decir $Id(x)=x$.

Algunas observaciones de las funciones invertibles. Sea $f:X \rightarrow Y$ una función invertible, entonces:

  • $f$ es inyectiva.

Demostración. Supongamos que no es inyectiva, entonces existen $x_1,x_2 \in X$ distintos tales que $f(x_1) = f(x_2)$. Como $f$ es invertible, entonces existe su función inversa $f^{-1}:Im(f) \rightarrow X$, en donde $$x_1 = f^{-1} \circ f(x_1) = f^{-1} \circ f(x_2) = x_2 $$ Siendo esta una contradicción, pues supusimos que eran distintos elementos. Así, la función es inyectiva.

$\square$

  • $f^{-1}$ es inyectiva.

Demostración. De manera similar a la demostración anterior, si $y_1,y_2 \in Dom(f^{-1})$ son tales que $f^{-1}(y_1) = f^{-1}(y_2)$, se tiene que al ser $f$ inyectiva, $$f(f^{-1}(y_1)) = f(f^{-1}(y_2)) \Rightarrow y_1=y_2$$ Llegando a que $f^{-1}$ es inyectiva.

$\square$

Así, te puedes dar una idea de lo que significan las funciones invertibles. Con estas proposiciones hemos probado además que la función $f^{-1}: Im(f) \rightarrow X$ es una biyección. ¿Te imaginas porqué? Pues resulta que la función $f^{-1}$ también es suprayectiva.

  • $f^{-1} \circ f = f \circ f^{-1}$

Demostración. Sabemos que $f^{-1} \circ f = Id$, entonces bastará demostrar que $f \circ f^{-1} = Id$. Para ello consideremos $y \in Dom(f^{-1})=Im(f) \subset Y$. Supongamos que $$f \circ f^{-1}(y)=w$$. Entonces $$f^{-1}(f \circ f^{-1}(y)) = f^{-1}(w). $$ Como la composición es asociativa, entonces: $$f^{-1}(f \circ f^{-1}(y)) = (f^{-1} \circ f) \circ f^{-1}(y) = f^{-1}(y) = f^{-1}(w)$$ Como $f^{-1}$ es inyectiva, entonces $y=w$.

$\square$

  • Sea $g:Im(f) \rightarrow Z$ una función invertible, entonces $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$ .

Demostración. Basta notar que por la asociatividad de las funciones:

$$ \begin{align*}
(g \circ f) \circ (f^{-1} \circ g^{-1}) &= g \circ (f \circ (f^{-1} \circ g^{-1})\\
&= g \circ ((f \circ f^{-1}) \circ g^{-1})\\
&= g \circ (Id \circ g^{-1}) \\
&= g \circ g^{-1} = Id
\end{align*}$$

$\square$

Más adelante…

Habiendo pasado por las funciones, su composición, sus propiedades y la inversa, utilizaremos estas definiciones para hablar de el tamaño de los conjuntos. Pues esta definición de funciones nos ayudan a decir «Cuántos elementos tiene un conjunto».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Demuestra que $f^{-1}$ es suprayectiva.
  2. Demuestra que $Dom(f^{-1})=Im(f)$.
  3. Demuestra que $(f \circ (g \circ h))^{-1} = h^{-1} \circ (g^{-1} \circ f^{-1})$.
  4. Da una condición suficiente para que una función no sea invertible.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Inversas de matrices de 2×2 con reducción gaussiana

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Es posible que sepas que una matriz $$A=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}$$de $2\times 2$ es invertible si y sólo si $ad-bc=0$, y que en ese caso la inversa está dada por $$B=\frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}.$$ De hecho, una vez que se propone a $B$ como esta matriz, es sencillo hacer la multiplicación de matrices y verificar que en efecto tanto $AB$ como $BA$ son la matriz identidad de $2\times 2$.

Sin embargo, la idea de esta entrada es deducir que $ad-bc$ tiene que ser distinto de $0$ para que $A$ sea invertible y que, en ese caso, la inversa tiene que ser de la forma que dijimos. En esta deducción no usaremos nunca la definición ni propiedades de determinantes.

El procedimiento

Lo que haremos es aplicar el procedimiento de reducción gaussiana para encontrar inversas, es decir, le haremos reducción gaussiana a la matriz $A’=\begin{pmatrix}
a & b & 1 & 0\\
c & d & 0 & 1
\end{pmatrix}$ obtenida de «pegar» a la matriz $A$ una matriz identidad a su derecha. Es un resultado conocido que si $A$ es invertible, entonces al terminar la reducción gaussiana de $A’$ la matriz de $2\times 2$ que queda a la izquierda será la identidad y la que quede a la derecha será la inversa de $A$.

Empecemos con una matriz $A=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}$ de $2\times 2$ cualquiera. Si ambos $a$ y $c$ son iguales a $0$, entonces la primer columna de $BA$ es $0$ para toda $B$, y por lo tanto $A$ no puede tener inversa. Así, una primera condición para que $A$ tenga inversa es que $a$ o $c$ sean distintos de cero. Si $a$ fuera $0$, el primer paso de reducción gaussiana sería intercambiar las filas, así que podemos suponer sin pérdida de generalidad que $a$ no es $0$. De este modo, el primer paso de reducción gaussiana es multiplicar la primer fila por $1/a$ para que el pivote sea $1$: $$\begin{pmatrix}
1 & \frac{b}{a}& \frac{1}{a} & 0\\
c & d & 0 & 1
\end{pmatrix}$$

El siguiente paso es hacer al resto de las entradas en la columna de ese primer pivote iguales a $0$. Para eso basta restar a la segunda fila $c$ veces la primera:

$$\begin{pmatrix}
1 & \frac{b}{a}& \frac{1}{a} & 0\\
0 & d – \frac{bc}{a} & -\frac{c}{a} & 1
\end{pmatrix}=\begin{pmatrix}
1 & \frac{b}{a}& \frac{1}{a} & 0\\
0 & \frac{ad-bc}{a} & -\frac{c}{a} & 1
\end{pmatrix}.$$

Si $ad-bc=0$, entonces el pivote de la segunda fila ya no quedaría en la segunda columna, y la forma escalonada reducida no tendría a la identidad a la izquierda. Así que una segunda condición para que $A$ sea invertible es que $ad-bc$ no sea cero. Notemos que si $ad-bc$ no es cero, entonces tampoco $a$ y $c$ son simultaneamente $0$, así que nuestra condición anterior ya está capturada con pedir que $ad-bc$ no sea cero.

Sabiendo que $ad-bc$ no es cero, el siguiente paso en la reducción gaussiana es multiplicar la segunda fila por $a/(ad-bc)$ para hacer el pivote igual a $1$:

$$\begin{pmatrix}
1 & \frac{b}{a}& \frac{1}{a} & 0\\
0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{pmatrix}.$$

Finalmente, para que el pivote de la segunda columna sea la única entrada no cero, tenemos que restar a la primera fila la segunda multiplicada por $-b/a$:

$$\begin{pmatrix}
1 & 0 & \frac{1}{a}+\frac{bc}{a(ad-bc)} & -\frac{b}{ad-bc}\\
0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{pmatrix}=\begin{pmatrix}
1 & 0 & \frac{d}{ad-bc} & -\frac{b}{ad-bc}\\
0 & 1 & -\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{pmatrix}.$$

Así, basta pedir $ad-bc$ para que la reducción gaussiana deje a la identidad en la matriz de $2\times 2$ de la izquierda y, al terminar el procedimiento, tenemos a la derecha a la inversa de $A$ que es la matriz:

$$\begin{pmatrix}
\frac{d}{ad-bc} & -\frac{b}{ad-bc}\\
-\frac{c}{ad-bc} & \frac{a}{ad-bc}
\end{pmatrix}=\frac{1}{ad-bc}\begin{pmatrix}
d & -b\\
-c & a
\end{pmatrix}.$$

Esto es a lo que queríamos llegar. Por supuesto, el camino fue largo y hay formas de llegar al mismo resultado de manera más corta, pero usando más teoría.

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario: