Mariposa de 7 equivalencias de matrices invertibles

2 respuestas

Introducción

Una de las nociones más importantes en álgebra lineal es la de «matriz invertible». Llamemos I_n a la matriz identidad de n\times n, es decir, a la que tiene 1 en cada entrada de la diagonal principal, y 0 en las demás.

Una matriz A de n\times n es invertible si existe una matriz B de n\times n tal que AB=I_n=BA.

Una consecuencia rápida es que dicha matriz B es única, así que le podemos dar la notación A^{-1}. De la definición (y asociatividad) se puede ver rápido que si A_1 y A_2 son invertibles, entonces su producto A_1A_2 también, con inversa A_2^{-1}A_1^{-1}, en otras palabras, «producto de invertibles es invertible».

Un detalle curioso de la definición es que pide no sólo que AB=I_n, sino que para la misma matriz B también se tenga que BA=I_n. Por un lado, a priori esto tiene sentido pues el producto de matrices no es conmutativo, es decir, ocurre a veces que AB\neq BA. Sin embargo, como veremos más adelante en esta entrada, en la definición de matriz invertible basta con tener una de estas igualdades.

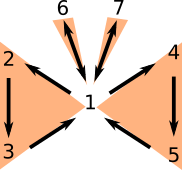
De hecho, la idea de esta entrada es presentar y demostrar varias equivalencias a la afirmación «A es una matriz invertible». La presentación sigue un poco el orden de ideas del capítulo 3.4 del libro Essential Linear Algebra with Applications: A Problem-Solving Approach de Titu Andreescu. La idea es explicar el siguiente diagrama, en donde agrupamos a las equivalencias en grupitos que corresponden a partes de una mariposa:

Algunas definiciones

Antes de enunciar el resultado principal, conviene recordar algunas definiciones y un par de resultados importantes.

Una operación elemental es aplicar a una matriz de las siguientes operaciones:

  • Intercambio de dos filas.
  • Multiplicar todas las entradas de alguna de sus filas por un elemento c no cero.
  • Sumar a una fila un múltiplo de otra fila.

Una matriz elemental es una matriz obtenida de aplicar a I_n exactamente una operación elemental.

Una fila de una matriz es una fila cero si todas sus entradas son iguales a cero. A la primer entrada no cero (de izquierda a derecha) de una fila que no sea fila cero se le llama pivote. Una matriz es escalonada reducida si cumple las siguientes tres propiedades:

  1. Todas las filas cero están hasta abajo.
  2. En todas las filas no cero los pivotes son iguales a 1.
  3. Si una fila no cero F_1 está arriba de otra fila no cero F_2, entonces el pivote de F_1 está estrictamente a la izquierda del pivote de F_2.
  4. Si una entrada tiene al pivote de una fila, entonces todas las demás entradas de la columna son iguales a 0.

Un resultado (no trivial) es que cualquier matriz se puede llevar a una (y sólo una) matriz escalonada reducida A_{\text{red}} usando únicamente operaciones elementales, a la cual le llamamos su forma escalonada reducida. Estas son todas las definiciones que necesitamos. Estamos listos para pasar al enunciado del teorema principal.

Teorema de la mariposa de equivalencias

Teorema: Sea A una matriz de n\times n con entradas en un campo F. Entonces, todas las siguientes afirmaciones son equivalentes:

  1. A es una matriz invertible.
  2. La forma escalonada reducida A_{\text{red}} de A es I_n.
  3. A es producto de matrices elementales.
  4. Para todo b\in F^n, el sistema de ecuaciones Ax=b tiene una única solución x\in F^n.
  5. Para todo b\in F^n, el sistema de ecuaciones Ax=b tiene una solución x\in F^n.
  6. Existe una matriz B de n\times n tal que AB=I_n.
  7. Existe una matriz B de n\times n tal que BA=I_n.

Por supuesto, estas no son todas las formas de caracterizar una matriz invertible. Hay otras formas de hacerlo en términos de determinantes, por ejemplo. En el camino recordaremos varias de las definiciones que están en este teorema.

Le llamo el teorema de la mariposa de equivalencias porque podemos agrupar a estos números en tres «grupos» principales de equivalencias «parecidas», que además nos van a recordar cómo va la prueba.

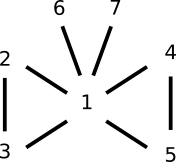
Primero veremos la equivalencia entre 1, 2 y 3 (un ala). Luego, entre 1,4,5 (otra ala). Después, entre 1 y 6 (antena derecha). Finalmente, entre 1 y 7 (antena izquierda).

Un par de lemas auxiliar

Antes de demostrar el teorema de equivalencias, enunciamos y argumentamos dos resultados útiles

Es fácil convencerse de que aplicar una operación elemental a una matriz A es lo mismo que multiplicar a A por la izquierda por la matriz elemental correspondiente a la operación. Como toda matriz A se puede llevar a su forma escalonada reducida mediante operaciones elementales, concluimos lo siguiente.

Lema 1: Para toda matriz A existe una matriz E que es producto de matrices elementales tal que EA es la forma escalonada reducida de A, es decir EA=A_{\text{red}}.

También es fácil convencerse de que cada matriz elemental es invertible, pues las operaciones elementales se pueden revertir, y la inversa de la matriz elemental M es precisamente la matriz elemental correspondiente a la operación inversa. Además, producto de matrices invertibles es invertible. De este modo, concluimos lo siguiente:

Lema 2: Si E es una matriz que es producto de matrices elementales, entonces E es invertible y también es producto de matrices elementales.

La demostración del teorema de la mariposa

Usaremos el diagrama de la mariposa para demostrar todas las equivalencias. Lo que haremos es probar una implicación por cada una de las siguientes flechas:


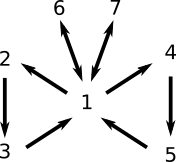
Empezamos con el ala izquierda de la mariposa.

(1) implica (2): Tomemos una matriz invertible A. Por el Lema 1, existe una matriz producto de elementales tal que EA=A_{\text{red}}. Como E y A son invertibles, entonces A_{\text{red}} también es invertible.

Si A_{\text{red}} tuviera una fila cero, digamos la j, no sería invertible. Esto sucede ya que para cualquier matriz B de n\times n tendríamos que la fila j de AB también sería cero, y entonces AB nunca sería I_n. Como sabemos que A_{\text{red}} es invertible, entonces todas sus filas no son cero y por lo tanto todas tienen pivote. Así, tenemos n pivotes y por lo tanto tiene que haber exactamente un pivote por columna. Como A_{\text{red}} es escalonada reducida, estos pivotes tienen que estar exactamente uno en cada entrada de la diagonal principal. Como además cada pivote es la única entrada no cero de su columna, concluimos que A_{\text{red}} es la identidad.

(2) implica (3): Tomemos una matriz A cuya forma escalonada reducida es la identidad. Por el Lema 1, existe una matriz producto de elementales tal que EA=A_{\text{red}}=I_n. Por el Lema 2, E es invertible y E^{-1} es producto de matrices elementales. Multiplicando por E^{-1} a la izquierda a la identidad EA=I_n obtenemos A=E^{-1}, es decir, A es producto de matrices elementales.

(3) implica (1): Finalmente, si A es producto de matrices elementales, por el Lema 2 tenemos que A es invertible.

Con esto terminamos la primer ala de la mariposa. Notemos que cierran un ciclo, así que a partir de ahora podemos usar libremente la equivalencia entre 1, 2 y 3. Hagamos la segunda ala.

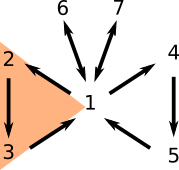
(1) implica (4): Supongamos que A es invertible y tomemos cualquier b en F^n. Notemos que A^{-1}b es solución de Ax=b pues satisface A(A^{-1}b)=I_n b=b. Además, si x y y son soluciones de Ax=b, tendríamos que Ax=Ay y mutiplicando por A^{-1} a la izquierda tendríamos que x=y. De este modo, Ax=b tiene una única solución para todo b en F^n.

(4) implica (5): Esta demostración es inmediata. Si Ax=b tiene una única solución, en particular tiene una solución.

(5) implica (1): Supongemos que Ax=b tiene una solución x en F^n para todo b en F^n. Afirmamos que esto implica que A_{\text{red}}x=b tiene solución para para todo b en F^n. Tomemos una b en F^n. Por el Lema 1, hay una matriz invertible E tal que A_{\red}=EA. Por hipótesis, existe una solución x para Ax=E^{-1}b. Tomemos esa x. Notemos que A_{\text{red}}x=(EA)x=E(Ax)=E(E^{-1}b)=b. Es decir, justo esa x es solución para A_{\text{red}}x=b.

En particular, A_{\text{red}}x=e_j tiene solución para cuando e_j es el vector cuya j-ésima entrada es 1 y las demás cero. Así, es imposible que la j-ésima fila de A_{\text{red}} sea cero, ya que en caso contrario Ax siempre tendría j-ésima entrada cero y Ax=e_j no tendría solución. Como ya vimos antes, si A_{\text{red}} no tiene filas cero, entonces es la identidad. Por la equivalencia entre (1) y (2) concluimos que A es invertible.

Esto termina las equivalencias en la segunda ala, así que ahora podemos usar libremente las implicaciones entre 1, 2, 3, 4 y 5. Ya nada más nos faltan las antenas.

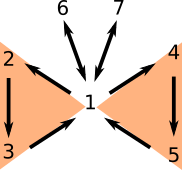
Por supuesto, las implicaciones (1) implica (6) y (1) implica (7) son triviales, pues la matriz de (1) en particular funciona para (6) y (7). Lo que falta ver son los regresos de estas implicaciones.

(6) implica (1): Supongamos que existe una matriz B tal que AB=I_n. Tomemos b en F^n. Notemos que Bb es solución de Ax=b pues A(Bb)=(AB)b=I_nb=b. De este modo, Ax=b tiene solución para todo b en F^n y por la equivalencia entre (1) y (5) tenemos que A es invertible. Si tomamos a su inversa A^{-1} y la multiplicamos a la izquierda en la hipótesis, obtenemos B=A^{-1}, de modo que también BA=I_n.

(7) implica (1): Supongamos que existe una matriz B tal que BA=I_n. Por la equivalencia entre (1) y (6), tenemos que B es invertible, de inversa B^{-1}. De este modo, A=(B^{-1}B)A=B^{-1}(BA)=B^{-1}I_n=B^{-1}. De este modo, A es la inversa de una matriz invertible y por tanto es invertible, y por lo tanto AB=B^{-1}B=I_n.

¡Listo! Con esto tenemos la equivalencia entre todas las afirmaciones.

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

2 comentarios en “Mariposa de 7 equivalencias de matrices invertibles”

  1. Diegochenko

    muy interesante cuando hice algebra lineal en la Universidad, durante la cursada seguí el grossman y llegue a decirme que fea materia. pero para el examen final la prepara siguiendo el «anton» y quede fascinado Saludos desde Argentina…

    Responder ↓
    1. LeoLeo Autor

      Hola Diegochenko. En efecto, la visión que uno tiene de las materias luego depende mucho del material con el que se estudie y de los profesores con quienes la toma. Gracias por el comentario.

      Responder ↓

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Este sitio usa Akismet para reducir el spam. Aprende cómo se procesan los datos de tus comentarios.