Introducción

Anteriormente vimos el concepto de composición entre funciones, que nos permiten saltar entre varios conjuntos de manera sencilla, revisamos algunas de sus propiedades y dimos algunos ejemplos. Ahora nos toca profundizar un poco más en la composición de funciones analizando un caso particular de funciones: las invertibles. Que en términos simples nos permiten deshacer los efectos de las operaciones.

Revirtiendo las cosas.

Pensemos por un momento en un cubo rubik, hay distintas técnicas para armarlo, pero por ahora nos enfocaremos en sus movimientos. La forma en que se usa el cubo, es moviendo sus caras hasta que todas las caras tengan un solo color. Imagina que tienes un cubo en tus manos, si mueves la cara que está hasta arriba, tienes dos formas de hacerlo, girar en sentido de las manecillas del reloj y girar en sentido contrario a las manecillas del reloj. No pasa nada si no estás seguro de tu movimiento, pues siempre puedes deshacer un movimiento rotando la misma cara que volteaste en sentido contrario. Incluso si mueves varias caras, podrás regresar al estado original si recuerdas exactamente las caras que volteaste y la dirección, pues para deshacer los movimientos, tendrás que empezar por la última cara que volteaste y deberás girarla al sentido contrario al que le diste vuelta. Por ejemplo esta imagen indica dos movimientos a las caras y la forma de «deshacer» los movimientos.

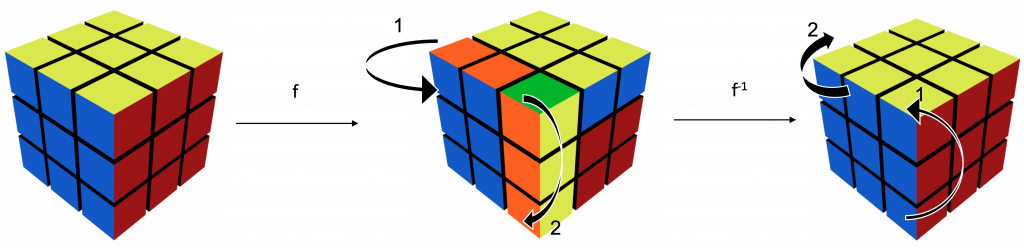
En la imagen también marcamos los movimientos de mover las dos caras como $f$, por ahora imagínate que ese movimiento de girar las dos caras como lo muestra la imagen, se llama el movimiento $f$. Mientras que el movimiento de deshacerlas se llama $f^{-1}$. Entonces si realizamos primero el movimiento $f$, el movimiento $f^{-1}$ revierte lo que hizo la primera, volviendo al estado inicial. Así es como vamos a pensar en la reversibilidad de las funciones, una manera de «volver a armar» el cubo.

Funciones reversibles

Diremos que una función es reversible si existe una función $f^{-1}:Im(f) \rightarrow X$ tal que $f ^{-1}\circ f = Id$ donde $Id$ es la función identidad, es decir, es la única función que asigna a cada elemento a sí mismo, es decir $Id(x)=x$.

Algunas observaciones de las funciones invertibles. Sea $f:X \rightarrow Y$ una función invertible, entonces:

• $f$ es inyectiva.

Demostración. Supongamos que no es inyectiva, entonces existen $x_1,x_2 \in X$ distintos tales que $f(x_1) = f(x_2)$. Como $f$ es invertible, entonces existe su función inversa $f^{-1}:Im(f) \rightarrow X$, en donde $$x_1 = f^{-1} \circ f(x_1) = f^{-1} \circ f(x_2) = x_2 $$ Siendo esta una contradicción, pues supusimos que eran distintos elementos. Así, la función es inyectiva.

$\square$

• $f^{-1}$ es inyectiva.

Demostración. De manera similar a la demostración anterior, si $y_1,y_2 \in Dom(f^{-1})$ son tales que $f^{-1}(y_1) = f^{-1}(y_2)$, se tiene que al ser $f$ inyectiva, $$f(f^{-1}(y_1)) = f(f^{-1}(y_2)) \Rightarrow y_1=y_2$$ Llegando a que $f^{-1}$ es inyectiva.

$\square$

Así, te puedes dar una idea de lo que significan las funciones invertibles. Con estas proposiciones hemos probado además que la función $f^{-1}: Im(f) \rightarrow X$ es una biyección. ¿Te imaginas porqué? Pues resulta que la función $f^{-1}$ también es suprayectiva.

• $f^{-1} \circ f = f \circ f^{-1}$

Demostración. Sabemos que $f^{-1} \circ f = Id$, entonces bastará demostrar que $f \circ f^{-1} = Id$. Para ello consideremos $y \in Dom(f^{-1})=Im(f) \subset Y$. Supongamos que $$f \circ f^{-1}(y)=w$$. Entonces $$f^{-1}(f \circ f^{-1}(y)) = f^{-1}(w). $$ Como la composición es asociativa, entonces: $$f^{-1}(f \circ f^{-1}(y)) = (f^{-1} \circ f) \circ f^{-1}(y) = f^{-1}(y) = f^{-1}(w)$$ Como $f^{-1}$ es inyectiva, entonces $y=w$.

$\square$

• Sea $g:Im(f) \rightarrow Z$ una función invertible, entonces $(g \circ f)^{-1} = f^{-1} \circ g^{-1}$ .

Demostración. Basta notar que por la asociatividad de las funciones:

$$ \begin{align*}
(g \circ f) \circ (f^{-1} \circ g^{-1}) &= g \circ (f \circ (f^{-1} \circ g^{-1})\\
&= g \circ ((f \circ f^{-1}) \circ g^{-1})\\
&= g \circ (Id \circ g^{-1}) \\
&= g \circ g^{-1} = Id
\end{align*}$$

$\square$

Más adelante…

Habiendo pasado por las funciones, su composición, sus propiedades y la inversa, utilizaremos estas definiciones para hablar de el tamaño de los conjuntos. Pues esta definición de funciones nos ayudan a decir «Cuántos elementos tiene un conjunto».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra que $f^{-1}$ es suprayectiva.
2. Demuestra que $Dom(f^{-1})=Im(f)$.
3. Demuestra que $(f \circ (g \circ h))^{-1} = h^{-1} \circ (g^{-1} \circ f^{-1})$.
4. Da una condición suficiente para que una función no sea invertible.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Composición de funciones
• Siguiente entrada del curso: Cardinalidad de conjuntos finitos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»