Archivo de la etiqueta: álgebra

Seminario de Resolución de Problemas: Coeficientes binomiales

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Los coeficientes binomiales aparecen en muchos problemas de matemáticas, y por ello es útil conocerlos bien y saber sus propiedades básicas. En esta entrada hablaremos de varios aspectos de los coeficientes binomiales: algebraicos, combinatorios y de teoría de números. Aunque resolvamos un problema con una técnica en particular, te recomendamos intentar usar las distintas herramientas en otros problemas, para conocer sus alcances y limitaciones.

Antes de empezar, ponemos una figura con un hecho curioso acerca de los coeficientes binomiales:

Coeficientes binomiales, Pascal y Fibonacci
«Las sumas de las diagonales del triángulo de Pascal dan los números de Fibonacci»

Definición algebraica de coeficientes binomiales

Como recordatorio, para $n\geq 0$ un entero, definimos $n!$ recursivamente como $0!=1$ y $n!=n(n-1)!$. En otras palabras, para $n\geq 1$ tenemos $$n!=1\cdot 2\cdot \ldots \cdot n.$$

Definimos para $n\geq 0$ un entero y $k$ un entero en $\{0,\ldots,n\}$al coeficiente binomial $n$ en $k$ como $$\binom{n}{k}:=\frac{n!}{k!(n-k)!}.$$ Si $n$ es un entero negativo o $k$ es un entero fuera del rango $\{0,\ldots,n\}$ es conveniente definir $\binom{n}{k}=0$.

A partir de la definición, es claro que $\binom{n}{n}=\binom{n}{0}=1$ para todo entero positivo $n$. Lo que no es inmediato a partir de la definición es que $\binom{n}{k}$ siempre sea un entero. Veremos eso en la siguiente sección.

Mientras tanto, veamos algunas propiedades de los coeficientes binomiales que se pueden verificar sin mostrar que $\binom{n}{k}$ es entero.

Propiedad (simetría). $\binom{n}{k}=\binom{n}{n-k}.$

Propiedad (fórmula de Pascal). $\binom{n+1}{k+1}=\binom{n}{k}+\binom{n}{k+1}.$

Propiedad (propiedad de entrada-salida). $\binom{n+1}{k+1}=\frac{n+1}{k+1}\binom{n}{k}.$

El siguiente problema se puede resolver usando estas identidades.

Propiedad (suma cambiando arriba). Muestra que para $n$ y $k$ enteros positivos se tiene que $$\sum_{j=0}^k \binom{n+j}{n} = \binom{n+k+1}{n+1}.$$

Sugerencia pre-solución. Primero, formula un problema equivalente usando la propiedad de simetría. Luego, procede por inducción y usa otra de las propiedades de coeficientes binomiales mencionada arriba.

Solución. Usando la propiedad de simetría de coeficientes binomiales, el problema es equivalente a demostrar que $$\sum_{j=0}^k \binom{n+j}{j} = \binom{n+k+1}{k}.$$ Fijemos un entero $n\geq 0$ y hagamos inducción sobre $k$. Para $k=0$, la identidad es cierta pues $$\binom{n}{0}=1=\binom{n+1}{0}.$$

Para $k=1$, tenemos que mostrar que $\binom{n}{0}+\binom{n+1}{1}=\binom{n+2}{1}$. El primer término se puede escribir como $\binom{n+1}{0}$, pues ambos son $1$. Así, lo que hay que mostrar es $$\binom{n+1}{0}+\binom{n+1}{1}=\binom{n+2}{1},$$ que es cierto por la fórmula de Pascal.

Suponiendo el resultado cierto para una $k$ dada, mostraremos que es cierto para $k+1$. Esto se sigue de la siguiente cadena de igualdades, en donde en la segunda igualdad usamos la hipótesis inductiva, y en la tercera la fórmula de Pascal:

\begin{align*}
\sum_{j=0}^{k+1} \binom{n+j}{j} &= \sum_{j=0}^{k} \binom{n+j}{j}+\binom{n+k+1}{k+1}\\
&=\binom{n+k+1}{k}+\binom{n+k+1}{k+1}\\
&=\binom{n+k+2}{k+1}.
\end{align*}

Esto termina la inducción.

$\square$

Existen otras formas de demostrar identidades con coeficientes binomiales, y de hecho una misma identidad se puede mostrar de varias formas. Veamos más técnicas.

Aspectos combinatorios de los coeficientes binomiales

El coeficiente binomial $\binom{n}{k}$ cuenta la cantidad de subconjuntos de tamaño $k$ de un conjunto de tamaño $n$. Argumentar esto es relativamente fácil, usando un argumento de doble conteo. Supongamos que dicha cantidad de subconjuntos es igual a $A$.

Respondamos la pregunta, ¿cuántos vectores de $k$ entradas existen, tales que las entradas son distintas y vienen de un conjunto de $n$ elementos? La pregunta es un poco distinta, pues como tenemos vectores, aquí sí importa el orden de los elementos. Supongamos que la respuesta es $B$.

Una forma de responder la pregunta es la siguiente. Primero, elegimos cuál subconjunto de tamaño $k$ conformará las entradas. Esto se puede hacer de $A$ formas (que aunque no sepamos cuánto vale, lo podemos usar). Luego, hay que ordenar las $k$ entradas elegidas, que se puede hacer de $k!$ maneras. Así, esto muestra que $B=k! A$.

Otra forma de responder la pregunta es la siguiente. Elegimos el primer elemento, que se puede hacer de $n$ formas. Luego el segundo, de entre los $n-1$ restantes, que se puede hacer de $n-1$ formas. Siguiendo de esta manera, el último de los $k$ hay que elegirlo entre $n-k+1$ restantes. Así, esta otra forma de contar dice que $$B=n\cdot(n-1)\cdot\ldots\cdot (n-k+1)=\frac{n!}{(n-k)!}.$$

Como ambas formas de contar son válidas, tenemos que $k!A=B=\frac{n!}{(n-k)!}$, de donde $A=\frac{n!}{k!(n-k)!}=\binom{n}{k}$.

Hay problemas que de lejos parecen preguntar algo de álgebra, pero que pueden ser interpretados en términos combinatorios para dar una solución.

Problema. Para $n$ un entero positivo, muestra que $$\sum_{k=1}^n k \binom{n}{k} = n 2^{n-1}.$$

Sugerencia pre-solución. Construye un problema de conteo cuya respuesta se pueda poner tanto en términos del lado izquierdo, como en términos del lado derecho.

Solución. Preguntémonos, ¿de cuántas formas se puede elegir un subconjunto de un conjunto de $n$ elementos en el que uno de sus elementos está pintado de azul?

Por un lado, primero se puede elegir qué elemento va a ser el azul. Hay $n$ formas de hacer esta elección, y ésta forza a que el elemento en azul esté en el subconjunto. Luego, de los $n-1$ elementos restantes hay que elegir un subconjunto para completar la elección, lo cual se puede hacer de $2^{n-1}$ formas posibles. Así, una forma de contar da $n2^{n-1}$.

Por otro lado, primero se puede decidir de qué tamaño $k$ va a ser el subconjunto. Como hay un elemento especial, el tamaño $k$ va de $1$ a $n$. Ya elegido $k$, hay $\binom{n}{k}$ formas de elegir cuál será el subconjunto. Ya elegido el subconjunto, hay $k$ formas de elegir cuál será el elemento pintado de azul. Así, otra posible respuesta, también correcta, es $\sum_{k=1}^n k \binom {n}{k}$.

Como estamos contando lo mismo con ambas expresiones, concluimos la igualdad del problema.

$\square$

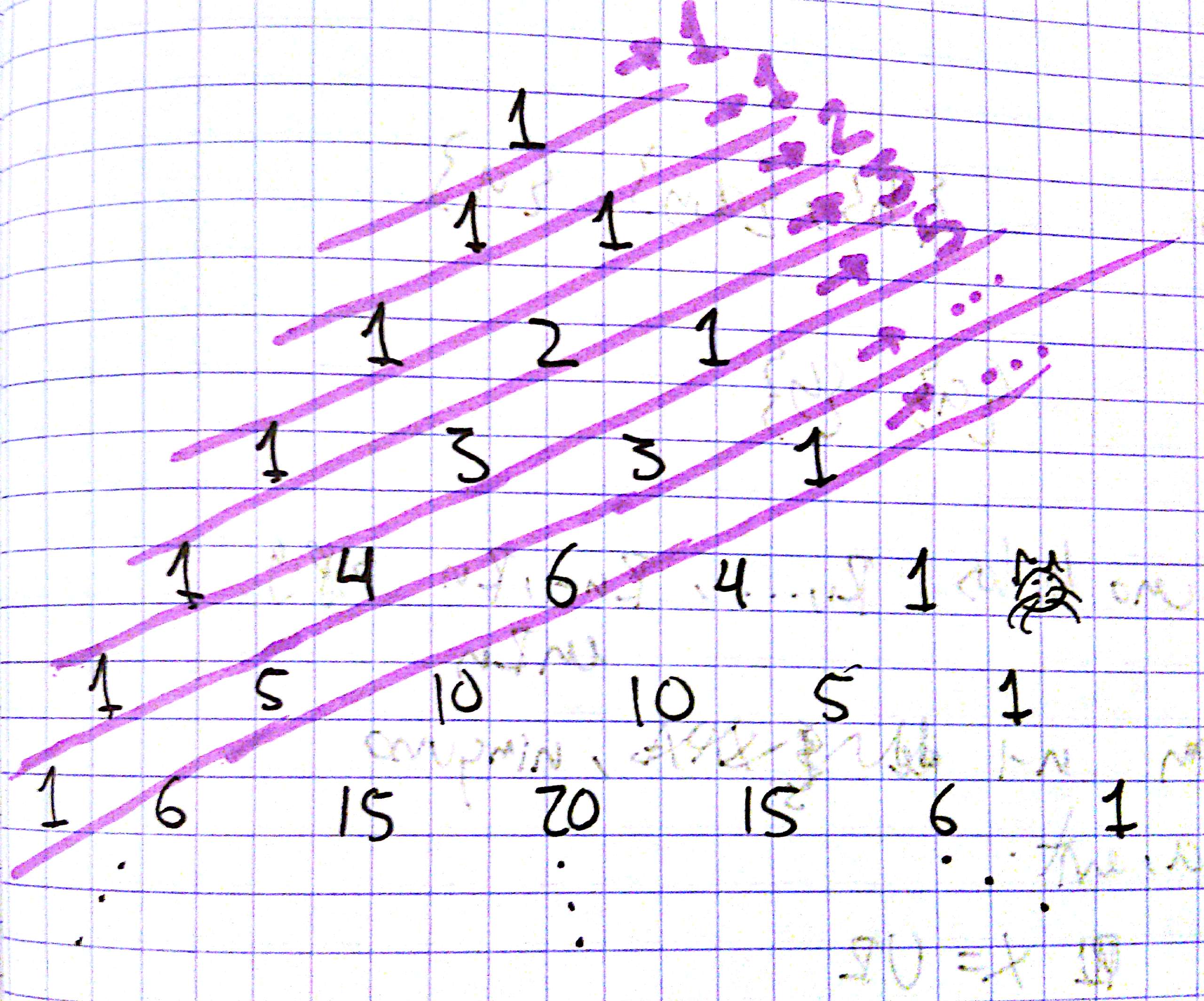
A este método de resolver problemas se le conoce como contar de dos formas distintas y funciona no sólo con coeficientes binomiales, sino también con cualquier otra expresión algebraica que tenga términos que se puedan interpretar de manera combinatoria. Hay otro ejemplo en el blog, en donde vemos cómo aparecen los números de Fibonacci en el triángulo de Pascal. En esa entrada también hablamos de cómo aparecen los coeficientes binomiales en el triángulo de Pascal.

Coeficientes binomiales y binomio de Newton

La interpretación combinatoria de los coeficientes binomiales nos da una demostración para la fórmula del binomio de Newton, que ya vimos en una entrada anterior. Aquí enunciamos la fómula como recordatorio.

Teorema (binomio de Newton). Para $a$ y $b$ números reales y $n$ un entero no negativo, se tiene que
\begin{align*}
(a+b)^n=\sum_{j=0}^n \binom{n}{j}a^{n-j}b^j.
\end{align*}

Si en el binomio de Newton ponemos $a=b=1$, obtenemos $$\binom{n}{0}+\binom{n}{1}+\ldots+\binom{n}{n}=(1+1)^n=2^n.$$ Otra forma de probar esta identidad es simplemente notar que tanto la suma de la izquierda como el término de la derecha cuentan la cantidad de subconjuntos de un conjunto de $n$ elementos: la de la izquierda los cuenta por tamaño, y el de la derecha decidiendo para cada elemento si está o no.

Si ponemos $a=1$, $b=-1$, obtenemos que $$\binom{n}{0}-\binom{n}{1}+\ldots+(-1)^n\binom{n}{n} = 0,$$ o bien $$\binom{n}{0}+\binom{n}{2}+\ldots = \binom{n}{1}+\binom{n}{3}+\ldots.$$

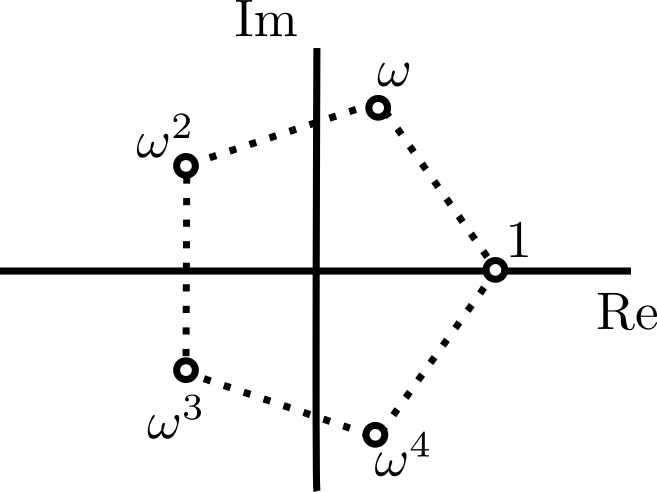
Se obtienen otras identidades de coeficientes binomiales interesantes si se usan raíces $n$-ésimas de la unidad, como ya vimos en la entrada de aritmética compleja.

Hay otras formas de usar el binomio de Newton para probar identidades de coeficientes binomiales.

Problema. Muestra que $$\binom{n}{0}^2+\binom{n}{1}^2+\ldots+\binom{n}{n}^2=\binom{2n}{n}.$$

Sugerencia pre-solución. Considera el polinomio $(1+x)^{2n}$.

Solución. Consideremos el polinomio $(1+x)^{2n}$ y determinemos el coeficiente de su término $x^n$.

Usando el binomio de Newton directamente, tenemos que $$(1+x)^{2n}=\sum_{j=0}^{2n} \binom{2n}{j}x^j,$$ de modo que el coeficiente de $x^n$ es $\binom{2n}{n}$.

Por otro lado, podemos escribir $(1+x)^{2n}=(1+x)^n(1+x)^n$. Usando el binomio de Newton, tenemos $$(1+x)^n=\sum_{j=0}^n \binom{n}{j} x^j.$$ Al multiplicar esta expresión consigo misma, los términos que quedan de grado $n$ son cuando, para cada $j$, elegimos en un paréntesis al término que tiene $x^j$ (que tiene coeficiente $\binom{n}{j}$) y en el otro al que tiene a $x^{n-j}$ (que tiene coeficiente $\binom{n}{n-j}$).

De esta forma, el coeficiente del término de grado $n$ es $$\sum_{j=0}^n \binom{n}{j} \binom{n}{n-j}.$$ Usando la identidad de simetría, podemos cambiar $\binom{n}{n-j}$ por $\binom{n}{j}$, para obtener $$\sum_{j=0}^n \binom{n}{j}^2.$$ Igualando ambas formas de encontrar el coeficiente, obtenemos la identidad deseada.

$\square$

Hay otras técnicas que usan herramientas de integrales o derivadas. Vimos un ejemplo de esto en una entrada anterior.

Coeficientes binomiales y teoría de números

El hecho de que los coeficientes binomiales son la respuesta a un problema de conteo, implica que son enteros no negativos. Alternativamente, esto se puede demostrar por inducción usando la identidad de Pascal.

Este hecho nos puede ayudar a resolver problemas de teoría de números. Veamos un ejemplo clásico.

Problema. Muestra que el producto de $n$ enteros consecutivos siempre es divisible entre $n!$.

Sugerencia pre-solución. Haz una división en casos para ver si se incluye al cero, si son sólo negativos o sólo positivos. Reduce el caso de negativos a positivos y usa notación adecuada para escribir al producto de dichos enteros usando un coeficiente binomial.

Solución. Si alguno de los enteros es $0$, entonces el producto es $0$, que es divisible entre cualquier número. Si son $n$ enteros negativos, entonces podemos cambiar el signo a todos y su producto diferirá, quizás, en un factor $-1$ que no afecta la divisibilidad, y habremos obtenido un problema con $n$ enteros positivos consecutivos. De esta manera, podemos enfocarnos en el caso de $n$ enteros positivos consecutivos.

Llamemos al primero $k+1$, para $k\geq 0$. Los demás son entonces $k+2,\ldots,k+n$. Su producto es
\begin{align*}
(k+1)(k+2)\ldots(k+n)&=\frac{k!}{k!}(k+1)(k+2)\ldots(k+n)\\
&=\frac{(n+k)!}{k!}\\
&=n!\binom{n+k}{k}.
\end{align*}

Como $\binom{n+k}{k}$ es un entero, tenemos que el lado derecho es un múltiplo de $n!$, como queríamos.

$\square$

Otro tipo de técnicas hablan de la divisibilidad de un coeficiente binomial. Por ejemplo si tenemos un primo $p$, sabemos que todos los siguiente coeficientes binomiales son enteros $$\binom{p}{1}, \binom{p}{2},\ldots,\binom{p}{p}.$$ Por su expresión en términos de factoriales, todos tienen a $p$ en el numerador, pero no tienen ningún divisor de $p$ distinto de $1$ en el denominador, pues $p$ es primo. Así, todos ellos son enteros divisibles entre $p$. Eso puede ayudar en problemas como el siguiente.

Problema. Muestra que si $p$ es un número primo, entonces $p^2$ divide a $\binom{2p}{p} -2$.

Sugerencia pre-solución. Formula un problema equivalente usando un resultado anterior.

Solución. Por un problema anterior, $$\binom{2p}{p}=\binom{p}{0}^2+\binom{p}{1}^2+\ldots+\binom{p}{p}^2.$$

Por la discusión previa, para $j=1,\ldots,p-1$ tenemos que $p\mid \binom{p}{j}$, así que $p^2\mid \binom{p}{j}^2$. De esta forma, trabajando módulo $2p$ tenemos \begin{align*}
\binom{2p}{p}&\equiv \binom{p}{0}^2+\binom{p}{p}^2 \\
&\equiv 1+1\equiv 2 \pmod{p^2}.
\end{align*}

Esto es justo lo que queríamos mostrar.

$\square$

Más problemas

Puedes encontrar más problemas de coeficientes binomiales en la sección 5.1 del libro Problem Solving through Problems de Loren Larson.

Álgebra Superior II: Raíces en los complejos y raíces de la unidad.

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En esta entrada veremos cómo resolver, en $\mathbb{C}$, la ecuación $w^n=z$, en donde $z$ es un complejo y $n$ es un entero positivo. Puedes pensar esto como que aprenderemos a obtener raíces en los complejos, pero sólo para $n$ entero. Más adelante hablaremos de la función exponencial compleja que nos permitirá elevar a otro tipo de exponentes.

Nuestra herramienta principal será la fórmula de De Moivre, que ya demostramos en una entrada anterior. Encontrar raíces $n$-ésimas es una herramienta más en nuestra caja para trabajar con números complejos, que hasta el momento ya incluye resolver ecuaciones cuadráticas complejas y sistemas de ecuaciones lineales complejos.

Introducción a raíces en los complejos

Pensemos en un ejemplo sencillo. ¿Cuáles son los complejos $w$ tales que $w^4=1$? En $\mathbb{R}$ tenemos dos de ellos: $1$ y $-1$. Como $$(-i)^4=i^4=(-1)^2=1,$$ en $\mathbb{C}$ tenemos otras dos soluciones: $i$ y $-i$. Así que tenemos $4$ soluciones en $\mathbb{C}$: $1$, $-1$, $i$ y $-i$.

Para mostrar que son las únicas en este sencillo caso, podemos hacer lo siguiente. Expresamos $1$ en forma polar $1=\text{cis}(0)$ y también, en forma polar, una solución $w=s\text{cis}(\alpha)$, con $\theta$ en $[0,2\pi)$. Por el teorema de De Moivre, tenemos que $$1=w^4=s^4\text{cis}(4\alpha).$$

Así, la norma $s$ de $w$ debe satisfacer $s^4=1$, y además $\text{cis}(4\alpha)$ debe ser $1$, por lo que $4\alpha$ debe ser un múltiplo entero de $2\pi$. La norma es un real positivo, así que la única solución para $s$ es $1$. Ahora, ¿cuántos argumentos $\alpha$ en $[0,2\pi)$ hacen que $4\alpha$ sea un múltiplo entero de $2\pi$?

Para determinar esto, notemos que $4\alpha$ está en $[0,8\pi)$, y ahí hay exactamente cuatro múltiplos enteros de $2\pi$, que son $$0,2\pi, 4\pi, 6\pi.$$ Esto es justo lo que limita las soluciones a que sean a lo más $4$.

Podemos continuar para verificar que en efecto son las soluciones que ya encontramos. Las soluciones para $\alpha$ en cada caso son $$0,\frac{\pi}{2},\pi,\frac{3\pi}{2}.$$ Concluimos entonces que las soluciones complejas de $w^4=1$ son, en forma polar,
\begin{align*}
w_1&=\text{cis}(0)\\
w_2&=\text{cis}\left(\frac{\pi}{2}\right)\\
w_3&=\text{cis}\left(\pi\right)\\
w_4&=\text{cis}\left(\frac{3\pi}{2}\right),
\end{align*}

que son exactamente $1,i,-1,-i$.

$\triangle$

El teorema de raíces en los complejos

La discusión anterior funciona en general para cualquier entero positivo $n$ y para cualquier complejo $\mathbb{C}$. Siempre tenemos exactamente $n$ soluciones y sabemos cómo se ven en forma polar.

Teorema. Sea $z=r\text{cis}(\theta)$ un número complejo, distinto de cero, dado en forma polar y $n$ un entero positivo. Existen exactamente $n$ elementos distintos de $\mathbb{C}$ tales que $w^n = z$. Están dados en forma polar por $$w_j=r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)$$ para $j=0,1,2\ldots,n-1$.

Demostración. Tomemos una solución $w$ y la escribimos en forma polar $w=s\text{cis}(\alpha)$, con $\alpha$ en $[0,2\pi)$. Usando que $w$ es solución y la fórmula de De Moivre, obtenemos que $$r\text{cis}(\theta)=s^n\text{cis}(n\alpha).$$ Como $s$ tiene que ser real positivo, obtenemos que $s=r^{1/n}$ (aquí estamos usando la raíz $n$-ésima en los reales).

El ángulo $n\alpha$ está en el intervalo $[0,2n\pi)$, y debe diferir en un múltiplo entero de $2\pi$ del ángulo $\theta$. Como $\theta$ está en $[0,2\pi)$, las únicas posibilidades para $n\alpha$ pueden ser los $n$ valores $$\theta, \theta+2\pi,\ldots, \theta+2(n-1)\pi,$$ de donde las soluciones para $\alpha$ son $$\frac{\theta}{n},\frac{\theta}{n}+\frac{2\pi}{n}, \ldots, \frac{\theta}{n} + (n-1)\frac{2\pi}{n},$$ respectivamente. Como son ángulos distintos en $[0,2\pi)$, obtenemos las posibles soluciones distintas $$r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)\quad \text{para $j=0,\ldots,n-1$}.$$

Verificar que en efecto son soluciones es sencillo, ya sea revirtiendo los pasos que hicimos, o usando directamente la fórmula de De Moivre. Esta verificación queda como tarea moral.

$\square$

Observa que el teorema dice que para obtener una raíz podemos empezar del complejo de norma $r^{1/n}$ y argumento $\frac{\theta}{n}$, y de ahí obtener el resto de las raíces en los complejos «rotando repetidamente $\frac{2\pi}{n}$ en el plano complejo». Esto muestra que las raíces forman los vértices de un $n$-ágono regular.

Nos costó un poco de trabajo mostrar que teníamos a lo más $n$ soluciones. En realidad, cualquier ecuación polinomial de grado $n$, es decir, de la forma $$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0$$ tiene a lo más $n$ soluciones. Esto lo veremos con toda generalidad en la última unidad, cuando hablemos de polinomios.

Ejemplos de obtener raíces en los complejos

Ejemplo. Encontremos todas las raíces séptimas del complejo $128\text{cis}\left(\frac{14\pi}{13}\right)$. Para empezar, notemos que $128^{1/7}=2$, de modo que todas las raíces tienen norma $2$.

Una de las raíces tiene argumento $\frac{14\pi}{7\cdot 13}=\frac{2\pi}{13}$ y el argumento del resto difiere en múltiplos enteros de $\frac{2\pi}{7}$. De esta forma, las raíces son

\begin{align*}
w_1&=2\text{cis}\left(\frac{2\pi}{13}\right)\\
w_2&=2\text{cis}\left(\frac{2\pi}{13}+\frac{2\pi}{7}\right)=2\text{cis}\left(\frac{40\pi}{91}\right)\\
w_3&=2\text{cis}\left(\frac{2\pi}{13}+\frac{4\pi}{7}\right)=2\text{cis}\left(\frac{66\pi}{91}\right)\\
w_4&=2\text{cis}\left(\frac{2\pi}{13}+\frac{6\pi}{7}\right)=2\text{cis}\left(\frac{92\pi}{91}\right)\\
w_5&=2\text{cis}\left(\frac{2\pi}{13}+\frac{8\pi}{7}\right)=2\text{cis}\left(\frac{118\pi}{91}\right)\\
w_6&=2\text{cis}\left(\frac{2\pi}{13}+\frac{10\pi}{7}\right)=2\text{cis}\left(\frac{144\pi}{91}\right)\\
w_7&=2\text{cis}\left(\frac{2\pi}{13}+\frac{12\pi}{7}\right)=2\text{cis}\left(\frac{170\pi}{91}\right).
\end{align*}

$\triangle$

Problema. Sabemos que $(2-3i)^4=-119+120i$. Encuentra las otras raíces cuartas de $-119+120i$.

Solución. Podríamos pasar $-119+120i$ a forma polar y usar el método anterior. Esto funciona y dará una solución. Pero veamos una solución alternativa más corta, que nos ayuda a entender mejor el teorema de raíces en los complejos.

De acuerdo con lo que probamos, las raíces varían únicamente en argumento, al que se le va sumando $\frac{\pi}{2}$. Es decir, si tenemos una raíz en el plano complejo, las demás se obtienen de ir rotando $\frac{\pi}{2}$ (recuerda que esto es $90^\circ$) desde el origen. Al ir rotando el punto $(2,-3)$ en el plano complejo en este ángulo, obtenemos los puntos $(-3,-2)$, $(-2,3)$ y $(3,2)$, de modo que las otras tres raíces son $-3-2i$, $-2+3i$ y $3+2i$.

Otra forma más de pensarlo es la siguiente. Si ya tenemos una raíz cuarta $w$ de un complejo $z$, entonces todas las raíces se obtienen multplicando por $1,i,-1, -i$. En efecto, por ejemplo, $$(iw)^4=i^4w^4=w^4=1.$$ Así, para el problema que nos interesa, las soluciones son

\begin{align*}w_1&=2-3i\\w_2&=i(2-3i)=3+2i\\w_3&=-(2-3i)=-2+3i\\w_4&=-i(2-3i)=-3-2i,\end{align*}
lo cual coincide con lo que habíamos encontrado antes.

$\triangle$

Raíces $n$-ésimas de la unidad

Un caso particular importante de la teoría desarrollada en la sección anterior es cuando $z$ es $1$. Sea $n$ un entero positivo y $w$ un complejo tal que $w^n=1$. A $w$ se le conoce como una raíz $n$-ésima de la unidad.

Teorema (de las raíces $n$-ésimas de la unidad). Sea $n$ un entero positivo. Existen exactamente $n$ raíces $n$-ésimas de la unidad distintas. Si $\omega$ es la que tiene el menor argumento positivo, entonces dichas raíces son $$1,\omega, \omega^2,\ldots, \omega^{n-1}.$$

La demostración se sigue fácilmente del teorema de raíces $n$-ésimas y queda como tarea moral. Cualquier raíz $n$-ésima $\omega$ tal que sus primeras potencias generen todas las raíces $n$-ésimas de la unidad se le conoce como una raíz primitiva.

Las raíces $n$-ésimas de la unidad tienen una interpretación geométrica bonita. Forman los vértices del $n$-ágono regular con $n$ vértices, sobre la circunferencia unitaria, donde uno de los vértices es $1$.

Ejemplo. Obtengamos las raíces quintas de la unidad. Primero, obtengamos la de menor argumento positivo, que por el teorema de raíces en los complejos, es $$\omega = \text{cis}\left(\frac{2\pi}{5}\right).$$ El resto de las raíces son entonces $\omega^2$, $\omega^3$, $\omega^4$ y $1$. Las podemos encontrar en el plano complejo como vértices del siguiente pentágono regular:

Ejemplo de raíces en los complejos: raíces quintas de la unidad
Raíces quintas de la unidad

Cualquiera de $\omega$, $\omega^2$, $\omega^3$ y $\omega^4$ son raíces primitivas, pero $1$ no es raíz primitiva pues sus potencias sólo son él mismo.

$\triangle$

Las raíces $n$-ésimas de la unidad se utilizan en muchos contextos. Aunque se puede trabajar con ellas de forma explícita, muchas veces se utilizan sólo las propiedades algebraicas que cumplen. A continuación enunciamos algunas.

Teorema. Sea $\omega$ una raíz primitiva $n$-ésima de la unidad. Las raíces $n$-ésimas de la unidad $$\omega_i = \omega^i $$ para $i=0,\ldots,n-1$ satisfacen las siguientes propiedades:

  • Para $n>1$, se tiene que $\omega_0+\ldots+\omega_{n-1}=0$.
  • Para $k=0,1,\ldots,n-1$, se tiene que $$(\omega_k)^{-1}=\overline{\omega_k}=\omega_{n-k}.$$
  • Se tiene que $\omega_0\cdot\ldots\cdot \omega_{n-1} = (-1)^{n+1}$.

Demostración. Empezamos con el primer inciso. Si $n>1$, tenemos que $1$ no es raíz primitiva, así que para el primer inciso sabemos que $\omega\neq 1$. Usamos la fórmula para suma de términos en una progresión geométrica:
\begin{align*}
\omega_0+\omega_1&+\ldots+\omega_{n-1}\\
&= 1+\omega+\ldots+\omega^{n-1}\\
&=\frac{1-\omega^n}{1-\omega}\\
&=\frac{1-1}{1-\omega}\\
&=0.
\end{align*}

Para la segunda parte, notemos que $$\omega_k\omega_{n-k}=\omega^k\omega^{n-k}=\omega^n=1,$$ lo cual prueba una de las igualdades. La otra igualdad se sigue del hecho general que el inverso de un complejo de norma $1$ es su conjugado, cuya demostración queda como tarea moral.

La tercera parte se sigue de la propiedad anterior. Al multiplicar todas las raíces de la unidad, podemos emparejar a cada raíz con su conjugado para obtener producto $1$. Las únicas excepciones es cuando emparejamos a un complejo consigo mismo, es decir, para cuando $\omega_k=\overline{\omega_k}$, lo cual sucede sólo cuando $\omega_k$ es real. Las únicas posibilidades son $1$ ó $-1$. El $1$ no tiene problema pues colabora con un factor $1$. Si $n$ es impar, $-1$ no es raíz $n$-ésima, así que no contribuye al producto. Si $n$ es par sí. Esto muestra lo que queremos pues $(-1)^{n+1}$ es $1$ si $n$ es impar y $-1$ si es par.

$\square$

Para un entero positivo $n$, llamemos $(U_n,\cdot)$ al conjunto de raíces $n$-ésimas de la unidad equipadas con el producto complejo.

Teorema. Para cada entero positivo $n$, se tiene que $(U_n,\cdot)$ es un grupo y es isomorfo a $(\mathbb{Z}_n,+)$.

Demostración. El producto de cualesquiera dos raíces $n$-ésimas es también una raíz $n$-ésima. Por el teorema anterior, los inversos multiplicativos de las raíces $n$-ésimas también son raíces $n$-ésimas. Esto basta para mostrar que se forma un grupo.

Para la segunda parte, notamos que ambos grupos son el grupo cíclico de $n$ elementos. Una correspondencia entre ellos está dada por mandar $[1]_n$ a cualquier raíz primitiva.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Encuentra las raíces cúbicas de $8-8i$ y dibújalas en el plano complejo.
  2. Verifica que las soluciones obtenidas en el teorema de raíces $n$-ésimas en efecto son soluciones.
  3. Muestra el teorema de las raíces $n$-ésimas de la unidad.
  4. Prueba que si $z$ es un complejo de norma $1$, entonces su inverso es su conjugado.
  5. Sea $\omega$ una raíz $n$-ésima primitiva de la unidad. Muestra que $w^k$ es una raíz primitiva si y sólo si $n$ y $k$ son primos relativos, es decir, $\MCD{n,k}=1$. Sugerencia: Usa lo que sabemos de soluciones a ecuaciones diofantinas lineales.
  6. Encuentra de manera explícita la parte real y la parte imaginaria de todas las raíces quintas de la unidad.
    Sugerencia: La ecuación $w^5-1=0$ se puede factorizar como $$(w-1)(w^4+w^3+w^2+w+1)$$ y $w^4+w^3+w^2+w+1$ se puede factorizar como $$\left(w^2+\frac{1+\sqrt{5}}{2}w+1\right)\left(w^2+\frac{1-\sqrt{5}}{2}w+1\right).$$ Usa lo que sabemos de resolver ecuaciones cuadráticas cojmplejas.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Superior II: Problemas de ecuaciones lineales y cambios de coordenadas en los complejos

Por Claudia Silva

Deja un comentario

Introducción

En las entradas anteriores platicamos de cómo resolver sistemas de ecuaciones lineales complejos, y de como pasar de coordenadas polares a rectangulares y viceversa. Ahora veremos un método más para resolver problemas de ecuaciones lineales en los complejos en tres variables. Además, haremos problemas de práctica de estos temas.

La regla de Kramer para tres variables

Cuando platicamos de resolver problemas de ecuaciones lineales complejas en dos variables, vimos que si el determinante no era $0$, entonces podíamos dar la solución de manera explícita. A esto se le conoce como la regla de Kramer. Veremos ahora cuál es la versión de esta regla para tres variables. A continuación enunciamos el método, y más abajo, en el video, se explica un poco más a detalle.

Proposición. Consideremos el siguiente sistema lineal de ecuaciones complejas en variables $x$, $y$ y $z$.
\begin{align*}
ax+by+cz&=j\\
dx+ey+fz&=k\\
gx+hy+iz&=l.
\end{align*}

Supongamos que el determinante $\Delta=\begin{vmatrix} a & b & c\\ d & e & f\\ g & h & i \end{vmatrix}$ no es $0$. Entonces, el sistema tiene una única solución, dada por
\begin{align*}
x&=\frac{\begin{vmatrix} j & b & c\\ k & e & f\\ l & h & i \end{vmatrix}}{\Delta},\\
y&=\frac{\begin{vmatrix} a & j & c\\ d & k & f\\ g & l & i \end{vmatrix}}{\Delta},\\
z&=\frac{\begin{vmatrix} a & b & j\\ d & e & k\\ g & h & l \end{vmatrix}}{\Delta}.
\end{align*}

No veremos la demostración de esta técnica, pues es uno de los temas que estudiarás en álgebra lineal con más generalidad. Sin embargo, veremos algunos ejemplos de cómo se aplica.

Problemas de ecuaciones lineales

Para comenzar, resolveremos un sistema de ecuaciones de dos variables.

Problema. Resuelve en $\mathbb{C}$ el siguiente sistema de ecuaciones:
\begin{align*}
iz+2w&=3+4i\\
2z-iw&=6-3i.
\end{align*}

Pasemos ahora a un ejemplo con tres variables. El el ejemplo 328 del libro Álgebra Superior de Bravo, Rincón, Rincón.

Problema. Resuelve en $\mathbb{C}$ el siguiente sistema de ecuaciones.
\begin{align*}
z_1+z_2+z_3&=6+4i\\
iz_1+(1+i)z_2+(1-i)z_3&=7+4i\\
z_i+iz_2-z_3&=2i.
\end{align*}

El problema está resuelto en los siguientes dos videos.

Problemas de cambio de coordenadas

Finalmente, veremos algunos problemas de cambio entre coordenadas polares y coordenadas rectangulares. Recordemos que la figura clave para cambiar entre coordenadas es la siguiente:

Cambios entre coordenadas polares y rectangulares
Cambio entre coordenadas polares y rectangulares

Problema. Calcula las coordenadas rectangulares del complejo cuyas coordenadas polares son $r=\sqrt{2}$ y $s=45^\circ$, y del complejo cuyas coordenadas polares son $r=3$ y $s=90^\circ$.

Problema. Expresa $7+7i$ y $4+2i$ en coordenadas polares.

Más adelante…

Tarea moral

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Seminario de Resolución de Problemas: Factorización de polinomios

Por Fabian Ferrari

Deja un comentario

Introducción

En la entradas anteriores se trataron algunos temas de identidades algebraicas y se profundizó en el binomio de Newton y la identidad de Gauss. En esta y la siguiente entrada hablaremos de polinomios. Por ahora, comenzaremos recordando las nociones básicas de la aritmética de polinomios y hablando un poco de la factorización de polinomios. Más adelante hablaremos del poderoso teorema de la identidad.

Recordatorio de polinomios

Tenemos que un polinomio de grado $n$, donde $n$ es un número entero no negativo, es una expresión algebraica de la forma

\begin{equation*}
a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0.
\end{equation*}

Dicha expresión también podemos denotarla como

\begin{equation*}
P(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0,
\end{equation*}

en donde $a_n$ es distinto de $0$.

Los elementos $\left\{ a_n, a_{n-1}, … , a_0\right\}$ se conocen como coeficientes. Si $a_n=1$, decimos que el polinomio es mónico.

Nota: El polinomio cuyos coeficientes son todos ceros, se le conoce como el polinomio cero y no tiene grado.

Si dos polinomios son idénticos coeficiente por coeficiente, decimos que dichos polinomios son iguales. Esta noción será de utilidad más adelante en la entrada del teorema de la identidad.

Si todos los coeficientes de un polinomio son enteros, decimos que es un polinomio sobre los enteros. Si los coeficientes son números reales, entonces es un polinomio sobre los reales. De manera similar definimos a los polinomios sobre los racionales, los complejos o incluso sobre $\mathbb{Z}_n$. Aunque parezca irrelevante, conocer las características de los coeficientes de un polinomio, nos da mucha información sobre su constitución. Hay resultados que, por ejemplo, se valen para los polinomios sobre los complejos, pero no para los polinomios sobre los reales.

Otra cosa que es de nuestro interés son las operaciones en los polinomios, y es que al igual que los números enteros, podemos sumar, multiplicar y dividir polinomios.

Algoritmo de la división para polinomios

Para los polinomios, al igual que en los números enteros, existe un algoritmo de la división. Este nos ayudará posteriormente para cuando queramos hacer factorización en polinomios.

Teorema. Sean los polinomios $P(x)$ y $Q(x)$ definidos sobre un campo $\mathbb{K}$ con $Q(x)$ distinto de cero. Entonces existen dos únicos polinomios $C(x)$ y $R(x)$ tales que

\begin{equation*}
P(x)=C(x)Q(x)+R(x),
\end{equation*}

donde $C(x)$ y $R(x)$ son el coeficiente y el residuo respectivamente, resultado de dividir $P(x)$ entre $Q(x)$, y se tiene que $R(x)$ es el polinomio $0$ o bien tiene grado menor o igual al grado de $C(x)$.

Ejemplo. Dados los polinomios $P(x)=x^2-3x-28$ y $Q(x)=x-5$, tenemos que $C(x)=x+2$ y $R(x)=-18$.

En efecto,

\begin{equation*}
x^2-3x-28=(x+2)(x-5)-18.
\end{equation*}

$\square$

Algoritmo de Euclides para polinomios

Al igual que en los enteros, el algoritmo de la división es de ayuda para determinar el máximo común divisor entre dos polinomios: simplemente seguimos los pasos del algoritmo de Euclides. Es por ello que tenemos el siguiente resultado.

Teorema. Si tenemos dos polinomios $P(x)$ y $Q(x)$ sobre un campo $\mathbb{K}$, tenemos que existen polinomios $S(x)$ y $T(x)$ tales que

\begin{equation*}
\MCD{P, Q}= PS+QT.
\end{equation*}

Aquí $\MCD{P, Q}$ es el máximo común divisor de $P(x)$ y $Q(x)$.

Otra forma de ver o de entender el máximo común divisor entre dos polinomios es como el producto de todos aquellos factores que tienen en común.

Problema: Encuentra polinomios $F(x)$ y $G(x)$ tales que

\begin{equation*}
(x^8-1)F(x)+(x^5-1)G(x)=x-1.
\end{equation*}

Sugerencia pre-solución. Recuerda cómo encontrar el máximo común divisor de dos enteros usando el algoritmo de Euclides. Además, usa una factorización para cancelar el factor $x-1$ de la derecha.

Solución. Definamos

\begin{align*}
A(x)&=x^7+x^6+x^5+x^4+x^3+x^2+x+1\\
B(x)&=x^4+x^3+x^2+x+1.
\end{align*}

Notemos que la ecuación es equivalente a

\begin{equation*}
A(x)F(x)+B(x)G(x)=1.
\end{equation*}

Tendría que suceder entonces que $A(x)$ y $B(x)$ sean primos relativos.

Aplicando el algoritmo de la división repetidamente, tenemos lo siguiente:

\begin{align*}
A(x)&=x^3B(x)+(x^2+x+1)\\
B(x)&=x^2(x^2+x+1)+(x+1)\\
x^2+x+1&=x(x+1)+1.
\end{align*}

Esto muestra que $A(x)$ y $B(x)$ son primos relativos, así que la combinación lineal que buscamos debe existir. Para encontrarla de manera explícita, invertimos los pasos. Trabajando hacia atrás, tenemos que

\begin{equation*}
\begin{split}
1 & =(x^2+x+1)-x(x+1)\\
& =(x^2+x+1)-x(B(x)-x^2(x^2+x+1))\\
& =(x^2+x+1)(x^3+1)-xB(x)\\
& =(x^3+1)(A(x)-x^3(B(x))-xB(x)\\
& =(x^3+1)A(x)-x^3(x^3+1)B(x)-xB(x)\\
& =(x^3+1)A(x)+(-x^6-x^3-x)B(x)
\end{split}
\end{equation*}

Así que podemos tomar a $F(x)=x^3+1$ y $G(x)=-x^6-x^3-x$.

$\square$

El teorema del factor

Sea $P(x)$ un polinomio sobre un dominio entero $D$. Decimos que un elemento $a$ de $D$ es raíz del polinomio $P(x)$ si $P(a)=0$. Si aplicamos el algoritmo de la división en los polinomios $P(x)$ y $x-a$ obtenemos el siguiente teorema, que es fundamental en la factorización de polinomios.

Teorema El elemento $a$ es raíz de $P(x)$ si y solo si $(x-a)$ es factor de $P(x)$.

Veamos cómo aplicar este teorema en un ejemplo concreto.

Problema. Dado $\omega=\cos\left(\frac{2\pi}{n}\right)+i\sin\left(\frac{2\pi}{n}\right)$, prueba que

\begin{equation*}
x^{n-1}+\ldots+x+1=(x-\omega)(x-\omega^2)\cdot\ldots\cdot(x-\omega^{n-1}).
\end{equation*}

Sugerencia pre-solución. Recuerda los resultados básicos de aritmética de los números complejos.

Solución. Por De Moivre tenemos que si

\begin{equation*}
\omega=\cos\left(\frac{2\pi}{n}\right)+i\sin\left(\frac{2\pi}{n}\right)=e^{\frac{2\pi i}{n}}
\end{equation*}

entonces $ \{1, \omega, \omega^2,…,\omega^{n-1}\}$ son raíces de $x^n-1=0$. Además, como $e^{\pi i}=-1$, tenemos que $\omega^n=1$.

Así, tenemos que $\omega^{n+1}=\omega$ y de manera general $\omega^{n+k}=\omega^k$.

Por otro lado,

\begin{equation*}
x^n-1=(x-1)(x^{n-1}+\ldots+x+1)
\end{equation*}

Y como $ \{1, \omega, \omega^2,\ldots,\omega^{n-1}\}$ son raíces de $x^n-1$, tenemos entonces que $\{\omega, \omega^2,\ldots,\omega^{n-1}\}$ deben de ser las raíces de $$x^{n-1}+\ldots+x+1.$$

Aplicando repetidamente el teorema del factor, tenemos que

\begin{equation*}
x^{n-1}+\ldots+x+1=(x-\omega)(x-\omega^2)\cdot\ldots\cdot(x-\omega^{n-1}).
\end{equation*}

$\square$

Un problema para números algebraicos

Un número real es algebraico si es raíz de un polinomio sobre los números enteros.

Problema. Prueba que $\sqrt{2}+\sqrt{3}$ es un número algebraico.

Sugerencia pre-solución. Realiza operaciones de suma, resta y producto con $\sqrt{2}+\sqrt{3}$ y con enteros. Ve si puedes encontrar un patrón de cómo se comportan.

Solución. Tenemos que encontrar un polinomio $P(x)$ sobre los número enteros de tal forma que $P(\sqrt{2}+\sqrt{3})=0$.

Si consideramos $x=\sqrt{2}+\sqrt{3}$, entonces $x^2=5+2\sqrt{6}$

Para $P(x)=x^2-5$, tenemos que $P(\sqrt{2}+\sqrt{3})=2\sqrt{6}$

Así,

\begin{equation*}
(P(\sqrt{2}+\sqrt{3}))^2=(2\sqrt{6})^2=144.
\end{equation*}

Ahora, si consideramos el polinomio

\begin{equation*}
Q(x)=(P(x))^2-144.
\end{equation*}

Tenemos que

\begin{equation*}
Q(\sqrt{2}+\sqrt{3})=(P(\sqrt{2}+\sqrt{3}))^2-144=0.
\end{equation*}

Por lo tanto como el polinomio $Q(x)=x^4-10x^2-119$ es un polinomio sobre los enteros, y como $Q(\sqrt{2}+\sqrt{3})=0$ concluimos que $\sqrt{2}+\sqrt{3}$ es un número algebraico.

$\square$

Más problemas

Puedes encontrar más problemas de aritmética y factorización de polinomios en la Sección 4.2 del libro Problem Solving through Problems de Loren Larson.

Álgebra Lineal I: Producto interior y desigualdad de Cauchy-Schwarz

Por Leonardo Ignacio Martínez Sandoval

11 respuestas

Introducción

Anteriormente, platicamos acerca de formas bilineales y de formas cuadráticas. Ahora veremos un tipo de formas bilineales especiales: las positivas y las positivas definidas. Las formas positivas definidas nos ayudan a definir qué es un producto interior. Esta es una noción fundamental que más adelante nos ayudará a definir distancias y ángulos.

Formas bilineales positivas y positivas definidas

Para hablar de geometría en espacios vectoriales, la siguiente noción es fundamental. Es importante notar que es una definición únicamente para formas bilineales simétricas.

Definición. Sea $b:V\times V\to \mathbb{R}$ una forma bilineal simétrica.

  • Diremos que $b$ es positiva si $b(x,x)\geq 0$ para todo vector $x$ de $V$.
  • Diremos que $b$ es positiva definida si $b(x,x)>0$ para todo vector $x\neq 0$ de $v$.

Tenemos una noción análoga para formas cuadráticas.

Definición. Sea $q:V\to \mathbb{R}$ una forma cuadrática con forma polar $b$. Diremos que $q$ es positiva si $b$ lo es, y diremos que es positiva definida si $b$ lo es.

Ejemplo 1. Como ya vimos antes, el producto punto de $\mathbb{R}^n$ es una forma bilineal simétrica. También es positiva definida, pues si tenemos $x=(x_1,\ldots,x_n)$, tenemos que $$x\cdot x = x_1^2+\ldots+x_n^2\geq 0,$$ y esta es una igualdad si y sólo si $x_1=\ldots=x_n=0$, lo cual sucede si y sólo si $x=0$.

$\triangle$

Ejemplo 2. Considera $V=\mathbb{R}_2[x]$ y consideremos la forma bilineal $b$ dada por $$b(p,q)=p(0)q(1)+p(1)q(0).$$ Esta es una forma bilineal simétrica pues \begin{align*}b(p,q)&=p(0)q(1)+p(1)q(0)\\&=q(0)p(1)+q(1)p(0)\\&=b(q,p).\end{align*} Notemos que $$b(p,p)=2p(0)p(1),$$ que no necesariamente es positivo. Por ejemplo, si tomamos el polinomio $p(x)=x-\frac{1}{2}$, tenemos que \begin{align*}b(p,p)&=2p(0)p(1)\\&=-2\cdot\frac{1}{2}\cdot\frac{1}{2}\\&=-\frac{1}{2}.\end{align*} Así, esta es una forma bilineal simétrica, pero no es positiva (y por lo tanto tampoco es positiva definida).

$\triangle$

Problema. Considera la forma cuadrática $Q$ en $M_{2}(\mathbb{R})$ que suma el cuadrado de las entradas de la diagonal de una matriz, es decir, aquella dada por $$Q\begin{pmatrix} a & b\\c & d\end{pmatrix}=a^2+d^2.$$ Determina su forma polar y si es positiva o positiva definida.

Solución. Para encontrar la forma polar $B$ de $Q$, usamos la identidad de polarización
\begin{align*}
B&\left(\begin{pmatrix}a&b\\c&d\end{pmatrix},\begin{pmatrix} e & f\\ g & h \end{pmatrix}\right)\\
&=\frac{(a+e)^2+(d+h)^2-a^2-e^2-d^2-h^2}{2}\\
&=\frac{2ae+2dh}{2}\\
&=ae+dh.
\end{align*}

Como $Q\begin{pmatrix}a&b\\c&d\end{pmatrix}=a^2+d^2\geq 0$, tenemos que $Q$ (y $B$) son positivas. Sin embargo, $Q$ no es positiva definida (ni $B$), pues por ejemplo, $$Q\begin{pmatrix}0&1\\1&0\end{pmatrix} = 0.$$

Producto interior

Estamos listos para definir aquellos espacios sobre los que podemos hacer geometría.

Definición. Sea $V$ un espacio vectorial sobre $\mathbb{R}$

  • Un producto interior en $V$ es una forma bilineal simétrica y positiva definida.
  • Decimos que $V$ es un espacio Euclideano si es de dimensión finita y está equipado con un producto interior.

Estamos siguiendo la convención del libro de Titu Andreescu, en donde es importante pedir que $V$ sea de dimensión finita para ser Euclideano.

Cuando estamos hablando de espacios con producto interior, o de espacios Euclideanos, tenemos una forma bilineal simétrica y positiva definida $b$. Sin embargo, en vez de usar constantemente $b(x,y)$, para simplificar la notación usaremos simplemente $\langle x, y\rangle$.

Definición. Si $V$ es un espacio con producto interior $\langle \cdot,\cdot \rangle$, definimos la norma de un vector $x$ como $$\Vert x \Vert =\sqrt{\langle x, x \rangle}.$$

Ejemplo. Como dijimos arriba, el producto punto en $\mathbb{R}^n$ es una forma bilineal simétrica, así que es un producto interior. Como $\mathbb{R}^n$ es de dimensión finita, entonces es un espacio Euclideano.

La norma de un vector $x=(x_1,\ldots,x_n)$ está dada por $\Vert x \Vert = \sqrt{x_1^2+\ldots+x_n^2},$ y geométricamente se interpreta como la distancia de $x$ al origen.

Un ejemplo más concreto es $\mathbb{R}^4$, en donde la norma del vector $(1,2,3,1)$ es $\sqrt{1^2+2^2+3^2+1^2}=\sqrt{15}$.

$\triangle$

La notación de producto interior quizás te recuerde la notación que se usa cuando hablamos de dualidad. Sin embargo, es muy importante que distingas los contextos. En el caso de dualidad, tenemos $$\langle \cdot, \cdot \rangle: V^\ast\times V \to \mathbb{R},$$ y en este contexto de producto interior tenemos $$\langle \cdot, \cdot \rangle: V\times V \to \mathbb{R}.$$ Más adelante, puede que te encuentres en tu preparación matemática con el teorema de representación de Riesz, a partir del cual tendrá sentido que se use la misma notación.

Desigualdad de Cauchy-Schwarz

A continuación presentamos un resultado fundamental es espacios con formas bilineales positivas y positivas definidas.

Teorema (desigualdad de Cauchy-Schwarz). Sea $b:V\times V\to \mathbb{R}$ una forma bilineal simétrica y $q$ su forma cuadrática asociada.

  • Si $b$ es positiva, entonces para todo $x$ y $y$ en $V$ tenemos que $$b(x,y)^2\leq q(x)q(y).$$ Si $x$ y $y$ son linealmente dependientes, se alcanza la igualdad.
  • Además, si $b$ es positiva definida y $x$ y $y$ son linealmente independientes, entonces la desigualdad es estricta.

Demostración. Supongamos primero solamente que $b$ es positiva. Consideremos la función $f:\mathbb{R}\to \mathbb{R}$ dada por $f(t)=q(x+ty)$. Como $q$ es forma cuadrática positiva, tenemos que $f(t)\geq 0$ para todo real $t$. Por otro lado, expandiendo y usando que $b$ es simétrica, tenemos que
\begin{align*}
f(t)&=q(x+ty)\\
&=b(x+ty,x+ty)\\
&=b(x,x)+2b(x,y)\cdot t + b(y,y) \cdot t^2\\
&=q(x) + 2b(x,y)\cdot t + q(y) \cdot t^2.
\end{align*}

En esta expresión, $q(x)$, $2b(x,y)$ y $q(y)$ son reales, así que $f(t)$ es un polinomio cuadrático en $t$. Como $f(t)\geq 0$ para todo $t$ en $\mathbb{R}$, el discriminante de este polinomio es no positivo, en otras palabras, $$(2b(x,y))^2-4q(x)q(y)\leq 0.$$

Sumando $4q(x)q(y)$ y dividiendo entre $4$ ambos lados de la desigualdad, obtenemos que $$b(x,y)^2\leq q(x)q(y),$$ la cual es la desigualdad que queremos.

Si $x$ y $y$ son linealmente dependientes, podemos despejar a uno en términos del otro. Sin perder generalidad, podemos suponer que $x=\alpha y$. En este caso, $$b(\alpha y,y)^2=\alpha^2 b(y,y)=q(\alpha(y))q(y),$$ así que se da la igualdad.

Ahora, supongamos además que $b$ es positiva definida y que se da la igualdad. Si esto sucede, el discriminante del polinomio cuadrático de arriba es igual a $0$ y por lo tanto el polinomio tiene una raíz $t$. En otras palabras, $q(x+ty)=0$. Pero como $q$ es positiva definida, esto implica que $x+ty=0$, de donde $x$ y $y$ son linealmente dependientes. Así, si $x$ y $y$ son linealmente independientes, tenemos que la desigualdad es estricta.

$\square$

El siguiente caso particular es uno de los más importantes y los más usados, por lo cual amerita que lo enunciemos separadamente.

Corolario. Sea $V$ un espacio vectorial sobre $\mathbb{R}$ equipado con un producto interior $\langle \cdot, \cdot \rangle$. Para cualesquiera $x,y$ en $V$ se cumple $|\langle x, y \rangle| \leq \Vert x \Vert \cdot \Vert y \Vert$.

Puede que te preguntes por qué enfatizamos los resultados de desigualdades. En varias partes de tu formación matemática trabajarás con espacios vectoriales en donde quieres hacer cálculo. Ahí, se define la convergencia y los límites en términos de una norma. Las desigualdades que probemos para espacios vectoriales son útiles para cuando se quiere demostrar la validez de ciertos límites. Más adelante mencionaremos algunas cosas adicionales al respecto.

Más adelante…

En esta entrada definimos el concepto de producto interior y vimos cómo el producto interior induce una norma en el espacio vectorial. El concepto de norma nos permite generalizar la noción de distancia y esto nos permitirá ver cómo se puede hacer cálculo en espacios vectoriales.

En las siguientes entradas veremos cómo se define esta norma para diferentes espacios vectoriales con diferentes productos interiores. Podremos ver entonces cómo se generalizan otras nociones que ya hemos visto en cursos anteriores; como el concepto de ángulo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Considera la función $q(w,x,y,z)=wx+yz$. Muestra que es una forma cuadrática en $\mathbb{R}^4$. Encuentra su forma polar y determina si es una forma cuadrática positiva y/o positiva definida.
  • Muestra que $$q(w,x,y,z)=x^2+y^2+z^2+xy+yz+zx$$ es una forma cuadrática en $\mathbb{R}^4$ y determina si es positiva y/o positiva definida.
  • Considera $V=\mathcal{C}[0,1]$ el espacio vectorial de funciones continuas en el intervalo $[0,1]$. Muestra que $$\langle f,g\rangle = \int_0^1 f(x)g(x)\, dx$$ define un producto interior en $V$. ¿Es $V$ un espacio Euclideano? Determina la norma de la función $f(x)=x^3$.
  • Sea $V=\mathbb{R}_2[x]$ el espacio vectorial de polinomios con coeficientes reales y de grado a lo más $1$. Muestra que $$\langle p,q\rangle = p(0)q(0)+p(1)q(1)+p(2)q(2)$$ hace a $V$ un espacio Euclideano.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»