Archivo de la categoría: Matemáticas

Posts de matemáticas, la ciencia más cercana a las artes.

Sucesiones de Cauchy

Por Lizbeth Fernández Villegas

Deja un comentario

$ \textit{ MATERIAL EN REVISIÓN}$

Introducción

En otros cursos, donde el conjunto de los números reales es el protagonista, se suele hablar de una propiedad: El conjunto $\mathbb{R}$ es completo. Esto puede concluirse a partir de 3 situaciones que son válidas en $\mathbb{R}:$

  1. El axioma del supremo o de completitud.
  2. La intersección de intervalos cerrados encajados cuya longitud tiende a cero es no vacía.
  3. Las sucesiones de Cauchy son convergentes en $\mathbb{R}$.

En las siguientes entradas veremos cómo las propiedades $2$ y $3$ son generalizadas a los espacios métricos. La primera no es posible, por ejemplo, en conjuntos métricos que no están ordenados. Pero tampoco basta que un conjunto tenga un orden en sus elementos para que todos sus subconjuntos acotados tengan un supremo en el conjunto. Este es el caso de algunos conjuntos acotados en el subespacio $\mathbb{Q}$ que tendrán supremo en $\mathbb{R}$ pero no en $\mathbb{Q}.$ ¿Puedes dar un ejemplo?

Recordemos que en la entrada de Convergencia vista anteriormente, hablamos de sucesiones $(x_n)_{n \in \mathbb{N}}\,$ que se aproximan a un punto $x$ en un espacio métrico $(X,d)$. Según la definición, $x_n \to x$ significa que dado $\varepsilon >0$ existe $N \in \mathbb{N}$ que cumple para cada $n \geq N, \, d(x_n,x)< \varepsilon.$ Esta definición compara la distancia entre cada punto de la sucesión con un punto fijo $x$. Sin embargo, ¿qué podemos decir de la distancia entre cualesquiera dos puntos de la sucesión?

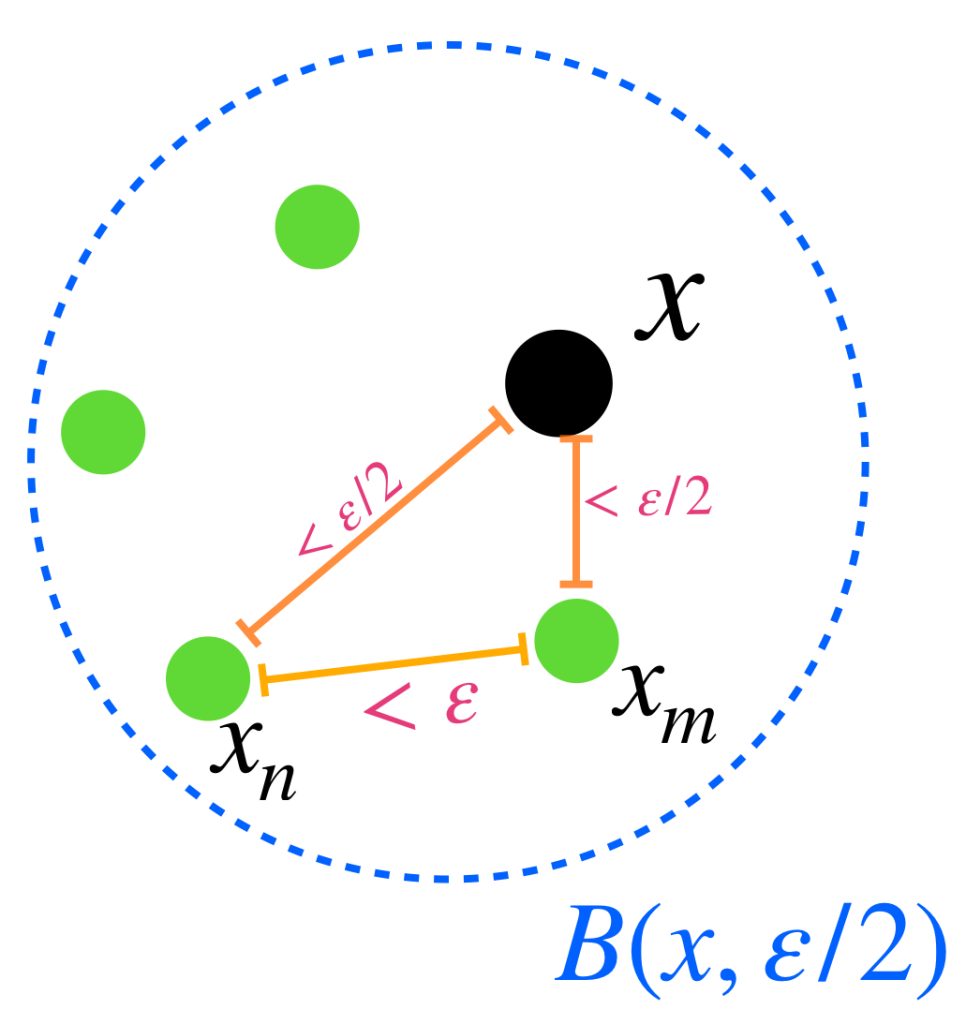
Sea $\varepsilon>0$. En una sucesión convergente $(x_n)_{n \in \mathbb{N}}\,$ ocurrirá que para algún $N \in \mathbb{N}$ si $n \geq N$ entonces $d(x_n,x)< \frac{\varepsilon}{2}.$

Sucesión convergente

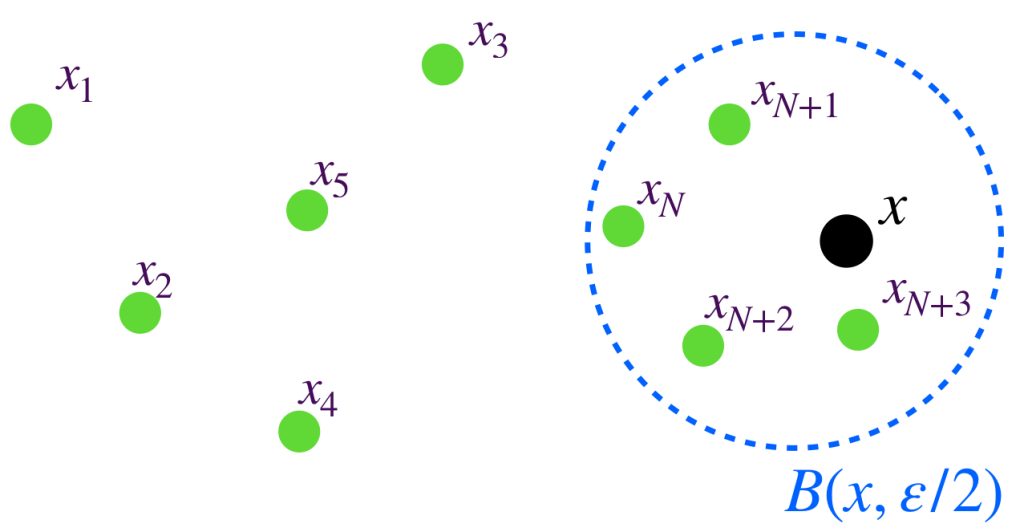
Podemos ver que mientras más se aproximan los puntos de la sucesión al punto de convergencia $x$, los puntos de la sucesión se acercan cada vez más entre ellos también.

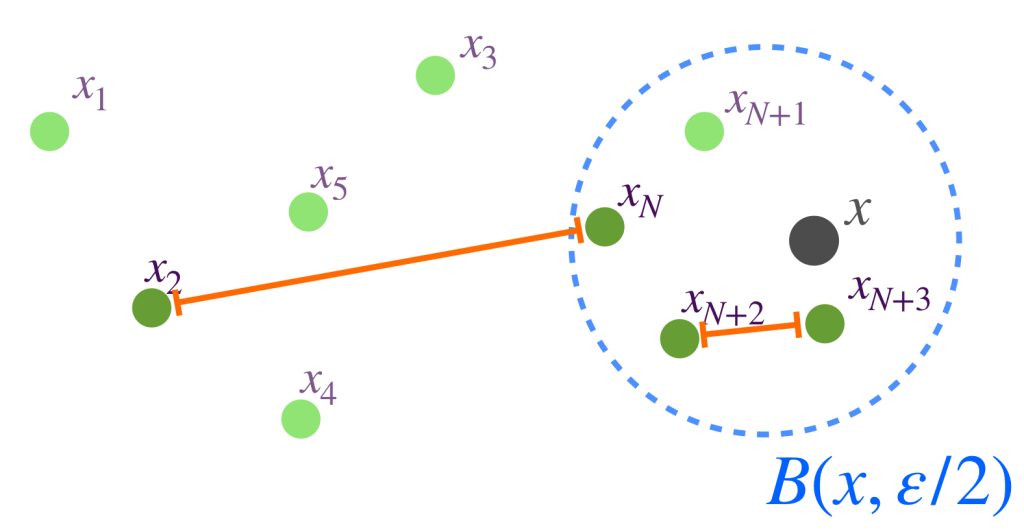
Los puntos de la bola abierta son más cercanos

Más aún, la desigualdad del triángulo garantiza que si $n,m \geq N$ entonces:
$$d(x_n,x_m) \leq d(x_n,x) + d(x,x_m) < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}<\varepsilon.$$ como lo expresa la siguiente imagen:

Hay puntos con distancias arbitrariamente pequeñas

Esto indica que es posible identificar un término de la sucesión, a partir del cual las distancias entre cualesquiera dos de ellos será arbitrariamente pequeña. Aunque ya vimos que esto pasa en sucesiones convergentes también puede ocurrir en algunas que no lo son. Cuando las sucesiones tienen esta característica son denominadas como sigue:

Definición sucesión de Cauchy: Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de un espacio métrico $(X,d).$ Decimos que es una sucesión de Cauchy si satisface la condición de Cauchy que es que:
$\forall \, \varepsilon>0,$ existe $N \in \mathbb{N}$ tal que $\forall \, n,m \geq N$ ocurre que $d(x_n,x_m)< \varepsilon.$

Proposición: Si una sucesión es de Cauchy entonces es acotada.

Demostración:
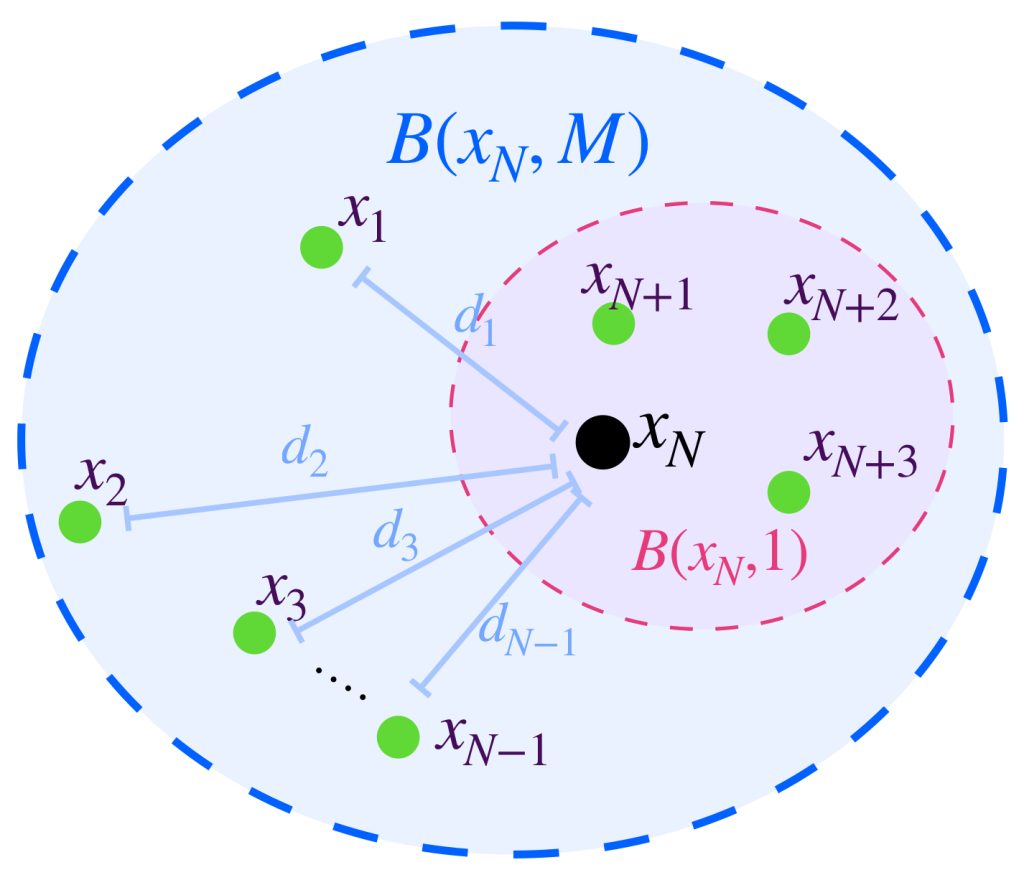
Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy. Entonces para $\varepsilon=1$ existe $N \in \mathbb{N}$ tal que $\forall \, n,m>N$ se cumple que $d(x_n,x_m)<1$ Entonces, $\forall \, m \geq N, d(x_N,x_m)< 1.$ Si definimos las distancias faltantes en los términos de la sucesión, es decir, las distancias $d_i= d(x_N,x_i)$ con $i=1,…,N-1$ y hacemos $M = máx \{ d_i,1 \} , i=1,…,N-1$ se concluye que existe una bola abierta que contiene todos los términos de la sucesión, la bola $B(x_N,M)$.

Una sucesión de Cauchy es acotada

A pesar de que una sucesión convergente es de Cauchy, no toda sucesión de Cauchy es convergente.

Ejemplo: La sucesión $(\frac{1}{n})_{n \in \mathbb{N}}$ en el subespacio euclideano $(0,1]$ es de Cauchy, pero no es convergente en $(0,1].$ La demostración se deja como ejercicio.

No obstante tenemos el siguiente resultado:

Proposición: Sea $(x_n)_{n \in \mathbb{N}}$ una sucesión de Cauchy en el espacio euclidiano $\mathbb{R}^n$, entonces la sucesión también es convergente.

Demostración:
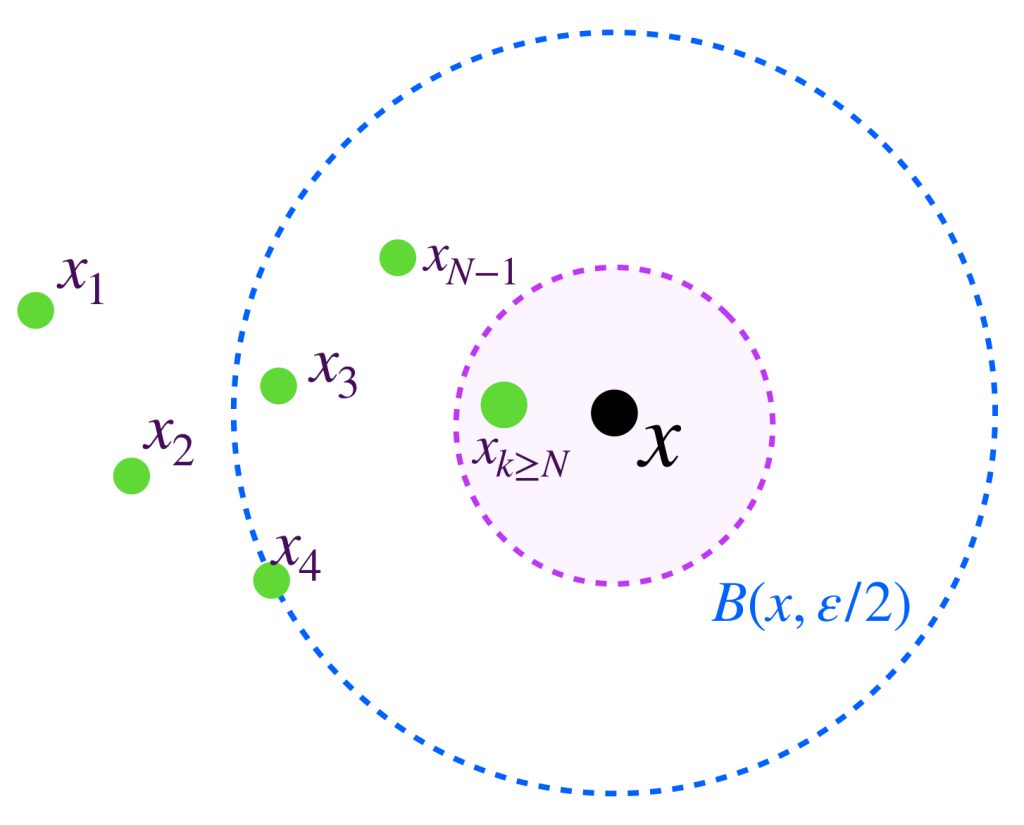
Si el conjunto de términos de la sucesión dado por $\{ x_n \} :=\{x_n:n \in \mathbb{N}\}$ es finito entonces es convergente. (Ejercicio de la tarea moral de la entrada de Convergencia). Pero si es infinito entonces, al ser también acotado (por la proposición anterior) se sigue que el conjunto de los términos de la sucesión tiene un punto de acumulación $x \in \mathbb{R}^n$. Esto es resultado del teorema de Bolzano-Weierstrass, que se ve en los cursos de cálculo y dice que todo conjunto infinito acotado en $\mathbb{R}^n$ tiene un punto de acumulación. (La demostración puede consultarse en el libro «Análisis Matemático, Introducción Moderna al Cálculo Superior» de Tom. M. Apóstol).

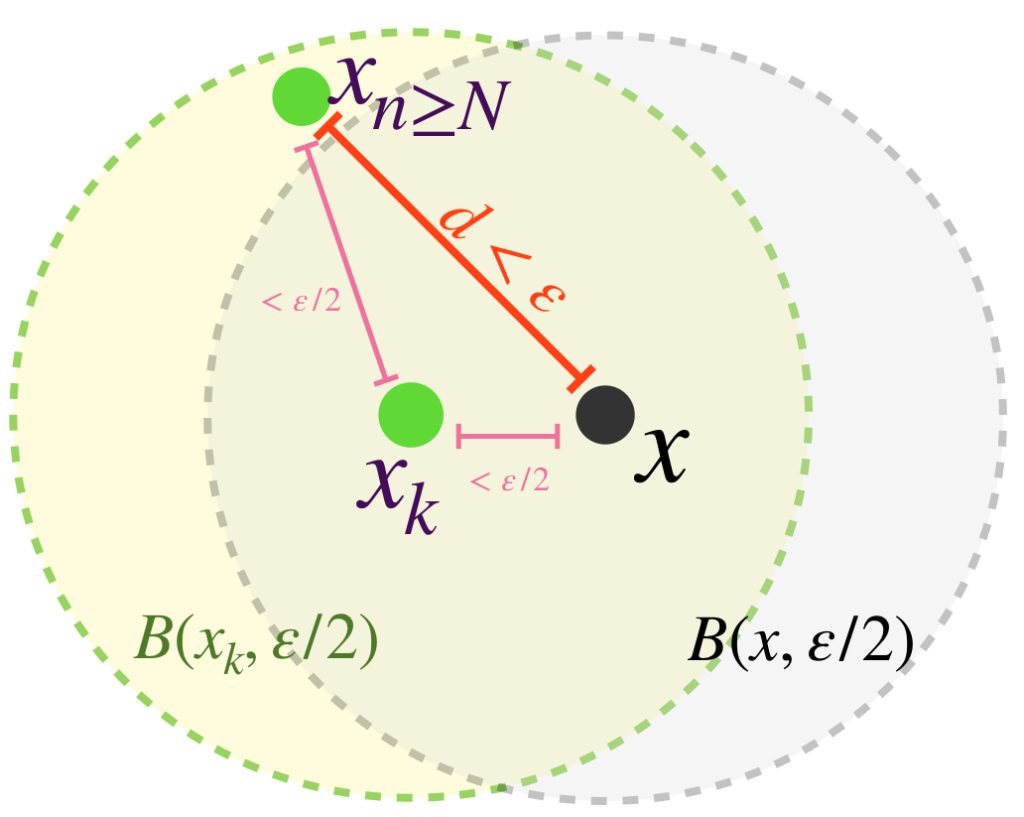
Sea $\varepsilon >0$. Como $(x_n)$ es de Cauchy entonces existe $N \in \mathbb{N}$ tal que $\forall \, n,m \geq N$ ocurre que $d(x_n,x_m)<\frac{\varepsilon}{2}$.

Como $x$ es punto de acumulación del conjunto $\{x_n\}$ podemos garantizar que existe un término de la sucesión $x_k \in B(x,\frac{\varepsilon}{2})$ con $k \geq N.$ (Se te pedirá argumentar esto al final de esta sección).

Existe $x_k \in B(x,\frac{\varepsilon}{2})$

Entonces, $\forall \, n \geq N$
\begin{align*}
d(x_n,x) &\leq d(x_n,x_k)+d(x_k,x) \\
&\leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2}\\
&= \varepsilon
\end{align*}
Por lo tanto $x_n \to x$.

$x_n \to x$

Finalizamos esta sección con la siguiente:

Proposición: Sea $(X,d)$ un espacio métrico y $(x_n)_{n \mathbb{N}}$ una sucesión de Cauchy en $X$. Entonces $(x_n)$ es convergente si y solo si tiene una subsucesión convergente.

Demostración: Queda como ejercicio.

Más adelante…

Ya que conocemos el concepto de las sucesiones de Cauchy procederemos a explorar espacios donde este tipo de sucesiones sí es convergente. Esto motiva la definición de espacio métrico completo que conoceremos en la siguiente entrada.

Tarea moral

  1. Demuestra que la sucesión $(\frac{1}{n})_{n \in \mathbb{N}}$ en el subespacio euclideano $(0,1]$ es de Cauchy, pero no es convergente en $(0,1].$
  2. En la demostración de la proposición anterior, prueba que que existe un término de la sucesión $(x_n)$ de $\mathbb{R}^n$, digamos $x_k$ tal que $x_k \in B(x,\frac{\varepsilon}{2})$ con $k \geq N.$
  3. Demuestra que si $(x_n)_{n \mathbb{N}}$ es una sucesión de Cauchy en un espacio $X$, entonces $(x_n)$ es convergente si y solo si tiene una subsucesión convergente.
  4. Sea $X = [1,\infty)$ y sea $d(x,y)=|\frac{1}{x}-\frac{1}{y}|$. Demuestra que $d$ es una métrica en $X.$
  5. Para cada $n \in \mathbb{N}$ definimos $x_n=n+1$. Prueba que la sucesión $(x_n)$ es de Cauchy en el espacio métrico del ejercicio anterior.

Enlaces

Geometría Moderna II: Principio de dualidad y Triángulo autopolar

Por Armando Arzola Pérez

Deja un comentario

Introducción

Gracias a la relación de polos y polares con respecto a una circunferencia, se tenían correspondencias entre todos los puntos y todas las rectas del plano. Por lo cual nace el Principio de dualidad. Así mismo analizaremos el Triángulo Autopolar junto con algunas propiedades.

Principio de Dualidad

El principio de Dualidad, donde la propiedad que nos dé como resultado de intercambiar las palabras de recta y punto resulta verdadera, además de que guarda sus propiedades.

Por ejemplo, se tiene la siguiente dualidad del teorema con respecto a su corolario.

Teorema. Dada una circunferencia, la polar de $P$ pasa por $Q$, entonces la polar de $Q$ pasa por $P$.

Corolario. Dada una circunferencia, sean $p$ y $q$ rectas tales que, el polo de $p$ está en $q$, entonces el polo de $q$ está en $p$.

Se puede ver que ambos son duales, se puede dar un ejemplo más sencillo.

Ejemplo. La unión de dos puntos es una recta, entonces la intersección de dos rectas es un punto.

Triángulo Autopolar

Definición. Se define como triángulo autopolar a aquel que, con respecto a una circunferencia, se tiene que cada vértice es el polo del lado opuesto, de tal modo que cada lado es polar del vértice opuesto.

Construcción. Se tiene una circunferencia $C(O,r)$, tomemos un punto $A$ dentro de la circunferencia y tracemos su inverso $A’$ y $a$ su polar. Ahora tomemos un punto $B$ en $a$ tal que $A’ \neq B$ y trazamos $b$ su polar, y por el Teorema Fundamental de Polos y Polares se tiene que $b$ pasa por $A$. Además, a la intersección de $a$ y $b$ la llamaremos $C$, y su polar de $c$ pasa por $A$ y $B$ puntos.

De esta forma tenemos el $ \triangle ABC$ es autopolar con respecto a $C(O,r)$.

Triángulo Autopolar

$\square$

Propiedades

Se tienen varias propiedades del triángulo autopolar.

1.- El ortocentro del triángulo autopolar es el centro de la circunferencia.

Demostración. De la figura anterior se tiene que:

La polar de $A$ es $a$ que es el lado $BC$ del $ \triangle ABC$ y $BC \perp OA$ por $A’$ inverso de $A$.

La polar de $B$ es $b$ que es el lado $CA$ del $ \triangle ABC$ y $CA \perp OB$ por $B’$ inverso de $B$.

La polar de $C$ es $c$ que es el lado $AB$ del $ \triangle ABC$ y $AB \perp OC$ por $C’$ inverso de $C$.

Por lo cual $AA’$, $CC’$ y $BB’$ son las alturas del $ \triangle ABC$ y estas se intersecan en $O$.

Por lo tanto, $O$ es el ortocentro del $\triangle ABC$.

$\square$

2.- Uno de sus vértices está dentro de la circunferencia y los otros dos fuera de esta.

3.- El ángulo del triángulo cuyo vértice está en la circunferencia es obtuso.

Más adelante…

Se abordará el tema de circunferencia Polar, en el cual veremos su relación con polos y polares.

Entradas relacionadas

Álgebra Lineal II: Aplicaciones de la forma canónica de Jordan

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En las entradas anteriores demostramos que cualquier matriz (o transformación lineal) tiene una y sólo una forma canónica de Jordan. Además, explicamos cómo se puede obtener siguiendo un procedimiento específico. Para terminar nuestro curso, platicaremos de algunas de las consecuencias del teorema de Jordan.

Clasificación de matrices por similaridad

Una pregunta que aún no hemos podido responder es la siguiente: si nos dan dos matrices $A$ y $B$ en $M_n(F)$, ¿son similares? Con la maquinaria desarrollada hasta ahora podemos dar una muy buena respuesta.

Proposición. Sean $A$ y $B$ matrices en $M_n(F)$ tales que el polinomio característico de $A$ se divide en $F$. Entonces, $A$ y $B$ son similares si y sólo si se cumplen las siguientes dos cosas:

  • El polinomio característico de $B$ también se divide en $M_n(F)$ y
  • $A$ y $B$ tienen la misma forma canónica de Jordan.

Demostración. Sea $J$ la forma canónica de Jordan de $A$.

Si $A$ y $B$ son similares, como $A$ es similar a $J$, se tiene que $B$ es similar a $J$. Entonces, $B$ tiene el mismo polinomio característico que $A$ y por lo tanto se divide en $F$. Además, como $J$ es similar a $B$, entonces por la unicidad de la forma canónica de Jordan, precisamente $J$ es la forma canónica de Jordan de $B$. Esto es un lado de nuestra proposición.

Supongamos ahora que el polinomio característico de $B$ también se divide en $M_n(F)$ y que la forma canónica de Jordan de $B$ también es $J$. Por transitividad de similaridad, $A$ es similar a $B$.

$\square$

Veamos un ejemplo de cómo usar esto en un problema específico.

Problema. Encuentra dos matrices en $M_2(\mathbb{R})$ que tengan como polinomio característico a $x^2-3x+2$, pero que no sean similares.

Solución. Las matrices $A=\begin{pmatrix} 1 & 0 \\ 0 & 2 \end{pmatrix}$ y $B=\begin{pmatrix} 1 & 1 \\ 0 & 2 \end{pmatrix}$ ya están en forma canónica de Jordan y son distintas, así que por la proposición anterior no pueden ser similares. Además, por ser triangulares superiores, en ambos casos el polinomio característico es $$(X-1)(X-2)=X^2-3X+2.$$

$\triangle$

El problema anterior fue sumamente sencillo. Piensa en lo difícil que sería argumentar con cuentas de producto de matrices que no hay ninguna matriz $P\in M_2(\mathbb{R})$ tal que $A=P^{-1}B P$.

Forma canónica de Jordan «para cualquier matriz»

Como en $\mathbb{C}[X]$ todos los polinomios se dividen, entonces tenemos el siguiente corolario del teorema de Jordan.

Corolario. Toda matriz en $M_n(\mathbb{C})$ tiene una única forma canónica de Jordan.

Aquí $\mathbb{C}$ es muy especial pues es un campo completo, es decir, en el cual cualquier polinomio no constante tiene por lo menos una raíz. En general esto no es cierto, y es muy fácil dar ejemplos: $x^2-2$ no tiene raíces en $\mathbb{Q}$ y $x^2+1$ no tiene raíces en $\mathbb{R}$.

Sin embargo, existe toda un área del álgebra llamada teoría de campos en donde se puede hablar de extensiones de campos. Un ejemplo de extensión de campo es que $\mathbb{C}$ es una extensión de $\mathbb{R}$ pues podemos encontrar «una copia de» $\mathbb{R}$ dentro de $\mathbb{C}$ (fijando la parte imaginaria igual a cero).

Un resultado importante de teoría de campos es el siguiente:

Teorema. Sea $F$ un campo y $P(X)$ un polinomio en $F[X]$. Existe una extensión de campo $G$ de $F$ tal que $P(X)$ se divide en $G$.

¿Puedes notar la consecuencia que esto trae para nuestra teoría de álgebra lineal? Para cualquier matriz en $M_n(F)$, podemos considerar a su polinomio característico y encontrar campo $G$ que extiende a $F$ en donde el polinomio se divide. Por el teorema de Jordan, tendríamos entonces lo siguiente.

Corolario. Sea $A$ una matriz en $M_n(F)$. Entonces, $A$ tiene una forma canónica de Jordan en un campo $G$ que extiende a $F$.

Por supuesto, la matriz $P$ invertible que lleva $A$ a su forma canónica quizás sea una matriz en $M_n(G)$.

Toda matriz compleja es similar a su transpuesta

Ya demostramos que para cualquier matriz $A$ en $M_n(F)$ se cumple que $\chi_A(X)=\chi_(A^T)(X)$. Esto implica que $A$ y su transpuesta $A^T$ tienen los mismos eigenvalores, traza y determinante. También vimos que $\mu_A(X)=\mu_{A^T}(X)$. Las matrices $A$ y $A^T$ comparten muchas propiedades. ¿Será que siempre son similares? A continuación desarrollamos un poco de teoría para resolver esto en el caso de los complejos.

Proposición. Sea $J_{\lambda,n}$ un bloque de Jordan en $M_n(F)$. Entonces, $J_{\lambda,n}$ y $J_{\lambda,n}^T$ son similares.

Demostración. Para bloques de Jordan, podemos dar explícitamente la matriz de similitud. Es la siguiente matriz, con unos en la diagonal no principal:

$$P=\begin{pmatrix} 0 & 0 & \ldots & 0 & 1 \\ 0 & 0 & \ldots & 1 & 0 \\ \vdots & & \ddots & \vdots & \\ 0 & 1 & \ldots & 0 & 0 \\ 1 & 0 & \ldots & 0 & 0 \end{pmatrix}.$$

Esta matriz es invertible, su inversa es ella misma y cumple lo siguiente (ver ejercicios). Si $A$ es una matriz en $M_n(F)$, entonces:

  • Si $A$ tiene columnas $C_1,\ldots, C_n$, entonces $AP$ tiene columnas $C_n, \ldots, C_1$.
  • Si $A$ tiene filas $R_1,\ldots, R_n$, entonces $PA$ tiene filas $R_n, \ldots, R_1$.

Para los bloques de Jordan, si revertimos el orden de las filas y luego el de las columnas, llegamos a la transpuesta. Así, $J_{\lambda,n}^T=PJ_{\lambda,n}P$ es la similitud entre las matrices dadas.

$\square$

La prueba anterior no funciona en general pues para matrices arbitrarias no pasa que $A^T=PAP$ (hay un contraejemplo en los ejercicios). Para probar lo que buscamos, hay que usar la forma canónica de Jordan.

Teorema. En $M_n(\mathbb{C})$, toda matriz es similar a su transpuesta.

Demostración. Sea $A$ una matriz en $M_n(\mathbb{C})$. Como en $\mathbb{C}$ todo polinomio se divide, tanto $A$ como $A^T$ tienen forma canónica de Jordan. Digamos que la forma canónica de Jordan es

\begin{equation}J=\begin{pmatrix} J_{\lambda_1,k_1} & 0 & 0 & \ldots & 0 \\ 0 & J_{\lambda_2,k_2} & 0 & \ldots & 0 \\ 0 & 0 & J_{\lambda_3,k_3} & \ldots & 0 \\ & \vdots & & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & J_{\lambda_d,k_d}\end{pmatrix}.\end{equation}

Si $P$ es la matriz de similitud, tenemos que $A=P^{-1}JP$ y al transponer obtenemos que:

$$A^T=P^T\begin{pmatrix} J_{\lambda_1,k_1}^T & 0 & 0 & \ldots & 0 \\ 0 & J_{\lambda_2,k_2}^T & 0 & \ldots & 0 \\ 0 & 0 & J_{\lambda_3,k_3}^T & \ldots & 0 \\ & \vdots & & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & J_{\lambda_d,k_d}^T\end{pmatrix}(P^T)^{-1}.$$

Como por la proposición anterior cada bloque de Jordan es similar a su transpuesta, existen matrices invertibles $Q_1,\ldots,Q_d$ tales $J_{\lambda_i,k_i}^T=Q_i^{-1}J_{\lambda_i,k_i}Q_i$ para todo $i\in\{1,\ldots,d\}$. Pero entonces al definir $Q$ como la matriz de bloques

$$Q=\begin{pmatrix} Q_1 & 0 & \ldots & 0 \\ 0 & Q_2 & \ldots & 0 \\ 0 & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & Q_d \end{pmatrix},$$

obtenemos la similaridad

$$A^T=P^TQ^{-1} \begin{pmatrix} J_{\lambda_1,k_1} & 0 & 0 & \ldots & 0 \\ 0 & J_{\lambda_2,k_2} & 0 & \ldots & 0 \\ 0 & 0 & J_{\lambda_3,k_3} & \ldots & 0 \\ & \vdots & & \ddots & \vdots \\ 0 & 0 & 0 & \ldots & J_{\lambda_d,k_d}\end{pmatrix} Q (P^T)^{-1}.$$

Así, $A$ y $A^T$ tienen la misma forma canónica de Jordan y por lo tanto son matrices similares.

$\square$

Más adelante…

¡Hemos terminado el curso de Álgebra Lineal II! Por supuesto, hay muchos temas de Álgebra Lineal adicionales que uno podría estudiar.

Un tema conectado con lo que hemos platicado es qué hacer con las matrices cuyo polinomio característico no se divide en el campo con el que estamos trabajando. Por ejemplo si tenemos una matriz $A$ en $M_n(\mathbb{R})$ cuyo polinomio característico no se divide, una opción es pensarla como matriz en $M_n(\mathbb{C})$ y ahí encontrar su forma canónica de Jordan. ¿Pero si queremos quedarnos en $\mathbb{R}$? Sí hay resultados que llevan una matriz a algo así como una «forma canónica» en $\mathbb{R}$ muy cercana a la forma canónica de Jordan.

Otro posible camino es profundizar en la pregunta de cuándo dos matrices en $M_n(F)$ son similares. Si tienen forma canónica de Jordan, ya dimos una buena caracterización en esta entrada. En los ejercicios encontrarás otra. Pero, ¿y si no tienen forma canónica de Jordan? Podríamos extender el campo a otro campo $G$ y comprar las formas canónicas ahí, pero en caso de existir la similaridad, sólo la tendremos en $M_n(G)$. Existe otra manera de expresar a una matriz en forma canónica, que se llama la forma canónica de Frobenius y precisamente está pensada para determinar si dos matrices son similares sin que sea necesario encontrar las raíces del polinomio característico, ni extender el campo.

Estos son sólo dos ejemplos de que la teoría de álgebra lineal es muy extensa. En caso de que estés interesado, hay mucho más por aprender.

Tarea moral

  1. Sea $A$ una matriz en $M_n(F)$ y tomemos $P$ en $M_n(F)$ la matriz
    $$P=\begin{pmatrix} 0 & 0 & \ldots & 0 & 1 \\ 0 & 0 & \ldots & 1 & 0 \\ \vdots & & \ddots & \vdots & \\ 0 & 1 & \ldots & 0 & 0 \\ 1 & 0 & \ldots & 0 & 0 \end{pmatrix}.$$
    • Demuestra que si $A$ tiene columnas $C_1,\ldots, C_n$, entonces $AP$ tiene columnas $C_n, \ldots, C_1$.
    • Demuestra que si $A$ tiene filas $R_1,\ldots,R_1$, entonces $PA$ tiene filas $R_n,\ldots,R_n$.
    • Concluye con cualquiera de los incisos anteriores que $P$ es invertible y su inversa es ella misma.
    • Tomemos explicitamente $n=2$ y $A=\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$. Encuentra explícitamente $PAP$. ¿Es $A^T$?
  2. ¿Cuál es la máxima cantidad de matrices que se pueden dar en $M_5(\mathbb{C})$ de manera que cada una de ellas tenga polinomio característico $x^2(x^2+1)(x+3)$ y tales que no haya dos de ellas que sean similares entre sí.
  3. Sea $A$ una matriz en $M_n(\mathbb{R})$ tal que su polinomio característico se divide en $\mathbb{R}$, con forma canónica de Jordan $J$. Sea $P(X)$ un polinomio en $\mathbb{R}[X]$.
    • Demuestra que el polinomio característico de $P(A)$ se divide en $\mathbb{R}$.
    • La forma canónica de Jordan de $P(A)$ no necesariamente será $P(J)$ pues puede que el polinomio altere el orden de los eigenvalores pero, ¿cómo se obtiene la forma canónica de $P(A)$ a partir de $J$?
  4. Sean $A$ y $B$ matrices en $M_n(F)$ cuyo polinomio característico se divide en $F$. Muestra que $A$ y $B$ son similares si y sólo si para cualquier polinomio $P(X)$ en $F[X]$ se tiene que $\text{rango}(P(A))=\text{rango}(P(B))$.
  5. Investiga sobre la forma canónica de Frobenius y sobre la variante a la forma canónica de Jordan restringida a $\mathbb{R}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Unicidad de la forma canónica de Jordan

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En la entrada anterior enunciamos el teorema de la forma canónica de Jordan y demostramos la existencia de dicha forma bajo ciertas hipótesis. Como corolario, quedó pensar cuál es la versión para matrices. En esta entrada enunciamos la versión para matrices (totalmente equivalente a la de transformaciones lineales) y nos enfocamos en mostrar la unicidad de la forma canónica de Jordan.

Unicidad de la forma canónica de Jordan

El siguiente teorema es totalmente análogo al enunciado en la entrada anterior. Recuerda que $\leq$ es un orden total fijo de $F$ (en $\mathbb{R}$, es el orden usual).

Teorema. Sea $A$ una matriz $M_n(F)$ cuyo polinomio característico $\chi_A(X)$ se divide en $F$. Entonces, existen únicos valores $\lambda_1\leq \ldots \leq \lambda_n$ en $F$ y únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} para los cuales $A$ es similar a la siguiente matriz de bloques de Jordan:

$$\begin{pmatrix} J_{\lambda_1,k_1} & 0 & \cdots & 0 \\ 0 & J_{\lambda_2,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{\lambda_d,k_d}\end{pmatrix}.$$

Usaremos esta versión para demostrar la unicidad, lo cual también implicará la unicidad para la versión de transformaciones lineales.

Mediante la demostración de existencia de la entrada anterior, llegamos a que si el polinomio característico de $A$ es

$$\chi_A(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r},$$

entonces $A$ es similar a una matriz conformada por matrices de bloques de Jordan $J_1,J_2,\ldots,J_r$, en donde cada $J_i$ es de tamaño $m_i$ y de bloques de Jordan de eigenvalor $\lambda_i$.

Si $A$ fuera similar a otra matriz $K$ de bloques de Jordan, podríamos agrupar por eigenvalores de los bloques $\kappa_1< \ldots < \kappa_s$ en matrices de bloques de Jordan tamaños $o_1,\ldots,o_s$, digamos $K_1,\ldots,K_s$. El polinomio característico de $K$ sería entonces

$$\chi_{K}(X)=(X-\kappa_1)^{o_1}(X-\kappa_2)^{o_2}\cdots(X-\kappa_s)^{o_s}.$$

Pero $K$ es similar a $A$, y entonces deben tener el mismo polinomio característico, así que conciden en raíces y multiplicidad. Esto demuestra que $r=s$ y como los $\lambda_i$ y los $\kappa_i$ están ordenados, también demuestra las igualdades $\lambda_i=\kappa_i$ y $m_i=o_i$ para todo $i\in\{1,\ldots,r\}.$

Sólo nos queda argumentar la igualdad entre cada $J_i$ y $K_i$ para $i\in\{1,\ldots,r\}$. Pero ambas una forma canónica de Jordan para la transformación nilpotente que se obtiene de restringir $T_{A-\lambda_i I}$ a $\ker(T_{A-\lambda_i I}^{m_i})$. Por la unicidad que demostramos para la forma canónica de Jordan para transformaciones nilpotentes, concluimos que $J_i=K_i$. Esto termina la demostración de la unicidad de la forma canónica de Jordan.

$\square$

Una receta para encontrar la forma canónica de Jordan

Ya con el teorema demostrado, ¿cómo juntamos todas las ideas para encontrar la forma canónica de Jordan de una matriz $A$ en $M_n(F)$ cuyo polinomio característico se divida en $F$? Podemos proceder como sigue.

  1. Encontramos el polinomio característico $\chi_A(X)$ y su factorización, digamos $$\chi_A(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r}.$$
  2. Nos enfocamos en encontrar las matrices de bloque de Jordan $J_i$ para cada eigenvalor $\lambda_i$. Sabemos que la matriz $J_i$ será de tamaño $m_i$.
  3. Para saber exactamente cuál matriz de bloques de Jordan es $J_i$, pensaremos en que tiene $b_1,b_2,\ldots,b_{m_i}$ bloques de Jordan de eigenvalor $\lambda_i$ de tamaños $1,2, \ldots,m_i$. Consideramos la matriz $A_i=A-\lambda_i I$. Los $b_1,\ldots,b_{m_i}$ son la solución al siguiente sistema de ecuaciones en las variables $x_1,\ldots,x_{m_i}$.
    \begin{align*}
    m_i&= 1\cdot x_1 + 2\cdot x_2 + 3 \cdot x_3 + \ldots + m_i \cdot x_{m_i}\\
    m_i-n+\text{rango}(A_i-\lambda_i I)&=0\cdot x_1 + 1\cdot x_2 + 2 \cdot x_3 + \ldots + (m_i-1) \cdot x_{m_i}\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^2)&= 0 \cdot x_1 + 0 \cdot x_2 + 1 \cdot x_3 + \ldots + (m_i-2)\cdot x_{m_i}\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^3)&= 0 \cdot x_1 + 0 \cdot x_2 + 0 \cdot x_3 + \ldots + (m_i-3)\cdot x_{m_i}\\
    &\vdots\\
    m_i-n+\text{rango}({A_i-\lambda_i I}^{m_i-1})&= 0\cdot x_1 + 0 \cdot x_2 + 0 \cdot x_3 + \ldots + 1 \cdot x_{m_i}.
    \end{align*}
  4. Juntamos todos los $J_i$ en una misma matriz y los ordenamos apropiadamente.

El paso número $3$ está motivado por lo que sabemos de las matrices nilpotentes, y es bueno que pienses por qué se estudia específicamente ese sistema de ecuaciones para cada eigenvalor $\lambda_i$ y multiplicidad $m_i$.

Ejemplo de obtener la forma canónica de Jordan

Veamos un ejemplo del procedimiento descrito en la sección anterior.

Ejemplo. Encontraremos la forma canónica de Jordan de la siguiente matriz: $$A=\begin{pmatrix}-226 & -10 & -246 & 39 & 246\\234 & 23 & 236 & -46 & -236\\-198 & -20 & -192 & 41 & 195\\-93 & 10 & -122 & 10 & 122\\-385 & -30 & -393 & 74 & 396\end{pmatrix}.$$

Con herramientas computacionales, podemos darnos cuenta de que el polinomio característico de esta matriz es $$\chi_A(X)=X^{5} – 11 X^{4} + 46 X^{3} – 90 X^{2} + 81 X- 27.$$

Este polinomio se puede factorizar como $$(X-1)^2(X-3)^3.$$ Así, la submatriz de bloques de Jordan $J_1$ de eigenvalor $1$ tendrá tamaño $2$ y la $J_3$ de eigenvalor $3$ tendrá tamaño $3$. Pero, ¿de qué tamaño son cada uno de los bloques de Jordan en cada una de estas matrices?

Para respondernos esto para $J_1$, notamos que sus bloques son de tamaño $1$ y $2$ solamente. Si hay $b_1$ bloques de tamaño $1$ y $b_2$ bloques de tamaño $2$, por la teoría desarrollada arriba tendremos:

\begin{align*}
b_1+2b_2&=2\\
b_2&=2-5+\text{rango}(A-I)=2-5+4=1.
\end{align*}

El rango de $A-I$ lo obtuvimos computacionalmente, pero recuerda que también puede ser obtenido con reducción gaussiana. Resolviendo el sistema, $b_2=1$ y entonces $b_1=0$. Concluimos que en $J_1$ hay un bloque de Jordan de tamaño $2$.

Para $J_3$, reciclemos las variables $b_i$ (para no introducir nuevas). Los bloques pueden ser de tamaño $1,2,3$. Supongamos que de estos tamaños respectivamente hay $b_1,b_2,b_3$ bloques. Los $b_i$ cumplen:

\begin{align*}
b_1+2b_2+3b_3&=3\\
b_2+2b_3&=3-5+\text{rango}(A-3I)=3-5+3=1\\
b_3&=3-5+\text{rango}((A-3I)^2)=3-5+2=0.
\end{align*}

Así, $b_3=0$, y en consecuencia $b_2=1$ y entonces $b_1=1$. Concluimos que $J_3$ tiene un bloque de tamaño $1$ y uno de tamaño $3$. Por lo tanto, la forma canónica de Jordan de $A$ es:

$$\begin{pmatrix} J_1 & 0 \\ 0 & J_3 \end{pmatrix} = \begin{pmatrix} J_{1,2} & 0 & 0 \\ 0 & J_{3,1} & 0 \\ 0 & 0 & J_{3,2} \end{pmatrix} = \begin{pmatrix}1 & 1 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0\\0 & 0 & 3 & 0 & 0\\0 & 0 & 0 & 3 & 1\\0 & 0 & 0 & 0 & 3\end{pmatrix}$$

$\triangle$

Otro problema sobre forma canónica de Jordan

La receta anterior funciona en general y da la forma canónica de Jordan. Esto es algo que probablemente en la práctica en aplicaciones no tendrás que hacer manualmente nunca, pues hay herramientas computacionales que te pueden ayudar. Sin embargo, es importante entender con profundidad el teorema y la receta de manera teórica, pues hay problemas conceptuales en los que no podrás usar herramientas computacionales. A continuación veremos un ejemplo.

Problema. Sea $A$ una matriz en $M_6(\mathbb{R})$ con polinomio característico $$\chi_A(X)=X^6-2X^4+X^2.$$

  • ¿Cuántas posibilidades hay para la forma canónica de Jordan de $A$?
  • Demuestra que si el rango de $A$ es $5$, entonces $A$ no es diagonalizable.

Solución. Podemos factorizar el polinomio característico de $A$ como sigue:

$$\chi_A(X)=X^2(X+1)^2(X-1)^2.$$

Así, la forma canónica de Jordan está conformada por una matriz de bloques de Jordan $J_0$ de eigenvalor $0$ y tamaño $2$; una $J_1$ de eigenvalor $1$ y tamaño $2$; y una $J_{-1}$ de eigenvalor $-1$ y tamaño $2$.

Cada $J_i$ tiene dos chances: o es un bloque de Jordan de tamaño $2$, o son dos bloques de Jordan de tamaño $1$. Así, en total tenemos $2\cdot 2 \cdot 2=8$ posibilidades.

Si $A$ es de rango $5$, entonces tendríamos en las cuentas de cantidad de bloques $b_1$ y $b_2$ para eigenvalor $0$ que

\begin{align*}
b_1+2b_2&=2\\
b_2&=2-6+\text{rango}(A)=2-6+5=1,
\end{align*}

de donde en $J_0$ tendría $1$ bloque de tamaño $2$ y ninguno de tamaño $1$. Si $A$ fuera diagonalizable, su diagonalización sería una forma canónica de Jordan donde para eigenvalor $0$ se tendrían $2$ bloques de tamaño $1$ y ninguno de tamaño $2$. Así, $A$ tendría dos formas canónicas de Jordan distintas, lo cual es imposible.

$\square$

Más adelante…

Con esta entrada terminamos de demostrar el teorema de la forma canónica de Jordan, uno de los teoremas más bonitos de álgebra lineal. ¿Te das cuenta de todo lo que utilizamos en su demostración? Forma matricial de transformaciones lineales, el teorema de Cayley-Hamilton, polinomio característico, subespacios estables, teoría de dualidad, sistemas de ecuaciones lineales, resultados auxiliares de polinomios, etc. Es un resultado verdaderamente integrador.

En la siguiente entrada, la última del curso, hablaremos de algunas de las consecuencias del teorema de la forma canónica de Jordan. Discutiremos cómo lo podemos utilizar para clasificar a las matrices por similaridad. Veremos una aplicación con respecto a una matriz y su transpuesta. También, esbozaremos un poco de por qué en cierto sentido el resultado no sólo vale para las matrices cuyo polinomio se divide sobre el campo, sino que para cualquier matriz. Con ello terminaremos el curso.

Tarea moral

  1. Calcula la forma canónica de Jordan $J$ de la matriz $$A=\begin{pmatrix} 1 & 0 & -3 \\ 1 & -1 & -6 \\ -1 & 2 & 5 \end{pmatrix}.$$ Además de encontrar $J$, encuentra de manera explícita una matriz invertible $P$ tal que $A=P^{-1}JP$.
  2. Calcula la forma canónica de Jordan de la matriz $$\begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 1 & 2 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 2 \end{pmatrix}$$
  3. Explica y demuestra cómo obtener lo siguiente para una matriz de bloques de Jordan:
    • Su polinomio característico.
    • Su polinomio mínimo.
    • Su determinante.
    • Su traza.
    • Sus eigenespacios.
  4. Justifica con más detalle por qué la receta que se propone para calcular la forma canónica de Jordan en efecto funciona. Necesitarás varios de los argumentos que dimos en la entrada anterior.
  5. Demuestra que una matriz $A\in M_n(F)$ para la cual su polinomio característico se divide en $F$ es diagonalizable si y sólo si cada bloque de cada matriz de bloques de la forma canónica de Jordan tiene tamaño $1$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

Álgebra Lineal II: Existencia de la forma canónica de Jordan

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

En las entradas anteriores demostramos que para cualquier matriz nilpotente existe (y es única) una matriz similar muy sencilla, hecha por lo que llamamos bloques de Jordan de eigenvalor cero. Lo que haremos ahora es mostrar una versión análoga de este resultado para una familia mucho más grande de matrices. De hecho, en cierto sentido tendremos un resultado análogo para todas las matrices.

Pensando en ello, lo que haremos en esta entrada es lo siguiente. Primero, generalizaremos nuestra noción de bloques de Jordan para contemplar cualquier eigenvalor. Estudiaremos un poco de los bloques de Jordan. Luego, enunciaremos el teorema que esperamos probar. Finalmente, daremos el primer paso hacia su demostración. En la siguiente entrada terminaremos la demostración y hablaremos de aspectos prácticos para encontrar formas canónicas de Jordan.

Enunciado del teorema de la forma canónica de Jordan

A continuación definimos a los bloques de Jordan para cualquier eigenvalor y tamaño.

Definición. Sea $F$ un campo. El bloque de Jordan de eigenvalor $\lambda$ y tamaño $k$ es la matriz $J_{\lambda,k}$ en $M_k(F)$ cuyas entradas son todas $\lambda$, a excepción de las que están inmediatamente arriba de la diagonal superior, las cuales son unos. En símbolos, $J_{\lambda,k}=[a_{ij}]$ con $$a_{ij}=\begin{cases} 1 & \text{si $j=i+1$}\\ \lambda & \text{si $i=j$} \\ 0 & \text{en otro caso.} \end{cases}$$

También podemos expresarlo de la siguiente manera:

$$J_{\lambda,k}=\begin{pmatrix} \lambda & 1 & 0 & \cdots & 0 & 0 \\ 0 & \lambda & 1 & \cdots & 0 & 0 \\ 0 & 0 & \lambda & \cdots & 0 & 0 \\ & \vdots & & \ddots & & \vdots \\ 0 & 0 & 0 & \cdots & \lambda & 1 \\ 0 & 0 & 0 & \cdots & 0 & \lambda \end{pmatrix},$$ en donde estamos pensando que la matriz es de $k\times k$.

Una última manera en la que nos convendrá pensar a $J_{\lambda,k}$ es en términos de los bloques de Jordan de eigenvalor cero: $J_{\lambda,k}=\lambda I_k + J_{0,k}$.

Definición. Una matriz de bloques de Jordan en $M_n(F)$ es una matriz diagonal por bloques en la que cada bloque en la diagonal es un bloque de Jordan.

Lo que nos gustaría demostrar es el siguiente resultado. En él, piensa en $\leq$ como algún orden total fijo de $F$ (para $\mathbb{R}$ es el orden usual, pero otros campos no necesariamente tienen un orden natural asociado).

Teorema. Sea $V$ un espacio vectorial de dimensión finita $n$ sobre el campo $F$ y $T:V\to V$ una transformación lineal tal que $\chi_T(X)$ se divide sobre $F$. Entonces, existen únicos valores $\lambda_1\leq \ldots \leq \lambda_n$ en $F$ y únicos enteros $k_1,\ldots,k_d$ tales que \begin{align*} &k_1+k_2+\ldots+k_d = n,\\ &k_1\leq k_2 \leq \ldots \leq k_d,\end{align*} para los cuales existe una base de $V$ en la cual $T$ tiene como forma matricial a la siguiente matriz de bloques de Jordan:

$$\begin{pmatrix} J_{\lambda_1,k_1} & 0 & \cdots & 0 \\ 0 & J_{\lambda_2,k_2} & \cdots & 0 \\ \vdots & & \ddots & \vdots \\ 0 & 0 & \cdots & J_{\lambda_d,k_d}\end{pmatrix}.$$

Por supuesto, este teorema también tiene una versión matricial, la cuál tendrás que pensar cómo escribir.

Un teorema de descomposición de kernels

Ya tenemos uno de los ingredientes que necesitamos para dar la demostración de la existencia de la forma canónica de Jordan: su existencia para las transformaciones nilpotentes. Otro de los ingredientes que usaremos es el teorema de Cayley-Hamilton. El tercer ingrediente es un resultado de descoposición de kernels de transformaciones evaluadas en polinomios.

Proposición. Sea $V$ un espacio vectorial sobre $F$. Sea $T:V\to V$ una transformación lineal. Y sean $P_1(X),\ldots,P_r(X)$ polinomios en $F[x]$ cuyo máximo común divisor de cualesquiera dos de ellos es el polinomio $1$. Entonces, $$\ker((P_1P_2\cdots P_r)(T))=\bigoplus_{i=1}^r \ker(P_i(T)).$$

Demostración. Para cada $i\in \{1,2,\ldots,r\}$ consideraremos a $Q_i(X)$ como el polinomio que se obtiene de multiplicar a todos los polinomios dados, excepto $P_i(X)$. Y por comodidad, escribiremos $P(X)=(P_1\cdots P_r)(X)$. Notemos que entonces $P(X)=(Q_iP_i)(X)$ para cualquier $i\in\{1,2,\ldots,r\}$.

Primero probaremos un resultado polinomial auxiliar. Veremos que $Q_1(X),\ldots,Q_r(X)$ tienen como máximo común divisor al polinomio $1$. En caso de no ser así, un polinomio $D(X)$ no constante dividiría a todos ellos. Sin pérdida de generalidad, $D$ es irreducible (tomando, por ejemplo $D(X)$ de grado mínimo con esta propiedad). Como $D(X)$ es irreducible y divide a $Q_r(X)$, entonces debe dividir a alguno de los factores de $Q_r(X)$, que sin pérdida de generalidad (por ejemplo, reetiquetando), es $P_1(X)$. Pero $D(X)$ también divide a $Q_1(X)$, así que debe dividir a alguno de sus factores $P_2(X),\ldots,P_r(X)$, sin pérdida de generalidad a $P_2(X)$. Pero entonces $D(X)$ divide a $P_1(X)$ y $P_2(X)$, lo cual contradice las hipótesis. Así, $Q_1(X),\ldots,Q_r(X)$ tienen como máximo común divisor al polinomio $1$. Por el lema de Bézout para polinomios (ver tarea moral), existen entonces polinomios $R_1(X),\ldots,R_r(X)$ tales que

\begin{equation}
\label{eq:bezout}(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(X)=1.
\end{equation}

Estamos listos para pasar a los argumentos de álgebra lineal. Veamos primero que cualquier elemento en la suma de la derecha está en el kernel de $P(T)$. Tomemos $v=v_1+\ldots+v_r$ con $v_i\in \ker(P_i(T))$. Al aplicar $P$ obtenemos

\begin{align*}
P(v)&=P(v_1)+\ldots+P(v_r)\\
&=Q_1(P_1(v_1))+\ldots+Q_r(P_r(v_r))\\
&=0+\ldots+0=0.
\end{align*}

Esto muestra que $v\in \ker(P(T))$, de donde se obtiene la primera contención que nos interesa.

Veamos ahora la segunda contención, que $\ker(P(T))=\bigoplus_{i=1}^r \ker(P_i(T))$. Tomemos $v\in \ker(P(T))$. Al aplicar \eqref{eq:bezout} en $T$ y evaluar en $v$ obtenemos que

\begin{align*}
v&=\text{Id}(v)=(1)(T)(v)\\
&=(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(T)(v)\\
&=(R_1Q_1)(T)(v)+\ldots+(R_rQ_r)(T)(v).
\end{align*}

Pero esto justo expresa a $v$ como elemento de $\ker(P_i(T))$ pues para cada $i$ tenemos

\begin{align*}
P_i(T)((R_iQ_i)(T)(v))&=(P_iR_i Q_i )(T)(v)\\
&=(R_i Q_i P_i)(T)(v)\\
&=R_i(T)P(T)(v)\\
&=R_i(0)=0,
\end{align*}

de modo que expresamos a $v$ como suma de vectores en $\ker(P_1(T)),\ldots,\ker(P_r(T))$.

Ya demostramos la igualdad de conjuntos, pero recordemos que en la igualdad de suma directa hay otra cosa que hay que probar: que el cero tiene una forma única de expresarse como suma de elementos de cada subespacio (aquella en donde cada elemento es cero). Supongamos entonces que $$0=v_1+\ldots+v_r$$ con $v_i\in \ker(P_i(T))$ para cada $i$. Si aplicamos $Q_i$ en esta igualdad, como tiene todos los factores $P_j$ con $j\neq i$ obtenemos $$0=Q_i(0)=Q_i(v_i).$$

Por otro lado, al aplicar nuevamente \eqref{eq:bezout} en $T$ y evaluar en $v_i$

\begin{align*}
v_i&=\text{Id}(v_i)=(1)(T)(v_i)\\
&=(R_1Q_1 + R_2Q_2 + \ldots + R_rQ_r)(T)(v_i)\\
&=(R_1Q_1)(T)(v_1)+\ldots+(R_rQ_r)(T)(v_i)\\
&=(R_iQ_i)(T)(v_i)\\
&=0.
\end{align*}

De esta forma, en efecto tenemos que los espacios están en posición de suma directa, que era lo último que nos faltaba verificar.

$\square$

Existencia de la forma canónica de Jordan

Estamos listos para demostrar la existencia de la forma canónica de Jordan. Supongamos que $V$ es un espacio vectorial de dimensión finita $n$ sobre $F$ y que $T:V\to V$ es una transformación lineal cuyo polinomio característico se divide en $F[x]$. Sabemos entonces que es de la siguiente forma:

$$\chi_T(X)=(X-\lambda_1)^{m_1}(X-\lambda_2)^{m_2}\cdots(X-\lambda_r)^{m_r},$$

donde $\lambda_1,\ldots,\lambda_r$ son eigenvalores distintos de $T$ y $m_1,\ldots,m_r$ son las multiplicidades algebraicas respectivas de estos eigenvalores como raíces de $\chi_T(X)$.

Por el teorema de Cayley-Hamilton, sabemos que $\chi_T(T)=0$, de modo que $\ker(\chi_T(T))=V$. Por la proposición de descomposición de la sección anterior aplicada a los polinomios $P_i(X)=(X-\lambda_i)^{m_i}$ (verifica que son primos relativos dos a dos) para $i\in\{1,\ldots,r\}$ tenemos entonces que $$V=\bigoplus_{i=1}^r \ker((T-\lambda_i \text{id})^{m_i}).$$

Pero, ¿cómo es la transformación $T-\lambda_i \text{id}$ restringida a cada $\ker((T-\lambda_i \text{id})^{m_i})$? ¡Es nilpotente! Precisamente por construcción, $(T-\lambda_i \text{id})^{m_i}$ se anula totalmente en este kernel. Así, por la existencia de la forma canónica de Jordan para matrices nilpotentes, hay una base $\beta_i$ para cada $\ker((T-\lambda_i \text{id})^{m_i})$ tal que $T-\lambda_i \text{id}$ restringida a ese kernel tiene como forma matricial una matriz $J_i$ de bloques de Jordan de eigenvalor cero. Pero entonces $T$ (restringida a dicho kernel) tiene como forma matricial a $J_i+\lambda_i I_{m_i}$, que es una matriz de bloques de Jordan de eigenvalor $\lambda$.

Con esto terminamos: como $V$ es la suma directa de todos esos kernel, la unión de bases $\beta_1,\ldots,\beta_r$ es una base para la cual $T$ tiene como forma matricial a una matriz de bloques de Jordan.

$\square$

Más adelante…

Hemos demostrado la existencia de la forma canónica de Jordan, pero aún nos falta demostrar su unicidad. Además de esto, también necesitaremos un mejor procedimiento para encontrarla. Haremos eso en la siguiente entrada.

Tarea moral

  1. Enuncia el teorema de la forma canónica de Jordan versión matrices.
  2. Investiga más sobre el lema de Bézout para polinomios y cómo se demuestra. Después de esto, expresa al polinomio $1$ como combinación lineal de los polinomios $x^2-1, x^3+1, x^2+5x+4$.
  3. Verifica que los polinomios $P_i(X)=(X-\lambda_i)^{k_i}$ de la demostración de la existencia de la forma canónica de Jordan cumplen las hipótesis de la proposición de descomposición de kernels.
  4. Sea $F$ un campo y $r,s$ elementos en $F$. Sea $n$ un entero. Demuestra que los bloques de Jordan $J_{r,n}$ y $J_{s,n}$ en $M_n(F)$ conmutan.
  5. Siguiendo las ideas de la demostración de existencia, encuentra la forma canónica de Jordan de la matriz $$\begin{pmatrix} 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 \\ 0 & 0 & 2 & 2 \\ 0 & 0 & 0 & 2 \end{pmatrix}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»