Introducción
Ante el modelado de situaciones, resulta útil identificar qué tan lejos está un objeto de convertirse en otro. Si se identifica una secuencia o patrón entre una situación y la siguiente, posiblemente se pueda comprobar que, tras varios cambios, nos aproximaremos a algún resultado específico. El Análisis Matemático ofrece herramientas que formalizan este estudio. En la sección que a continuación presentamos trabajaremos más con la noción de cercanía a través de distancias que van tendiendo a cero. Esta vez lo haremos con una sucesión que toma elementos del espacio métrico. Se verá bajo qué condiciones estos puntos se acercan cada vez más a cierto punto en el espacio métrico. Comencemos con la siguiente:
Definición sucesión: Sea $(X,d)$ un espacio métrico. Decimos que una función $x: \mathbb{N} \to X$ es una sucesión en $X$.
Podemos pensar entonces que una sucesión elige, para cada número natural $n$, un elemento $x_n$ del conjunto $X$. Vamos a denotar una sucesión como $(x_n)_{n \in \mathbb{N}}.$
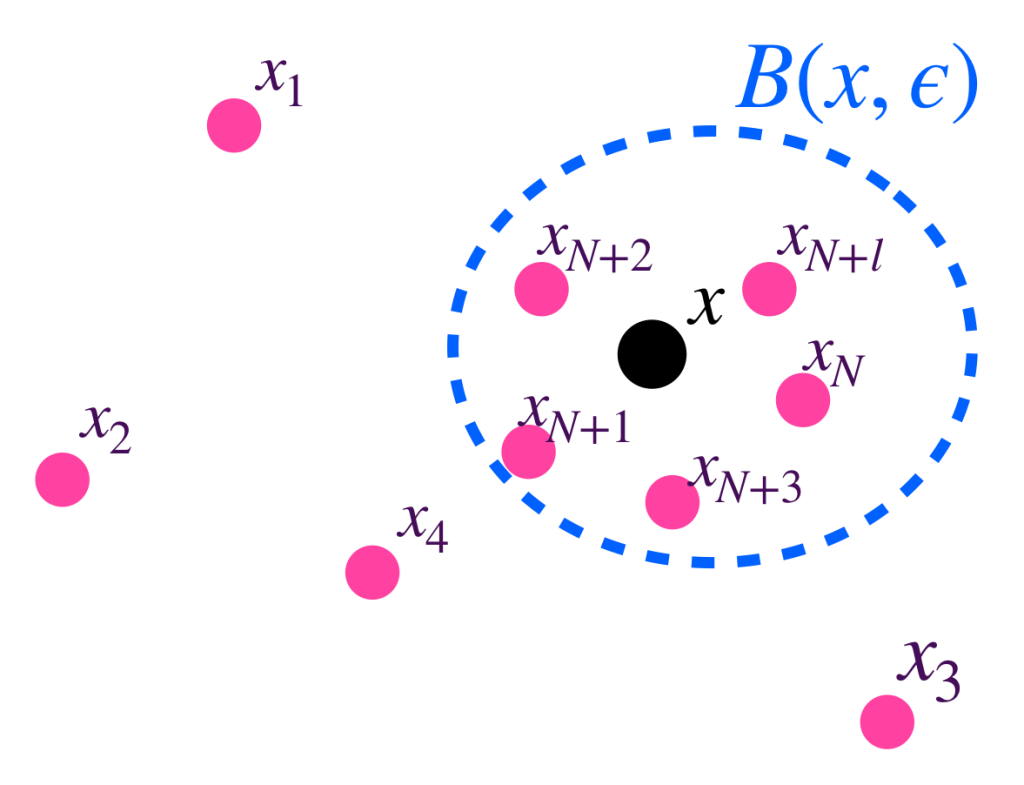
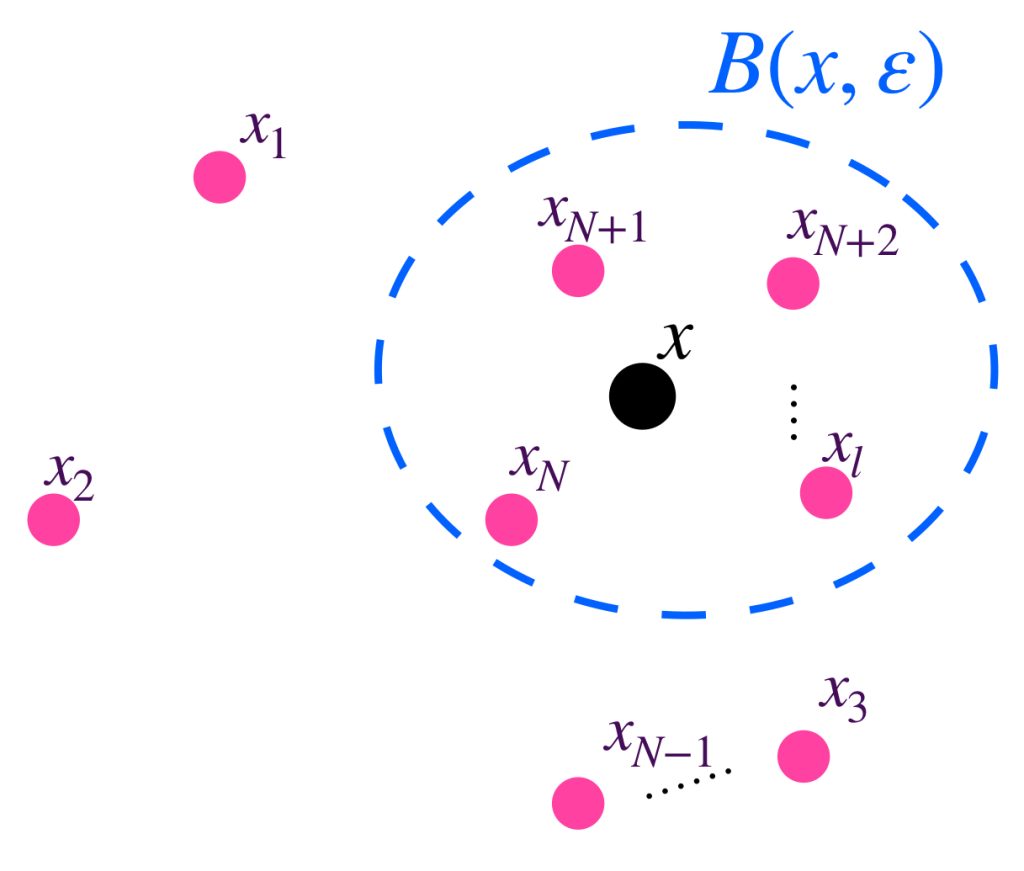
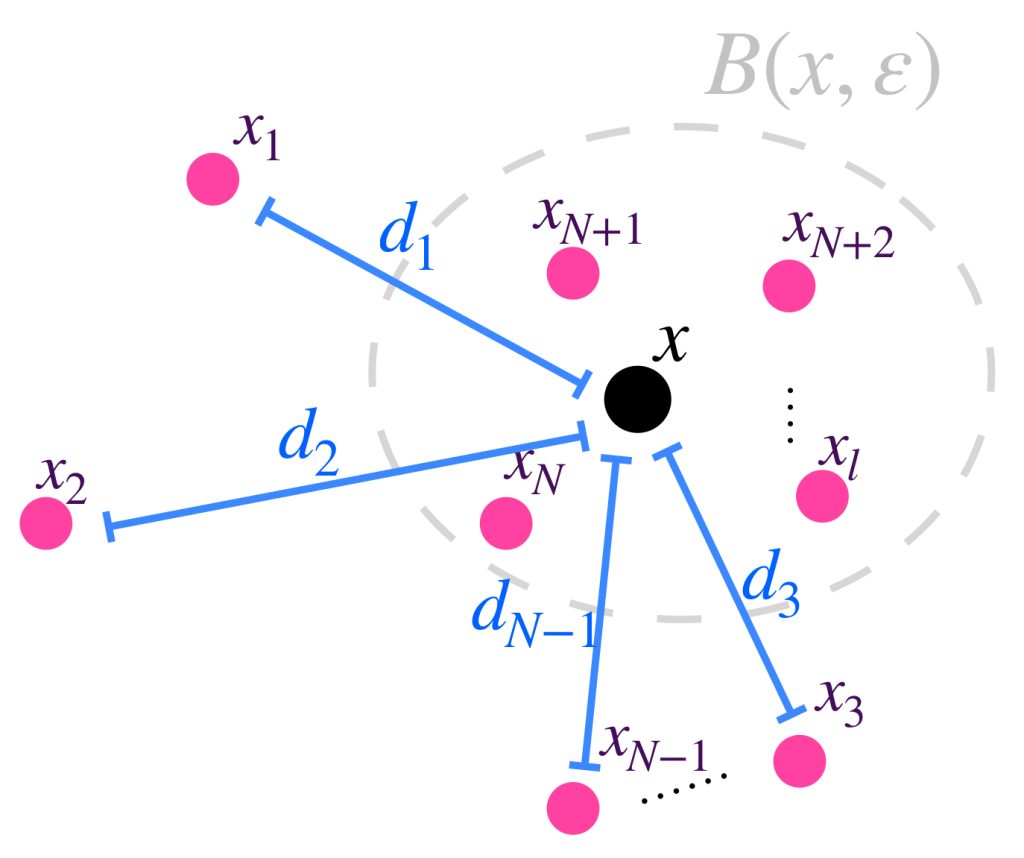
¿Bajo qué condiciones podemos decir que la sucesión se aproxima cada vez más a cierto punto $x$ en $(X,d)$? Para que esto ocurra se espera que, siempre que se fije una distancia $\varepsilon >0$ como referencia, se pueda asegurar que los últimos elementos de la sucesión, tengan una distancia al punto $x$ menor que $\varepsilon$, es decir, que exista un número natural $N \,$ de modo que todos los puntos asignados por la sucesión a partir de la posición $N$, estén “dentro” de la bola de radio $\varepsilon$ con centro en $x$, el punto de convergencia. De manera formal, tenemos la:
Definición sucesión convergente: Vamos a decir que una sucesión $(x_n)_{n \in \mathbb{N}} \,$ es convergente en $(X,d)$ si existe $x \in X$ tal que para todo $\varepsilon >0$ existe $N \in \mathbb{N}$ tal que para todo $n \geq N$ ocurre que $d(x_n,x)<\varepsilon$.
Si es así, diremos que $(x_n)_{n \in \mathbb{N}} \,$ converge a $x$ y se indicará en la notación como:
$$x_n \to x$$
o como:
$$\underset{n \to \infty}{lim} \, x_n =x$$
Nota: $x_n \to x \text{ en } X \iff d(x_n,x) \to 0 \text{ en } \mathbb{R}$.
Si la sucesión no es convergente decimos que es divergente.
Ahora veamos que una sucesión no puede converger a dos puntos diferentes:
Proposición: Si $(x_n)_{n \in \mathbb{N}} \,$ es una sucesión convergente en $X$ entonces el límite $\underset{n \to \infty}{lim} \, x_n$ es único.
Demostración:
Supongamos que $x_n \to x_a \,$ y $\, x_n \to x_b \,$ en $X$. Sea $\varepsilon>0$. Siguiendo la definición de convergencia se tiene que para todo $\frac{\varepsilon}{2} >0$ existen números naturales $N_a\, $ y $\, N_b\, $ tales que para todo $n\geq N_a, \, d(x_n,x_a)< \frac{\varepsilon}{2}$ y para todo $n\geq N_b, \, d(x_n,x_b)< \frac{\varepsilon}{2}$. Si elegimos $N = max\{N_a,N_b\}$ las dos condiciones anteriores se satisfacen. Entonces, para toda $n\geq N$,
$0 \leq d(x_a,x_b) \leq d(x_a,x_n)+d(x_n,x_b) \leq \frac{\varepsilon}{2}+\frac{\varepsilon}{2}= \varepsilon$
Nota entonces que $\forall \, \varepsilon >0,$ la distancia entre $x_a$ y $x_b$ queda acotada por $0 \leq d(x_a,x_b) \leq \varepsilon.$
En conclusión, $d(x_a,x_b)=0$, por lo tanto los puntos de convergencia son iguales.
Es importante mencionar que la convergencia de una sucesión depende tanto de la métrica como del conjunto a considerar. Una sucesión puede ser convergente en un espacio métrico pero no serlo en otro. Por ejemplo, la sucesión que a cada natural $n$ le asigna el número $\frac{1}{n}$ cumple que $(\frac{1}{n}) \to 0$ en $\mathbb{R}$ con la métrica euclideana, pero en el subespacio euclideano $(0,1]$ no es convergente, pues $0$ no está en el subespacio.
Definición subsucesión de $(x_n)_{n \in \mathbb{N}}$. Una subsucesión $(x_{k(n)})_{n \in \mathbb{N}}$ es una composición de la sucesión $(x_n)_{n \in \mathbb{N}}$ con una función estrictamente creciente, $k:\mathbb{N} \to \mathbb{N}$.
Esto significa que una subsucesión tomará elementos en $X$ de la sucesión, en el mismo orden en que aparecen, aunque es posible que vaya descartando algunos.
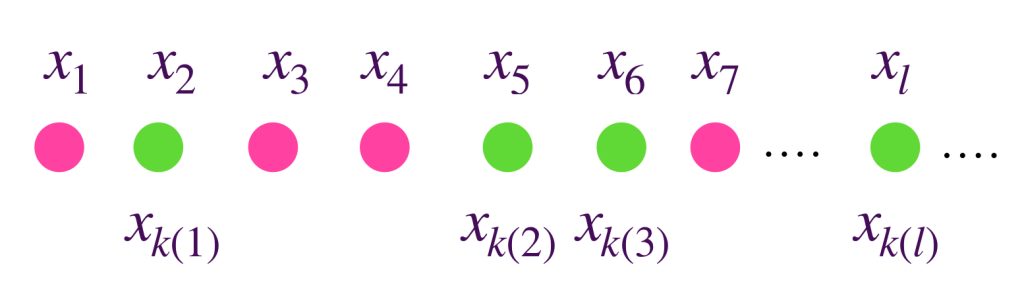
Hay una relación entre el límite de una sucesión y los de sus subsucesiones:
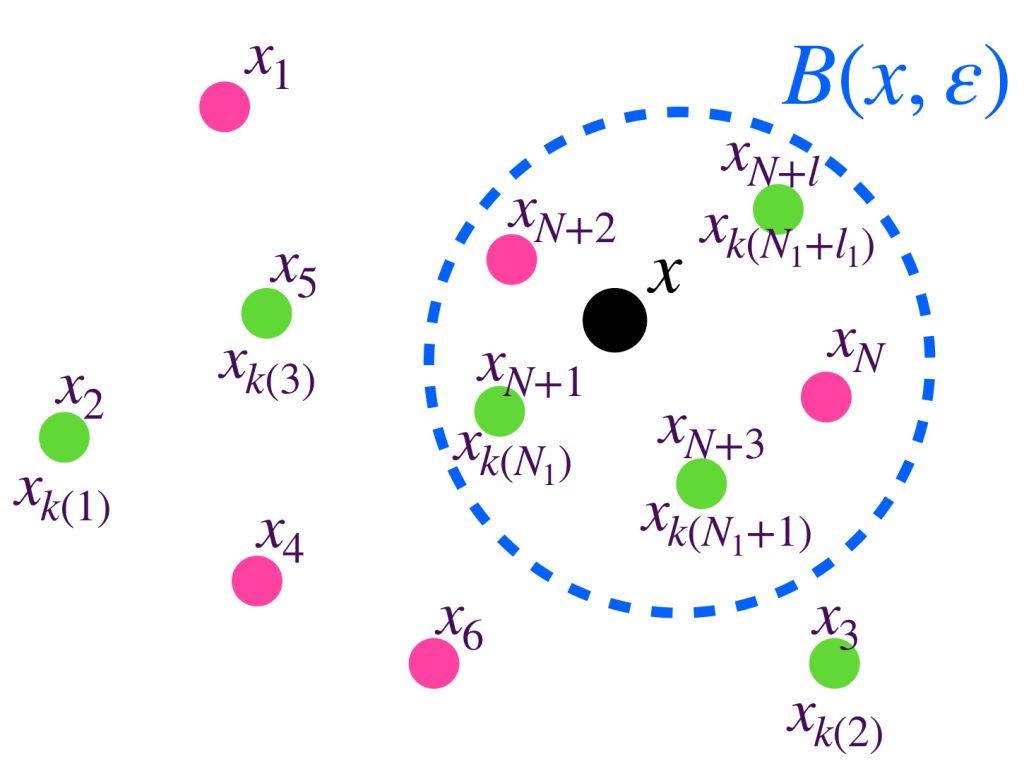
Proposición: Una sucesión $(x_n)_{n \in \mathbb{N}}$ converge a $x$ en $X$ si y solo si toda subsucesión $(x_{k(n)})_{n \in \mathbb{N}}$ converge a $x$ en $X$.
Demostración:
Sea $(x_{k(n)})_{n \in \mathbb{N}}$ una subsucesión de $(x_n)_{n \in \mathbb{N}}$. Como $(x_n)_{n \in \mathbb{N}}$ converge entonces existe $N \in \mathbb{N}$ tal que para todo $n \geq N, \, d(x_n,x) < \varepsilon$. Ya que $k: \mathbb{N} \to \mathbb{N}$ es estrictamente creciente, tenemos que para todo $j \geq N, \, k(j) \geq k(N) \geq N$. Así, $d(x_k(j),x)< \varepsilon$, lo cual demuestra que $(x_{k(n)}) \to x$. El regreso es trivial, pues es posible definir una subsucesión como la sucesión misma.
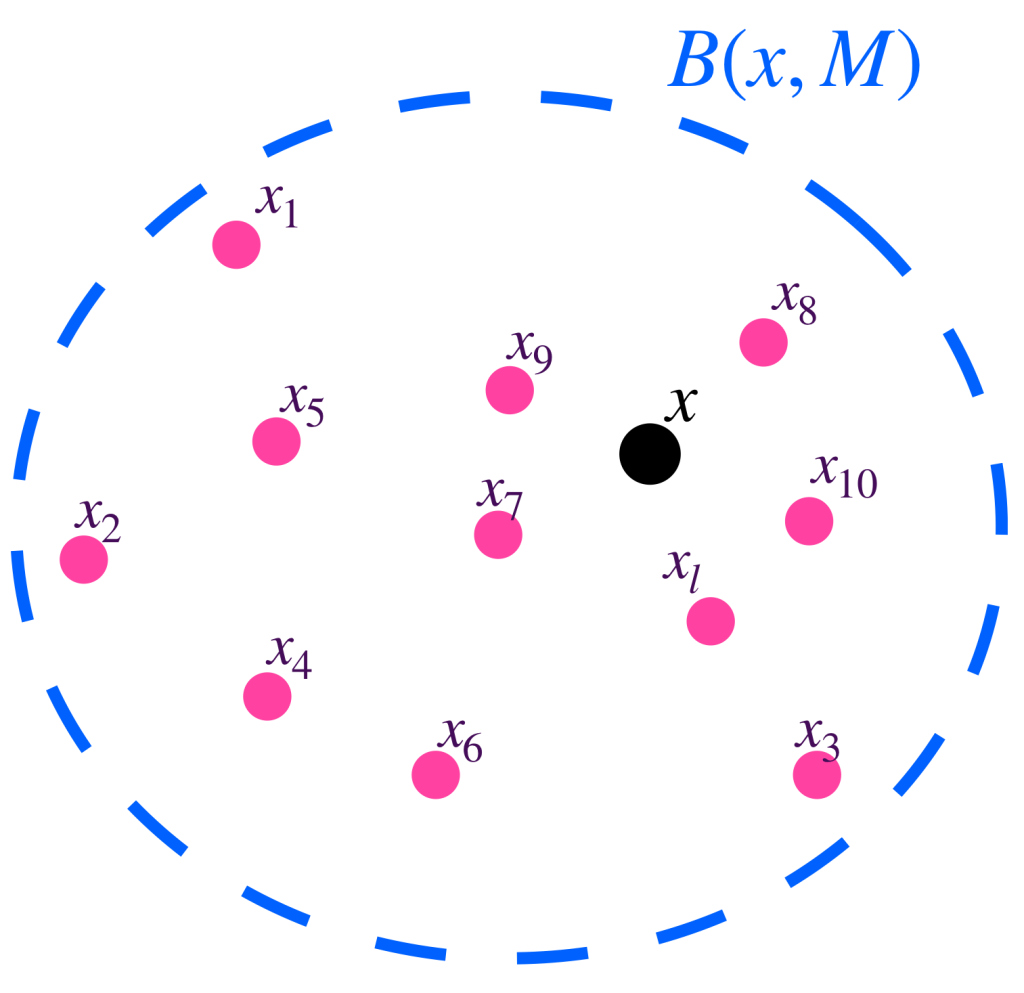
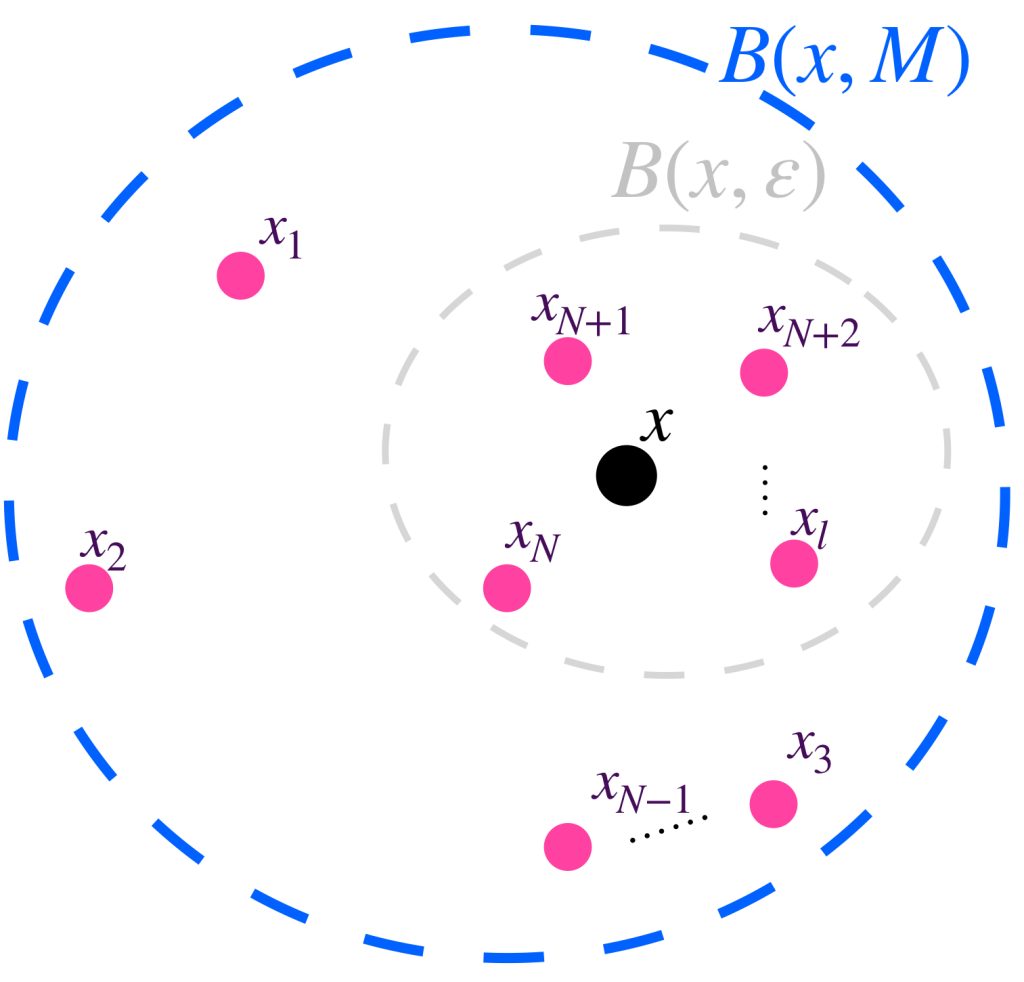
Definición: Diremos que una sucesión $(x_n)_{n \in \mathbb{N}}$ en $X$ es acotada si existe $M \in \mathbb{R}$ y $x \in X$ tales que $\forall \, n \in \mathbb{N}$ ocurre que $d(x,x_n) \leq M$.
Esto significa que una sucesión es acotada si todos los puntos $x_n,$ con $n \in \mathbb{N}$ están en una bola abierta con centro en algún punto $x$ del espacio métrico.
¿Es posible concluir que una sucesión es convergente si sabemos que es una sucesión acotada? Al final se te propondrá dar un ejemplo de una sucesión acotada que no sea convergente.
En contraparte, tenemos la siguiente:
Proposición: Toda sucesión convergente es acotada.
Demostración:
Sea $(x_n)_{n \in \mathbb{N}} \,$ una sucesión que converge a $x$ en $X$. Buscamos «encerrar» todos los puntos de la sucesión en una bola abierta. Si suponemos $\varepsilon = 1$, existe $N \in \mathbb{N}$ tal que para todo $n \geq N, \, d(x_n,x)<1$. Hasta aquí ya logramos «encerrar» todos los puntos de la sucesión a partir de $x_N$.
Para encerrar los elementos que van antes en la sucesión, considera las distancias entre $x$ y cada uno de esos puntos como $d_i = d(x_i,x), \, i=1,…,N-1$.
Si hacemos $M = máx\{d_i,1\}, \, i=1,…,N-1$, se consigue que para todo $n \in \mathbb{N}, \, d(x_n,x)<M$ con lo cual se demuestra que la sucesión es acotada.
Los últimos resultados que expondremos en esta entrada son muy importantes, en el sentido en que suele acudirse a ellos para otras demostraciones. Te sugerimos tenerlos presentes.
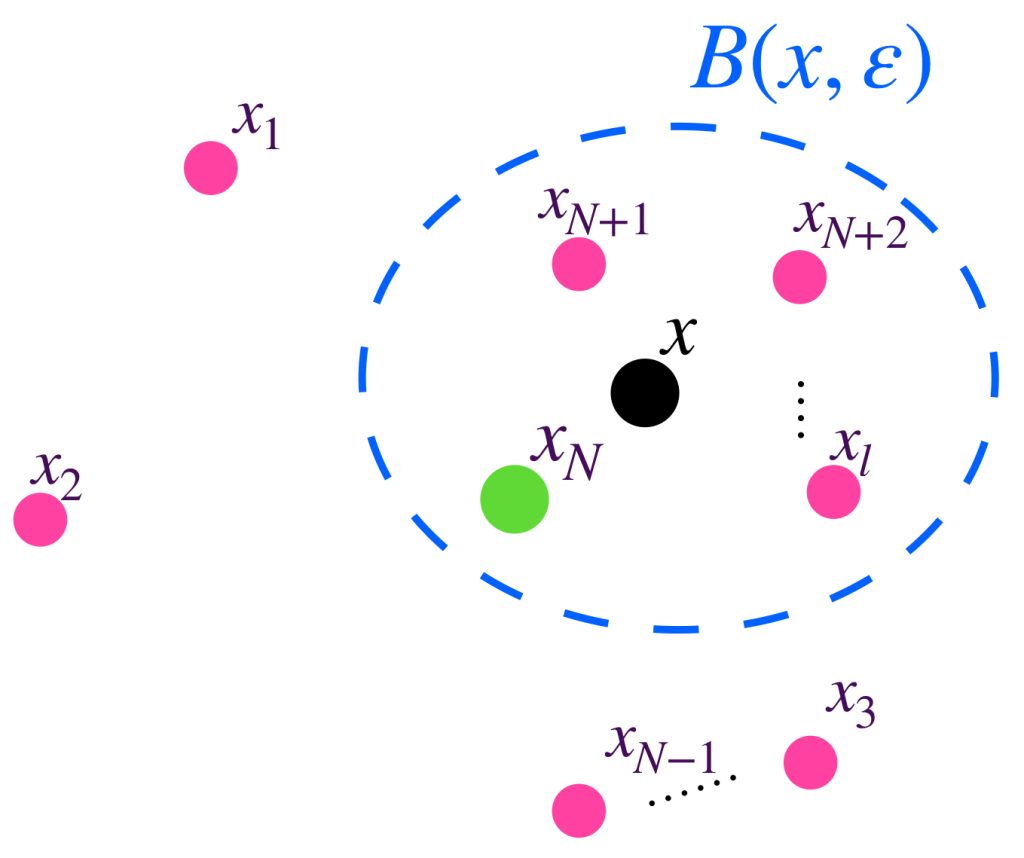
Proposición: Si $x_n \to x$ en $X$ entonces $x$ es un punto de contacto del conjunto $\{x_n \,|n \in \mathbb{N}\}$.
Según la definición, basta con demostrar que toda bola abierta de radio $\varepsilon >0$ con centro en $x$ interseca al conjunto $\{x_n\}$. La demostración se deja como ejercicio.
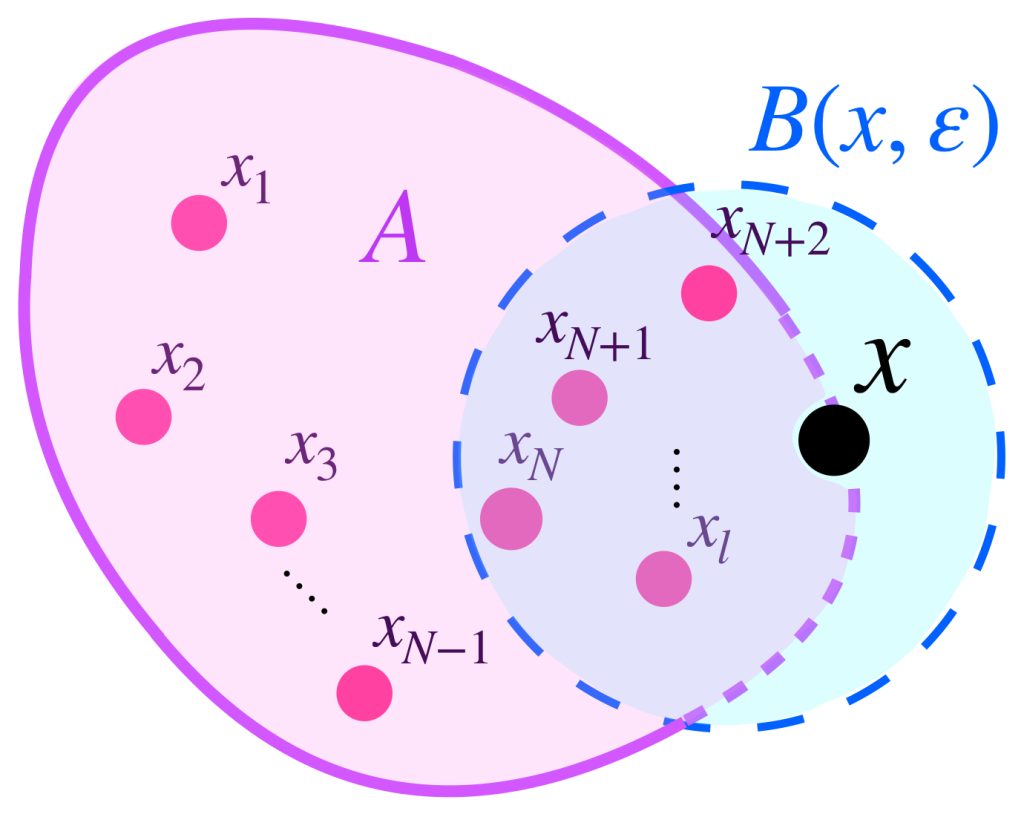
Proposición: Sea $A \subset X$ y $x \in X$. Entonces $x \in \overline{A}$ si y solo si existe una sucesión $(x_n)_{n \in \mathbb{N}}$ en $A$ tal que $x_n \to x$ en $X$.
Demostración:
El regreso se concluye a partir de la proposición anterior.
Si $x \in \overline{A}$ entonces todas las bolas abiertas con centro en $x$ intersecan al conjunto $A$. Así, para cada $n \in \mathbb{N}$, podemos elegir un punto $x_n \in B(x, \frac{1}{n}) \cap A$. Como $d(x,x_n)< \frac{1}{n} \to 0$ en $\mathbb{R}$, se concluye que $x_n \to x$ en $X$.
Más adelante…
Tendremos un acercamiento a un espacio métrico cuyos elementos son los subconjuntos cerrados de otro espacio métrico. Al definir la distancia entre estos subconjuntos cerrados veremos que, si una sucesión de ellos converge, entonces lo hace en un subconjunto cerrado. Ya que eso significa que la distancia tiende a cero, y la distancia entre dos elementos es cero cuando son iguales, podemos esperar que los subconjuntos de la sucesión se parecerán cada vez más, al subconjunto al cual convergen.
Tarea moral
- Prueba que si $(x_n) \to x$ en $X$ entonces $x$ es un punto de contacto del conjunto $\{x_n \,|n \in \mathbb{N}\}$.
- Demuestra que una sucesión constante converge.
- ¿Puede una sucesión ser convergente en el espacio discreto? ¿Bajo qué condiciones?
- Da un ejemplo de una sucesión en $\mathbb{Q}$ que converge en $\mathbb{R}$ pero no en $\mathbb{Q}$.
- Sea $A \subset X$. Demuestra que $x$ es un punto interior de $A$ si y solo si para toda $(x_n)_{n \in \mathbb{N}}$ que converge a $x$ en $X$, existe $N>0$ tal que $\forall \, n \geq N, x_n \in A$.
- Demuestra que $x \in X$ es un punto frontera de $A \subset X$ si y solo si existen sucesiones $(a_n)_{n \in \mathbb{N}}$ en $A$ y $(b_n)_{n \in \mathbb{N}}$ en $X\setminus A$ que convergen a $x$.
- Demuestra que si la imagen de una sucesión es finita entonces la sucesión es convergente.
- Da un ejemplo de una sucesión acotada que no sea convergente.