Introducción
En esta sección mostraremos los fundamentos de uno de los términos más importantes de las matemáticas. Una descripción histórica la presenta Yanina del Carmen Rodríguez Reyes, en la tesis «Desarrollo histórico-pedagógico del concepto de compacidad» en la Universidad de Panamá, República de Panamá 2018.
«La compacidad surgió de uno de los periodos más productivos de la actividad matemática. En la segunda mitad del siglo XIX en Europa las matemáticas avanzadas comenzaron a tomar la forma que conocemos actualmente. Muchos matemáticos, incluyendo Weierstrass, Hausdorff y Dedekind estaban preocupados por los fundamentos de las matemáticas y comenzaron a hacer muchas rigurosidades de las ideas que durante siglos habían sido dadas por sentado. Mientras que algunos de los trabajos del siglo XIX se pueden remontar a las preocupaciones matemáticas de los antiguos griegos, el nivel de rigor y la abstracción refleja una revolución en el pensamiento matemático. Fréchet fue influenciado por muchos contemporáneos y predecesores pero parece que merece el crédito como el padre de la compacidad. Fue Fréchet quien dio el nombre al concepto en un documento que conduce a su tesis doctoral de 1906. Fréchet también define por primera vez espacios métricos aunque no usando ese término y de hecho incursiona en el análisis funcional proporcionando así un contexto para el cual la importancia de la compacidad se hizo indiscutible”. (Rodríguez, 2018).
Conjuntos compactos
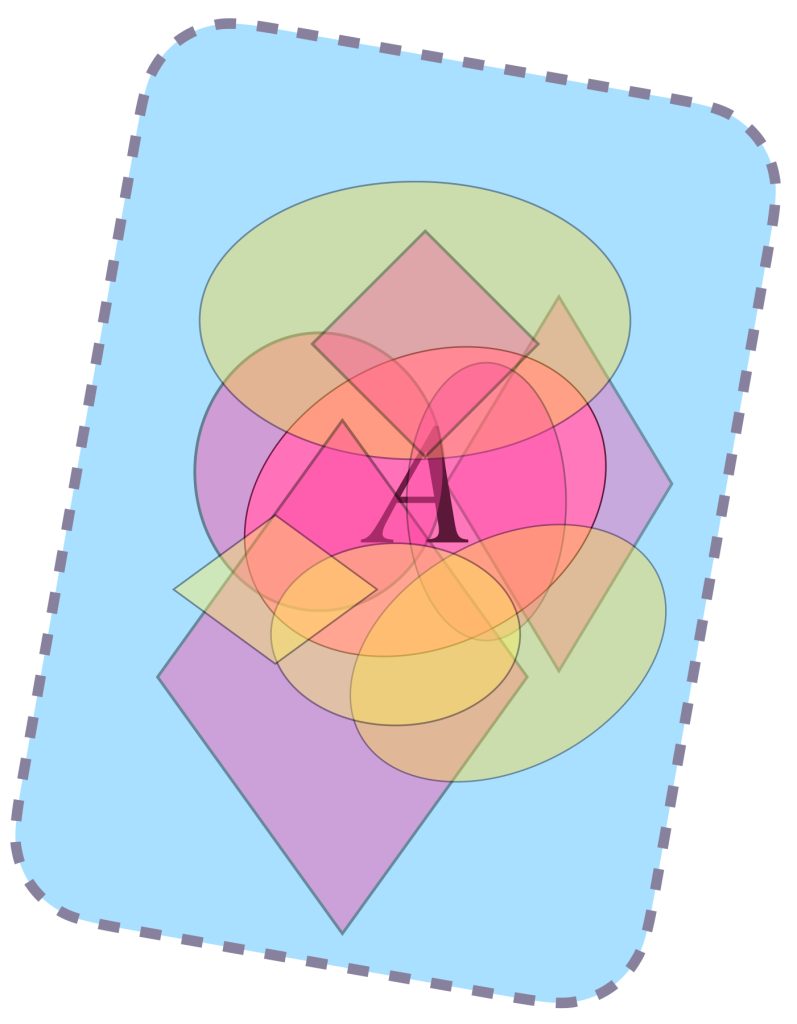
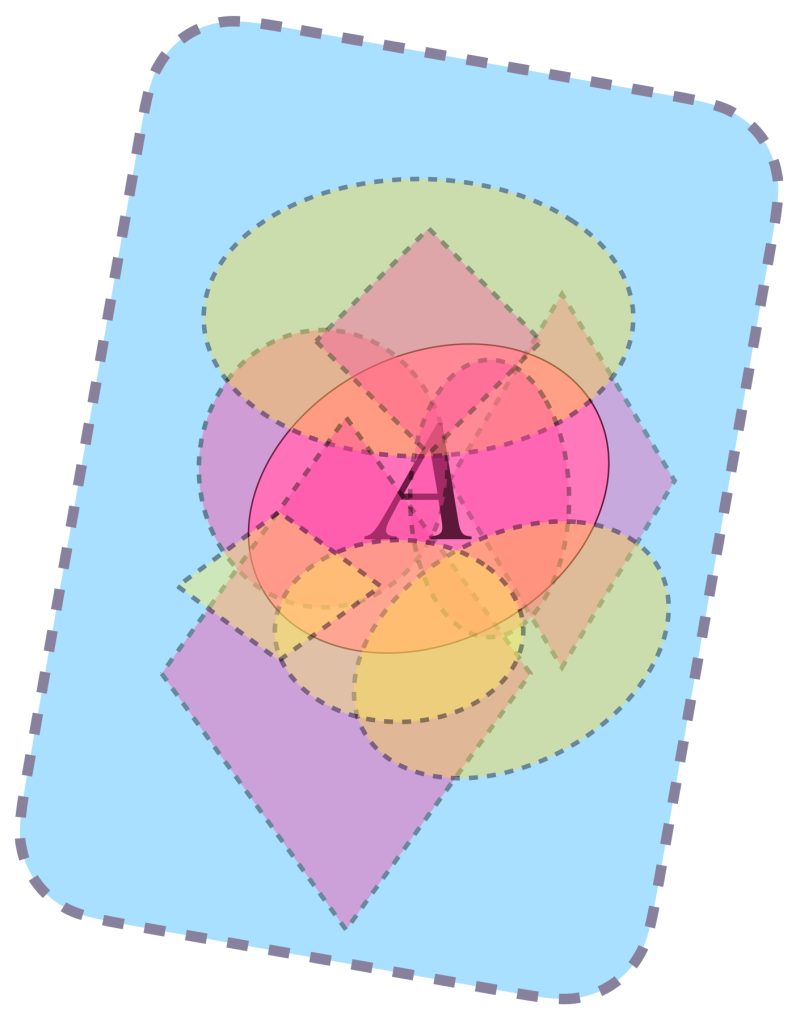
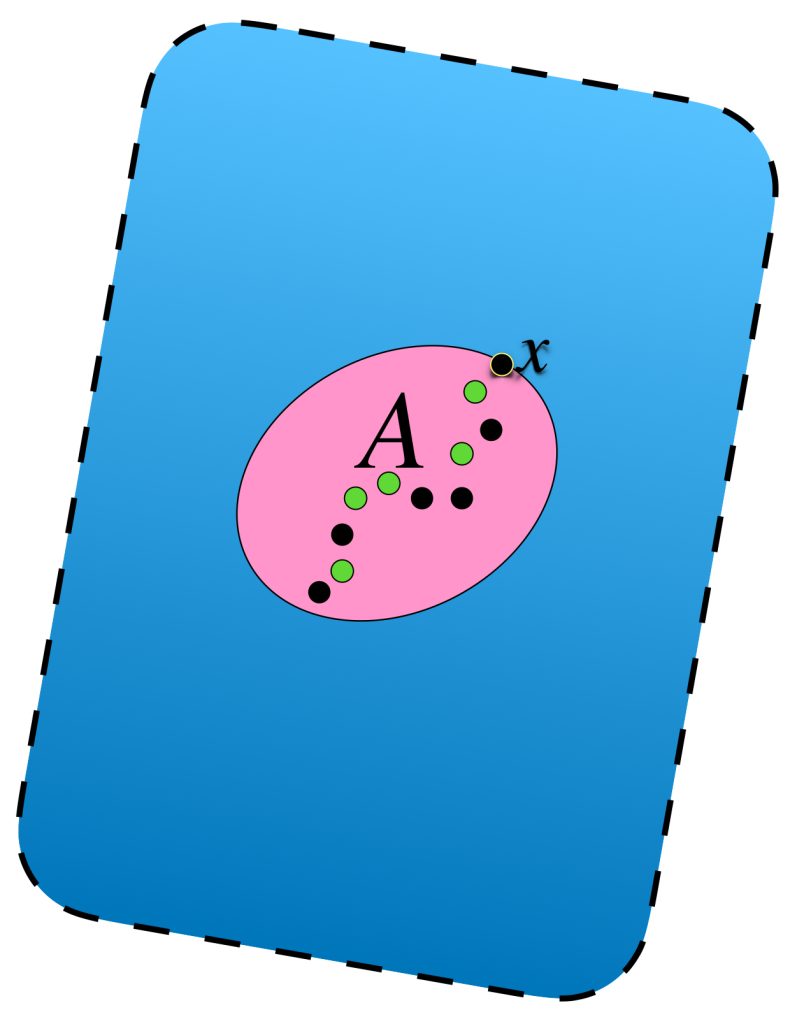
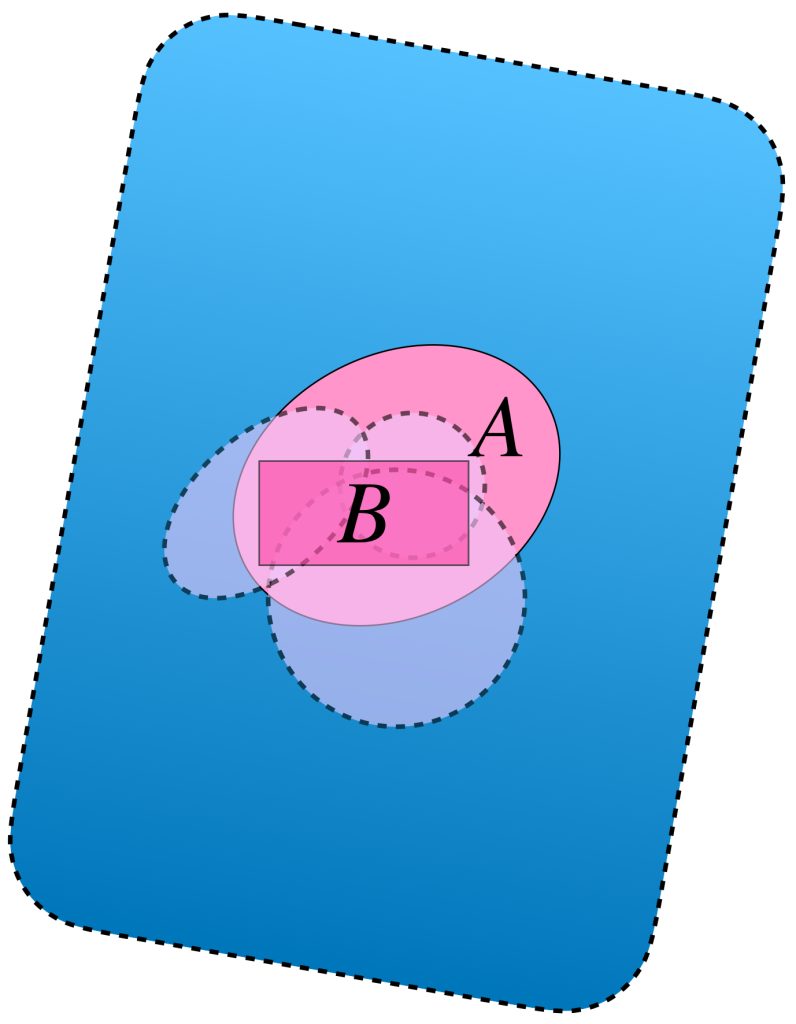
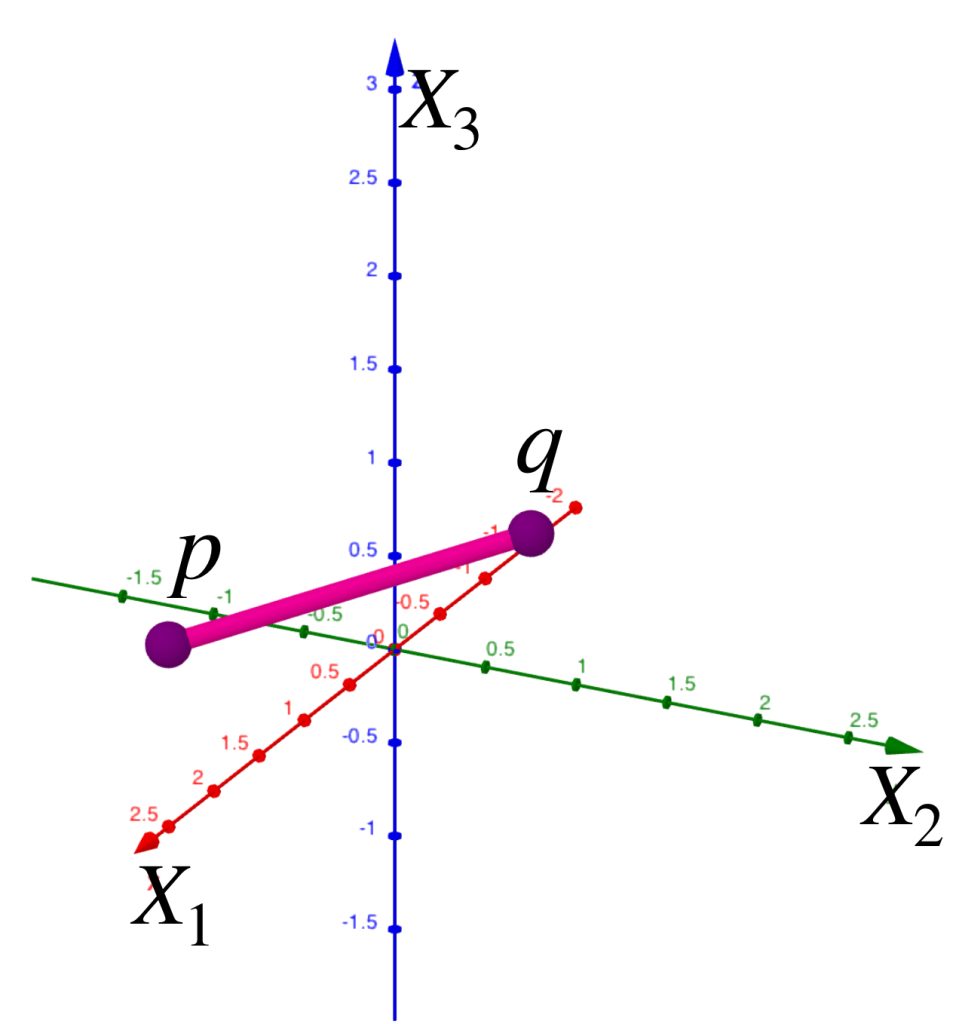
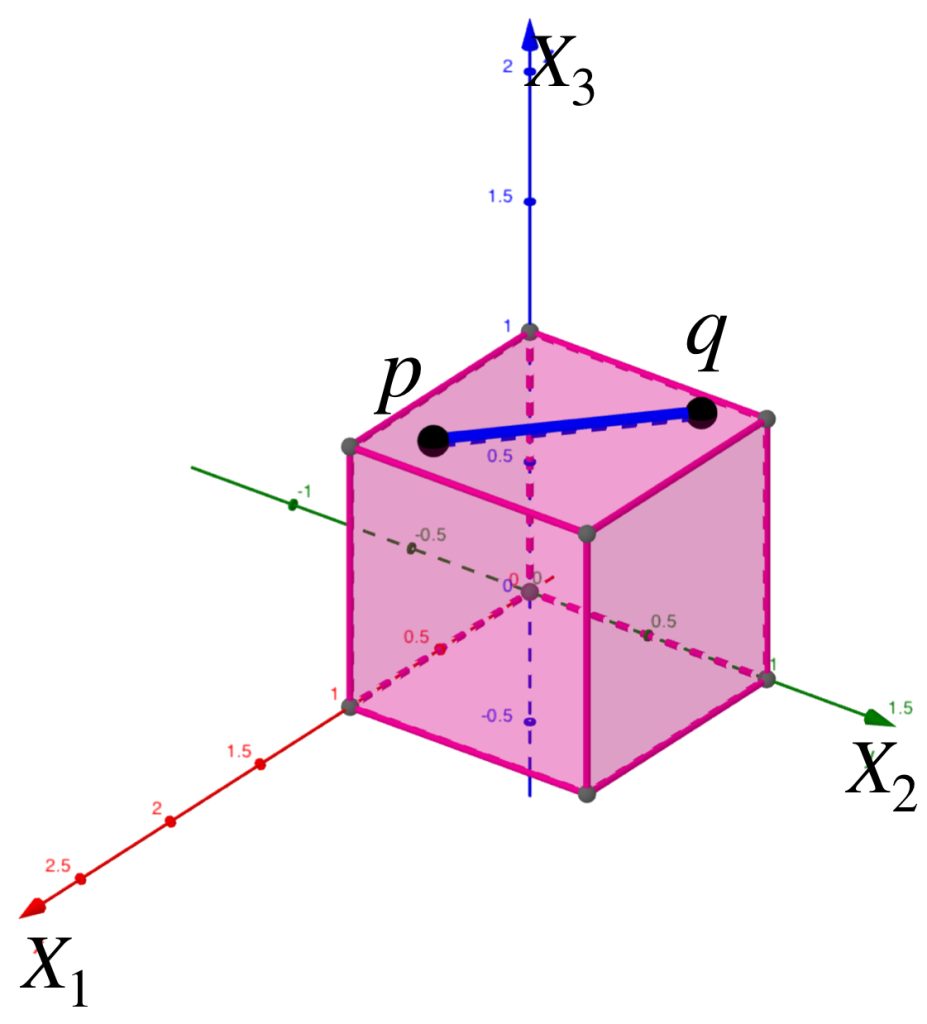
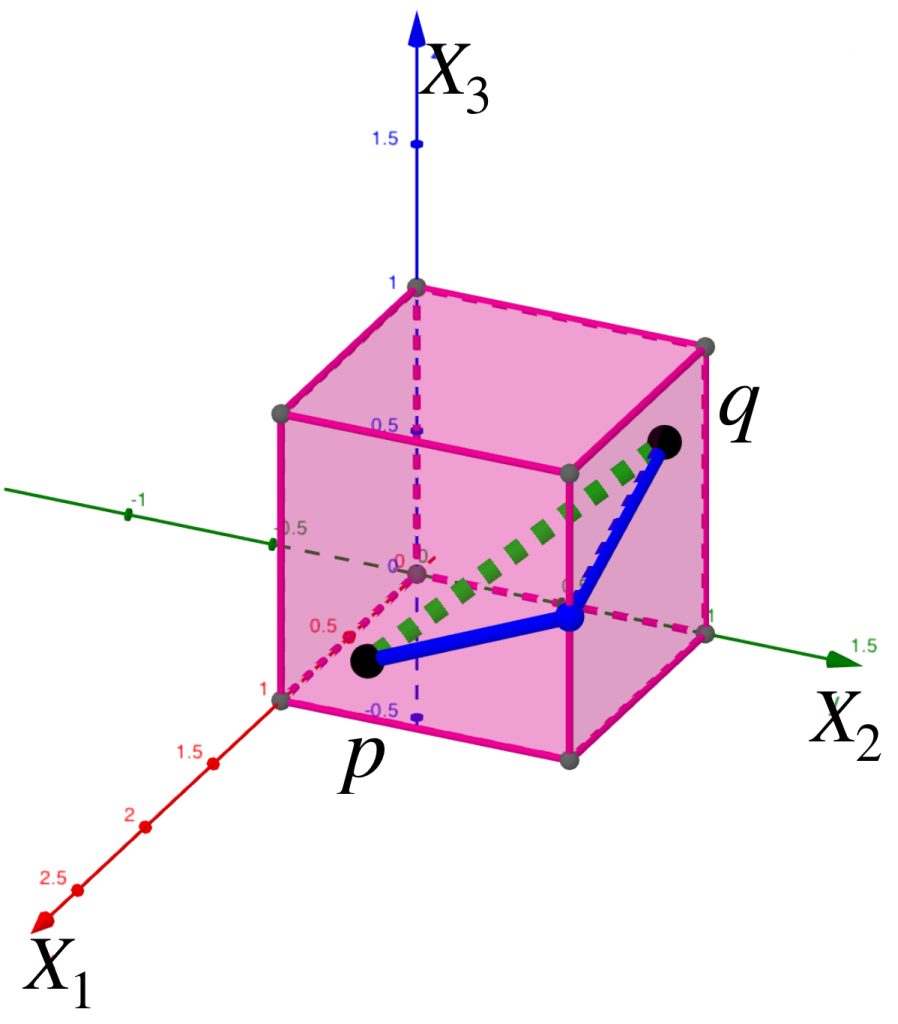
Sea $(X,d)$ un espacio métrico y $A \subset X$. Podemos pensar en «cubrir» este subconjunto a través de otros a modo de la siguiente imagen, es decir, conjuntos cuya unión logre contener a $A.$
La cantidad de subconjuntos que forman parte de la cubierta elegida puede ser finita, numerable o no numerable, entonces, para ser formales, cada subconjunto se puede indexar con los elementos de algún conjunto $\mathcal{I}$. Así tenemos la siguiente:
Definición. Cubierta de un conjunto: Sea $A \subset X$. Decimos que una familia de subconjuntos $\mathcal{C} = \{A_{i} \subset X : i \in \mathcal{I} \}$ es una cubierta de $A$ en $X$ si
$$A \subset \underset{i \in \mathcal{I}}{\cup} \, A_{i} \,$$
Definición. Cubierta abierta: Si para toda $i \in \mathcal{I}$ se cumple que el conjunto $A_i$ es abierto, diremos que $\mathcal{C}$ es una cubierta abierta de $A$ en $X$.
Definición. Subcubierta: Si tomamos conjuntos de una cubierta $\mathcal{C}$, digamos, una familia $\mathcal{C’} \subset \mathcal{C} \, $ y $\, \mathcal{C’}$ es también una cubierta de $A$ diremos que $\mathcal{C’}$ es una subcubierta de $\mathcal{C}$.
Definición. Conjunto compacto: Sea $A$ un conjunto de un espacio métrico $(X,d)$. Decimos que $A$ es un conjunto compacto si dada cualquier cubierta abierta $\mathcal{C}$ de $A$, existe una subcubierta finita de $\mathcal{C}.$
El concepto de compacidad suele tomar mayor relevancia cuando en un espacio topológico se considera el subespacio generado por el conjunto compacto. En estos casos se le denomina espacio topológico compacto.
Según la definición, para demostrar que un conjunto $A$ no es compacto, bastará con identificar una cubierta de la cual no sea posible extraer una subcubierta finita (conjuntos cuya unión logre contener el conjunto $A$).
Ejemplos
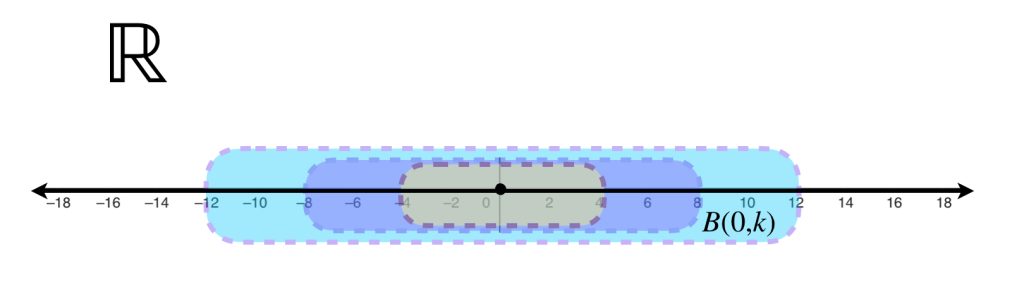
El conjunto $\mathbb{R}$ con la métrica euclidiana no es compacto.
Demostración:
El conjunto de intervalos abiertos con centro en $0$ y radio $n, \, n \in \mathbb{N}$ es decir, $\mathcal{C}=\{(-n,n):n \in \mathbb{N}\}$ es una cubierta abierta de $\mathbb{R}.$ Pero si consideramos un subconjunto finito $\mathcal{C’} \subset \mathcal{C}$ entonces $\mathcal{C’} = \{(-k_1,k_1),(-k_2,k_2),…,(-k_m,k_m)\}$ con $k_1,k_2,…,k_m \in \mathbb{N}.$ Sea $k=máx\{k_1,k_2,…,k_m\}$ podemos ver que la unión de los elementos en $\mathcal{C’}$ es el intervalo $(-k,k)$ que claramente, no contiene a $\mathbb{R}$, por lo tanto $\mathbb{R}$ no es compacto.
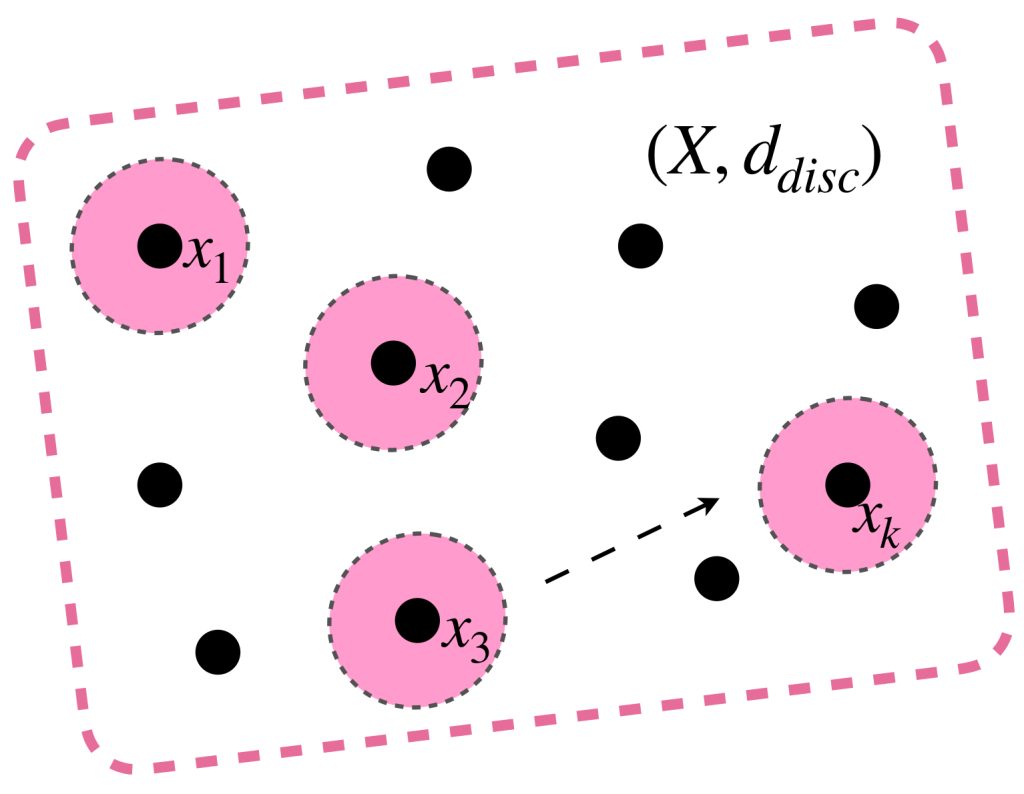
Un espacio discreto es compacto si y solo si es finito
Considera un conjunto $X$ con la métrica discreta. Entonces, para cada $x \in X$ el conjunto $\{ x \}$ es abierto, así $\mathcal{C}=\{\{x\}:x \in X\}$ es una cubierta abierta de $X.$ Un subconjunto finito de esta cubierta estaría dada por $\mathcal{C’}=\{\{x_1\},\{x_2\},…,\{x_k\}\}, \, k \in \mathbb{N}$ cuya unión de conjuntos contiene $k$ elementos. Por lo tanto, si $X$ es infinito no es compacto con la métrica discreta. La prueba de que si $X$ es finito entonces es compacto se deja como ejercicio al final de esta sección.
Proposición. Si $A$ es un conjunto compacto en $(X,d)$, entonces toda sucesión en $A$ tiene una subsucesión que converge en $A$.
Demostración:
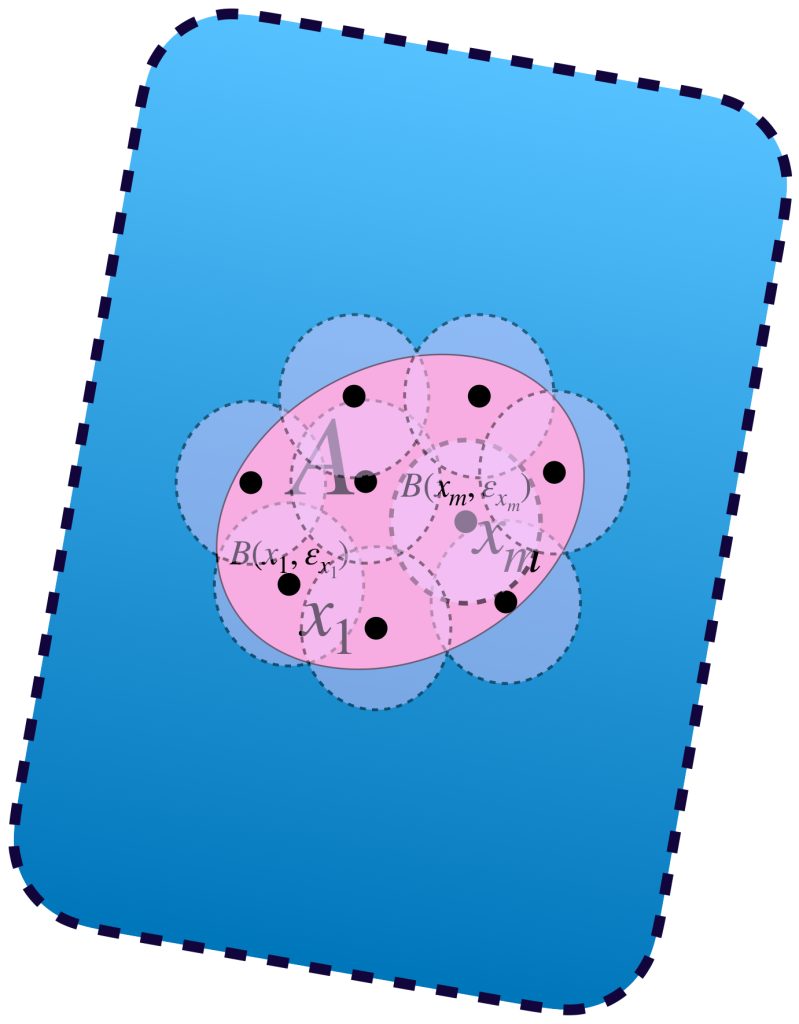
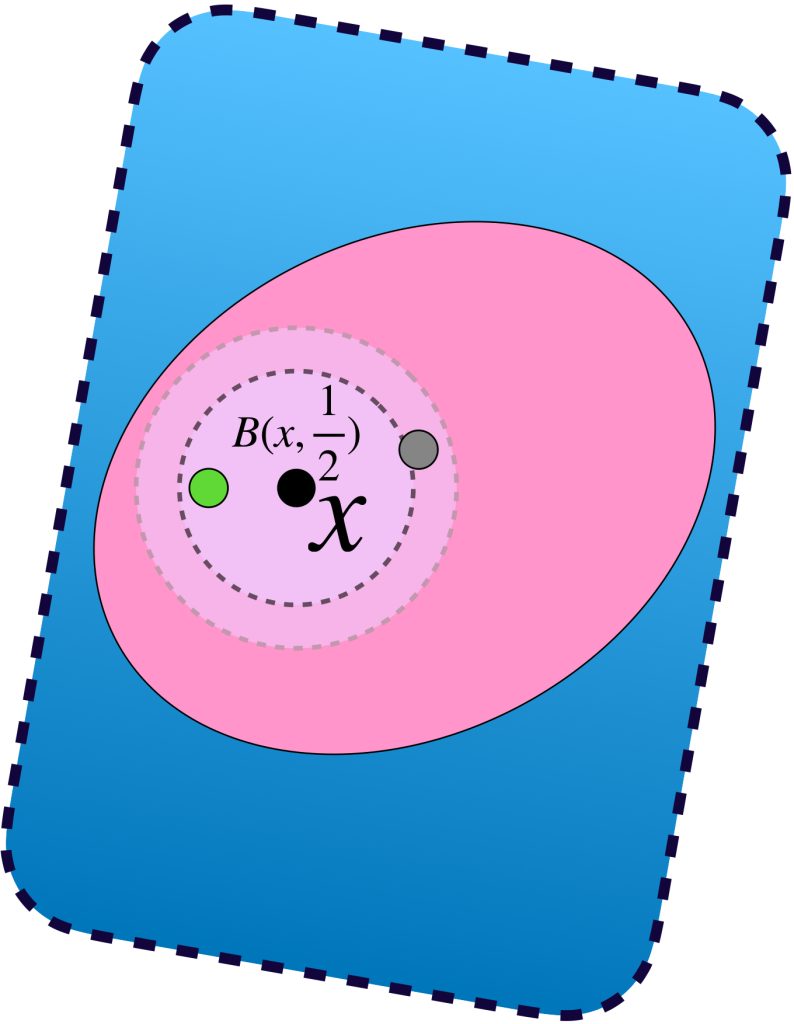
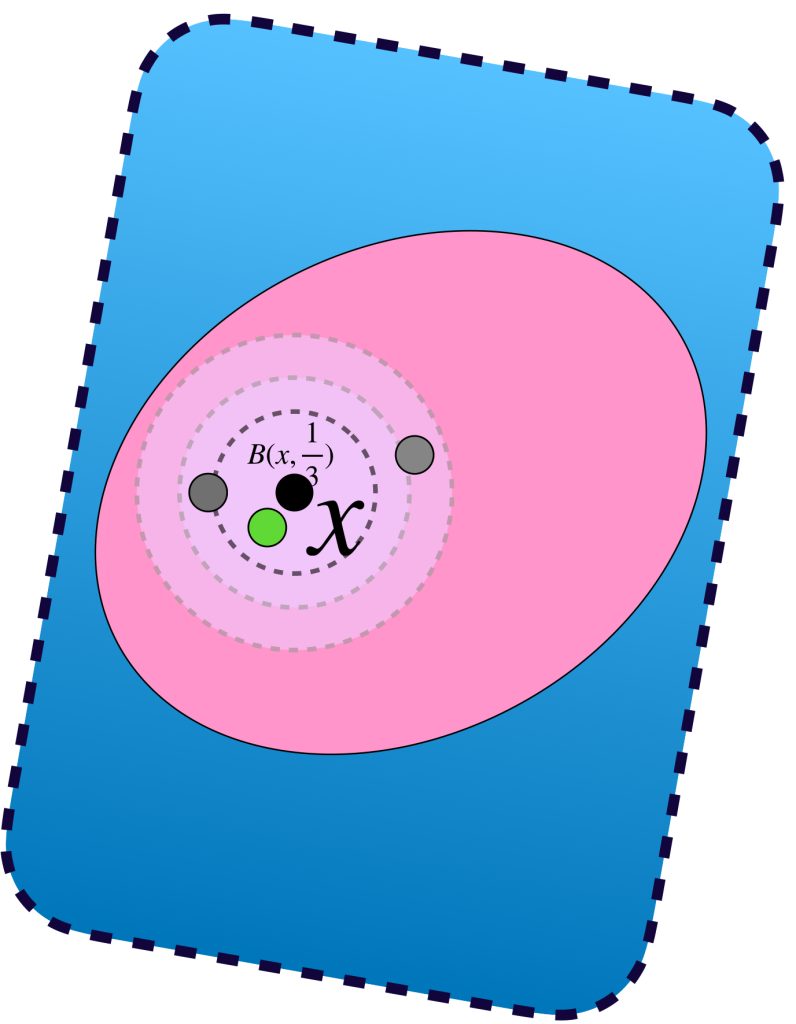
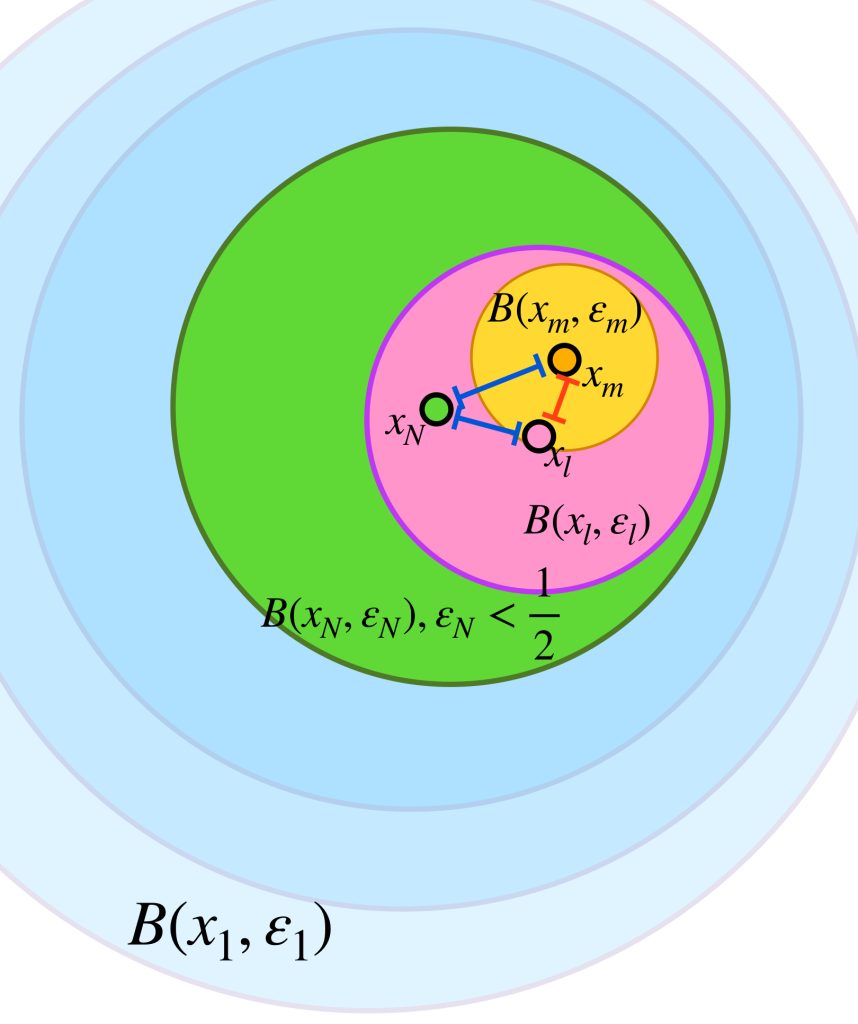
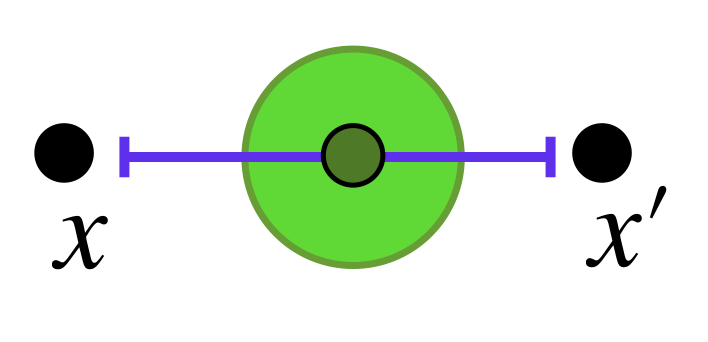
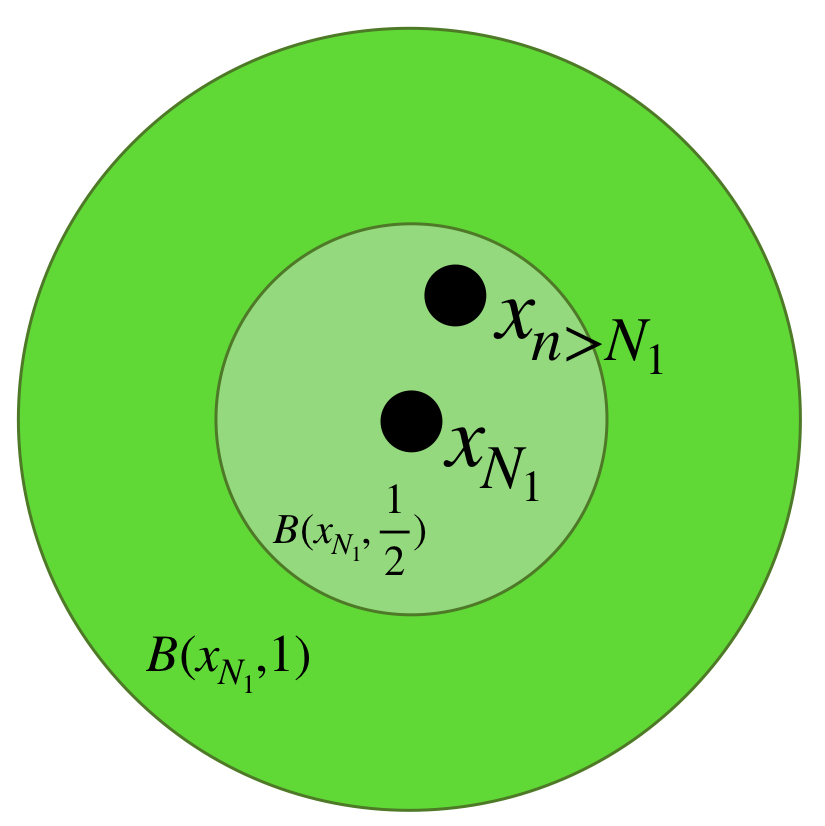
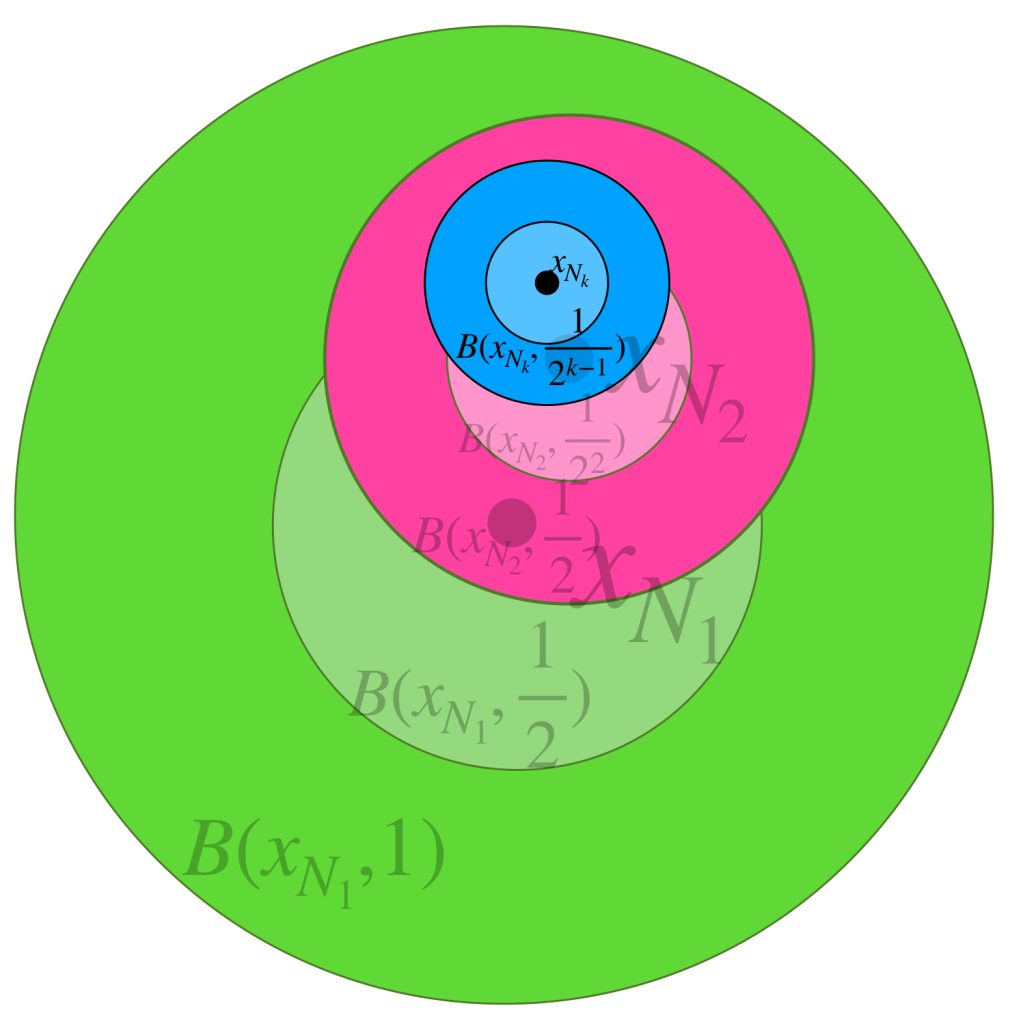
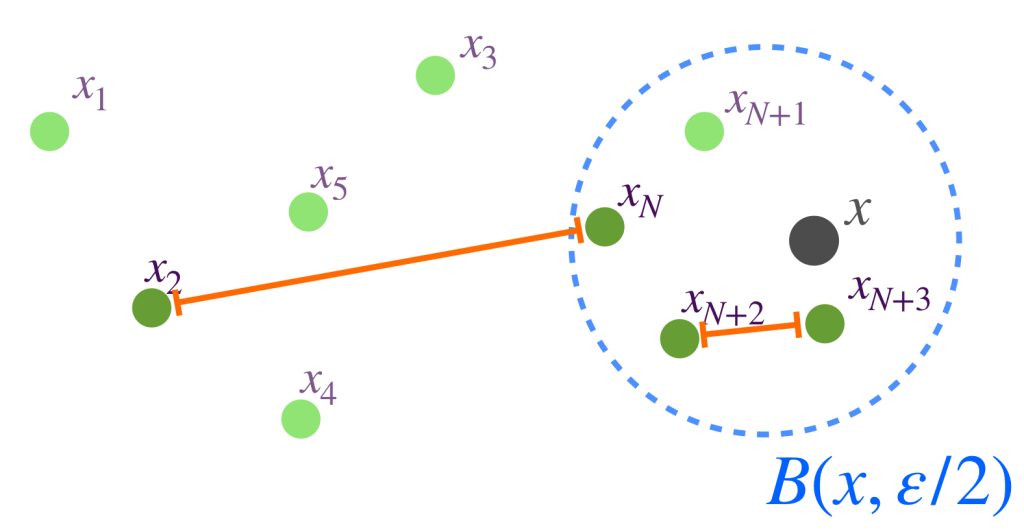
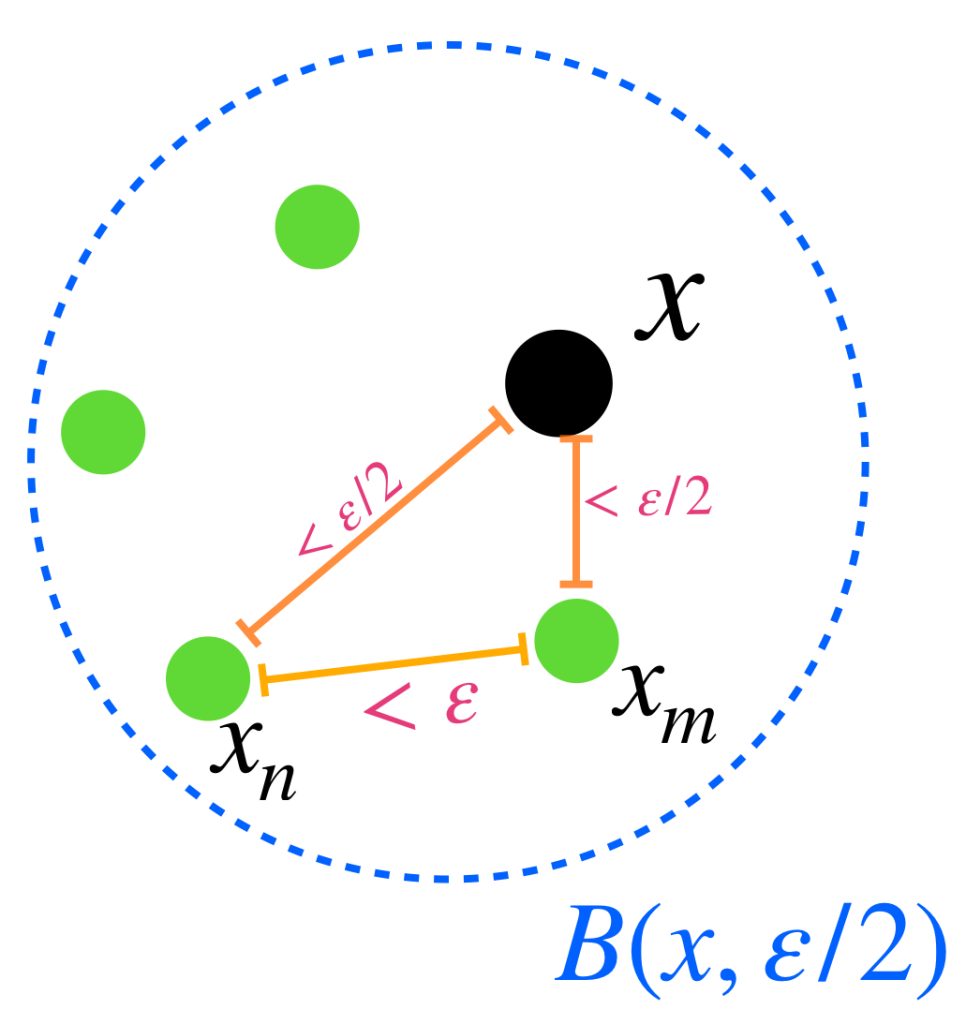
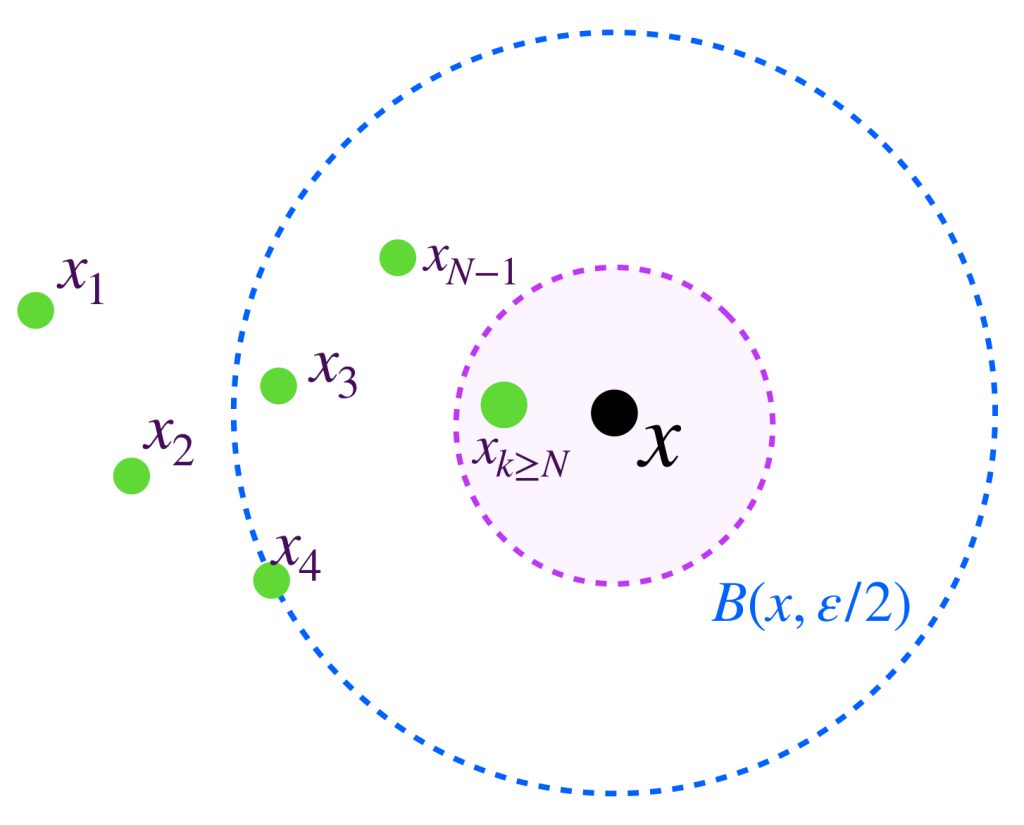
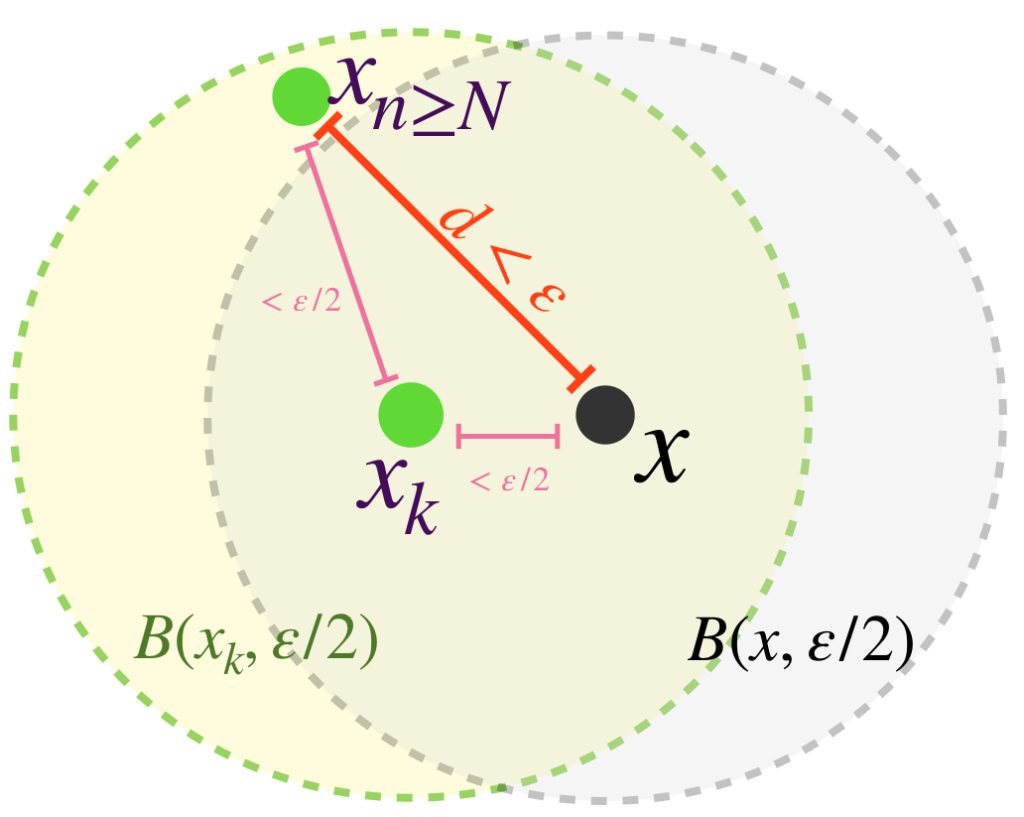
Sea $A \subset X$ compacto y $(x_n)_{n \in \mathbb{N}} \,$ una sucesión en $A$. Demostraremos primero que existe un punto $x \in A$ tal que toda bola abierta con centro en $x$ tiene una subsucesión de $(x_n)$. Supón por el contrario que no es así, es decir, para todo punto $x \in A$ existe $\varepsilon_x >0$ y existe $k_x \in \mathbb{N}$ tal que para toda $k \geq k_x, \, x_k \, \notin \, B(x,\varepsilon_x).$
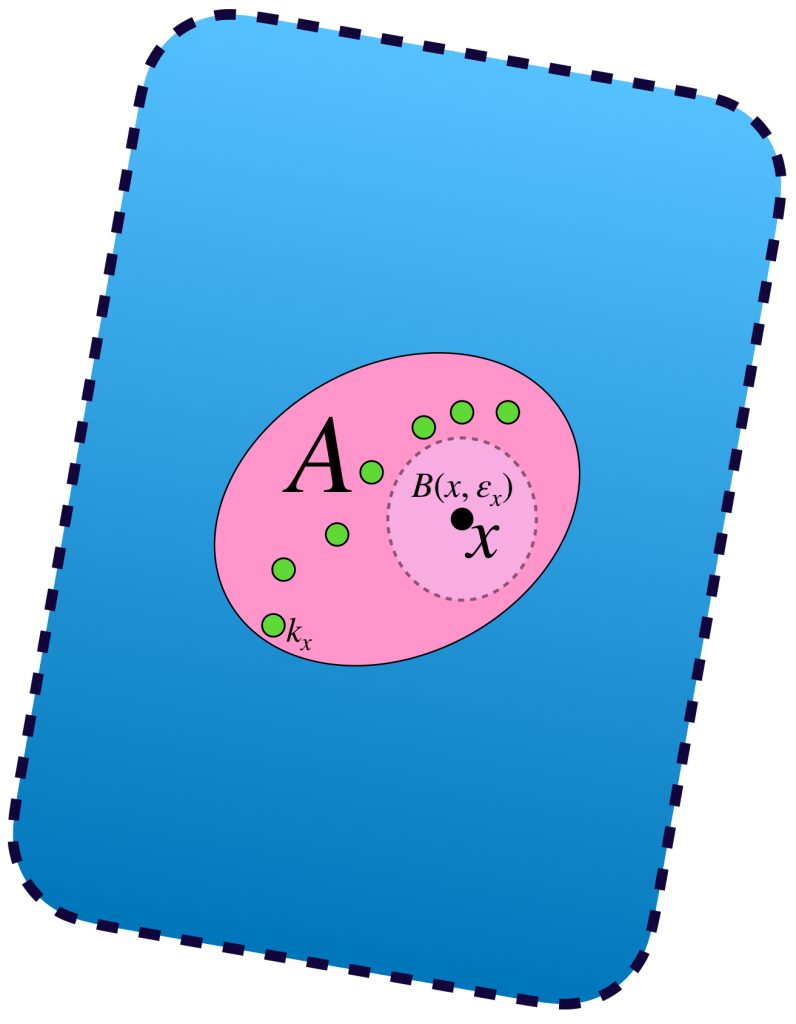
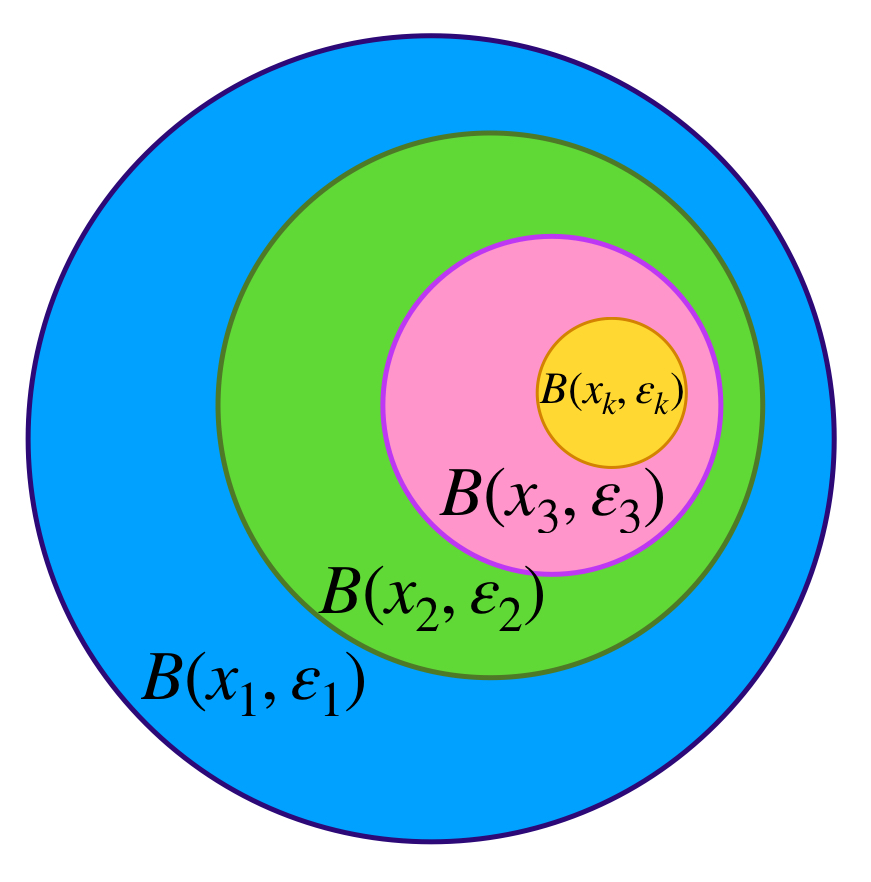
El conjunto de todas estas bolas abiertas, $\{B(x, \varepsilon_x): x \in A\}$ es una cubierta abierta del conjunto $A$. Como $A$ es compacto, existe $\{B(x_1, \varepsilon_{x_1}),B(x_2, \varepsilon_{x_2}),…,B(x_m, \varepsilon_{x_m})\}$ subcubierta finita. Sea $l =: máx \{k_{x_1},k_{x_2},…,k_{x_3}$ entonces para toda $k \geq l,$ el término $x_k \notin \underset{1\leq i \leq m}{\cup} \, B(x_i, \varepsilon_{x_i}) \supset A,$ en consecuencia $x _k \notin A$ lo cual es una contradicción, pues todos los términos de la sucesión están en $A$, por lo tanto existe un punto $x \in A$ tal que toda bola abierta con centro en $x$ tiene una subsucesión de $(x_n)$.
Sea $x \in A$ dicho punto. Por la propiedad mencionada es posible seleccionar un punto $x_{k_j}$ de la sucesión que esté en cada bola $B(x,\frac{1}{j}), \, j \in \mathbb{N}$ tal que no se repita con los anteriores y conserven el orden de la sucesión original. Por lo tanto $(x_{k_j})$ es subsucesión de $(x_n)$ y $x_{k_{j}} \to x$.
Así probamos que toda sucesión de un conjunto compacto tiene una subsucesión que converge en él.
Proposición: Si $A \subset X$ es compacto entonces es cerrado y acotado.
Demostración:
Recordemos que un conjunto es cerrado si y solo si es igual a su cerradura. Como $A \subset \overline{A}$ basta demostrar que $\overline{A} \subset A$. Sea $x \in \overline{A}$ entonces existe una sucesión $(x_n)_{n \in \mathbb{N}}$ en $A$ que converge en $x$ (Visto en Convergencia). Pero por la proposición que acabamos de ver, $(x_n)$ tiene una subsucesión que converge en $A$. Por la unicidad del límite, ese punto de convergencia es $x$, por lo tanto $x \in A$.
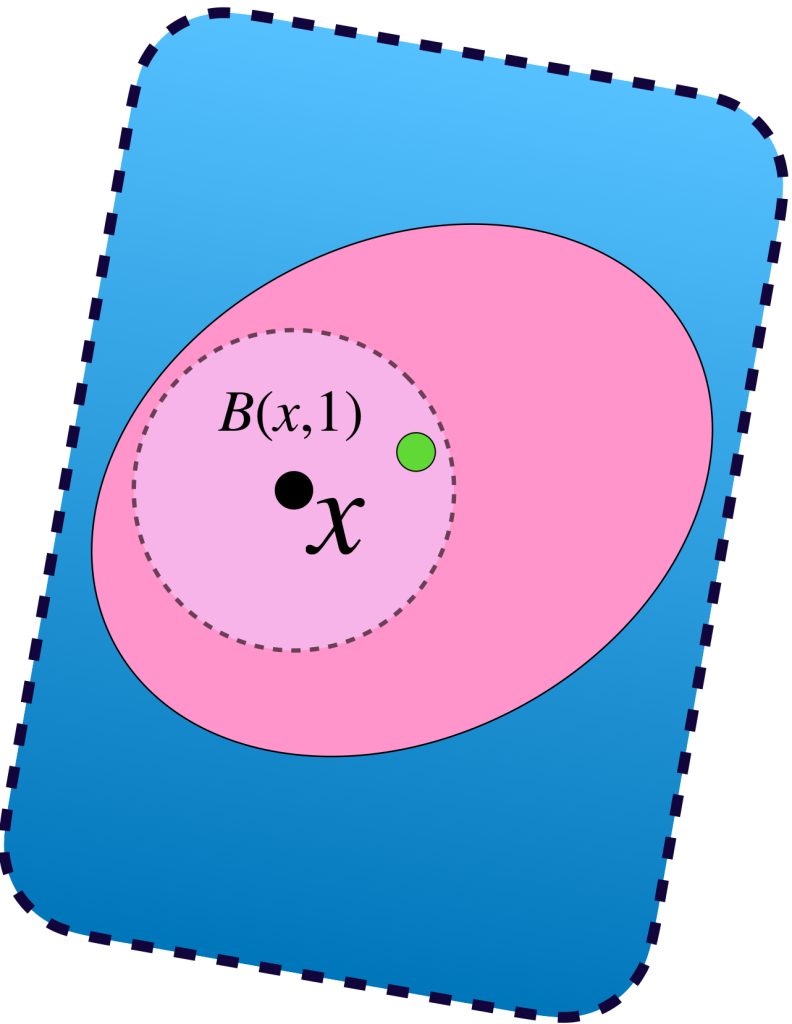
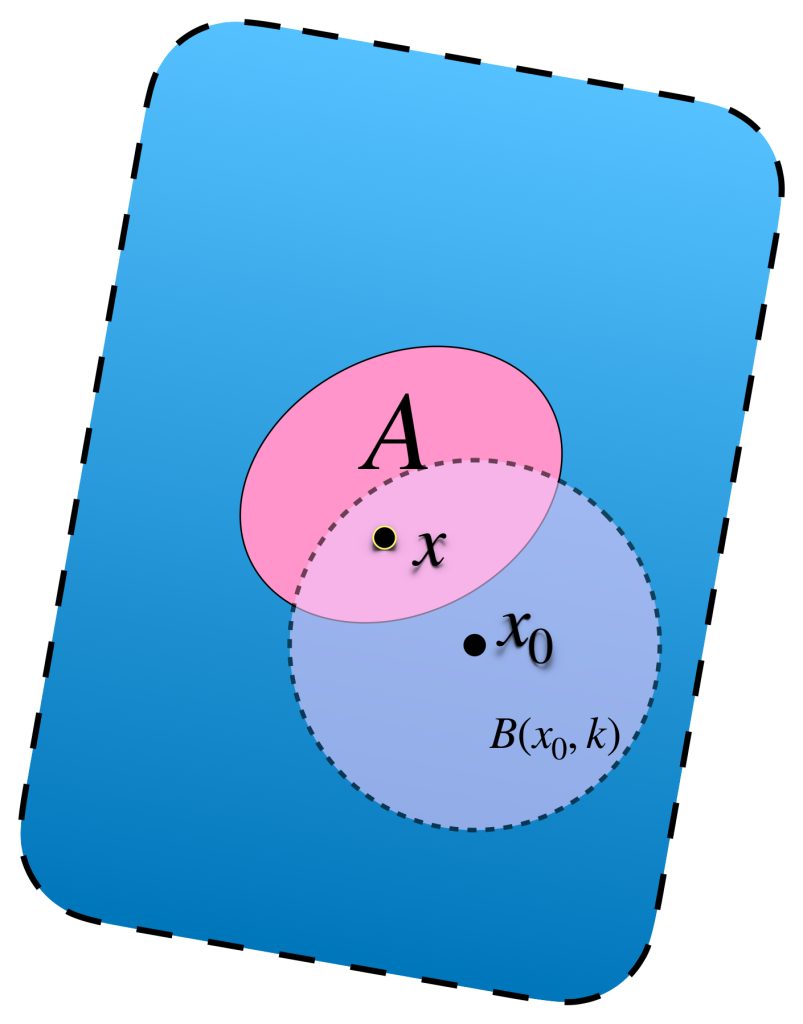
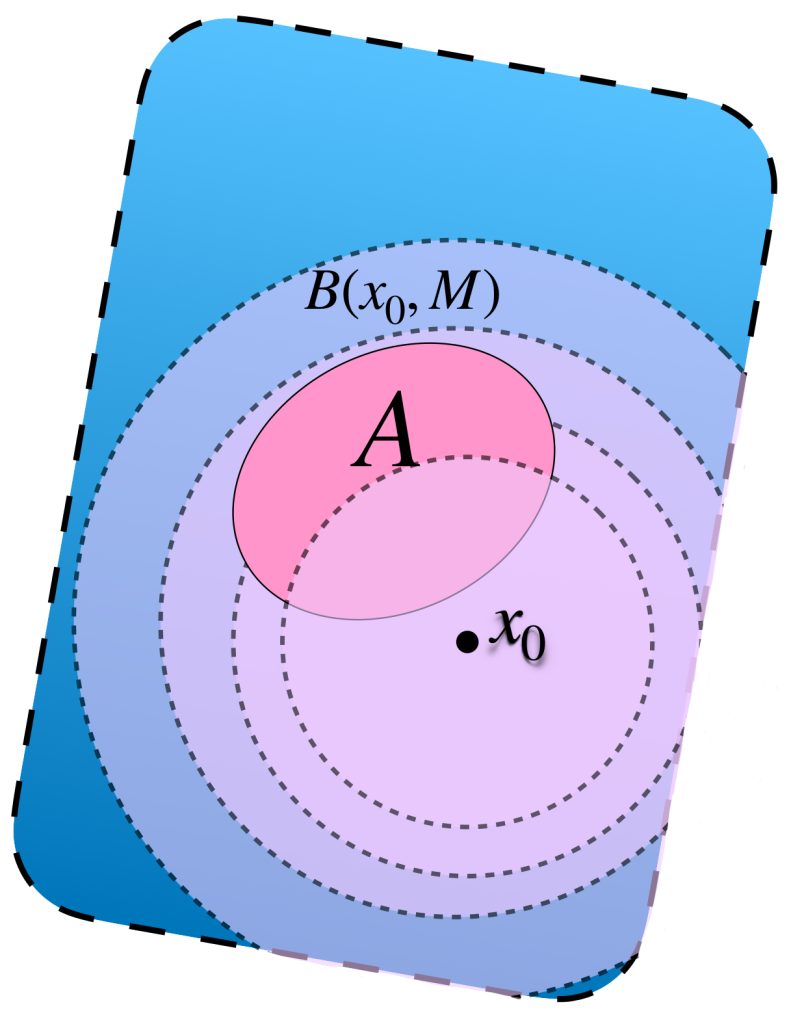
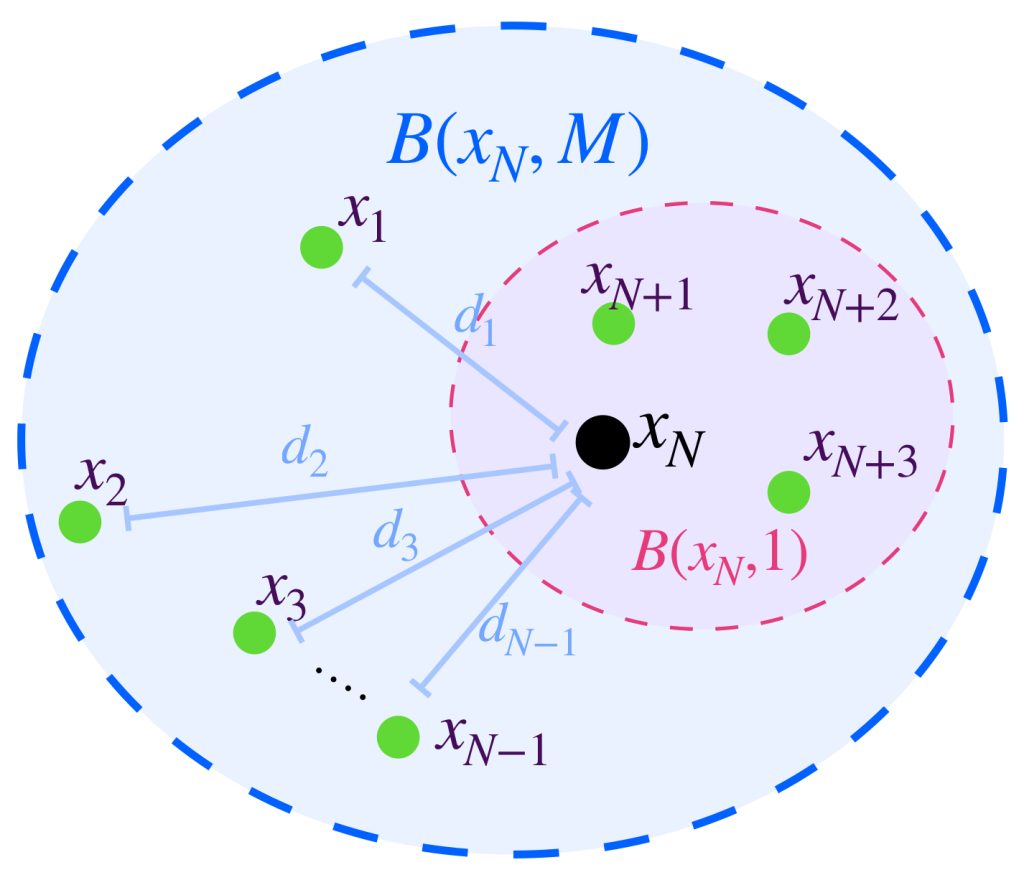
Para probar que $A$ es acotado notemos lo siguiente. Si fijamos un punto $x_0 \in X$, podemos poner cada $x \in A$ en una bola abierta con centro en $x_0$ y radio mayor a la distancia $d(x,x_0).$ Elegimos el radio como un número natural $k \,$ suficientemente grande, tal que $d(x,x_0)<k.$ Entonces $x \in B(x_0,k).$
En consecuencia el conjunto de bolas abiertas $\{B(x_0,n):n \in \mathbb{N}\}$ es una cubierta abierta del conjunto $A$ que, como es compacto, tiene una subcubierta finita $\{B(x_0,n_1), B(x_0,n_2),…,B(x_0,n_m)\}$. Sea $M =: máx \{n_1,n_2,…,n_m\}$ entonces $A \subset B(x_0,M)$ por lo tanto $A$ es acotado.
Ejemplos
A continuación recordamos un resultado conocido de los cursos de cálculo:
Teorema de Heine Borel: Considera $\mathbb{R}^n$ con la métrica euclidiana y $A \subset \mathbb{R}^n.$ Entonces $A$ es un conjunto compacto si y solo si es cerrado y acotado.
No obstante, hay espacios métricos en los que no es suficiente que un conjunto sea cerrado y acotado para que sea compacto:
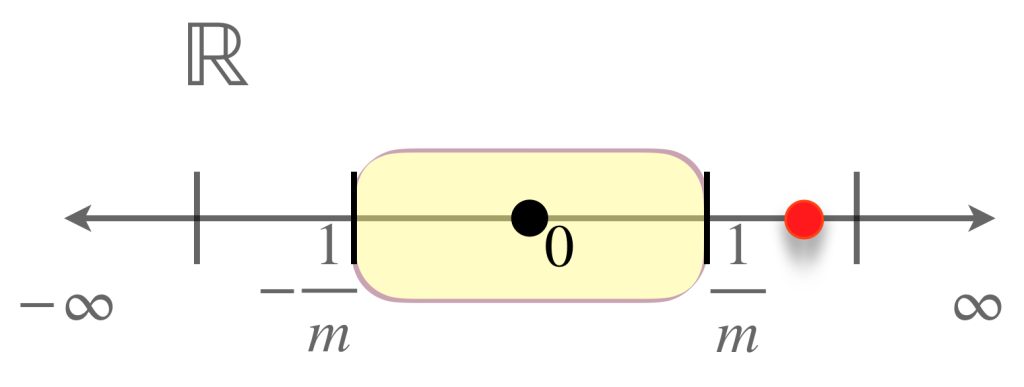
Ejercicio: Considera el conjunto $\mathbb{R}$ y $d$ definida como $d(x,y)=min\{1, |x-y|\}, \, x,y \in \mathbb{R}$ entonces tenemos lo siguiente:
- $d$ es una métrica en $\mathbb{R}.$
- $d$ induce en $\mathbb{R}$ los mismos conjuntos abiertos que la métrica usual. Entonces un conjunto es compacto en $(\mathbb{R},d)$ si y solo si lo es en $(\mathbb{R},d_2).$
- El conjunto $[0,\infty)$ es cerrado y acotado en $(\mathbb{R},d),$ pero no es compacto, pues no lo es en $(\mathbb{R},d_2).$
Veamos una propiedad que hereda la compacidad a un subconjunto de un conjunto compacto:
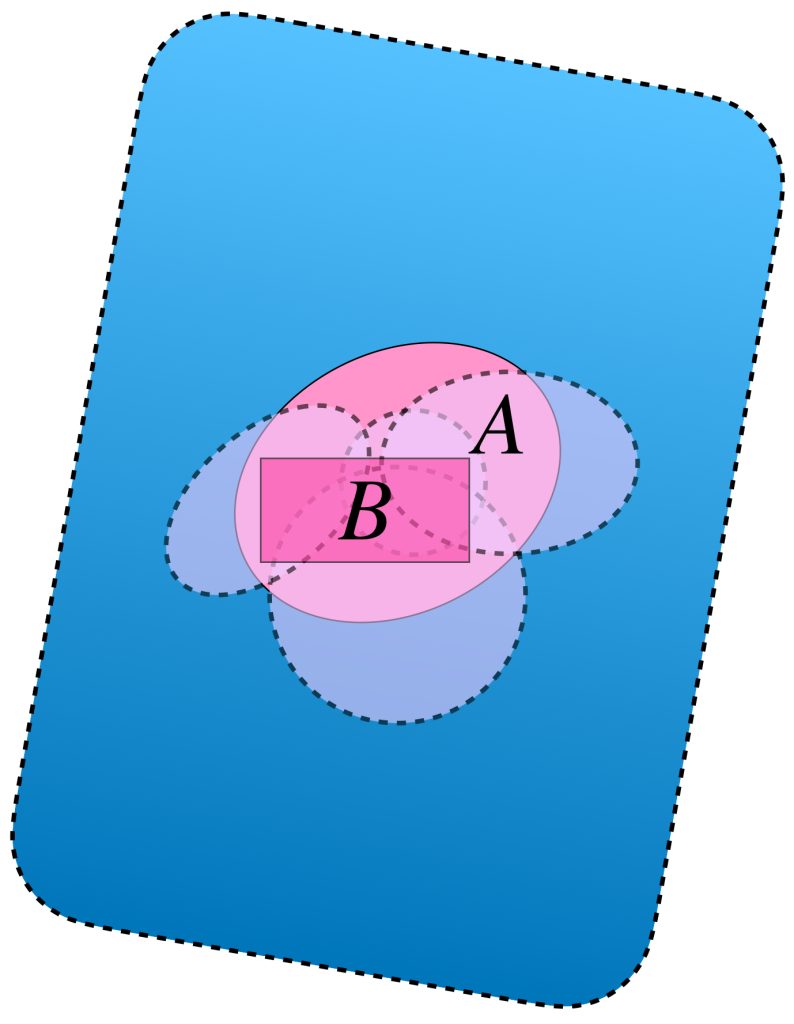
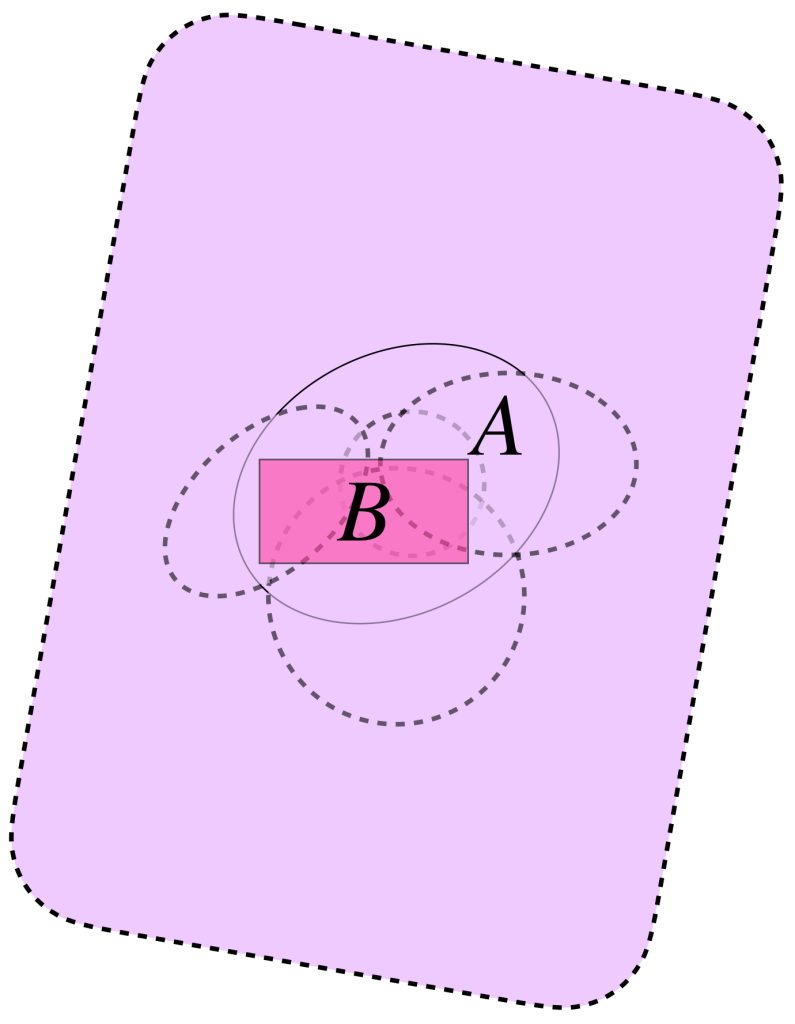
Proposición: Un subconjunto cerrado $B$ de un conjunto compacto $A$ también es compacto.
Demostración:
Sea $B \subset A$ con $B$ cerrado y $A$ compacto. Considera $\mathcal{C} = \{B_{i} \subset X : i \in \mathcal{I} \}$ una cubierta abierta de $B$.
Dado que $B \subset A,$ si agregamos $X \setminus B$ a la cubierta de $B$ tenemos que $\mathcal{C} \cup \{X \setminus B\}$ es una cubierta abierta de $A.$
Al ser el conjunto $A$ compacto, se sigue que esta cubierta tiene una subcubierta finita que satisface:
$$B \subset A \subset B_{i_1} \cup…\cup B_{i_n} \cup (X \setminus A).$$ con $n \in \mathbb{N}.$
Por lo tanto $\mathcal{C’}=B_{i_1},…,B_{i_n}$ es una subcubierta finita de $\mathcal{C}$ lo cual concluye que $B$ es compacto.
Finalizamos esta sección con los siguientes resultados para así cumplir con una deuda pendiente.
Teorema: Considera $ \{ A_{\alpha} : \alpha \in \mathcal{A} \}$ una colección de subconjuntos compactos de un espacio métrico $(X,d).$ Si ocurre que cualquier intersección finita de elementos de $\{A_{\alpha}\}$ es no vacía, entonces la intersección de todos los elementos también es no vacía. Es decir:
$$\underset{\alpha \in \mathcal{A}}{\bigcap} \, A_{\alpha} \, \neq \emptyset$$
Demostración:
Supón por el contrario que la intersección es vacía. Sea $A_1 \in \{A_{\alpha}\}$ entonces no existe punto de $A_1$ que pertenezca al mismo tiempo, a todos los elementos de $\{A_{\alpha}\}$
Sea $C_{\alpha} := X \setminus A_{\alpha}.$ Entonces $ \{ C_{\alpha} : \alpha \in \mathcal{A} \}$ es una cubierta abierta de $A_1$ que, por ser compacto, tiene una subcubierta finita, así:
$A_1 \subset (C_{\alpha_1} \cup … \cup C_{\alpha_n})$ p.a. ${\alpha_1},…{\alpha_n}, \in \mathcal{A}$
En consecuencia $A_{\alpha_1} \cap … \cap A_{\alpha_n} = \emptyset$ lo cual no es cierto, por lo tanto
$$\underset{\alpha \in \mathcal{A}}{\bigcap} \, A_{\alpha} \, \neq \emptyset$$
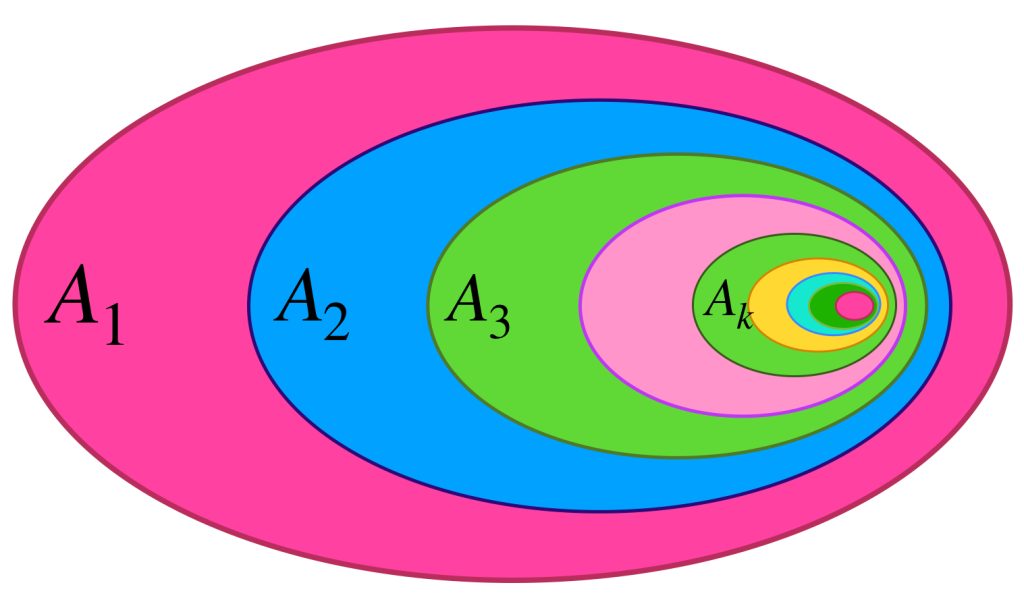
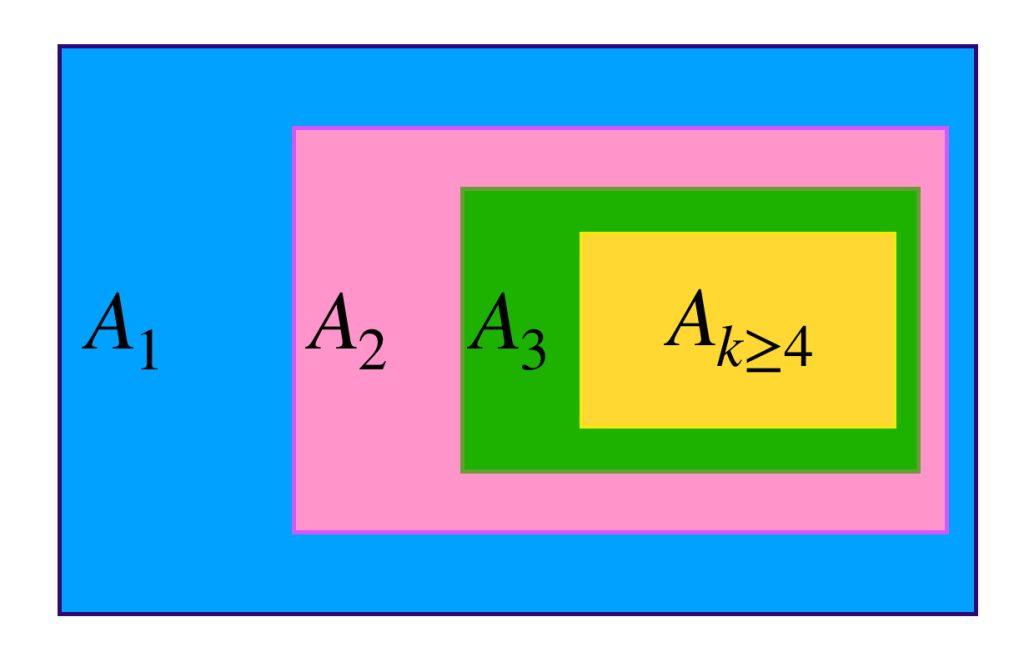
Corolario: Si $ \{ A_{n} : n \in \mathbb{N} \}$ es una colección de subconjuntos compactos no vacíos de un espacio métrico $(X,d)$ tales que para cada $n \in \mathbb{N} , \, A_n \supset A_{n+1}$ se cumple que $\underset{n \in \mathbb{N}}{\bigcap} \, A_n \neq \emptyset .$
En la entrada Convergencia uniforme y continuidad se enunció el siguiente resultado. Vamos a retomarla ahora con demostración.
Proposición: Sea $A$ un espacio métrico compacto, $(f_n)_{n \in \mathbb{N}}$ una sucesión de funciones continuas con $f_n:A \to \mathbb{R}, n \in \mathbb{N}$ tal que $(f_n)$ converge puntualmente a una función continua $f$. Si para cada $x \in A$ y $n \in \mathbb{N} \, f_n(x) \geq f_{n+1}(x),$ entonces $(f_n)$ converge a $f$ uniformemente en $A.$
Demostración:
Para cada $n \in \mathbb{N}$ definimos $g_n := f_n – f.$ Entonces $(g_n)_{n \in \mathbb{N}} \,$ es una sucesión de funciones continuas en $A.$ Es sencillo probar que $(g_n)_{n \in \mathbb{N}} \,$ converge puntualmente a $0.$
Sea $\varepsilon >0.$ Ahora, para cada $n \in \mathbb{N}$ definimos un conjunto con los puntos de $A$ que bajo la función $g_n \,$ quedan fuera de la bola de radio $\varepsilon$ con centro en $0.$ Formalmente:
$A_n:= \{a \in A: g_n(a) \notin \, B(0,\varepsilon)\}$
Nota que este conjunto es complemento de la imagen inversa de la función continua $g_n \,$ en la bola abierta $B(0,\varepsilon).$ Por lo tanto $A_n$ es cerrado en $A.$ Esa propiedad se vio en Funciones continuas en espacios métricos. Arriba vimos que cada conjunto cerrado de un compacto hereda la compacidad, en consecuencia cada $A_n$ es compacto.
Nota además que para cada $n \in \mathbb{N}, \, A_{n+1} \subset A_n.$ La intersección de todos estos conjuntos es vacía, pues si existe $x_0 \in \underset{\n \in \mathbb{N}}{\cap} \, A_n$ entonces para toda $n \in \mathbb{N}, \, g_n(a) \notin \, B(0,\varepsilon)$ lo cual no puede ser, pues $g_n(x_0) \to 0.$ A partir del corolario visto un par de lineas arriba se sigue que existe $N \in \mathbb{N}$ tal que $A_N$ es vacío. Entonces, para todo $k \geq N, \, A_k = \emptyset.$ Así para cada $a \in A$ se cumple que $0 \leq g_n(a) < \varepsilon.$ Por lo tanto $(f_n)$ converge a $f$ uniformemente en $A.$
Más adelante…
Conoceremos los efectos que producen algunas funciones al ser aplicadas en conjuntos compactos. ¿Será posible conservar la compacidad al enviar conjuntos de un espacio métrico a otro? ¿Qué propiedades tendrá la imagen de una función continua?
Tarea moral
- Resuelve el ejercicio planteado arriba.
- Prueba que un espacio discreto finito es compacto. ¿Es necesario que tenga asociada la métrica discreta?
- Demuestra que cada subconjunto infinito de un conjunto compacto posee un punto de acumulación en el conjunto compacto.
- Da un ejemplo de un conjunto $A$ que sea cerrado pero no acotado y una cubierta abierta y numerable de $A$ que no tenga una subcubierta finita.
- Prueba que si $A$ es cerrado y $B$ es compacto, entonces $A \cap B$ es compacto.
- Prueba que la intersección arbitraria de conjuntos compactos es compacta.
- Demuestra que una sucesión de Cauchy en un conjunto compacto es convergente.
- Sea $(X,d)$ un espacio métrico y $A \subset X$ un conjunto compacto. Demuestra que el subespacio $(A,d)$ es completo.
Enlaces
- Análisis Matemático.
- Enlace a entrada anterior.
- Enlace a entrada siguiente.