Introducción

Tres teoremas importantes en la razón cruzada son el Teorema de Pascal, Brianchon y Pappus. Con estos se muestran propiedades de colinealidad y concurrencia.

Teorema de Pascal

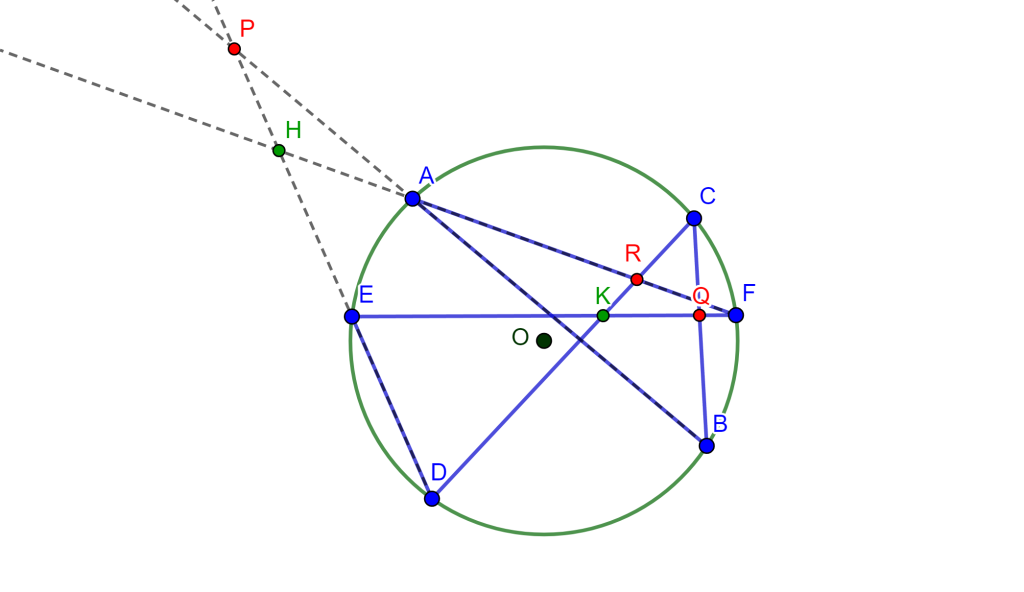
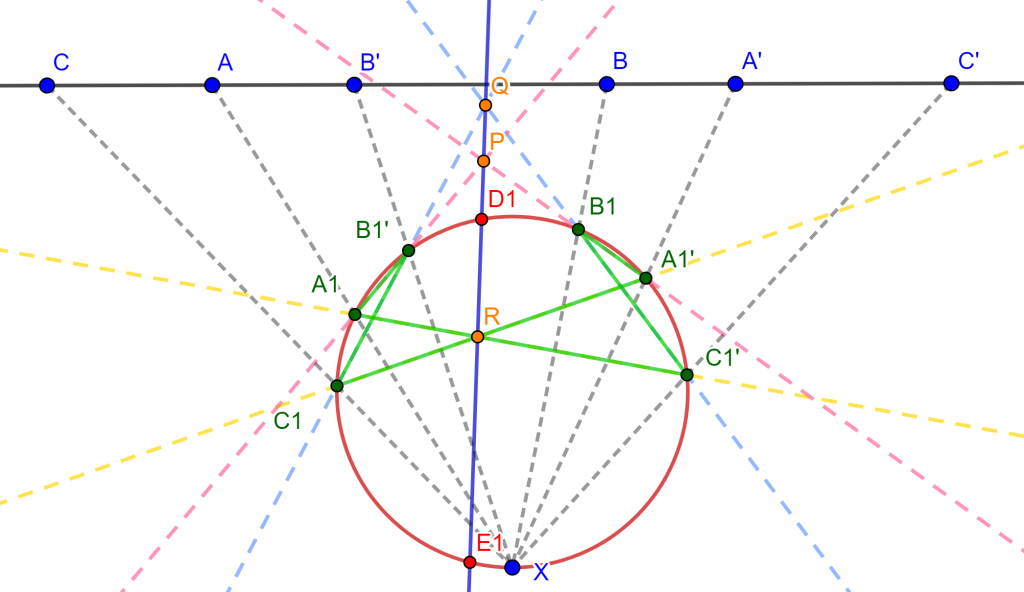
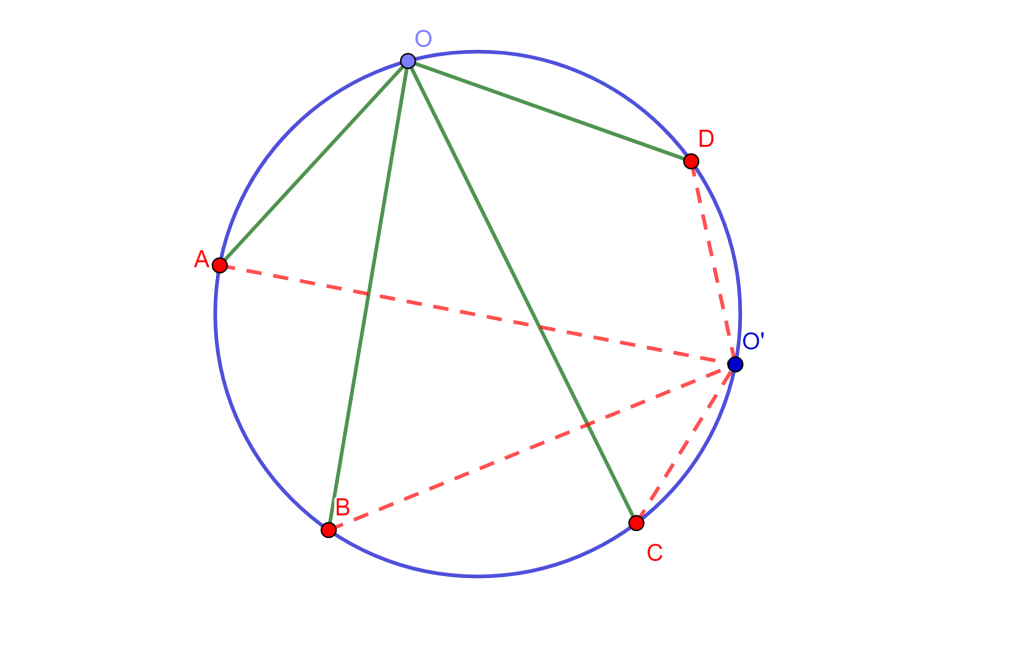
Sea un hexágono inscrito en una circunferencia, los puntos de intersección de sus lados opuestos son colineales.

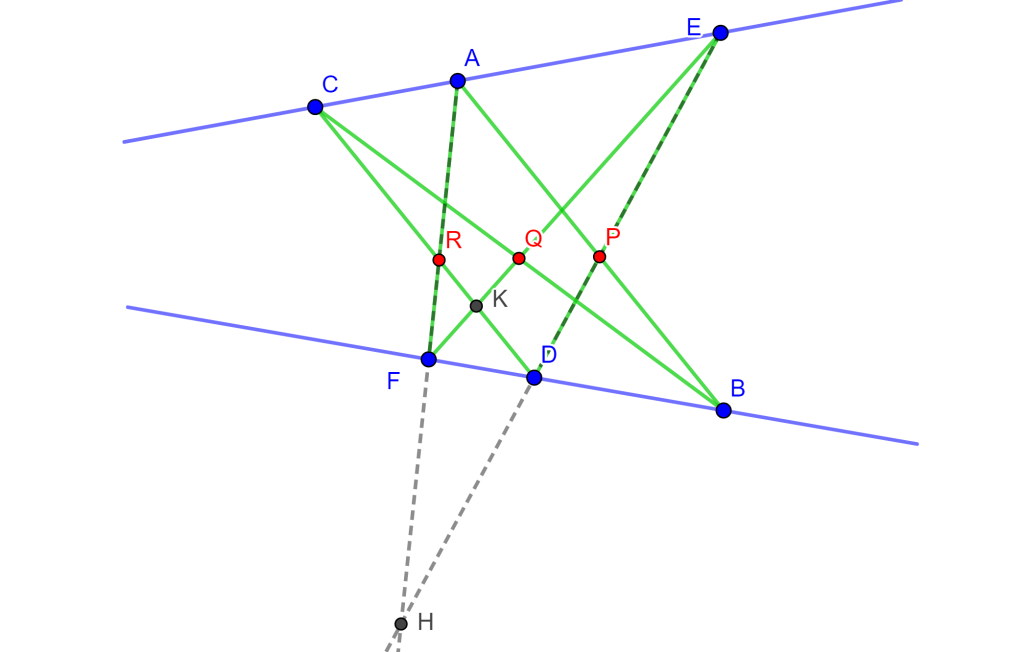
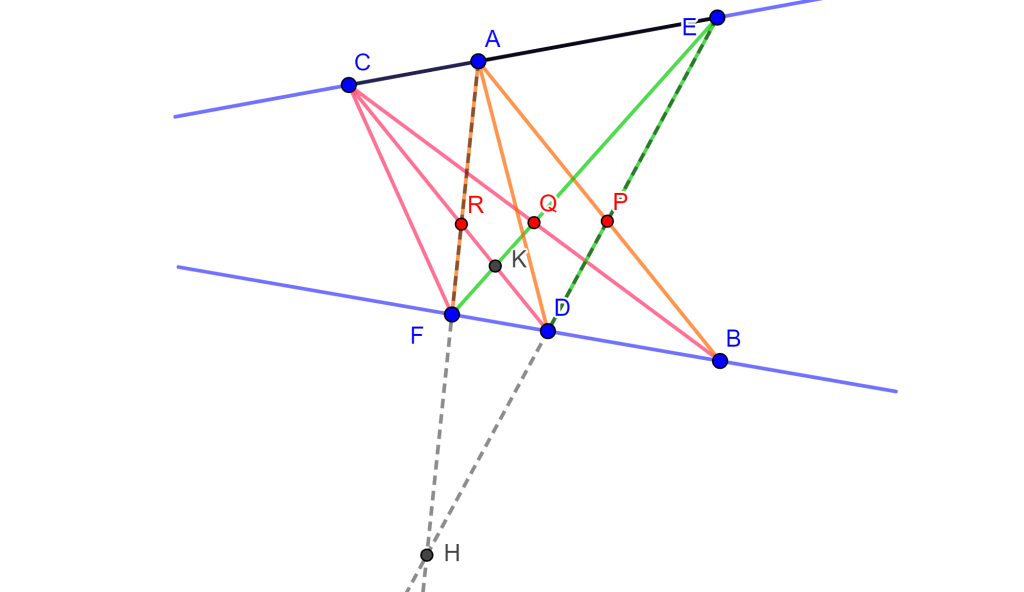
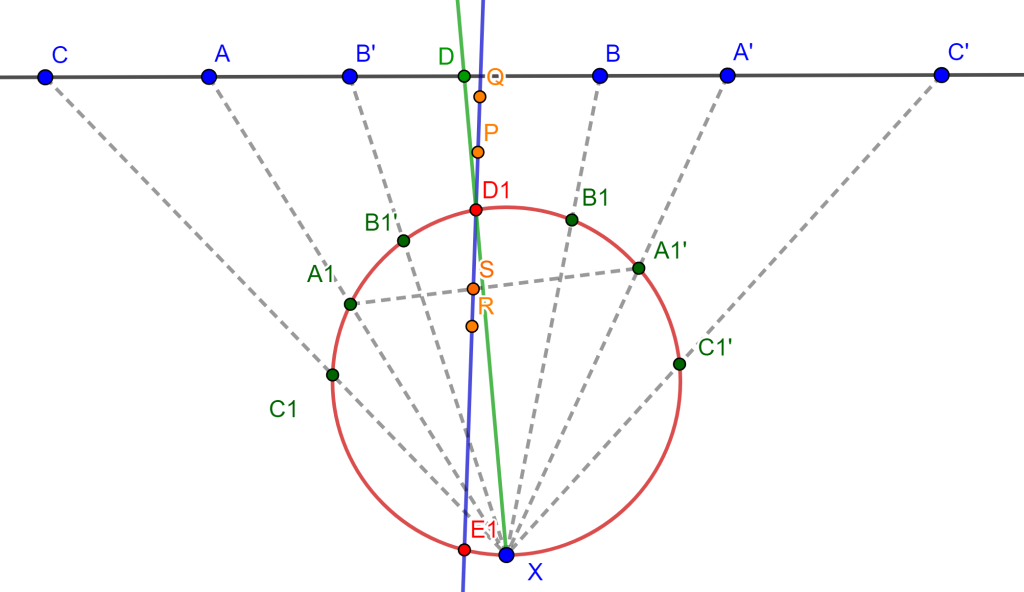
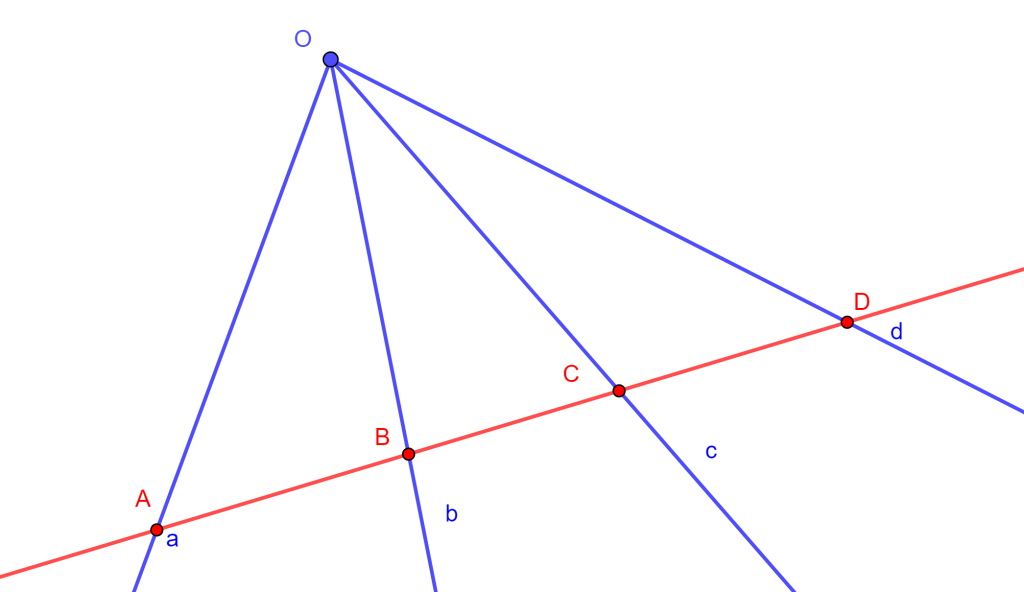
Demostración. Sea el hexágono inscrito $ABCDEF$ en la circunferencia $O$, donde sus lados opuestos $AB,DE$, $BC,EF$ y $CD,FA$ se intersecan en los puntos $P,Q$ y $R$ son colineales. Ahora $FA$ interseca a $DE$ en $H$ y $EF$ interseca a $CD$ en $K$.

Por propiedades de razón cruzada en la circunferencia se tiene $A\{EDBF\}=C\{EDBF\}$ y por lo cual $\{EDPH\}=\{EKQF\}$, como se observa en la siguiente imagen.

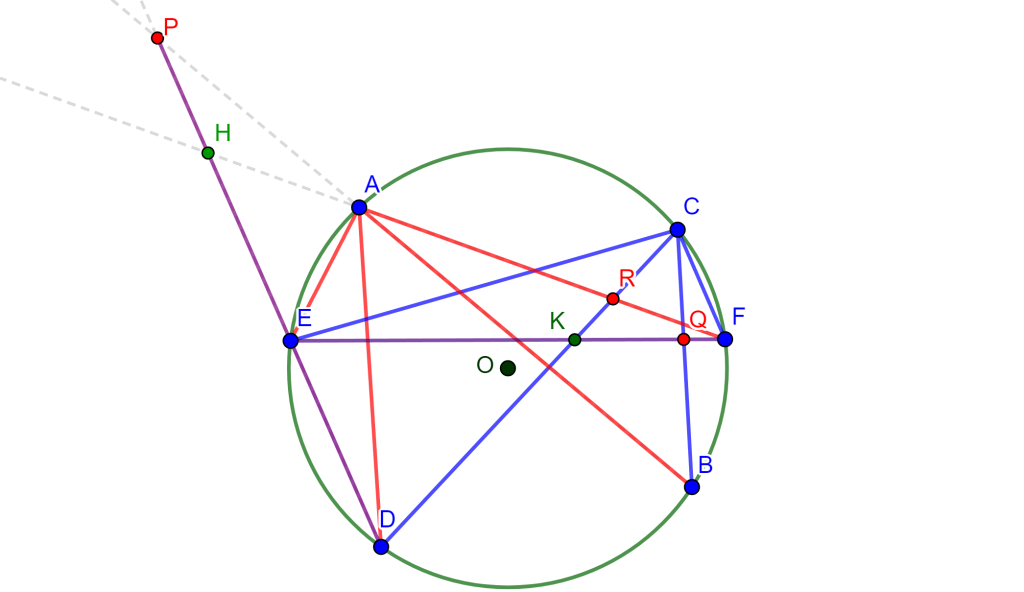
Así mismo se tiene que al unir $R$ con estos puntos se cumple la propiedad $R\{EDPH\}=R\{EKQF\}$. Donde $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, por ende estos dos haces coinciden en la primera, segunda y cuarta recta, y al tener 3 rectas y una constante distinta de -1, es posible construir una única cuarta recta tal que la razón cruzada sea la constante elegida por ello $RP$ coincide con $RQ$. Y, por lo tanto, $PQR$ son colineales y a esta es la línea de Pascal del hexágono.

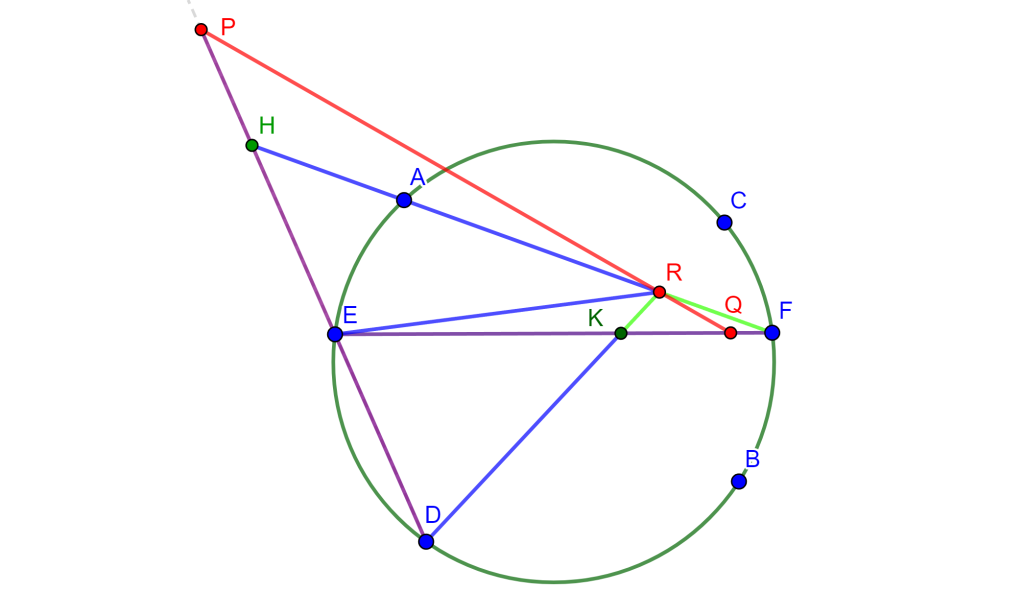
$\square$

Teorema de Brianchon

Este es un teorema dual al de Pascal, el cual es aplicable a hexágonos circunscritos a cualquier sección cónica. En nuestro caso se mostrará para una circunferencia.

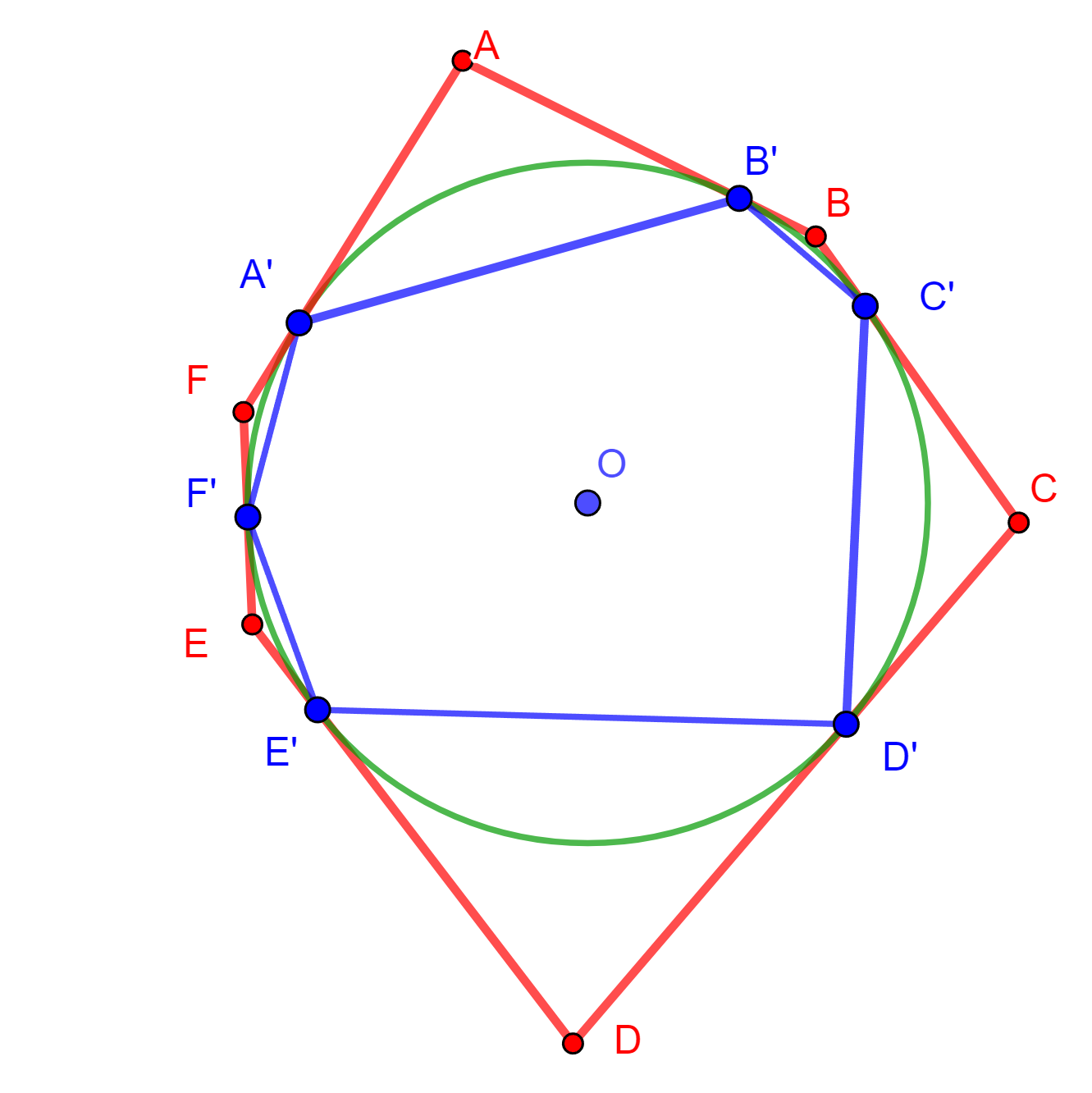
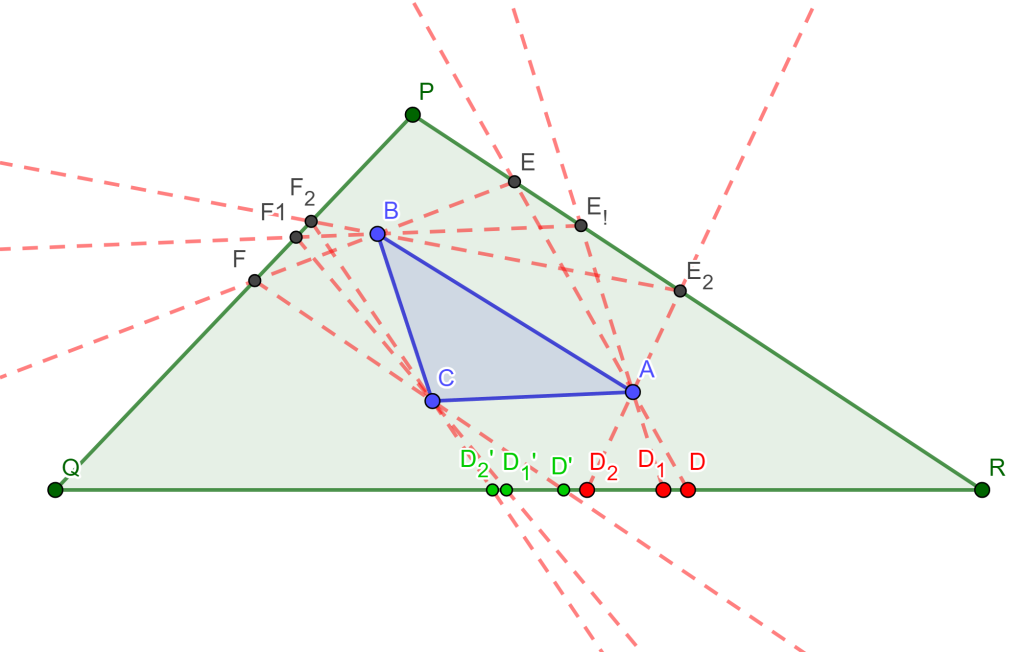
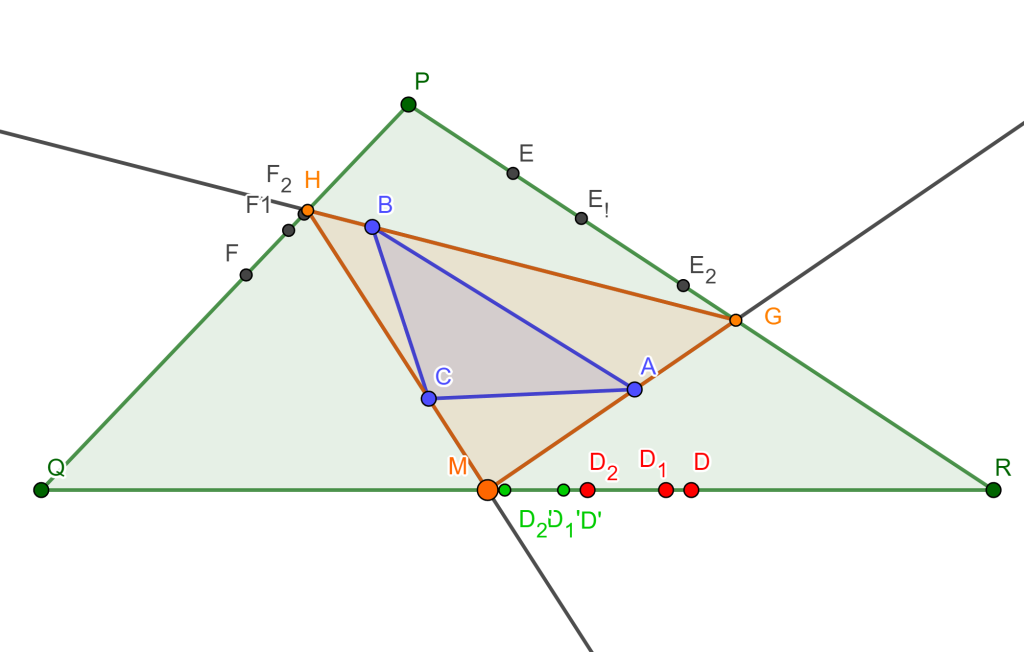
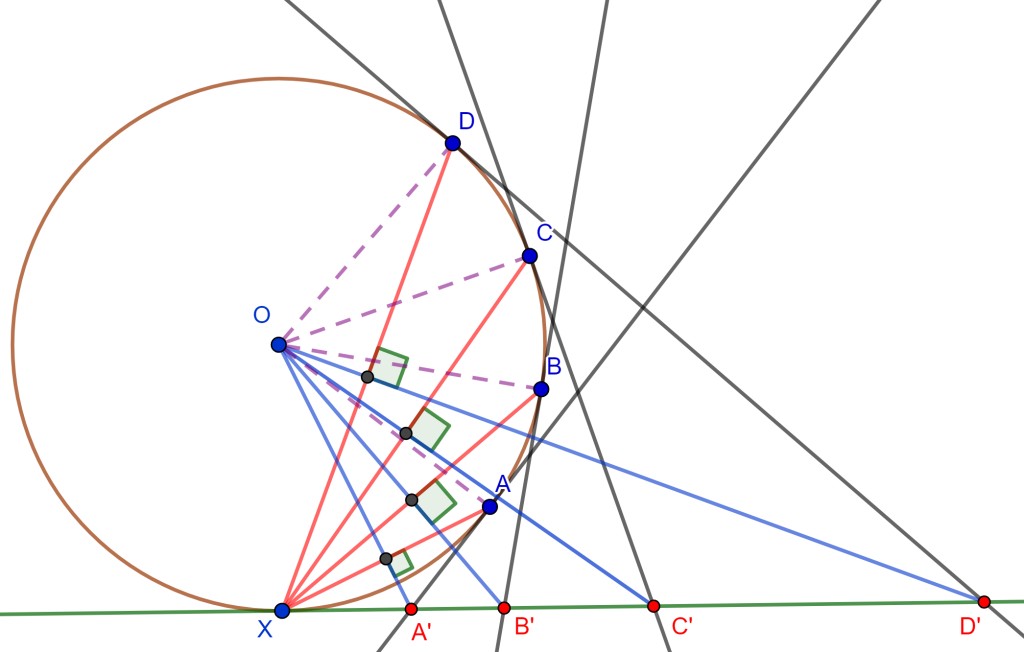
Teorema. Sea un hexágono circunscrito a una circunferencia, entonces las líneas que unen sus vértices opuestos son concurrentes.

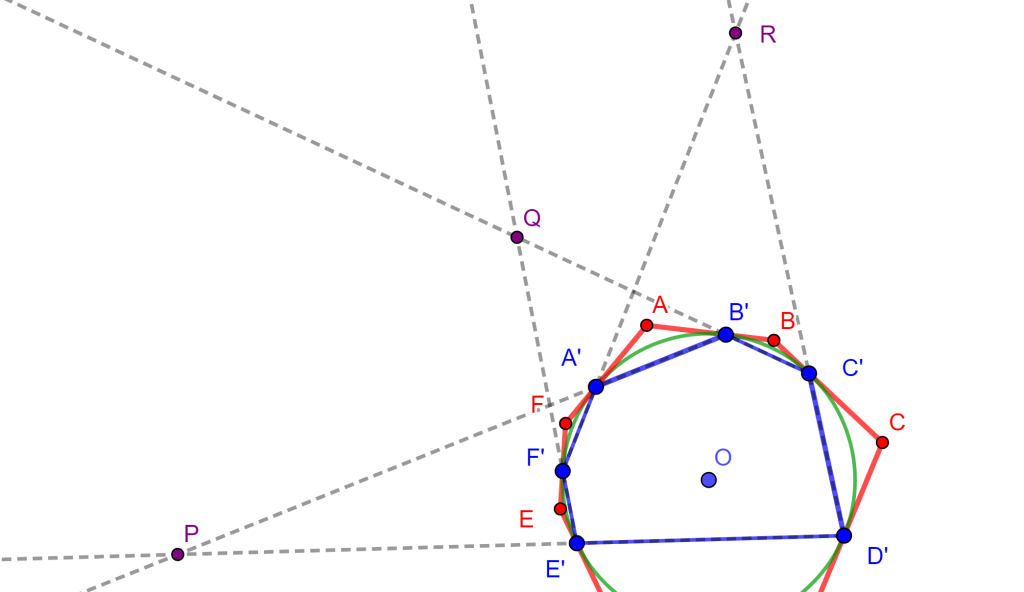
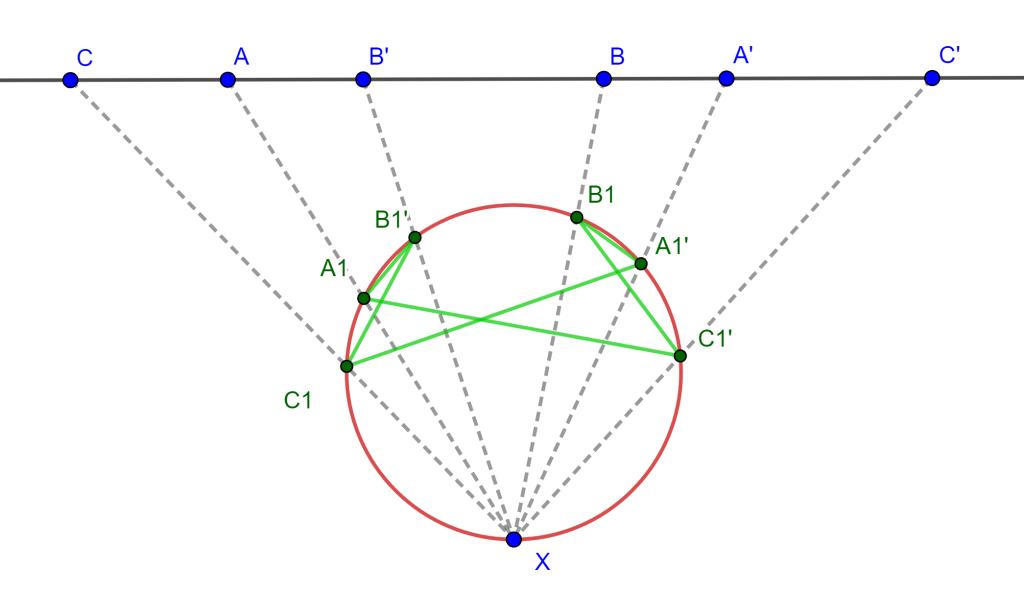
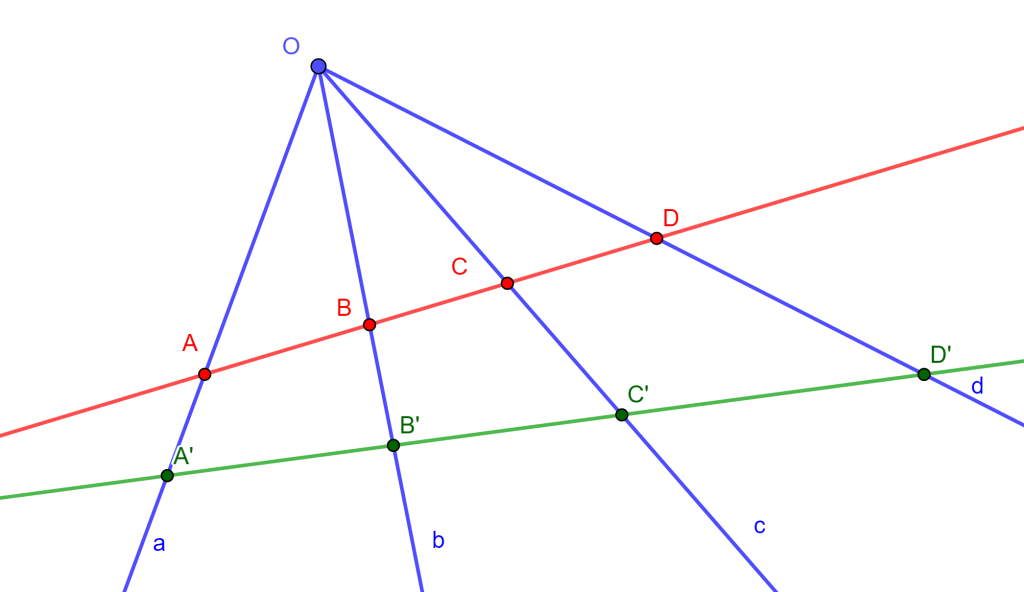
Demostración. Sea el hexágono $ABCDEF$ circunscrito a la circunferencia $O$, ahora los puntos de tangencia de los lados del hexágono $ABCDEF$ son los vértices del hexágono $A’B’C’D’E’F’$.

Si observamos los lados opuestos del hexágono $A’B’C’D’E’F’$ estos se intersecan de la siguiente forma:

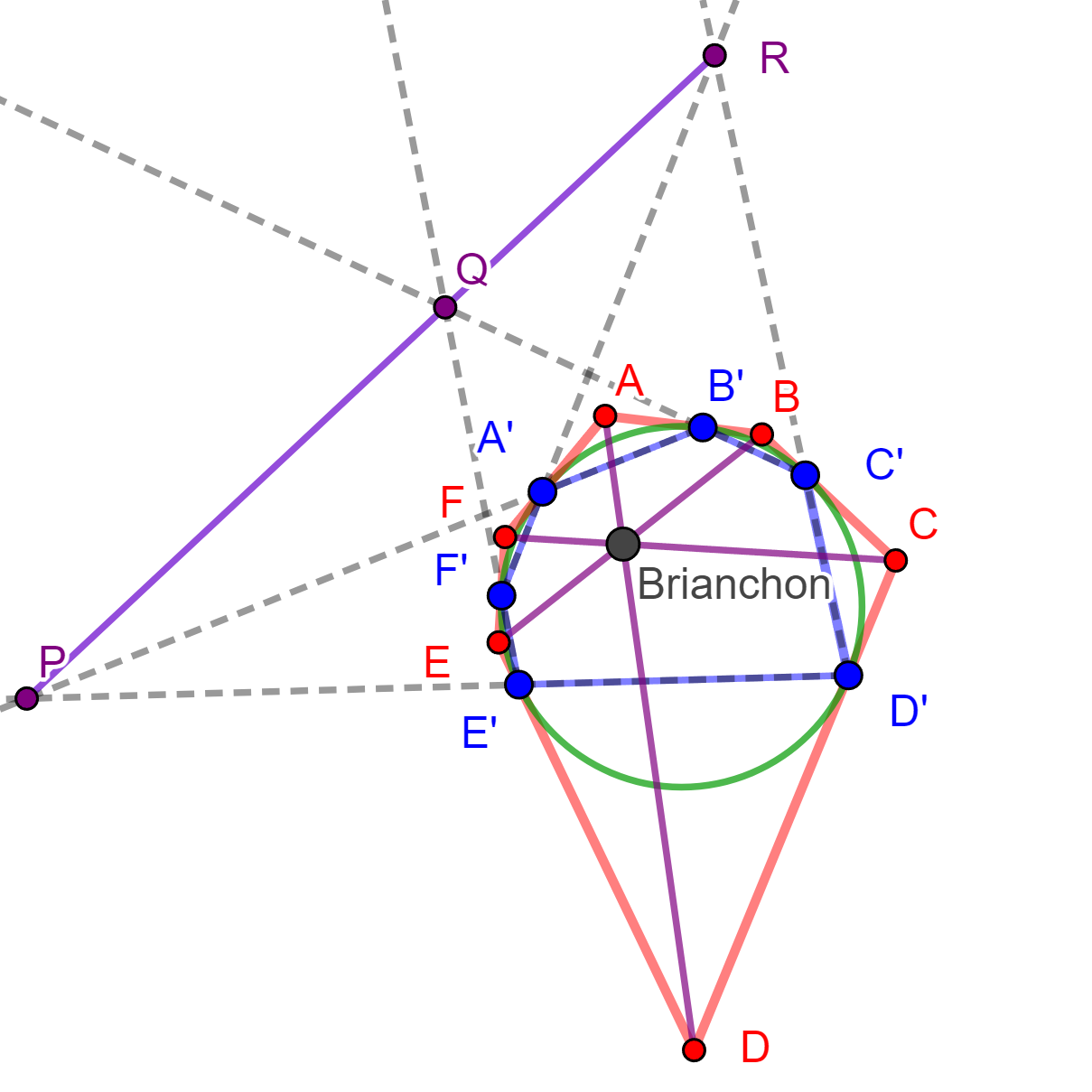
Por propiedad de los Polos y Polares, las polares de $A$ y $D$ pasan por $P$ y la polar de $P$ es $AD$. De igual forma, la polar de $Q$ es $BE$ y la polar de $R$ es $CF$, y por el Teorema de Pascal el hexágono inscrito $A’B’C’D’E’F’$ los puntos de intersección de sus lados opuestos $P$, $Q$ y $R$ son colineales, y por lo cual sus polares $AD$, $BE$ y $CF$ son concurrentes y a este es el punto de Brianchon.

$\square$

Teorema de Pappus

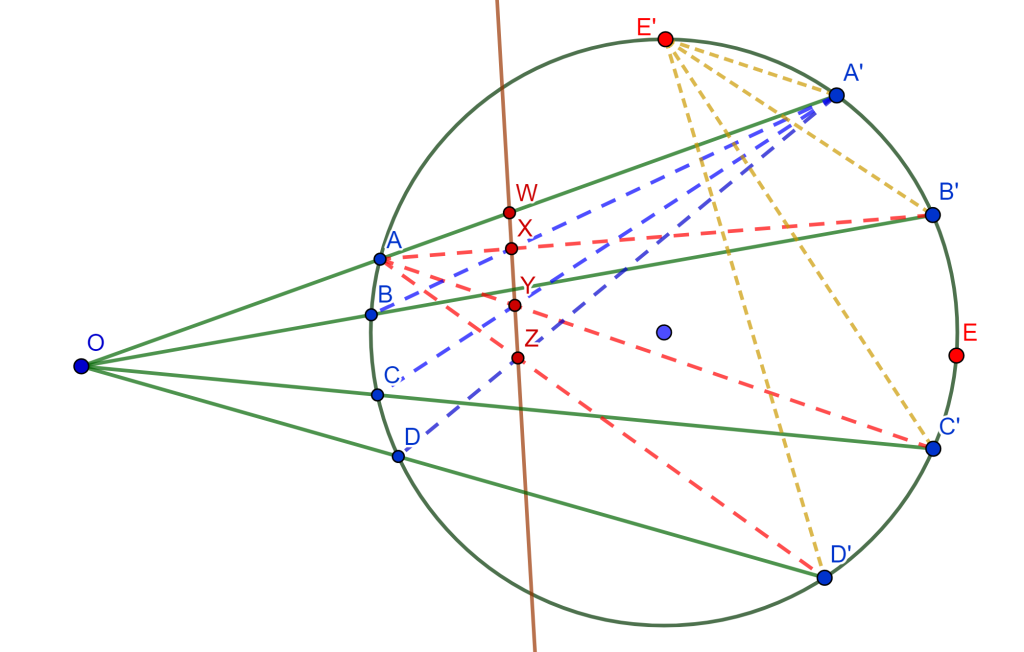
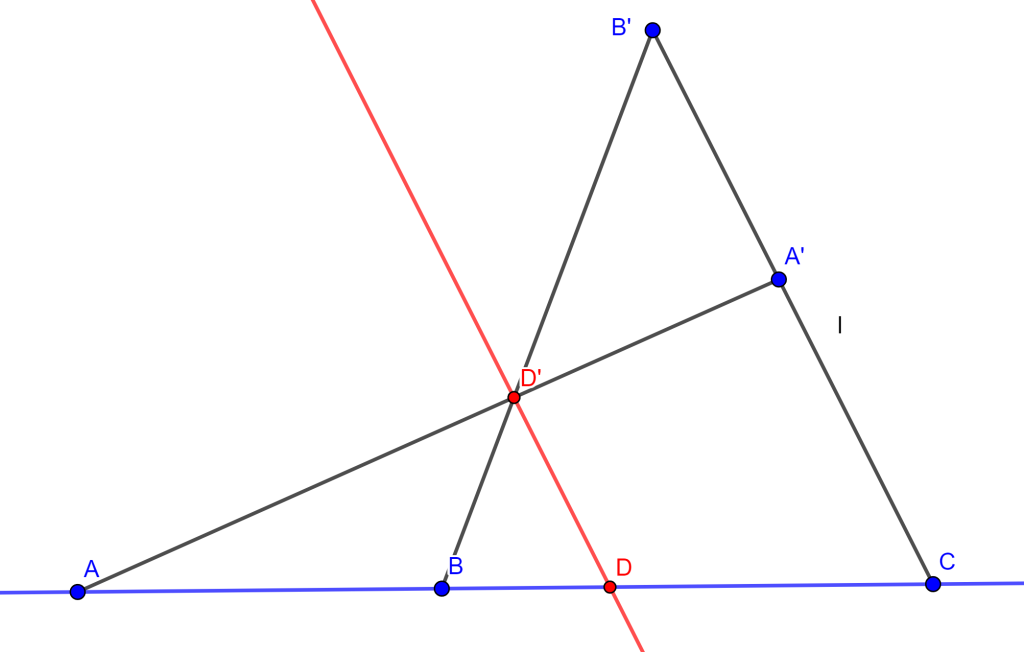
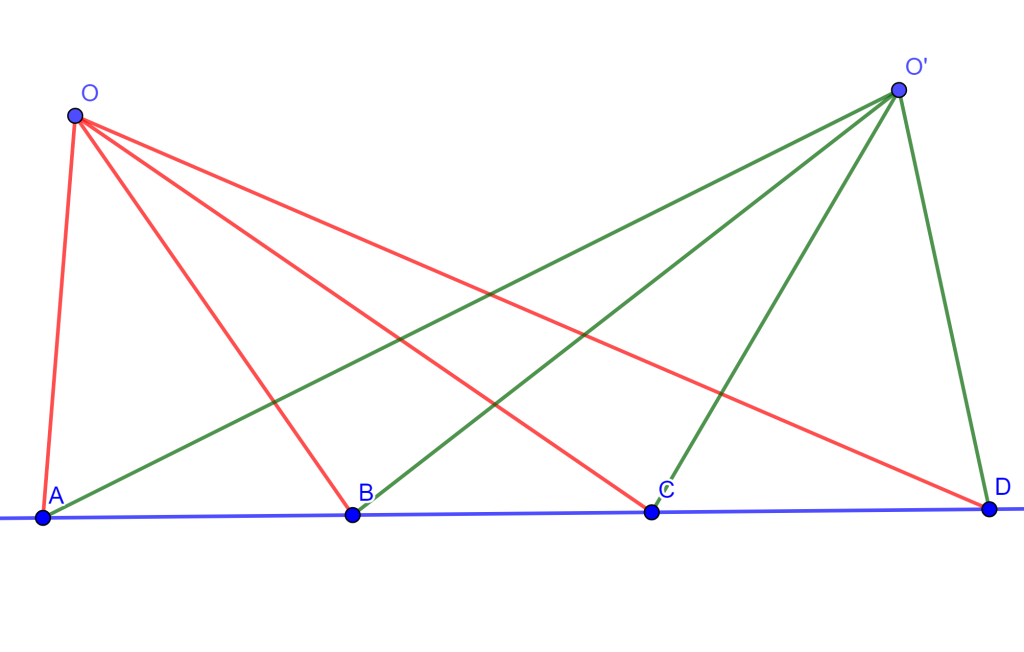
Si los vértices de un hexágono están alternativamente en dos líneas rectas, entonces la intersección de los pares de lados opuestos genera puntos los cuales son colineales.

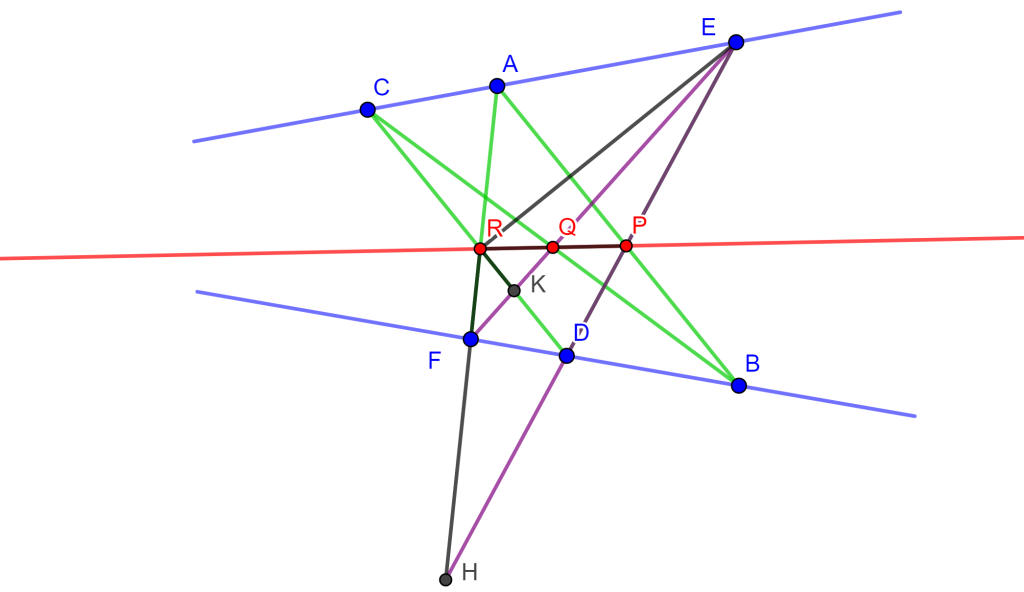
Demostración. Este es un caso especial del Teorema de Pascal para un hexágono inscrito en una sección cónica. Sea el hexágono $ABCDEF$, donde la intersección de los lados opuestos son:

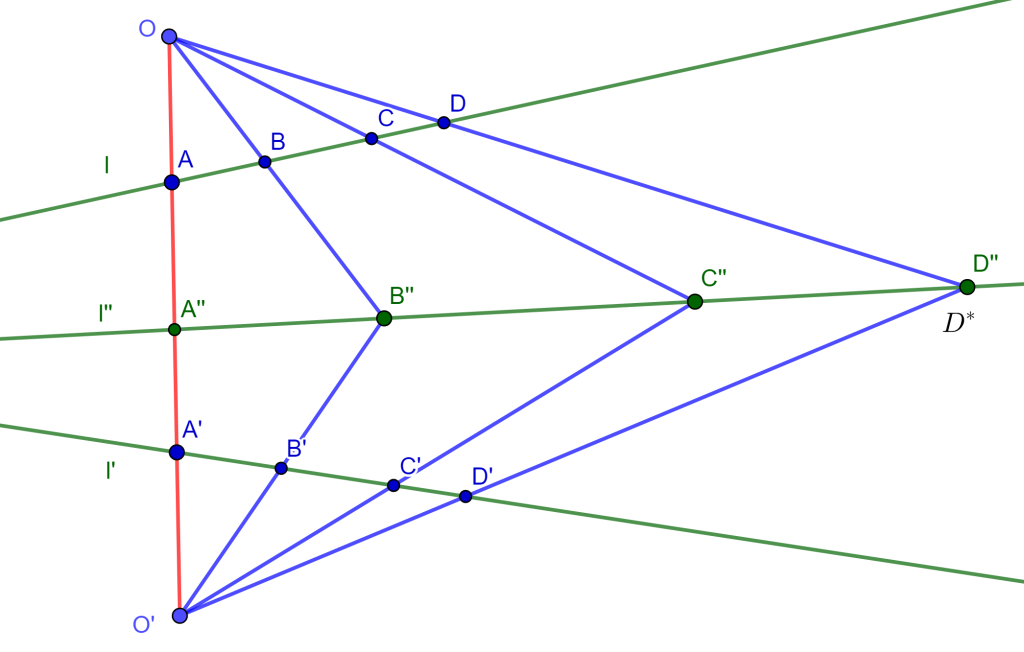
Se tiene que $AF$ interseca a $ED$ en $H$, y $EF$ interseca a $CD$ en $K$.

Por lo cual $A\{EBDF\}$ es igual a $C\{EBDF\}$, entonces $\{EPDH\}=\{EQKF\}$.

Uniendo $RQ$ los cuatro puntos de las líneas $ED$ y $EF$, se tiene que $R\{EPDH\}=R\{EQKF\}$.
Ahora como $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, entonces $RP$ y $RQ$ coinciden, por lo tanto, $P$, $Q$ y $R$ son colineales.

$\square$

Más adelante…

Otro tema interesante por abordar es la involución tanto en Hileras de puntos como Haces de líneas.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Puntos autocorrespondientes y regla geométrica de la falsa posición
• Siguiente entrada del curso: Hileras de puntos en involución

Introducción

Se seguirá viendo resultados y problemas relacionados con la razón cruzada, en esta entrada se abordará los Puntos autocorrespondientes y la regla geométrica de la falsa posición.

Puntos Autocorrespondientes

Sean $A,B,C$ y $A’,B’,C’$ dos conjuntos de puntos en una misma línea recta, por ende para un punto cualquiera $D$ en la recta le corresponde un punto $D’$ que nos dará como resultado $\{ ABCD \}=\{ A’B’C’D’ \}$.

Problema 1. El problema cae en la siguiente incógnita ¿Existirá un punto $D$ que se corresponda al mismo?, de tal forma que $\{ ABCD \}=\{ A’B’C’D \}$.

Demostraremos que puede haber uno, dos o ningún punto, a este punto existente se le llamará «punto autocorrespondiente» con respecto a las dos razones cruzadas.

Demostración. Trácese cualquier circunferencia en el plano y tómese un punto $X$ en esta, y únanse los puntos $A,B,C,A’,B’,C’$ a $X$, y las intersecciones con la circunferencia y estas rectas se denotarán como $A_1, B_1, C_1, A_1′, B_1′, C_1’$.

Notese que tenemos un hexagono inscrito con lados $A_1C_1’$, $A_1B_1’$, $C_1A_1’$, $B_1C_1’$, $B_1A_1’$, $B_1’C_1$, y la existencia del punto $D$ depende de que este hexágono cumpla el Teorema de Pascal.
El Teorema de Pascal dice que «Los puntos de intersección de los lados opuestos de un hexágono inscrito en una circunferencia son colineales». Es de esta forma que la intersección de $A_1B_1’$ y $A_1’B_1$ se cortan en $P$, $B_1’C_1$ y $B_1C_1’$ en $Q$, $A_1C_1’$ y $A_1’C_1$ en $R$, de esta forma se tiene la recta $PQ$ la cual corta a la circunferencia en $D_1$ y $E_1$.

Ahora las rectas $XD_1$ y $XE_1$ cortarán la recta de los haces en los puntos $D$ y $E$ correspondientemente, estos son los dos puntos buscados. Sea $S$ la intersección de $PQ$ con $A_1A_1’$.

Entonces se tienen las siguientes igualdades:

$\{ ABCD \}=X\{ A_1B_1C_1D_1\}$

por propiedad 1 de razón cruzada de la circunferencia se tiene:

$X\{ A_1B_1C_1D_1\}=A_1’\{ A_1B_1C_1D_1\}$

Por razón cruzada se tiene:

$A_1’\{ A_1B_1C_1D_1\}=\{SPRD_1\}= A_1\{ A_1’B_1’C_1’D_1 \}$

Por razón cruzada por la circunferencia:

$A_1\{ A_1’B_1’C_1’D_1 \} = X\{ A_1’B_1’C_1’D_1\} = \{ A’B’C’D \}$

Por lo tanto, $\{ ABCD \}=\{ A’B’C’D \}$ y es equivalente para $E$.

$\square$

Ahora, si $PQ$ es tangente a la circunferencia, solo existirá un punto autocorrespondiente, y si la recta $PQ$ no corta a la circunferencia, entonces no existe ningún punto autocorrespondiente.

Regla geométrica de la falsa posición

Esta regla viene del siguiente problema:

Problema 2. Construir un triángulo el cual sus lados pasan por los vértices de un triángulo dado y cuyos vértices se encuentran en los lados de otro triángulo dado.

Solución. El triángulo a encontrar debe tener sus lados, los cuales deben pasar por los vértices del triángulo $PQR$, y sus vértices en los lados del triángulo $ABC$.

Sea un punto $D$ en $QR$, trácese $DA$ que corte a $PR$ en $E$, $EB$ que corte $PQ$ en $F$, y $FC$ que corte a $QR$ en $D’$, si $D$ y $D’$ son el mismo ya tendríamos el triángulo buscado. Por lo cual se vuelve a hacer lo mismo para $D_1$ obteniendo $D_1’$ y $D_2$ obteniendo $D_2’$, si estos son puntos iguales ya lo tendríamos resuelto, pero no es así, por ende se construirán los puntos autocorrespondientes a partir de $D,D_1,D_2,D’,D_1′,D_2’$.
Si estos puntos $M$ y $N$ existen, y pasamos por uno de ellos, en este caso $M$ para construir el triángulo buscado, nos daríamos cuenta de que regresamos a $M$ y estaría solucionado, pero como menciones estos triángulos existen si existen los puntos autocorrespondientes.

$\square$

Más adelante…

Se verán tres teoremas importantes respecto al tema de Razón Cruzada, los cuales son Teoremas de Pascal, Brianchon y Pappus.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Razón cruzada en la circunferencia
• Siguiente entrada del curso: Teoremas de Pascal, Brianchon y Pappus