3.4 Circunferencia Polar

Introducción

Como ya se vio en la entrada anterior de Triángulo Autopolar, se puede tener un triángulo autopolar dada una circunferencia y no solo eso, sino que además se puede tener un número infinito de triángulos autopolares dada una circunferencia, pero solamente existe una circunferencia (Circunferencia Polar) de la cual un triángulo dado sea autopolar.

Circunferencia Polar

Como mencione, solo existe una circunferencia de la cual un triángulo dado sea autopolar, donde el triángulo debe de ser obtuso. Por lo cual si se cumple lo anterior se tiene una circunferencia que se denomina «Circunferencia Polar» del triángulo.

Construcción Circunferencia Polar

Dado $A$ un punto dado y $BC$ una recta dada. Supongamos $O$ el centro de la circunferencia, dado que la polar de $B$ pasa por $A$ y perpendicular a $BO$, y la polar de $C$ pasa por $A$ y perpendicular a $CO$, entonces $O$ es el ortocentro del triángulo $\triangle ABC$.

Ahora como el polo $A$ es el vértice, y el pie de la altura $D$ el cual pertenece a la polar de $A$ son puntos inversos, entonces $r= \sqrt{AO \times DO} $, de esta forma encontramos la circunferencia polar del triángulo $\triangle ABC $ la cual es única.

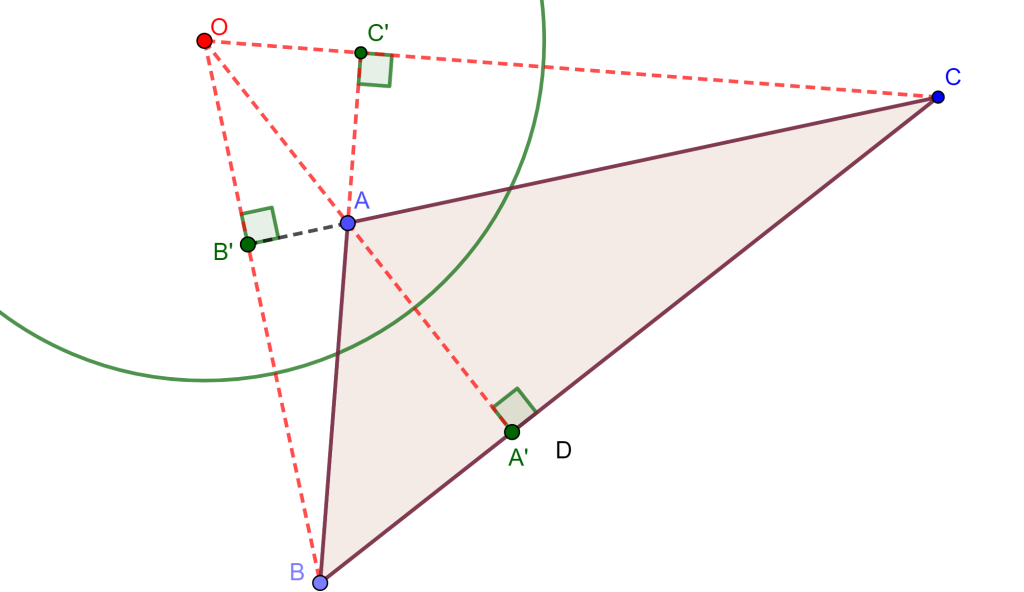
El triángulo $\triangle ABC $ es autopolar.

Propiedad 1

Cualquier circunferencia la cual tiene una cuerda como altura del triángulo es ortogonal a la circunferencia polar del triángulo.

Propiedad 2

De la construcción anterior se tiene:

Si un triángulo es autopolar con respecto a una circunferencia, entonces el triángulo es obtusángulo.

Demostración

Se sabe que el $\triangle ABC$ es autopolar con respecto a la circunferencia $C(O,r)$ y se tiene que $O$ es el ortocentro. Además, $OA \times OA’ = OC \times OC’ = OB \times OB’ =r^2$.

Ahora supongamos $O$ interno al triángulo $\triangle ABC$, entonces los puntos inversos de cada par estarían en lados contrarios de sus respectivas líneas respecto a $O$ centro de inversión, entonces $OA \times OA’ = OC \times OC’ = OB \times OB’ =-r^2$. Por lo cual $O$ debe de ser un punto externo al triángulo $\triangle ABC$.

Entonces $\angle BAC$ es un angulo externo a $\triangle B’BA$, entonces $\angle BAC= \angle BB’A + \angle ABB’ = \pi /2 + \angle ABB’$, se tiene que $\angle BAC > \pi /2$. Por lo tanto, el $\triangle ABC$ es obtusangulo. $_\blacksquare $

Teorema

El circuncirculo de un triángulo autopolar y su circunferencia de los nueve puntos son mutuamente inversas con respecto a la circunferencia polar.

Propiedad 3

Tres de los cuatro triángulos de un grupo ortocentrico son obtusos.

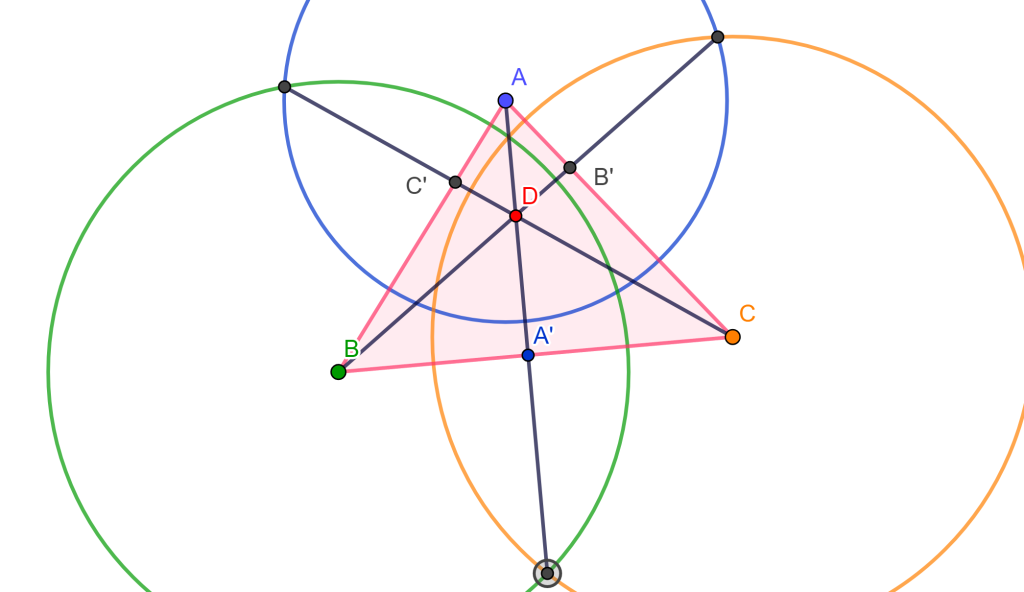
Los triángulos $DAB$, $DBC$ y $ DCA$ son obtusos en $D$, se tienen $r_C$, $r_A$ y $r_B$ los radios de las circunferencias polares $C$, $A$ y $B$ de estos triángulos respectivamente.

Entonces se tiene $r^2_B=BA’ \times BC$ y $r^2_C=A’C \times BC$, de lo anterior se obtiene $r^2_B + r^2_C = (BA’ \times A’C) BC = BC^2$.

De esta forma las circunferencias $B$ y $C$ son ortogonales, como $A’$ y $C$ son puntos inversos con respecto a la circunferencia $B$, $A’A$ es la polar de $C$ respecto a la circunferencia $B$ y pasa por los puntos de intersección de las circunferencias $B$ y $C$, por lo cual se tiene el siguiente teorema.

Teorema

Dados los tres triángulos obtusos de un grupo ortocentrico sus circunferencias polares son ortogonales en pares, y sus puntos de intersección están en los tres lados de un cuadrángulo que pasa por el vértice común de los ángulos obtusos.

Más adelante…

Se tiene pensado abordar los 10 problemas de Apolonio.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Principio de dualidad y Triángulo Autopolar
• Siguiente entrada del curso: Los diez problemas de Apolonio