3.3 Principio de dualidad y Triángulo Autopolar
Introducción
Gracias a la relación de polos y polares con respecto a una circunferencia, se tenían correspondencias entre todos los puntos y todas las rectas del plano. Por lo cual nace el Principio de dualidad. Así mismo analizaremos el Triángulo Autopolar junto con algunas propiedades.
Principio de Dualidad
El principio de Dualidad, donde la propiedad que nos dé como resultado de intercambiar las palabras de recta y punto resulta verdadera, además de que guarda sus propiedades.
Por ejemplo, se tiene la siguiente dualidad del teorema con respecto a su corolario.
Teorema: Dada una circunferencia, la polar de $P$ pasa por $Q$, entonces la polar de $Q$ pasa por $P$.
Corolario: Dada una circunferencia, sean $p$ y $q$ rectas tales que, el polo de $p$ está en $q$, entonces el polo de $q$ está en $p$.
Se puede ver que ambos son duales, se puede dar un ejemplo más sencillo:
La unión de dos puntos es una recta, entonces la intersección de dos rectas es un punto.
Triángulo Autopolar
Definición: Se define como triángulo autopolar a aquel que, con respecto a una circunferencia, se tiene que cada vértice es el polo del lado opuesto, de tal modo que cada lado es polar del vértice opuesto.
Construcción del Triángulo Autopolar
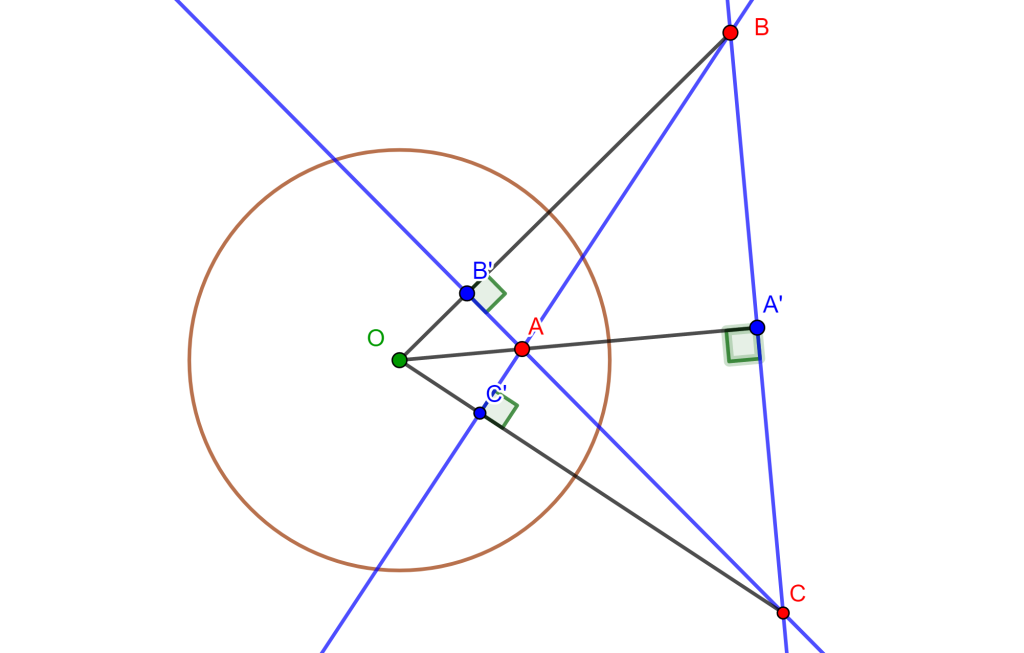
Se tiene una circunferencia $C(O,r)$, tomemos un punto $A$ dentro de la circunferencia y tracemos su inverso $A’$ y $a$ su polar. Ahora tomemos un punto $B$ en $a$ tal que $A’ \neq B$ y trazamos $b$ su polar, y por el Teorema Fundamental de Polos y Polares se tiene que $b$ pasa por $A$. Además, a la intersección de $a$ y $b$ la llamaremos $C$, y su polar de $c$ pasa por $A$ y $B$ puntos.
De esta forma tenemos el $ \triangle ABC$ es autopolar con respecto a $C(O,r)$
Propiedades
Se tienen varias propiedades del triángulo autopolar:
1.- El ortocentro del triángulo autopolar es el centro de la circunferencia.
Demostración
De la figura anterior se tiene que:
La polar de $A$ es $a$ que es el lado $BC$ del $ \triangle ABC$ y $BC \perp OA$ por $A’$ inverso de $A$.
La polar de $B$ es $b$ que es el lado $CA$ del $ \triangle ABC$ y $CA \perp OB$ por $B’$ inverso de $B$.
La polar de $C$ es $c$ que es el lado $AB$ del $ \triangle ABC$ y $AB \perp OC$ por $C’$ inverso de $C$.
Por lo cual $AA’$, $CC’$ y $BB’$ son las alturas del $ \triangle ABC$ y estas se intersecan en $O$.
Por lo tanto, $O$ es el ortocentro del $\triangle ABC$ $_\blacksquare$
2.- Uno de sus vértices está dentro de la circunferencia y los otros dos fuera de esta.
3.- El ángulo del triángulo cuyo vértice está en la circunferencia es obtuso.
Más adelante…
Se abordará el tema de circunferencia Polar.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Relaciones Armónicas
- Siguiente entrada del curso: Circunferencia Polar