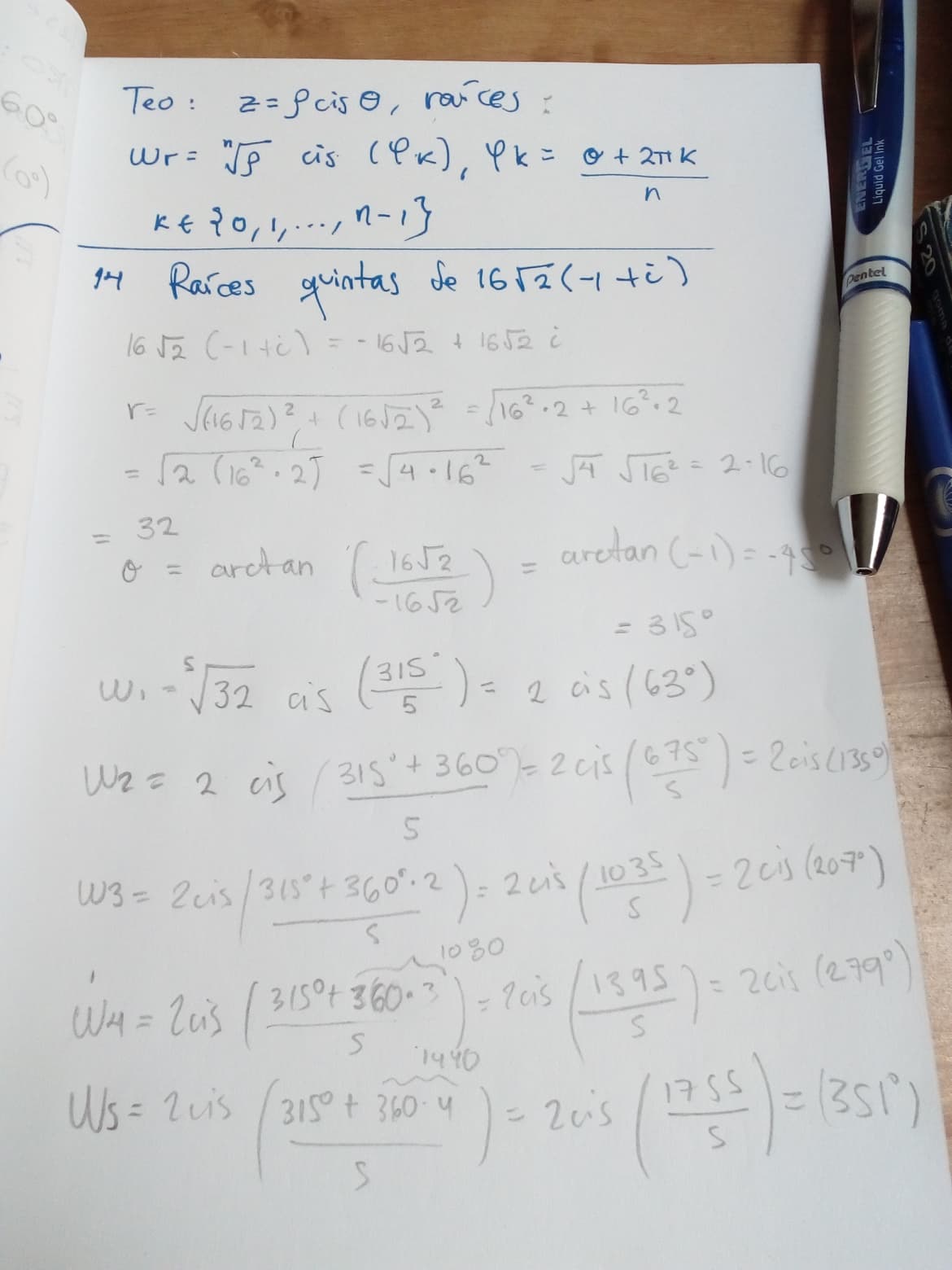Introducción
En esta entrada practicaremos los conceptos aprendidos en entradas anteriores, como el concepto de grado y de la función que induce un polinomio. De la misma forma veremos como aplicar el algoritmo de la división y los teoremas del residuo y del factor en algunos ejercicios básicos.
Conociendo ya a los polinomios y sus operaciones básicas, pasaremos a unos ejercicios sencillos que involucran los conceptos de polinomios que son el grado, la evaluación y raíz.
Problemas de grado de un polinomio
Problemas de evaluación
Problemas de divisibilidad y teorema del factor
Más adelante…
Ya que nos encargamos de practicar las herramientas que llevamos hasta ahora, pasaremos a ver un nuevo concepto en los polinomios, el máximo común divisor, esta nueva definición será análoga al concepto que desarrollamos para los enteros, por lo que existirá un gran paralelismo entre ambos y una gran cantidad de propiedades que probamos para los enteros, también se podrán probar para los polinomios.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestra que $x-a$ divide a $x-b$ si y solo si $a=b$.
- Si $f(x)$ y $g(x)$ son polinomios tales que $f(x)$ divide a $g(x)$ y $g(x)$ divide a $f(x)$, entonces existe $c\in \mathbb{R}$ tal que $f(x)=c g(x)$.
- Si $f(x)=x^2 +1$ y $g(x) = x^3-x+3$, evalúa $f\circ g(x)$ en $x=2$.
- Si $f(x)$ y $g(x)$ son polinomios, ¿Quién es el grado de $f\circ g(x)$?
- Demuestra que si $f(x)$ tiene grado mayor que $0$, entonces $f$ no tiene un inverso multiplicativo.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Algoritmo de la división, teorema del factor y teorema del residuo
- Entrada siguiente del curso: Máximo común divisor de polinomios y algoritmo de Euclides
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»