Archivo de la etiqueta: elipse

Geometría Analítica II: Cilindros sobre cónicas

Por Brian Manzano

Deja un comentario

Introducción

Con esta entrada comenzamos nuestra exploración de los objetos en el espacio de tres dimensiones. Lo primero que haremos es estudiar los cilindros que se construyen sobre cónicas. La mayoría de nosotros tiene una noción bastante buena sobre ellos, o por lo menos de los «cilindros usuales», en donde las secciones horizontales son círculos. Sin embargo, si bien entendemos muy bien su forma de manera intuitiva, ¿cómo los podemos representar en el lenguaje matemático?

A continuación definiremos qué entenderemos por un cilindro sobre una cónica. Veremos algunos ejemplos y luego haremos cilindros con objetos que hemos estudiado en el curso de Geometría Analítica I: con cónicas.

Definición de cilindros sobre curvas

Los cilindros que conocemos de manera intuitiva comienzan con una circunferencia y luego esta se extiende sin cambios a lo largo de un eje. Los cilindros con los que nos encontramos cotidianamente (por ejemplo, un vaso) se extienden sólo de manera acotada. Pero podemos pensar en qué sucedería si los extendemos indefinidamente. Si hacemos esto, llegamos a la siguiente definición.

Definición. Un cilindro es una superficie en $\mathbb{R}^3$ que se pueda obtener tomando un plano $\Pi$, tomando en él una curva $\mathcal{C}$ y tomando para cada punto $p$ de $\mathcal{C}$ una recta ortogonal a $\Pi$ que pase por $p$. La unión de estas rectas son el cilindro. A cada una de las rectas le llamamos una directriz del cilindro y a la curva $\mathcal{C}$ le llamamos la curva generatriz del cilindro.

Así, un cilindro es un conjunto de lineas paralelas que se encuentran «guiadas» o «dirigidas» de acuerdo a una curva plana. Podemos imaginarlo como sigue: dibujamos la curva sobre un papel, y luego sobre ella pegamos palos perpendiculares a la hoja

Cilindros a partir de cónicas

La definición de cilindro, tal y como está arriba, no restringe el tipo de cónicas que podemos tener. Sin embargo, hay una familia de cónicas que conocemos bien debido a cursos anteriores: las cónicas. Ya que podemos elegir con libertad la curva plana, pensemos en lo que sucede si usamos de las cónicas que conocemos. Para simplificar la situación, supondremos que dibujamos la cónica en el plano XY y entonces que las directrices son perpendiculares al plano $XY$, es decir, paralelas al eje $Z$. Podemos entonces hacer ejemplos de acuerdo a subfamilia de cónicas que usemos.

Cilindros elípticos

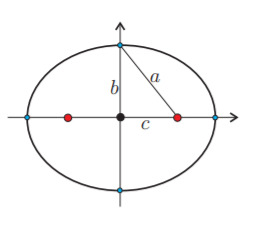
Recordemos que una elipse en el plano $XY$ puede pensarse (salvo rotaciones y traslaciones) como el lugar geométrico de los puntos $(x,y)$ que satisfacen una ecuación del estilo $$\frac{x^2}{a^2}+\frac{y^2}{b^2} =1,$$ donde $a$ y $b$ son parámetros que determinan la longitud de los ejes de la elipse.

Si ahora pensamos en todo $\mathbb{R}^3$ y nos preguntamos por el lugar geométrico de los puntos $(x,y,z)$ que satisfacen la ecuación, la respuesta es similar. Los valores de $(x,y)$ están dados por la ecuación y el valor de $z$ no está restringido de ninguna manera por la ecuación, de modo que puede ser lo que sea. ¡Hemos logrado «levantar la cónica» a líneas perpendiculares al plano $XY$!

De tener $a=b$, tendremos un cilindro circular en el origen. Si $a=b=1$, entonces es un cilindro mucho más especial, pues es uno que se obtiene de levantar la circunferencia unitaria canónica.

Por supuesto, pudimos haber comenzado con una elipse en el plano $YZ$, que tendría una ecuación del estilo $$\frac{y^2}{a^2}+\frac{z^2}{b^2} =1.$$ En este caso, el valor de $x$ sería libre, así que puede valer lo que sea. Así, esta ecuación pensada en todo $\mathbb{R}^3$ nos daría un cilindro cuya curva directriz es una elipse, y cuyas generatrices son paralelas al eje $x$.

Cilindros parabólicos

Para crear cilindros parabólicos podemos proceder de la misma manera. Para ellos, comenzamos con una parábola, por ejemplo, en el plano $XY$. Sabemos que una parábola así está dada, salvo rotaciones y traslaciones, por una ecuación del siguiente tipo: $$y^2 = 2px.$$ Una vez más, si en vez de pensar en esto como una ecuación en $\mathbb{R}^2$, la pensamos como una ecuación en $\mathbb{R}^3$, entonces el valor de $z$ es arbitrario y entonces al tomar el lugar geométrico en efecto obtenemos una línea perpendicular al plano $XY$ por cada punto de la parábola.

Cilindros hiperbólicos

La tercer familia sería la de cilindros hiperbólicos. En este caso, la curva generatriz es una hipérbola. Recordemos que salvo rotaciones y traslaciones, una hipérbola es el lugar geométrico de los puntos $(x,y)$ del plano $XY$ tales que satisfacen una ecuación del estilo $$\frac{x^2}{a^2}-\frac{y^2}{b^2} =1.$$ Al pensar a esta ecuación como una restricción para puntos $(x,y,z)$ de $\mathbb{R}^3$, obtenemos entonces un cilindro hiperbólico.

Problemas ejemplo de cilindros

Para aterrizar las ideas anteriores, veamos algunos ejemplos concretos.

Ejemplo. Tomemos el lugar geométrico de los puntos $(x,y,z) \in $ $\mathbb{R} ^3$ que cumplen con la siguiente ecuación: $$\frac{x^2}{4}+\frac{y^2}{25} = 1.$$

Podemos comenzar detectando la ausencia de la variable $z$, con lo que las generatrices serán rectas paralelas al eje $Z$. De hecho, el eje del cilindro precisamente será será el eje $Z$. Esto no siempre ocurre ya que no necesariamente el centro de la curva dada está en el origen del plano $XY$, pero debido a que no tenemos constantes que acompañen los valores $x$ o $y $ su centro no se encontrará desplazado.

¿Qué nos dicen los valores $4,25$ que acompañan a sus variables correspondientes ?Con todo en mente veamos su gráfica

Gráfica de la ecuación en el plano XY

Veamos desde otra perspectiva, no solo sobre el plano, sino con una vista incluyendo el otro eje coordenado obtenemos la siguiente gráfica.

Gráfica de la ecuación en 3D
Ejemplo

$\square$

Ejemplo. Tomemos el lugar geométrico en $\mathbb{R}^3$ de los puntos $(x,y,z)$ que cumplen la siguiente ecuación: $$y^2=6x.$$

De manera muy similar notamos que la ausencia de la variable $z$ llevara a que su directriz se encuentre en el plano $XY$ de forma que vista desde este plano:

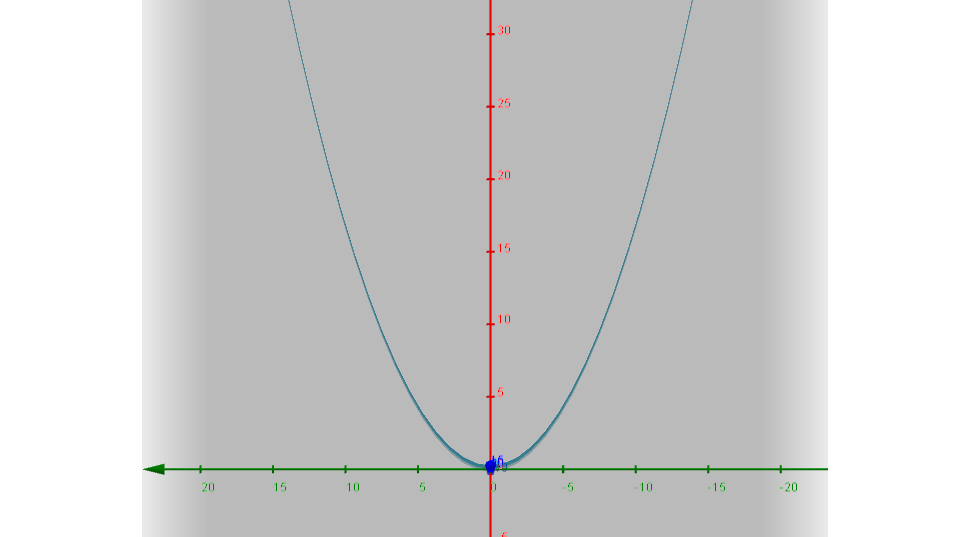
¿Puedes decir a que cónica pertenece esta gráfica?

Agregando la perspectiva con el eje faltante obtenemos:

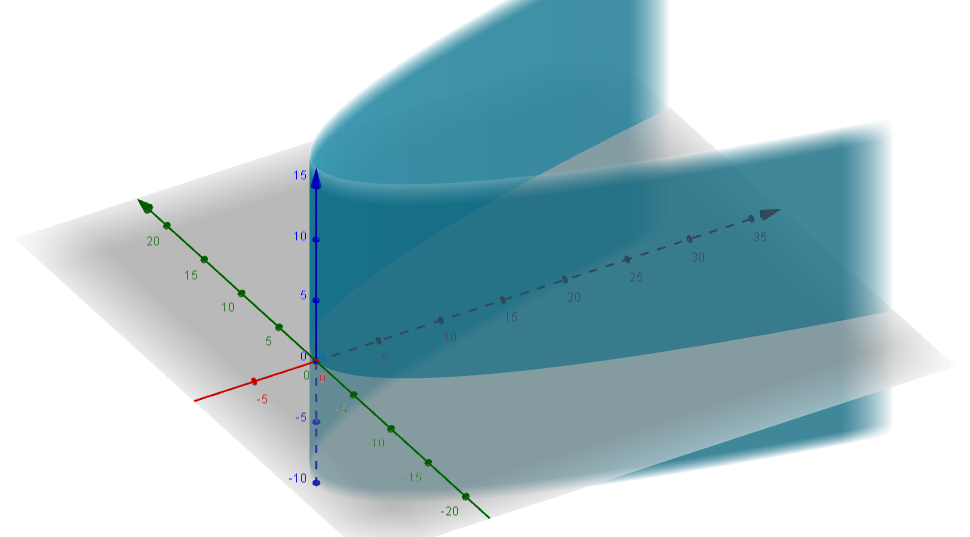
Nota importante. Como habrás notado al graficar obtenemos estas representaciones que parecen estar cortadas o seccionadas por planos paralelos al $XY$ , en realidad estos cilindros se extienden sin límite.

$\square$

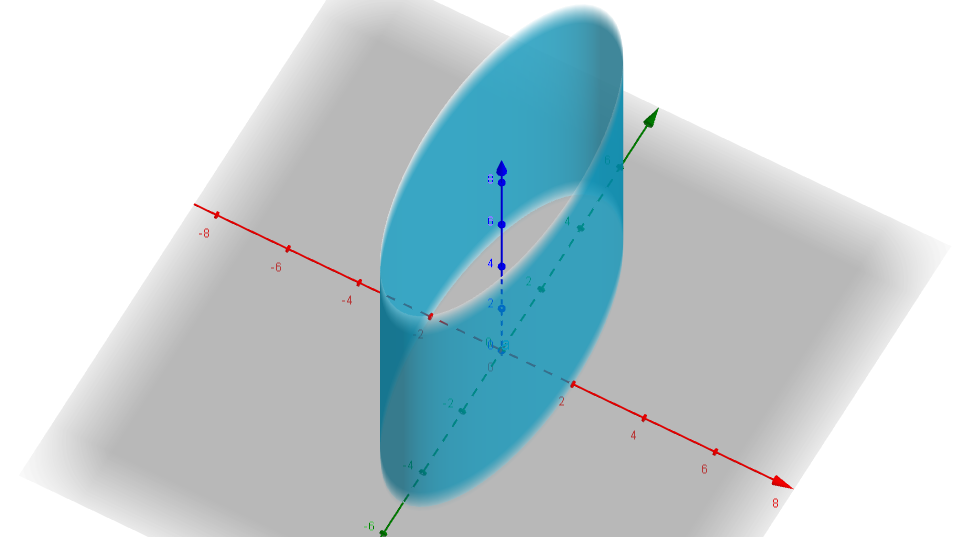
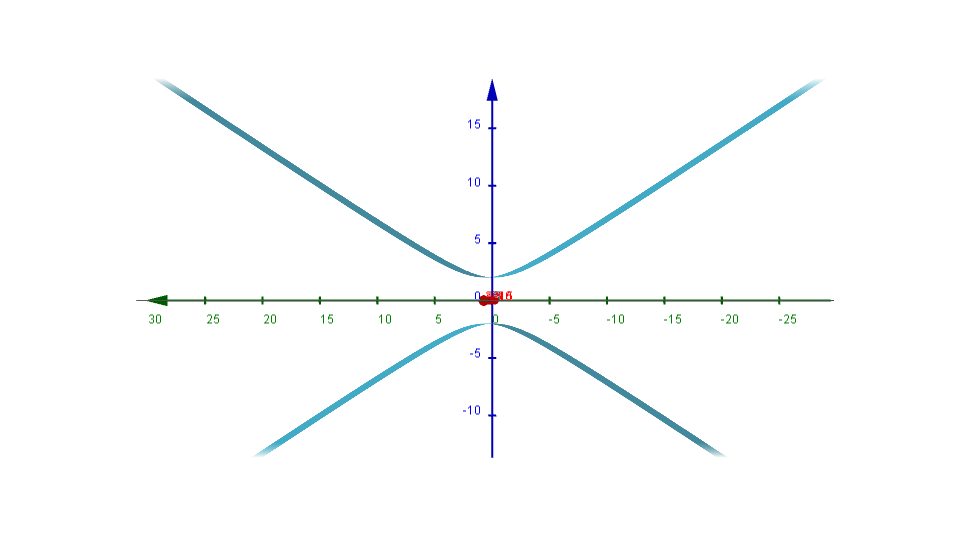
Ejemplo. Para la siguiente ecuación: $$\frac{z^2}{4}-\frac{y^2}{9} = 1,$$ ¿cuál es el lugar geométrico de los puntos $(x,y,z)$ en $\mathbb{R}^3$ que la cumplen?

Notemos ahora que además de representar otro tipo de cónica tenemos ahora un cambio importante, ya no contamos de manera explicita con la $y$ en la ecuación, ¿Qué cambios conllevara esto? ¿En que plano podremos observar la cónica correspondiente?

Veamos si tu intuición fue correcta

Gráfica de la ecuación en el plano YZ

Desde otra perspectiva donde podremos ver su profundidad, tenemos ahora que las generatrices se extienden desde $- \infty$ hasta $\infty$.

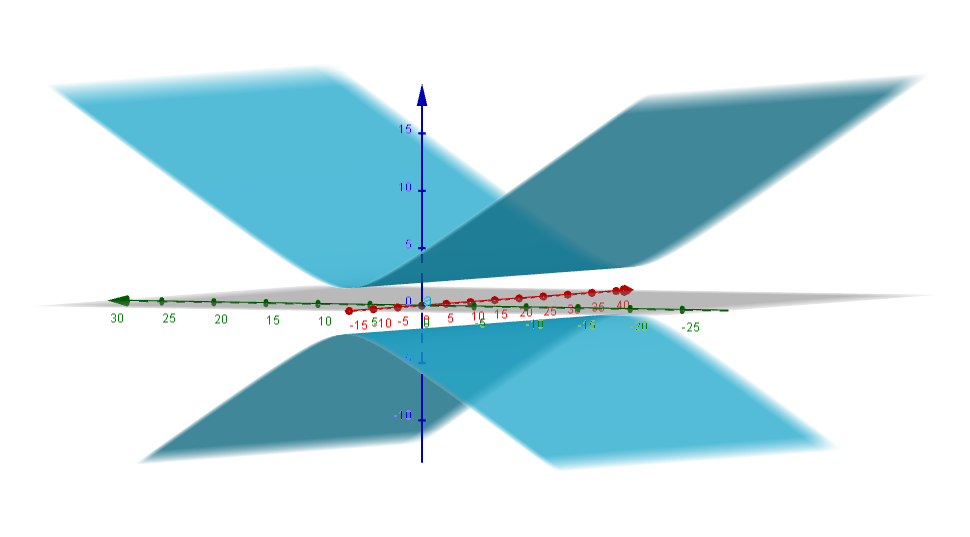
$\square$

Más adelante…

En esta primer entrada del curso hablamos de los primeros objetos geométricos de tres dimensiones que nos interesan: los cilindros con cierta curva generatriz. En la siguiente entrada veremos otra manera con la cual podemos crear un objeto de tres dimensiones a partir de rectas: las superficies de revolución. Un poco más adelante estudiaremos una versión más general de objetos que podemos obtener de esta manera: los conjuntos cero de ecuaciones de segundo grado en tres variables.

Tarea moral

Estos ejercicios te ayudaran a comprender de mejor forma los conceptos vistos.

  1. Reescribe las ecuaciones de los ejemplos que dimos para que sus directrices se encuentren en diferentes planos.
    Sugerencia: Nota qué pasa con el tercer ejemplo.
  2. Ahora que hemos cambiado los planos donde se encuentran las directrices, grafica estas ecuaciones, ¿Cómo cambian los cilindros? Realiza un cambio de variable para el segundo ejemplo haciendo el reemplazo $x\to x-3$. ¿Qué cambia? ¿pasa lo mismo para el primer ejemplo?
  3. Determina la ecuación para un cilindro parabólico cuya parábola directriz esté contenida en el plano XY y cuyo foco sea el punto $(2, 0)$ de este plano. Hay varias de estas parábolas. Puedes usar la que gustes.
  4. Gráfica los cilindros asociados a cada una de las siguientes ecuaciones:
    1. $x^2-z^2=0$.
    2. $(y-9)^2+(z-4)^2=0$.
    3. $x^2=y$.

Entradas relacionadas

Geometría Analítica I: Teoremas de clasificación de polinomios cuadráticos y curvas cuadráticas

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Nos hemos estado preparando para enunciar formalmente los resultados de clasificación que nos dirán «cómo son todas las cónicas algebraicamente», o bien que nos dirán «cómo se ven conjuntos de ceros de cualquier polinomio cuadrático en dos variables». En una entrada anterior hablamos de qué es un resultado de clasificación en matemáticas. Después, definimos con toda precisión cuáles son los objetos que clasificaremos: los polinomios cuadráticos en dos variables y las curvas cuadráticas. Finalmente, establecimos las nociones de equivalencia afín y equivalencia isométrica que usaremos para dar nuestra clasificación.

En esta entrada finalmente enunciaremos con toda precisión los teoremas de clasificación que nos interesan. La demostración de estos teoremas no es directa, así que nos tomará algunas entradas más preparar la teoría necesaria para poder hacerlo.

Teoremas de clasificación isométrica

Los primeros teoremas que demostraremos serán bajo la equivalencia dada por las isometrías. Daremos teoremas para clasificar tanto polinomios cuadráticos en dos variables, como curvas cuadráticas.

El resultado para PCDVs es un poco más abstracto. La clasificación es un poco aparatosa, pues habrá muchos posibles parámetros involucrados. Pero tiene la ventaja de que es el que podremos demostrar a partir de las técnicas de matrices que ya conocemos y de algunas más que desarrollaremos sobre la marcha.

El resultado para curvas cuadráticas es muy intuitivo, pues lo podemos pensar en términos puramente geométricos: nos dirá que cualquier curva cuadrática se puede llevar, sin alterar su métrica, a una curva cuadrática mucho más fácil de describir, que viene de una «lista corta» de posibilidades. Como las transformaciones permitidas son las isometrías, esto es lo que más se parece a nuestro entendimiento de «ser la misma figura».

Veamos qué dice cada resultado. El primer teorema clasifica PCDVs a través de isometrías.

Teorema. Cualquier polinomio cuadrático en dos variables es isométricamente equivalente a exactamente alguno de los siguientes polinomios:

  1. A algún polinomio de la forma $\frac{x^2}{a^2}+\frac{y^2}{b^2}-1$ para $a\geq b$ reales distintos de cero
  2. A algún polinomio de la forma $\frac{x^2}{a^2}-\frac{y^2}{b^2}-1$ para $a\geq b$ reales distintos de cero
  3. A algún polinomio de la forma $y^2-cx$ para $c$ real distinto de cero
  4. A algún polinomio de la forma $c^2x^2-y^2$ para $c$ real distinto de cero
  5. A algún polinomio de la forma $c^2x^2-1$ para $c$ real distinto de cero
  6. Al polinomio $x^2$
  7. A algún polinomio de la forma $c^2x^2+y^2$ para $c$ real distinto de cero
  8. A algún polinomio de la forma $\frac{x^2}{a^2}+\frac{x^2}{b^2}+1$ para $a,b$ reales distintos de cero
  9. A algún polinomio de la forma $c^2x^2+1$ para $c$ real distinto de cero

El segundo teorema clasifica curvas cuadráticas bajo isometrías, y será un corolario del teorema anterior.

Teorema. Cualquier curva cuadrática del plano es isométricamente equivalente a exactamente una de las siguientes:

  1. A alguna elipse canónica con centro en $(0,0)$ y focos en el eje $x$
  2. A alguna hipérbola canónica con centro en $(0,0)$ y focos en el eje $x$
  3. A alguna parábola canónica de vértice $(c,0)$ y directriz $y=-c$
  4. A dos rectas que se intersectan en el origen
  5. A dos rectas paralelas de la forma $x=c$ y $x=-c$
  6. A la recta $x=0$
  7. Al origen $(0,0)$
  8. Al conjunto vacío

Teoremas de clasificación afín

Después de realizar la clasificación isométrica, agrandaremos un poco el conjunto de transformaciones que usaremos: permitiremos utilizar cualquier transformación afín. Al hacer esto, tenemos más transformaciones y por lo tanto deberíamos esperar que nuestra clasificación tenga menos posibilidades. En efecto este es el caso.

De hecho, la razón por la cual hacemos esto es que al permitir a todas las transformaciones afines nuestros polinomios cuadráticos en dos variables (o curvas cuadráticas) quedan clasificadas en muy muy pocos tipos: una cantidad finita. A continuación enunciamos los resultados concretos.

El primer teorema es para polinomios cuadráticos en dos variables.

Teorema. Cualquier polinomio cuadrático en dos variables es afínmente equivalente a exactamente uno de los siguientes polinomios:

  1. $x^2+y^2-1$
  2. $x^2-y^2-1$
  3. $y^2-x$
  4. $x^2-y^2$
  5. $x^2+1$
  6. $x^2$
  7. $x^2+y^2$
  8. $x^2+y^2+1$
  9. $x^2+1$

¡Este resultado es fantástico! Existen muchísimas expresiones de la forma $Ax^2+Bxy+Cy^2+Dx+Ey+F$ y el teorema anterior nos dice que, en realidad, podemos «resumirlas» únicamente en nueve posibilidades muy fáciles de enunciar.

Como corolario, obtendremos el segundo resultado para clasificación mediante transformaciones afines: el correspondiente a las curvas cuadráticas.

Teorema. Cualquier curva cuadrática del plano es afínmente equivalente a exactamente una de las siguientes posibilidades:

  1. La circunferencia unitaria
  2. La hipérbola unitaria
  3. La parábola unitaria
  4. Las rectas $y=x$ y $y=-x$
  5. Las rectas $x=1$ y $x=-1$
  6. La recta $x=0$
  7. El origen
  8. El conjunto vacío

Una vez más, es increíble que existiendo tantísimas curvas cuadráticas en el plano, sea posible resumirlas a tan solo ocho posibilidades.

Y, ¿por qué sirve esta clasificación?

En el transcurso de las siguientes entradas nos encontraremos con muchas situaciones concretas en las que clasificar una cónica será de utilidad. Mientras tanto discutimos esto de manera un poco informal. Imagina que comenzamos con el siguiente polinomio cuadrático en dos variables: $$P((x,y))=x^2-5xy-y^2+2x-y+5.$$

Tras hacer una figura en el plano usando alguna herramienta computacional, obtenemos que la curva cuadrática definida por $P$ se ve como en la siguiente figura.

Parece ser que esta es una hipérbola. Una de las ventajas del teorema de clasificación isométrica de curvas cuadráticas es que nos dirá que, en efecto, esto es una hipérbola. De hecho, tendremos una manera práctica de encontrar de manera explícita la transformación $T$ que manda el polinomio $P$ que define esta hipérbola $\mathcal{H}$ a un polinomio isométricamente equivalente $P’$ de una hipérbola canónica $\mathcal{H}’$.

¿Cuáles son los focos de $\mathcal{H}$? ¿Cuál es el centro de $\mathcal{H}$? ¿Cuál es la longitud de sus ejes? Esto no se aprecia claramente a partir del polinomio $P$. Sin embargo, la hipérbola $\mathcal{H}’$ tiene ecuación canónica, así que en $P’$ podemos leer fácilmente los focos, ejes y centro de $\mathcal{H’}$. Y luego usando precisamente la transformación $T$ podemos transferir esta información que sabemos de $\mathcal{H}’$ a $\mathcal{H}$. Por ejemplo, usando que $T$ es isometría obtenemos que $\mathcal{H}$ y $\mathcal{H}’$ tienen la misma longitud de ejes.

Más adelante…

En las siguientes entradas nos enfocaremos en demostrar los teoremas de clasificación aquí enunciados. Antes de hacer esto, debemos desarrollar un poco más de teoría. Por un lado, necesitamos comprender cómo las traslaciones nos pueden ayudar a «eliminar los términos lineales» de algunos polinomios cuadráticos. Luego, necesitamos comprender cómo las rotaciones nos pueden ayudar a «eliminar el término cruzado $xy$».

Las traslaciones las podremos entender fácilmente. Sin embargo, las rotaciones que «eliminan el término cruzado» requerirán que entendamos un nuevo procedimiento para matrices simétricas: el de diagonalizarlas. Esto nos llevará a discutir los eigenvalores, eigenvectores y el polinomio característico de la matriz.

Tarea moral

  1. Demuestra que cualesquiera dos segmentos del plano son afínmente equivalentes.
  2. Demuestra que cualesquiera dos rectángulos del plano son afínmente equivalentes.
  3. Resuelve los siguientes incisos:
    1. Prueba que dos cuadrados del plano son isométricamente equivalentes si y sólo si tienen la misma longitud de lado.
    2. Demuestra que cualquier cuadrado es isométricamente equivalente a algún cuadrado de vértices $(0,0)$, $(c,0)$, $(0,c)$ y $(c,c)$ para $c>0$.
    3. Demuestra que el cuadrado de vértices $(0,0)$, $(c,0)$, $(0,c)$ y $(c,c)$ tiene diagonal de longitud $\sqrt{2}c$.
    4. Usa todo lo anterior para demostrar que en cualquier cuadrado de lado $c$ se tiene que la diagonal mide $\sqrt{2}c$.
  4. En el teorema de clasificación afín de PCDV tenemos que cualquier PCDV es afínmente equivalente a exactamente una de las posibilidades enunciadas. En particular, esto implica que de esos nueve polinomios, no hay dos de ellos que sean afínmente equivalentes entre sí. Demuestra esto.
  5. Enuncia y demuestra un teorema de clasificación isométrico y un teorema de clasificación afín para triángulos en el plano.

Entradas relacionadas

Geometría Analítica I: Propiedades de elipses

Por Héctor Morales

3 respuestas

Introducción

En la entrada anterior definimos qué es una elipse, hablamos de una técnica para trazar una y cómo esta técnica, nos conduce naturalmente a su definición analítica: una elipse es la curva que define al conjunto de puntos que cumplen que la suma a dos puntos distintos llamados focos es constante. Finalmente vimos cómo escribir la ecuación canónica de la elipse; a partir de esta ecuación canónica podemos leer toda su información geométrica.

Ahora, para finalizar nuestro estudio de las elipses, vamos a hablar de sus elementos, propiedades focales y sus propiedades métricas. Verás cómo algunos problemas de aplicación motivan el estudio formal de estas propiedades y extenderemos algunas de ellas para el estudio de las cónicas que nos faltan. Sin más preámbulo, abordaremos el tema.

Elementos de una elipse

En la entrada anterior hicimos mención a algunos de los elementos que componen una elipse. Como mencionamos, a partir de la ecuación canónica puedes leer directamente información como el eje menor y el eje mayor; conociendo estos dos ejes, puedes deducir cuáles son sus vértices y sus focos. Haciendo más cuentas puedes deducir cuál es su lado recto y directrices.

En la siguiente figura puedes observar un diagrama que muestra todos los elementos de la elipse y en la siguiente tabla puedes ver qué relación guardan unos con otros. Es importante que sepamos extraer toda la información geométrica que nos sea posible cuando se nos presente una ecuación en su forma canónica.

Breve resumen de los elementos de una elipse. Estos elementos tienen análogos cuando tratamos con otras secciones cónicas.
Elemento dentro de la elipse canónicaExpresión analítica
Longitud del eje mayor$$2a$$
Coordenadas de los vértices$$(\pm a,0)$$
Longitud del eje menor$$2b$$
Coordenadas de los co-vértices$$(0,\pm b)$$
Coordenadas de los focos$(\pm c,0) \quad \text{donde} \quad c^{2}=a^{2}+b^{2}$
Excentricidad$$\varepsilon=\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}=\sqrt{1-\frac{b^{2}}{a^{2}}}$$

Como puedes notar, la última fila se refiere a una propiedad de la elipse que no hemos discutido: la excentricidad. La excentricidad normalmente denotada como $\epsilon$ es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. Pronto veremos que a partir de la excentricidad, podemos definir a las tres secciones cónicas como el lugar geométrico de los puntos $\mathbf{X}$ cuya razón de sus distancias a un foco $\mathbf{p}$ y a una recta $\ell$ es una constante fija. Profundizaremos en el estudio de la excentricidad a lo largo de esta unidad, por el momento fijemos la idea de que las elipses necesariamente deben tener una excentricidad menor que uno; es decir $\epsilon < 1$.

Otra observación importante: estas reglas se refieren a una elipse centrada en el origen que tiene una ecuación canónica $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$. No es el objetivo de esta unidad hablar de traslaciones y rotaciones; pero debes saber que si la elipse tiene el centro fuera del origen en un punto $(h,k)$, su ecuación se ve así: $\frac{x^{2}-h}{a^{2}}+\frac{y^{2}-k}{b^{2}}=1$. El estudio de elipses rotadas se aborda comúnmente en un segundo curso de geometría analítica.

Propiedad focal de la elipse

La propiedad focal de la elipse es es que cualquier fotón que sale de uno de los focos, se refleja dentro de la elipse para llegar al otro foco. Si no estás familiarizado con el fotón, imagina la siguiente situación: estás en un cuarto con paredes reflejantes y con forma elíptica; si tu te paras en uno de los focos del cuarto y apuntas con una linterna hacia algún punto en las paredes, el rayo de luz de tu linterna impactará directamente en el otro foco.

Existen dos formas de formalizar la propiedad que describimos en el párrafo anterior; la primera consiste en tomar el círculo de radio $2\mathbf{a}$ centrado en el foco $\mathbf{p}$ (este círculo contiene el otro foco $\mathbf{q}$, puesto que ahora $2 a>d(p, q)$) y luego ver que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a la elipse $\mathcal{E}$. La segunda forma de resolver este problema nos va a permitir abordar el clásico «problema del bombero», entonces dejaremos el primero como tarea moral.

Para hablar del problema del bombero observa la siguiente figura, supongamos que un bombero está para en el punto $\mathbf{p}$ y hay un incendio en el punto $\mathbf{q}$. Pero tiene su cubeta vacía, y entonces tiene que pasar primero a llenarla a un río cuyo borde es la recta $\mathcal{l}$. El problema consiste en saber cuál es la trayectoria óptima que debe seguir el bombero. Es decir, ¿para cuál punto $x \in \mathcal{l}$? se tiene que $\mathrm{d}(\mathbf{p}, \boldsymbol{x})+\mathrm{d}(\boldsymbol{x}, \mathbf{q})$ es mínima.

Nota cómo no hemos específicado de qué lado del río está el fuego; si estuviera del otro lado que el bombero, cualquier trayectoria al fuego tiene que pasar por $\mathcal{l}$ y entonces debe irse por la línea recta de $\mathbf{p}$ a $\mathbf{q}$ y tomar agua en $\boldsymbol{x}_{0}=\ell \cap \overline{\mathbf{p q}}$ (ver la siguiente figura). Entonces, si fuego y bombero están del mismo lado del río $\mathcal{l}$ podemos pensar en un «fuego virtual», que es el reflejado de $\mathbf{q}$ en $\mathcal{l}$, llamémosle $\mathbf{q}_{0}$, que cumple que $\mathrm{d}(\mathbf{x}, \mathbf{q})=\mathrm{d}\left(\mathbf{x}, \mathbf{q}_{0}\right)$ para todo $\mathbf{x} \in \mathcal{l}$, (para $\mathbf{q}$ y $\mathbf{q}_{0}$, \mathcal{l} es su mediatriz). La solución es, por el caso anterior, $\mathbf{x}_{0}=\ell \cap \overline{\mathbf{p q}_{0}}$.

Pero observa cómo además de que el ángulo $\alpha$ con el que llega el bombero a $\mathcal{l}$ es igual al ángulo de «de reflexión» con el que sale corriendo al fuego (ya con la cubeta llena), e igual al ángulo con el que seguiría su trayecto al fuego virtual; y que esta propiedad determina el punto de mínimo recorrido $\mathbf{x}_{0}$; es fácil convencerse de que para cualquier otro punto de $\mathcal{l}$ los ángulos de llegada y de salida son distintos. Si los bomberos fueran fotones que salen de $\mathbf{p}$ y $\mathcal{l}$ es un espejo, el único que llega a $\mathbf{q}$ es el fotón de recorrido mínimo.

Para aterrizar nuestro problema del bombero al caso de las elipses, considera ahora que $\mathbf{p}$ y $\mathbf{q}$ son los focos de una elipse y $\mathbf{x}_{0}$ un punto en ella. Sea $\mathcal{l}$ la recta que pasa por $\mathbf{x}_{0}$ y bisecta (por fuera) los segmentos de $\mathbf{p}$ y $\mathbf{q}$ a $\mathbf{x}_{0}$. Por construcción, y considerando la solución al problema del bombero, cualquier otro punto $\mathbf{x} \in \mathcal{l}$ tiene mayor suma de distancias a los focos y por tanto está fuera de la elipse. Esto demuestra que $\mathcal{l}$ es la tangente a la elipse en el punto $\mathbf{x}_{0}$, y por lo tanto, queda demostrada la propiedad focal de la elipse.

Antes de dar por terminada esta sección, te invito a que experimentes con el siguiente recuadro interactivo de GeoGebra: en él podrás ver cómo funciona esta propiedad focal de las elipses para elipses de diferentes tamaños y posiciones. ¿Puedes ver qué pasa con esta propiedad para el caso degenerado de la elipse? ¿Qué pasa si los focos son el mismo punto?

Propiedades métricas de la elipse

Tocaremos brevemente el tema de las propiedades métricas de la elipse; lo haremos sólo superficialmente pues una demostración formal se escapa de lo que planeamos cubrir en este curso. Si no estás familiarizado con los términos que aparecen en esta sección, no te preocupes, enfócate en entender cómo se llegó a los resultados y tenlos como referencia por si los ocupas en algún otro curso un poco más enfocado a las aplicaciones de las elipses.

La primera de sus propiedades métricas que vamos a abordar es el área de la elipse: considera que esta propiedad se refiere a la elipse con ecuación:

\begin{equation}
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\end{equation}

La ecuación anterior, puede ser reescrita como

\begin{equation}
y(x)=b \sqrt{1-x^{2} / a^{2}}.
\end{equation}

Para toda $x \in[-a, a]$, esta curva es la mitad superior de la elipse. Entonces, el doble de la integral $y(x)$ sobre le intervalo $[-a, a]$ será el área de la elipse:

\begin{equation}
\begin{aligned}
A_{\text {ellipse }} &=\int_{-a}^{a} 2 b \sqrt{1-\frac{x^{2}}{a^{2}}} d x \
&=\frac{b}{a} \int_{-a}^{a} 2 \sqrt{a^{2}-x^{2}} d x .
\end{aligned}
\end{equation}

La segunda integral es el área del círculo con radio $a$, la cual vale $\pi a^{2}$. Entonces,

\begin{equation}
A_{\text {ellipse }}=\frac{b}{a} \pi a^{2}=\pi a b.
\end{equation}

La circunferencia de una elipse, es decir, el análogo del perímetro para las circunferencias presenta un problema: ¡es bastante difícil de obtener! pues hay que calcular una integral que no puede ser evaluada en términos de funciones elementales. De momento, pondremos sólo la fórmula, pues es un resultado bastante útil. Si te interesa ver cómo se llegó a este resultado, puedes revisar la siguiente fuente.

\begin{equation}
C \approx \pi[3(a+b)-\sqrt{(3 a+b)(a+3 b)}]=\pi\left[3(a+b)-\sqrt{10 a b+3\left(a^{2}+b^{2}\right)}\right]
\end{equation}

La última de estas propiedades métricas que veremos superficialmente será la curvatura; esto te podría resultar especialmente útil si por ejemplo quisieras calcular la curvatura de la trayectoria para una partícula que se mueve trazando una parábola. La curvatura para una elipse con ecuación canónica $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$ será:

\begin{equation}
\kappa=\frac{1}{a^{2} b^{2}}\left(\frac{x^{2}}{a^{4}}+\frac{y^{2}}{b^{4}}\right)^{-\frac{3}{2}}.
\end{equation}

Más adelante…

En esta entrada y en la anterior profundizamos en las propiedades de la elipse. Seguiremos nuestro estudio de las secciones cónicas definiendo a las hipérbolas, veremos que a pesar de ser figuras muy distintas, guardan una relación estrecha con los círculos y las elipses. Al igual que para las figuras que hemos visto hasta el momento, entenderemos cómo llegar a una expresión analítica y aprenderemos a leer toda la información geométrica que contiene.

Tarea moral

  • Demuestra la propiedad focal de la elipse sin resolver el problema del bombero. Sugerencia. toma el círculo de radio $2\mathbf{a}$ centrado en un foco $\mathbf{p}$ y luego ve que para los puntos de este círculo, su mediatriz con $\mathbf{q}$ es tangente a una elipse.
  • Halle la ecuación de la elipse con centro en el origen que satisface las condiciones dadas; construya la curva:
  1. La longitud del eje mayor es $10$ y l del eje menor $8$; los focos están sobre el eje $y$.
  2. El eje menor mide $10$ y un vértice es $(6,0)$.
  3. El lado recto mide $\frac{32}{7}$ y uno de los extremos del eje menor está en $(4,0)$.
  • Obten el área de la elipse que tiene la siguiente ecuación:

$$
\frac{x^{2}}{16}+\frac{y^{2}}{25}=1
$$

  • Obtenga una aproximación del perímetro de la siguiente elipse:

$$
\frac{x^{2}}{25}+\frac{y^{2}}{225}=1
$$

  • Obtenga la curvatura de la siguiente elipse en el punto $(3,2)$:

$$
\frac{x^{2}}{16}+\frac{y^{2}}{9}=1
$$

Entradas relacionadas

Geometría Analítica I: Elipses

Por Héctor Morales

Deja un comentario

Introducción

Probablemente recuerdas un ejercicio muy común que se hace en las primarias en México: cuando se enseña a los niños sobre el Sistema Solar, comúnmente se les pide hacer una maqueta con esferas de unicel. Si alguna vez hiciste este ejercicio, tal vez recuerdas que las supuestas trayectorias de estos planetas en nuestra maqueta se distribuían como una serie de círculos concéntricos que iban aumentando en tamaño, con el «Sol» en su centro.

Por otro lado, si te interesa la astronomía, seguramente estás familiarizado con las Leyes de Kepler, una de ellas nos dice «Todos los planetas se mueven alrededor del Sol siguiendo órbitas elípticas. El Sol está en uno de los focos de la elipse.» Entonces, resulta que las trayectorias de los planetas no son círculos, si no «elipses», y todo este tiempo nuestra maqueta estuvo mal (¿o no tanto?). Si las elipses son tan importantes como para permitirnos visualizar el movimiento de un planeta, podrás darte cuenta de la importancia de tener una descripción analítica de esta figura; y por qué nos interesa estudiarla a fondo.

En esta entrada haremos justo eso: discutiremos desde cómo trazar una elipse en papel, pasando por su definición formal hasta obtener una expresión analítica que nos permitirá leer toda la información geométrica de la figura.

Dibujando y definiendo una elipse

Si alguna vez has visto un arbusto con forma elíptica (algo así como un círculo achatado), tal vez te has preguntado ¿cómo obtuvo esa forma? El método más sencillo para dibujar una elipse consiste en fijar dos tachuelas a una superficie de papel, amarrar holgadamente un hilo entre ellas y luego, manteniendo la tensión del hilo, girar el lápiz. Si intentas por tu cuenta este procedimiento, podrás ver que obtuviste una figura como la siguiente:

Elipse dibujada con el «Método del
Jardinero»

Esta figura es una de las secciones cónicas que estudiaremos durante el curso; como ya lo sugiere el método que usamos para dibujarla («Método del jardinero»), su definición tiene tres elementos importantes: dos puntos fijos y un tercer punto que se mueve manteniendo una suma de distancias totales constante. Sin más preámbulos, abordemos la definición de elipse con la que trabajaremos.

Definición. Las elipses son el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos llamados focos es constante. De tal manera que una elipse $\mathcal{E}$ queda totalmente determinada por la ecuación:

\begin{equation}
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
\end{equation}

donde $\mathbf{p}$ y $\mathbf{q}$ son los focos y $a$ es una constante positiva, llamada semieje mayor, tal que 2 a>d(\mathbf{p}, \mathbf{q}).

Un pregunta natural que te puede surgir al considerar esta definición es el por qué incluir el coeficiente $2$. La respuesta es que se incluye para que quede claro que si los focos coinciden, $\mathbf{p}=\mathbf{q}$, entonces se obtiene un círculo de radio $a$ y centro en el foco; dicho de una forma más explícita ¡Resulta que los círculos son un tipo especial de elipse!

Antes de continuar te invito a que manipules el siguiente recuadro interactivo de GeoGebra para familiarizarte con las elipses. Observa cómo cambiar el eje mayor y el eje menor la redefine totalmente; además cómo la figura es totalmente dependiente de la posición de sus focos.

Ahora, debes considerar que esta ecuación, poniéndole coordenadas a los focos, incluye raíces cuadradas por las distancias, lo cual la hace ver un poco intimidante. Veamos un caso especial que nos permitirá escribir a la ecuación de la elipse de una forma más agradable. Con este desarrollo, queremos llegar a la ecuación canónica de la elipse.

Supongamos que el centro de la elípse $\mathcal{E}$, i.e., el punto medio entre los focos, está en el origen y que además los focos están en el eje $x .$ Entonces tenemos que $\mathbf{p}=(c, 0)$ y $\mathbf{q}=(-c, 0)$ para alguna $c$ tal que $0<c<a$ (donde ya suponemos que la elipse no es un círculo al pedir $0<c$ ). Es fácil ver que entonces la intersección de $\mathcal{E}$ con el eje $x$ consiste de los puntos $(a, 0) \mathrm{y}$ $(-a, 0)$, pues la ecuación $(2.8)$ para puntos $(x, 0)$ es

\begin{equation}
|x-c|+|x+c|=2 a
\end{equation}

que sólo tiene las soluciones $x=a$ y $x=-a$, y de aquí el nombre de «semieje mayor» para la constante $a$. Como el eje $y$ es ahora la mediatriz de los focos, en él, es decir en los puntos $(0, y)$, la ecuación se vuelve:

\begin{equation}
\sqrt{c^{2}+y^{2}}=a
\end{equation}

que tiene soluciones $y=\pm b$, donde $b>0$, llamado el semieje menor de la elipse $\mathcal{E}$. es tal que:

\begin{equation}
b^{2}=a^{2}-c^{2} .
\end{equation}

Puedes guiarte con la siguiente figura para entender el desarrollo que acabamos de hacer:

Semieje mayor y semieje menor de una elipse.

Ahora sí, consideremos la ecuación $(2.8)$, que $\operatorname{con} \mathrm{x}=(x, y) \mathrm{y}$ la definición de nuestros focos se expresa:

$$
\sqrt{(x-c)^{2}+y^{2}}+\sqrt{(x+c)^{2}+y^{2}}=2 a
$$

Si elevamos al cuadrado directamente a esta ecuación, en el lado izquierdo nos quedaría un incomodo término con raíces. Así que conviene pasar a una de las dos raíces al otro lado, para obtener

$$
\sqrt{(x-c)^{2}+y^{2}}=2 a-\sqrt{(x+c)^{2}+y^{2}}
$$

Elevando al cuadrado se tiene

$$
(x-c)^{2}+y^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+(x+c)^{2}+y^{2}
$$

$$
x^{2}-2 c x+c^{2}=4 a^{2}-4 a \sqrt{(x+c)^{2}+y^{2}}+x^{2}+2 c x+c^{2}
$$

$$
4 a \sqrt{(x+c)^{2}+y^{2}}=4 a^{2}+4 c x
$$

$$
a \sqrt{(x+c)^{2}+y^{2}}=a^{2}+c x
$$

Elevando de nuevo al cuadrado, nos deshacemos de la raíz, y después, agrupando términos, obtenemos

$$
a^{2}\left((x+c)^{2}+y^{2}\right)=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$

$$
a^{2} x^{2}+2 a^{2} c x+a^{2} c^{2}+a^{2} y^{2}=a^{4}+2 a^{2} c x+c^{2} x^{2}
$$

$$
\left(a^{2}-c^{2}\right) x^{2}+a^{2} y^{2}=a^{2}\left(a^{2}-c^{2}\right)
$$

$$
b^{2} x^{2}+a^{2} y^{2}=a^{2} b^{2}
$$

que, dividiendo entre $a^{2} b^{2}$, se escribe finalmente como

\begin{equation}
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
\end{equation}

llamada la ecuación canónica de la elipse centrada en el origen.

Después de este largo desarrollo pudimos llegar a una ecuación sencilla que nos permite leer toda la información geométrica de la elipse: su centro y la magnitud de su semieje mayor y semieje menor. Observa cómo ahora podemos demostrar sencillamente una de las afirmaciones que hicimos en esta entrada: si en la ecuación canónica de la elipse centrada en el origen hacemos $a=b$, es decir, forzamos a que la figura tenga el semieje mayor y el semieje menor iguales obtenemos la ecuación $x^2+y^2=a^2$ que es la expresión analítica de una circunferencia centrada en el origen.

Con estas herramientas estamos listos para realizar algunos ejercicios. En el primero obtendremos la ecuación de la elipse a partir de la definición, y en el segundo veremos cómo podemos extraer toda la información geométrica de la elipse a partir de su ecuación.

Ejercicio. Encuentra la ecuación de la elipse con fonoces en $(0,3)$ y $(0,-3)$ para la cual la suma de las distancias del foco a cada uno de sus puntos es $6\sqrt{3}$.

Utilizando la definición propuesta al inicio de esta entrada, nuestra elipse será el conjunto de puntos que cumplen la condición:

$$
d(\mathbf{x}, \mathbf{p})+d(\mathbf{x}, \mathbf{q})=2 a
$$

Aplicando la fórmula de la distancia que utilizando en la primera unidad del curso y considerando el valor de la constante $2a$ tenemos que

$$
\sqrt{x^{2}+(y-3)^{2}}+\sqrt{x^{2}+(y+3)^{2}}=6 \sqrt{3}
$$

Esto, lo podemos reescribir como

$$
\sqrt{x^{2}+(y-3)^{2}}=6 \sqrt{3}-\sqrt{x^{2}+(y+3)^{2}}
$$

Si elevamos ambos lados al cuadrado, llegamos a que

$$
x^{2}+(y-3)^{2}=108-12 \sqrt{3} \sqrt{x^{2}+(y+3)^{2}}+x^{2}+(y+3)^{2}
$$

Si te das cuenta, podemos cancelar algunos términos; y en nuestro caso nos conviene dividir ambos lados de la ecuación anterior entre $12$.Si reducimos la expresión anterior, tenemos que

$$
\sqrt{3} \sqrt{x^{2}+(y+3)^{2}}=9+y
$$

Una vez más elevamos ambos lados al cuadrado y llegamos a que

$$
3 x^{2}+2 y^{2}=54
$$

Lo cual es lo mismo a

$$
\frac{x^{2}}{27}+\frac{y^{2}}{18}=1
$$

que es la ecuación de la elipse en su forma canónica.

Ejercicio. ¿Cuál es la ecuación canónica de la elipse que tiene como vértices a los puntos $(\pm 8,0)$ y como focos a $(\pm 5,0)$?

Los focos están en el eje $x$, entonces el eje mayor estará también sobre el eje $x$. Así, la ecuación tendrá esta forma

$$
\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1
$$

Como los vértices son $(\pm 8,0)$, entonces $a=8$ y $a^{2} = 64$. Y puesto que los focos son $(\pm 5,0)$, entonces $c=5$ y $c^2 = 25$. Ahora, sabemos que los focos y los vértices están relacionados por la siguiente ecuación $c^{2}=a^{2}-b^{2}$. Si resolvemos para $b^2$ tenemos que $b^2=39$. Por lo tanto, la ecuación canónica de esta elipse será:

$$
\frac{x^{2}}{64}+\frac{y^{2}}{39}=1
$$

Más adelante…

En esta entrada aprendimos lo básico sobre una elipse: su definición, sus elementos y la ecuación canónica que la representa. Nos falta hablar de sus propiedades focales y del concepto de excentricidad, estos términos serán el tema de la siguiente entrada. Una vez que hayamos concluido nuestro estudio de las elipses, empezaremos a hablar de hipérbolas.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Dibuja la elipse $\frac{x^{2}}{36}+\frac{y^{2}}{4}=1$ en algún programa de computadora e identifica sus elementos. Sugerencia: puedes utilizar GeoGebra, Mathematica, Matlab, Python o GNU plot.
  • Considera la siguiente ecuación de elipse $9 x^{2}+4 y^{2}=36$; encuentra sus focos, su semieje mayor, su semieje menor y dibújala.
  • Encuentra el área de una elipse con semieje mayor $a$ y semieje menor $b$. Sugerencia: Considera la ecuación canónica de una elipse centrada en el origen, despeja para $x$ e integra sobre $x$ sólo un cuadrante; eligiendo correctamente los límites de integración. El resultado de la integral multiplícalo por $4$. Cuidado, la integral es trigonométrica.

Entradas relacionadas

Casos extremos

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasEn los problemas de matemáticas tenemos objetos con propiedades. De entre los objetos con una propiedad, a veces es bueno elegir uno en especial para verificar nuestras conjeturas. En otras ocasiones, estos objetos extremos tienen propiedades que los hacen cumplir lo que pide el problema.

En estos videos veremos ejemplos en los cuales la existencia (¡o no existencia!) de objetos extremos o especiales nos permite resolver problemas.

Ir a los videos…