Archivo de la etiqueta: descenso infinito

Seminario de Resolución de Problemas: Sucesiones monótonas y acotadas

Por Leonardo Ignacio Martínez Sandoval

Introducción

En entradas anteriores hablamos de sucesiones aritméticas y geométricas. También hablamos de sucesiones periódicas y pre-periódicas. Cuando una sucesión es de cualquiera de estos tipos, entonces no es tan compleja pues depende de pocos parámetros. Hay otros dos sentidos en los que podemos restringir una sucesión: orden y en tamaño. Esto nos da, respectivamente, las definiciones de sucesiones monótonas y acotadas.

Por un lado, para hablar de sucesiones acotadas se necesita una noción de distancia. Por otro, para hablar de sucesiones monótonas se necesita de una noción de orden. En las siguientes secciones veremos ejemplos numéricos, pero mucho de lo que discutimos en esta entrada es generalizable a espacios métricos o conjuntos ordenados arbitrarios.

A menos que digamos lo contrario, supondremos que las sucesiones de las que hablamos empiezan con un término de subíndice $0$ , aunque esto en realidad no afecta las ideas que discutimos.

Sucesiones acotadas

Las sucesiones acotadas son aquellas que siempre están «cerca de un punto». Cuando estamos hablando de sucesiones de reales, o de elementos en un conjunto linealmente ordenado, podemos hablar de cotas por arriba y por abajo.

Definición. Sea ${x_{n}}$ una sucesión de reales. Decimos que ${x_{n}}$ es:

Inferiormente acotada si existe un real $m$ tal que $x_{n} \geq m$ para todo entero $n \geq 0$ .
Superiormente acotada si existe un real $M$ tal que $x_{n} \leq M$ para todo entero $n \geq 0$ .
Acotada si es inferiormente acotada y superiormente acotada.

Se puede usar como definición alternativa del tercer punto la conclusión de siguiente proposición. Esto permite definir sucesiones acotadas en cualquier espacio normado.

Proposición. Sea ${x_{n}}$ una sucesión de reales. Se tiene que ${x_{n}}$ es acotada si y sólo si existe un real $A \geq 0$ tal que $| x_{n} | \leq A$ para todo entero $n \geq 0$ .

Cualquier sucesión periódica de reales toma sólo una cantidad finita de valores, así que es acotada. ¿Cómo son las sucesiones aritméticas y geométricas que son acotadas?

Problema. La sucesión ${x_{n}}$ está definida para $n \geq 1$ y está dada por $x_{n} = 3 + \sqrt{3 + \sqrt{3 + \sqrt{\dots \sqrt{3 + \sqrt{3}}}}},$ en donde tenemos $n$ signos de raíz cuadrada. Muestra que esta sucesión es acotada.

Sugerencia pre-solución. La notación es algo difícil. Usa una mejor notación, conjetura una cota superior trabajando hacia atrás, y pruébala por inducción.

Solución. El primer término es $3 + \sqrt{3}$ y para $n \geq 1$ tenemos $x_{n + 1} = 3 + \sqrt{x_{n}} \geq 0.$ Falta ver que la sucesión está acotada superiormente.

Trabajemos hacia atrás, suponiendo que podemos mostrar por inducción que un real $C$ es cota superior. Al hacer el paso inductivo, nos bastaría que $3 + \sqrt{C} \leq C .$ Esto se cumple para muchos valores de $C$ , por ejemplo, podemos tomar $C = 9$ .

Hagamos la prueba formalmente. Mostraremos que ${x_{n}}$ está acotada superiormente por $9$ . El primer término es $3 + \sqrt{3}$ , que está acotado por $9$ . Si $x_{n}$ está acotado por $9$ , entonces $x_{n + 1} = 3 + \sqrt{x_{n}} \leq 3 + \sqrt{9} \leq 3 + 3 \leq 9.$ Esto termina la inducción y muestra que ${x_{n}}$ es acotada.

Sucesiones monótonas

Otra forma de limitar los «movimientos» de una sucesión es a través de una noción de orden. Las siguientes definiciones son para sucesiones de reales, pero es sencillo extenderlas a cualquier conjunto parcialmente ordenado.

Definición. Sea ${x_{n}}$ una sucesión de reales. Decimos que ${x_{n}}$ es:

Creciente si para todo par de enteros enteros $k > l \geq 0$ se tiene que $x_{k} \geq x_{l}$ .
Estrictamente creciente si para todo par de enteros enteros $k > l \geq 0$ se tiene que $x_{k} > x_{l}$ .
Decreciente si para todo par de enteros enteros $k > l \geq 0$ se tiene que $x_{k} \leq x_{l}$ .
Estrictamente decreciente si para todo par de enteros enteros $k > l \geq 0$ se tiene que $x_{k} < x_{l}$ .

Las sucesiones monótonas son aquellas que cumplen alguna de las definiciones anteriores.

Aunque la definición requiere que cierta desigualdad se cumpla para todo par de índices $k > l \geq 0$ , basta con demostrar que se cumple para $k = n + 1$ y $l = n$ , es decir, para índices consecutivos. Esto típicamente se reduce a demostrar una desigualdad. Hablaremos más adelante de técnicas para resolver desigualdades, pero por el momento veremos un ejemplo sencillo.

Problema. Muestra que la sucesión ${x_{n}}$ dada por $x_{n} = {(1 + \frac{1}{n})}^{n}$ es estrictamente creciente.

Sugerencia pre-solución. Basta con que pruebes la desigualdad para subíndices consecutivos. Para hacer esto, usa el binomio de Newton y modifica el problema a comparar ciertos términos.

Solución. Tenemos que mostrar que ${(1 + \frac{1}{n})}^{n} \leq {(1 + \frac{1}{n + 1})}^{n + 1} .$

Para mostrar esto, primero demostraremos la siguiente desigualdad auxiliar para $0 \leq k \leq n + 1$ : $\begin{matrix} (1) & (\binom{n}{k}) \frac{1}{n^{k}} \leq (\binom{n + 1}{k}) \frac{1}{(n + 1)^{k}} . \end{matrix}$

Si $k = n + 1$ , la desigualdad se cumple pues el término izquierdo es $0$ . Para $0 \leq k \leq n$ , esta desigualdad es equivalente a la desigualdad $\frac{(\binom{n + 1}{k})}{(\binom{n}{k})} \geq {(\frac{n + 1}{n})}^{k} .$ Usando la expresión en términos de factoriales y simplificando el lado izquierdo, tenemos que
$\begin{aligned} \frac{(\binom{n + 1}{k})}{(\binom{n}{k})} & = \frac{\frac{(n + 1)!}{k! (n + 1 - k)!}}{\frac{n!}{k! (n - k)!}} \\ = (\frac{n + 1}{n}) \cdot (\frac{n}{n - 1}) \cdot \dots \cdot (\frac{n + 2 - k}{n + 1 - k}) \end{aligned}$

Afirmamos que cada uno de los $k$ términos de la derecha es mayor o igual a $\frac{n + 1}{n}$ . Para ello, basta mostrar que la sucesión ${\frac{m + 1}{m}}$ definida para $m \geq 1$ es decreciente. Pero esto es fácil de ver, pues cada término es $\frac{m + 1}{m} = 1 + \frac{1}{m}$ que claramente decrece conforme $m$ crece. Con esto terminamos la prueba de la desigualdad auxiliar (1).

Sumando la desigualdad (1) para todos los valores de $k$ de $0$ a $n + 1$ y usando el binomio de Newton, obtenemos la desigualdad deseada.

Más allá de sucesiones monótonas

De entre las sucesiones monótonas, hay algunas que podemos entender mejor. Una sucesión de reales puede ser estrictamente creciente, y no irse a infinito. Por ejemplo, considera la sucesión: $0.3, 0.33, 0.333, 0.3333, \dots$ en donde de un término al siguiente se agrega un dígito $3$ . Esta sucesión es estrictamente creciente, pero todos los términos son menores a $\frac{1}{3}$ .

Hay diferentes grados de información que podemos tener de una sucesión con respecto a cuánto crece. En cada uno de los siguientes puntos, cada vez sabemos mejor qué tanto crece la sucesión:

Saber que la sucesión es creciente
Saber que es estrictamente creciente
Determinar si es acotada superiormente
Conocer qué tan rápido crece

Por supuesto, hay una jerarquía análoga para funciones decrecientes.

Veamos un ejemplo de entender bien el crecimiento de una sucesión. El siguiente problema apareció en uno de los concursos de matemáticas Pierre Fermat que organiza el IPN.

Problema. Considera una sucesión ${a_{n}}$ de reales tal que $a_{0} > 0$ y para cada $n \geq 0$ se cumple que $a_{n + 1} = a_{n} + \frac{1}{a_{n}}$ . Muestra que $a_{200} > 20$ .

Sugerencia pre-solución. En vez de entender la sucesión ${a_{n}}$ , modifica el problema a entender la sucesión ${a_{n}^{2}}$ , que es más fácil de estudiar cómo crece. En cierta forma, tendrás que generalizar el problema, entendiendo qué tan grande es cada término.

Solución. Es fácil ver que la sucesión es creciente. Para ello podemos probar simultáneamente por inducción que cada término es positivo y mayor que el anterior. Sin embargo, esto es todavía muy débil para nuestros fines: aún no sabemos si la sucesión superará $20$ y, peor aún, no sabemos si sucederá antes del término $200$ .

Quedémonos con el hecho de que $a_{n}$ es de términos positivos. Pero en vez de estudiar cómo crece ${a_{n}}$ , mejor estudiamos cómo crece ${a_{n}^{2}}$ . Observemos que
$\begin{aligned} a_{n + 1}^{2} & = {(a_{n} + \frac{1}{a_{n}})}^{2} \\ = a_{n}^{2} + 2 + \frac{1}{a_{n}^{2}} \\ > a_{n}^{2} + 2, \end{aligned}$

de modo que podemos probar inductivamente que $a_{n}^{2} \geq 2 n$ . De aquí, deducimos que $a_{n} \geq \sqrt{2 n}$ . En particular, $a_{200} \geq \sqrt{400} = 20$ .

Descenso infinito

Una herramienta bastante útil para la resolución de problemas con enteros es el siguiente resultado. En cierto sentido, habla de cómo son las sucesiones monótonas y acotadas de enteros.

Teorema (principio del descenso infinito). No existen sucesiones estrictamente decrecientes e inferiormente acotadas de enteros.

De manera similar, no existen sucesiones estrictamente crecientes y superiormente acotadas de enteros.

Veamos un ejemplo de la Olimpiada Centroamericana de Matemáticas.

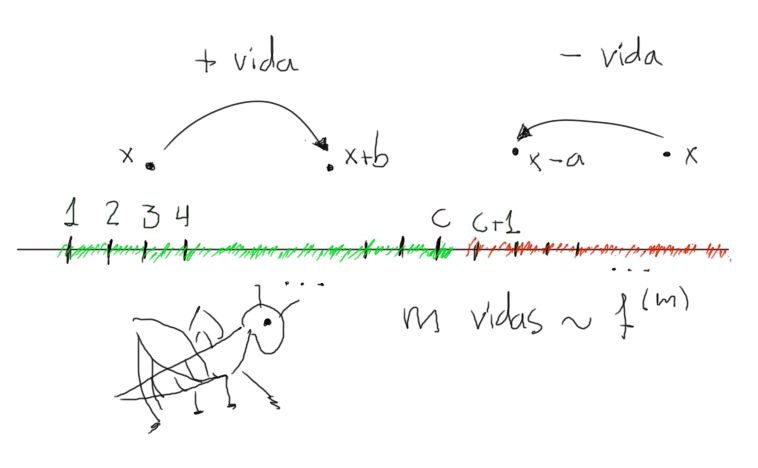
Problema. Aplicar un desliz a un entero positivo $n \geq 5$ consiste en cambiar a $n$ por $\frac{n + p^{2}}{p}$ , con $p$ un divisor primo de $n$ . Muestra que tras aplicar repetidamente deslices a un entero $n \geq 5$ , siempre se llega a $5$ .

Sugerencia pre-solución. Usa el principio de descenso infinito.

Solución. Si comenzamos con $n = 5$ , la única opción es pasar a $\frac{5 + 25}{5} = 6$ . Si comenzamos con $n = 6$ , ambos deslices (con $2$ ó $3$ ) nos llevan a $5$ .

Veremos que a partir de cualquier entero $n \geq 7$ , tras aplicar deslices siempre se llega a $5$ .

Afirmamos lo siguiente:

Si $n$ es primo, sólo tiene un desliz que lo pasa a $n + 1$ .
Para $n \geq 7$ no primo, aplicar un desliz lo disminuye en al menos $2$ .
Para $n \geq 5$ , aplicar un desliz lo lleva a un número mayor o igual a $5$ .

La primera afirmación es fácil de ver, pues si $n = p$ , el único divisor primo que tiene es $p$ y así, el único desliz que tiene lo manda a $\frac{p^{2} + p}{p} = p + 1 = n + 1.$

Para la segunda afirmación, necesitamos mostrar que si $n \geq 7$ no es primo y $p$ lo divide, entonces $\frac{n + p^{2}}{p} \leq n - 2.$ Reescribiendo esta afirmación, necesitamos mostrar que $n p \geq p^{2} + n + 2 p .$ Como $n$ no es primo, $n = p q$ con $q \geq 2$ . Como $p$ es primo, $p \geq 2$ .

Reescribiendo la desigualdad que queremos mostrar en términos de $p$ y $q$ , y cancelando un factor $p$ de ambos lados, lo que necesitamos es $p q \geq p + q + 2.$ restando $p + q - 1$ de ambos lados y factorizando el lado izquierdo, esto es equivalente a $(p - 1) (q - 1) \geq 3.$

Hagamos un análisis de casos para los primos $p$ y $q$

Si $p = q = 2$ entonces $n = 4$ , que no es un caso que nos interese.
Si $p = 2$ y $q = 3$ , o $p = 3$ y $q = 2$ , entonces $n = 6$ , pero para la segunda afirmación estamos suponiendo $n \geq 7$ .
Así, $p \geq 3$ y $q \geq 3$ , de modo que $(p - 1) (q - 1) \geq 4$ , que implica la desigualdad que queremos.

Esto prueba la segunda afirmación.

La tercera afirmación se prueba notando que tras el desliz, un número se va a $\frac{n}{p} + p \geq 2 \sqrt{n} \geq 2 \sqrt{5} > 4$ , y como esta esta expresión es entera, se tiene $\frac{n}{p} + p \geq 5$ .

Estamos listos para dar la prueba. Por la tercer afirmación, la sucesión siempre es $\geq 5$ . Si acaso la sucesión crece, fue porque teníamos un primo $p$ que pasó a $p + 1$ . Pero entonces $p + 1$ no es primo y al paso siguiente es menor o igual a $p - 1$ por la segunda afirmación. Así, cada dos pasos, la sucesión decrece estrictamente, a menos que pase por $6$ . Por el principio de descenso infinito, no es posible que siempre decrezca. Así, en algún momento pasa por $6$ , y entonces al paso siguiente será $5$ .

Más problemas

Esta entrada es una extensión de las secciones 1, 2 y 3 del curso de sucesiones que impartí para los entrenadores de la Olimpiada Mexicana de Matemáticas. Puedes consultar las notas de este curso en el siguiente PDF, en donde hay más problemas de práctica:

Curso de Sucesiones Descarga

Un problema de saltamontes en cuarentena

Por Adán Medrano

Deja un comentario

Nota de Leo: Esta es una entrada invitada de Adán Medrano Martín del Campo. Nos platicará de un problema de saltamontes (de hecho, de dos) y de funciones en los enteros.

$Tu \in Casa$

Esto nos aconsejó muy atinadamente el Dr. Hugo López-Gatell Ramírez hace unos pocos días, ya que México y la mayoría del mundo está en cuarentena a causa de la enfermedad COVID19.

Cada vez más y más personas buscamos nuevas actividades para hacer en casa. Junto con Leo Martínez, David Torres (aka Gato) y Pablo Meré, administro el grupo de facebook InsOMMnia, el cual sirve de plataforma para discutir y realizar actividades olímpicamente productivas. A modo de amenizar la cuarentena, hice un video en vivo explicando la solución a un problema que me pareció particularmente agradable por varias razones:

Apareció en el examen de selección del equipo rumano de la IMO 2019
Es parecido al problema 5 de la OMM 2019
Es, en cierto sentido, un problema de saltamontes

En esta entrada, quisiera platicarles el problema y su solución. Antes de esto, recordemos el problema que apareció en la OMM 2019.

La Momia: OMM 2019

Problema 5. Sean $a > b$ dos números enteros positivos, primos relativos entre sí. En un camino recto, en el cual está marcado cada centímetro $n$ , para todo entero $n$ , un saltamontes hará algunos saltos comenzando en la marca de $0$ cm y siguiendo las siguientes reglas:

Cuando cierto minuto sea múltiplo de $a$ y no múltiplo de $b$ , saltará $a$ centímetros hacia adelante.
Cuando cierto minuto sea múltiplo de $b$ y no múltiplo de $a$ , saltará $b$ centímetros hacia atrás.
Cuando cierto minuto sea múltiplo de $a$ y múltiplo de $b$ , saltará $a - b$ centímetros hacia adelante.
Cuando un minuto no es múltiplo de $a$ ni de $b$ , el saltamontes no se mueve del lugar en el que está.

Determina todas las marcas a las que puede llegar el saltamontes.

Nota de Leo: Este es un excelente problema para explorarse buscando un patrón.

Sin dar un spoiler de la solución a dicho problema, el enunciado puede traducirse al siguiente problema de equivalente.

Problema 5′: Sean $a > b$ enteros primos positivos primos relativos entre sí y sea $f : N \to Z$ la función dada por
$f (n) = a ⌊ \frac{n}{a} ⌋ - b ⌊ \frac{n}{b} ⌋ .$
Determina la imagen de $f$ .

Uno puede jugar un poco con la función definida arriba, y llegar a la respuesta usando propiedades de dicha función. El objetivo de mostrarles este enunciado equivalente, es que muchas veces ciertos problemas que hablan de ciertos procesos pueden describirse (y resolverse) en términos de funciones construidas apropiadamente.

El problema que resolveremos cae en la categoría opuesta, pues es un problema sobre una función, al cual se le puede dar una interpretación de un saltamontes haciendo… algo.

El Vampiro: Romania TST 2019

Problema: Sean $a < b < c$ enteros positivos y sea $f : N \to N$ una función dada por
$f (n) = {\begin{cases} n - a & n > c \\ f (f (n + b)) & n \leq c \end{cases}$
Determina la cantidad de enteros positivos $n$ tales que $f (n) = n$ .

«Y eso qué tiene que ver con un saltamontes?» podrías pensar en este momento. ¡Ha ha! Mira ahora este problema de saltamontes.

Problema’: Sean $a < b < c$ enteros positivos. Un saltamontes se encuentra sobre un entero $n > 0$ en la recta real positiva, donde hay pasto en los enteros positivos menores o iguales que $c$ , y lava en los enteros mayores a $c$ . Inicialmente, el saltamontes tiene una vida, y mientras el saltamontes tenga al menos una vida, se dispondrá a saltar de la siguiente manera:

Si el saltamontes se encuentra en el pasto, el saltamontes gana una vida y salta $b$ enteros hacia adelante.
Si el saltamontes se encuentra en la lava, el saltamontes pierde una vida y salta $a$ enteros hacia atrás.

Cuando el saltamontes tiene $0$ vidas, este muere y deja de moverse. Determina todas las posiciones iniciales del saltamontes tal que el saltamontes morirá en su posición inicial.

Saltamontes, lava, pasto y vidas — Problema visto como vidas, pasto, lava y saltamontes.

A que no se lo esperaban. (Honestamente yo tampoco, pero últimamente tengo más tiempo libre). Tal vez este problema inspire algún mini juego en alguna entrega futura de The Legend of Zelda.

Y, ¿cómo resolvemos algo así?

El Santo: venciendo a la momia y al vampiro

Spoiler Alert:

A continuación resolveremos los problemas, en caso que estés intentándolos y no quieras ver sus soluciones

La clave para ambos problemas es: ¡usar residuos y propiedades de las funciones en juego!

Solución al problema 5 del nacional

Notemos que al dividir $n$ entre $a$ y entre $b$ , obtenemos
$n = a ⌊ \frac{n}{a} ⌋ + r_{a}$ y $n = b ⌊ \frac{n}{b} ⌋ + r_{b}$
donde

$0 \leq r_{a} \leq a - 1$ y $0 \leq r_{b} \leq b - 1$
son precisamente los residuos que resultan de la división. Notemos entonces que

$\begin{aligned} f (n) & = a ⌊ \frac{n}{a} ⌋ - b ⌊ \frac{n}{b} ⌋ \\ = (n - b ⌊ \frac{n}{b} ⌋) - (n - a ⌊ \frac{n}{a} ⌋) \\ = r_{b} - r_{a} \end{aligned}$

por lo que $f (n)$ simplemente depende de la diferencia entre $r_{b}$ y $r_{a}$ . Por el Teorema Chino del Residuo, o simplemente mirando exclusivamente a los múltiplos de $a$ y de $b$ entre $1$ y $a b$ , aparecen como diferencia todos los posibles enteros en el intervalo

$[- a + 1, b - 1]$
lo cual compone la imagen de $f$ , que es lo que buscábamos.

¡Genial! Mirar los residuos fue clave en el problema de saltamontes del nacional. En particular, no lo usamos en nuestra solución, pero $f$ resulta ser una función periódica, con periodo $a b$ . Esto es gracias a que $a$ y $b$ son primos relativos, y por lo tanto cada pareja de residuos $r_{a}, r_{b}$ se repiten exactamente cada $a b$ enteros.

La periodicidad será una propiedad clave en la solución del problema del selectivo rumano. Comenzamos mostrando una exploración del problema.

Exploración del problema del selectivo rumano

Los puntos $n$ tales que $f (n) = n$ son llamados puntos fijos. En la formulación como problema de saltamontes, corresponden a que el saltamontes muera justo donde empezó: «muera» es que ya no haya $f$ , empieza con una vida, osea una $f$ .

Notemos que si $n > c$ , entonces $n$ no es un punto fijo, pues

$f (n) = n - a \neq n .$
Esto nos dice que los puntos fijos son menores o iguales que $c$ . Ahora, notemos que (recordemos que $a < b < c$ )

$\begin{aligned} f (c) & = f (f (c + b)) \\ = f (c + b - a) = c + b - 2 a \end{aligned}$

y esto nos lleva a considerar que números cercanos a $c$ , dentro de un intervalo de tamaño $b - a$ , tendrán un valor similar. En efecto, si $0 \leq r < b - a$ entonces

$\begin{aligned} f (c - r) & = f (f (c - r + b)) \\ = f (c - r + b - a) \\ = c - r + b - 2 a . \end{aligned}$
Ahora, veamos que restando $b - a$ a $c$ , perdemos este patrón, pues

$\begin{aligned} f (c - b + a) & = f (f (c + a)) \\ = f (c) \\ = c + b - 2 a \end{aligned}$
¡Hemos regresado a un valor ya conocido! Esto nos lleva a la hipótesis de que $f$ es periódica con periodo $b - a$ en el intervalo $[1, c]$ . Formalicemos estas observaciones.

Un par de lemas para el problema rumano

La manera de enunciar formalmente las observaciones anteriores esto es, por ejemplo, via el siguiente lema:

Lema 1: Sea $n = c - r - k (b - a)$ un entero positivo menor o igual que $c$ donde $k \geq 0$ y $0 \leq r < b - a$ . Entonces
$f (n) = c - r + b - 2 a .$

(Prueba del lema 1): Procederemos por descenso en los enteros positivos. Construiremos una secuencia de valores iguales, con distinta cantidad de $f$ ’s compuestas, de la siguiente manera: comenzamos con
$z_{0} = n = c - r - k (b - a)$
y definimos

$z_{i + 1} = {\begin{cases} z_{i} - a & z_{i} > c \\ z_{i} + b & z_{i} \leq c \end{cases}$

para todo $i \geq 0$ . Además, escribiremos

$z_{i} = c - r - y_{i} b + x_{i} a$
donde $x_{0} = y_{0} = k$ , y ambas secuencias ${x_{i}}$ y ${y_{i}}$ decrecen, definiendo

$x_{i + 1} = {\begin{cases} x_{i} - 1 & z_{i} > c \\ x_{i} & z_{i} \leq c \end{cases}$ y

$y_{i + 1} = {\begin{cases} y_{i} & z_{i} > c \\ y_{i} - 1 & z_{i} \leq c \end{cases}$
Habiendo definido esto, tenemos que

$f (n) = f^{(1 + x_{i} - y_{i})} (z_{i})$
para todo $i \geq 0$ .

Observemos que si $y_{i} = - 1$ entonces $z_{i} = c - r + b + x_{i} a > c$ si se cumple que $x_{i} \geq - 1$ . Más aún, observemos el siguiente lema:

Lema 2: Para todo $i \geq 0$ , tenemos que $y_{i} \geq 0$ implica que $y_{i + 1} \leq x_{i + 1}$ .

(Prueba del lema 2): Procedemos por inducción. Para $i = 0$ esto es claro, pues
$y_{1} = k - 1 < k = x_{1} .$
Ahora, supongamos que $x_{i} \geq y_{i} \geq 0$ . Si $x_{i} > y_{i}$ entonces

$x_{i + 1} \geq x_{i} - 1 \geq y_{i} \geq y_{i + 1} .$
Si $x_{i} = y_{i}$ entonces tenemos que

$z_{i} = c - r - y_{i} (b - a) \leq c$
por lo que $z_{i + 1} = z_{i} + b$ y esto implica que

$x_{i + 1} = x_{i} > y_{i} - 1 = y_{i + 1} .$

Hemos probado pues que las secuencias ${x_{i}}$ y ${y_{i}}$ decrecen, y mientras $y_{i} \geq 0$ , tendremos que $x_{i + 1} \geq y_{i + 1}$ . ¿Cómo hemos de proseguir con esto?

La clave es notar la existencia de la menor $m$ tal que $y_{m} = - 1$ , donde es claro que $y_{m - 1} = 0$ . Si $m = 1$ entonces $y_{0} = x_{0} = k = 0$ , y ya hemos cubierto ese caso arriba, así que asumiremos que $m > 1$ . Tenemos que $y_{m - 2} \geq 0$ por lo que, por el lema 2,

$x_{m - 1} \geq y_{m - 1} = 0$
y como $y_{m} = y_{m - 1} - 1$ entonces $x_{m} = x_{m - 1} \geq 0$ . Esto implica que

$\begin{aligned} z_{m} & = c - r + b + x_{m} a \\ \geq c - r + b \\ > c \end{aligned}$
por lo que para todo $j > m$ se tiene que $x_{j + 1} = x_{j} - 1$

$z_{m + x_{m} + 1} = c - r + b - a$
y tenemos que $y_{m + x_{m} + 1} = x_{m + x_{m} + 1} = - 1$ , lo que muestra que

$\begin{aligned} f (n) & = f (z_{m + x_{m} + 1}) \\ = f (c - r + b - a) \\ = c - r + b - 2 a . \end{aligned}$

Juntando todo

Vaya, después de arduo trabajo hemos mostrado la periodicidad de $f$ . Lo que falta únicamente, es usar esto para hacer una conclusión sobre los puntos fijos. Notemos que los únicos valores de $f$ en el dominio $[1, c]$ son $c - r + b - 2 a$ para $0 \leq r < b - a$ , así que solo estos valores pueden ser puntos fijos de $f$ . De hecho, cada uno de esos valores es un punto fijo si y solo si podemos encontrar una $k \geq 0$ tal que

$c - r - k (b - a) = c - r + b - 2 a$ , lo cual sucede si y sólo si $(k + 1) (b - a) = a$ , o bien justo cuando $b - a ∣ a$ , por lo que si $b - a$ divide a $a$ , todos nuestros $b - a$ valores son puntos fijos, y si $b - a$ no divide a $a$ , ningún valor es un punto fijo. Hemos concluido entonces.

Antes de regresar a la cuarentena

Espero que hayan pasado un rato agradable pensando en este problema, y espero que hayan entendido 4 lecciones:

Quédate en casa
Quédate en casa
Quédate en casa
Es una buena idea usar residuos y secuencias jugando con enteros.

Con esto me despido y, ¡hasta la próxima!

Casos extremos