Seminario de Resolución de Problemas: Vectores en geometría

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

Anteriormente, comenzamos esta serie de entradas de geometría platicando de algunas técnicas euclideanas o sintéticas que se pueden usar para resolver problemas en el plano. Después, tomamos herramientas de la geometría analítica, las cuales nos permiten poner problemas en términos de coordenadas y ecuaciones. Lo que haremos ahora es ver varios ejemplos del uso de vectores en geometría.

A diferencia de la geometría analítica, cuando hablamos de soluciones por vectores estamos hablando de aquellas que aprovechan la estructura de espacio vectorial en $\mathbb{R}^2$. En otras palabras, usamos argumentos en los cuales pensamos a los puntos del plano como vectores, los cuales tienen una dirección y una magnitud. Los vectores tienen operaciones de suma y de producto por un escalar. Además, tienen producto punto, norma y transformaciones dadas por matrices. Apenas tocaremos la superficie del tipo de teoría que se puede usar. Un buen curso de álgebra lineal te puede dar más herramientas para resolver problemas geométricos.

Interpretar puntos como vectores

Pongamos un origen $O$ en el plano. A cada punto $P$ le corresponden ciertas coordenadas dadas por parejas de reales $(x,y)$, que identificaremos con $P$. Al origen le corresponden las coordenadas $(0,0)$. Si tenemos otro punto $Q=(w,z)$, entonces su suma es el vector $P+Q=(x+w,y+z)$. Si tomamos un real $r$, el vector $rP$ es el vector de coordenadas $(rx,ry)$.

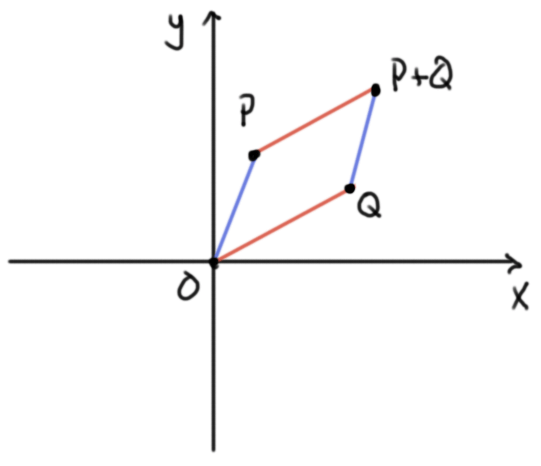
Suma de vectores
Suma de vectores

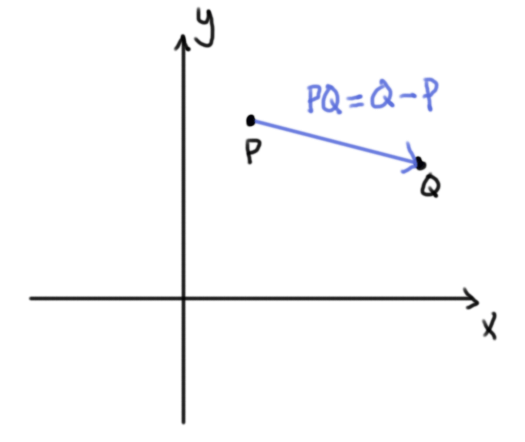
La suma $P+Q$ se puede encontrar mediante la ley del paralelogramo: los puntos $O,P,P+Q,Q$ hacen un paralelogramo en ese orden cíclico. La resta $Q-P$ está definida por $Q+(-1)P$, y la llamamos el vector $PQ$. Geométricamente coincide con el vector que va «de $P$ a $Q$». Observa que el orden es importante y que $OP=P$.

Resta de vectores
Resta de vectores

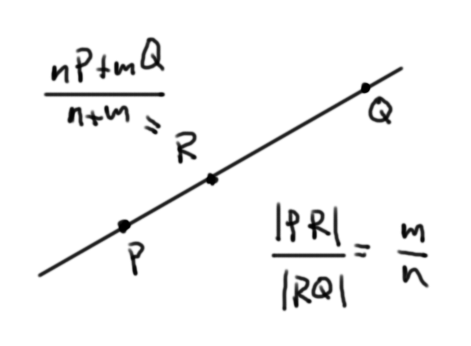
Proposición (de la razón). Si tenemos dos puntos $P$ y $Q$ distintos y $m,n$ son reales, entonces podemos encontrar al único punto $R$ en la recta por $P$ y $Q$ tal que $$\frac{PR}{RQ}=\frac{m}{n}$$ así: $$R=\frac{n}{m+n}P + \frac{m}{m+n} Q.$$

Punto en una recta con cierta razón
Punto en una recta con cierta razón

Veamos dos problemas en los que se usan estas ideas de vectores en geometría, en particular, la proposición de la razón.

Problema. En el triángulo $ABC$ se toman puntos $D,E,F$ sobre los segmentos $BC,CA,AB$ tales que $\frac{BD}{DC}=\frac{CE}{EA}=\frac{AF}{FB}=\frac{1}{4}$. Muestra que $ABC$ y $DEF$ tienen el mismo gravicentro.

Sugerencia pre-solución. Encuentra una fórmula en términos vectoriales para el gravicentro de un triángulo $ABC$.

Solución. Tomemos un triángulo $PQR$ y pensemos a sus vértices como vectores. Afirmamos que su gravicentro $X$ es el punto correspondiente a $\frac{P+Q+R}{3}$ Demostraremos esto.

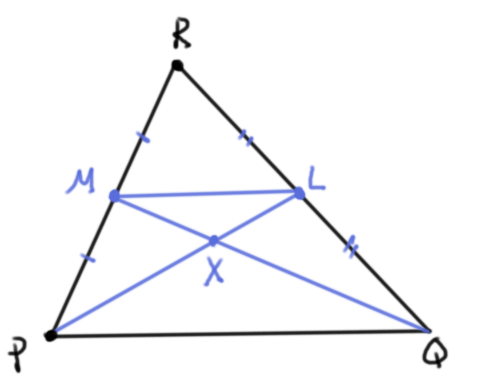
El gravicentro está a un tercio del punto medio hacia el vértice correspondiente
Razón del gravicentro en la mediana

Primero haremos un argumento de geometría sintética. El gravicentro es por definición el punto de intersección de las medianas de un triángulo. Si $L$ es el punto medio de $QR$ y $M$ es el punto medio de $RP$, entonces $X$ es el punto de intersección de $PL$ y $QM$. Tenemos que $$\frac{RL}{LQ}=1=\frac{RM}{MP},$$ así que por el teorema de Tales se tiene que la recta por $L$ y $M$ es paralela al lado $PQ$, y $\frac{LM}{PQ}=\frac{1}{2}$. Esto muestra que los triángulos $XLM$ y $XPQ$ son semejantes en razón $1$ a $2$. Por lo tanto, $\frac{LX}{XP}=\frac{1}{2}$.

Ahora hagamos el argumento vectorial, pensando a los puntos como vectores. El punto $L$ está a la mitad de $QR$, así que por la proposición de la razón, $$L=\frac{Q+R}{2}.$$ El punto $X$ cumple $\frac{LX}{XP}=\frac{1}{2}$, así que de nuevo por la proposición de la razón.
\begin{align*}
X&=\frac{2L+P}{2+1}\\
&=\frac{Q+R+P}{3}\\
&=\frac{P+Q+R}{3}.
\end{align*}

Esto es el resultado auxiliar que queríamos mostrar. Regresemos al problema.

De acuerdo al resultado auxiliar, el gravicentro de $ABC$ es $$G:=\frac{A+B+C}{3}.$$ Usando una vez más la proposición de la razón, los puntos $D$, $E$ y $F$ los podemos calcular como sigue:
\begin{align*}
D&=\frac{4B+C}{4+1}=\frac{4B+C}{5}\\
E&=\frac{4C+A}{4+1}=\frac{4C+A}{5}\\
F&=\frac{4A+B}{4+1}=\frac{4A+B}{5}.
\end{align*}

De esta forma, el gravicentro $G’$ de $DEF$ lo podemos encontrar como sigue:
\begin{align*}
G’&=\frac{D+E+F}{3}\\
&=\frac{\frac{4B+C}{5}+\frac{4C+A}{5}+\frac{4A+B}{5}}{3}\\
&=\frac{A+B+C}{3}\\
&=G.
\end{align*}

Esto termina la solución del problema.

$\square$

Problema. En el paralelogramo $ABCD$ el punto $F$ es el punto medio de $CD$. Muestra que el segmento $AF$ corta a la diagonal $BD$ en un punto $E$ tal que $\frac{DE}{DB}=\frac{1}{3}$.

Sugerencia pre-solución. Hay varias formas de hacer las cuentas en este problema, pero el uso de una notación adecuada te hará simplificar muchas operaciones.

Solución. Pensemos a los puntos de la figura como vectores. Coloquemos al punto $A$ en el origen. El punto $C$ está dado por $B+D$, de modo que $$F:=\frac{C+D}{2}=\frac{B+2D}{2}.$$

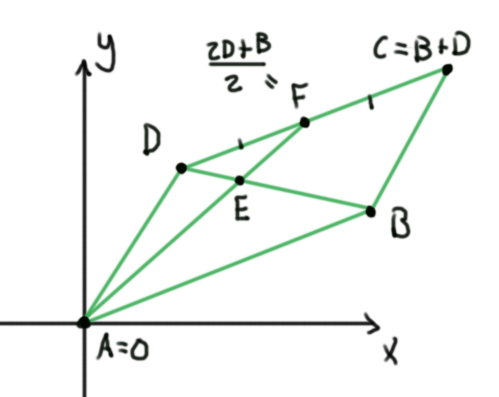
Vectores en geometría: problema de paralelogramo
Figura auxiliar para problema de paralelogramo

Para encontrar al punto $E$, notemos que está en las rectas $AF$ y $BD$. De esta forma, deben existir reales $r$ y $s$ tales que $$E=rF$$ y $$E=sB+(1-s)D.$$ Expresando $F$ en términos de $B$ y $D$ en la primer ecuación, tenemos que $$E=\frac{rB+2rD}{2}=\frac{rB}{2}+rD.$$ De ambas expresiones para $E$, concluimos que
\begin{align*}
s=\frac{r}{2}\\
1-s=r.
\end{align*}

Este sistema de ecuaciones tiene solución $r=\frac{2}{3}$, $s=\frac{1}{3}$, y por lo tanto $E=\frac{B+2D}{3}$. De aquí se obtiene $\frac{DE}{EB}=\frac{1}{2}$, o bien $\frac{DE}{DB}=\frac{DE}{DE+EB}=\frac{1}{3}$, como queríamos mostrar.

$\square$

Producto punto, norma y ángulos

Para dos vectores $P=(x,y)$ y $Q=(w,z)$ definimos su producto punto como la cantidad $P\cdot Q = xw+yz$. El productos puntos es:

  • Conmutativo: $P\cdot Q = Q\cdot P$
  • Abre sumas: $P\cdot (Q+R)=P\cdot Q + P\cdot R$
  • Saca escalares: $(rP)\cdot Q = r(P\cdot Q)$.

La norma de $P$ se define como $\norm{P}=\sqrt{P\cdot P}$, y coincide con la distancia de $P$ al origen. La norma de $PQ$ es entonces $\norm{PQ}=\sqrt{(Q-P)\cdot (Q-P)}$ y coincide con la distancia de $P$ a $Q$.

El ángulo entre dos vectores $PQ$ y $RS$ se define como el ángulo cuyo coseno es $$\frac{PQ \cdot RS}{\norm{PQ}\norm{RS}},$$ y coincide precisamente con el ángulo (orientado) geométrico entre las rectas $PQ$ y $RS$. De esta forma, las rectas $PQ$ y $RS$ son perpendiculares si y sólo si el producto punto $PQ\cdot RS$ es cero.

Problema. Sea $ABC$ un triángulo con sus vértices pensados como vectores. Sean $H$ y $O$ su ortocentro y circuncentro respectivamente. Supongamos que el circuncentro $O$ está en el origen. Muestra que $H=A+B+C$.

Sugerencia pre-solución. Trabaja hacia atrás. Define al punto $A+B+C$ y ve que las rectas que unen a los vértices con este punto en efecto son alturas. Para calcular los ángulos, usa el producto punto y sus propiedades.

Solución. Como el circuncentro equidista de $A$. $B$ y $C$, tenemos que $$\norm{A}=\norm{B}=\norm{C}.$$ Tomemos el punto $H’=A+B+C$.

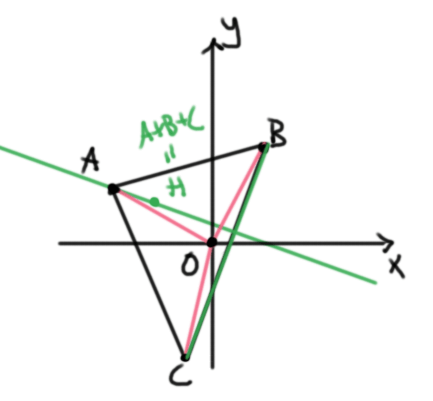
Vectores en geometría para encontrar el ortocentro
Ortocentro con vectores

Calculemos el ángulo entre las rectas $BC$ y $AH’$, haciendo su producto punto:
\begin{align*}
BC\cdot AH’ &= (C-B)\cdot (H’-A)\\
&=(C-B)\cdot(C+B)\\
&=C\cdot C + C\cdot B – B\cdot C – B\cdot B\\
&=\norm{C}^2 – \norm{B}^2\\
&=0.
\end{align*}

Observa que estamos usando la linealidad y conmutatividad del producto punto. Al final usamos que $A$ y $C$ tienen la misma norma.

Esto muestra que la recta $AH’$ es la altura al lado $BC$. De manera análoga, $BH’$ y $CH’$ son las alturas a los lados $CA$ y $AB$ respectivamente. Por lo tanto, $H’$ es el ortocentro, así que $H=A+B+C$.

$\square$

Cualquier triángulo $ABC$ en el plano se puede trasladar para que su circuncentro $O$ quede en el origen. El ortocentro estará en $H=A+B+C$ y el gravicentro, como vimos antes, en $G=\frac{A+B+C}{3}$, que es un múltiplo escalar de $H$. Por lo tanto, $O$, $H$ y $G$ están alineados. Acabamos de demostrar con vectores en geometría un clásico resultado euclideano.

Teorema (recta de Euler). En cualquier triángulo $ABC$, el circuncentro $O$, el gravicentro $G$ y el ortocentro $H$ están alineados. Además, $$\frac{OG}{GH}=\frac{1}{2}.$$

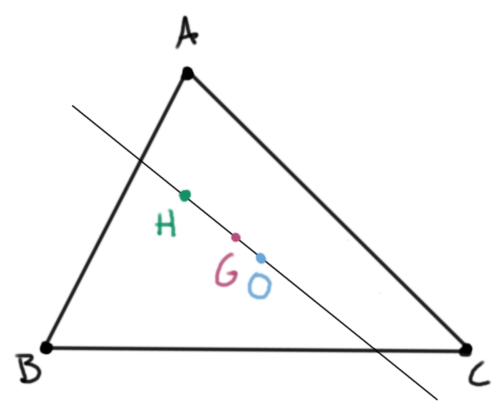
Teorema de la recta de Euler
Teorema de la recta de Euler

Si el circuncentro no está en el origen, ahora podemos usar el teorema de la recta de Euler y la proposición de la razón para concluir que $G=\frac{2O+H}{3}$. Usando que $G=\frac{A+B+C}{3}$, obtenemos el siguiente corolario

Corolario. Sea $ABC$ un triángulo en el plano, $H$ su ortocentro y $O$ su circuncentro. Entonces al pensar a los puntos como vectores tenemos que $$A+B+C=2O+H.$$

Más problemas

Puedes encontrar más problemas del uso de vectores en geometría en la sección 8.3 del libro Problem Solving through Problems de Loren Larson.

Álgebra Superior II: Continuidad y diferenciabilidad de polinomios reales

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

Al inicio de esta unidad, hablamos de las propiedades algebraicas de $\mathbb{R}[x]$, definimos sus operaciones y argumentamos por qué se puede usar la notación de potencias. Luego hablamos de las propiedades aritméticas de los polinomios cuando hablamos de divisibilidad, máximo común divisor y factorización en irreducibles. Vimos una aplicación de esto a la solución de desigualdades. Lo que queremos hacer ahora es pensar a los polinomios como funciones de $\mathbb{R}$ en $\mathbb{R}$ y entender las propiedades analíticas que tienen, es decir en términos de cálculo. Nos interesa saber qué les sucede cuando su entrada es grande, la continuidad y la diferenciabilidad de polinomios.

Estas propiedades tienen consecuencias algebraicas importantes. La continuidad de polinomios nos permite encontrar raíces reales en ciertos intervalos. La diferenciabilidad de polinomios nos ayuda a encontrar la multiplicidad de las raíces. Supondremos que manejas conocimientos básicos de cálculo y de manipulación de límites, pero de cualquier forma recordaremos algunas definiciones y daremos esbozos de la demostración de algunos resultados.

Límites a reales y límites a infinito

Recordemos dos definiciones de cálculo, que se aplican para funciones arbitrarias definidas en todos los reales.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función y $a, b$ reales. Decimos que $$\lim_{x\to a} f(x) = b$$ si para todo $\epsilon >0$ existe un $\delta > 0 $ tal que cuando $0<|x-a|<\delta$, entonces $|f(x)-b|<\epsilon$. En palabras, decimos que el límite de $f$ cuando $x$ tiende a $a$ es $b$.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función. Decimos que $$\lim_{x\to \infty} f(x) = \infty$$ si para todo $M>0$ existe un $r > 0 $ tal que cuando $x>r$, entonces $f(x)>M$. En palabras, decimos que el límite de $f$ cuando $x$ tiende a infinito es infinito.

De manera análoga se pueden definir límites cuando $x$ tiende a menos infinito, y definir qué quiere decir que el límite sea menos infinito. La siguiente proposición se prueba en textos de cálculo.

Proposición (propiedades de límites). Sean $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ funciones y $a$, $b$, $c$ reales. Si $$\lim_{x\to a} f(x) = b \quad \text { y } \quad \lim_{x\to a} g(x)= c,$$ entonces:

  • «El límite de la suma es la suma de los límites», en símbolos, $$\lim_{x\to a} (f+g)(x) = b+c.$$
  • «El límite del producto es el producto de los límites», en símbolos, $$\lim_{x\to a} (fg)(x)=bc.$$

La proposición anterior es sólo para cuando los límites son reales. Hay resultados para cuando algunos de los límites son infinitos, pero en general hay que tener cuidado.

La primer propiedad analítica de los polinomios es saber cómo es su comportamiento cuando $x$ se hace infinito o menos infinito. Si el polinomio es constante, entonces este límite es simplemente su valor en cualquier punto. Para polinomios de grado mayor o igual a $1$, su comportamiento queda resumido en la siguiente proposición.

Proposición (límites a infinito). Tomemos al polinomio $p(x)$ en $\mathbb{R}[x]$ dado por $$p(x)=a_0+a_1x+a_2x^2+\ldots+a_nx^n,$$ en donde $n\geq 1$ y $a_n\neq 0$.

  • Si $a_n>0$ y $p(x)$ es de grado par entonces $$\lim_{x\to \infty} p(x) = \lim_{x\to-\infty} p(x)= \infty,$$
  • Cuando $a_n>0$ y $p(x)$ es de grado impar entonces $$\lim_{x\to \infty} p(x) = \infty \quad \text { y } \quad \lim_{x\to -\infty} p(x)=-\infty$$
  • Si $a_n<0$ y $p(x)$ es de grado par entonces $$\lim_{x\to \infty} p(x) = \lim_{x\to-\infty} p(x)= -\infty,$$
  • Cuando $a_n<0$ y $p(x)$ es de grado impar entonces $$\lim_{x\to \infty} p(x) = -\infty \quad \text { y } \quad \lim_{x\to -\infty} p(x)=\infty.$$

Demostración. Vamos a hacer una de las demostraciones. Mostraremos que para cuando $a_n>0$ y el grado es par, entonces $$\lim_{x\to \infty} p(x) = \infty.$$ Las demás se siguen haciendo cambios de signo cuidadosos y usando que una potencia impar de un real negativo es un real negativo, y una potencia par es siempre un real positivo. Pensar en estas demostraciones queda como tarea moral.

Tomemos entonces $p(x)$ un polinomio de grado par y con coeficiente principal $a_n>0$. Intuitivamente, tenemos que mostrar que si $x$ es muy grande, entonces $p(x)$ es tan grande como queramos. Tomemos un real $M>0$. Como haremos $x$ grande, podemos suponer que $x>1$.

Como el término $a_nx^n$ es positivo, basta mostrar como resultado auxiliar que si $x$ es suficentemente grande, entonces $$a_nx^n >M+|a_0+a_1x+\ldots+a_{n-1}x^{n-1}|,$$ ya que si esto sucede, tendríamos que:
\begin{align*}
a_nx^n&>M+|a_0+a_1x+\ldots+a_{n-1}x^{n-1}|\\
&=M+|-a_0-a_1x-\ldots-a_{n-1}x^{n-1}|\\
&>M-a_0-a_1x-\ldots-a_{n-1}x^{n-1},
\end{align*}

y de aquí, pasando todo excepto a $M$ a la izquierda, tendríamos $p(x)>M$.

Para probar el resultado auxiliar, tomemos $A$ como el máximo de los valores absolutos $|a_0|,\ldots,|a_{n-1}|$. Por la desigualdad del triángulo y usando $x>1$ tenemos que

\begin{align*}
M+|a_0&+a_1x+\ldots+a_{n-1}x^{n-1}|\\
&\leq M+|a_0|+|a_1 x| + \ldots + |a_{n-1}x^{n-1}|\\
&\leq M+A(1+x+\ldots+x^{n-1})\\
&< M+nA\\
&<(M+nA)x^{n-1}
\end{align*}

De esta forma, para mostrar nuestra desigualdad auxiliar basta mostrar que para $x$ suficientemente grande, tenemos que $(M+nA)x^{n-1}<a_nx^n$. Pero como $x>0$, esta desigualdad es equivalente a $x>\frac{M+nA}{a_n}$.

Recapitulando, para cualquier $M>0$, si $x>\frac{M+nA}{a_n}$, entonces $p(x)>M$. Esto termina la demostración.

$\square$

Podemos usar la proposición anterior para comparar polinomios cuando su variable tiende a infinito.

Ejemplo. Mostraremos que existe una $M$ suficientemente grande tal que si $x>M$, entonces $$\frac{1}{2}x^7-x^6-x-1>x^6+1000x^5+1000000.$$ Pasando todo del lado izquierdo, nos queda la desigualdad equivalente $$\frac{1}{2}x^7-2x^6-1000x^5-x-999999>0.$$ Aquí tenemos un polinomio $p(x)$ de grado impar y coeficiente principal positivo. Por la proposición anterior, $\lim_{x\to \infty} p(x) = \infty$, de modo que la $M$ que estamos buscando existe.

$\triangle$

Continuidad de polinomios

Antes de llegar a diferenciabilidad de polinomios, haremos un paso intermedio. Recordemos otra definición de cálculo.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función y $a$ un real. Decimos que $f$ es continua en $a$ si $$\lim_{x\to a} f(x) = f(a).$$ Decimos que $f$ es continua si es continua en todo real.

Por la proposición de propiedades de límites, la suma o producto de funciones continuas es continua. Las funciones constantes son continuas. La función identidad $I:\mathbb{R}\to \mathbb{R}$ dada por $I(x)=x$ es continua. Estos tres hechos nos ayudan a demostrar que todos los polinomios son funciones continuas sin tener que recurrir a la definición de límite.

Teorema. Cualquier polinomio $p(x)$ en $\mathbb{R}[x]$ pensado como una función $p:\mathbb{R}\to \mathbb{R}$ es una función continua.

Demostración. Supongamos que $p(x)$ está dado por $$p(x)=a_0+a_1x+\ldots+a_nx^n.$$

Para toda $i$ de $0$ a $n$ tenemos que la función $x\mapsto a_i$ es constante y por lo tanto es continua. Si $i>0$, la función $x\mapsto x^i$ es producto de $i$ veces la identidad consigo misma. Como la identidad es continua y producto de continuas es continua, entonces $x\mapsto x^i$ es continua.

De nuevo, usando que producto de funciones continuas es continua, tenemos que $x\mapsto a_ix^i$ es una función continua. De esta forma, $p(x)$ es la suma de $n+1$ funciones continuas, y por lo tanto es una función continua.

$\square$

El resultado anterior nos ayuda a usar teoremas versátiles de cálculo en nuestro estudio de polinomios. Recordemos el teorema del valor intermedio.

Teorema (del valor intermedio). Sea $f:\mathbb{R}\to \mathbb{R}$ una función continua. Sean $a<b$ dos reales. Entonces entre $a$ y $b$, la función $f$ toma todos los valores entre $f(a)$ y $f(b)$.

Veamos cómo el teorema del valor intermedio nos permite encontrar raíces de polinomios.

Problema 1. Muestra que el polinomio $p(x)=x^7-5x^5+x^2+3$ tiene por lo menos una raíz en el intervalo $[0,2]$.

Solución. Al evaluar al polinomio en cero, obtenemos $p(0)=3$. Al evaluarlo en $2$, obtenemos
\begin{align*}
p(2)&=2^7-5\cdot 2^5+x^2 + 3\\
&=128-160+4+3\\
&=-25.
\end{align*}

Como los polinomios son funciones continuas, podemos aplicar el teorema del valor intermedio. Concluimos que $p(x)$ toma todos los valores de $-25$ a $2$ en el intervalo $[0,2]$. En particular, existe un real $r$ en $[0,2]$ tal que $p(r)=0$.

$\triangle$

El teorema del valor intermedio nos ayuda a demostrar que un polinomio tiene una raíz en cierto intervalo. Sin embargo, no es de tanta utilidad para decir exactamente cuál es esa raíz. Es un resultado existencial en vez de ser constructivo. Veamos un ejemplo más, que muestra una proposición que quedó pendiente en una entrada anterior.

Problema 2. Sea $p(x)$ un polinomio cuadrático, mónico e irreducible en $\mathbb{R}[x]$. Muestra que $p(r)>0$ para todo real $r$.

Solución. Procedamos por contradicción. Supongamos que $p(r)\leq 0$ para algún real $r$.

Como $p(x)$ es mónico, su coeficiente principal es $1$, que es positivo. Como $p(x)$ es cuadrático, es de grado par. Por la proposición de límites a infinito, existe un real $t>r$ tal que $p(t)>0$. Por el teorema del valor intermedio, existiría un real $s$ en el intervalo $[r,t]$ tal que $p(s)=0$. Pero esto es imposible, pues entonces por el teorema del factor $x-s$ divide a $p(x)$ y esto contradice que $p(x)$ es irreducible.

$\triangle$

Como muestra el problema anterior, se pueden combinar los límites de polinomios a infinito y menos infinito, y sus propiedades de continuidad. Otra aplicación es mostrar que todo polinomio de grado impar tiene por lo menos una raíz real. Esto se verá en otra entrada.

Por supuesto, otros resultados de continuidad también se pueden usar en todos los polinomios, como el teorema del valor extremo. Aplicándolo directamente, concluimos lo siguiente.

Proposición. Sean $a<b$ reales y $p(x)$ un polinomio en $\mathbb{R}$. Entonces $p(x)$ está acotado en el intervalo $[a,b]$ y existen reales $r$ y $s$ en dicho intervalo tales que $p(r)$ y $p(s)$ son el mínimo y máximo de $p(x)$ en $[a,b]$, respectivamente.

Diferenciabilidad de polinomios

Es momento de hablar de diferenciabilidad de polinomios. Recordemos una última definición de cálculo.

Definición. Sea $f:\mathbb{R}\to \mathbb{R}$ una función. Decimos que $f$ es diferenciable en $a$ si el límite $$\lim_{h\to 0} \frac{f(a+h)-f(a)}{h}$$ existe. En este caso, a ese límite lo denotamos por $f'(a)$. Una función es diferenciable si es diferenciable en todo real. A la función $f’:\mathbb{R}\to \mathbb{R}$ le llamamos la derivada de $f$.

Al igual que en el caso de continuidad, la suma y producto de funciones diferenciales es diferenciable. Si $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ son diferenciables, entonces la derivada de $f+g$ está dada por $$(f+g)'(x)=f'(x)+g'(x)$$ y la derivada de $fg$ está dada por la regla de la cadena $$(fg)'(x)=f'(x)g(x)+f(x)g'(x).$$

Las funciones constantes son diferenciables, y su derivada es la función constante $0$. La función identidad es diferenciable, y su derivada es la función constante $1$. Esto es sencillo de mostrar y queda como tarea moral.

Proposición. Sea $n\geq 1$ un entero. El polinomio $p(x)=x^n$ es diferenciable, y su derivada es la función $p'(x)=nx^{n-1}$.

Demostración. Haremos la prueba por inducción. Si $n=1$, el polinomio es $p(x)=x$, y su derivada es $p'(x)=1=1\cdot x^0$, como queremos. Supongamos que el resultado es cierto para el entero $n\geq 1$ y tomemos $p(x)=x^{n+1}=x^n\cdot x$. Por hipótesis inductiva, $x\mapsto x^n$ es diferenciable. Como $p(x)$ es producto de dos funciones diferenciables, entonces es diferenciable.

Usando la regla de la cadena, la hipótesis inductiva de la fórmula y la derivada de $x\mapsto x$, tenemos que $$p'(x)=(nx^{n-1})(x)+(x^n)(1)=(n+1)x^n.$$ Esto termina la demostración.

$\square$

Con todos estos ingredientes podemos mostrar la diferenciabilidad de todos los polinomios. Los detalles quedan como tarea moral.

Teorema (diferenciabilidad de polinomios). Sea $p(x)$ un polinomio en $\mathbb{R}[x]$ dado por $$p(x)=a_0+a_1x+\ldots+a_nx^n,$$ Entonces $p(x)$ pensado como función es diferenciable y su derivada es un polinomio. Si $p(x)$ es constante, su derivada es el polinomio $0$. En otro caso, su derivada es el polinomio $$a_1+2a_2x+3a_3x^2+\ldots+na_nx^{n-1}.$$

Ejemplo. El polinomio $x^7+3x^2-1$ es diferenciable. Su derivada es el polinomio $7x^6+6x$.

$\triangle$

Ya que sabemos que los polinomios son diferenciables, podemos usar todas las herramientas de cálculo diferencial, como:

No profundizaremos en esto, pues es el contenido de un buen curso de cálculo, o bien de material de algún texto en el área, como el libro de Cálculo de Spivak.

A nosotros nos interesa una consecuencia algebraica de que los polinomios tengan derivada. Como la derivada de un polinomio es otro polinomio, entonces la derivada es diferenciable. Por ello, un polinomio $p(x)$ se puede derivar iteradamente tantas veces como se quiera. Al polinomio obtenido de derivar $n$ veces le llamamos la $n$-ésima derivada y lo denotamos por $p^{(n)}(x)$. En la siguiente entrada veremos cómo la repetida diferenciabilidad de polinomios nos ayuda a detectar la multiplicidad de sus raíces.

Más adelante…

En la siguiente sección nos encargaremos de realizar varios problemas para repasar las definiciones y propiedades que acabamos de enunciar, y posteriormente ocuparemos todo lo aprendido para explotar el conocimiento que tenemos de los polinomios.

En particular, nos será útil el concepto de diferenciabilidad pues con este podemos dar una definición precisa de lo que significa que la raíz de un polinomio sea múltiple.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Estudia el resto de los casos de la proposición de límites de polinomios cuando la entrada va a menos infinito y a infinito.
  2. Muestra usando la definición de límite que las funciones constantes y la función identidad son continuas.
  3. Demuestra por definición que las funciones constantes son diferenciables y que su derivada es la función constante $0$. Demuestra por definición que la función identidad es diferenciable y que su derivada es la función constante $1$.
  4. Muestra que existe un real $x$ en el cual los polinomios $p(x)=x^5+x^3+x$ y $q(x)=100x^4+10x^2$ son iguales. Sugerencia. Reescribe esta igualdad en términos de encontrar una raíz de un sólo polinomio.
  5. Completa los detalles del teorema de diferenciabilidad de polinomios.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Álgebra Lineal I: Eigenvalores y eigenvectores de transformaciones y matrices

Por Leonardo Ignacio Martínez Sandoval

10 respuestas

Introducción

En entradas anteriores ya establecimos los fundamentos para hablar de determinantes. Dimos su definición para el caso de vectores y el caso de matrices/transformaciones lineales. Enunciamos y demostramos varias de sus propiedades. Luego dedicamos toda una entrada a ver formas de calcularlos. Finalmente, vimos que nos pueden ayudar para entender mucho mejor a los sistemas de ecuaciones lineales. Entender bien estos conceptos te será de gran utilidad en tu formación matemática.

Además, los determinantes son un paso natural en uno de nuestros objetivos del curso: entender por qué las matrices simétricas reales son diagonalizables. Recuerda que una matriz $A$ en $M_n(F)$ es diagonalizable si existe una matriz diagonal $D$ y una matriz invertible $P$, ambas en $M_n(F)$, de modo que $$A=P^{-1}DP.$$

Lo que haremos en esta entrada es hablar de esos valores que aparecen en la matriz diagonal $D$ en el caso de que $A$ sea diagonalizable. Resulta que estos valores están relacionados con una pregunta muy natural en términos de lo que le hace la matriz a ciertos vectores. Y mejor aún, como veremos, hay un método para encontrar estos valores por medio de un determinante. Vamos poco a poco.

Eigenvalores y eigenvectores para transformaciones lineales

Sea $V$ un espacio vectorial sobre un campo $F$ y sea $T:V\to V$ una transformación lineal. Para fijar ideas, pensemos en $\mathbb{R}^n$ por el momento. A veces, $T$ simplemente la cambia la magnitud a un vector, sin cambiarle la dirección. Es decir, hay algunos vectores para los cuales $T$ se comporta simplemente como la multiplicación por un escalar. En símbolos, hay vectores $v$ tales que existe un valor $\lambda$ tal que $T(v)=\lambda v$.

Por supuesto, al vector $0$ siempre le pasa esto, pues como $T$ es lineal, se tiene que $T(0)=0=\lambda\cdot 0$ para cualquier escalar $\lambda$. Resulta que cuando se estudian estos vectores y escalares especiales, lo más conveniente es quitar al vector $0$ de la discusión. Estas ideas llevan a la siguiente definición.

Definición. Un eigenvalor de una transformación lineal $T:V\to V$ es un escalar $\lambda$ tal que $\lambda \text{id} – T$ no es invertible. En otras palabras, $\lambda$ es un escalar tal que existe un vector no cero en el kernel de $\lambda \text{id} – T$. A un vector $v\neq 0$ en $V$ tal que $$(\lambda \text{id} – T)v=0,$$ se le conoce como un eigenvector de $T$.

En otras palabras, $v$ es un eigenvector correspondiente a $T$ si $v$ no es cero y $T(v)=\lambda v$. A los eigenvalores y eigenvectores de $T$ también se les conoce en la bibliografía como valores propios y vectores propios de $T$.

Observa que si al conjunto de eigenvectores para un eigenvalor $\lambda$ le agregamos el vector $0$, entonces obtenemos el kernel de una transformación lineal, que sabemos que es un subespacio vectorial.

Veamos un par de ejemplos para que queden más claras las ideas.

Ejemplo 1. Consideremos a la transformación lineal $T:\mathbb{R}^3\to \mathbb{R}^3$ dada por $$T(x,y,z)=(-2x+15y+18z,3y+10z,z).$$

Observa que
\begin{align*}
T(1,0,0)&=(-2,0,0)\\
&=-2(1,0,0),
\end{align*}

que
\begin{align*}
T(-19,-5,1)&=((-2)(-19)+15(-5)+18,3(-5)+10, 1)\\
&=(28+75-18,-15+10,1)\\
&=(-19,-5,1),
\end{align*}

y que

\begin{align*}
T(3,1,0)&=(-6+15,3,0)\\
&=(9,3,0)\\
&=3(3,1,0).
\end{align*}

Estas igualdades muestran que $(1,0,0)$ es un eigenvector de $T$ con eigenvalor $-2$, que $(-19,-5,1)$ es un eigenvector de $T$ con eigenvalor $1$ y $(3,1,0)$ es un eigenvector de $T$ con eigenvalor $3$.

$\triangle$

Ejemplo 2. Consideremos al espacio vectorial $\mathbb{R}[x]$ de polinomios con coeficientes reales. Tomemos la transformación lineal $T$ que manda a un polinomio a su segunda derivada. ¿Quiénes son los eigenvalores y eigenvectores de $T$?

Para que $p$ sea un eigenvector con eigenvalor $\lambda$, tiene que suceder que $$p»=T(p)=\lambda p.$$

Como $p$ no es el vector cero, tiene un cierto grado. Si $\lambda \neq 0$, entonces la igualdad anterior no puede suceder, pues si $p$ es de grado mayor o igual a $2$, entonces el grado de $p»$ es menor al de $\lambda p$, y si el grado de $p$ es $0$ ó $1$, su segunda derivada es $0$, y no puede pasar $\lambda p = 0$. Así, el único eigenvalor que puede tener $T$ es $\lambda = 0$. Observa que sí es válido que los eigenvalores sean cero (los eigenvectores no).

Cuando $\lambda = 0$, tiene que pasar que $p»$ sea $0\cdot p$, es decir, el polinomio cero. Los únicos polinomios tales que su derivada es cero son los constantes y los lineales. Pero el polinomio cero por definición no es eigenvector.

Así, la respuesta final es que el único eigenvalor de $T$ es $0$, y sus eigenvectores correspondientes son los polinomios constantes distintos de cero, y los polinomios lineales.

$\triangle$

Eigenvalores y eigenvectores para matrices

Tenemos una definición similar para matrices. Sea $A$ una matriz en $M_n(F)$.

Definición. Un escalar $\lambda$ en $F$ es un eigenvalor de $A$ si la matriz $\lambda I_n – A$ no es invertible. En otras palabras, si existe un vector no cero $X$ en $F^n$ tal que $AX=\lambda X$. A un tal vector $X$ se le conoce como un eigenvector correspondiente al eigenvalor $\lambda$.

En otras palabras, los eigenvalores y eigenvectores de $A$ son exactamente los eigenvalores y eigenvectores de la transformación $T_A:\mathbb{F}^n\to \mathbb{F}^n$ dada por $T_A(v)=Av$.

Además, si elegimos cualquier base $B$ de un espacio de dimensión finita $V$ y $A$ es la matriz de $T$ con respecto a la base $B$, entonces para cualquier escalar $\lambda$ se tiene que $\lambda I_n – A$ es la matriz de $\lambda \text{id} – T$ con respecto a esta misma base. De aquí se deduce que los eigenvalores de $T$ son los mismos que los eigenvalores de $A$. Dos matrices que representan a $T$ difieren sólo en un cambio de base, así que obtenemos el siguiente resultado fundamental.

Proposición. Si $A$ es una matriz en $M_n(F)$ y $P$ es una matriz invertible, entonces $A$ y $P^{-1}AP$ tienen los mismos eigenvalores. En otras palabras, matrices similares tienen los mismos eigenvalores.

En el primer ejemplo tomamos la transformación lineal $T:\mathbb{R}^3\to \mathbb{R}^3$ tal que $$T(x,y,z)=(-2x+15y+18z,3y+10z,z).$$ Su matriz en la base canónica de $\mathbb{R}^3$ es $$A=\begin{pmatrix} -2 & 15 & 18\\ 0 & 3 & 10\\ 0 & 0 & 1 \end{pmatrix}.$$ En el ejemplo vimos que los eigenvalores eran $-2$, $1$ y $3$, que precisamente conciden con las entradas en la diagonal de $A$. Esto no es casualidad. El siguiente resultado muestra esto, y es una primer evidencia de la importancia de los determinantes para encontrar los eigenvalores de una matriz.

Proposición. Si $A$ es una matriz triangular (superior o inferior) en $M_n(F)$, entonces sus eigenvalores son exactamente las entradas en su diagonal principal.

Demostración. Haremos el caso para cuando $A$ es triangular superior. El otro caso queda de tarea moral.

Queremos encontrar los valores $\lambda$ para los cuales la matriz $\lambda I_n – A$ no sea invertible. La matriz $A$ es triangular superior, así que la matriz $\lambda I_n – A$ también, pues las entradas de $A$ se vuelven negativas, y luego sólo se altera la diagonal principal.

Si las entradas diagonales de $A$ son $a_{11},\ldots,a_{nn}$, entonces las entradas diagonales de $\lambda I_n -A$ son $$\lambda – a_{11},\ldots,\lambda-a_{nn}.$$

La matriz $\lambda I_n – A$ no es invertible si y sólo si su determinante es igual a cero. Como es una matriz triangular superior, su determinante es el producto de sus entradas diagonales, es decir, $$\det(\lambda I_n – A) = (\lambda – a_{11})\cdot\ldots\cdot(\lambda – a_{nn}).$$

Este producto es $0$ si y sólo si $\lambda$ es igual a alguna entrada $a_{ii}$. De esta forma, los únicos eigenvalores de $A$ son las entradas en su diagonal.

$\square$

Si $A$ es una matriz diagonalizable, entonces es semejante a una matriz diagonal $D$. Por la proposición anterior, los eigenvalores de $A$ serían entonces las entradas en la diagonal principal de $D$. Esto nos da una intuición muy importante: si acaso pudiéramos encontrar todos los eigenvalores de $A$, entonces eso podría ser un paso parcial hacia diagonalizarla.

Encontrar eigenvalores es encontrar las raíces de un polinomio

La siguiente proposición conecta eigenvalores, polinomios y determinantes.

Proposición. Sea $A$ una matriz en $M_n(F)$. Entonces la expresión $$\det(\lambda I_n – A)$$ está en $F[\lambda]$, es decir, es un polinomio en la variable $\lambda$ con coeficientes en $F$. Además, es de grado exactamente $n$.

Demostración. La fórmula para el determinante
\begin{align*}
\begin{vmatrix}
\lambda – a_{11} & -a_{12} & \ldots & -a_{1n}\\
-a_{21} & \lambda – a_{22} & \ldots & -a_{1n}\\
\vdots & & \ddots & \\
-a_{n1} & -a_{n2} & \ldots & \lambda – a_{nn}
\end{vmatrix}
\end{align*}

en términos de permutaciones nos dice que el determinante es sumas de productos de entradas de $A$. Cada una de las entradas es un polinomio en $F[\lambda]$, ya sea constante, o lineal. Como $F[\lambda]$ es cerrado bajo sumas y productos, esto prueba la primer parte de la afirmación.

Para probar que el grado es exactamente $n$, notemos que cada sumando de la expresión multiplica exactamente $n$ entradas. Como las entradas a lo mucho son de grado uno en $F[\lambda]$, entonces cada sumando es un polinomio de grado a lo más $n$. Hay una única forma que el grado sea $n$: cuando se elige la permutación identidad y entonces se obtiene el sumando $$(\lambda-a_{11})\cdot\ldots\cdot(\lambda-a_{nn}).$$

Esto termina la prueba.

$\square$

La proposición anterior nos asegura entonces que la siguiente definición tiene sentido.

Definición. Para $A$ una matriz en $M_n(F)$, el polinomio característico de $A$ es el polinomio $\chi_A(\lambda)$ en $F[\lambda]$ dado por $$\chi_A(\lambda) = \det(\lambda I_n – A).$$

De esta forma, $\lambda$ es un eigenvalor de $A$ si y sólo si es una raíz del polinomio $\chi_A(\lambda)$. Esto son buenas y malas noticias. Por un lado, nos cambia un problema de álgebra lineal a uno de polinomios, en donde a veces tenemos herramientas algebraicas que nos ayudan a encontrar raíces. Sin embargo, como se ve en cursos anteriores, también hay otros polinomios para los cuales es muy difícil encontrar sus raíces de manera exacta. Lo que salva un poco esa situación es que sí existen métodos para aproximar raíces numéricamente de manera computacional.

A pesar de la dificultad de encontrar raíces, sin duda tenemos consecuencias interesantes de esta conexión. Consideremos como ejemplo el siguiente resultado.

Proposición. Una matriz $A$ en $M_n(F)$ tiene a lo más $n$ eigenvalores distintos. Lo mismo es cierto para una transformación lineal $T:V\to V$ para $V$ un espacio vectorial de dimensión $n$.

Demostración. La matriz $A$ tiene tantos eigenvalores como raíces en $F$ tiene su polinomio característico. Como el polinomio característico es de grado exactamente $n$, tiene a lo más $n$ raíces en $F$.

La parte de transformaciones queda de tarea moral.

$\square$

Ya que encontramos los eigenvalores de una matriz o transformación, es posible que queramos encontrar uno o más eigenvectores correspondientes a ese eigenvalor. Observa que eso corresponde a encontrar una solución no trivial al sistema lineal de ecuaciones homogéneo de la forma $$(I_n-A) X = 0.$$ Para ello ya tenemos muchas herramientas, como hacer reducción Gaussiana.

Terminamos esta entrada con un ejemplo de cómo encontrar los valores propios y vectores propios en un caso concreto.

Problema. Encuentra los eigenvalores de la matriz $$A=\begin{pmatrix}1 & 0 & 0\\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}$$ considerándola como:

  • Una matriz en $M_3(\mathbb{R})$
  • Una matriz en $M_3(\mathbb{C})$.

En el caso de $M_n(\mathbb{R})$, encuentra un eigenvector para cada eigenvalor.

Solución. Para encontrar los eigenvalores, tenemos que encontrar el determinante $$\begin{vmatrix}\lambda – 1 & 0 & 0\\ 0 & \lambda & 1 \\ 0 & -1 & \lambda \end{vmatrix}.$$

Usando expansión de Laplace en la primer columna y haciendo las operaciones, obtenemos que el determinante de $\lambda I_3 – A$ es el polinomio $$(\lambda-1)(\lambda^2+1).$$

Aquí es importante la distinción de saber en qué campo estamos trabajando. Si estamos en $M_3(\mathbb{R})$, la única raíz del polinomio es $1$. Si estamos en $M_3(\mathbb{C})$, obtenemos otras dos raíces: $i$ y $-i$.

Ahora, para cuando $A$ es matriz en $M_3(\mathbb{R})$, necesitamos encontrar un eigenvector para el eigenvalor $1$. Esto equivale a encontrar una solución al sistema de ecuaciones $$(I_3-A)X=0,$$ es decir, a $$\begin{pmatrix}0 & 0 & 0\\ 0 & 1 & 1 \\ 0 & -1 & 1\end{pmatrix}X=0.$$

Una solución para este sistema es $X=(1,0,0)$. Y en efecto, $(1,0,0)$ es eigenvector de $A$ para el eigenvalor $1$ pues no es el vector cero y $$\begin{pmatrix}1 & 0 & 0\\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 + 0 + 0 \\ 0 + 0 + 0 \\ 0 + 0 + 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}.$$

$\triangle$

Observa que la matriz anterior no es diagonalizable en $M_n(\mathbb{R})$, pues si lo fuera tendría que ser semejante a una matriz diagonal $D$ con entradas $i$ y $-i$ en la diagonal, pero entonces $D$ no sería una matriz en $M_n(\mathbb{R})$. Esto nos da otra intuición con respecto a la diagonalización de una matriz: si acaso una matriz en $M_n(F)$ es diagonalizable, entonces su polinomio característico debe tener puras raíces en $F$. Esta es una condición necesaria, pero aún no es suficiente.

Más adelante…

En esta entrada definimos el concepto de eigenvalor y eigenvector para una transformación lineal y para una matriz; y vimos algunas de las propiedades que cumplen. En la siguiente entrada estudiaremos el concepto de polinomio característico utilizando los conceptos que hemos visto en esta entrada y enunciaremos (sin demostración) dos teoremas muy importantes. Luego, pondremos en práctica lo que hemos estudiado resolviendo algunos ejercicios.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • En la entrada vimos que los eigenvalores de una transformación $T$ son los eigenvalores de cualquier matriz que la represente. ¿Es cierto que los eigenvectores de $T$ son los eigenvectores de cualquier matriz que lo represente?
  • Muestra que una transformación lineal $T:V\to V$ para $V$ un espacio vectorial de dimensión $n$ tiene a lo más $n$ eigenvalores distintos.
  • Encuentra los eigenvalores de las matrices de permutación.
  • Para un real $\theta\in[0,2\pi)$ se define la matriz $$A(\theta):=\begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix}.$$ Muestra que $A(\theta)$ tiene eigenvalores reales si y sólo si $\theta=0$ \o $\theta=\pi$. Sugerencia: Encuentra el polinomio característico (que es cuadrático) y calcula su discrimintante. Si es negativo, no tiene soluciones reales.
  • Sea $A$ una matriz en $M_n(F)$. Muestra que la matriz transpuesta $^t A$ tiene los mismos eigenvalores que $A$, y de hecho, el mismo polinomio característico que $A$. Sugerencia. Recuerda que una matriz y su transpuesta tienen el mismo determinante.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Álgebra Lineal I: Problemas de cálculo de determinantes

Por Ayax Calderón

3 respuestas

Para esta entrada del blog haremos uso de las propiedades vistas en la entrada de propiedades de determinantes para facilitar las cuentas a la hora de calcular determinantes de matrices que un primera instancia podrían parecer complicadas. Asimismo, haciendo uso de estas propiedades, se demostrará el teorema de expansión de Laplace.

Problemas resueltos

Problema 1. Considera la siguiente matriz

$$A=\begin{pmatrix}
1 & 1 & 1\\
1 & 2 & 1\\
1 & 1 & 2\end{pmatrix}$$

y calcula $\det (A^{-1})$.

Solución. Como el determinante es multiplicativo, sabemos que $\det(A^{-1})=\frac{1}{\det A}$ , por lo que nos bastará con calcular $\det A$.
Es fácil ver que $\det A = 1(4-1)- 1(2-1)+1(1-2)=2-1-1=1.$
Así, $\det (A^{-1})=1$.

$\triangle$

Problema 2. Sea $A\in M_n(\mathbb{R}).$

  1. Muestra que si $n^2-n+1$ entradas de $A$ son iguales a $0$, entonces $\det A =0$.
  2. Muestra que se puede escoger $A$ de tal manera que $\det A \neq 0$ tiene $n^2-n+1$ entradas iguales.
  3. Muestra que si $n^2-n+2$ entradas de $A$ son iguales, entonces $\det A = 0$.

Demostración.

  1. Afirmamos que la matriz $A$ tiene una columna en la que todas las entradas son cero. Supongamos que cada columna de $A$ tiene a los más $n-1$ ceros, entonces la matriz $A$ tiene a lo más $n^2 -n$ ceros, lo cuál contradice nuestra hipótesis, por lo tanto existe una columna en la cuál todas las entradas son iguales a cero. Por lo tanto $\det A = 0$.
  2. Consideremos la matriz $A=[a_{ij}]$ dado por $a_{ij}=1$ si $i\neq j$ y $a_{ij}=i$ si $i=j$. De esta manera nos aseguramos de que $n^2-n+1$ entradas son iguales a $1$, pero $\det A \neq 0$, pues si sustraemos el primer renglón de cada uno de los siguientes renglones obtenemos una matriz triangular superior con entradas diagonales distintas de cero, por lo que $\det A \neq 0$.
  3. Si $A$ tiene $n^2-n+2$ entradas iguales (digamos a un número $k$), entonces $A$ tiene a lo más $n-2$ entradas distintas a $k$. Por lo tanto, a lo más $n-2$ columnas de $A$ contienen una entrada distinta de $k$, es decir, al menos dos columnas de $A$ tienen todas sus entradas iguales a $k$, entonces $\rank(A)<n$. Por consiguiente $\det A=0$.

$\square$

Teorema de Expansión de Laplace

Sea $A=[a_{ij}]\in M_n(F)$ una matriz y sea $C_{i,j}$ el cofactor de $a_{ij}$.

(a) (Expansión con respecto a una columna $j$) Para cada $j\in\{1,2,\dots , n\}$ tenemos $$ \det A = \displaystyle\sum _{i=1}^n a_{ij}C_{ij}.$$

(b) (Expansión con respecto a una columna $i$). Para cada $i\in \{1,2,\dots , n\}$ tenemos $$\det A = \displaystyle\sum _{j=1}^n a_{ij}C_{ij}.$$

Demostración. (a) Tomemos $j\in \{1,2,\dots , n\}$ fija , y sea $B=(e_1,\dots, e_n)$ la base canónica de $F^n$ y sea $C_1,\dots, C_n \in F^n$ las columnas de $A$, tales que $C_k=\displaystyle\sum_{i=1}^{n} a_{ik}e_i$ para toda $k$. Se sigue que

$$\det A = \det _{B}(C_1, \dots, C_n)=\det_B(C_1,\dots, C_{j-1}, \displastyle\sum_{i=1}^{n}a_{ij}e_i, C_{j+1},\dots C_n)$$

$$=\displaystyle\sum_{i=1}^n a_{ij}\det_B(C_1,\dots, C_{j-1}, e_i, C_{j+1},\dots , C_n ).$$

Nos falta ver que $X_{ij}:=\det_B(C_1,\dots, C_{j-1}, e_i, C_{j+1},\dots , C_n)= C_{ij}$. Mediante una serie de $n-j$ intercambios de columnas, podemos poner la $j-$ésima columna del determinante $X_{ij}$ en la última posición, y mediante una sucesión de $n-i$ intercambios de renglones podemos poner el $i-$ésimo renglón en la última posición, lo que nos da

$$X_{ij}=(-1)^{n-1+n-j}=\det \begin{pmatrix}
a_{11} & \dots & a_{i,j-1} & a_{1,j+1} & \dots & a_{1n} & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots\\
a_{n1} & \dots & a_{n,j-1} & a_{n,j+1} & \dots & a_{nn} & 0\\
a_{i1} & \dots & a_{i,j-1} & a_{i,j+1} & \dots & a_{in} & 1\end{pmatrix}.$$

El último determinante es precisamente $C_{ij}$, y como $(-1)^{n-i+n-j}=(-1)^{i+j}$ se sigue el resultado deseado.

(b) La prueba para este inciso se sigue del inciso anterior y tomando en cuenta que $\det A = \det (^tA)$.

$\square$

Problema 3. Sean $x,y,z \in \mathbb{R}$, $A=
\begin{pmatrix}
0 & y & z\\
z & x & 0\\
y & 0 & x\end{pmatrix}$

y $B=
\begin{pmatrix}
0 & z & y\\
y & x & 0\\
z & 0 & x\end{pmatrix}$. Calcula el determinante de la matriz $$C=\begin{pmatrix}y^2+z^2 & xy & xz\\
xy & x^2+z^2 & yz\\
xz & yz & x^2 + y^2\end{pmatrix}.$$

Solución. Note que $^tA=B$, entonces $\det A = \det B$. Calculemos $\det A$

$$\det A = -z(yx)+y(-zx)=-2xyz$$

Además notemos que $\begin{pmatrix}
0 & y & z\\
z & x & 0\\
y & 0 & x\end{pmatrix} \begin{pmatrix}
0 & z & y\\
y & x & 0\\
z & 0 & x\end{pmatrix} = \begin{pmatrix}y^2+z^2 & xy & xz\\
xy & x^2+z^2 & yz\\
xz & yz & x^2 + y^2\end{pmatrix} $

o bien, $AB=C$.
Así, $\det C= (\det A)^2= (-2xyz)^2 = 4x^2y^2z^2.$

$\triangle$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Procedimiento gráfico para resolver una desigualdad polinomial

Por Claudia Silva

Deja un comentario

Introducción

El objetivo de esta sección es conocer el conjunto de puntos que cumplen cierta desigualdad polinomial. Para ello, nos apoyamos de considerar al polinomio como una función, y de herramientas algebraicas para darnos idea de la gráfica de tal función, y la región en el plano correspondiente a la solución de la desigualdad.

Procedimiento para resolver desigualdades polinomiales

Primero, explicación breve del procedimiento

Luego, un ejemplo de graficación y solución a una desigualdad polinomial. Olvidé mencionar que, finalmente, la solución, observando la gráfica, es $S=\{x \in \mathbb{R} | f(x) \geq 0 \}= (-\infty,-1) \cup \{0\} \cup [2,\infty)$.

Finalmente, otro ejercicio de encontrar una solución de una desigualdad polinomial:

Más adelante…

Cómo mencionamos en las entradas pasadas, la siguiente tarea que nos concierne es estudiar las propiedades de los polinomios como funciones, para esto nos armaremos de las herramientas del cálculo

Tarea moral

  1. Encuentra el conjunto solución de números reales de la desigualdad $x^3-2x^2+x-2>0$. Nota que $i$ es solución del polinomio.
  2. Encuentra el conjunto solución de números reales de la desigualdad $(x+1)(x^2-3x+2)>x^2-1$.
  3. Demuestra que $x^4-x+1$ siempre es positivo. Considera los casos en que $x$ está en $(-\infty,0],[0,1]$ y $[1,\infty)$.
  4. Encuentra el conjunto solución de números reales de la desigualdad $\frac{1}{x^2+1}>x+1$.
  5. Encuentra el conjunto solución de números reales de la desigualdad $\frac{x-1}{(x-2)(x-3)}>1$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»