Introducción

Las funciones continuas son bonitas pues tienen la propiedad del valor intermedio y además alcanzan sus valores extremos. Las funciones diferenciables en un intervalo también tienen un par de teoremas que hablan acerca de algo que sucede “dentro del intervalo”. Estos son el teorema de Rolle, del cual platicamos en la entrada anterior, y el teorema del valor medio. Ambos nos permiten encontrar en el intervalo un punto en el que la derivada tiene un valor específico.

Teorema de Rolle. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Supongamos que $f(a)=f(b)$. Entonces existe un punto $c\in (a,b)$ tal que $f'(c)=0$.

Teorema del valor medio. Sean $a<b$ reales y $f:[a,b]\to \mathbb{R}$ una función continua en el intervalo $[a,b]$ y diferenciable en el intervalo $(a,b)$. Entonces existe un punto $c\in (a,b)$ tal que $$f'(c)=\frac{f(b)-f(a)}{b-a}.$$

En la entrada anterior vimos aplicaciones del teorema de Rolle a resolución de problemas matemáticos. En esta entrada hablaremos brevemente de la intuición geométrica del teorema del valor medio, de algunas de sus consecuencias inmediatas y de cómo usar al teorema y sus consecuencias para resolver problemas concretos.

La intuición geométrica del teorema del valor medio

El teorema del valor medio dice que una función diferenciable en $(a,b)$ y continua en $[a,b]$ cumple que hay un punto $c$ tal que el valor de la derivada en $c$ es igual a la pendiente de la recta que une los puntos del plano $(a,f(a))$ y $(b,f(b))$. En la siguiente figura, se marca en azul el punto $c$ en donde la pendiente de la tangente es lo que queremos, es decir, la pendiente entre los puntos rojos.

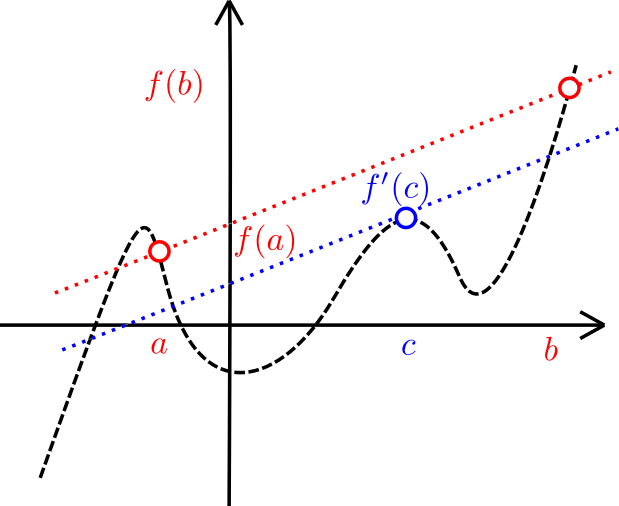
En varios problemas en los que se usa el teorema del valor medio, o bien en los cuales se pide demostrar enunciados parecidos a lo que dice el teorema del valor medio, es conveniente hacer una figura para entender la intuición geométrica del problema.

Consecuencias del teorema del valor medio

Si $f$ y $g$ son funciones continuas en $[a,b]$ y diferenciables en $(a,b)$ entonces se pueden deducir los siguientes resultados a partir del teorema del valor medio. No profundizamos en las demostraciones, y dejamos su verificación como un ejercicio de práctica.

Proposición. Si $f'(x)=0$ para toda $x$ en $(a,b)$, entonces $f$ es constante.

Proposición. Si $f'(x)=g'(x)$ para toda $x$ en $(a,b)$, entonces existe una constante $c$ tal que $f(x)=g(x)+c$ para toda $x$.

Proposición. Si $f'(x)>0$ para toda $x$ en $(a,b)$, entonces $f$ es una función estrictamente creciente. Si $f'(x)<0$ en $(a,b)$, entonces $f$ es una función estrictamente decreciente.

Cuando $f'(x)\geq 0$ y $f'(x)\leq 0$, tenemos resultados análogos que dicen que es no decreciente y no creciente, respectivamente.

Veamos algunas aplicaciones de los resultados anteriores.

Problema. Sean $f:\mathbb{R}\to \mathbb{R}$ y $g:\mathbb{R}\to \mathbb{R}$ funciones tales que para todo par de reales $x$ y $y$ se cumple que $$|f(x)+g(y)-f(y)-g(x)|\leq (x-y)^2.$$ Demuestra que $f$ y $g$ varían sólo por una constante aditiva.

Sugerencia pre-solución. Identifica cuál de las proposiciones anteriores puedes usar. Hay que tener cuidado con las hipótesis, pues en el enunciado no se habla de la diferenciabilidad de ninguna de las funciones involucradas.

Solución. Podría ser tentador usar la segunda proposición que enunciamos arriba, pero no tenemos hipótesis acerca de la diferenciabilidad de $f$ o de $g$. Sin embargo, vamos a mostrar que sí se puede mostrar que $f-g$ es diferenciable en todo real, y que su derivada es $0$ en todo real. Para ello, definamos $h=f-g$ y notemos que la hipótesis dice que $|h(x)-h(y)|\leq (x-y)^2.$

A partir de aquí, notemos que por la hipótesis, para $x\neq y$, $$\frac{|h(y)-h(x)|}{|y-x|}\leq \frac{(y-x)^2}{|y-x|} = |y-x|,$$ y el límite de esta última expresión conforme $y\to x$ es $0$, de modo que $$\left|\lim_{y\to x} \frac{h(y)-h(x)}{y-x}\right|=\lim_{y\to x} \frac{|h(y)-h(x)|}{|y-x|} = 0.$$ Esto muestra que para cualquier $x$ se tiene que $h$ es diferenciable en $x$ y su derivada es igual $0$ en todo $x$. De este modo, $h$ es una función constante, y por lo tanto existe un $c$ tal que $f(x)=g(x)+c$ para todo $x$.

$\square$

Veamos cómo el teorema del valor medio nos puede ayudar a demostrar desigualdades.

Problema. Sea $f:\mathbb{R}\to \mathbb{R}$ una función dos veces diferenciable tal que $f”(x)\geq 0$ para todo $x$. Demuestra que para todo par de reales $a$ y $b$ con $a<b$ se tiene que $$f\left(\frac{a+b}{2}\right) \leq \frac{f(a)+f(b)}{2}.$$

Sugerencia pre-solución. Haz una figura para convencerte de que el resultado es cierto. En el enunciado del problema, la función está siendo enunciada en tres valores, $a$, $b$ y $\frac{a+b}{2}$. Esto te dará una pista de dónde usar el teorema del valor medio.

Solución. Por el teorema del valor medio, existe un real $r$ en el intervalo $\left(a,\frac{a+b}{2}\right)$ para el cual $$\frac{f\left(\frac{a+b}{2}\right)-f(a)}{\frac{a+b}{2}-a} = f'(r).$$

De manera similar, existe un real $s$ en el intervalo $\left(\frac{a+b}{2},b\right)$ para el cual $$\frac{f(b)-f\left(\frac{a+b}{2}\right)}{b-\frac{a+b}{2}} = f'(s).$$

Como $f”(x)>0$ para todo real $x$, tenemos que $f’$ es una función creciente, y como $r<s$, tenemos entonces que $f'(r)<f'(s)$. De esta forma, $$ \frac{f\left(\frac{a+b}{2}\right)-f(a)}{\frac{a+b}{2}-a}<\frac{f(b)-f\left(\frac{a+b}{2}\right)}{b-\frac{a+b}{2}}.$$ Notemos que el denominador de ambos lados es $\frac{b-a}{2}$. Cancelando los denominadores y reacomodando los términos en esta desigualdad, obtenemos la desigualdad deseada.

$\square$

Problemas resueltos con el teorema del valor medio y otras técnicas

Veamos algunos problemas que combinan el teorema del valor medio con otras técnicas de solución de problemas.

Problema. Sea $f(x)$ una función diferenciable en $(0,1)$ y continua en $[0,1]$ con $f(0)=0$ y $f(1)=1$. Muestra que existen puntos distintos $a,b,c,d$ en el intervalo $[0,1]$ tales que $$\frac{1}{f'(a)}+ \frac{1}{f'(b)} + \frac{1}{f'(c)} + \frac{1}{f'(d)} = 4.$$

Sugerencia pre-solución. Para resolver el problema, hay que combinar el teorema del valor medio con el teorema del valor intermedio. El primer paso del problema es encontrar reales $p<q<r$ tales que $f$ valga en ellos $1/4$, $2/4$ y $3/4$.

Solución. Como $f(0)=0$, $f(1)=1$ y $0<1/4<1$, por el teorema del valor intermedio existe un real $p$ en $(0,1)$ tal que $f(p)=1/4$. De manera similar, existe un real $q$ en $(p,1)$ tal que $f(q)=2/4$ y un real $r$ en $(q,1)$ tal que $f(r)=3/4$.

Aplicando el teorema del valor medio a los intervalos $[0,p]$, $[p,q]$, $[q,r]$ y $[r,1]$ obtenemos reales $a,b,c,d$ respectivamente tales que

\begin{align*}
f'(a)&=\frac{f(p)-f(0)}{p-0}=\frac{1/4}{p}\\
f'(b)&=\frac{f(q)-f(p)}{q-p}=\frac{1/4}{q-p} \\
f'(c)&=\frac{f(r)-f(q)}{r-q}=\frac{1/4}{r-q} \\
f'(d)&=\frac{f(1)-f(r)}{1-r}=\frac{1/4}{1-r}.
\end{align*}

Estos son los valores de $a,b,c,d$ que queremos pues

\begin{align*}
\frac{1}{f'(a)}+ \frac{1}{f'(b)} + \frac{1}{f'(c)} + \frac{1}{f'(d)} &= 4(1-r+r-q+q-p+p)\\
&=4.
\end{align*}

$\square$

Problema. Sean $a$, $b$ y $c$ números distintos. Muestra que la siguiente expresión $$\frac{(x-a)(x-b)}{(c-a)(c-b)}+ \frac{(x-b)(x-c)}{(a-b)(a-c)} + \frac{(x-c)(x-a)}{(b-c)(b-c)}$$ no depende del valor de $x$.

Sugerencia pre-solución. Encuentra la derivada de la expresión. Puedes aprovechar la simetría para hacer menos cuentas.

Solución. Usando la regla del producto, la derivada del primer sumando es
\begin{align*}
\frac{(x-a)+(x-b)}{(c-a)(c-b)}&=\frac{(2x-a-b)(b-a)}{(a-b)(b-c)(c-a)}\\
&=\frac{2x(b-a)+a^2-b^2}{(a-b)(b-c)(c-a)}.
\end{align*}

Por simetría, las derivadas de los otros dos términos tienen el mismo denominador que esta y en el numerador tienen, respectivamente,
\begin{align*}
&2x(c-b)+b^2-c^2\quad \text{y}\\
&2x(a-c)+c^2-a^2,
\end{align*} de modo que al sumar las tres expresiones obtenemos cero. Así, la derivada de la expresión es cero y por lo tanto es constante.

$\square$

Hay otro argumento para resolver el problema anterior, que usa teoría de polinomios. A grandes rasgos, la expresión es un polinomio de grado $2$, que toma tres veces el valor $1$, de modo que debe ser igual al polinomio constante $1$.

Más problemas

Hay más ejemplos de problemas relacionados con el teorema del valor medio en la Sección 6.6 del libro Problem Solving through Problems de Loren Larson.