Archivo de la etiqueta: paralelogramo

Álgebra Superior I: Determinante de matrices y propiedades

Por Eduardo García Caballero

Deja un comentario

Introducción

Uno de los conceptos más importantes en el álgebra lineal es la operación conocida como determinante. Si bien este concepto se extiende a distintos objetos, en esta entrada lo revisaremos como una operación que se puede aplicar a matrices cuadradas. Como veremos, el determinante está muy conectado con otros conceptos que hemos platicado sobre matrices

Definición para matrices de $2\times 2$

A modo de introducción, comenzaremos hablando de determinantes para matrices de $2\times 2$. Aunque este caso es sencillo, podremos explorar algunas de las propiedades que tienen los determinantes, las cuales se cumplirán de manera más genera. Así, comencemos con la siguiente definición.

Definición. Para una matriz $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$, definimos su determinante como
\[
\operatorname{det}(A) = ad – bc.
\]

Basándonos en esta definición, podemos calcular los determinantes
\[
\operatorname{det}
\begin{pmatrix} 9 & 3 \\ 5 & 2 \end{pmatrix}=9\cdot 2 – 3\cdot 5 = 3
\]
y
\[
\operatorname{det}
\begin{pmatrix} 4 & -3 \\ 12 & -9 \end{pmatrix}
=
4\cdot (-9)-(-3)\cdot 12= 0.
\]

Otra notación que podemos encontrar para determinantes es la notación de barras. Lo que se hace es que la matriz se encierra en barras verticales, en vez de paréntesis. Así, los determinantes anteriores también se pueden escribir como
\[
\begin{vmatrix} 9 & 3 \\ 5 & 2 \end{vmatrix} = 3
\qquad
\text{y}
\qquad
\begin{vmatrix} 4 & -3 \\ 12 & -9 \end{vmatrix} = 0.
\]

Primeras propiedades del determinante

El determinante de una matriz de $2\times 2$ ayuda a detectar cuándo una matriz es invertible. De hecho, esto es algo que vimos previamente, en la entrada de matrices invertibles. En ella, dijimos que una matriz $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ es invertible si y sólo si se cumple que $ad – bc \ne 0$. ¡Aquí aparece el determinante! Podemos reescribir el resultado de la siguiente manera.

Teorema. Una matriz de la forma $A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}$ es invertible si y sólo si $\det(A) \ne 0$. Cuando el determinante es distinto de cero, la inversa es $A^{-1} = \frac{1}{\det(A)}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}$.

Otra propiedad muy importante que cumple el determinante para matrices de $2\times 2$ es la de ser multiplicativo; es decir, para matrices $A$ y $B$ se cumple que $\operatorname{det}(AB) = \operatorname{det}(A) \operatorname{det}(B)$. La demostración de esto se basa directamente en las definiciones de determinante y de producto de matrices. Hagamos las cuentas a continuación para matrices $A=\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}$ y $B=\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}.$

Tenemos que:
\begin{align*}
\operatorname{det}(AB)
&=
\operatorname{det}
\left(
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\right)
\\[5pt]
&=
\operatorname{det}
\begin{pmatrix}
a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\
a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22}
\end{pmatrix}
\\[5pt]
&=
(a_{11}b_{11} + a_{12}b_{21})(a_{21}b_{12} + a_{22}b_{22})-(a_{11}b_{12} + a_{12}b_{22})(a_{21}b_{11} + a_{22}b_{21})
\\[5pt]
&=
a_{11}a_{22}b_{11}b_{22} – a_{12}a_{21}b_{11}b_{22} – a_{11}a_{22}b_{12}b_{21} + a_{12}a_{21}b_{12}b_{21}
\\[5pt]
&=
(a_{11}a_{22} – a_{12}a_{21})(b_{11}b_{22} – b_{12}b_{21})
\\[5pt]
&=
\operatorname{det}
\begin{pmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{pmatrix}
\operatorname{det}
\begin{pmatrix}
b_{11} & b_{12} \\
b_{21} & b_{22}
\end{pmatrix}
\\[5pt]
&=
\operatorname{det}(A)\operatorname{det}(B).
\end{align*}

Interpretación geométrica del determinante de $2\times 2$

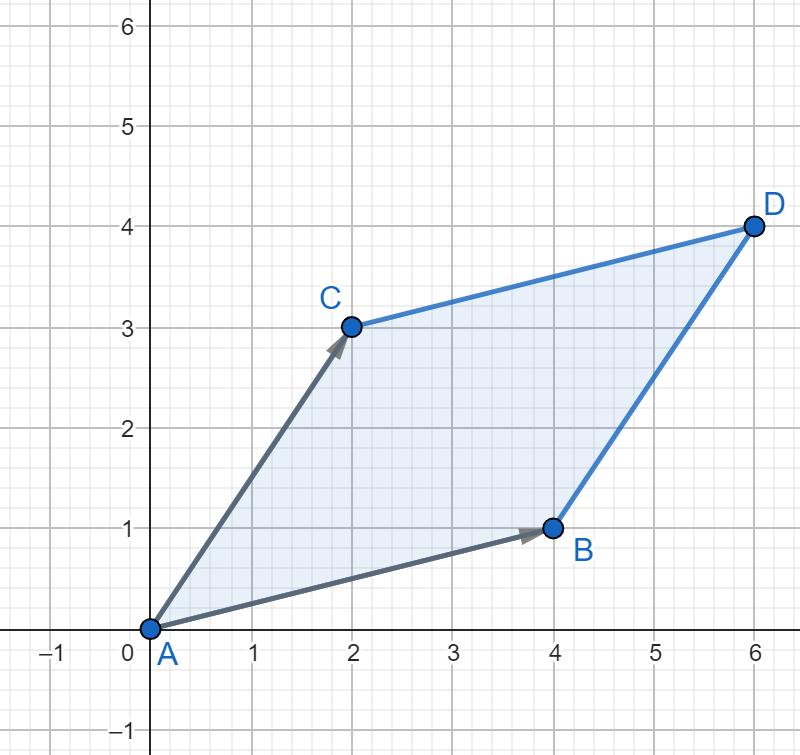
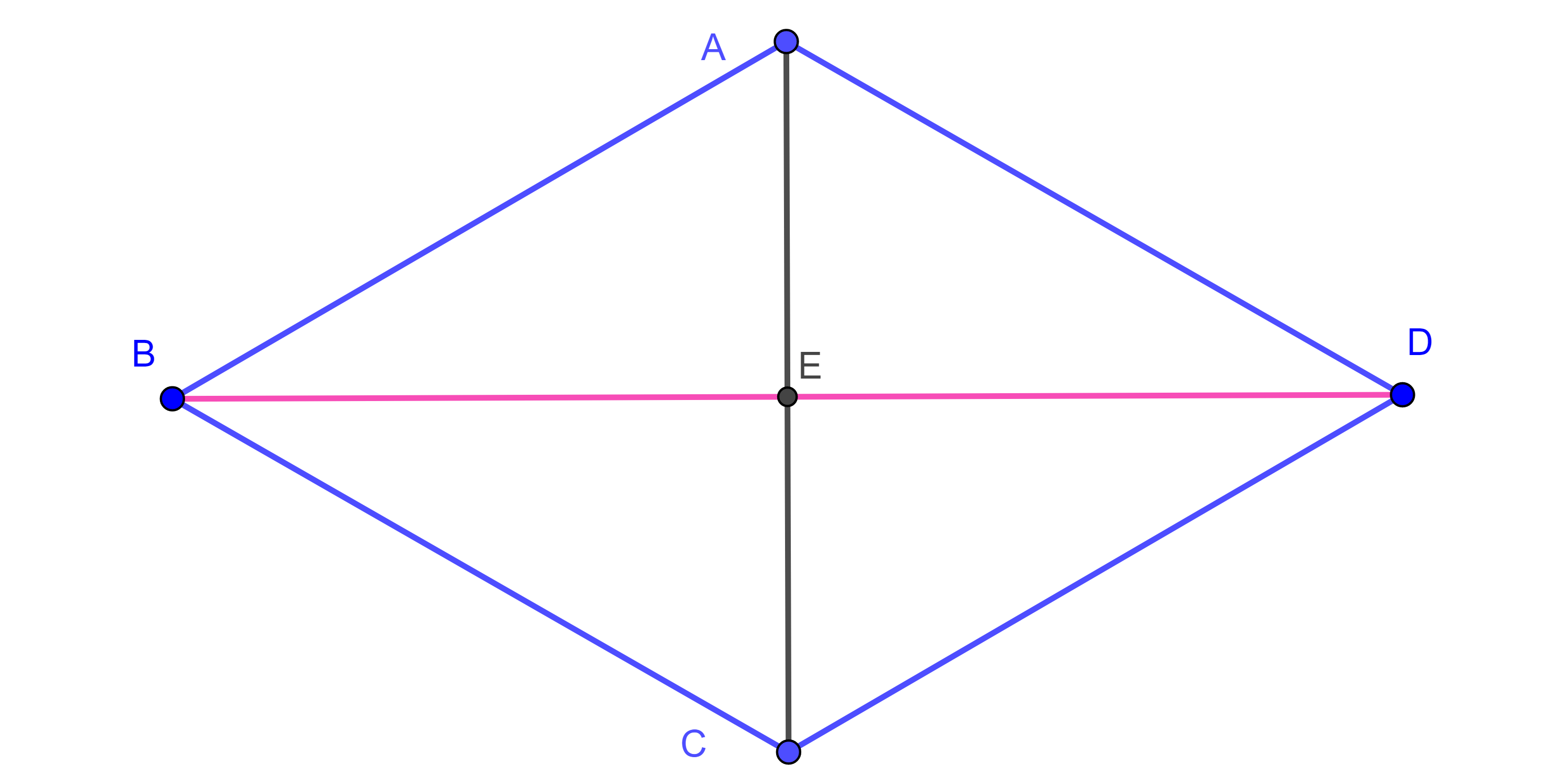
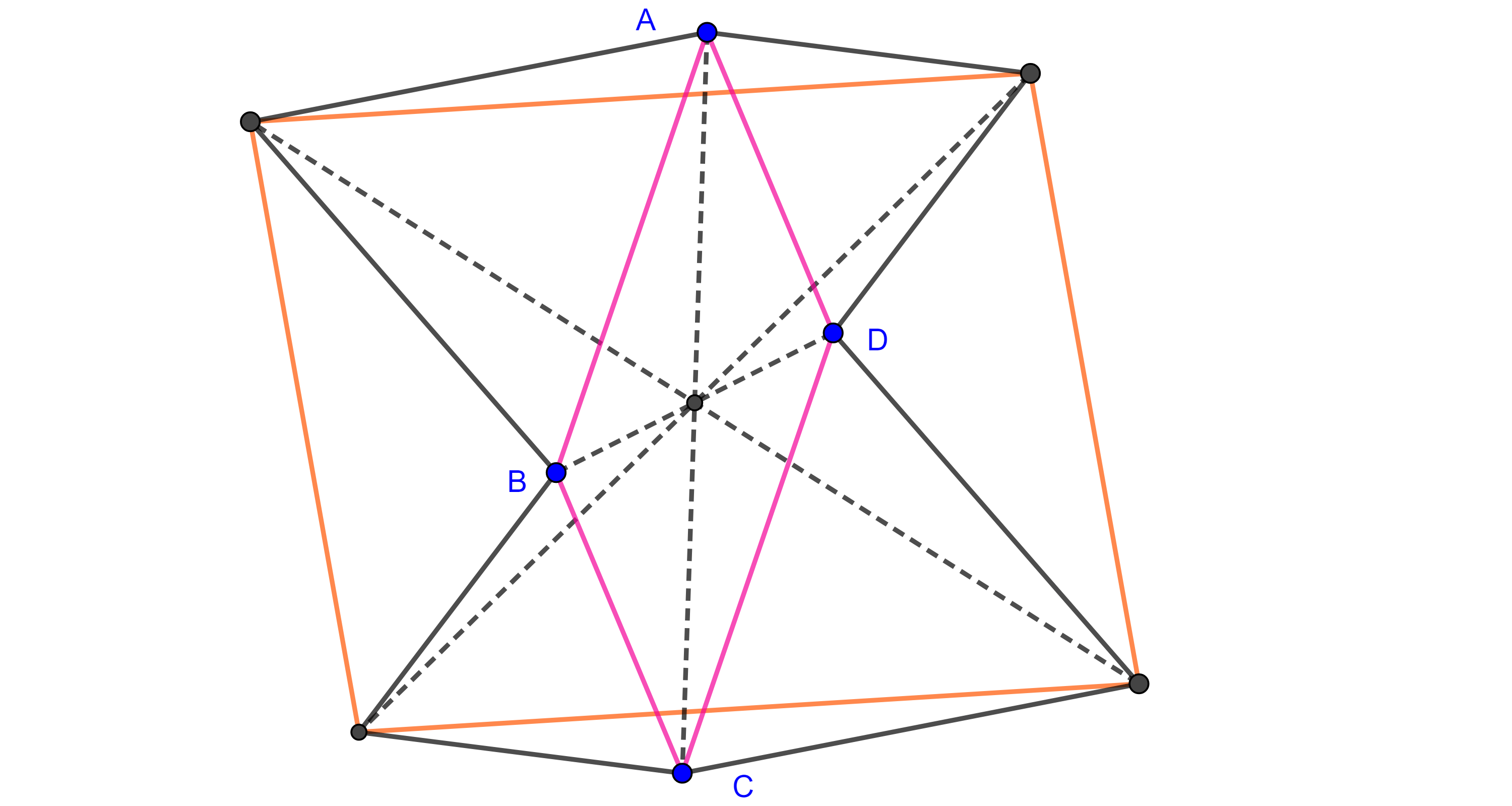
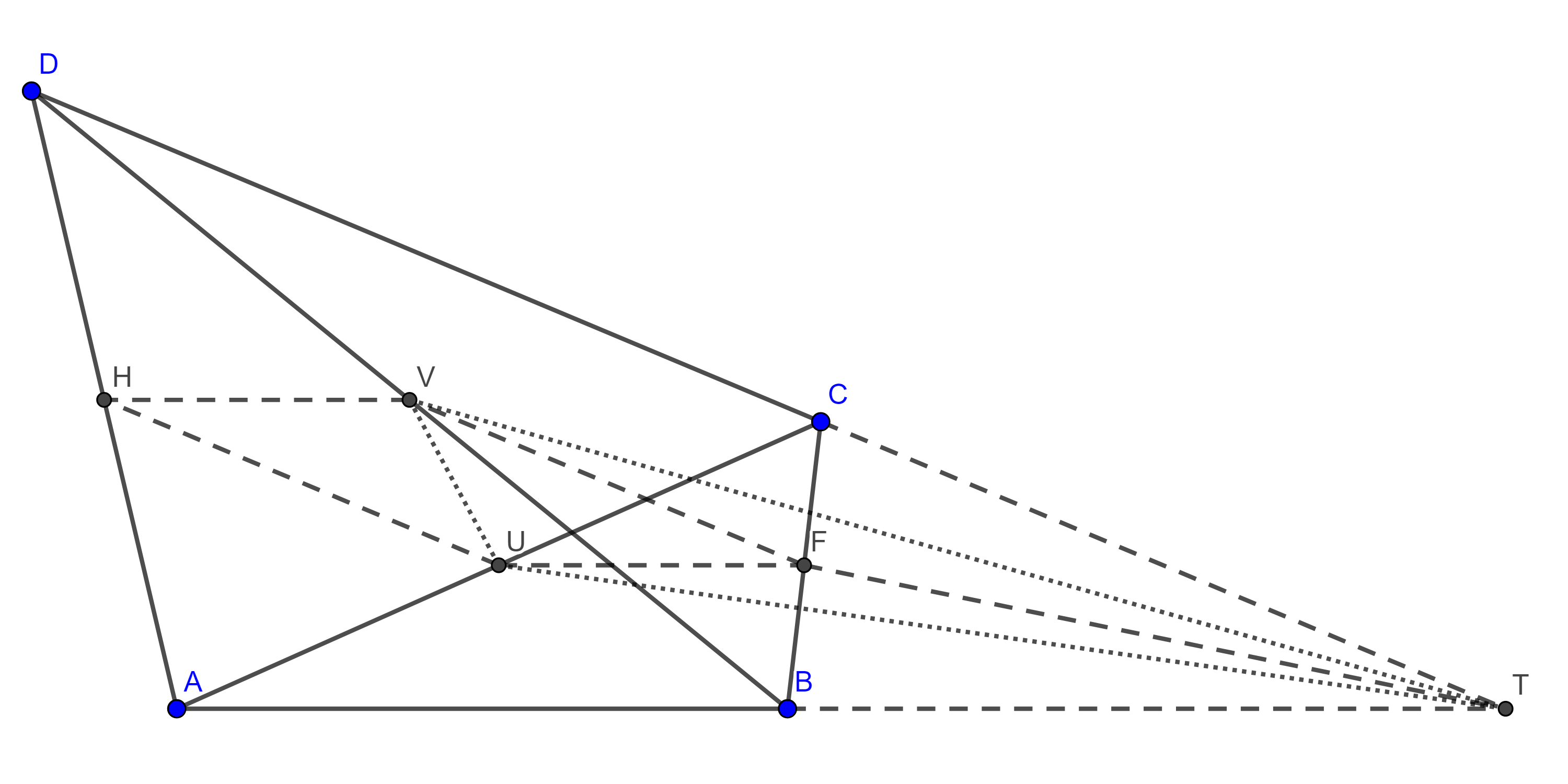
El determinante también tiene una interpretación geométrica muy interesante. Si tenemos una matriz de $2\times 2$, entonces podemos pensar a cada una de las columnas de esta matriz como un vector en el plano. Resulta que el determinante es igual al área del paralelogramo formado por estos vectores.

Por ejemplo, si consideramos la matriz
\[
\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix},
\]
podemos ver que el vector asociado a su primera columna es el vector $(4,1)$, mientras que el vector asociado a su segunda columna es $(2,3)$:

Así, el paralelogramo $ABDC$ de la figura anterior formado por estos dos vectores tiene área igual a
\[
\operatorname{det}
\begin{pmatrix} 4 & 2 \\ 1 & 3 \end{pmatrix}
= 4\cdot 3 – 2\cdot 1 = 10.
\]

No daremos la demostración de este hecho, pues se necesita hablar más sobre la geometría del plano. Sin embargo, las ideas necesarias para este resultado pueden consultarse en un curso de Geometría Analítica I.

Definición recursiva

También nos interesa hablar de determinantes de matrices más grandes. De hecho, nos interesa hablar del determinante de cualquier matriz cuadrada. La definición formal requiere de varios conocimientos de Álgebra Lineal I. Sin embargo, por el momento podemos platicar de cómo se obtienen los determinantes de matrices recursivamente. Con esto queremos decir que para calcular el determinante de matrices de $3\times 3$, necesitaremos calcular varios de matrices de $2\times 2$. Así mismo, para calcular el de matrices de $4\times 4$ requeriremos calcular varios de matrices de $3\times 3$ (que a su vez requieren varios de $2\times 2$).

Para explicar cómo es esta relación de poner determinantes de matrices grandes en términos de matrices más pequeñas, primeramente definiremos la función $\operatorname{sign}$, la cual asigna a cada pareja de enteros positivos $(i,j)$ el valor
\[
\operatorname{sign}(i,j) = (-1)^{i+j}.
\]
A partir de la función $\operatorname{sign}$ podemos hacer una matriz cuya entrada $a_{ij}$ es $\operatorname{sign}(i,j)$. Para visualizarla más fácilmente, podemos pensar que a la entrada $a_{11}$ (la cual se encuentra en la esquina superior izquierda) le asigna el signo “$+$”, y posteriormente va alternando los signos del resto de entradas. Por ejemplo, los signos correspondientes a las entradas de la matriz de $3 \times 3$
\[
\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}
\]
serían
\[
\begin{pmatrix}
+ & – & + \\
– & + & – \\
+ & – & +
\end{pmatrix},
\]
mientras que los signos correspondientes a las entradas de la matriz de $4 \times 4$
\[
\begin{pmatrix}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34} \\
a_{41} & a_{42} & a_{43} & a_{44}
\end{pmatrix}
\]
serían
\[
\begin{pmatrix}
+ & – & + & – \\
– & + & – & + \\
+ & – & + & – \\
– & + & – & +
\end{pmatrix}.
\]

Ya que entendimos cómo se construyen estas matrices, el cálculo de determinantes se realiza como sigue.

Estrategia. Realizaremos el cálculo de determinante de una matriz de $n \times n$ descomponiéndola para realizar el cálculo de determinantes de matrices de $(n-1) \times (n-1)$. Eventualmente llegaremos al calcular únicamente determinantes de matrices de $2 \times 2$, para las cuales ya tenemos una fórmula. Para esto, haremos los siguientes pasos repetidamente.

  1. Seleccionaremos una fila o columna arbitraria de la matriz original (como en este paso no importa cuál fila o columna seleccionemos, buscaremos una que simplifique las operaciones que realizaremos; generalmente nos convendrá seleccionar una fila o columna que cuente en su mayoría con ceros).
  2. Para cada entrada $a_{ij}$ en la fila o columna seleccionada, calculamos el valor de
    \[
    \operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{ij}),
    \]
    donde $A_{ij}$ es el la matriz que resulta de quitar la fila $i$ y la columna $j$ a la matriz original.
  3. El determinante de la matriz será la suma de todos los términos calculados en el paso anterior.

Veamos algunos ejemplos de cómo se utiliza la estrategia recién descrita.

Ejemplo con matriz de $3\times 3$

Consideremos la matriz de $3 \times 3$
\[
\begin{pmatrix}
3 & 1 & -1 \\
6 & -1 & -2 \\
4 & -3 & -2
\end{pmatrix}.
\]

A primera vista no hay alguna fila o columna que parezca simplificar los cálculos, por lo cual podemos proceder con cualquiera de estas; nosotros seleccionaremos la primera fila.
\[
\begin{pmatrix}
\fbox{3} & \fbox{1} & \fbox{-1} \\
6 & -1 & -2 \\
4 & -3 & -2
\end{pmatrix}.
\]

Para cada término de la primera fila, calculamos el producto
\[
\operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{i,j}),
\]
obteniendo
\begin{align*}
\operatorname{sign}(1,1) \cdot (a_{11}) \cdot \operatorname{det}(A_{11})
&= +(3)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
\blacksquare & -1 & -2 \\
\blacksquare & -3 & -2
\end{pmatrix}
\\[5pt]
&= +(3)\operatorname{det} \begin{pmatrix} -1 & -2 \\ -3 & -2 \end{pmatrix}
\\[5pt]
&= +(3)[(-1)(-2) – (-2)(-3)]
\\[5pt]
&= +(3)(-4)
\\[5pt]
&= -12,
\\[10pt]
\operatorname{sign}(1,2) \cdot (a_{12}) \cdot \operatorname{det}(A_{12})
&= -(1)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
6 & \blacksquare & -2 \\
4 & \blacksquare & -2
\end{pmatrix}
\\[5pt]
&= -(1)\operatorname{det}
\begin{pmatrix} 6 & -2 \\ 4 & -2 \end{pmatrix}
\\[5pt]
&=-(1)[(6)(-2) – (-2)(4)]
\\[5pt]
&=-(1)(-4)
\\[5pt]
&=4,
\\[10pt]
\operatorname{sign}(1,3) \cdot (a_{13}) \cdot \operatorname{det}(A_{13})
&= +(-1)\operatorname{det}
\begin{pmatrix}
\blacksquare & \blacksquare & \blacksquare \\
6 & -1 & \blacksquare \\
4 & -3 & \blacksquare
\end{pmatrix}
\\[5pt]
&= +(-1)\operatorname{det} \begin{pmatrix} 6 & -1 \\ 4 & -3 \end{pmatrix}
\\[5pt]
&= +(-1)[(6)(-3) – (-1)(4)]
\\[5pt]
&= +(-1)(-14)
\\[5pt]
&= 14.
\end{align*}

Finalmente, el determinante de nuestra matriz original será la suma de los términos calculados; es decir,
\[
\begin{pmatrix}
3 & 1 & -1 \\
6 & -1 & -2 \\
4 & -3 & -1
\end{pmatrix}
=
(-12) + (4) + (14) = 6.
\]

Ejemplo con matriz de $4\times 4$

En el siguiente ejemplo veremos cómo el escoger una fila o columna en específico nos puede ayudar a simplificar mucho los cálculos.

Consideremos la matriz
\[
\begin{pmatrix}
4 & 0 & 2 & 2 \\
-1 & 3 & -2 & 5 \\
-2 & 0 & 2 & -3 \\
1 & 0 & 4 & -1
\end{pmatrix}.
\]

Observemos que el valor de tres de las entradas de la segunda columna es $0$. Por esta razón, seleccionaremos esta columna para descomponer la matriz:
\[
\begin{pmatrix}
4 & \fbox{0} & 2 & 2 \\
-1 & \fbox{3} & -2 & 5 \\
-2 & \fbox{0} & 2 & -3 \\
1 & \fbox{0} & 4 & -1
\end{pmatrix}.
\]

El siguiente paso será calcular el producto
\[
\operatorname{sign}(i,j) \cdot a_{ij} \cdot \operatorname{det}(A_{ij}),
\]
para cada entrada de esta columna. Sin embargo, por la elección de columna que hicimos, podemos ver que el valor de $a_{ij}$ es 0 para tres de las entradas, y por tanto también lo es para el producto que deseamos calcular. De este modo, únicamente nos restaría calcular el producto
\begin{align*}
\operatorname{sign}(2,2) \cdot a_{22} \cdot \operatorname{det}(A_{22})
&=
+(3)\operatorname{det}
\begin{pmatrix}
4 & \blacksquare & 2 & 2 \\
\blacksquare & \blacksquare & \blacksquare & \blacksquare \\
-2 & \blacksquare & 2 & -3 \\
1 & \blacksquare & 4 & -1
\end{pmatrix}
\\[5pt]
&= +(3)\operatorname{det}
\begin{pmatrix}
4 & 2 & 2 \\
-2 & 2 & -3 \\
1 & 4 & -1
\end{pmatrix}.
\end{align*}
Se queda como ejercicio al lector concluir que el resultado de este último producto es 30.

De este modo, obtenemos que
\[
\operatorname{det}
\begin{pmatrix}
4 & 0 & 2 & 2 \\
-1 & 3 & -2 & 5 \\
-2 & 0 & 2 & -3 \\
1 & 0 & 4 & -1
\end{pmatrix}
= 0 + 30 + 0 + 0 = 30.
\]

Aunque esta definición recursiva nos permite calcular el determinante de una matriz cuadrada de cualquier tamaño, rápidamente se vuelve un método muy poco práctico (para obtener el determinante de una matriz de $6 \times 6$ tendríamos que calcular hasta 60 determinantes de matrices de $2 \times 2$). En el curso de Álgebra Lineal I se aprende otra definición de determinante a través de permutaciones, de las cuales se desprenden varios métodos más eficientes para calcular determinante. Hablaremos un poco de estos métodos en la siguiente entrada.

Las propiedades de $2\times 2$ también se valen para $n\times n$

Las propiedades que enunciamos para matrices de $2\times 2$ también se valen para determinantes de matrices más grandes. Todo lo siguiente es cierto, sin embargo, en este curso no contamos con las herramientas para demostrar todo con la formalidad apropiada:

  • El determinante es multiplicativo: Si $A$ y $B$ son matrices de $n\times n$, entonces $\operatorname{det}(AB) = \operatorname{det}(A)\operatorname{det}(B)$.
  • El determinante detecta matrices invertibles: Una matriz $A$ de $n\times n$ es invertible si y sólo si su determinante es distinto de $0$.
  • El determinante tiene que ver con un volumen: Los vectores columna de una matriz $A$ de $n\times n$ hacen un paralelepípedo $n$-dimensional cuyo volumen $n$-dimensional es justo $\det{A}$.

Más adelante…

En esta entrada conocimos el concepto de determinante de matrices, vimos cómo calcularlo para matrices de distintos tamaños y revisamos cómo se interpreta cuando consideramos las matrices como transformaciones de flechas en el plano. En la siguiente entrada enunciaremos y aprenderemos a usar algunas de las propiedades que cumplen los determinantes.

Tarea moral

  1. Calcula los determinantes de las siguientes matrices:
    • $\begin{pmatrix} 5 & 8 \\ 3 & 9 \end{pmatrix}, \begin{pmatrix} 10 & 11 \\ -1 & 9 \end{pmatrix}, \begin{pmatrix} 31 & 38 \\ 13 & -29 \end{pmatrix}$
    • $\begin{pmatrix} 1 & 5 & 2 \\ 3 & -1 & 8 \\ 0 & 2 & 5 \end{pmatrix}, \begin{pmatrix} 1 & 8 & 4 \\ 0 & 5 & -3 \\ 0 & 0 & -1 \end{pmatrix}, \begin{pmatrix} 1 & 1 & 1 \\ 2 & 2 & 2 \\ 3 & 3 & 3 \end{pmatrix}$
    • $\begin{pmatrix} 5 & 7 & -1 & 2 \\ 3 & 0 & 1 & 0 \\ 2 & -2 & 2 & -2 \\ 5 & 1 & 1 & 0 \end{pmatrix}, \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{pmatrix}$
  2. Demuestra que para una matriz $A$ y un entero positivo $n$ se cumple que $\det(A^n)=\det(A)^n$.
  3. Sea $A$ una matriz de $3\times 3$. Muestra que $\det(A)=\det(A^T)$.
  4. Sea $A$ una matriz invertible de $2\times 2$. Demuestra que $\det(A)=\det(A^{-1})^{-1}$.
  5. ¿Qué le sucede al determinante de una matriz $A$ cuando intercambias dos filas? Haz algunos experimentos para hacer una conjetura, y demuéstrala.

Entradas relacionadas

Geometría Moderna I: Paralelogramos

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

En esta entrada presentamos a el primer tipo de cuadriláteros que estudiaremos, los paralelogramos, algunas de sus propiedades serán frecuentemente usadas durante el curso.

Definición 1. Un cuadrilátero es una figura geométrica que consiste en cuatro vértices y cuatro lados. Si los vértices de un cuadrilátero son $A$, $B$, $C$ y $D$ y los lados $AB$, $BC$, $CD$ y $AD$ entonces lo denotamos como $\square ABCD$.

Decimos que los lados de un cuadrilátero son adyacentes u opuestos de acuerdo a si tienen o no un vértice en común.

Similarmente diremos que los vértices de un cuadrilátero son adyacentes u opuestos si son extremos de un mismo lado o no. Los segmentos que unen vértices opuestos son las diagonales del cuadrilátero.

Un cuadrilátero es convexo si sus diagonales se intersecan en el interior del cuadrilátero.

Figura 1

Proposición 1. La suma de los ángulos internos de todo cuadrilátero convexo es $2\pi$.

Demostración. Sea $\square ABCD$ convexo, consideremos $BD$, entonces la suma de los ángulos internos del cuadrilátero será igual a la suma de los ángulos internos de los dos triángulos $\triangle ABD$ y $\triangle CBD$, esto es, $2\pi$.

$\blacksquare$

Algunas propiedades de paralelogramos

Definición 2. Un paralelogramo es un cuadrilátero convexo cuyos pares de lados opuestos son paralelos.

Teorema 1. En todo paralelogramo se cumple lo siguiente:

  • los lados opuestos y los ángulos opuestos son iguales,
  • los ángulos adyacentes son suplementarios,
  • cada diagonal divide al paralelogramo en dos triángulos congruentes,
  • las dos diagonales del paralelogramo lo dividen en dos parejas de triángulos congruentes,
  • las diagonales se intersecan en su punto medio.

Demostración. Sea $\square ABCD$ un paralelogramo.

Como la diagonal $BD$ es transversal a $AB$ y $DC$ y estos son paralelos, entonces $\angle DBA = \angle BDC$.

Similarmente $BD$ es transversal a $AD$ y a $BC$, por lo que $\angle ADB = \angle CBD$.

Figura 2

$\triangle ABD$ y $\triangle CDB$ tienen en común al lado $BD$ y por criterio ALA, $\triangle ABD \cong \triangle CDB$.

Es decir,
$AB = CD$, $AD = CB$ y $\angle A = \angle C$,
además $\angle D = \angle ADB + \angle BDC = \angle CBD + \angle DBA = \angle B$.

Así los lados y ángulos opuesto son iguales.

Veamos que los los ángulos adyacentes son suplementarios,
$\angle A + \angle B = \angle A + \angle CBD + \angle DBA $
$= \angle A + \angle ADB + \angle DBA = \pi$.

Similarmente,
$\angle A + \angle D = \angle C + \angle B = \angle C + \angle D = \pi$.

Por otro lado, si consideramos la diagonal $AD$, al igual que en el caso anterior, tendremos que $\angle BAC = \angle DCA$ y $\angle CAD = \angle ACB$.

Figura 3

Sea $E = AC \cap BD$, por criterio ALA, $\triangle EAB \cong \triangle ECB$ y $\triangle EAD \cong \triangle ECB$, por lo que $AE = CE$ y $BE = DE$.

$\blacksquare$

Rectángulo

Definición 3. Un rectángulo es un cuadrilátero con cuatro ángulos rectos.

Proposición 2. Todo rectángulo es paralelogramo.

Demostración. Como dos lados opuestos son perpendiculares a un tercer lado entonces son paralelos entre sí. Similarmente los otros dos lados opuestos son paralelos entre sí. Por lo tanto, un rectángulo es paralelogramo.

Figura 4

$\blacksquare$

Proposición 3. Un paralelogramo es rectángulo si y solo si sus diagonales tienen la misma longitud.

Demostración. Sea $\square ABCD$ paralelogramo y supongamos que $AC = BD$.

Por el teorema anterior, $AD = BC$, y los triángulos $\triangle ADC $ y $\triangle BCD$ comparten a $CD$ como lado en común, por criterio LLL, $\triangle ADC \cong \triangle BCD$, en particular $\angle C = \angle D$.

Figura 5

Pero por el teorema 1, $\angle A = \angle C$ y $\angle B = \angle D$.

Por tanto, $\angle A = \angle C = \angle D = \angle B$.

Por la proposición 1,
$4\angle A = \angle A + \angle C + \angle B + \angle D = 2 \pi$
$\Rightarrow \angle A = \angle C = \angle B = \angle D = \dfrac{\pi}{2}$.

Así, $\square ABCD$ es rectángulo.

$\blacksquare$

Ahora supongamos que $\square ABCD$ es rectángulo y probemos que $AC = BD$.

Figura 6

Por hipótesis $\angle D = \angle C$, como $\square ABCD$ es paralelogramo entonces $AD = BC$, además $CD$ es un lado en común de $\triangle ADC$ y $\triangle BCD$, por criterio LAL, $\triangle ADC \cong \triangle BCD$.

Por lo tanto, $AC = BD$.

$\blacksquare$

Rombo

Definición 4. Un rombo es un cuadrilátero con cuatro lados iguales.

Proposición 4. Todo rombo es paralelogramo.

Demostración. Sea $\square ABCD$ un rombo.

Por criterio LLL, $\triangle ABD \cong \triangle CDB$, en particular $\angle ADB = \angle CBD$, como $BD$ es transversal a $AD$ y a $BC$ y los ángulos alternos internos son iguales entonces $AD \parallel BC$.

Figura 7

De manera similar se ve que $AB \parallel CD$.

Concluimos que $\square ABCD$ es paralelogramo.

$\blacksquare$

Proposición 5. Un paralelogramo es un rombo si y solo si sus diagonales son perpendiculares.

Demostración. Sea $\square ABCD$ paralelogramo y supongamos que $AC \perp BD$, veamos que es rombo.

Figura 8

Sea $E = AC \cap BD$, por hipótesis $\angle DEA = \angle AEB$, como $\square ABCD$ es paralelogramo, por el teorema 1, $BE = DE$, además $AE$ es un lado en común de $\triangle AED$ y $\triangle AEB$, por criterio LAL, $\triangle AED \cong \triangle AEB$, en particular $AD = AB$.

Como $\square ABCD$ es paralelogramo los lados opuestos son iguales, por lo tanto, $CD = AB = AD = BC$.

Así, $\square ABCD$ es rombo.

$\blacksquare$

Ahora supongamos que $\square ABCD$ es rombo veamos que $AC \perp BD$.

Figura 9

Sea $E = AC \cap BD$, como $\square ABCD$ es paralelogramo, $BE = DE$, por criterio LLL, $\triangle ABE \cong \triangle ADE$, por lo que $\angle AEB = \angle DEA$.

Por ser opuestos por el vértice, $\angle AEB = \angle CED$ y $\angle DEA = \angle BEC$, por lo que $\angle CED = \angle AEB = \angle DEA = \angle BEC$, y como $\angle CED + \angle AEB + \angle DEA + \angle BEC = 2\pi$, entonces $\angle CED = \angle AEB = \angle DEA = \angle BEC =\dfrac{\pi}{2}$.

Por lo tanto, $AC \perp BD$.

$\blacksquare$

Segmento medio del triángulo

Proposición 6. Si un cuadrilátero convexo tiene un par de lados opuestos paralelos e iguales entre si entonces los restantes lados opuestos son paralelos e iguales entre sí.

Demostración. Sea $\square ABCD$ convexo tal que $AD = BC$ y $AD \parallel BC$.

Tracemos $BD$, como $AD \parallel BC$ entonces $\angle ADB = \angle CBD$, por criterio LAL, $\triangle ADB \cong \triangle CBD$, en particular $AB = CD$ y $\angle DBA = \angle BDC$.

Figura 10

Como $BD$ es transversal a $AB$ y a $CD$ y $\angle DBA = \angle BDC$, entonces $AB \parallel CD$.

En consecuencia, $\square ABCD$ es paralelogramo.

$\blacksquare$

Teorema 2. Del segmento medio del triángulo. El segmento que une puntos medios de dos lados de un triángulo es paralelo e igual a la mitad del lado restante.

Demostración. Sean $\triangle ABC$, $M$ y $N$ los puntos medios de $AB$ y $AC$ respectivamente.

Extendemos $MN$ hasta un punto $O$ del lado de $N$ tal que $MN = NO$.

Figura 11

Como $N$ es punto medio de $AC$ entonces $AN = CN$, por construcción $MN = NO$ y $\angle ANM = \angle CNO$ por ser opuestos por el vértice.

Por criterio LAL, $\triangle ANM \cong \triangle CNO$ por lo que $CO = AM = BM$ y $\angle NMA = \angle NOC$.

Como $MO$ es transversal a $AB$ y a $CO$ y los ángulos alternos internos $\angle NMA$, $\angle NOC$ son iguales entonces $AB \parallel CO$.

En el cuadrilátero $\square MBCO$ los lados opuestos $MB$ y $CO$ son paralelos e iguales, por la proposición 6, $MO \parallel BC$ y $MO = BC$ pero $MN = \dfrac{MO}{2}$.

Por lo tanto $MN = \dfrac{BC}{2}$ y $MN \parallel BC$.

$\blacksquare$

Problema de Thébault

Definición 5. Un cuadrado es un cuadrilátero con cuatro lados iguales y cuatro ángulos rectos. Decimos que la intersección de las diagonales de un cuadrado es el centro del cuadrado.

Teorema 3. Los centros de cuadrados construidos externamente sobre los lados de un paralelogramo son los vértices de un cuadrado y las diagonales del cuadrado y las del paralelogramo son concurrentes.

Demostración. Sea $\square ABCD$ paralelogramo y sean $\square ABB’’A’$, $\square BCC’’B’$, $\square CDD’’C’$ y $\square ADD’A’’$ cuadrados construidos sobre $AB$, $BC$, $CD$ y $DA$ respectivamente y $O_{1}$, $O_{2}$, $O_{3}$, $O_{4}$ sus respectivos centros.

Como un cuadrado es un caso particular de un rectángulo y un rombo, sus diagonales son perpendiculares y tienen la misma longitud, y como es un paralelogramo las diagonales se bisecan.

De esto concluimos que las diagonales de un cuadrado lo dividen en cuatro triángulos rectángulos, isósceles y congruentes entre sí.

Por otro lado, como $\square ABCD$ es paralelogramo entonces $AD = BC$ y $AB = CD$.

$\Rightarrow$
$\begin{equation} \triangle AA’O_{1} \cong \triangle ABO_{1} \cong \triangle CDO_{3} \cong \triangle CC’O_{3}, \end{equation}$
$\begin{equation} \triangle AA’’O_{4} \cong \triangle ADO_{4} \cong \triangle BCO_{2} \cong \triangle CC’’O_{2}. \end{equation}$

Figura 12

Por ser $\square ABCD$ paralelogramo,
$\angle A = \angle C$, $\angle B = \angle D$, $\angle A + \angle B = \pi$.

Veamos que $\triangle AO_{1}O_{4}$ y $\triangle CO_{3}O_{2}$ son congruentes.

Por $(1)$, $AO_{1} = CO_{3}$, por $(2)$, $AO_{4} = CO_{2}$,
notemos que $\angle A’’AA’ = \pi – \angle A = \angle B = \angle D = \pi – \angle C = \angle C’’CC’$.

$\Rightarrow \angle O_{4}AO_{1} = \angle O_{4}AA’’ + \angle A’’AA’ + \angle A’AO_{1}$
$= \angle O_{2}CC’’ + \angle C’’CC’ + \angle C’CO_{3} = \angle O_{2}CO_{3}$

Por criterio LAL, $\triangle AO_{1}O_{4} \cong \triangle CO_{3}O_{2}$, por lo que $ O_{1}O_{4} = O_{2}O_{3}$.

De manera similar se muestra que $\triangle AO_{1}O_{4} \cong \triangle BO_{1}O_{2} \cong \triangle DO_{3}O_{4}$, y así,
$\begin{equation} O_{2}O_{3} = O_{1}O_{4} = O_{1}O_{2} = O_{3}O_{4}. \end{equation}$

Como $\triangle AO_{1}O_{4} \cong \triangle BO_{1}O_{2}$, entonces $\angle AO_{1}O_{4} = \angle BO_{1}O_{2}$.

$\Rightarrow \angle O_{2}O_{1}O_{4} = \angle BO_{1}O_{4} – \angle BO_{1}O_{2}$
$= \angle BO_{1}A + \angle AO_{1}O_{4} – \angle BO_{1}O_{2} = \angle BO_{1}A = \dfrac{\pi}{2}$.

De manera similar se ve que
$\begin{equation} \angle O_{1}O_{4}O_{3} = \angle O_{4}O_{3}O_{2} = \angle O_{3}O_{2}O_{1} = \angle AO_{1}O_{4} = \dfrac{\pi}{2}. \end{equation}$.

Como $\square O_{1}O_{2}O_{3}O_{4}$ tienen cuatro lados iguales por $(3)$, y cuatro ángulos rectos por $(4)$, entonces es un cuadrado.

Veamos que las cuatro diagonales son concurrentes, consideremos $O_{2}O_{4}$ diagonal del cuadrado y $BD$ diagonal del paralelogramo.

Sea $E = O_{2}O_{4} \cap BD$. En $\triangle EBO_{2}$ y $\triangle EDO_{4}$ tenemos que $\angle BEO_{2} = \angle DEO_{4}$ por ser opuestos por el vértice, $\angle O_{2}BE = \angle O_{2}BC + \angle CBD = \angle O_{4}DA + \angle ADB$.

Por lo tanto, $\angle EO_{2}B = \angle EO_{4}D$, además $BO_{2} = DO_{4}$.

Por criterio LAL, $\triangle EBO_{2} \cong \triangle EDO_{4}$, por lo que $BE = DE$ y $O_{2}E = O_{4}E$
$\Rightarrow O_{2}O_{4}$ y $BD$ se intersecan en su punto medio.

Como $\square ABCD$ y $\square O_{1}O_{2}O_{3}O_{4}$ son paralelogramos sus diagonales se intersecan en su punto medio y por lo anterior todas concurren en $E$.

$\blacksquare$

Más adelante…

En la siguiente entrada veremos un resultado muy importante de las matemáticas, el teorema de Pitágoras y algunas aplicaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que si un cuadrilátero convexo tiene alguna de las siguientes características entonces es un paralelogramo.
    $i)$los dos pares de lados opuestos son iguales,
    $ii)$los dos pares de ángulos opuestos son iguales,
    $iii)$los ángulos adyacentes son suplementarios,
    $iv)$las diagonales se bisecan.
  2.  Construye un cuadrado sobre un segmento dado.
  3. Si trazamos rectas paralelas a los lados de un paralelogramo por un punto de una de sus diagonales se forman 4 cuadriláteros, muestra que los dos cuadriláteros por donde no pasa la diagonal tienen la misma área.
Figura 13
  1. Demuestra que si una recta biseca a un lado de un triangulo y es paralela a otro de los lados del triangulo entonces biseca al lado restante.
  2. $i)$ Muestra que el punto medio de la hipotenusa de un triangulo rectángulo equidista a los tres vértices del triangulo.
    $ii)$ Recíprocamente prueba que si en un triangulo un punto en uno de sus lados equidista a los tres vértices entonces el triángulo es rectángulo.
  3. Prueba que si construimos triángulos equiláteros exteriormente sobre los lados de un paralelogramo, entonces los cuatro vértices construidos son los vértices de un paralelogramo, y muestra que las diagonales de los dos paralelogramos son concurrentes.
Figura 14

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Moderna I: Teoremas de Varignon y Van Aubel

Por Rubén Alexander Ocampo Arellano

Deja un comentario

Introducción

Con esta entrada damos inicio a la cuarta unidad que tratará sobre cuadriláteros. Comenzaremos hablando sobre el paralelogramo de Varignon y el teorema de Van Aubel.

Área del cuadrilátero

A partir de la ubicación de las diagonales de un cuadrilátero podemos establecer una clasificación de estos.

Un cuadrilátero es convexo si sus dos diagonales se encuentran dentro de él, es cóncavo si tiene una diagonal dentro y otra fuera de él, y es cruzado si las dos diagonales se ubican fuera del cuadrilátero.

El teorema de Varignon nos habla sobre el área de un cuadrilátero en general y ya que no es tan intuitivo definir el área de un cuadrilátero cruzado es necesario introducir el concepto de área orientada.

Consideraremos el área de un triángulo como positiva si recorremos sus vértices en el sentido opuesto a las manecillas del reloj y como negativa en caso contrario.

De esta manera tenemos que para un triángulo $\triangle ABC$,
$(\triangle ABC) = (\triangle BCA) = (\triangle CAB) $
$= – (\triangle CBA) = – (\triangle ACB) = – (\triangle BAC)$.

Figura 1

Definición 1. Definimos el área de un cuadrilátero $\square ABCD$ como la suma de las áreas de los triángulos que se forman al considerar una de sus diagonales, esto es,
$(\square ABCD) = (\triangle ABC) + (\triangle CDA)$.

Notemos que como resultado de esta definición el área del cuadrilátero cruzado resulta ser la diferencia de las áreas de los triángulos que se forman al considerar la intersección cruzada de los lados.

Paralelogramo de Varignon

Teorema 1, de Varignon.
$i)$ Los puntos medios de los lados de un cuadrilátero convexo son los vértices de un paralelogramo, conocido como paralelogramo de Varignon, cuyo perímetro es la suma de las diagonales del cuadrilátero,
$ii)$ el área del paralelogramo de Varignon es la mitad del área del cuadrilátero.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$ y $M_{da}$ los puntos medios de $AB$, $BC$, $CD$ y $DA$ respetivamente.

Figura 2

Notemos que $M_{ab}M_{bc}$ y $M_{cd}M_{da}$ son segmentos medios de $\triangle ABC$ y $\triangle DAC$ por lo que $M_{ab}M_{bc} \parallel CA \parallel M_{cd}M_{da}$ y $2M_{ab}M_{bc} = CA = 2M_{cd}M_{da}$.

De manera análoga podemos ver que $M_{ab}M_{da} \parallel DB \parallel M_{bc}M_{cd}$ y $2M_{ab}M_{da} = BD = 2M_{bc}M_{cd}$.

Por lo tanto los lados opuestos de $\square M_{ab}M_{bc}M_{cd}M_{da}$ son paralelos y $M_{ab}M_{bc} + M_{bc}M_{cd} + M_{cd}M_{da} + M_{da}M_{ab} = \dfrac{CA + BD + CA +BD}{2} = CA + BD$.

Para calcular el área de  $\square M_{ab}M_{bc}M_{cd}M_{da}$ primero notemos que $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ son semejantes pues $M_{ab}M_{da} \parallel BD$.

También sabemos que $M_{ab}M_{da} = \dfrac{BD}{2}$, por lo que las alturas desde $A$, $h$ y $h’$ de $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ respectivamente, también cumplirán que $h = \dfrac{h’}{2}$.

Por lo tanto,
$(\triangle AM_{ab}M_{da}) = \dfrac{M_{ab}M_{da} \times h}{2}$
$= \dfrac{\frac{1}{2}DBD \times \frac{1}{2}h’}{2} = \dfrac{1}{4} \dfrac{BD \times h’}{2} $
$= \dfrac{1}{4} (\triangle ABD)$.

De manera similar podemos encontrar las áreas de $\triangle BM_{bc}M_{ab}$, $\triangle CM_{cd}M_{bc}$ y $\triangle DM_{da}M_{cd}$.

En consecuencia,
$(\square M_{ab}M_{bc}M_{cd}M_{da}) = (\square ABCD) – (\triangle AM_{ab}M_{da}) – (\triangle BM_{bc}M_{ab}) – (\triangle CM_{cd}M_{bc}) – (\triangle DM_{da}M_{cd})$
$= (\square ABCD) – \dfrac{1}{4} ((\triangle ABD) + (\triangle BCD) + (\triangle CDB) + (\triangle DAC))$
$= (\square ABCD) – \dfrac{2}{4}(\square ABCD) $
$ = \dfrac{(\square ABCD)}{2}$.

$\blacksquare$

Corolario. Sea $\square ABCD$ un cuadrilátero convexo, entonces su cuadrilátero de Varignon
$i)$ es un rombo si y solo si $AC = BD$,
$ii)$ es un rectángulo si y solo si $AC \perp BD$,
$iii)$ es un cuadrado si y solo si $AC = BD$ y $AC \perp BD$.

Demostración. Sean $E$, $F$, $G$, $H$, los puntos medios de $BC$, $CD$, $DA$, $AB$, respectivamente como $EF$ y $FG$ son segmentos medios de $\triangle DBC$ y $\triangle ADC$, entonces, $2EF = BD$, $EF \parallel BD$ y $2FG = AC$, $FG \parallel AC$.

Figura 3

$i)$ $\square EFGH$ es un rombo, entonces por definición $EF = FG \Leftrightarrow AC = BD$.

$ii)$ $\square EFGH$ es un rectángulo, entonces por definición $EF \perp FG \Leftrightarrow AC \perp BD$.

$iii)$ Es consecuencia de $i)$ y $ii)$.

$\blacksquare$

Centroide de un cuadrilátero

Definición 2. Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se llaman bimedianas.

Al segmento que une los puntos medios de las diagonales de un cuadrilátero se le conoce como recta de Newton.

Teorema 2. Las bimedianas de un cuadrilátero convexo y su recta de Newton son concurrentes y se bisecan entre sí, el punto de concurrencia es el centroide del cuadrilátero.

Demostración. Sea $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$, $M_{da}$, $M$, $N$, los puntos medios de $AB$, $BC$, $CD$, $DA$, $AC$, $BD$, respectivamente.

$M_{ab}M_{cd}$ y $M_{bc}M_{da}$ son las diagonales del paralelogramo de Varignon, por lo tanto, se intersecan en $J$ su punto medio.

Figura 4

Por otra parte, $M_{ab}M$ es un segmento medio de $\triangle ABC$, por lo que $M_{ab}M \parallel BC$; $NM_{cd}$ es un segmento medio de $\triangle DBC$, por lo tanto, $NM_{cd} \parallel BC$, y así $NM_{cd} \parallel M_{ab}M$.

Igualmente vemos que $M_{ab}N \parallel MM{cd}$.

Por lo tanto, $\square M_{ab}NM_{cd}M$ es un paralelogramo, en consecuencia las diagonales $M_{ab}M_{cd}$ y $NM$ se intersecan en $J$ su punto medio.

En conclusión, $J$ es el punto medio de $M_{ab}M_{cd}$, $M_{bc}M_{da}$ y $NM$.

$\blacksquare$

Construcción de un cuadrilátero

Problema. Construye un cuadrilátero $\square ABCD$ conociendo $AB$, $BC$, $CD$, $DA$ y $M_{ab}M_{cd}$ donde $M_{ab}$ y $M_{cd}$ son los puntos medios de $AB$ y $CD$ respectivamente.

Solución. Primero construimos el paralelogramo $\square M_{ab}NM_{cd}M$, donde $M$ y $N$ son los puntos medios de las diagonales $AC$ y $BD$, de la siguiente manera.

De la demostración del teorema 2 sabemos que $M_{ab}M = NM_{cd} = \dfrac{BC}{2}$ y $M_{ab}N = MM_{cd} = \dfrac{AD}{2}$ (figura 4).

También sabemos que la diagonal de un paralelogramo lo divide en dos triángulos congruentes, por lo que basta construir un triángulo de lados $M_{ab}M_{cd}$, $\dfrac{BC}{2}$  y $\dfrac{AD}{2}$ y luego trazar paralelas por $M_{ab}$ y $M_{cd}$ a los lados del triángulo construido completando así el paralelogramo.

De manera similar construimos el paralelogramo $\square M_{ab}M_{bc}M_{cd}M_{da}$ donde $M_{bc}$ y $M_{da}$ serían los puntos medios de $BC$ y $AD$ respectivamente.

Sabemos también que $M_{bc}M \parallel AB$ por lo que trazamos la paralela $AB$ a $M_{bc}M$ por $M_{ab}$ tal que $AM_{ab} = M_{bc}B = \dfrac{AB}{2}$.

Con $A$ y $B$ construidos, por $M_{bc}$ trazamos $ABC$ tal que $BM_{bc} = M_{bc}C = \dfrac{BC}{2}$, similarmente construimos $D$.

$\blacksquare$

Teorema de Van Aubel

Teorema 3, de Van Aubel. Los segmentos que unen los centros de cuadrados construidos externamente sobre lados opuestos de un cuadrilátero convexo son perpendiculares y tienen la misma longitud.

Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $\square EFBA$, $\square BGHC$, $\square DCIJ$, $\square LADK$, cuadrados construidos externamente sobre los lados de $\square ABCD$ y $O_1$, $O_2$, $O_3$, $O_4$, sus respectivos centros.

Figura 5

Sea $M = LB \cap ED$, como $AL = AD$ y $AB = AE$ y $\angle LAB = \angle DAE$, por criterio de congruencia LAL, $\triangle LAB \cong \triangle DAE$,
$\Rightarrow LB = DE$ y $\angle AEM = \angle ABM$.

Por lo tanto, $\square MEBA$ es cíclico, así, $\angle EMB = \angle EAB$, es decir $LB \perp DE$.

Considera $N$ el punto medio de $BD$, $NO_4$ y $NO_3$ son segmentos medios de $\triangle BDE$ y $\triangle DBL$ respectivamente.

Esto implica que $2NO_4 = DE$ y $NO_4 \parallel DE$ y $2NO_3 = LB$ y $NO_4 \parallel LB$.

Por lo tanto, $NO_4 = NO_3$ y $NO_4 \perp NO_3$.

Igualmente vemos que $NO_1 = NO_2$ y $NO_1 \perp NO_2$.

Sea $V = O_1O_3 \cap O_2O_4$, por criterio de congruencia LAL, $NO_1O_3 \cong NO_2O_4$,
$\Rightarrow O_1O_3 = O_2O_4$ y $\angle VO_1N = \angle VO_2N$.

Por lo tanto, $\square VNO_1O_2$ es cíclico, y así $O_1O_3 \perp O_2O_4$.

$\blacksquare$

Definición 3. Nos referiremos al cuadrilátero $\square O_1O_1O_3O_4$ como cuadrilátero externo de Van Aubel y a la intersección de sus diagonales como punto externo de Van Aubel.

Centroide del cuadrilátero de Van Aubel

Teorema 4. Un cuadrilátero y su cuadrilátero externo de Van Aubel tienen el mismo centroide.

Demostración. Sean $\square ABCD$ y $\square O_1O_2O_3O_4$ su cuadrilátero externo de Van Aubel, $M$ y $N$ los puntos medios de $AC$ y $BD$, y $V$ el punto externo de Van Aubel.

Figura 6

En el teorema anterior vimos que $NV$ es una cuerda común a las circunferencias cuyos diámetros son $O_1O_2$ y $O_3O_4$, por lo tanto la línea que une sus centros $M_{1,2}M_{3,4}$ biseca a $NV$ y $M_{1,2}M_{3,4} \perp NV$.

De manera análoga podemos ver que $MV$ es una cuerda común a las circunferencias cuyos diámetros son $O_2O_3$ y $O_4O_1$ y por lo tanto la línea que une sus centros $M_{2,3}M_{4,1}$ biseca a $MV$ y $M_{2,3}M_{4,1} \perp MV$.

Por otra parte, por el teorema de Van Aubel las diagonales del cuadrilátero de Van Aubel son perpendiculares y tienen la misma longitud. Entonces por el corolario, su paralelogramo de Varignon $\square M_{1,2}M_{2,3}M_{3,4}M_{4,1}$ es un cuadrado, en particular, $M_{1,2}M_{3,4} \perp M_{2,3}M_{4,1}$.

En consecuencia, en $\triangle MNV$, $M_{1,2}M_{2,3} \parallel MV$ y $M_{1,2}M_{2,3}$ pasa por el punto medio de $NV$, por lo tanto $M_{1,2}M_{2,3}$ biseca a $MN$.

Igualmente podemos ver que $M_{2,3}M_{4,1}$ biseca a $MN$.

Por el teorema 2 sabemos que el punto medio $J$ de $MN$ es el centroide de $\square ABCD$ y que la intersección de las bimedianas $M_{1,2}M_{3,4}$ y $M_{2,3}M_{4,1}$ es el centroide de $\square O_1O_2O_3O_4$.

$\blacksquare$

Más adelante…

En la siguiente entrada continuaremos el estudio de los cuadriláteros cíclicos que comenzamos en la entada teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Muestra que un cuadrilátero es dividido por una de sus diagonales en dos triángulos de igual área si y solo si la diagonal biseca a la otra diagonal.
  2.  Verifica que el teorema de Varignon se cumple para los cuadriláteros cóncavo y cruzado.
  3. Sean $\square ABCD$ un cuadrilátero $U$ y $V$ los puntos medios de $\overline{AC}$ y $\overline{BD}$ respectivamente y $T$ la intersección de $\overline{AB}$ con $\overline{CD}$. Prueba que $(\triangle TUV) = \dfrac{(\square ABCD)}{4}$.
    Sugerencia. Considera $H$ y $F$ los puntos medios de $\overline{AD}$ y $\overline{BC}$ y los cuadriláteros $\square ACBD$, $\square CUFT$ y $\square BVFT$ para calcular el área de los triángulos $\triangle UVF$, $\triangle UFT$ y $\triangle VFT$.
Figura 7
  1. Construye un cuadrilátero dados dos ángulos opuestos, la longitud de las diagonales y el ángulo entre las diagonales.
  2. Verifica que el teorema de Van Aubel se cumple cuando los cuadrados son construidos internamente, y también para los para los cuadriláteros cóncavo y cruzado.
  3. Muestra que en un cuadrilátero convexo los puntos medios de sus diagonales y los puntos medios de las diagonales de su cuadrilátero externo de Van Aubel, forman un cuadrado, y que el punto externo de Van Aubel pertenece al circuncírculo de este cuadrado.

Entradas relacionadas

Fuentes

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Geometría Analítica I: El espacio vectorial R²

Por Elsa Fernanda Torres Feria

6 respuestas

Introducción

En la entrada anterior llegamos a una equivalencia entre un punto en el plano euclidiano y parejas de números $(x,y)$, donde $x, y \in \mathbb{R}$. Podemos imaginarnos entonces el conjunto de todas las parejas ordenadas de números reales como $\mathbb{R} \times \mathbb{R} = \mathbb{R}^2$, donde $\times$ hace referencia al producto cartesiano (en general para conjuntos $A$ y $B$, $A \times B := \{ (a,b) : a \in A, b \in B \}$).

Con esto en mente, es posible imaginaros a los postulados de Euclides ya no como afirmaciones incuestionables, sino como consecuencias de una geometría construida a partir de las parejas de números reales. Ahora nuestra base será la teoría de conjuntos, los números reales y las parejas ordenadas. Usaremos los axiomas y propiedades que tienen para construir nuestros objetos.

Para entender mejor cómo se trabajará en el espacio formado por todas las parejas $(x,y)$ de reales, comencemos esta entrada hablando de los números reales.

Los números reales

Como advertencia, esta sección tiene muchos símbolos. Es normal. Muy muy a grandes rasgos, lo que queremos recordar aquí es que los reales se pueden sumar, restar, multiplicar y dividir (excepto divisiones entre cero). Y que todas estas operaciones tienen propiedades bonitas.

A partir de este punto, pensaremos en los reales como algo que sabemos con seguridad puede ser construido, y tomaremos como ciertos todos los axiomas que éstos cumplen. Los axiomas se pueden resumir en la siguiente frase, que desglosaremos una vez enunciada:

«$\mathbb{R}$ es un campo ordenado y completo»

Que $\mathbb{R}$ sea un campo hace referencia a que como conjunto, tiene las operaciones de suma ($+$) y producto ($\cdot$) definidas tales que:

  • $\mathbb{R}$ con la suma, es un grupo conmutativo.
    • La suma es asociativa, es decir: $ \forall a,b,c \in \mathbb{R}$, se tiene que $(a+b)+c=a+(b+c)$ ($\forall$ se lee para todo).
    • Existe $ 0 \in \mathbb{R}$ tal que $\forall a \in \mathbb{R}$, $a+0=a=0+a$.
    • Existe $ b \in \mathbb{R}$ tal que $a+b=0=b+a$. ($b=-a$).
    • Es conmutativa, es decir, $\forall a,b \in \mathbb{R}$, se tiene que $a+b=b+a$.
  • $\mathbb{R} \setminus \{0\}$ (los reales sin el elemento cero) con el producto, es un grupo conmutativo; de manera análoga a la suma tenemos:
    • El producto es asociativo: $\forall a,b,c \in \mathbb{R}$, se tiene que $(ab)c=a(bc)$ (nota que estamos omitiendo el símbolo de multiplicación).
    • Existe $ 1 \in \mathbb{R}$ tal que $\forall a \in \mathbb{R}$, $a\cdot1=a=1\cdot a$.
    • Existe $ b \in \mathbb{R}$ tal que $ab=1=ba$. ($b=\frac{1}{a}$).
    • Es conmutativo, es decir, $\forall a,b \in \mathbb{R}$, se tiene que $ab=ba$.
  • La suma y el producto se distribuyen: $\forall a,b,c \in \mathbb{R}$, se tiene que $a(b+c)=ab+ac$.

Que sea ordenado nos indica que tenemos una relación que es un orden total y es compatible con la suma y el producto. $\forall a,b,c\in \mathbb{R}$:

  • Se cumple exactamente una de las siguientes relaciones: $a<b$, $b<a$, $a=b$.
  • Si $a \leq b$ y $b \leq c$, entonces $a \leq c$.
  • Si $a \leq b$, entonces $a+c \leq b+c$.
  • Si $a,b \geq 0$ , entonces $ab \geq 0$.

Por último, que sea completo es una noción formal en la cual no nos enfocaremos mucho, pero que a grandes rasgos quiere decir que en los números reales «no hay hoyos», lo cual es muy importante para cuando se quiere usar este sistema numérico para hacer cálculo diferencial e integral.

Por lo que vimos en la entrada anterior, podemos representar cualquier punto en el espacio euclidiano con una pareja de números reales. Ya que hemos dado un pequeño repaso formal de la estructura de $\mathbb{R}$ (todo esto lo cumple cada entrada de un punto $(a,b)$), demos el siguiente paso y exploremos el espacio vectorial $\mathbb{R}^2$.

Espacio vectorial $\mathbb{R}^2$

Comencemos definiendo formalmente un concepto que exploramos en la entrada anterior: el vector.

Definición. Un vector $v$ con dos entradas, es una pareja ordenada de números reales $v=(x,y)$.

Ejemplos. Algunos vectores en $\mathbb{R}^2$ son:

  • $(1,4)$
  • $(-3,2)$
  • $(\pi,1)$
  • $(2.3,-e)$

Utiliza el siguiente interactivo de GeoGebra: mueve el punto $C$ y explora cómo el vector cambia con esta acción.

Definición. El conjunto de todos los vectores con dos elementos (ambos reales) es $\mathbb{R}^2$. En símbolos tenemos que:

$\mathbb{R}^2=\{(x,y): x,y \in \mathbb{R} \}$

Si realizaste la tarea moral anterior, te habrás dado cuenta que podemos encontrar ciertas regiones geométricas al imponer condiciones sobre las entradas de un vector. En la tarea se hace referencia a áreas muy determinadas conocidas como cuadrantes, pero no son las únicas regiones existentes. Hagamos un ejercicio de esto.

Problema. Ubica dentro del plano de dos dimensiones las siguientes regiones geométricas definidas al imponer ciertas restricciones en las entradas de un vector:

  1. $\{ (x,y) \in \mathbb{R}^2 : x \leq 0, y \geq 1 \}$
  2. $\{ (x,y) \in \mathbb{R}^2 : x \geq \pi , y \leq \pi \}$
  3. $\{ (x,y) \in \mathbb{R}^2 : x \geq y \}$

Solución. Para encontrar estas áreas basta con ubicar la región en la que se vale cada condición por separado. La intersección de las regiones será la región que buscamos. Esto se vale para los dos primeros incisos.

Utiliza el siguiente interactivo de GeoGebra en el que ya están las condiciones para visualizar la primera región geométrica para localizar la región del segundo inciso.

¿Qué pasa con el inciso 3? Puede parecer más complicado porque ahora las coordenadas están conectadas en una sola restricción. Antes de introducir la condición en GeoGebra, imagina cuál es la región en la que la condición se cumple.

Ahora, utilicemos el siguiente interactivo para usar lo que ya sabemos y determinar intuitivamente cuál es el área que determina la condición $x \geq y$. Pensemos en el caso específico $x = 1$, $y$ puede ser a lo más $1$ ($y \leq 1$); al restringir nuestra $x$ podemos obtener dos condiciones a partir de las cuales ya sabemos cómo encontrar la región en las que se cumplen. Si ves el interactivo, notarás que la intersección de las regiones es únicamente la recta definida por $x=1$ pero no toda, sino que sólo a partir de cuando $y=1$ hacia abajo. ¿qué pasa si mueves los deslizadores para cambiar los valores de $x$ y $y$ ? Se obtienen segmentos de recta correspondientes a un valor de $x$ fijo que comienzan cuando $y$ es menor o igual a ese valor.

Resulta que estos segmentos de recta se obtienen para cualquier valor de $x$. ¿qué pasa ahora cuando unes todas estas líneas? En este punto es importante recordar que en $\mathbb{R}$ hay un real entre cada dos reales. Entonces, se puede construir el segmento de recta del que hemos hablado. Por lo que la únión de todas estas rectas define un área, ¿ya imaginas cuál es? Verifícalo al escribir la condición $y \leq x$ en el interactivo anterior.

$\triangle$

La suma en $\mathbb{R}^2$

Regresando a la teoría, el siguiente paso lógico después de definir ciertos objetos (en este caso vectores), es averiguar cómo operan. Definamos entonces la suma y el producto escalar de vectores haciendo uso del conocimiento que ya tenemos acerca de las operaciones en los reales.

Definición. Sean $v_1, v_2 \in \mathbb{R}^2$ dados por $v_1=(x_1,y_1)$ y $v_1=(y_1,y_2)$. Su suma está dada por el vector

$v_1+v_2 := (x_1+x_2,y_1+y_2)$

Esto es, que la suma de vectoes se hace entrada a entrada y esta bien definida pues al final lo que estamos sumando son números reales.

Ejemplos.

  • $(-3,4) + (2,2)=(-3+2,4+2)=(-1,6)$
  • $(7,4) + (2,1)=(7+2,4+1)=(9,5)$
  • $(-3.-7) + (1,2)=(-3+1,-7+2)=(-2,-5)$

En el siguiente interactivo podrás ver el primer ejemplo de manera gráfica en el plano, donde los vectores de colores son los que se suman y el vector negro es el resultante.

Además de poder obtener el vector suma de manera algebraica hay otra manera más de hacerlo: En el mismo interactivo hay una copia de cada vector de color, escoge uno de los dos vectores de la suma y transpórtalo por completo y paralelo a sí mismo para que su punto de inicio no sea el origen, si no el punto donde termina el otro vector. Por ejemplo, deja el vector azul en su lugar y transporta al verde para que su punto de partida sea la flecha del vector azul. Si lo hiciste correctamente, notarás que ahora ese vector transportado termina en donde el vector resultante de la suma (negro) termina. Resulta que si quieres sumar dos vectores, puedes avanzar desde el origen hasta las coordenadas de uno de ellos y ahora »tomando» como origen ese punto al que llegaste, avanzar las coordenadas del otro vector. Al final llegarás al punto del vector resultante de la suma. Este método es conocido como el método del paralelogramo.

El producto escalar en $\mathbb{R}^2$

Otra operación importante en $\mathbb{R}^2$ es el producto escalar, que intuitivamente combina a un real y a un vector y «reescala» al vector por el factor dado por el número real.

Definición. Para $r$ un número real y $v_1 \in \mathbb{R}^2$ dado por $v_1=(x,y)$, el producto escalar $rv$ está dado por:

$rv:=(rx,ry)$

Ejemplos.

  • $4(7,3.5)=(28,14)$
  • $2(5,3)=(10,6)$
  • $2.3(6,3)=(13.8,6.9)$

Utiliza el siguiente interactivo moviendo el deslizador del valor $a$ que multiplica al vector $(5,3)$ para interiorizar lo que implica multiplicar un vector por un escalar. Si lo notas, lo único que hace es reescalarlo, y si el escalar es negativo, entonces le cambia el sentido, pero no la dirección.

Una última cosa que es muy importante mencionar es que hasta ahora no hemos dicho cómo multiplicar dos (o más vectores). Sólo tenemos un producto que toma un escalar (un real) y lo multiplica con un vector, cuyo resultado acaba siendo un vector.

Más adelante…

En esta entrada dimos un breve repaso acerca de los números reales que nos sirvió para entender el espacio $\mathbb{R}^2$ y las operaciones dentro de este. El desarrollo aquí hecho servirá como herramienta para construir la representación algebraica de una recta.

Tarea moral

  • Sean $v=(8,9)$, $w=(3,-2)$, $u=(-5-4)$. Calcula y dibuja las siguientes operaciones de vectores:
    • $5v+3u$
    • $u-3w$
    • $2.5v+9w-u$
  • Demuestra en $\mathbb{R}$ que si $-1$ es el inverso aditivo de $1$, entonces $-a$ es el inverso aditivo de $a$.
  • Por los axiomas, sabemos que la conmutatividad se vale para la suma de reales, es decir, que si $a$ y $b$ son reales, entonces $a+b=b+a$. Pero en esta entrada definimos una nueva suma: la de vectores. De entrada, no sabemos qué propiedades cumple. A partir de las definiciones que dimos, y de los axiomas de los reales, demuestra que también se tiene $u+v=v+u$ para $u$ y $v$ vectores en $\mathbb{R}^2$.
  • Determina, si es posible, las regiones siguientes geométricas. Si dicha región es vacía, argumenta por qué.
    • $\{ (x,y) \in \mathbb{R}^2 : x \leq y, y \geq x \}$
    • $\{ (x,y) \in \mathbb{R}^2 : x \leq y, y > x \}$
    • $\{ (x,y) \in \mathbb{R}^2 : x \leq 3, y > \pi \}$
  • En el interactivo de producto escalar siempre sucede que la línea que pasa por el extremo del vector verde y el extremo del vector rojo siempre pasa por el origen. ¿Por qué sucede esto?

Seminario de Resolución de Problemas: Vectores en geometría

Por Leonardo Ignacio Martínez Sandoval

2 respuestas

Introducción

Anteriormente, comenzamos esta serie de entradas de geometría platicando de algunas técnicas euclideanas o sintéticas que se pueden usar para resolver problemas en el plano. Después, tomamos herramientas de la geometría analítica, las cuales nos permiten poner problemas en términos de coordenadas y ecuaciones. Lo que haremos ahora es ver varios ejemplos del uso de vectores en geometría.

A diferencia de la geometría analítica, cuando hablamos de soluciones por vectores estamos hablando de aquellas que aprovechan la estructura de espacio vectorial en $\mathbb{R}^2$. En otras palabras, usamos argumentos en los cuales pensamos a los puntos del plano como vectores, los cuales tienen una dirección y una magnitud. Los vectores tienen operaciones de suma y de producto por un escalar. Además, tienen producto punto, norma y transformaciones dadas por matrices. Apenas tocaremos la superficie del tipo de teoría que se puede usar. Un buen curso de álgebra lineal te puede dar más herramientas para resolver problemas geométricos.

Interpretar puntos como vectores

Pongamos un origen $O$ en el plano. A cada punto $P$ le corresponden ciertas coordenadas dadas por parejas de reales $(x,y)$, que identificaremos con $P$. Al origen le corresponden las coordenadas $(0,0)$. Si tenemos otro punto $Q=(w,z)$, entonces su suma es el vector $P+Q=(x+w,y+z)$. Si tomamos un real $r$, el vector $rP$ es el vector de coordenadas $(rx,ry)$.

Suma de vectores
Suma de vectores

La suma $P+Q$ se puede encontrar mediante la ley del paralelogramo: los puntos $O,P,P+Q,Q$ hacen un paralelogramo en ese orden cíclico. La resta $Q-P$ está definida por $Q+(-1)P$, y la llamamos el vector $PQ$. Geométricamente coincide con el vector que va «de $P$ a $Q$». Observa que el orden es importante y que $OP=P$.

Resta de vectores
Resta de vectores

Proposición (de la razón). Si tenemos dos puntos $P$ y $Q$ distintos y $m,n$ son reales, entonces podemos encontrar al único punto $R$ en la recta por $P$ y $Q$ tal que $$\frac{PR}{RQ}=\frac{m}{n}$$ así: $$R=\frac{n}{m+n}P + \frac{m}{m+n} Q.$$

Punto en una recta con cierta razón
Punto en una recta con cierta razón

Veamos dos problemas en los que se usan estas ideas de vectores en geometría, en particular, la proposición de la razón.

Problema. En el triángulo $ABC$ se toman puntos $D,E,F$ sobre los segmentos $BC,CA,AB$ tales que $\frac{BD}{DC}=\frac{CE}{EA}=\frac{AF}{FB}=\frac{1}{4}$. Muestra que $ABC$ y $DEF$ tienen el mismo gravicentro.

Sugerencia pre-solución. Encuentra una fórmula en términos vectoriales para el gravicentro de un triángulo $ABC$.

Solución. Tomemos un triángulo $PQR$ y pensemos a sus vértices como vectores. Afirmamos que su gravicentro $X$ es el punto correspondiente a $\frac{P+Q+R}{3}$ Demostraremos esto.

El gravicentro está a un tercio del punto medio hacia el vértice correspondiente
Razón del gravicentro en la mediana

Primero haremos un argumento de geometría sintética. El gravicentro es por definición el punto de intersección de las medianas de un triángulo. Si $L$ es el punto medio de $QR$ y $M$ es el punto medio de $RP$, entonces $X$ es el punto de intersección de $PL$ y $QM$. Tenemos que $$\frac{RL}{LQ}=1=\frac{RM}{MP},$$ así que por el teorema de Tales se tiene que la recta por $L$ y $M$ es paralela al lado $PQ$, y $\frac{LM}{PQ}=\frac{1}{2}$. Esto muestra que los triángulos $XLM$ y $XPQ$ son semejantes en razón $1$ a $2$. Por lo tanto, $\frac{LX}{XP}=\frac{1}{2}$.

Ahora hagamos el argumento vectorial, pensando a los puntos como vectores. El punto $L$ está a la mitad de $QR$, así que por la proposición de la razón, $$L=\frac{Q+R}{2}.$$ El punto $X$ cumple $\frac{LX}{XP}=\frac{1}{2}$, así que de nuevo por la proposición de la razón.
\begin{align*}
X&=\frac{2L+P}{2+1}\\
&=\frac{Q+R+P}{3}\\
&=\frac{P+Q+R}{3}.
\end{align*}

Esto es el resultado auxiliar que queríamos mostrar. Regresemos al problema.

De acuerdo al resultado auxiliar, el gravicentro de $ABC$ es $$G:=\frac{A+B+C}{3}.$$ Usando una vez más la proposición de la razón, los puntos $D$, $E$ y $F$ los podemos calcular como sigue:
\begin{align*}
D&=\frac{4B+C}{4+1}=\frac{4B+C}{5}\\
E&=\frac{4C+A}{4+1}=\frac{4C+A}{5}\\
F&=\frac{4A+B}{4+1}=\frac{4A+B}{5}.
\end{align*}

De esta forma, el gravicentro $G’$ de $DEF$ lo podemos encontrar como sigue:
\begin{align*}
G’&=\frac{D+E+F}{3}\\
&=\frac{\frac{4B+C}{5}+\frac{4C+A}{5}+\frac{4A+B}{5}}{3}\\
&=\frac{A+B+C}{3}\\
&=G.
\end{align*}

Esto termina la solución del problema.

$\square$

Problema. En el paralelogramo $ABCD$ el punto $F$ es el punto medio de $CD$. Muestra que el segmento $AF$ corta a la diagonal $BD$ en un punto $E$ tal que $\frac{DE}{DB}=\frac{1}{3}$.

Sugerencia pre-solución. Hay varias formas de hacer las cuentas en este problema, pero el uso de una notación adecuada te hará simplificar muchas operaciones.

Solución. Pensemos a los puntos de la figura como vectores. Coloquemos al punto $A$ en el origen. El punto $C$ está dado por $B+D$, de modo que $$F:=\frac{C+D}{2}=\frac{B+2D}{2}.$$

Vectores en geometría: problema de paralelogramo
Figura auxiliar para problema de paralelogramo

Para encontrar al punto $E$, notemos que está en las rectas $AF$ y $BD$. De esta forma, deben existir reales $r$ y $s$ tales que $$E=rF$$ y $$E=sB+(1-s)D.$$ Expresando $F$ en términos de $B$ y $D$ en la primer ecuación, tenemos que $$E=\frac{rB+2rD}{2}=\frac{rB}{2}+rD.$$ De ambas expresiones para $E$, concluimos que
\begin{align*}
s=\frac{r}{2}\\
1-s=r.
\end{align*}

Este sistema de ecuaciones tiene solución $r=\frac{2}{3}$, $s=\frac{1}{3}$, y por lo tanto $E=\frac{B+2D}{3}$. De aquí se obtiene $\frac{DE}{EB}=\frac{1}{2}$, o bien $\frac{DE}{DB}=\frac{DE}{DE+EB}=\frac{1}{3}$, como queríamos mostrar.

$\square$

Producto punto, norma y ángulos

Para dos vectores $P=(x,y)$ y $Q=(w,z)$ definimos su producto punto como la cantidad $P\cdot Q = xw+yz$. El productos puntos es:

  • Conmutativo: $P\cdot Q = Q\cdot P$
  • Abre sumas: $P\cdot (Q+R)=P\cdot Q + P\cdot R$
  • Saca escalares: $(rP)\cdot Q = r(P\cdot Q)$.

La norma de $P$ se define como $\norm{P}=\sqrt{P\cdot P}$, y coincide con la distancia de $P$ al origen. La norma de $PQ$ es entonces $\norm{PQ}=\sqrt{(Q-P)\cdot (Q-P)}$ y coincide con la distancia de $P$ a $Q$.

El ángulo entre dos vectores $PQ$ y $RS$ se define como el ángulo cuyo coseno es $$\frac{PQ \cdot RS}{\norm{PQ}\norm{RS}},$$ y coincide precisamente con el ángulo (orientado) geométrico entre las rectas $PQ$ y $RS$. De esta forma, las rectas $PQ$ y $RS$ son perpendiculares si y sólo si el producto punto $PQ\cdot RS$ es cero.

Problema. Sea $ABC$ un triángulo con sus vértices pensados como vectores. Sean $H$ y $O$ su ortocentro y circuncentro respectivamente. Supongamos que el circuncentro $O$ está en el origen. Muestra que $H=A+B+C$.

Sugerencia pre-solución. Trabaja hacia atrás. Define al punto $A+B+C$ y ve que las rectas que unen a los vértices con este punto en efecto son alturas. Para calcular los ángulos, usa el producto punto y sus propiedades.

Solución. Como el circuncentro equidista de $A$. $B$ y $C$, tenemos que $$\norm{A}=\norm{B}=\norm{C}.$$ Tomemos el punto $H’=A+B+C$.

Vectores en geometría para encontrar el ortocentro
Ortocentro con vectores

Calculemos el ángulo entre las rectas $BC$ y $AH’$, haciendo su producto punto:
\begin{align*}
BC\cdot AH’ &= (C-B)\cdot (H’-A)\\
&=(C-B)\cdot(C+B)\\
&=C\cdot C + C\cdot B – B\cdot C – B\cdot B\\
&=\norm{C}^2 – \norm{B}^2\\
&=0.
\end{align*}

Observa que estamos usando la linealidad y conmutatividad del producto punto. Al final usamos que $A$ y $C$ tienen la misma norma.

Esto muestra que la recta $AH’$ es la altura al lado $BC$. De manera análoga, $BH’$ y $CH’$ son las alturas a los lados $CA$ y $AB$ respectivamente. Por lo tanto, $H’$ es el ortocentro, así que $H=A+B+C$.

$\square$

Cualquier triángulo $ABC$ en el plano se puede trasladar para que su circuncentro $O$ quede en el origen. El ortocentro estará en $H=A+B+C$ y el gravicentro, como vimos antes, en $G=\frac{A+B+C}{3}$, que es un múltiplo escalar de $H$. Por lo tanto, $O$, $H$ y $G$ están alineados. Acabamos de demostrar con vectores en geometría un clásico resultado euclideano.

Teorema (recta de Euler). En cualquier triángulo $ABC$, el circuncentro $O$, el gravicentro $G$ y el ortocentro $H$ están alineados. Además, $$\frac{OG}{GH}=\frac{1}{2}.$$

Teorema de la recta de Euler
Teorema de la recta de Euler

Si el circuncentro no está en el origen, ahora podemos usar el teorema de la recta de Euler y la proposición de la razón para concluir que $G=\frac{2O+H}{3}$. Usando que $G=\frac{A+B+C}{3}$, obtenemos el siguiente corolario

Corolario. Sea $ABC$ un triángulo en el plano, $H$ su ortocentro y $O$ su circuncentro. Entonces al pensar a los puntos como vectores tenemos que $$A+B+C=2O+H.$$

Más problemas

Puedes encontrar más problemas del uso de vectores en geometría en la sección 8.3 del libro Problem Solving through Problems de Loren Larson.