Introducción
Con esta entrada concluimos la unidad tres y en general temas relacionados con el triángulo, hablaremos de la circunferencia de Brocard y el primer triángulo de Brocard, veremos como se relacionan con los puntos de Brocard.
Circunferencia de Brocard
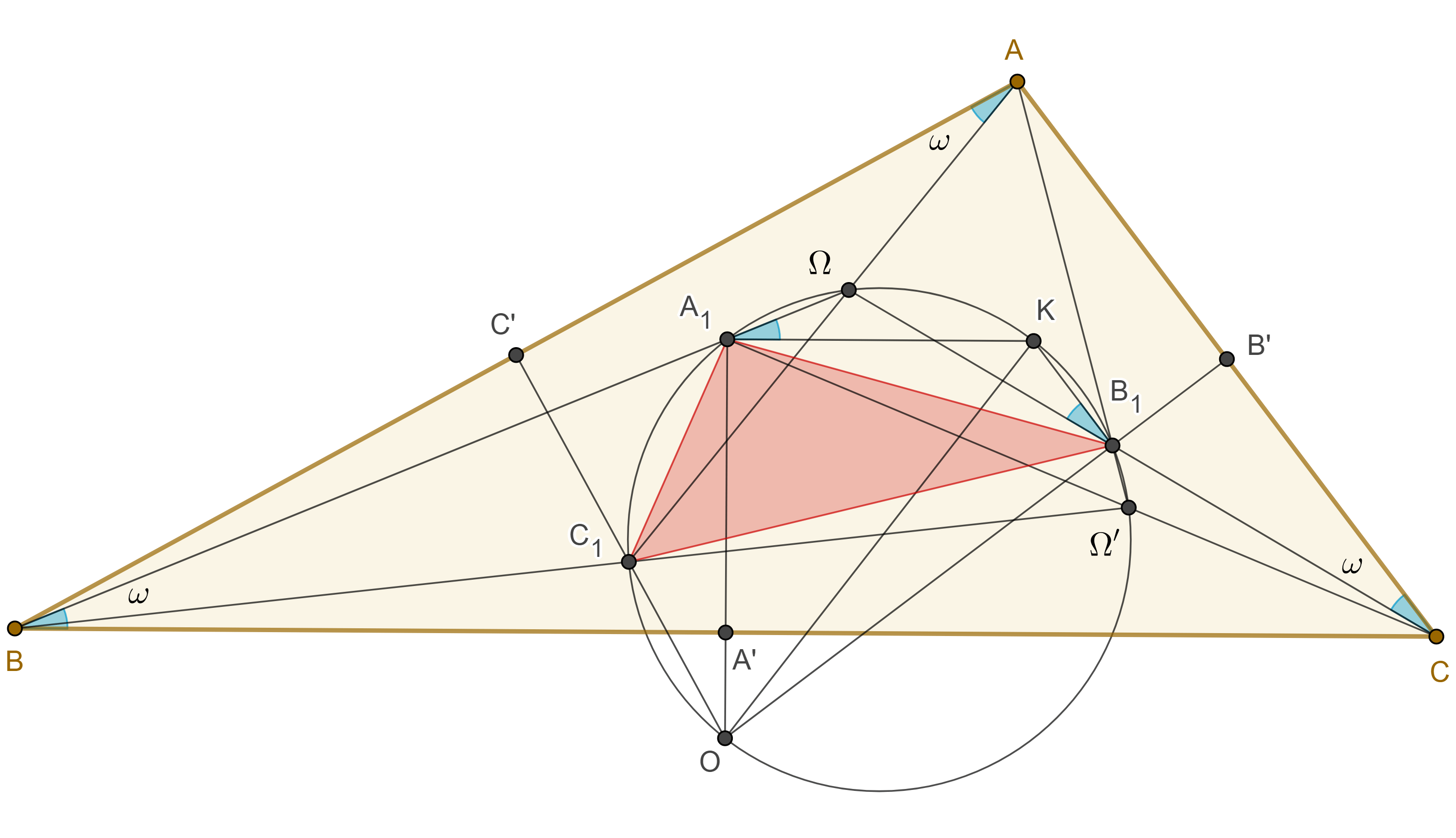
Definición. La circunferencia $\Gamma(KO)$ que tiene como diámetro el segmento que une el punto simediano $K$ y el circuncentro $O$ de un triángulo se conoce como circunferencia de Brocard.
El triángulo cuyos vértices son las segundas intersecciones de las mediatrices de un triángulo con su circunferencia de Brocard es el primer triángulo de Brocard.
Observación. Recordemos que el centro de la primera circunferencia de Lemoine es el punto medio entre el punto simediano y el circuncentro de un triángulo, por lo tanto, la circunferencia de Brocard y la primera circunferencia de Lemoine son concéntricas.
Teorema 1. Los puntos de Brocard están en la circunferencia de Brocard.
Demostración. En $\triangle ABC$ sea $\Omega$ el primer punto de Brocard, $K$ el punto simediano, $O$ el circuncentro y $A’$, $B’$, $C’$, los puntos medios de $BC$, $CA$ y $AB$ respectivamente.
Recordemos que las distancias de $K$ a los lados del triángulo son proporciónales a estos,
$d(K, BC) = a \dfrac{2(\triangle ABC)}{a^2 + b^2 + c^2}$
En un ejercicio de la entrada anterior se pide mostrar que
$\dfrac{1}{\tan \omega} = \cot \omega = \dfrac{a^2 + b^2 + c^2}{4(\triangle ABC)}$.
Donde $\omega$ es el ángulo de Brocard y $a$, $b$, $c$ los lados de $\triangle ABC$.
Por lo tanto, $d(K, BC) = \dfrac{a}{2} \tan \omega$.
Sea $A_1 = OA’ \cap B\Omega$, en $\triangle A_1BA’$, $A’A_1 = \dfrac{a}{2} \tan \omega$.
Esto implica que $A_1K \parallel BC$, como $OA_1$ es mediatriz de $BC$ entonces $\angle OA_1K = \dfrac{\pi}{2}$, y por lo tanto $A_1 \in \Gamma (KO)$.
De manera similar si consideramos $B_1$ la intersección del rayo $C\Omega$ con la mediatriz de $CA$, podemos ver $B_1K \parallel CA$ y que $B_1 \in \Gamma(KO)$.
Como $A_1K \parallel BC$ y $B_1K \parallel CA$ entonces $\angle KA_1\Omega = \omega = \angle KB_1\Omega$.
En consecuencia, el cuadrilátero $\square \Omega A_1B_1K$ es cíclico, pero el circuncírculo de $\triangle A_1B_1K$, es la circunferencia de Brocard.
Por lo tanto, el primer punto de Brocard $\Omega$, está en la circunferencia de Brocard.
Sea $\Omega’$ el segundo punto de Brocard, como $A_1$ y $B_1$ están en las mediatrices de $BC$ y $CA$ entonces $\triangle A_1BC$ y $\triangle B_1CA$ son isósceles y $\angle A_1CB = \angle B_1AC = \angle \Omega’CB = \angle \Omega’AC = \omega$.
Esto implica que $CA_1$ y $AB_1$ se intersecan en $\Omega’$.
Ya que $A_1K \parallel BC$ y $B_1K \parallel CA$, entonces, $\angle \Omega’A_1K = \omega$ y $\angle KB_1\Omega’ = \pi – \omega$.
Esto implica que $\square A_1\Omega B_1K$ es cíclico, y así el segundo punto de Brocard está en la circunferencia de Brocard.
$\blacksquare$
Corolario 1. Un triángulo y su primer triángulo de Brocard están en perspectiva desde los puntos de Brocard.
Demostración. En el teorema anterior vimos que $BA_1$ y $CB_1$ se intersecan en el primer punto de Brocard, de manera similar se puede ver que $A$, $C_1$ y $\Omega$ son colineales.
También mostramos que $CA_1 \cap AB_1 = \Omega’$, de manera análoga podemos ver que $BC_1$ pasa por $\Omega’$.
Por lo tanto $\Omega$ y $\Omega’$ son centros de perspectiva de $\triangle ABC$ y $\triangle A_1B_1C_1$.
$\blacksquare$
Corolario 2. $\triangle ABC$ y su primer triángulo de Brocard son semejantes.
Demostración. Como $B_1K \parallel CA$, $A_1K \parallel BC$ y tomando en cuenta que $\square A_1C_1B_1K$ es cíclico entonces $\angle ACB = \pi – \angle A_1KB_1 = \angle B_1C_1A_1$.
De manera similar vemos que $\angle A = \angle A_1$ y $\angle B = \angle B_1$.
$\blacksquare$
Conjugado isotómico del punto simediano
En la entrada triángulos en perspectiva vimos que si dos triángulos tienen dos centros de perspectiva entonces existe un tercero, en la siguiente proposición describimos este punto.
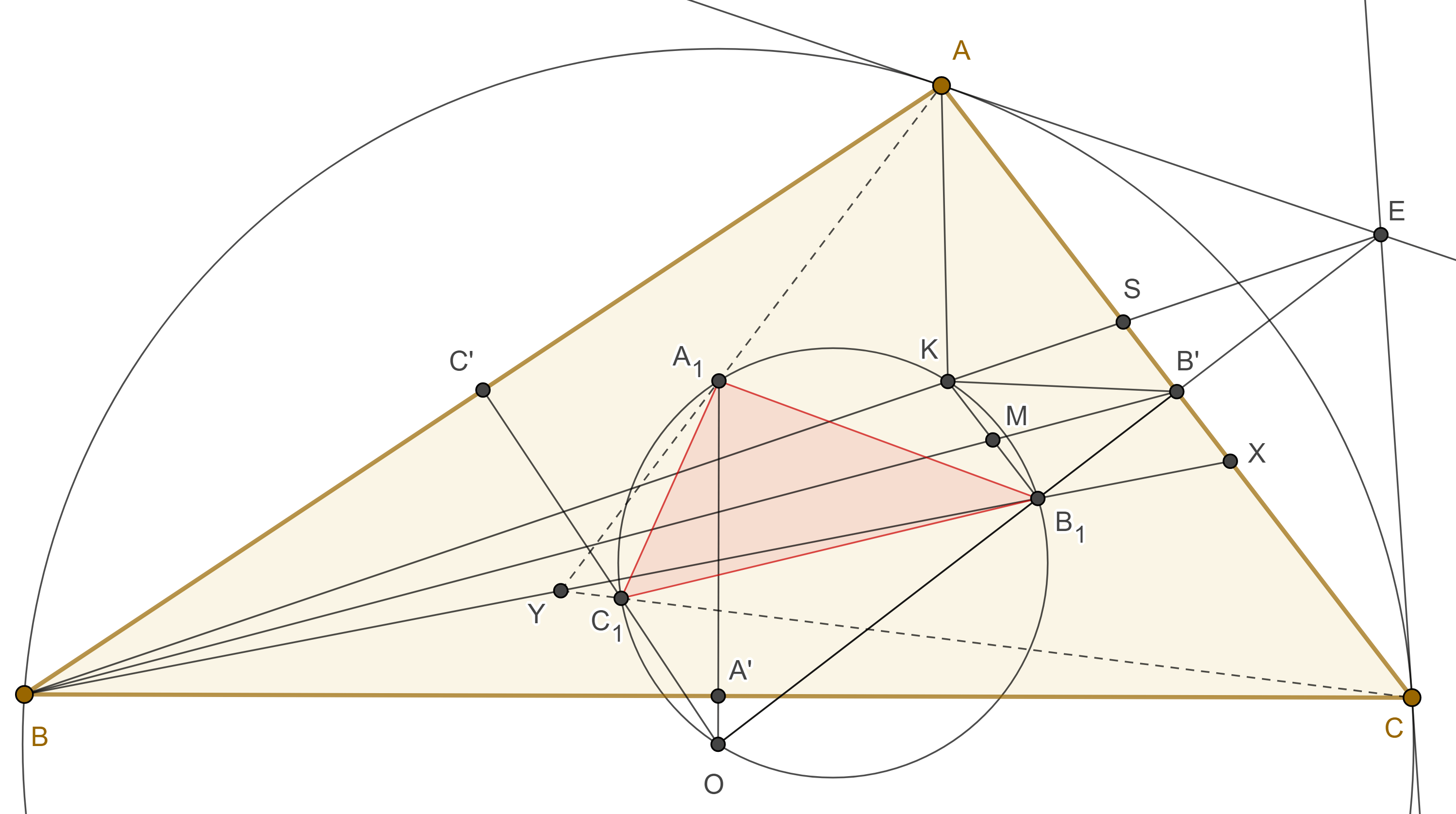
Proposición 1. El tercer centro de perspectiva entre un triángulo y su triángulo de Brocard es el conjugado isotómico del punto simediano respecto del triángulo original.
Demostración. Bajo la misma notación del teorema anterior, Recordemos que la $A$-simediana y la $A$-exsimediana son conjugadas armónicas respecto de $AB$, $AC$.
También sabemos que $BK$ y la $A$-exsimediana se intersecan en un punto exsimediano, es decir el punto de intersección de las tangentes por $A$ y $C$ al circuncírculo de $\triangle ABC$.
Sea $S = BK \cap AC$, entonces la hilera $BKSE$ es armónica, así, el haz $B’(BKSE)$ es armónico.
Tomando en cuenta que $OB_1B’E$ es una recta.
En el teorema anterior vimos que $B_1K \parallel AC$, entonces las otras tres rectas del haz bisecan a $B_1K$, es decir $BB’$ biseca a $B_1K$.
Sea $X = BB_1 \cap AC$, como $\triangle BB_1K$ y $\triangle BXS$ son semejantes entonces $B’$ es el punto medio entre $X$ y $S$.
Por lo tanto, $BK$, $BB_1$, son rectas isotómicas, es decir, unen puntos isotómicos con el vértice opuesto.
Igualmente vemos que $AK$, $AA_1$ y $CK$, $CC_1$ son rectas isotómicas, como las simedianas concurren en $K$, entonces, $AA_1$, $BB_1$, $CC_1$concurren en u punto $Y$.
$\blacksquare$
Centroide del triángulo de Brocard
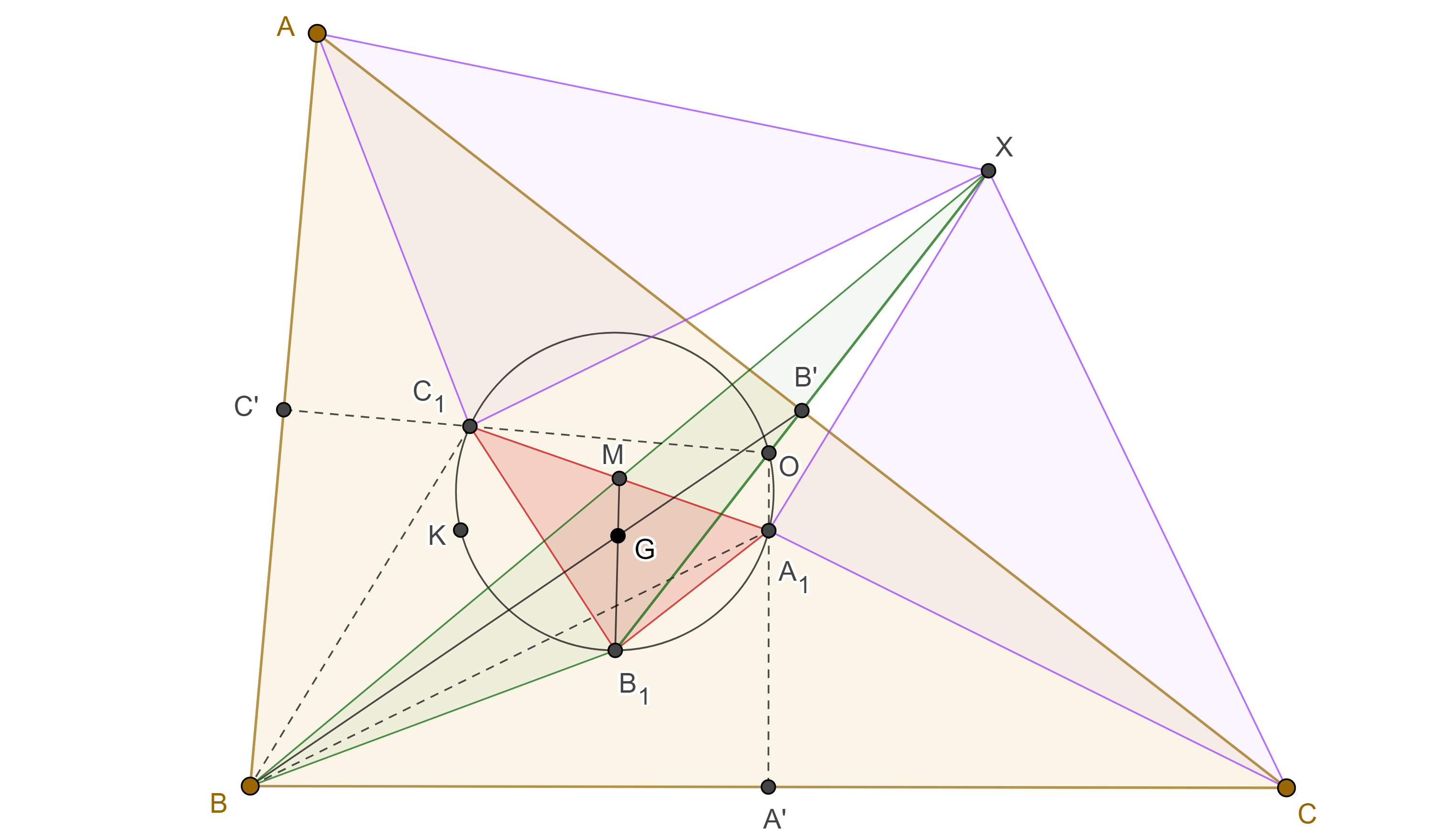
Teorema 2. El centroide de un triángulo y el centroide de su primer triángulo de Brocard coinciden.
Demostración. Nuevamente emplearemos la notación del teorema 1.
$A_1$, $B_1$ y $C_1$ están en las mediatrices de $BC$, $CA$ y $AB$ entonces $\triangle A_1BC$, $\triangle B_1CA$, $\triangle C_1AB$ son isósceles, además son semejantes, pues $\angle A_1BC = \angle B_1CA = \angle C_1AB = \omega$, por lo tanto,
$\dfrac{AC_1}{AB_1} = \dfrac{AB}{CA}$ y $\dfrac{CA_1}{CB_1} = \dfrac{BC}{CA}$.
Sea $X$ la reflexión de $B_1$ respecto de $CA$, entonces
$\angle C_1AX = \angle C_1AC + \angle CAX $
$= \angle C_1AC + \angle B_1AC = \angle C_1AC + \omega $
$= \angle A$,
además $\dfrac{AC_1}{AX} = \dfrac{AC_1}{AB_1} =\dfrac{AB}{CA}$.
Por criterio de semejanza LAL, $\triangle ABC \sim \triangle AC_1X$, igualmente podemos ver que $\triangle ABC \sim \triangle XA_1C$.
Por lo tanto, $\triangle AC_1X \sim \triangle XA_1C$, pero $AX = AB_1 = B_1C = CX$, así que $\triangle AC_1X$ y $\triangle XA_1C$ son congruentes.
En consecuencia, $C_1X = A_1C = A_1B$ y $XA_1 = AC_1 = C_1B$, esto implica que $\square C_1BA_1X$ es un paralelogramo y por lo tanto $A_1C_1$ y $BX$ se cortan en su punto medio $M$.
En $\triangle B_1BX$, $B_1M$ y $BB’$ son medianas, donde $B’$ es el punto medio de $B_1X$ y $CA$, por lo tanto, su intersección $G$, triseca a ambas medianas de $\triangle B_1BX$.
Pero el centroide de $\triangle ABC$ y de $\triangle A_1B_1C_1$ es el único punto con esa propiedad, por lo tanto, su centroide es el mismo.
$\blacksquare$
Concurrencia en el centro de los nueve puntos.
Proposición 3. Las perpendiculares a los lados de un triángulo desde los puntos medios de su primer triángulo de Brocard concurren en el centro de los nueve puntos.
Demostración. Sean $\triangle ABC$ y $\triangle A_1B_1C_1$ su primer triángulo de Brocard, $D$, $E$, $F$, los puntos medios de $B_1C_1$, $C_1A_1$, $A_1B_1$ respectivamente.
Notemos que las perpendiculares por $D$, $E$, $F$, a $BC$, $CA$, $AB$, respectivamente, son paralelas a $OA_1$, $OB_1$, $OC_1$ respectivamente, donde $O$ es el circuncentro de $\triangle ABC$.
Como $\triangle A_1B_1C_1$ y $\triangle DEF$, están en homotecia desde $G$, el centroide de $\triangle A_1B_1C_1$, y razón $\dfrac{- 1}{2}$, entonces los tres pares de rectas paralelas son pares de rectas homotéticas, pues pasan por puntos homólogos.
Como $OA_1$, $OB_1$, $OC_1$, concurren en $O$ entonces sus correspondientes rectas homotéticas concurren en el correspondiente punto homólogo, $O’$.
Entonces $O$, $G$ y $O’$ son colineales en ese orden y $\dfrac{OG}{2} = GO’$.
Como $G$ también es el centroide de $\triangle ABC$ entonces $O’$ es el centro de los nueve puntos de $\triangle ABC$.
$\blacksquare$
Punto de Steiner
Proposición 4. Las rectas paralelas (perpendiculares) por los vértices de un triángulo a los respectivos lados de su primer triángulo de Brocard concurren en el circuncírculo del triángulo original, el punto de concurrencia se conoce como punto de Steiner (Tarry).
Demostración. Si $\triangle A_1B_1C_1$ es el primer triángulo de Brocard de $\triangle ABC$, sea $S$ la intersección de la paralela a $A_1C_1$ por $B$ y la paralela a $A_1B_1$ por $C$.
$\angle BSC = \angle C_1A_1B_1 = \angle BAC$, por lo tanto, $S$ se encuentra en el arco $\overset{\LARGE{\frown}}{AB}$.
De manera análoga vemos que $CS$ y la paralela a $B_1C_1$ por $A$ se intersecan en el circuncírculo de $\triangle ABC$.
Por lo tanto, las paralelas concurren en $S$.
Considera $T$ el punto diametralmente opuesto a $S$, entonces $AT \perp AS \Rightarrow AT \perp B_1C_1$.
De manera similar vemos que $BT \perp A_1C_1$ y $CT \perp A_1B_1$.
Por lo tanto, las perpendiculares concurren en el circuncírculo de $\triangle ABC$.
$\blacksquare$
Más adelante…
Con la siguiente entrada comenzaremos la última unidad en la que hablaremos sobre cuadriláteros, mostraremos algunos teoremas que establecen propiedades análogas a la de los triángulos, como, cuando un cuadrilátero tiene un incírculo o la formula de Euler que mide la distancia entre el incentro y el circuncentro pero esta vez para cuadriláteros.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Construye un triángulo, dado su primer triángulo de Brocard.
- Muestra que la recta que une los vértices de un triángulo con los correspondientes vértices de su primer triángulo de Brocard dividen a los lados opuestos del triángulo original en el inverso de la razón de los cuadrados de los lados adyacentes.
- Prueba que la reflexión del punto simediano respecto del centro de los nueve puntos de un triángulo es el centro de la circunferencia de Brocard de su triángulo anticomplementario.
- Muestra que el punto simediano y el circuncentro de un triángulo son el punto de Steiner y el punto de Tarry de su primer triángulo de Brocard.
- El triángulo cuyos vértices son las segundas intersecciones de las simedianas de un triángulo con su circunferencia de Brocard es el segundo triángulo de Brocard, demuestra que:
$i)$ los vértices del segundo triángulo de Brocard son los puntos medios de las cuerdas del circuncírculo de su triángulo de referencia determinadas por sus simedianas,
$ii)$ las circunferencias del grupo directo e indirecto que son tangentes a los lados de un mismo ángulo de un triángulo se intersecan en los vértices de su segundo triángulo de Brocard.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Puntos de Brocard.
- Siguiente entrada del curso: Teoremas de Varignon y Van Aubel.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 279-284.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 277-282.
- Shively, L., Introducción a la Geómetra Moderna. México: Ed. Continental, 1961, pp 73-75.
- Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 106-124.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»