Geometría Moderna I: Teoremas de Varignon y Van Aubel

Introducción

Con esta entrada damos inicio a la cuarta unidad que tratará sobre cuadriláteros. Comenzaremos hablando sobre el paralelogramo de Varignon y el teorema de Van Aubel.

Área del cuadrilátero

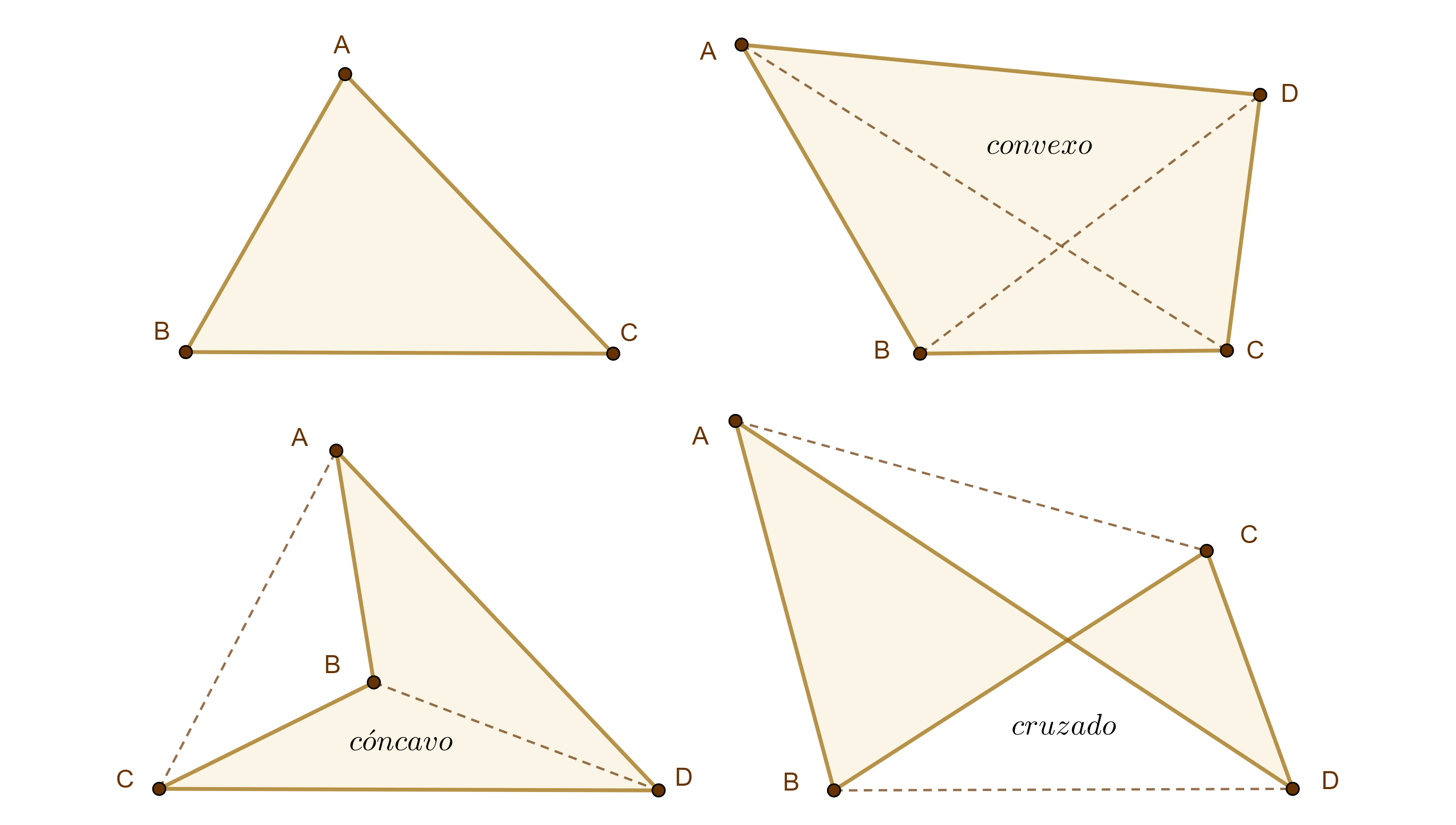
A partir de la ubicación de las diagonales de un cuadrilátero podemos establecer una clasificación de estos.

Un cuadrilátero es convexo si sus dos diagonales se encuentran dentro de él, es cóncavo si tiene una diagonal dentro y otra fuera de él, y es cruzado si las dos diagonales se ubican fuera del cuadrilátero.

El teorema de Varignon nos habla sobre el área de un cuadrilátero en general y ya que no es tan intuitivo definir el área de un cuadrilátero cruzado es necesario introducir el concepto de área orientada.

Consideraremos el área de un triángulo como positiva si recorremos sus vértices en el sentido opuesto a las manecillas del reloj y como negativa en caso contrario.

De esta manera tenemos que para un triángulo $△ A B C$ ,
$(△ A B C) = (△ B C A) = (△ C A B)$
$= - (△ C B A) = - (△ A C B) = - (△ B A C)$ .

Definición 1. Definimos el área de un cuadrilátero $A B C D$ como la suma de las áreas de los triángulos que se forman al considerar una de sus diagonales, esto es,
$(A B C D) = (△ A B C) + (△ C D A)$ .

Notemos que como resultado de esta definición el área del cuadrilátero cruzado resulta ser la diferencia de las áreas de los triángulos que se forman al considerar la intersección cruzada de los lados.

Paralelogramo de Varignon

Teorema 1, de Varignon.
$i)$ Los puntos medios de los lados de un cuadrilátero convexo son los vértices de un paralelogramo, conocido como paralelogramo de Varignon, cuyo perímetro es la suma de las diagonales del cuadrilátero,
$i i)$ el área del paralelogramo de Varignon es la mitad del área del cuadrilátero.

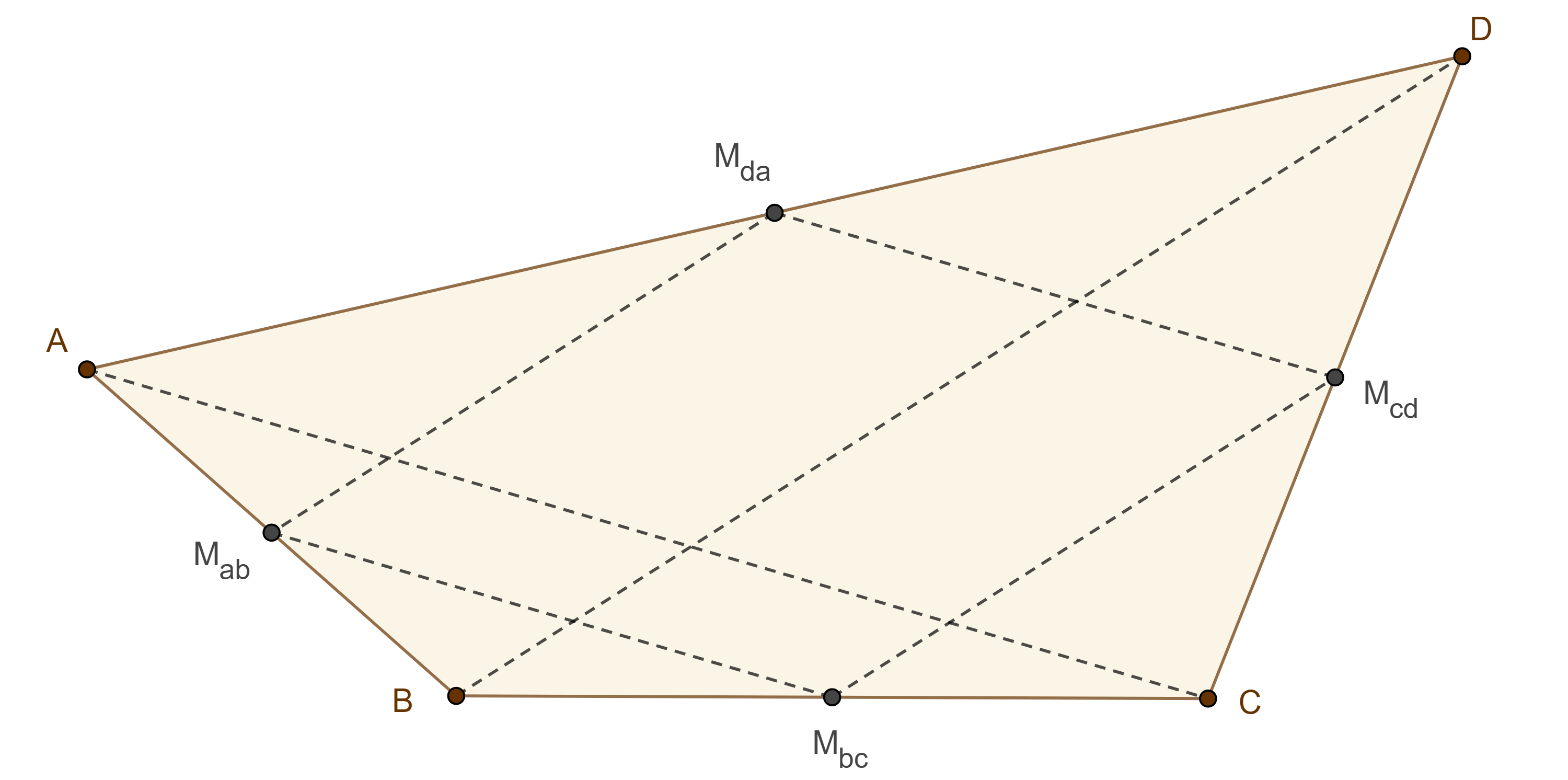
Demostración. Sean $A B C D$ un cuadrilátero convexo y $M_{a b}$ , $M_{b c}$ , $M_{c d}$ y $M_{d a}$ los puntos medios de $A B$ , $B C$ , $C D$ y $D A$ respetivamente.

Notemos que $M_{a b} M_{b c}$ y $M_{c d} M_{d a}$ son segmentos medios de $△ A B C$ y $△ D A C$ por lo que $M_{a b} M_{b c} ∥ C A ∥ M_{c d} M_{d a}$ y $2 M_{a b} M_{b c} = C A = 2 M_{c d} M_{d a}$ .

De manera análoga podemos ver que $M_{a b} M_{d a} ∥ D B ∥ M_{b c} M_{c d}$ y $2 M_{a b} M_{d a} = B D = 2 M_{b c} M_{c d}$ .

Por lo tanto los lados opuestos de $M_{a b} M_{b c} M_{c d} M_{d a}$ son paralelos y $M_{a b} M_{b c} + M_{b c} M_{c d} + M_{c d} M_{d a} + M_{d a} M_{a b} = \frac{C A + B D + C A + B D}{2} = C A + B D$ .

Para calcular el área de $M_{a b} M_{b c} M_{c d} M_{d a}$ primero notemos que $△ A M_{a b} M_{d a}$ y $△ A B D$ son semejantes pues $M_{a b} M_{d a} ∥ B D$ .

También sabemos que $M_{a b} M_{d a} = \frac{B D}{2}$ , por lo que las alturas desde $A$ , $h$ y $h^{'}$ de $△ A M_{a b} M_{d a}$ y $△ A B D$ respectivamente, también cumplirán que $h = \frac{h^{'}}{2}$ .

Por lo tanto,
$(△ A M_{a b} M_{d a}) = \frac{M_{a b} M_{d a} \times h}{2}$
$= \frac{\frac{1}{2} D B D \times \frac{1}{2} h^{'}}{2} = \frac{1}{4} \frac{B D \times h^{'}}{2}$
$= \frac{1}{4} (△ A B D)$ .

De manera similar podemos encontrar las áreas de $△ B M_{b c} M_{a b}$ , $△ C M_{c d} M_{b c}$ y $△ D M_{d a} M_{c d}$ .

En consecuencia,
$(M_{a b} M_{b c} M_{c d} M_{d a}) = (A B C D) - (△ A M_{a b} M_{d a}) - (△ B M_{b c} M_{a b}) - (△ C M_{c d} M_{b c}) - (△ D M_{d a} M_{c d})$
$= (A B C D) - \frac{1}{4} ((△ A B D) + (△ B C D) + (△ C D B) + (△ D A C))$
$= (A B C D) - \frac{2}{4} (A B C D)$
$= \frac{(A B C D)}{2}$ .

Corolario. Sea $A B C D$ un cuadrilátero convexo, entonces su cuadrilátero de Varignon
$i)$ es un rombo si y solo si $A C = B D$ ,
$i i)$ es un rectángulo si y solo si $A C ⊥ B D$ ,
$i i i)$ es un cuadrado si y solo si $A C = B D$ y $A C ⊥ B D$ .

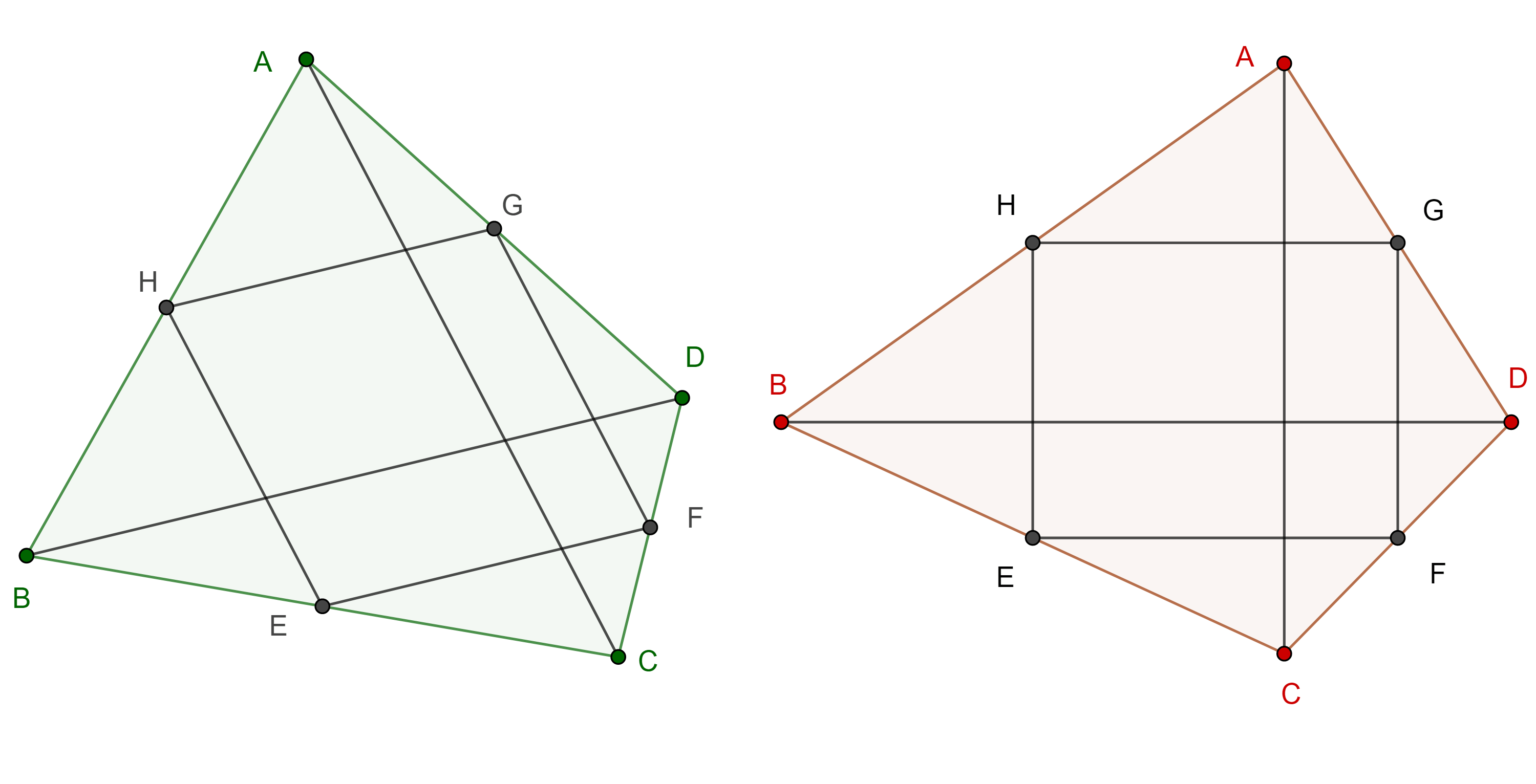
Demostración. Sean $E$ , $F$ , $G$ , $H$ , los puntos medios de $B C$ , $C D$ , $D A$ , $A B$ , respectivamente como $E F$ y $F G$ son segmentos medios de $△ D B C$ y $△ A D C$ , entonces, $2 E F = B D$ , $E F ∥ B D$ y $2 F G = A C$ , $F G ∥ A C$ .

$i)$ $E F G H$ es un rombo, entonces por definición $E F = F G \Leftrightarrow A C = B D$ .

$i i)$ $E F G H$ es un rectángulo, entonces por definición $E F ⊥ F G \Leftrightarrow A C ⊥ B D$ .

$i i i)$ Es consecuencia de $i)$ y $i i)$ .

Centroide de un cuadrilátero

Definición 2. Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se llaman bimedianas.

Al segmento que une los puntos medios de las diagonales de un cuadrilátero se le conoce como recta de Newton.

Teorema 2. Las bimedianas de un cuadrilátero convexo y su recta de Newton son concurrentes y se bisecan entre sí, el punto de concurrencia es el centroide del cuadrilátero.

Demostración. Sea $A B C D$ un cuadrilátero convexo y $M_{a b}$ , $M_{b c}$ , $M_{c d}$ , $M_{d a}$ , $M$ , $N$ , los puntos medios de $A B$ , $B C$ , $C D$ , $D A$ , $A C$ , $B D$ , respectivamente.

$M_{a b} M_{c d}$ y $M_{b c} M_{d a}$ son las diagonales del paralelogramo de Varignon, por lo tanto, se intersecan en $J$ su punto medio.

Por otra parte, $M_{a b} M$ es un segmento medio de $△ A B C$ , por lo que $M_{a b} M ∥ B C$ ; $N M_{c d}$ es un segmento medio de $△ D B C$ , por lo tanto, $N M_{c d} ∥ B C$ , y así $N M_{c d} ∥ M_{a b} M$ .

Igualmente vemos que $M_{a b} N ∥ M M c d$ .

Por lo tanto, $M_{a b} N M_{c d} M$ es un paralelogramo, en consecuencia las diagonales $M_{a b} M_{c d}$ y $N M$ se intersecan en $J$ su punto medio.

En conclusión, $J$ es el punto medio de $M_{a b} M_{c d}$ , $M_{b c} M_{d a}$ y $N M$ .

Construcción de un cuadrilátero

Problema. Construye un cuadrilátero $A B C D$ conociendo $A B$ , $B C$ , $C D$ , $D A$ y $M_{a b} M_{c d}$ donde $M_{a b}$ y $M_{c d}$ son los puntos medios de $A B$ y $C D$ respectivamente.

Solución. Primero construimos el paralelogramo $M_{a b} N M_{c d} M$ , donde $M$ y $N$ son los puntos medios de las diagonales $A C$ y $B D$ , de la siguiente manera.

De la demostración del teorema 2 sabemos que $M_{a b} M = N M_{c d} = \frac{B C}{2}$ y $M_{a b} N = M M_{c d} = \frac{A D}{2}$ (figura 4).

También sabemos que la diagonal de un paralelogramo lo divide en dos triángulos congruentes, por lo que basta construir un triángulo de lados $M_{a b} M_{c d}$ , $\frac{B C}{2}$ y $\frac{A D}{2}$ y luego trazar paralelas por $M_{a b}$ y $M_{c d}$ a los lados del triángulo construido completando así el paralelogramo.

De manera similar construimos el paralelogramo $M_{a b} M_{b c} M_{c d} M_{d a}$ donde $M_{b c}$ y $M_{d a}$ serían los puntos medios de $B C$ y $A D$ respectivamente.

Sabemos también que $M_{b c} M ∥ A B$ por lo que trazamos la paralela $A B$ a $M_{b c} M$ por $M_{a b}$ tal que $A M_{a b} = M_{b c} B = \frac{A B}{2}$ .

Con $A$ y $B$ construidos, por $M_{b c}$ trazamos $A B C$ tal que $B M_{b c} = M_{b c} C = \frac{B C}{2}$ , similarmente construimos $D$ .

Teorema de Van Aubel

Teorema 3, de Van Aubel. Los segmentos que unen los centros de cuadrados construidos externamente sobre lados opuestos de un cuadrilátero convexo son perpendiculares y tienen la misma longitud.

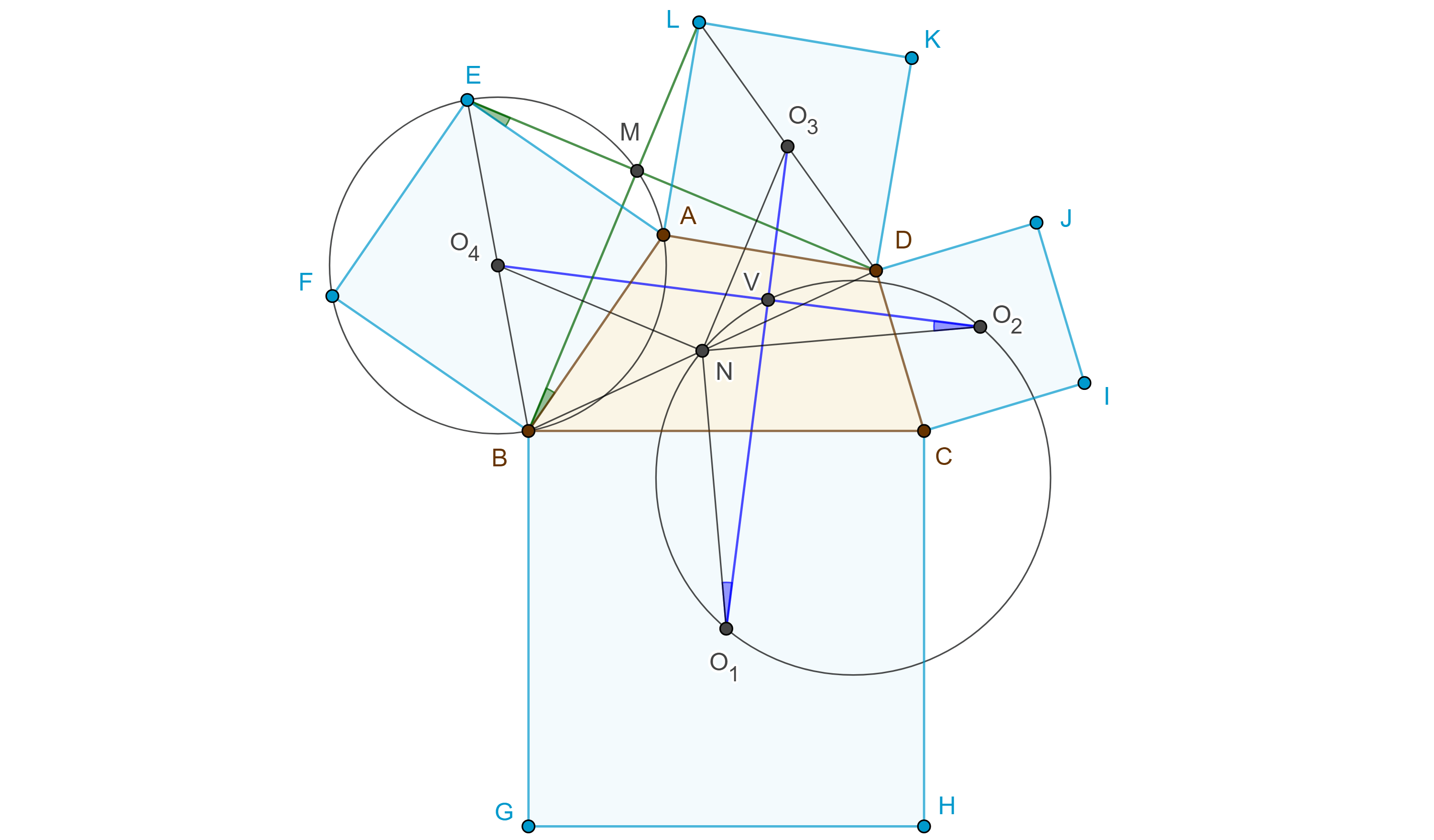
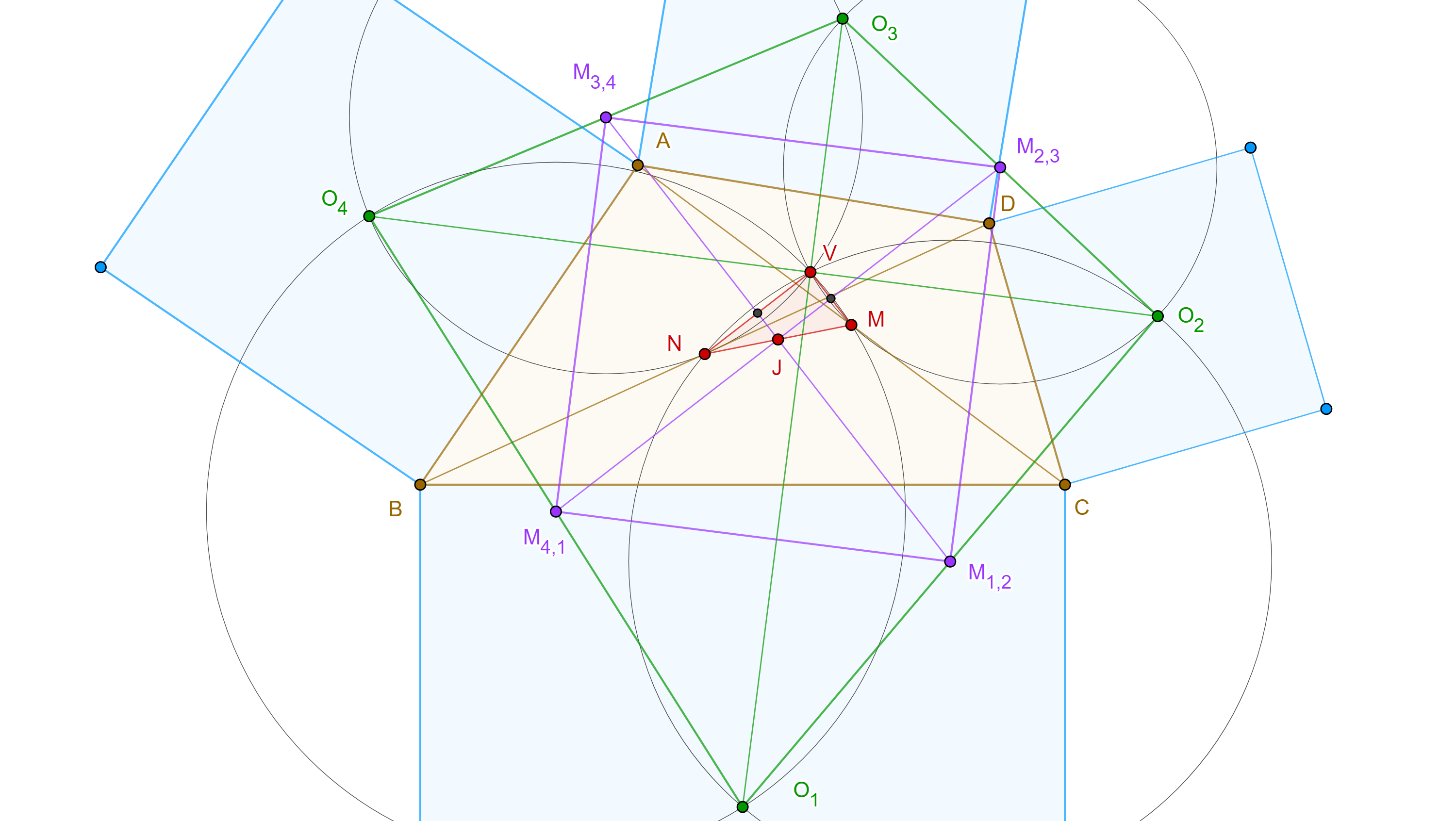
Demostración. Sean $A B C D$ un cuadrilátero convexo y $E F B A$ , $B G H C$ , $D C I J$ , $L A D K$ , cuadrados construidos externamente sobre los lados de $A B C D$ y $O_{1}$ , $O_{2}$ , $O_{3}$ , $O_{4}$ , sus respectivos centros.

Sea $M = L B \cap E D$ , como $A L = A D$ y $A B = A E$ y $∠ L A B = ∠ D A E$ , por criterio de congruencia LAL, $△ L A B ≅ △ D A E$ ,
$\Rightarrow L B = D E$ y $∠ A E M = ∠ A B M$ .

Por lo tanto, $M E B A$ es cíclico, así, $∠ E M B = ∠ E A B$ , es decir $L B ⊥ D E$ .

Considera $N$ el punto medio de $B D$ , $N O_{4}$ y $N O_{3}$ son segmentos medios de $△ B D E$ y $△ D B L$ respectivamente.

Esto implica que $2 N O_{4} = D E$ y $N O_{4} ∥ D E$ y $2 N O_{3} = L B$ y $N O_{4} ∥ L B$ .

Por lo tanto, $N O_{4} = N O_{3}$ y $N O_{4} ⊥ N O_{3}$ .

Igualmente vemos que $N O_{1} = N O_{2}$ y $N O_{1} ⊥ N O_{2}$ .

Sea $V = O_{1} O_{3} \cap O_{2} O_{4}$ , por criterio de congruencia LAL, $N O_{1} O_{3} ≅ N O_{2} O_{4}$ ,
$\Rightarrow O_{1} O_{3} = O_{2} O_{4}$ y $∠ V O_{1} N = ∠ V O_{2} N$ .

Por lo tanto, $V N O_{1} O_{2}$ es cíclico, y así $O_{1} O_{3} ⊥ O_{2} O_{4}$ .

Definición 3. Nos referiremos al cuadrilátero $O_{1} O_{1} O_{3} O_{4}$ como cuadrilátero externo de Van Aubel y a la intersección de sus diagonales como punto externo de Van Aubel.

Centroide del cuadrilátero de Van Aubel

Teorema 4. Un cuadrilátero y su cuadrilátero externo de Van Aubel tienen el mismo centroide.

Demostración. Sean $A B C D$ y $O_{1} O_{2} O_{3} O_{4}$ su cuadrilátero externo de Van Aubel, $M$ y $N$ los puntos medios de $A C$ y $B D$ , y $V$ el punto externo de Van Aubel.

En el teorema anterior vimos que $N V$ es una cuerda común a las circunferencias cuyos diámetros son $O_{1} O_{2}$ y $O_{3} O_{4}$ , por lo tanto la línea que une sus centros $M_{1, 2} M_{3, 4}$ biseca a $N V$ y $M_{1, 2} M_{3, 4} ⊥ N V$ .

De manera análoga podemos ver que $M V$ es una cuerda común a las circunferencias cuyos diámetros son $O_{2} O_{3}$ y $O_{4} O_{1}$ y por lo tanto la línea que une sus centros $M_{2, 3} M_{4, 1}$ biseca a $M V$ y $M_{2, 3} M_{4, 1} ⊥ M V$ .

Por otra parte, por el teorema de Van Aubel las diagonales del cuadrilátero de Van Aubel son perpendiculares y tienen la misma longitud. Entonces por el corolario, su paralelogramo de Varignon $M_{1, 2} M_{2, 3} M_{3, 4} M_{4, 1}$ es un cuadrado, en particular, $M_{1, 2} M_{3, 4} ⊥ M_{2, 3} M_{4, 1}$ .

En consecuencia, en $△ M N V$ , $M_{1, 2} M_{2, 3} ∥ M V$ y $M_{1, 2} M_{2, 3}$ pasa por el punto medio de $N V$ , por lo tanto $M_{1, 2} M_{2, 3}$ biseca a $M N$ .

Igualmente podemos ver que $M_{2, 3} M_{4, 1}$ biseca a $M N$ .

Por el teorema 2 sabemos que el punto medio $J$ de $M N$ es el centroide de $A B C D$ y que la intersección de las bimedianas $M_{1, 2} M_{3, 4}$ y $M_{2, 3} M_{4, 1}$ es el centroide de $O_{1} O_{2} O_{3} O_{4}$ .

Más adelante…

En la siguiente entrada continuaremos el estudio de los cuadriláteros cíclicos que comenzamos en la entada teorema de Ptolomeo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Muestra que un cuadrilátero es dividido por una de sus diagonales en dos triángulos de igual área si y solo si la diagonal biseca a la otra diagonal.
Verifica que el teorema de Varignon se cumple para los cuadriláteros cóncavo y cruzado.
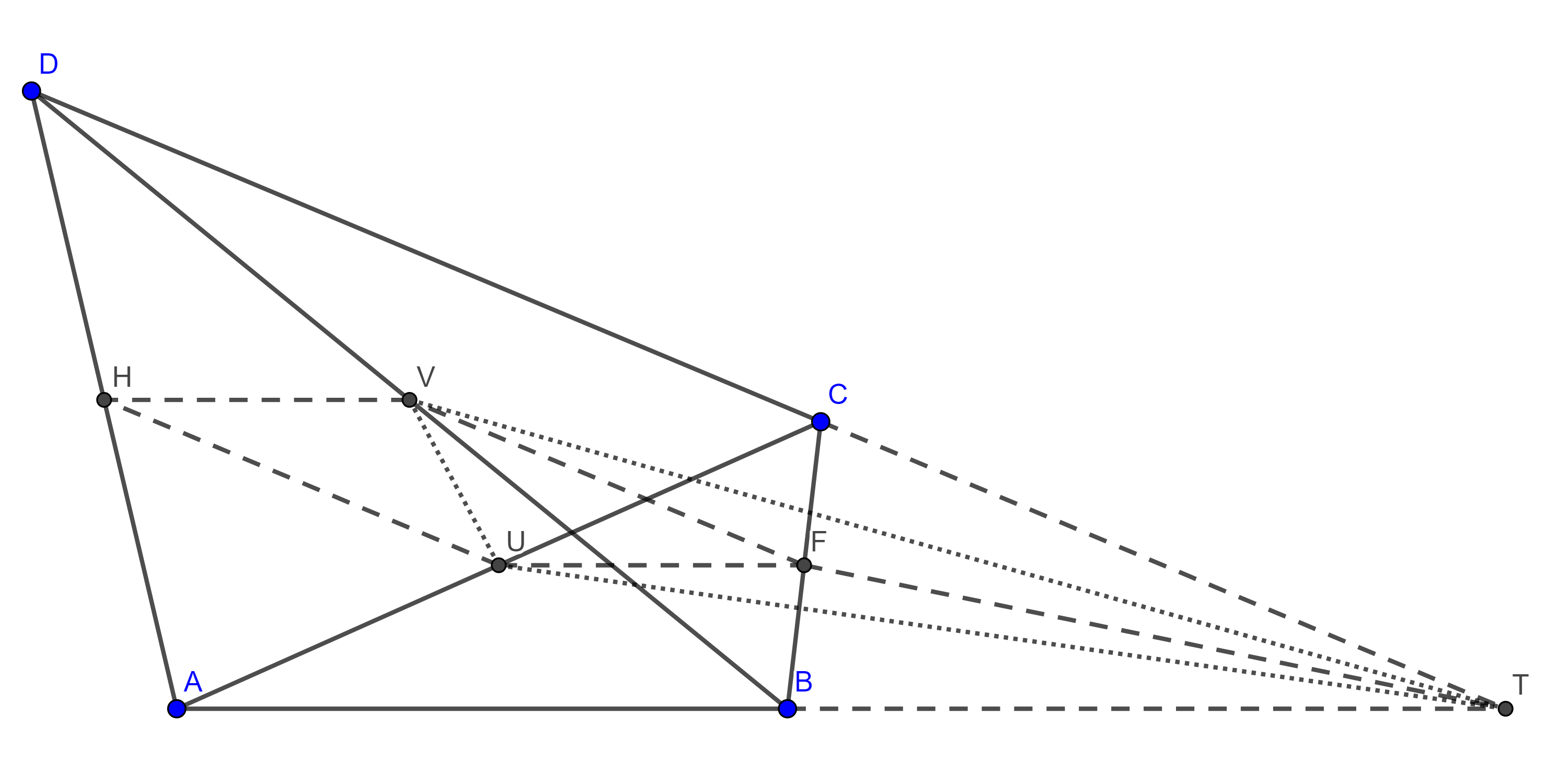
Sean $A B C D$ un cuadrilátero $U$ y $V$ los puntos medios de $\overset{―}{A C}$ y $\overset{―}{B D}$ respectivamente y $T$ la intersección de $\overset{―}{A B}$ con $\overset{―}{C D}$ . Prueba que $(△ T U V) = \frac{(A B C D)}{4}$ .
Sugerencia. Considera $H$ y $F$ los puntos medios de $\overset{―}{A D}$ y $\overset{―}{B C}$ y los cuadriláteros $A C B D$ , $C U F T$ y $B V F T$ para calcular el área de los triángulos $△ U V F$ , $△ U F T$ y $△ V F T$ .

Construye un cuadrilátero dados dos ángulos opuestos, la longitud de las diagonales y el ángulo entre las diagonales.
Verifica que el teorema de Van Aubel se cumple cuando los cuadrados son construidos internamente, y también para los para los cuadriláteros cóncavo y cruzado.
Muestra que en un cuadrilátero convexo los puntos medios de sus diagonales y los puntos medios de las diagonales de su cuadrilátero externo de Van Aubel, forman un cuadrado, y que el punto externo de Van Aubel pertenece al circuncírculo de este cuadrado.

Entradas relacionadas

Ir a Geometría Moderna I.
Entrada anterior del curso: Circunferencia de Brocard.
Siguiente entrada del curso: Cuadrilátero cíclico.
Otros cursos.

Fuentes

Altshiller, N., College Geometry. New York: Dover, 2007, pp 124-127.
Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 51-56.
Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 6-13.
D. Pellegrinetti., The Six-Point Circle for the Quadrangle. International Journal of Geometry, Vol. 8 (Oct., 2019), No. 2, pp 5–13.

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

El blog de Leo

Aprendiendo, creando y compartiendo matemáticas

Geometría Moderna I: Teoremas de Varignon y Van Aubel

Introducción

Área del cuadrilátero

Paralelogramo de Varignon

Centroide de un cuadrilátero

Construcción de un cuadrilátero

Teorema de Van Aubel

Centroide del cuadrilátero de Van Aubel

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Me gusta esto:

Deja una respuesta Cancelar la respuesta

Introducción

Área del cuadrilátero

Paralelogramo de Varignon

Centroide de un cuadrilátero

Construcción de un cuadrilátero

Teorema de Van Aubel

Centroide del cuadrilátero de Van Aubel

Más adelante…

Tarea moral

Entradas relacionadas

Fuentes

Agradecimientos

Comparte esto:

Me gusta esto:

Deja una respuesta Cancelar la respuesta