Introducción

En esta entrada presentamos a el primer tipo de cuadriláteros que estudiaremos, los paralelogramos, algunas de sus propiedades serán frecuentemente usadas durante el curso.

Definición 1. Un cuadrilátero es una figura geométrica que consiste en cuatro vértices y cuatro lados. Si los vértices de un cuadrilátero son $A$, $B$, $C$ y $D$ y los lados $AB$, $BC$, $CD$ y $AD$ entonces lo denotamos como $\square ABCD$.

Decimos que los lados de un cuadrilátero son adyacentes u opuestos de acuerdo a si tienen o no un vértice en común.

Similarmente diremos que los vértices de un cuadrilátero son adyacentes u opuestos si son extremos de un mismo lado o no. Los segmentos que unen vértices opuestos son las diagonales del cuadrilátero.

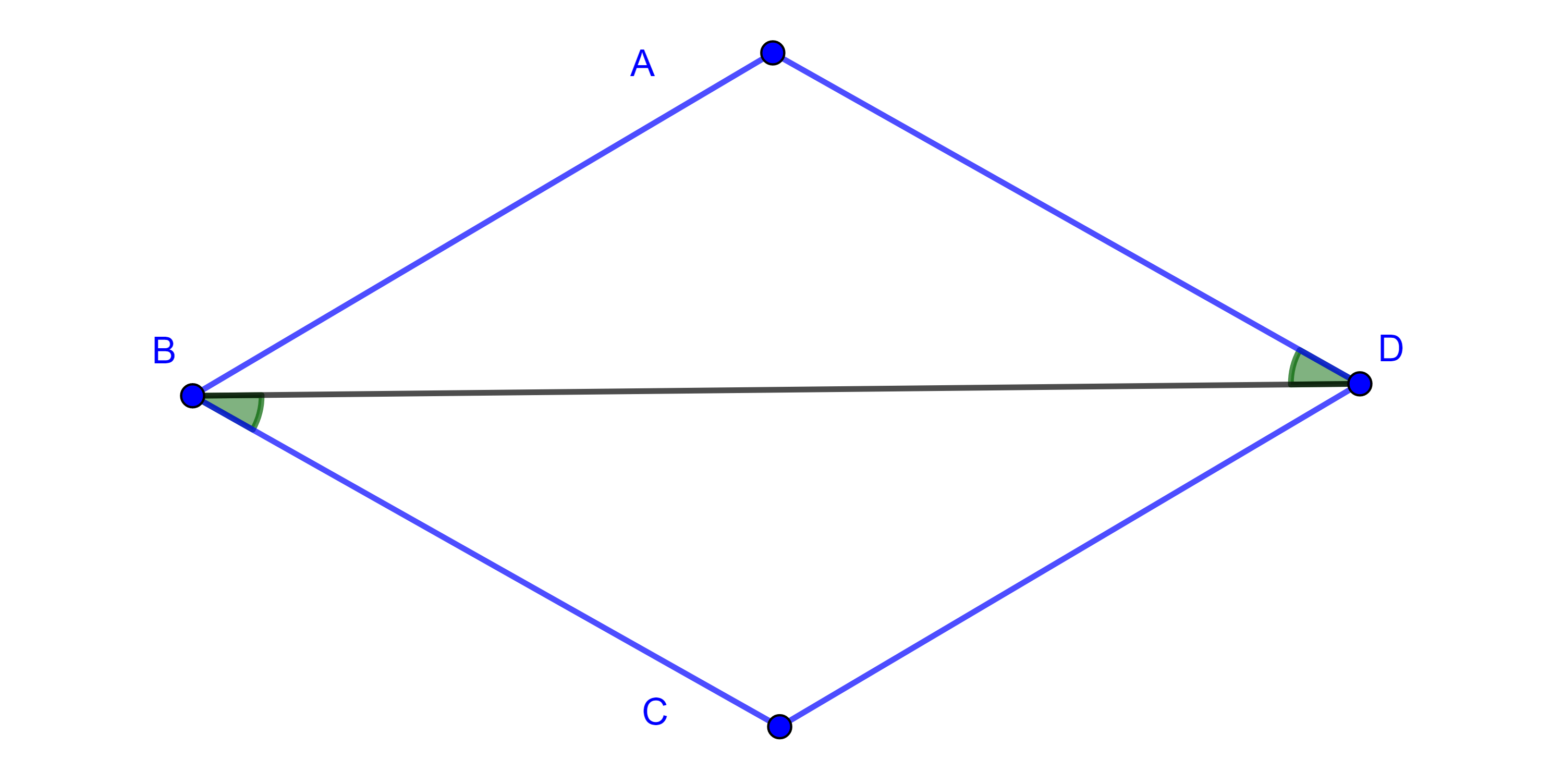
Un cuadrilátero es convexo si sus diagonales se intersecan en el interior del cuadrilátero.

Proposición 1. La suma de los ángulos internos de todo cuadrilátero convexo es $2\pi$.

Demostración. Sea $\square ABCD$ convexo, consideremos $BD$, entonces la suma de los ángulos internos del cuadrilátero será igual a la suma de los ángulos internos de los dos triángulos $\triangle ABD$ y $\triangle CBD$, esto es, $2\pi$.

$\blacksquare$

Algunas propiedades de paralelogramos

Definición 2. Un paralelogramo es un cuadrilátero convexo cuyos pares de lados opuestos son paralelos.

Teorema 1. En todo paralelogramo se cumple lo siguiente:

• los lados opuestos y los ángulos opuestos son iguales,
• los ángulos adyacentes son suplementarios,
• cada diagonal divide al paralelogramo en dos triángulos congruentes,
• las dos diagonales del paralelogramo lo dividen en dos parejas de triángulos congruentes,
• las diagonales se intersecan en su punto medio.

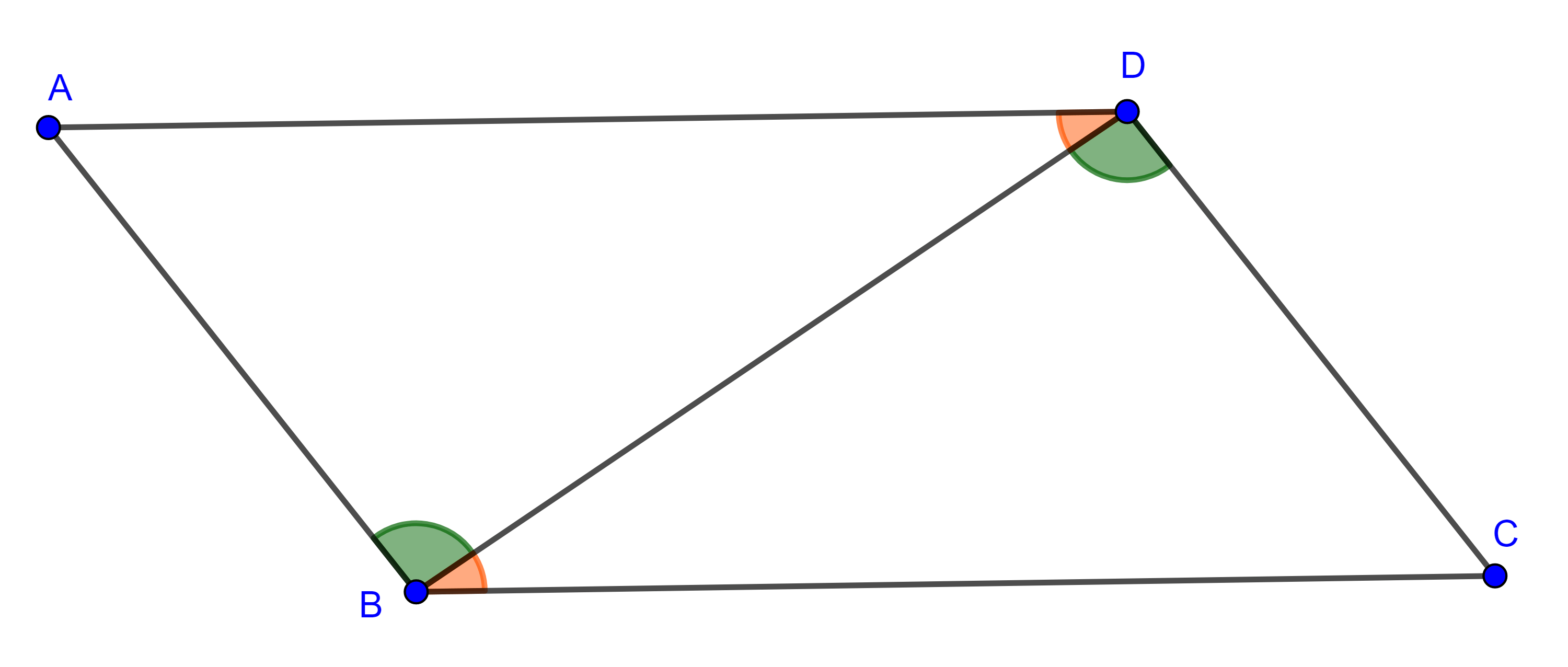
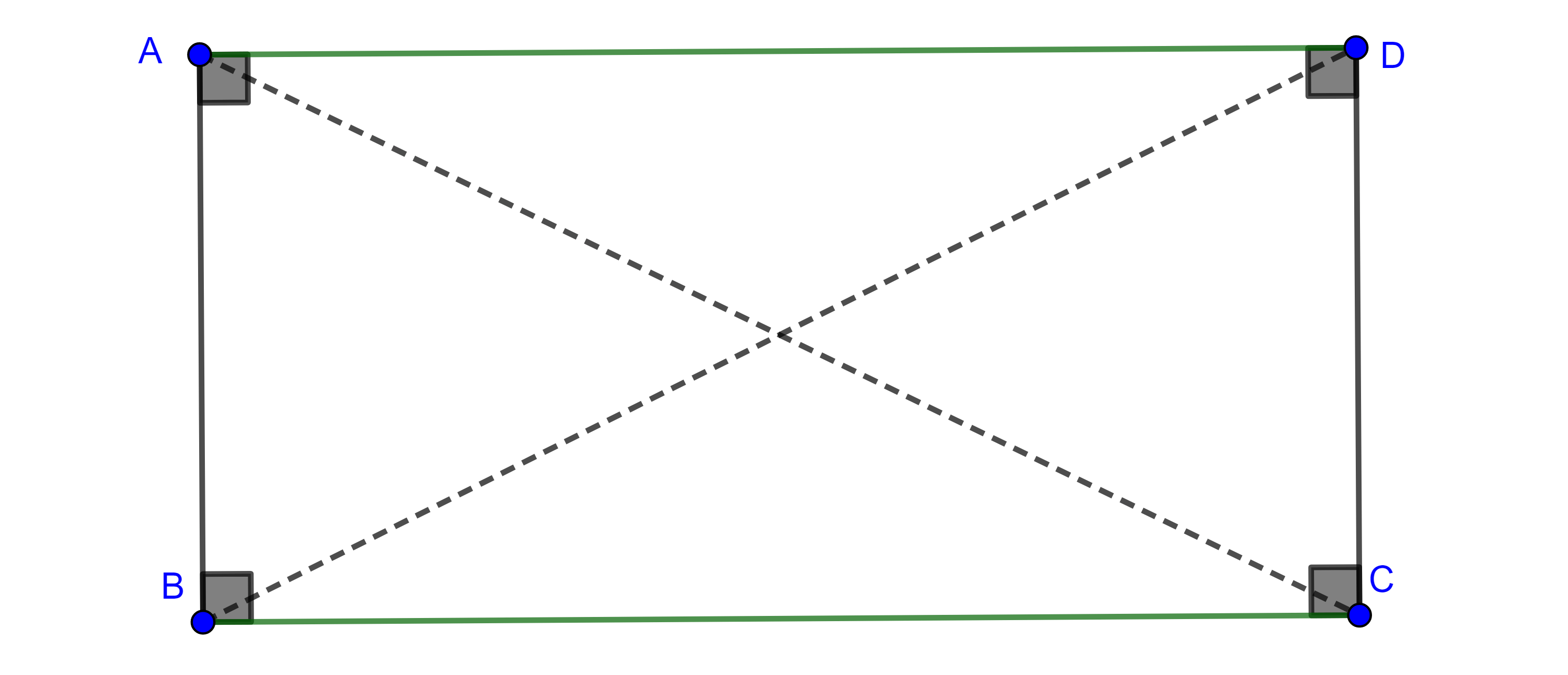
Demostración. Sea $\square ABCD$ un paralelogramo.

Como la diagonal $BD$ es transversal a $AB$ y $DC$ y estos son paralelos, entonces $\angle DBA = \angle BDC$.

Similarmente $BD$ es transversal a $AD$ y a $BC$, por lo que $\angle ADB = \angle CBD$.

$\triangle ABD$ y $\triangle CDB$ tienen en común al lado $BD$ y por criterio ALA, $\triangle ABD \cong \triangle CDB$.

Es decir,
$AB = CD$, $AD = CB$ y $\angle A = \angle C$,
además $\angle D = \angle ADB + \angle BDC = \angle CBD + \angle DBA = \angle B$.

Así los lados y ángulos opuesto son iguales.

Veamos que los los ángulos adyacentes son suplementarios,
$\angle A + \angle B = \angle A + \angle CBD + \angle DBA $
$= \angle A + \angle ADB + \angle DBA = \pi$.

Similarmente,
$\angle A + \angle D = \angle C + \angle B = \angle C + \angle D = \pi$.

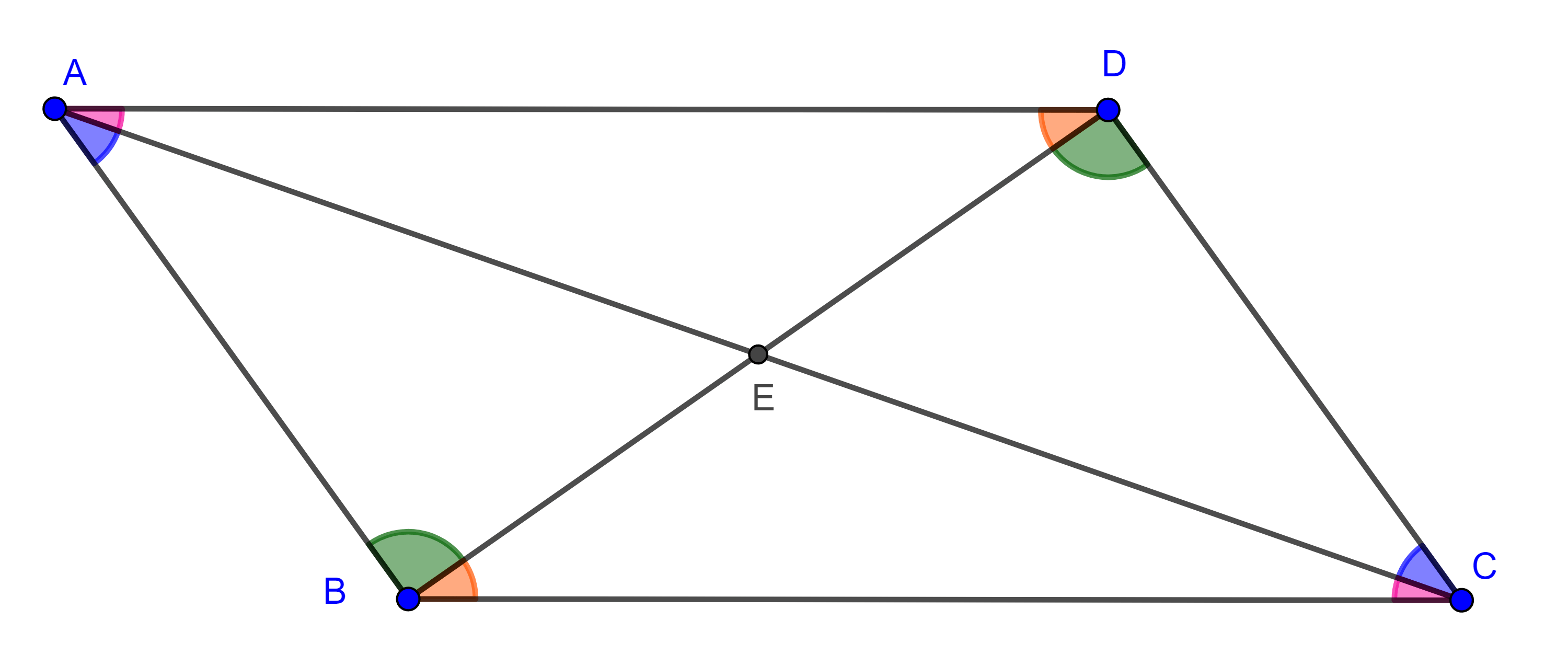
Por otro lado, si consideramos la diagonal $AD$, al igual que en el caso anterior, tendremos que $\angle BAC = \angle DCA$ y $\angle CAD = \angle ACB$.

Sea $E = AC \cap BD$, por criterio ALA, $\triangle EAB \cong \triangle ECB$ y $\triangle EAD \cong \triangle ECB$, por lo que $AE = CE$ y $BE = DE$.

$\blacksquare$

Rectángulo

Definición 3. Un rectángulo es un cuadrilátero con cuatro ángulos rectos.

Proposición 2. Todo rectángulo es paralelogramo.

Demostración. Como dos lados opuestos son perpendiculares a un tercer lado entonces son paralelos entre sí. Similarmente los otros dos lados opuestos son paralelos entre sí. Por lo tanto, un rectángulo es paralelogramo.

$\blacksquare$

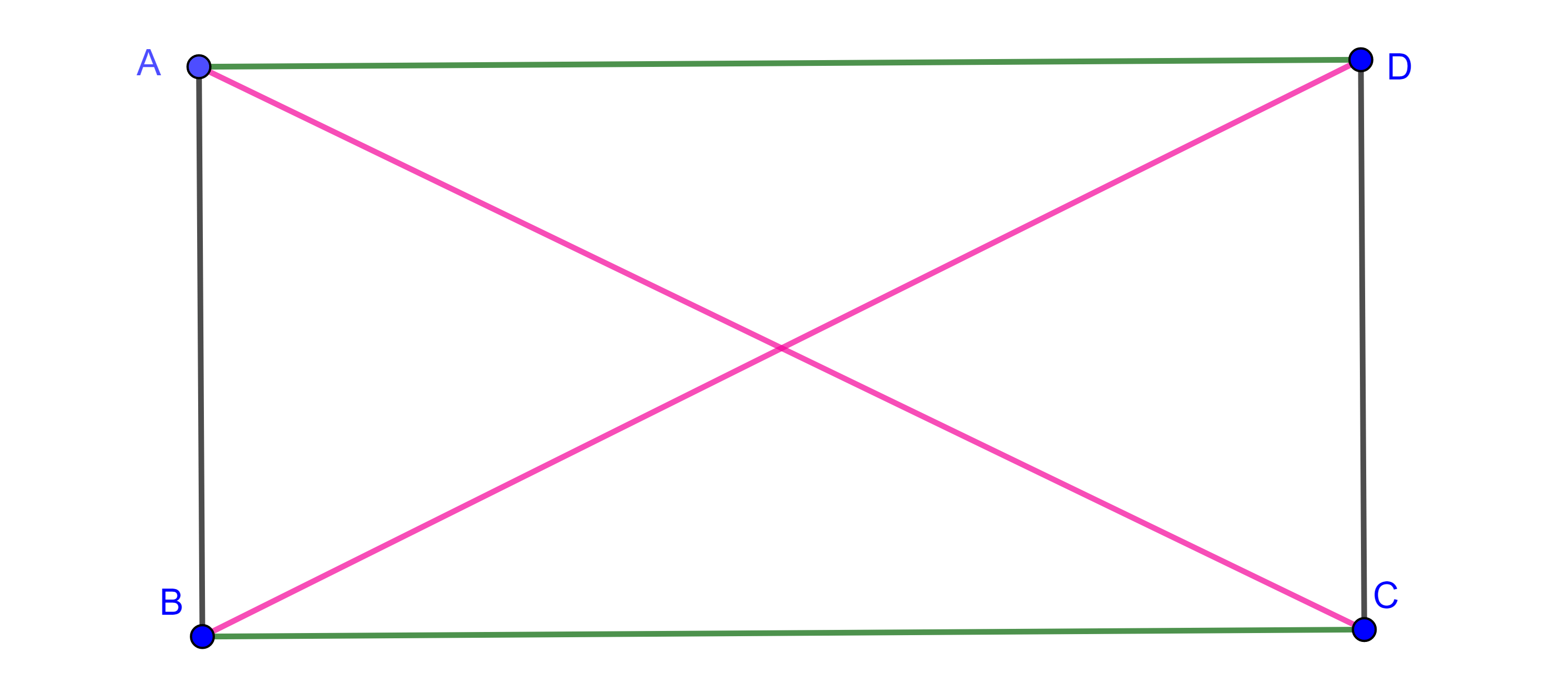
Proposición 3. Un paralelogramo es rectángulo si y solo si sus diagonales tienen la misma longitud.

Demostración. Sea $\square ABCD$ paralelogramo y supongamos que $AC = BD$.

Por el teorema anterior, $AD = BC$, y los triángulos $\triangle ADC $ y $\triangle BCD$ comparten a $CD$ como lado en común, por criterio LLL, $\triangle ADC \cong \triangle BCD$, en particular $\angle C = \angle D$.

Pero por el teorema 1, $\angle A = \angle C$ y $\angle B = \angle D$.

Por tanto, $\angle A = \angle C = \angle D = \angle B$.

Por la proposición 1,
$4\angle A = \angle A + \angle C + \angle B + \angle D = 2 \pi$
$\Rightarrow \angle A = \angle C = \angle B = \angle D = \dfrac{\pi}{2}$.

Así, $\square ABCD$ es rectángulo.

$\blacksquare$

Ahora supongamos que $\square ABCD$ es rectángulo y probemos que $AC = BD$.

Por hipótesis $\angle D = \angle C$, como $\square ABCD$ es paralelogramo entonces $AD = BC$, además $CD$ es un lado en común de $\triangle ADC$ y $\triangle BCD$, por criterio LAL, $\triangle ADC \cong \triangle BCD$.

Por lo tanto, $AC = BD$.

$\blacksquare$

Rombo

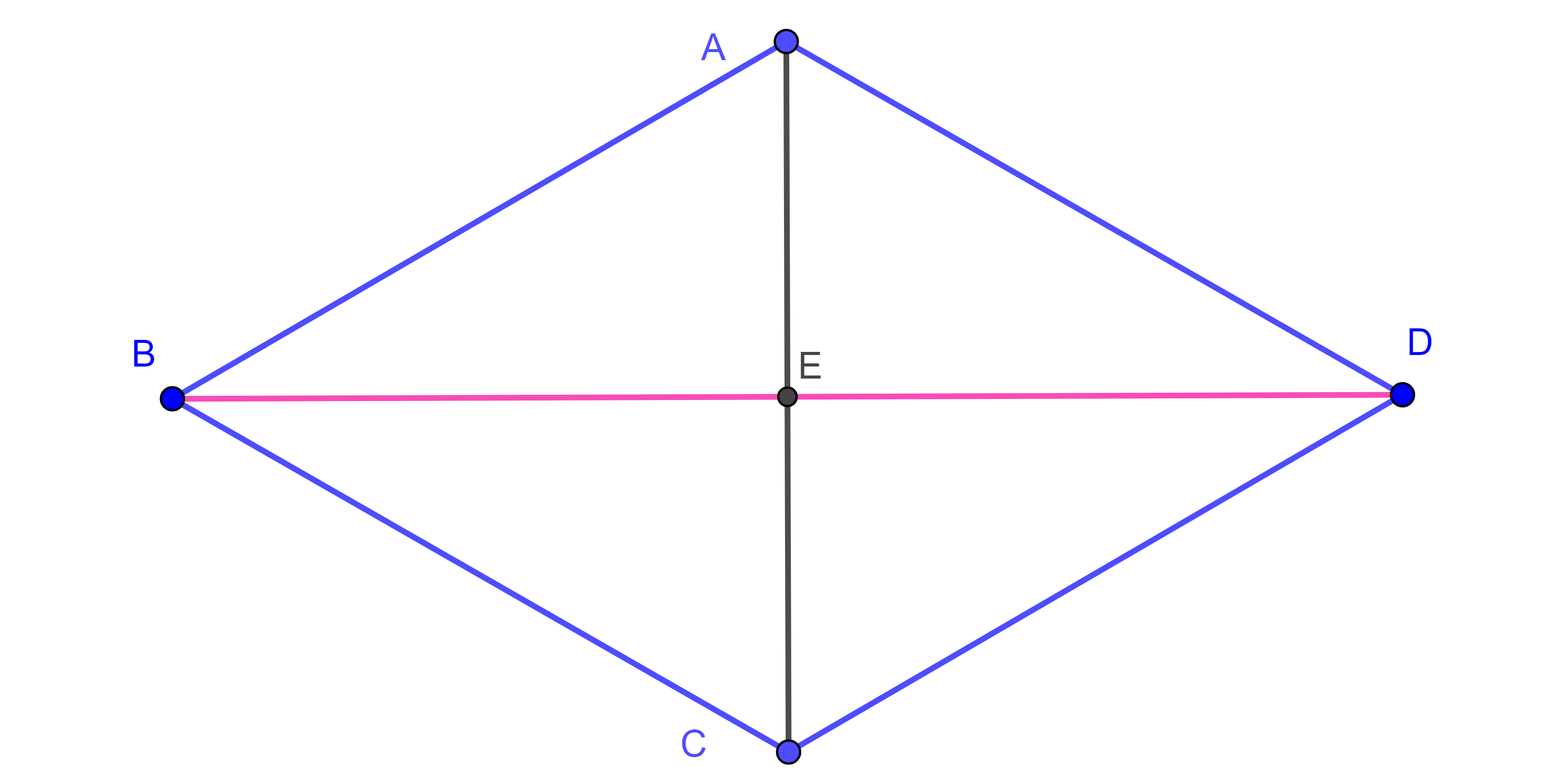
Definición 4. Un rombo es un cuadrilátero con cuatro lados iguales.

Proposición 4. Todo rombo es paralelogramo.

Demostración. Sea $\square ABCD$ un rombo.

Por criterio LLL, $\triangle ABD \cong \triangle CDB$, en particular $\angle ADB = \angle CBD$, como $BD$ es transversal a $AD$ y a $BC$ y los ángulos alternos internos son iguales entonces $AD \parallel BC$.

De manera similar se ve que $AB \parallel CD$.

Concluimos que $\square ABCD$ es paralelogramo.

$\blacksquare$

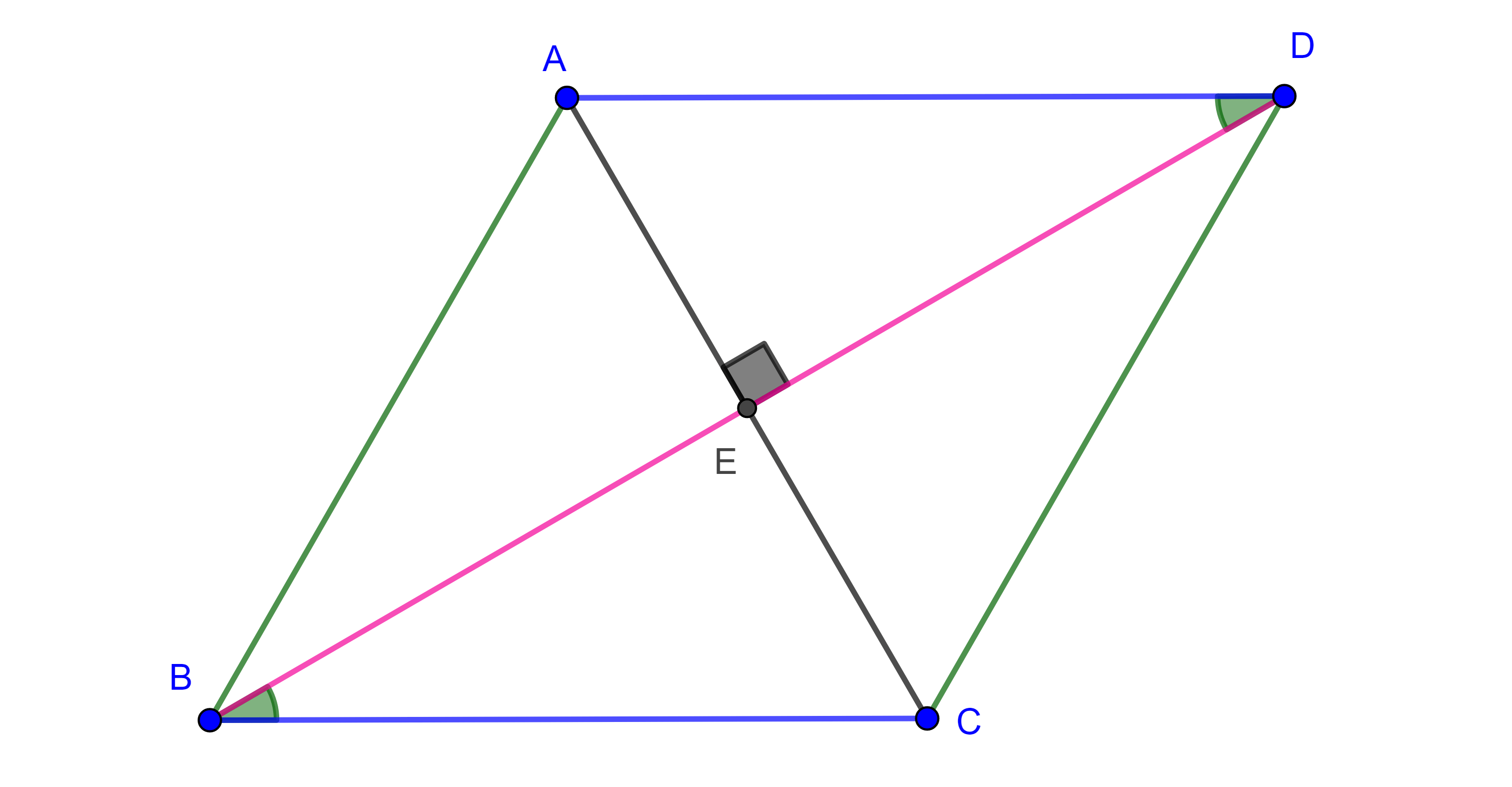
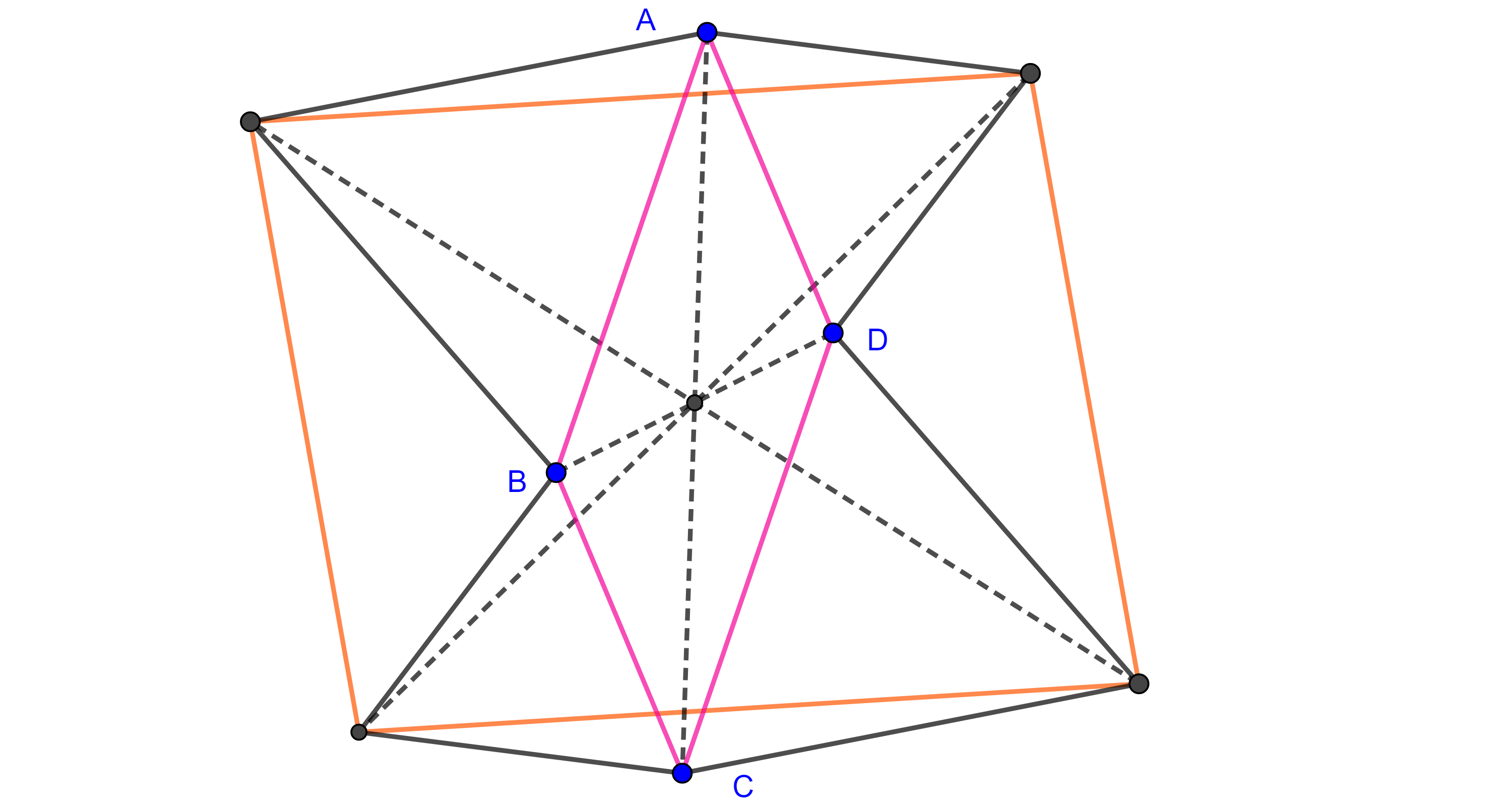
Proposición 5. Un paralelogramo es un rombo si y solo si sus diagonales son perpendiculares.

Demostración. Sea $\square ABCD$ paralelogramo y supongamos que $AC \perp BD$, veamos que es rombo.

Sea $E = AC \cap BD$, por hipótesis $\angle DEA = \angle AEB$, como $\square ABCD$ es paralelogramo, por el teorema 1, $BE = DE$, además $AE$ es un lado en común de $\triangle AED$ y $\triangle AEB$, por criterio LAL, $\triangle AED \cong \triangle AEB$, en particular $AD = AB$.

Como $\square ABCD$ es paralelogramo los lados opuestos son iguales, por lo tanto, $CD = AB = AD = BC$.

Así, $\square ABCD$ es rombo.

$\blacksquare$

Ahora supongamos que $\square ABCD$ es rombo veamos que $AC \perp BD$.

Sea $E = AC \cap BD$, como $\square ABCD$ es paralelogramo, $BE = DE$, por criterio LLL, $\triangle ABE \cong \triangle ADE$, por lo que $\angle AEB = \angle DEA$.

Por ser opuestos por el vértice, $\angle AEB = \angle CED$ y $\angle DEA = \angle BEC$, por lo que $\angle CED = \angle AEB = \angle DEA = \angle BEC$, y como $\angle CED + \angle AEB + \angle DEA + \angle BEC = 2\pi$, entonces $\angle CED = \angle AEB = \angle DEA = \angle BEC =\dfrac{\pi}{2}$.

Por lo tanto, $AC \perp BD$.

$\blacksquare$

Segmento medio del triángulo

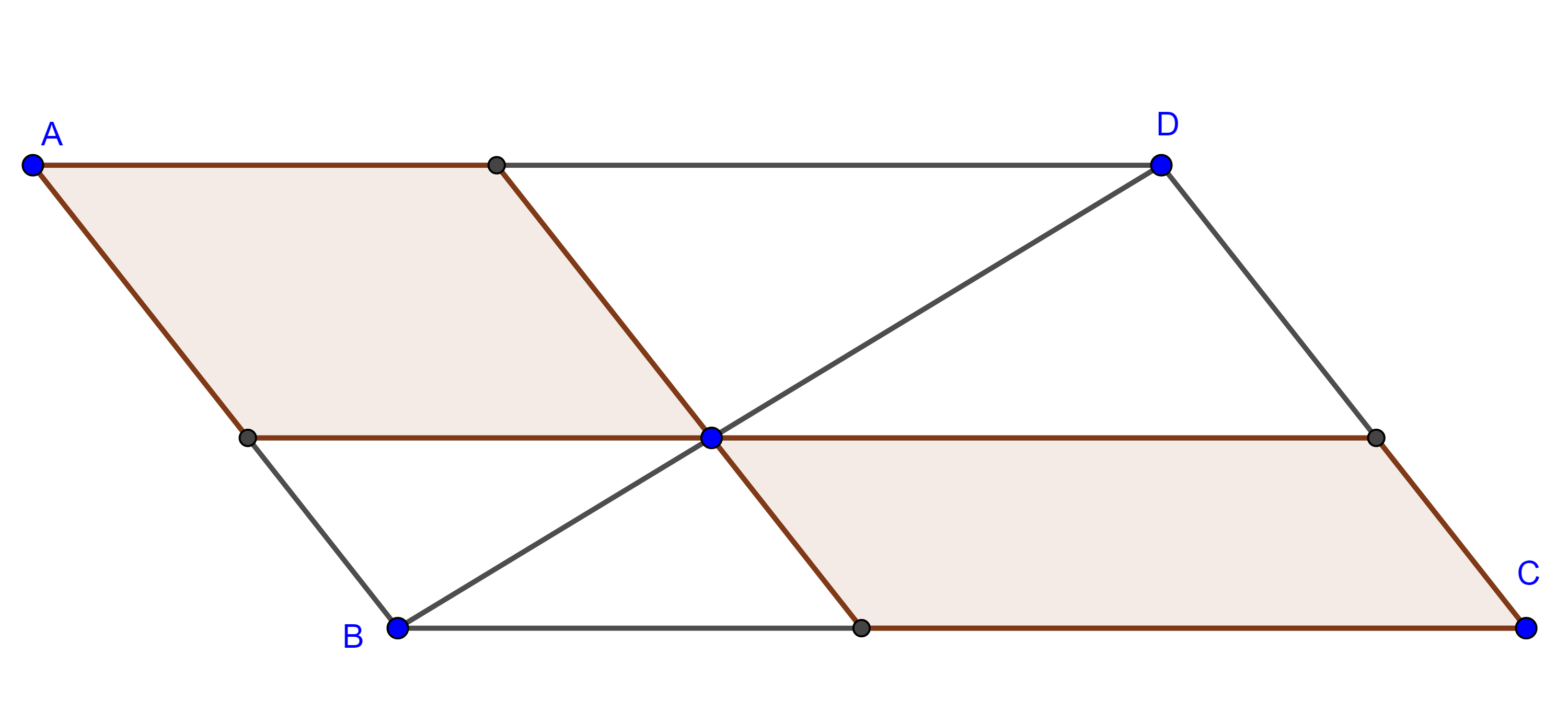
Proposición 6. Si un cuadrilátero convexo tiene un par de lados opuestos paralelos e iguales entre si entonces los restantes lados opuestos son paralelos e iguales entre sí.

Demostración. Sea $\square ABCD$ convexo tal que $AD = BC$ y $AD \parallel BC$.

Tracemos $BD$, como $AD \parallel BC$ entonces $\angle ADB = \angle CBD$, por criterio LAL, $\triangle ADB \cong \triangle CBD$, en particular $AB = CD$ y $\angle DBA = \angle BDC$.

Como $BD$ es transversal a $AB$ y a $CD$ y $\angle DBA = \angle BDC$, entonces $AB \parallel CD$.

En consecuencia, $\square ABCD$ es paralelogramo.

$\blacksquare$

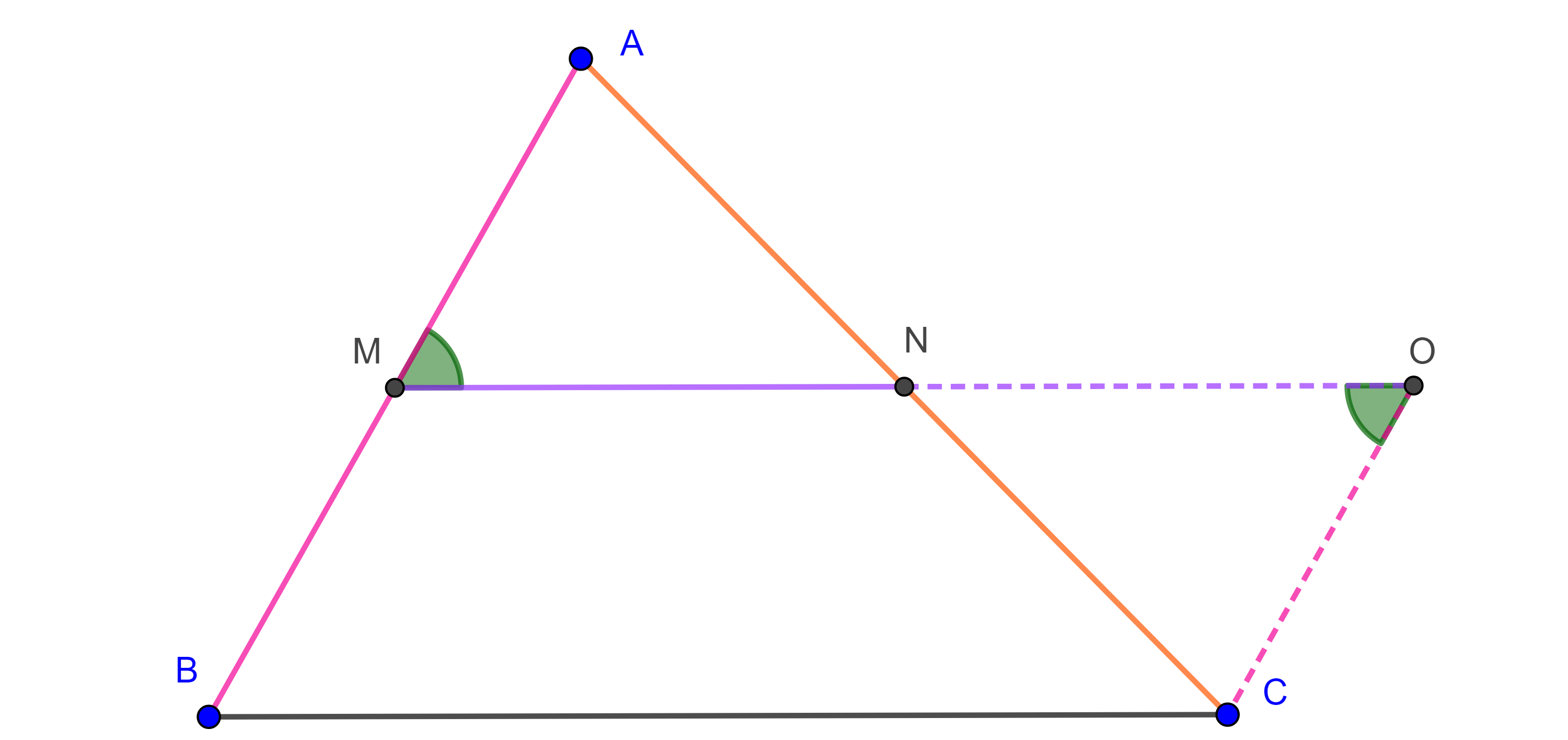
Teorema 2. Del segmento medio del triángulo. El segmento que une puntos medios de dos lados de un triángulo es paralelo e igual a la mitad del lado restante.

Demostración. Sean $\triangle ABC$, $M$ y $N$ los puntos medios de $AB$ y $AC$ respectivamente.

Extendemos $MN$ hasta un punto $O$ del lado de $N$ tal que $MN = NO$.

Como $N$ es punto medio de $AC$ entonces $AN = CN$, por construcción $MN = NO$ y $\angle ANM = \angle CNO$ por ser opuestos por el vértice.

Por criterio LAL, $\triangle ANM \cong \triangle CNO$ por lo que $CO = AM = BM$ y $\angle NMA = \angle NOC$.

Como $MO$ es transversal a $AB$ y a $CO$ y los ángulos alternos internos $\angle NMA$, $\angle NOC$ son iguales entonces $AB \parallel CO$.

En el cuadrilátero $\square MBCO$ los lados opuestos $MB$ y $CO$ son paralelos e iguales, por la proposición 6, $MO \parallel BC$ y $MO = BC$ pero $MN = \dfrac{MO}{2}$.

Por lo tanto $MN = \dfrac{BC}{2}$ y $MN \parallel BC$.

$\blacksquare$

Problema de Thébault

Definición 5. Un cuadrado es un cuadrilátero con cuatro lados iguales y cuatro ángulos rectos. Decimos que la intersección de las diagonales de un cuadrado es el centro del cuadrado.

Teorema 3. Los centros de cuadrados construidos externamente sobre los lados de un paralelogramo son los vértices de un cuadrado y las diagonales del cuadrado y las del paralelogramo son concurrentes.

Demostración. Sea $\square ABCD$ paralelogramo y sean $\square ABB’’A’$, $\square BCC’’B’$, $\square CDD’’C’$ y $\square ADD’A’’$ cuadrados construidos sobre $AB$, $BC$, $CD$ y $DA$ respectivamente y $O_{1}$, $O_{2}$, $O_{3}$, $O_{4}$ sus respectivos centros.

Como un cuadrado es un caso particular de un rectángulo y un rombo, sus diagonales son perpendiculares y tienen la misma longitud, y como es un paralelogramo las diagonales se bisecan.

De esto concluimos que las diagonales de un cuadrado lo dividen en cuatro triángulos rectángulos, isósceles y congruentes entre sí.

Por otro lado, como $\square ABCD$ es paralelogramo entonces $AD = BC$ y $AB = CD$.

$\Rightarrow$
$\begin{equation} \triangle AA’O_{1} \cong \triangle ABO_{1} \cong \triangle CDO_{3} \cong \triangle CC’O_{3}, \end{equation}$
$\begin{equation} \triangle AA’’O_{4} \cong \triangle ADO_{4} \cong \triangle BCO_{2} \cong \triangle CC’’O_{2}. \end{equation}$

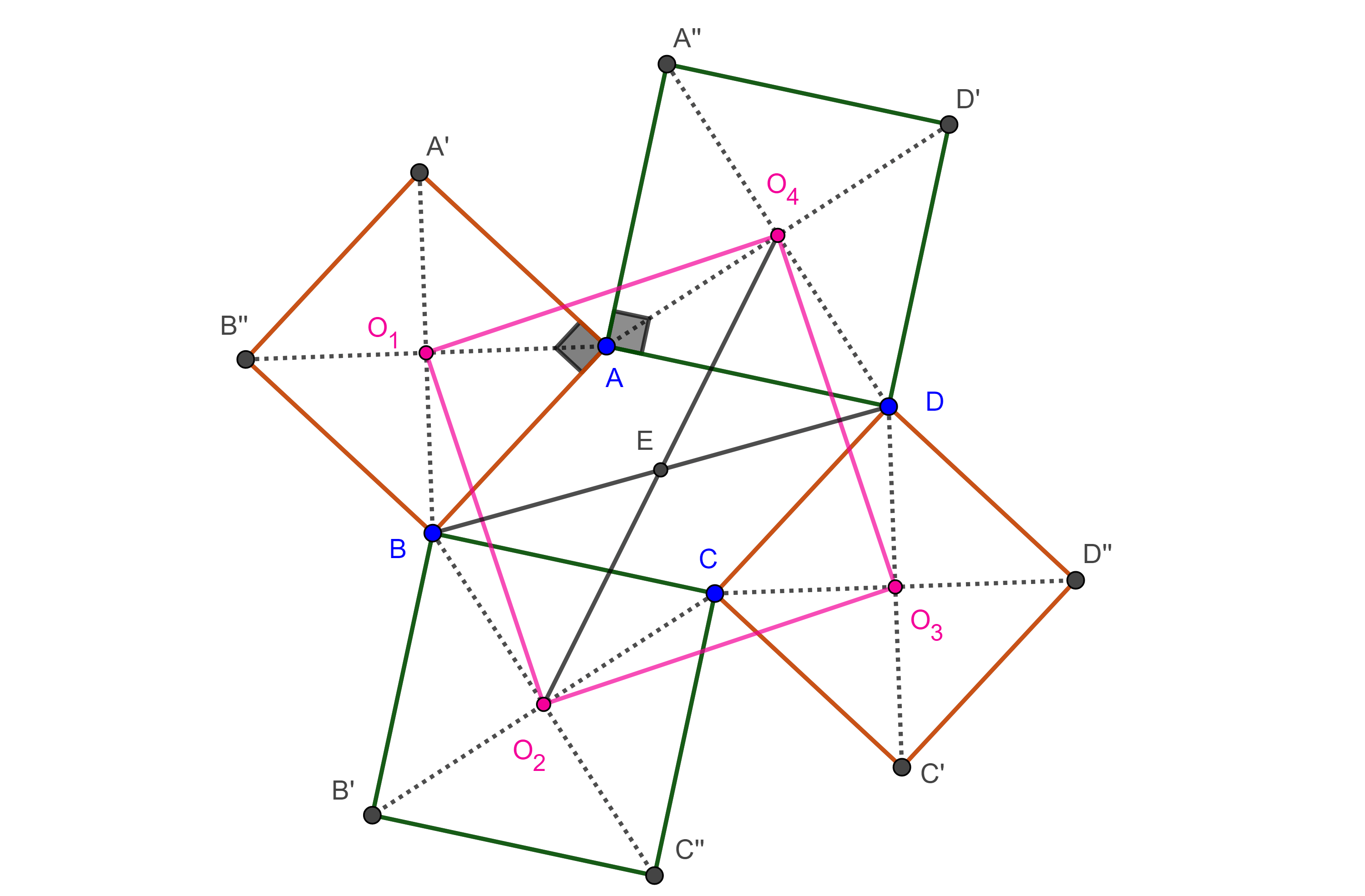
Por ser $\square ABCD$ paralelogramo,
$\angle A = \angle C$, $\angle B = \angle D$, $\angle A + \angle B = \pi$.

Veamos que $\triangle AO_{1}O_{4}$ y $\triangle CO_{3}O_{2}$ son congruentes.

Por $(1)$, $AO_{1} = CO_{3}$, por $(2)$, $AO_{4} = CO_{2}$,
notemos que $\angle A’’AA’ = \pi – \angle A = \angle B = \angle D = \pi – \angle C = \angle C’’CC’$.

$\Rightarrow \angle O_{4}AO_{1} = \angle O_{4}AA’’ + \angle A’’AA’ + \angle A’AO_{1}$
$= \angle O_{2}CC’’ + \angle C’’CC’ + \angle C’CO_{3} = \angle O_{2}CO_{3}$

Por criterio LAL, $\triangle AO_{1}O_{4} \cong \triangle CO_{3}O_{2}$, por lo que $ O_{1}O_{4} = O_{2}O_{3}$.

De manera similar se muestra que $\triangle AO_{1}O_{4} \cong \triangle BO_{1}O_{2} \cong \triangle DO_{3}O_{4}$, y así,
$\begin{equation} O_{2}O_{3} = O_{1}O_{4} = O_{1}O_{2} = O_{3}O_{4}. \end{equation}$

Como $\triangle AO_{1}O_{4} \cong \triangle BO_{1}O_{2}$, entonces $\angle AO_{1}O_{4} = \angle BO_{1}O_{2}$.

$\Rightarrow \angle O_{2}O_{1}O_{4} = \angle BO_{1}O_{4} – \angle BO_{1}O_{2}$
$= \angle BO_{1}A + \angle AO_{1}O_{4} – \angle BO_{1}O_{2} = \angle BO_{1}A = \dfrac{\pi}{2}$.

De manera similar se ve que
$\begin{equation} \angle O_{1}O_{4}O_{3} = \angle O_{4}O_{3}O_{2} = \angle O_{3}O_{2}O_{1} = \angle AO_{1}O_{4} = \dfrac{\pi}{2}. \end{equation}$.

Como $\square O_{1}O_{2}O_{3}O_{4}$ tienen cuatro lados iguales por $(3)$, y cuatro ángulos rectos por $(4)$, entonces es un cuadrado.

Veamos que las cuatro diagonales son concurrentes, consideremos $O_{2}O_{4}$ diagonal del cuadrado y $BD$ diagonal del paralelogramo.

Sea $E = O_{2}O_{4} \cap BD$. En $\triangle EBO_{2}$ y $\triangle EDO_{4}$ tenemos que $\angle BEO_{2} = \angle DEO_{4}$ por ser opuestos por el vértice, $\angle O_{2}BE = \angle O_{2}BC + \angle CBD = \angle O_{4}DA + \angle ADB$.

Por lo tanto, $\angle EO_{2}B = \angle EO_{4}D$, además $BO_{2} = DO_{4}$.

Por criterio LAL, $\triangle EBO_{2} \cong \triangle EDO_{4}$, por lo que $BE = DE$ y $O_{2}E = O_{4}E$
$\Rightarrow O_{2}O_{4}$ y $BD$ se intersecan en su punto medio.

Como $\square ABCD$ y $\square O_{1}O_{2}O_{3}O_{4}$ son paralelogramos sus diagonales se intersecan en su punto medio y por lo anterior todas concurren en $E$.

$\blacksquare$

Más adelante…

En la siguiente entrada veremos un resultado muy importante de las matemáticas, el teorema de Pitágoras y algunas aplicaciones.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que si un cuadrilátero convexo tiene alguna de las siguientes características entonces es un paralelogramo.
   $i)$los dos pares de lados opuestos son iguales,
   $ii)$los dos pares de ángulos opuestos son iguales,
   $iii)$los ángulos adyacentes son suplementarios,
   $iv)$las diagonales se bisecan.
2.  Construye un cuadrado sobre un segmento dado.
3. Si trazamos rectas paralelas a los lados de un paralelogramo por un punto de una de sus diagonales se forman 4 cuadriláteros, muestra que los dos cuadriláteros por donde no pasa la diagonal tienen la misma área.

4. Demuestra que si una recta biseca a un lado de un triangulo y es paralela a otro de los lados del triangulo entonces biseca al lado restante.
5. $i)$ Muestra que el punto medio de la hipotenusa de un triangulo rectángulo equidista a los tres vértices del triangulo.
   $ii)$ Recíprocamente prueba que si en un triangulo un punto en uno de sus lados equidista a los tres vértices entonces el triángulo es rectángulo.
6. Prueba que si construimos triángulos equiláteros exteriormente sobre los lados de un paralelogramo, entonces los cuatro vértices construidos son los vértices de un paralelogramo, y muestra que las diagonales de los dos paralelogramos son concurrentes.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Desigualdad del triángulo y lugar geométrico.
• Siguiente entrada del curso: Teorema de Pitágoras.
• Otros cursos.

Fuentes

• Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 1-6.
• Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 6.
• Wikipedia
• Geometría interactiva
• Geometry Help
• Cut the Knot
• Wolfram MathWorld

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»