Introducción
Con esta entrada damos inicio a la cuarta unidad que tratará sobre cuadriláteros. Comenzaremos hablando sobre el paralelogramo de Varignon y el teorema de Van Aubel.
Área del cuadrilátero
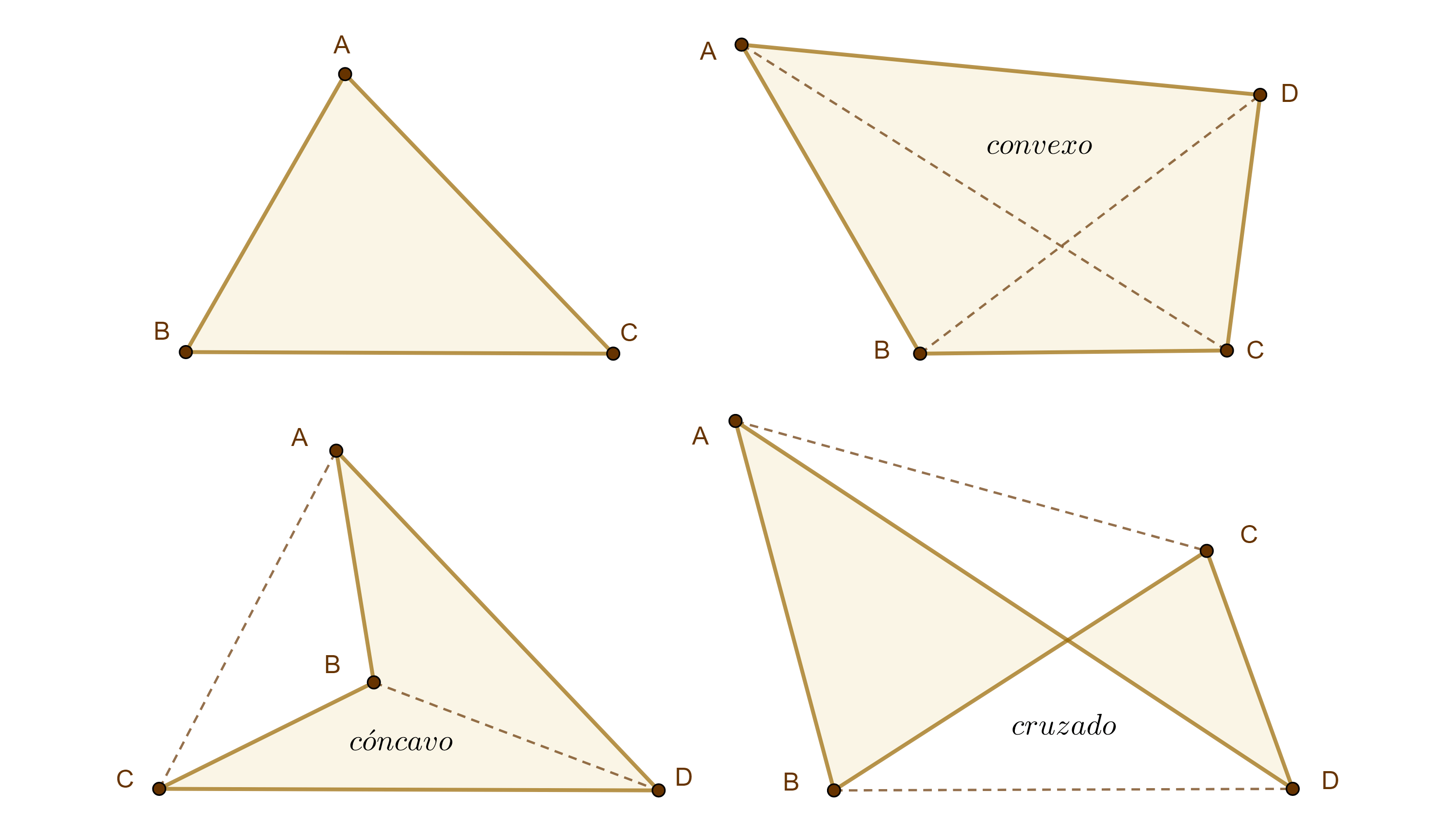
A partir de la ubicación de las diagonales de un cuadrilátero podemos establecer una clasificación de estos.
Un cuadrilátero es convexo si sus dos diagonales se encuentran dentro de él, es cóncavo si tiene una diagonal dentro y otra fuera de él, y es cruzado si las dos diagonales se ubican fuera del cuadrilátero.
El teorema de Varignon nos habla sobre el área de un cuadrilátero en general y ya que no es tan intuitivo definir el área de un cuadrilátero cruzado es necesario introducir el concepto de área orientada.
Consideraremos el área de un triángulo como positiva si recorremos sus vértices en el sentido opuesto a las manecillas del reloj y como negativa en caso contrario.
De esta manera tenemos que para un triángulo $\triangle ABC$,
$(\triangle ABC) = (\triangle BCA) = (\triangle CAB) $
$= – (\triangle CBA) = – (\triangle ACB) = – (\triangle BAC)$.
Definición 1. Definimos el área de un cuadrilátero $\square ABCD$ como la suma de las áreas de los triángulos que se forman al considerar una de sus diagonales, esto es,
$(\square ABCD) = (\triangle ABC) + (\triangle CDA)$.
Notemos que como resultado de esta definición el área del cuadrilátero cruzado resulta ser la diferencia de las áreas de los triángulos que se forman al considerar la intersección cruzada de los lados.
Paralelogramo de Varignon
Teorema 1, de Varignon.
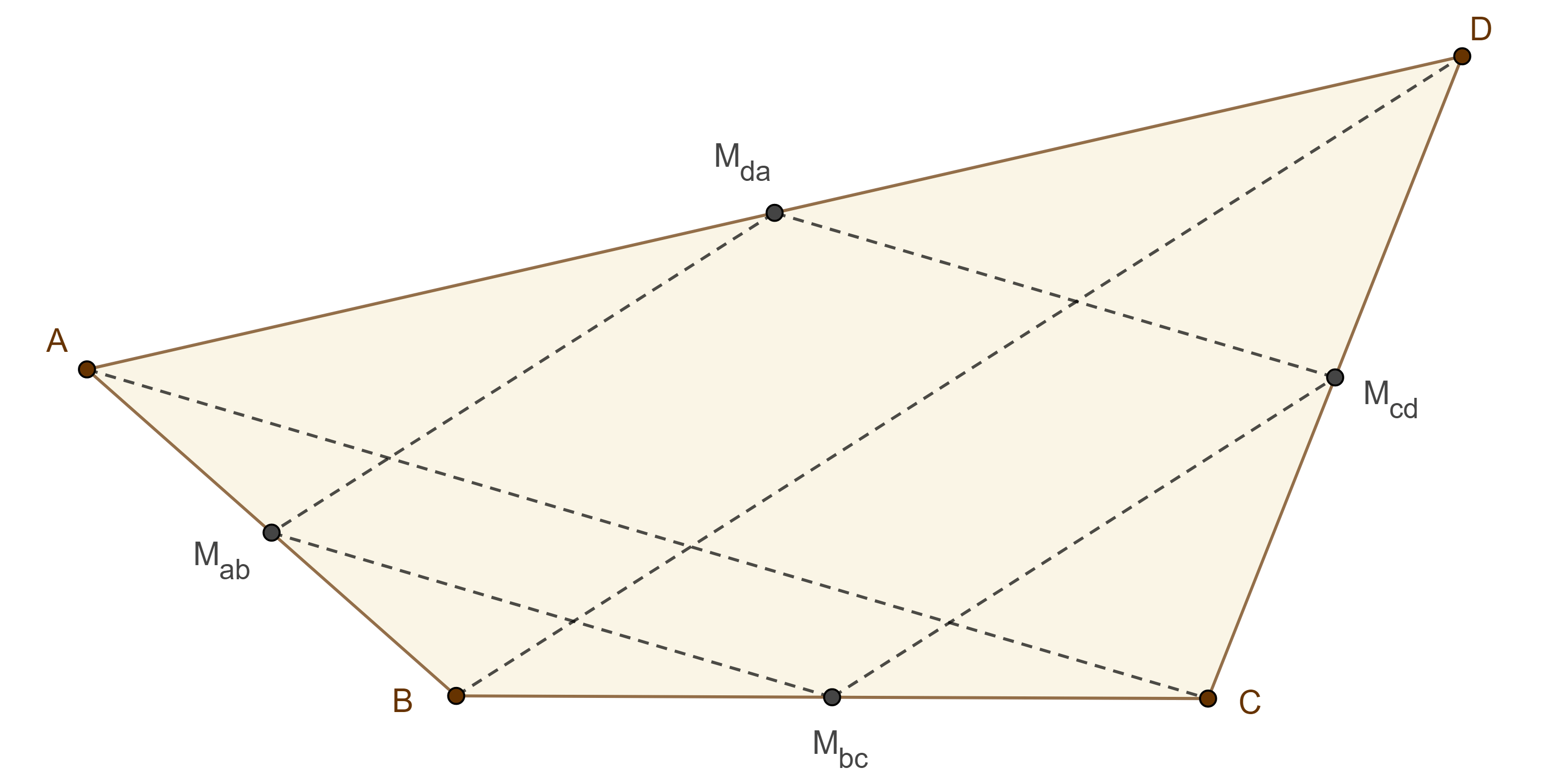
$i)$ Los puntos medios de los lados de un cuadrilátero convexo son los vértices de un paralelogramo, conocido como paralelogramo de Varignon, cuyo perímetro es la suma de las diagonales del cuadrilátero,
$ii)$ el área del paralelogramo de Varignon es la mitad del área del cuadrilátero.
Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$ y $M_{da}$ los puntos medios de $AB$, $BC$, $CD$ y $DA$ respetivamente.
Notemos que $M_{ab}M_{bc}$ y $M_{cd}M_{da}$ son segmentos medios de $\triangle ABC$ y $\triangle DAC$ por lo que $M_{ab}M_{bc} \parallel CA \parallel M_{cd}M_{da}$ y $2M_{ab}M_{bc} = CA = 2M_{cd}M_{da}$.
De manera análoga podemos ver que $M_{ab}M_{da} \parallel DB \parallel M_{bc}M_{cd}$ y $2M_{ab}M_{da} = BD = 2M_{bc}M_{cd}$.
Por lo tanto los lados opuestos de $\square M_{ab}M_{bc}M_{cd}M_{da}$ son paralelos y $M_{ab}M_{bc} + M_{bc}M_{cd} + M_{cd}M_{da} + M_{da}M_{ab} = \dfrac{CA + BD + CA +BD}{2} = CA + BD$.
Para calcular el área de $\square M_{ab}M_{bc}M_{cd}M_{da}$ primero notemos que $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ son semejantes pues $M_{ab}M_{da} \parallel BD$.
También sabemos que $M_{ab}M_{da} = \dfrac{BD}{2}$, por lo que las alturas desde $A$, $h$ y $h’$ de $\triangle AM_{ab}M_{da}$ y $\triangle ABD$ respectivamente, también cumplirán que $h = \dfrac{h’}{2}$.
Por lo tanto,
$(\triangle AM_{ab}M_{da}) = \dfrac{M_{ab}M_{da} \times h}{2}$
$= \dfrac{\frac{1}{2}DBD \times \frac{1}{2}h’}{2} = \dfrac{1}{4} \dfrac{BD \times h’}{2} $
$= \dfrac{1}{4} (\triangle ABD)$.
De manera similar podemos encontrar las áreas de $\triangle BM_{bc}M_{ab}$, $\triangle CM_{cd}M_{bc}$ y $\triangle DM_{da}M_{cd}$.
En consecuencia,
$(\square M_{ab}M_{bc}M_{cd}M_{da}) = (\square ABCD) – (\triangle AM_{ab}M_{da}) – (\triangle BM_{bc}M_{ab}) – (\triangle CM_{cd}M_{bc}) – (\triangle DM_{da}M_{cd})$
$= (\square ABCD) – \dfrac{1}{4} ((\triangle ABD) + (\triangle BCD) + (\triangle CDB) + (\triangle DAC))$
$= (\square ABCD) – \dfrac{2}{4}(\square ABCD) $
$ = \dfrac{(\square ABCD)}{2}$.
$\blacksquare$
Corolario. Sea $\square ABCD$ un cuadrilátero convexo, entonces su cuadrilátero de Varignon
$i)$ es un rombo si y solo si $AC = BD$,
$ii)$ es un rectángulo si y solo si $AC \perp BD$,
$iii)$ es un cuadrado si y solo si $AC = BD$ y $AC \perp BD$.
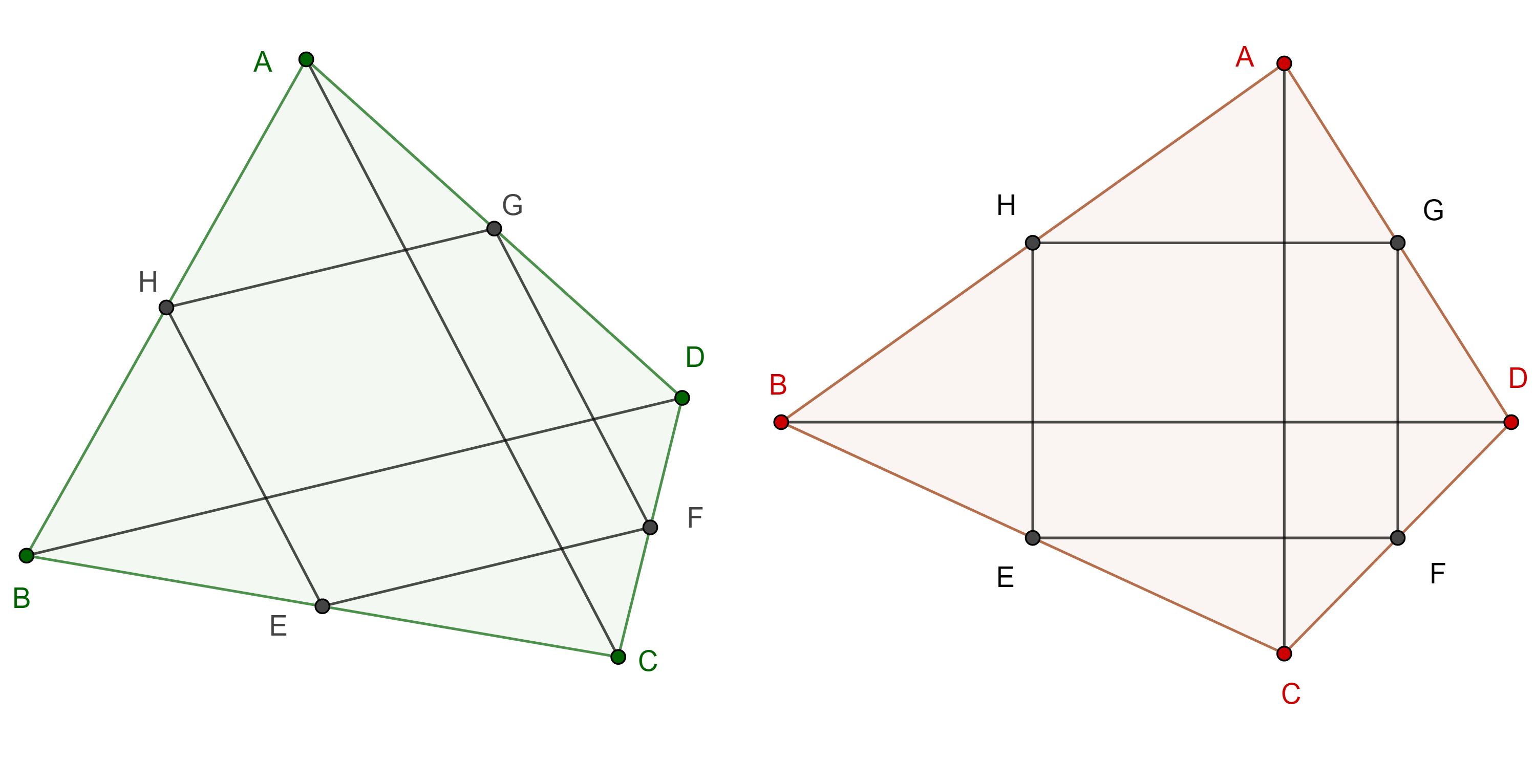
Demostración. Sean $E$, $F$, $G$, $H$, los puntos medios de $BC$, $CD$, $DA$, $AB$, respectivamente como $EF$ y $FG$ son segmentos medios de $\triangle DBC$ y $\triangle ADC$, entonces, $2EF = BD$, $EF \parallel BD$ y $2FG = AC$, $FG \parallel AC$.
$i)$ $\square EFGH$ es un rombo, entonces por definición $EF = FG \Leftrightarrow AC = BD$.
$ii)$ $\square EFGH$ es un rectángulo, entonces por definición $EF \perp FG \Leftrightarrow AC \perp BD$.
$iii)$ Es consecuencia de $i)$ y $ii)$.
$\blacksquare$
Centroide de un cuadrilátero
Definición 2. Los segmentos que unen los puntos medios de los lados opuestos de un cuadrilátero se llaman bimedianas.
Al segmento que une los puntos medios de las diagonales de un cuadrilátero se le conoce como recta de Newton.
Teorema 2. Las bimedianas de un cuadrilátero convexo y su recta de Newton son concurrentes y se bisecan entre sí, el punto de concurrencia es el centroide del cuadrilátero.
Demostración. Sea $\square ABCD$ un cuadrilátero convexo y $M_{ab}$, $M_{bc}$, $M_{cd}$, $M_{da}$, $M$, $N$, los puntos medios de $AB$, $BC$, $CD$, $DA$, $AC$, $BD$, respectivamente.
$M_{ab}M_{cd}$ y $M_{bc}M_{da}$ son las diagonales del paralelogramo de Varignon, por lo tanto, se intersecan en $J$ su punto medio.
Por otra parte, $M_{ab}M$ es un segmento medio de $\triangle ABC$, por lo que $M_{ab}M \parallel BC$; $NM_{cd}$ es un segmento medio de $\triangle DBC$, por lo tanto, $NM_{cd} \parallel BC$, y así $NM_{cd} \parallel M_{ab}M$.
Igualmente vemos que $M_{ab}N \parallel MM{cd}$.
Por lo tanto, $\square M_{ab}NM_{cd}M$ es un paralelogramo, en consecuencia las diagonales $M_{ab}M_{cd}$ y $NM$ se intersecan en $J$ su punto medio.
En conclusión, $J$ es el punto medio de $M_{ab}M_{cd}$, $M_{bc}M_{da}$ y $NM$.
$\blacksquare$
Construcción de un cuadrilátero
Problema. Construye un cuadrilátero $\square ABCD$ conociendo $AB$, $BC$, $CD$, $DA$ y $M_{ab}M_{cd}$ donde $M_{ab}$ y $M_{cd}$ son los puntos medios de $AB$ y $CD$ respectivamente.
Solución. Primero construimos el paralelogramo $\square M_{ab}NM_{cd}M$, donde $M$ y $N$ son los puntos medios de las diagonales $AC$ y $BD$, de la siguiente manera.
De la demostración del teorema 2 sabemos que $M_{ab}M = NM_{cd} = \dfrac{BC}{2}$ y $M_{ab}N = MM_{cd} = \dfrac{AD}{2}$ (figura 4).
También sabemos que la diagonal de un paralelogramo lo divide en dos triángulos congruentes, por lo que basta construir un triángulo de lados $M_{ab}M_{cd}$, $\dfrac{BC}{2}$ y $\dfrac{AD}{2}$ y luego trazar paralelas por $M_{ab}$ y $M_{cd}$ a los lados del triángulo construido completando así el paralelogramo.
De manera similar construimos el paralelogramo $\square M_{ab}M_{bc}M_{cd}M_{da}$ donde $M_{bc}$ y $M_{da}$ serían los puntos medios de $BC$ y $AD$ respectivamente.
Sabemos también que $M_{bc}M \parallel AB$ por lo que trazamos la paralela $AB$ a $M_{bc}M$ por $M_{ab}$ tal que $AM_{ab} = M_{bc}B = \dfrac{AB}{2}$.
Con $A$ y $B$ construidos, por $M_{bc}$ trazamos $ABC$ tal que $BM_{bc} = M_{bc}C = \dfrac{BC}{2}$, similarmente construimos $D$.
$\blacksquare$
Teorema de Van Aubel
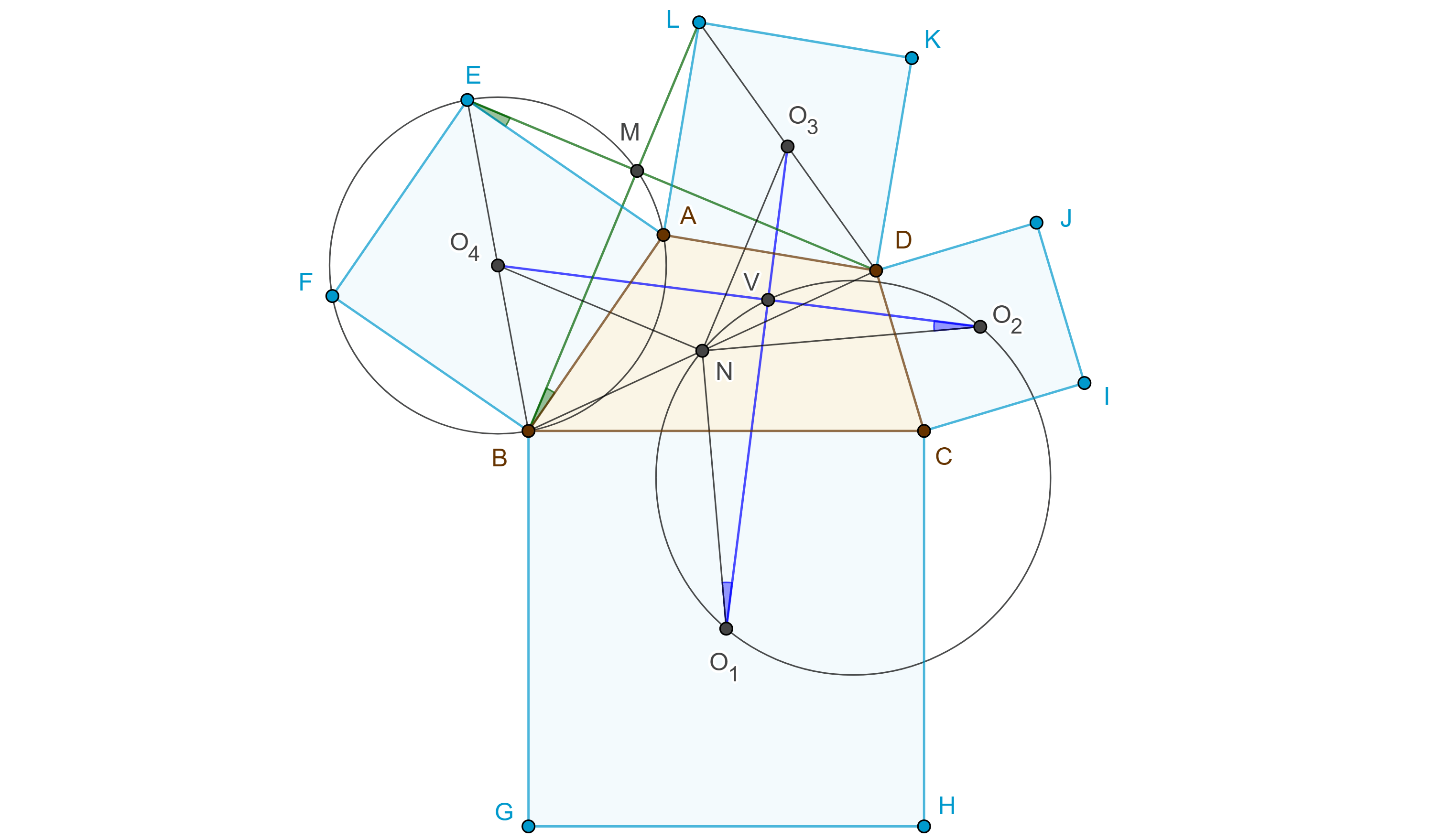
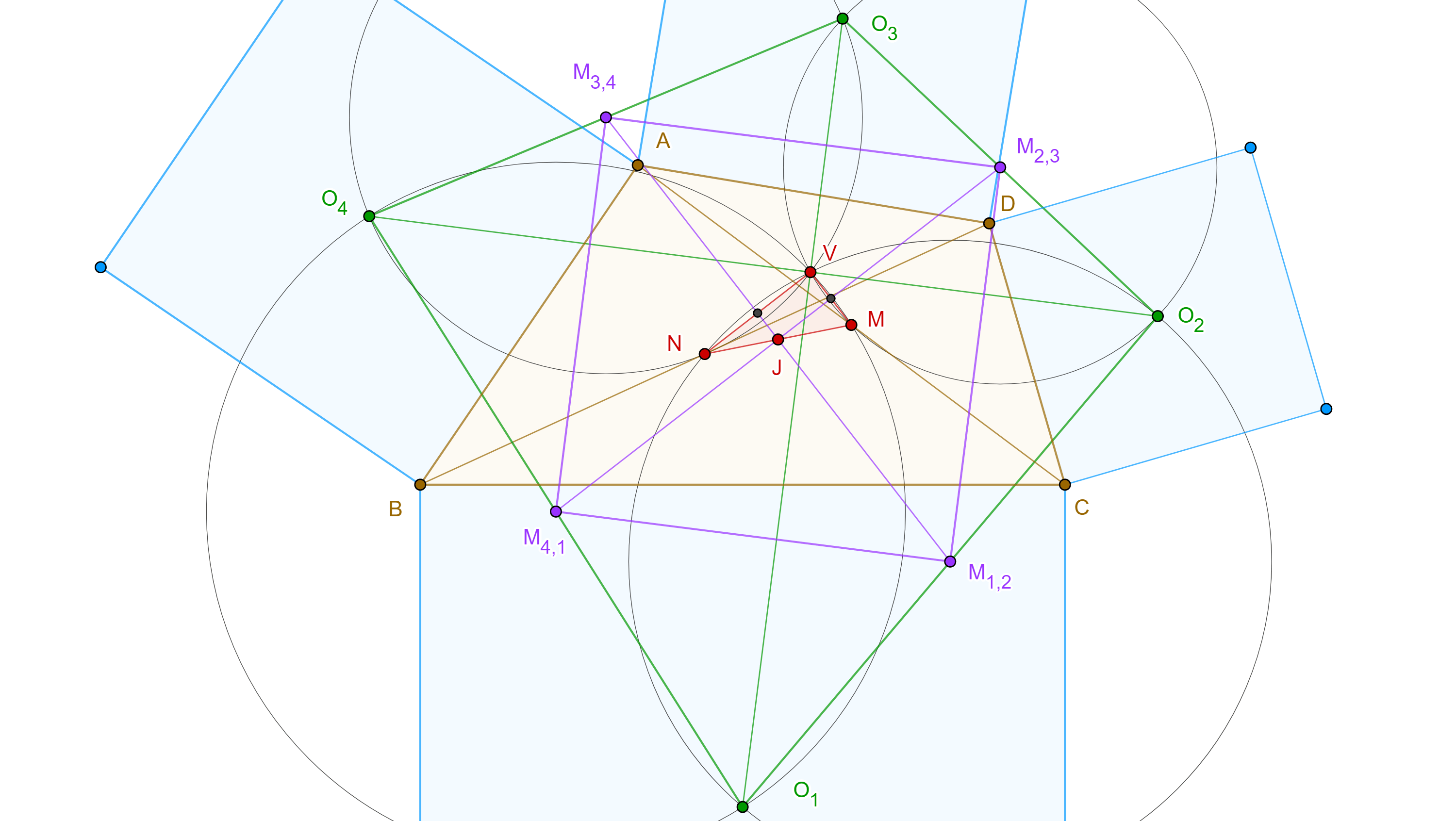
Teorema 3, de Van Aubel. Los segmentos que unen los centros de cuadrados construidos externamente sobre lados opuestos de un cuadrilátero convexo son perpendiculares y tienen la misma longitud.
Demostración. Sean $\square ABCD$ un cuadrilátero convexo y $\square EFBA$, $\square BGHC$, $\square DCIJ$, $\square LADK$, cuadrados construidos externamente sobre los lados de $\square ABCD$ y $O_1$, $O_2$, $O_3$, $O_4$, sus respectivos centros.
Sea $M = LB \cap ED$, como $AL = AD$ y $AB = AE$ y $\angle LAB = \angle DAE$, por criterio de congruencia LAL, $\triangle LAB \cong \triangle DAE$,
$\Rightarrow LB = DE$ y $\angle AEM = \angle ABM$.
Por lo tanto, $\square MEBA$ es cíclico, así, $\angle EMB = \angle EAB$, es decir $LB \perp DE$.
Considera $N$ el punto medio de $BD$, $NO_4$ y $NO_3$ son segmentos medios de $\triangle BDE$ y $\triangle DBL$ respectivamente.
Esto implica que $2NO_4 = DE$ y $NO_4 \parallel DE$ y $2NO_3 = LB$ y $NO_4 \parallel LB$.
Por lo tanto, $NO_4 = NO_3$ y $NO_4 \perp NO_3$.
Igualmente vemos que $NO_1 = NO_2$ y $NO_1 \perp NO_2$.
Sea $V = O_1O_3 \cap O_2O_4$, por criterio de congruencia LAL, $NO_1O_3 \cong NO_2O_4$,
$\Rightarrow O_1O_3 = O_2O_4$ y $\angle VO_1N = \angle VO_2N$.
Por lo tanto, $\square VNO_1O_2$ es cíclico, y así $O_1O_3 \perp O_2O_4$.
$\blacksquare$
Definición 3. Nos referiremos al cuadrilátero $\square O_1O_1O_3O_4$ como cuadrilátero externo de Van Aubel y a la intersección de sus diagonales como punto externo de Van Aubel.
Centroide del cuadrilátero de Van Aubel
Teorema 4. Un cuadrilátero y su cuadrilátero externo de Van Aubel tienen el mismo centroide.
Demostración. Sean $\square ABCD$ y $\square O_1O_2O_3O_4$ su cuadrilátero externo de Van Aubel, $M$ y $N$ los puntos medios de $AC$ y $BD$, y $V$ el punto externo de Van Aubel.
En el teorema anterior vimos que $NV$ es una cuerda común a las circunferencias cuyos diámetros son $O_1O_2$ y $O_3O_4$, por lo tanto la línea que une sus centros $M_{1,2}M_{3,4}$ biseca a $NV$ y $M_{1,2}M_{3,4} \perp NV$.
De manera análoga podemos ver que $MV$ es una cuerda común a las circunferencias cuyos diámetros son $O_2O_3$ y $O_4O_1$ y por lo tanto la línea que une sus centros $M_{2,3}M_{4,1}$ biseca a $MV$ y $M_{2,3}M_{4,1} \perp MV$.
Por otra parte, por el teorema de Van Aubel las diagonales del cuadrilátero de Van Aubel son perpendiculares y tienen la misma longitud. Entonces por el corolario, su paralelogramo de Varignon $\square M_{1,2}M_{2,3}M_{3,4}M_{4,1}$ es un cuadrado, en particular, $M_{1,2}M_{3,4} \perp M_{2,3}M_{4,1}$.
En consecuencia, en $\triangle MNV$, $M_{1,2}M_{2,3} \parallel MV$ y $M_{1,2}M_{2,3}$ pasa por el punto medio de $NV$, por lo tanto $M_{1,2}M_{2,3}$ biseca a $MN$.
Igualmente podemos ver que $M_{2,3}M_{4,1}$ biseca a $MN$.
Por el teorema 2 sabemos que el punto medio $J$ de $MN$ es el centroide de $\square ABCD$ y que la intersección de las bimedianas $M_{1,2}M_{3,4}$ y $M_{2,3}M_{4,1}$ es el centroide de $\square O_1O_2O_3O_4$.
$\blacksquare$
Más adelante…
En la siguiente entrada continuaremos el estudio de los cuadriláteros cíclicos que comenzamos en la entada teorema de Ptolomeo.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Muestra que un cuadrilátero es dividido por una de sus diagonales en dos triángulos de igual área si y solo si la diagonal biseca a la otra diagonal.
- Verifica que el teorema de Varignon se cumple para los cuadriláteros cóncavo y cruzado.
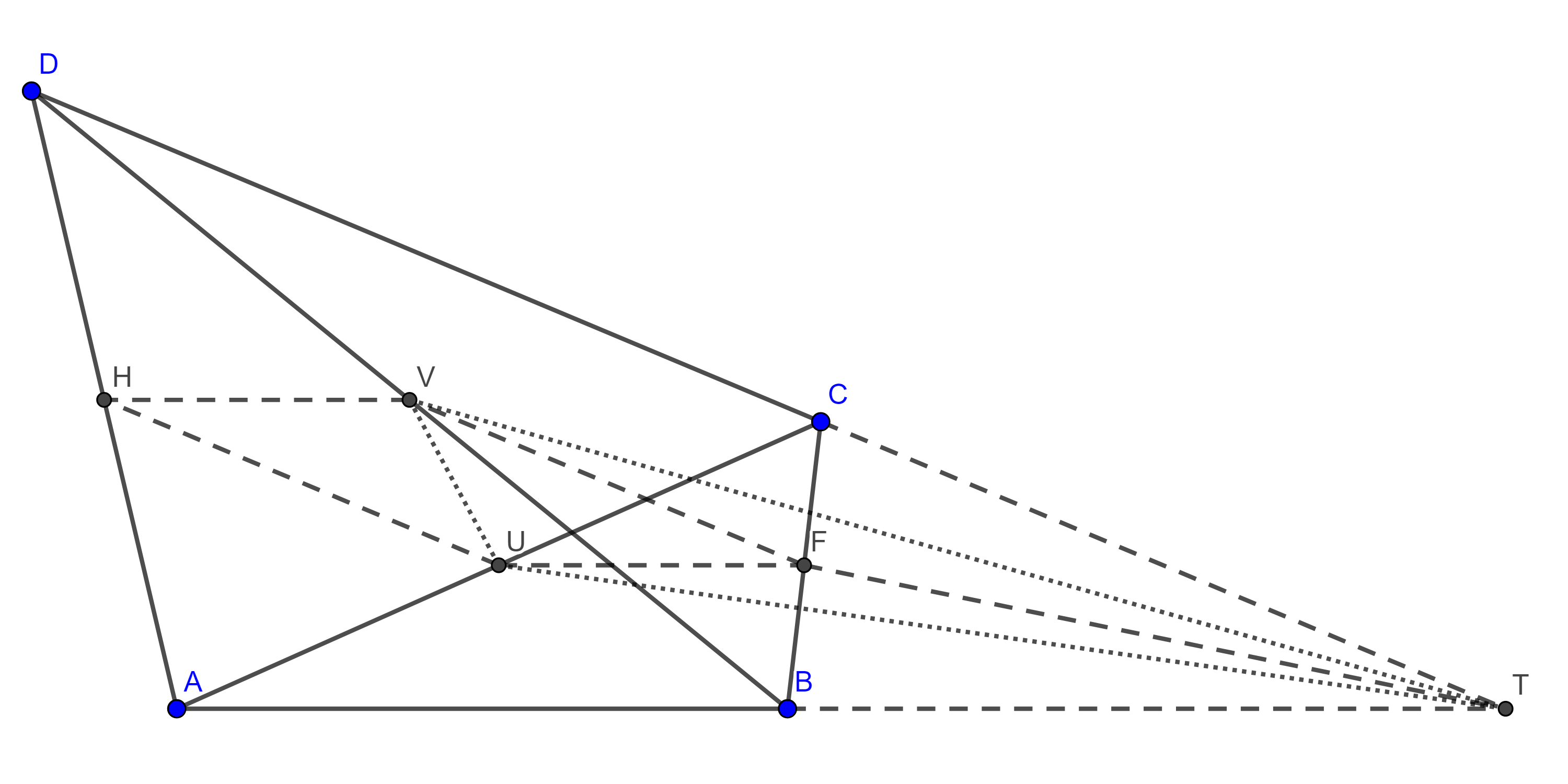
- Sean $\square ABCD$ un cuadrilátero $U$ y $V$ los puntos medios de $\overline{AC}$ y $\overline{BD}$ respectivamente y $T$ la intersección de $\overline{AB}$ con $\overline{CD}$. Prueba que $(\triangle TUV) = \dfrac{(\square ABCD)}{4}$.
Sugerencia. Considera $H$ y $F$ los puntos medios de $\overline{AD}$ y $\overline{BC}$ y los cuadriláteros $\square ACBD$, $\square CUFT$ y $\square BVFT$ para calcular el área de los triángulos $\triangle UVF$, $\triangle UFT$ y $\triangle VFT$.
- Construye un cuadrilátero dados dos ángulos opuestos, la longitud de las diagonales y el ángulo entre las diagonales.
- Verifica que el teorema de Van Aubel se cumple cuando los cuadrados son construidos internamente, y también para los para los cuadriláteros cóncavo y cruzado.
- Muestra que en un cuadrilátero convexo los puntos medios de sus diagonales y los puntos medios de las diagonales de su cuadrilátero externo de Van Aubel, forman un cuadrado, y que el punto externo de Van Aubel pertenece al circuncírculo de este cuadrado.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Circunferencia de Brocard.
- Siguiente entrada del curso: Cuadrilátero cíclico.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 124-127.
- Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 51-56.
- Santos, J., Tesis Geometría del Cuadrilátero. 2010, pp 6-13.
- D. Pellegrinetti., The Six-Point Circle for the Quadrangle. International Journal of Geometry, Vol. 8 (Oct., 2019), No. 2, pp 5–13.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»