Introducción
En esta entrada introduciremos un nuevo concepto: el de circunferencias ortogonales. Veremos cómo se relaciona este concepto con el de eje radical, que estudiamos en la entrada anterior.
Circunferencias ortogonales
La definición que nos interesa estudiar ahora es la siguiente.
Definición. Dos circunferencias $\mathcal{C_1}$ y $\mathcal{C_2}$ que se intersecan en un punto $P$ son ortogonales si sus tangentes en $P$ forman un ángulo recto.
Hagamos algunas observaciones de esta definición. Primero, dos circunferencias tangentes no pueden ser ortogonales pues si el punto de tangencia es $P$, entonces tienen la misma tangente en $P$. Así, las circunferencias deben intersectarse en al menos dos puntos $P$ y $Q$. Por simetría, las tangentes en $P$ son ortogonales si y sólo si las tangentes en $Q$ lo son.
Además, si los centros son $O_1$ y $O_2$, respectivamente, entonces sabemos que $O_1P$ es ortogonal a la tangente a $\mathcal{C}_1$ por $P$ y análogamente $O_2P$ es ortogonal a la tangente a $\mathcal{C}_2$ por $P$. Así, las tangentes son ortogonales si y sólo si los radios $O_1P$ y $O_2P$ lo son.
Algunas conexiones entre circunferencias ortogonales y eje radical
Veamos un primer resultado que relaciona circunferencias ortogonales y el eje radical.
Teorema. Sean $\mathcal{C_1}$ y $\mathcal{C_2}$ circunferencias de centros distintos. Si $\mathcal{C}_3$ es ortogonal a ambas circunferencias, entonces su centro $O_3$ se encuentra en el eje radical de ambas.
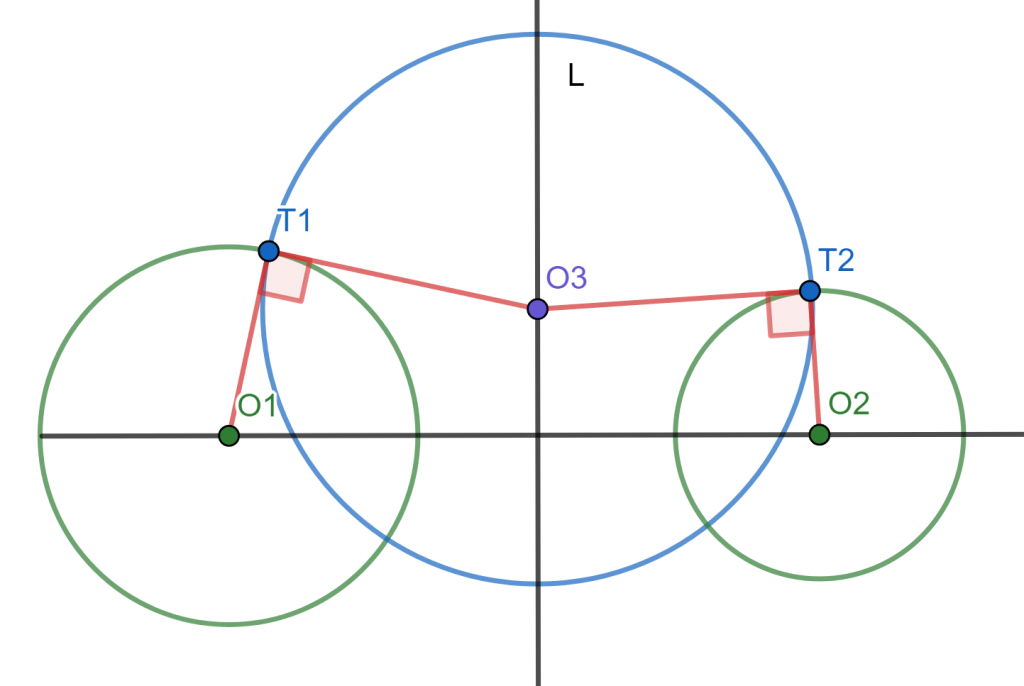
Demostración. Denotaremos por $T_1$ a uno de los puntos de intersección de $\mathcal{C}_1$ y $\mathcal{C}_3$, y por $T_2$ a uno de los puntos de intersección de $\mathcal{C}_2$ y $\mathcal{C}_3$ (ver la figura a continuación). Debemos mostrar que $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$, es decir, que $$\text{Pot}(O_3,\mathcal{C}_1)=\text{Pot}(O_3,\mathcal{C}_2).$$
Como $O_3T_2$ y $O_3T_1$ son radios de $\mathcal{C}_3$, entonces $$O_3T_1^2=O_3T_2^2.$$
En la entrada de potencia de un punto vimos que podemos calcular la potencia en términos de la longitud de una tangente como sigue: $$\text{Pot}(O_3,\mathcal{C}_1)=O_3T_1^2=O_3T_2^2=\text{Pot}(O_3,\mathcal{C}_2).$$
Así, concluimos lo que queríamos, que $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$.
$\square$
El siguiente resultado es similar, y en cierto sentido es un «regreso» del anterior.
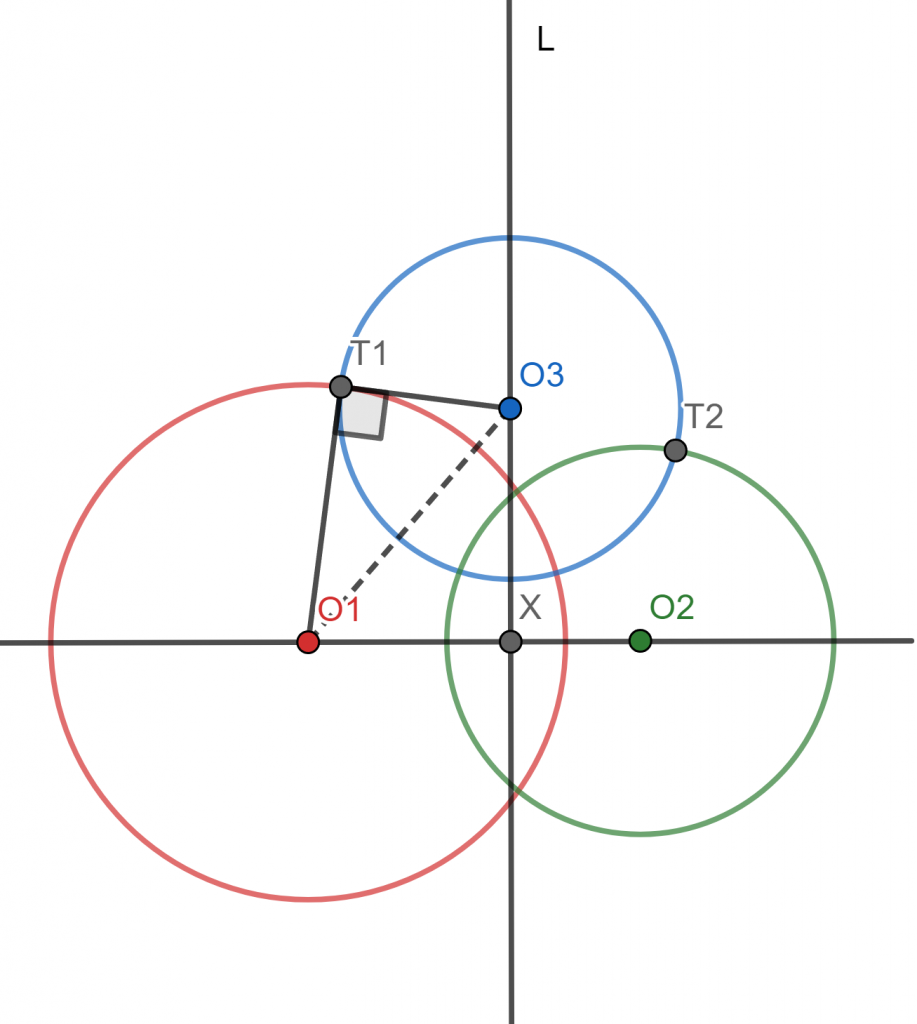
Teorema. Sean $\mathcal{C_1}$ y $\mathcal{C_2}$ circunferencias de centros distintos. Sea $\mathcal{C}_3$ una circunferencia cuyo centro $O_3$ está en el eje radical de las dos circunferencias dadas. Si $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_2$, entonces también es ortogonal a $\mathcal{C}_1$.
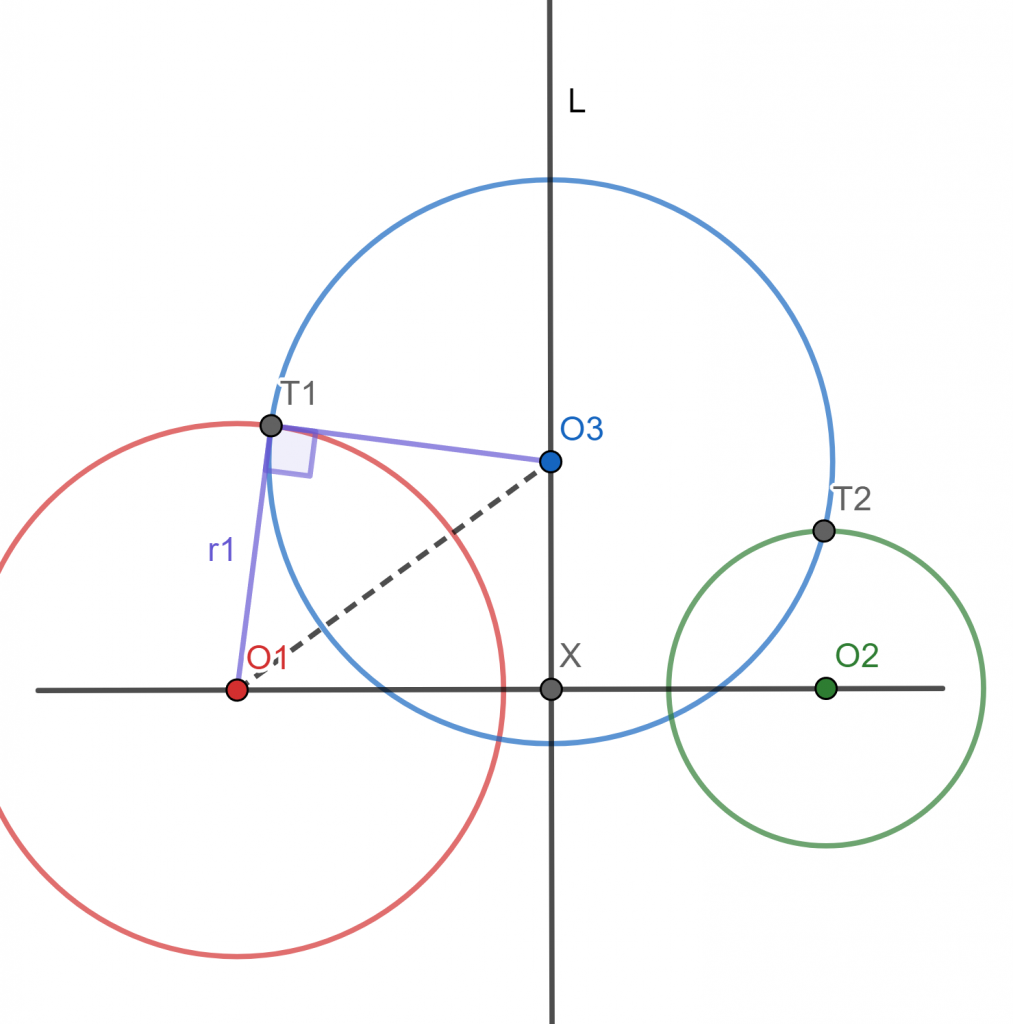
Demostración. Tomaremos como referencia la figura anterior. A partir de las hipótesis, queremos demostrar que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$. Sea $r_1$ el radio de $\mathcal{C}_1$. Por el teorema de Pitágoras, lo que queremos sucede si y sólo si $$O_3O_1^2-r_1^2= O_3T_1^2.$$
Dado que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_2$, el triángulo $\triangle O_3T_2O_2$ es rectángulo. Por el teorema de Pitágoras se cumple entonces que $O_3O_2^2-r_2^2= O_3T_2^2$. Como $O_3$ está en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$, y por cómo se calcula la potencia en términos de la distancia al centro y del radio, tenemos que: $$O_3O_2^2 – r_2^2=\text{Pot}(O_2,\mathcal{C}_3)=\text{Pot}(O_2,\mathcal{C}_2)=O_3O_1^2-r_1^2.$$
De este modo, $$O_3T_1^2=O_3T_2^2=O_3O_2^2-r_2^2=O_3O_1^2-r_1^2.$$
Esto es justo lo que necesitábamos para concluir que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$.
$\square$
Posición de una circunferencia ortogonal a dos dadas con respecto a su eje radical
Veamos un resultado más, que nos habla acerca de la posición de una circunferencia en relación a otras dos a las que es tangente.
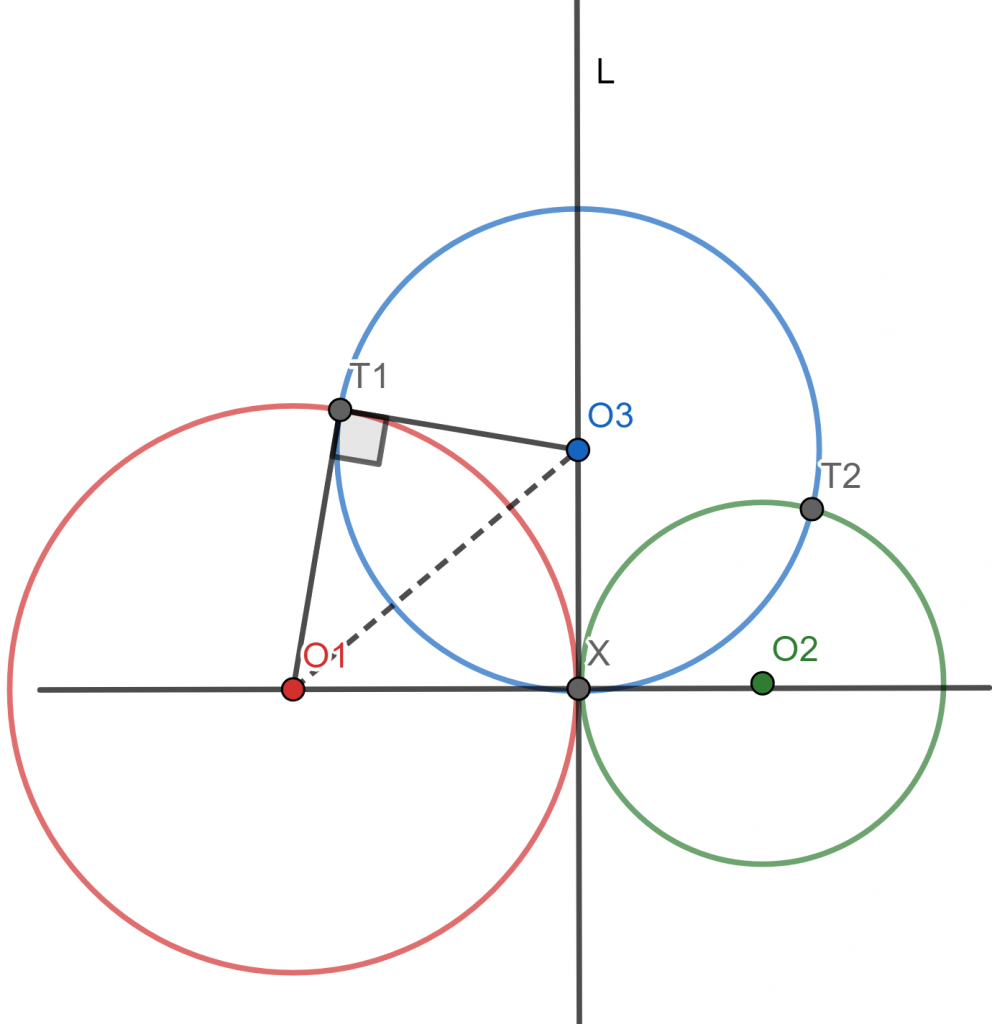
Teorema. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias de centros distintos $O_1$ y $O_2$. Sea $\mathcal{C}_3$ una circunferencia ortogonal a $\mathcal{C}_1$ y $\mathcal{C}_2$. La circunferencia $\mathcal{C}_3$ está posicionada con respecto a la línea de los centros $O_1O_2$ de acuerdo a los siguientes tres casos:
- Si $\mathcal{C}_1$ y $\mathcal{C}_2$ se intersectan en dos puntos, entonces $\mathcal{C}_3$ no intersecta a $O_1O_2$.
- Si $\mathcal{C}_1$ y $\mathcal{C}_2$ son tangentes, entonces $\mathcal{C}_3$ es tangente a $O_1O_2$.
- Si $\mathcal{C}_1$ y $\mathcal{C}_2$ no se intersectan, entonces $\mathcal{C}_3$ intersecta a $O_1O_2$ en dos puntos.
Demostración. Sea $\mathcal{C}_3$ una circunferencia ortogonal a dos circunferencias dadas $\mathcal{C}_1$ y $\mathcal{C}_2$. Sean $r_1$, $r_2$, $r_3$ los radios de $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$, respectivamente. Sea $X$ la intersección de $O_1O_2$ con el eje radical $l$ de las circunferencias $\mathcal{C}_1$ y $\mathcal{C}_2$. Sea $T_1$ un punto de intersección de $O_3$ con $O_1$ y $T_1$ un punto de intersección de $O_3$ con $O_2$. La figura a continuación muestra el dibujo para el primer caso.
Dado que $\mathcal{C}_3$ es ortogonal a $\mathcal{C}_1$ y $\mathcal{C}_2$, se tienen dos triángulos rectángulos: $$\triangle O_3T_1O_1 \quad \text{y} \quad \triangle O_3XO_1.$$
Por el teorema de Pitágoras, tenemos que $$O_3T_1^2+r_1^2=O_3O_1^2=O_1X^2+O_3X^2,$$
de donde $r_1^2-O_1X^2=O_3X^2-r_3^2$. Tratemos ahora sí cada caso por separado.
Caso 1. Supongamos que $\mathcal{C}_1$ y $\mathcal{C}_2$ se intersectan en dos puntos. Mostraremos que $\mathcal{C}_3$ no intersecta a $O_1O_2$.
Como las circunferencias se intersectan en dos puntos, el eje radical es la recta que une las intersecciones. Por ello, $r_1>|O_1X|$. Usando las cuentas de arriba:
\begin{align*}
& r_1>|O_1X|\\
\Rightarrow &r_1^2>O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 >0\\
\Rightarrow & O_3X^2-r_3^2>0\\
\Rightarrow & O_3X^2>r_3^2.
\end{align*}
Esto último sucede si y sólo si $|O_3X|>r_3$. Esto nos dice que $X$ está fuera de la circunferencia $\mathcal{C}_3$ y entonces dicha circunferencia no intersecta a $O_1O_2$.
Caso 2. Supongamos ahora que $\mathcal{C}_1$ y $\mathcal{C}_2$ son tangentes. Debemos demostrar que $\mathcal{C}_3$ es tangente a $O_1O_2$. En este caso, $r_1=|O_1X|$. Y entonces tenemos la siguiente cadena de implicaciones:
\begin{align*}
& r_1>=O_1X|\\
\Rightarrow &r_1^2=O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 =0\\
\Rightarrow & O_3X^2-r_3^2=0\\
\Rightarrow & O_3X^2=r_3^2.
\end{align*}
Esto, junto con el hecho de que $O_3X$ es perpendicular a $O_1O_2$, implica que $O_1O_2$ es tangente a $\mathcal{C}_3$.
Caso 3. Finalmente, supongamos que $\mathcal{C}_1$ y $\mathcal{C}_2$ no se intersectan. Debemos mostrar que $\mathcal{C}_3$ sí intersecta a $O_1O_2$ en dos puntos. Para ello basta mostrar que $|O_3X|<r_3$. La suposición de que las circunferencias no se intersectan implica que $r_1<|O_1X|$.
Una vez más procedemos con las siguientes implicaciones:
\begin{align*}
& r_1<|O_1X|\\
\Rightarrow &r_1^2<O_1X^2\\
\Rightarrow &r_1^2-O_1X^2 <0\\
\Rightarrow & O_3X^2-r_3^2<0\\
\Rightarrow & O_3X^2<r_3^2.
\end{align*}
Por ello, $|O_3X|<r_3$, como queríamos.
$\square$
Más adelante…
Hemos abordado algunos resultados de circunferencias ortogonales. Lo que haremos en la siguiente entrada es estudiar a las familiar coaxiales de circunferencias. Sabemos que cualesquiera dos circunferencias tienen un eje radical pero, ¿qué sucede tenemos más de dos circunferencias que comparten eje radical?
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Eje radical de 2 circunferencias
- Siguiente entrada del curso: Familias coaxiales